Diagnostics of Bolted Joints in Vibrating Screens Based on a Multi-Body Dynamical Model
Abstract
:1. Introduction
1.1. Problems in Vibrating Sieving Screen Operation and Diagnostics
1.2. Diagnostics of Bolted Joints Loosening in Structures
2. Materials and Methods
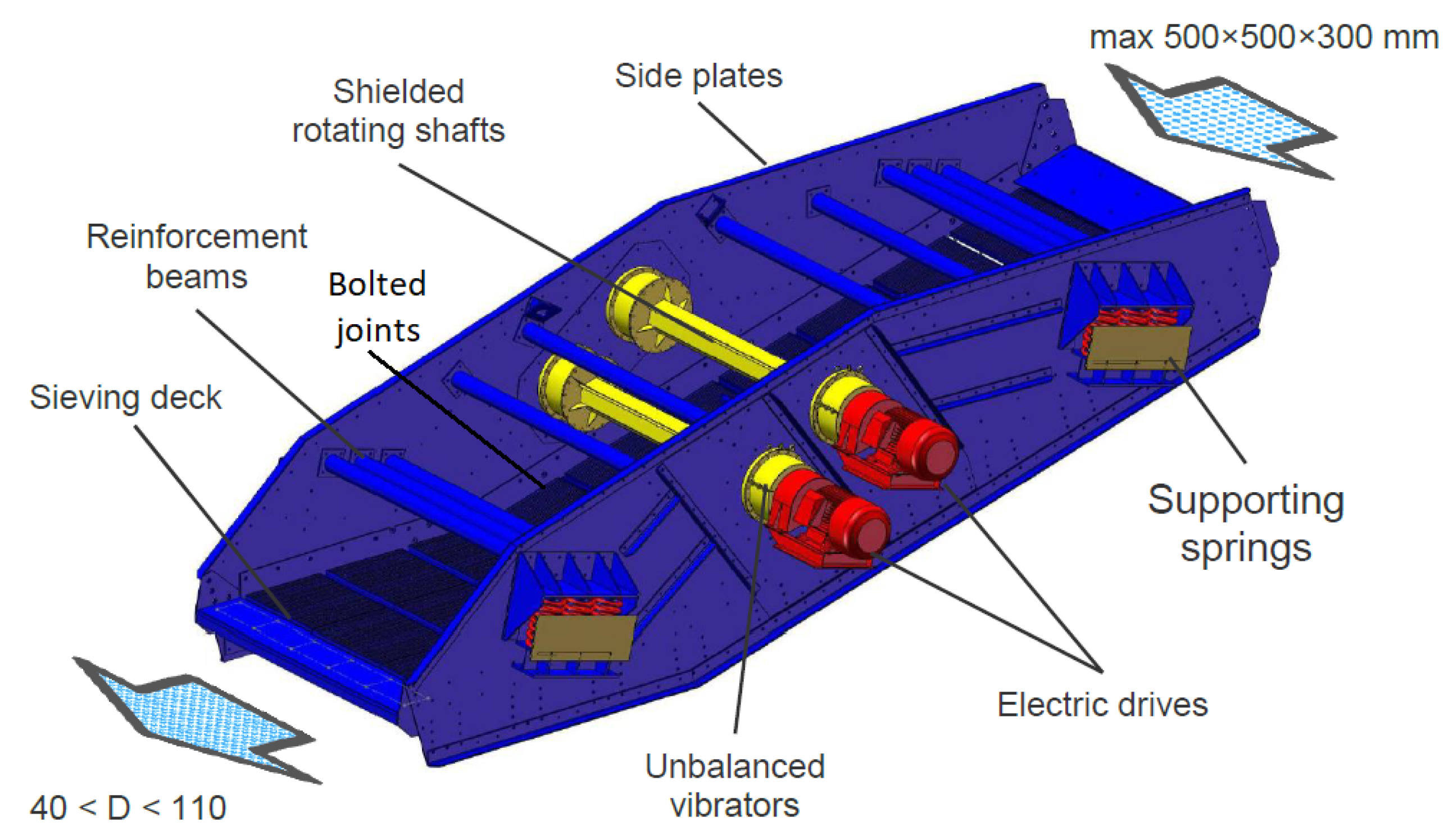
2.1. Design of Industrial Sieving Screen
2.2. Vibrating Screen Dynamics and Failures
2.3. Measuring Equipment
3. Methodology of the Bolted Joints Diagnostics in Vibrating Screens
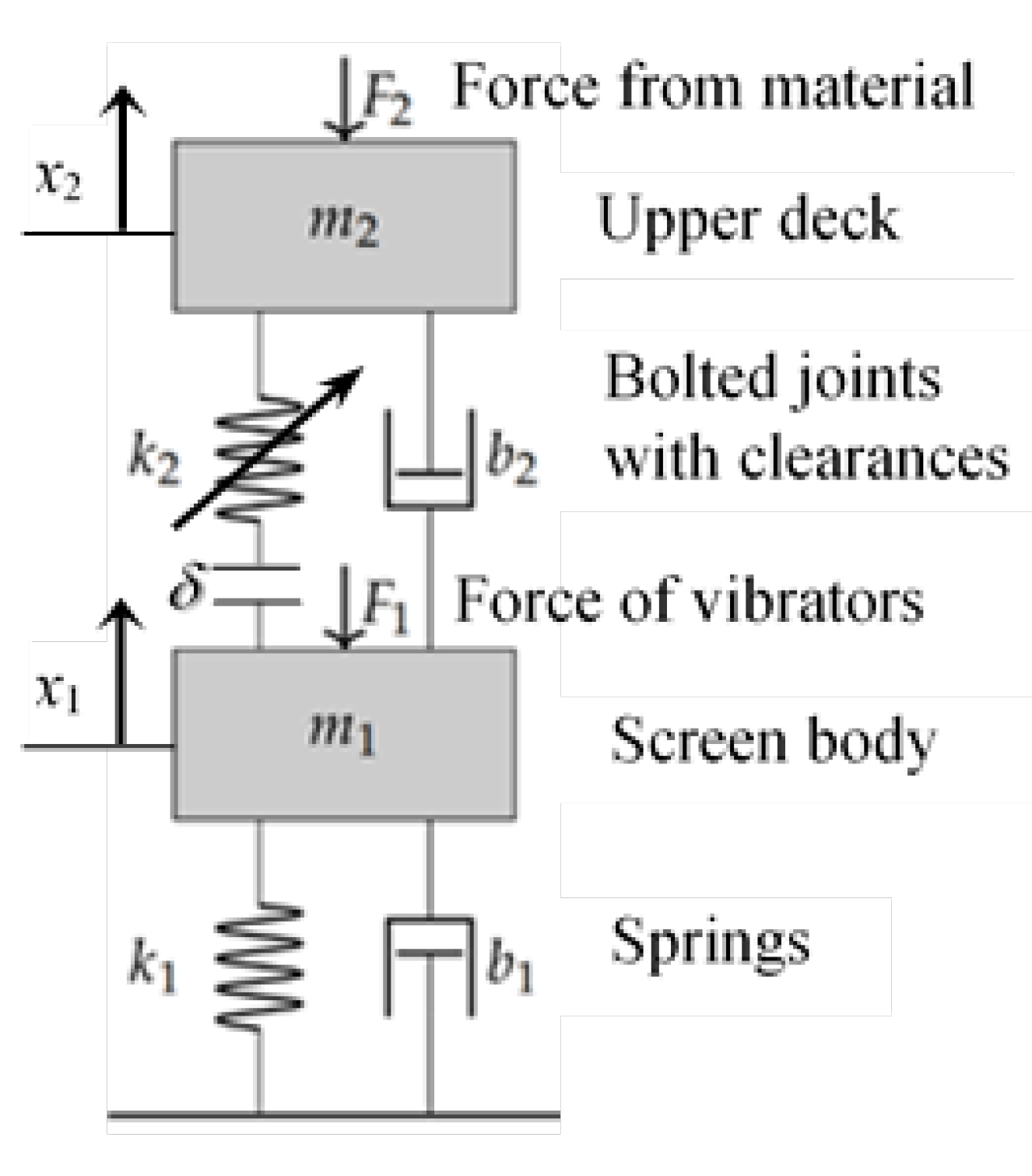
3.1. Equation of Motion
3.1.1. Modal Analysis
3.1.2. Damping Ratio
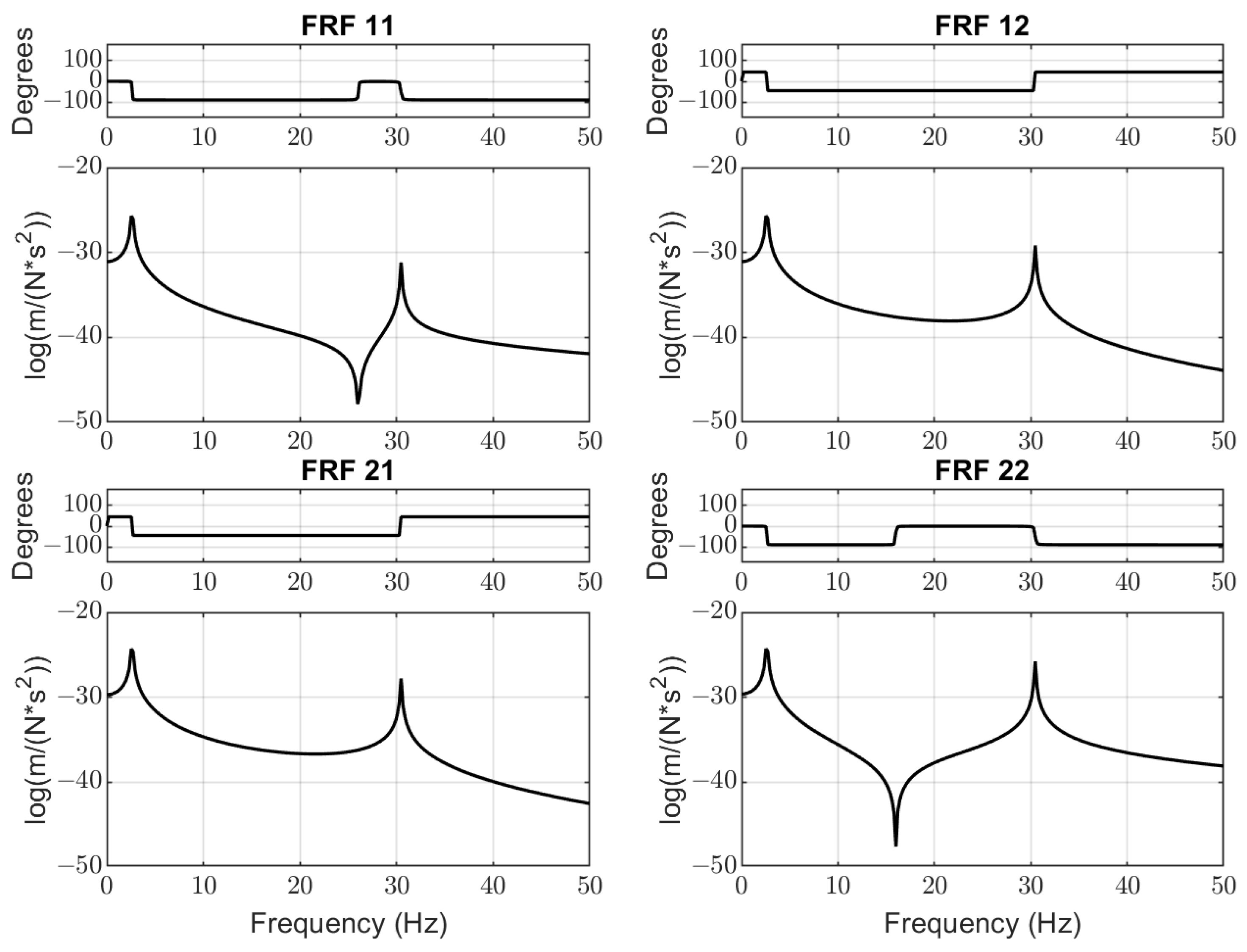
3.1.3. Frequency Response Functions
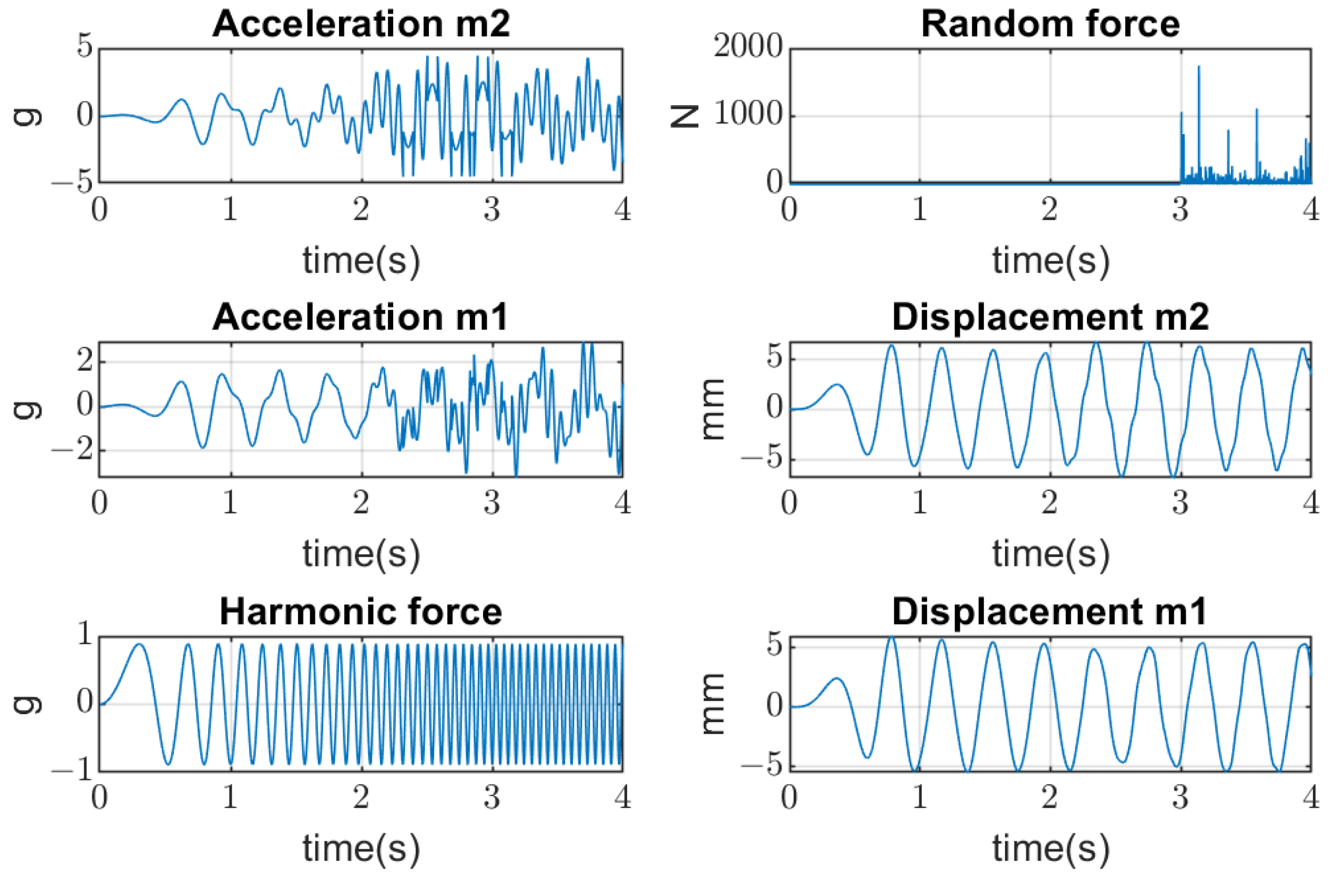
3.2. Impulsive Non-Gaussian Noise
3.3. Dynamical Model of the Vibrating Screen
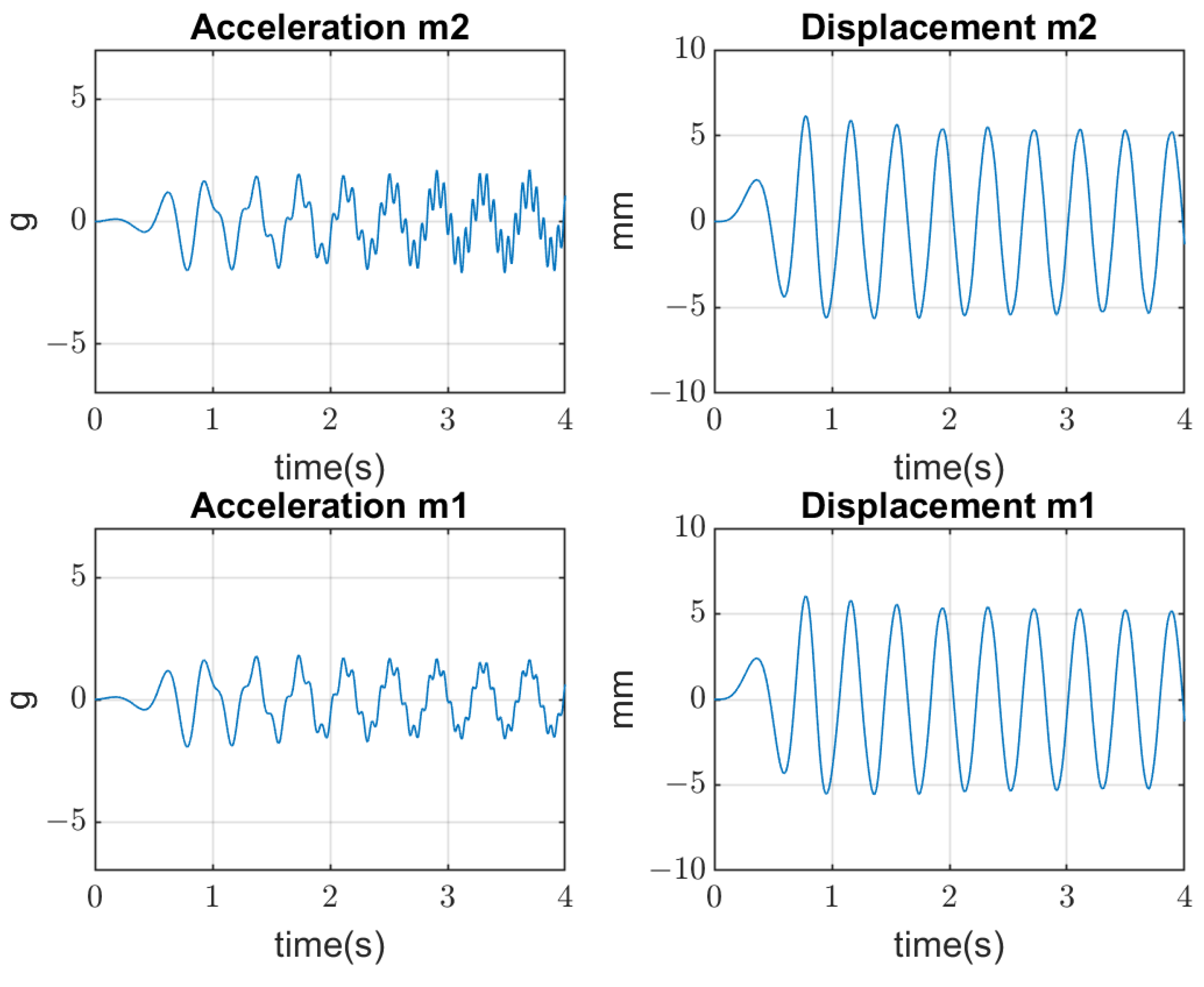
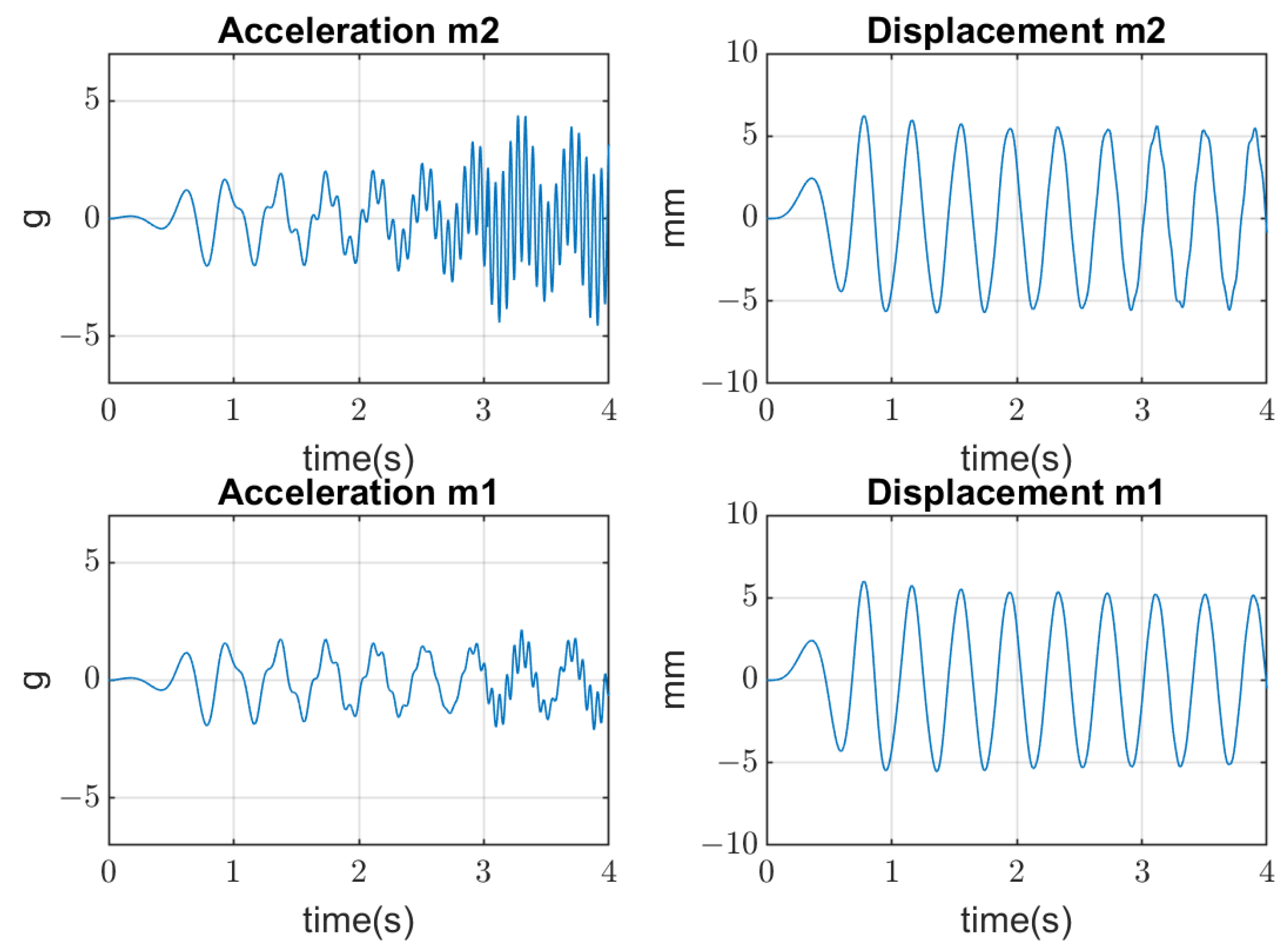
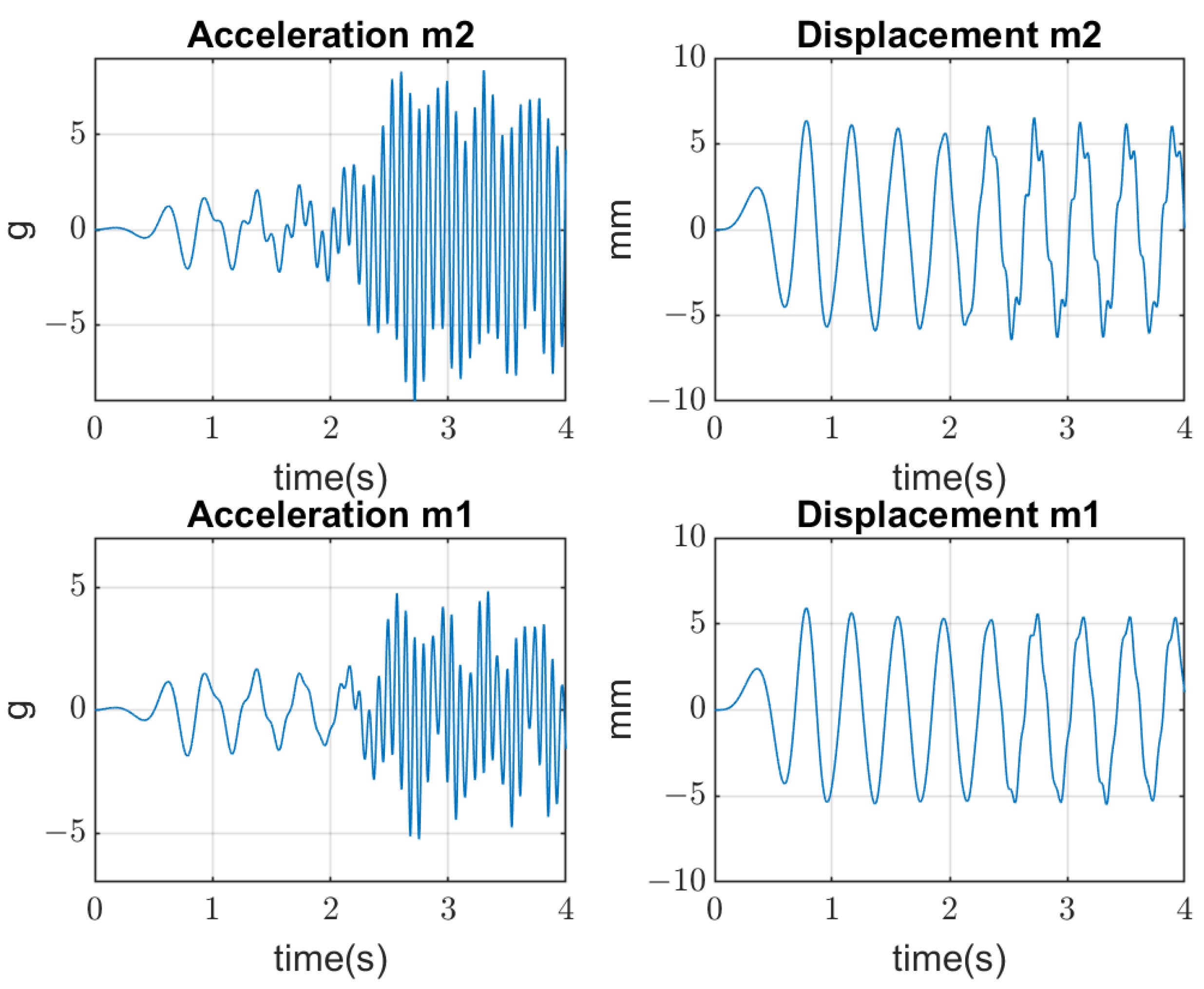
4. Results of Simulation
4.1. Analysis of Frequency Response Functions
- FRF: from (vibrators’ force F1) to (displacement of mass m1);
- FRF: from (vibrators’ force F1) to (displacement of mass m2);
- FRF: from (material impacts force F2) to (displacement of mass m1);
- FRF: from (material impacts force F2) to (displacement of mass m2).
4.2. Dynamical Model Simulation
4.3. System Detuning from the Resonance
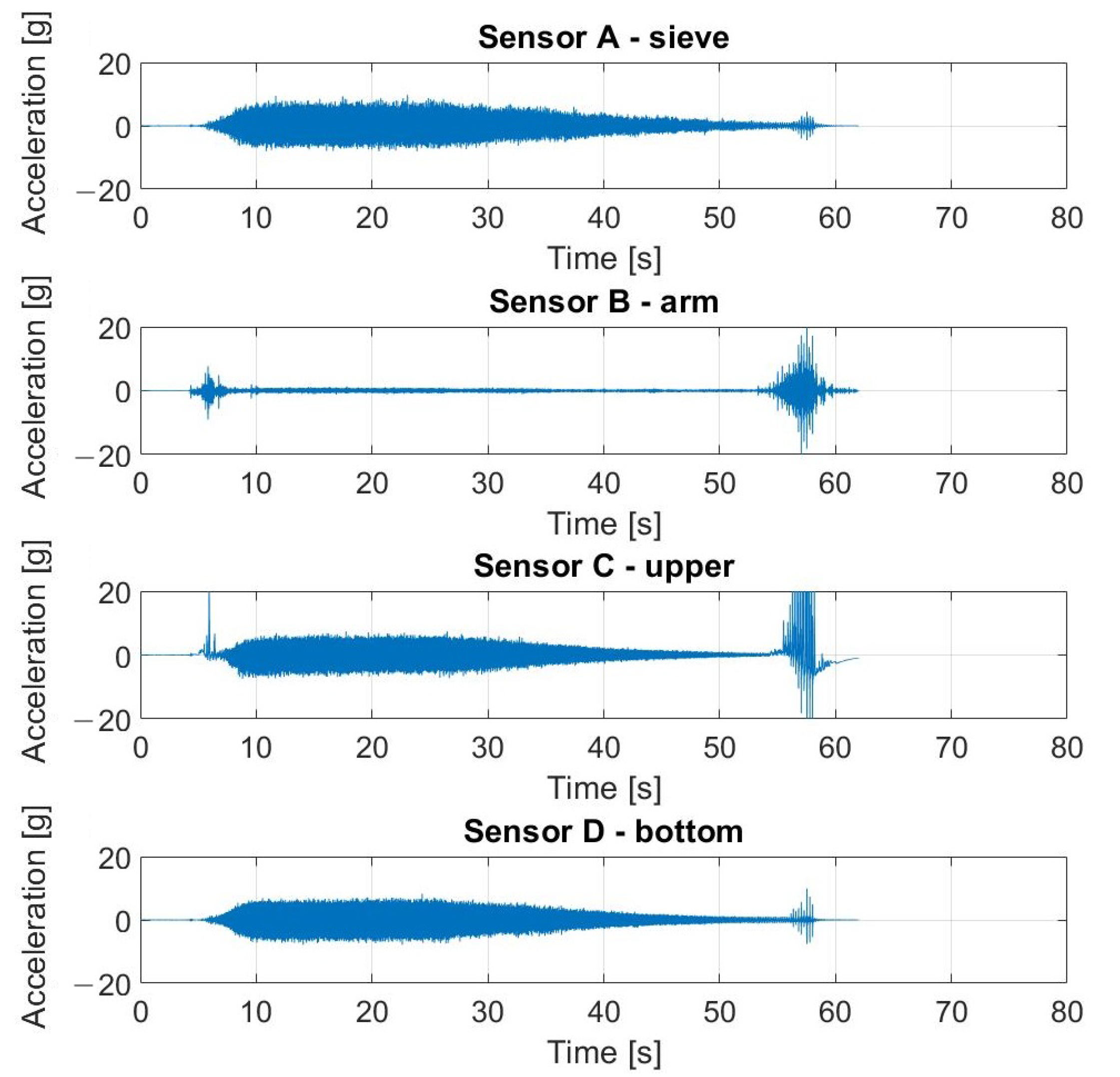
5. Measurements on a Laboratory Vibrating Screen
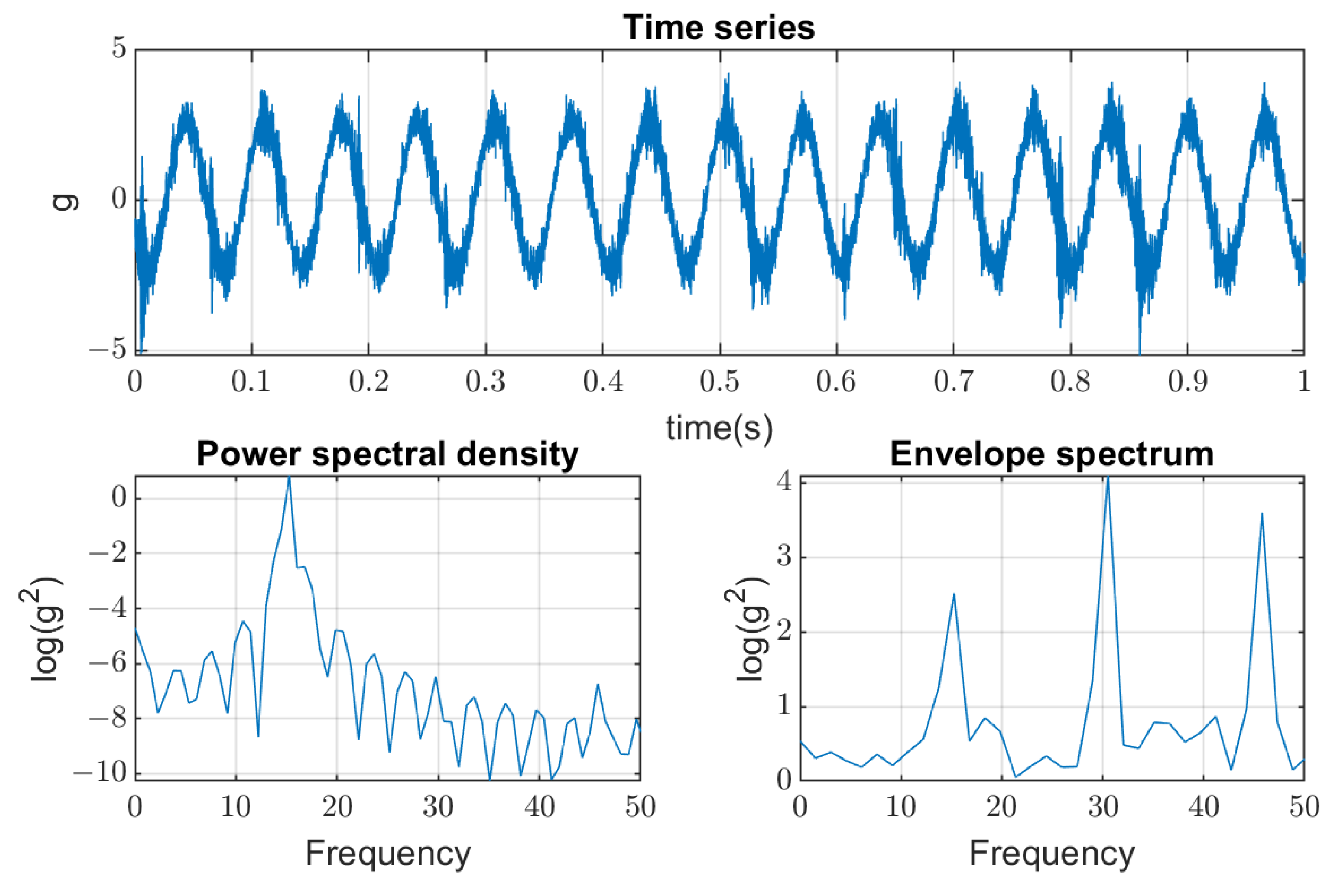
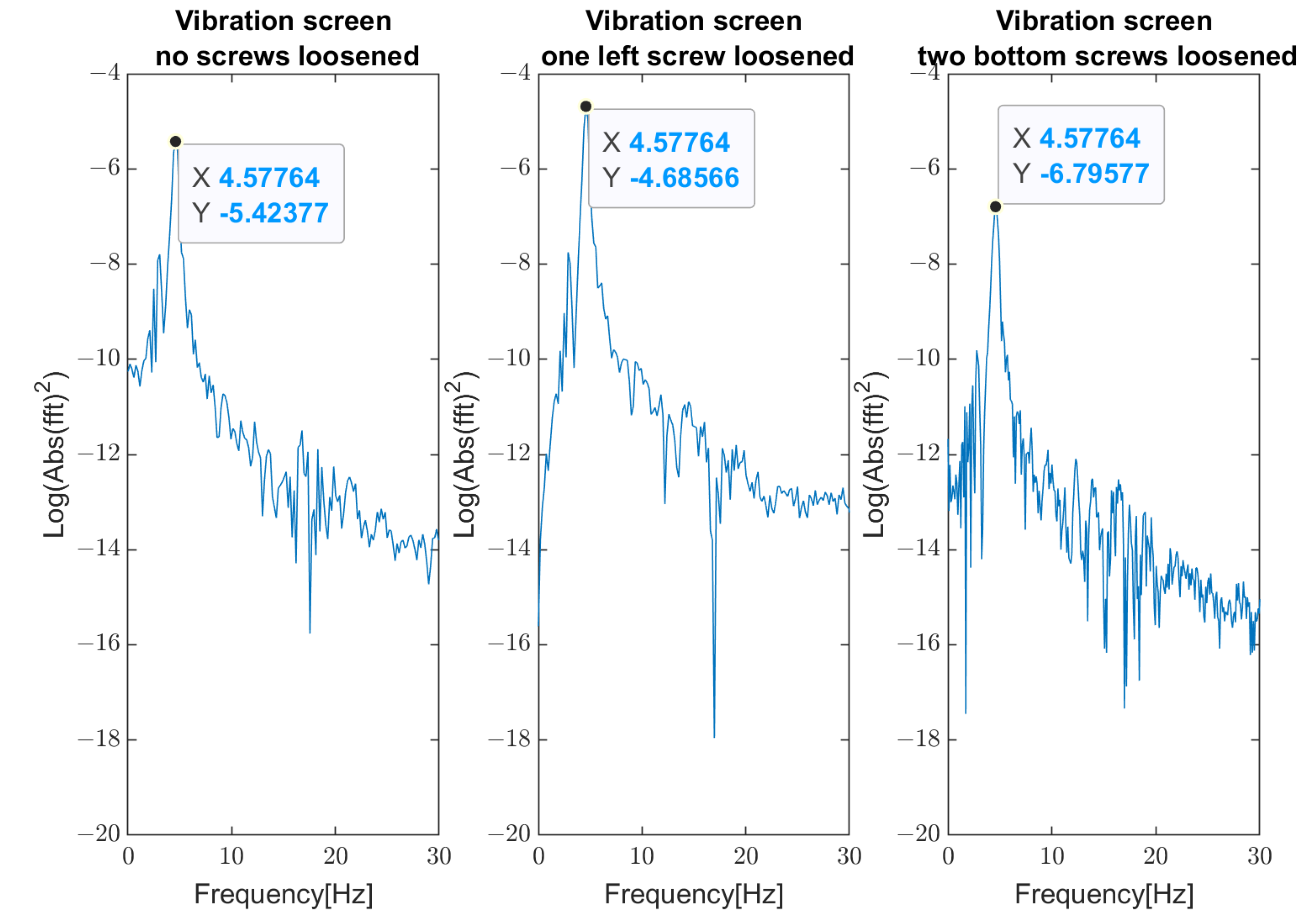
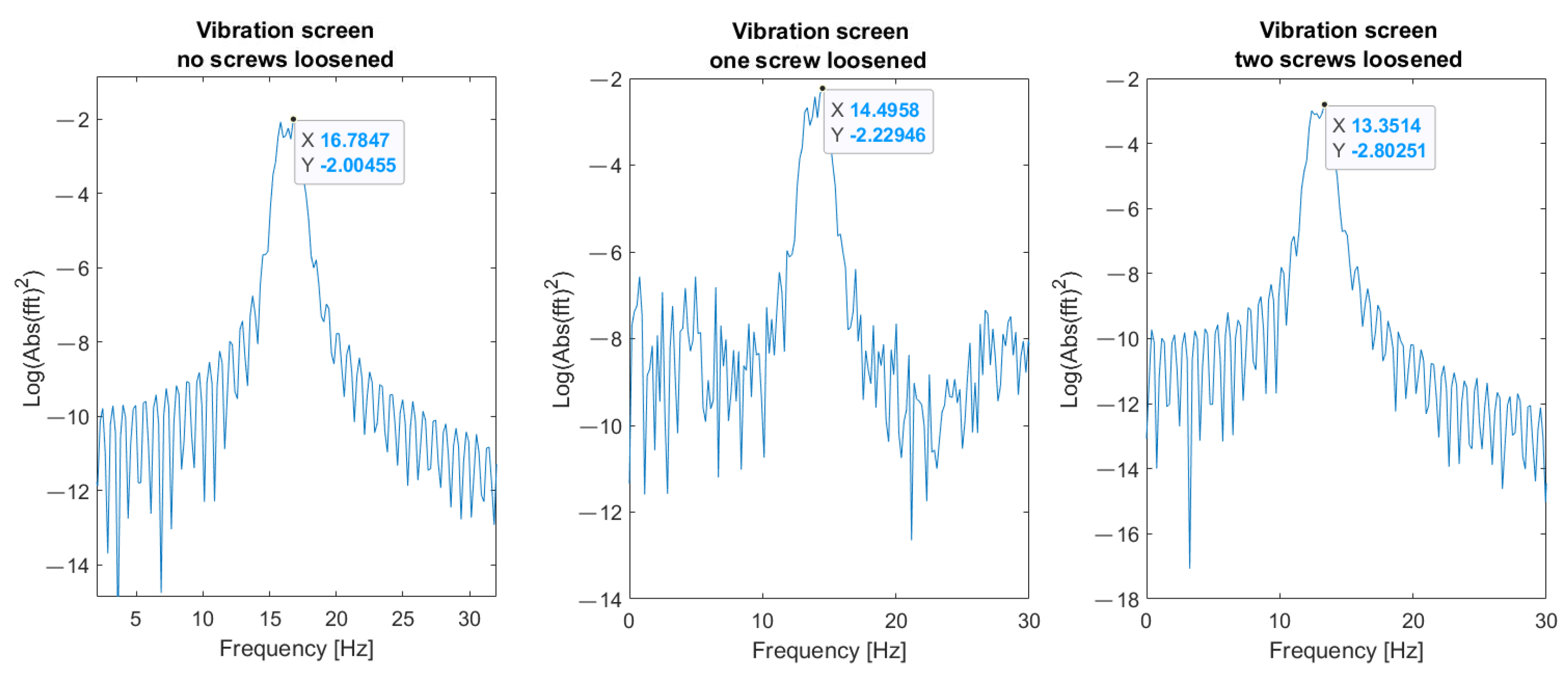
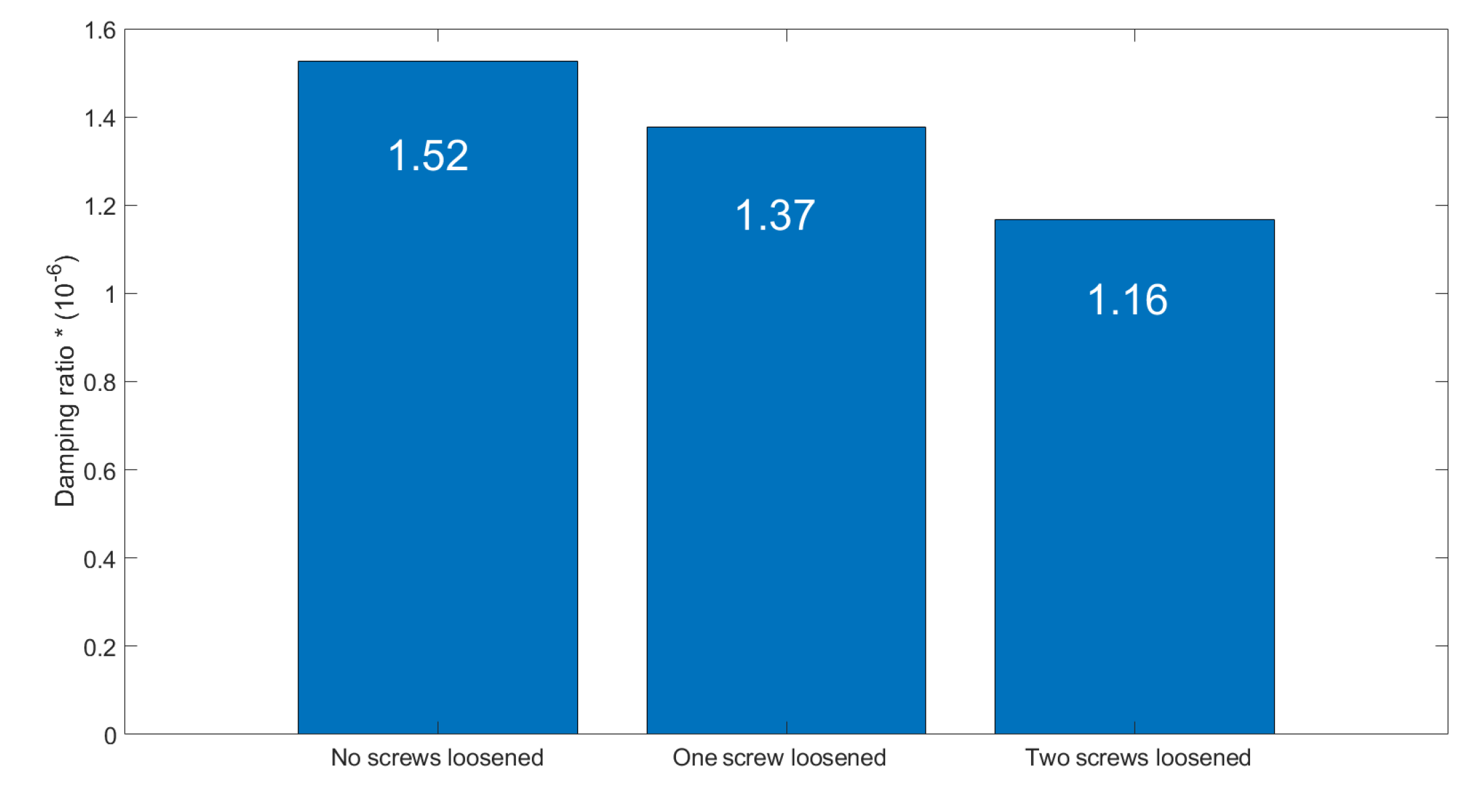
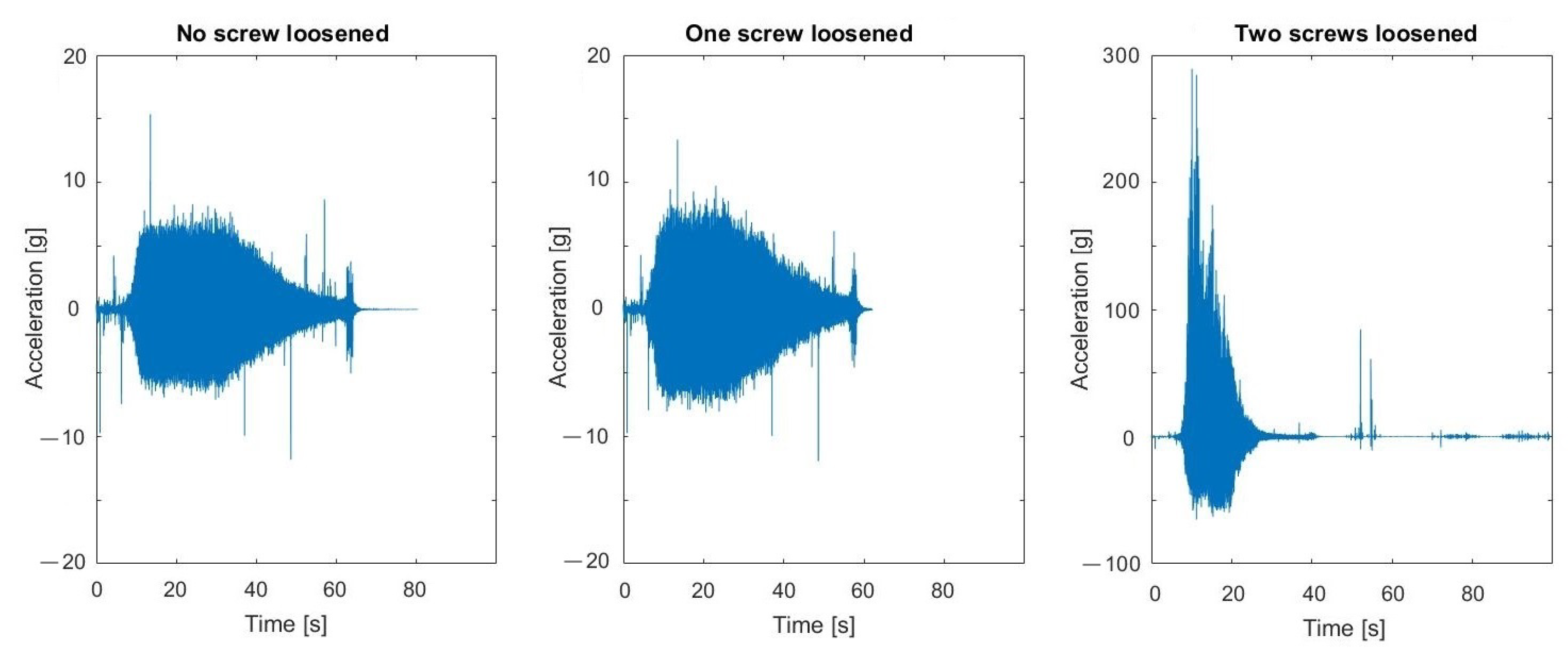
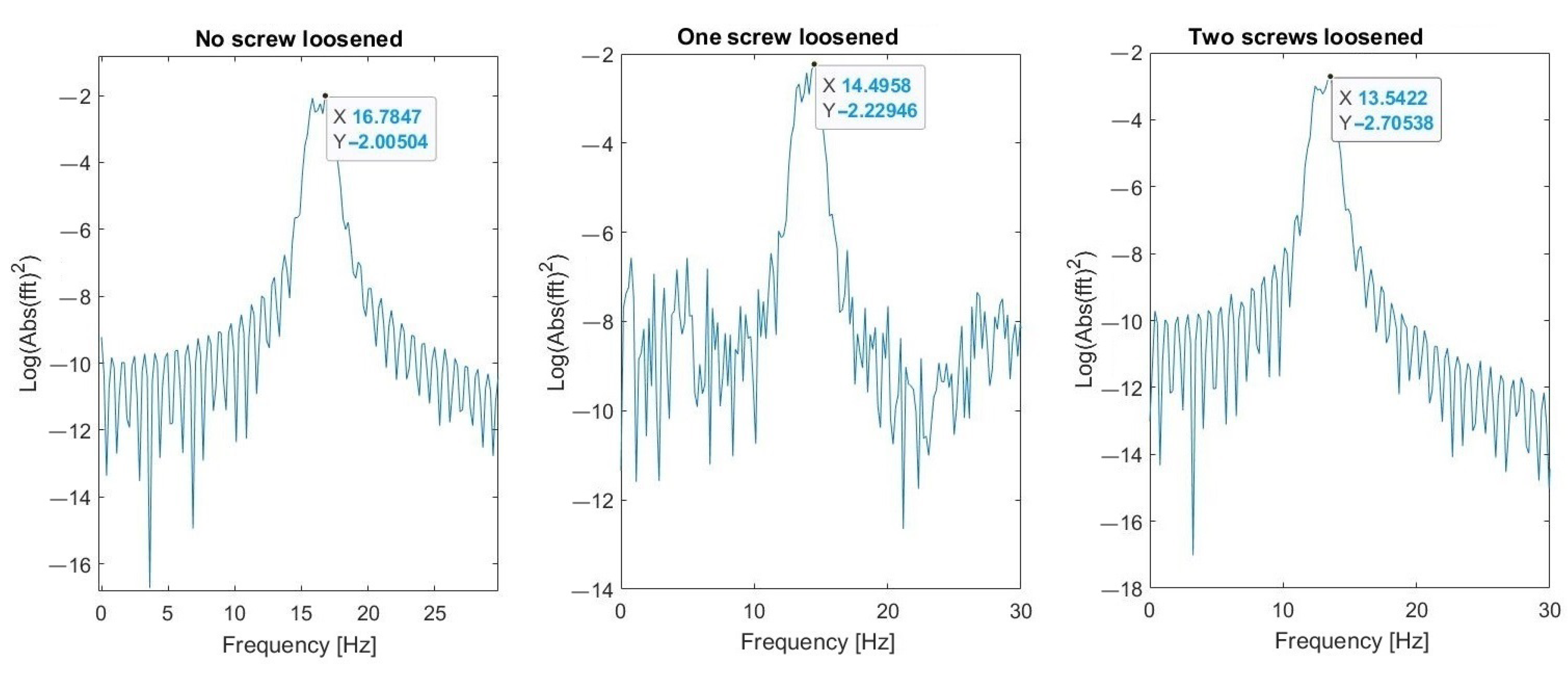
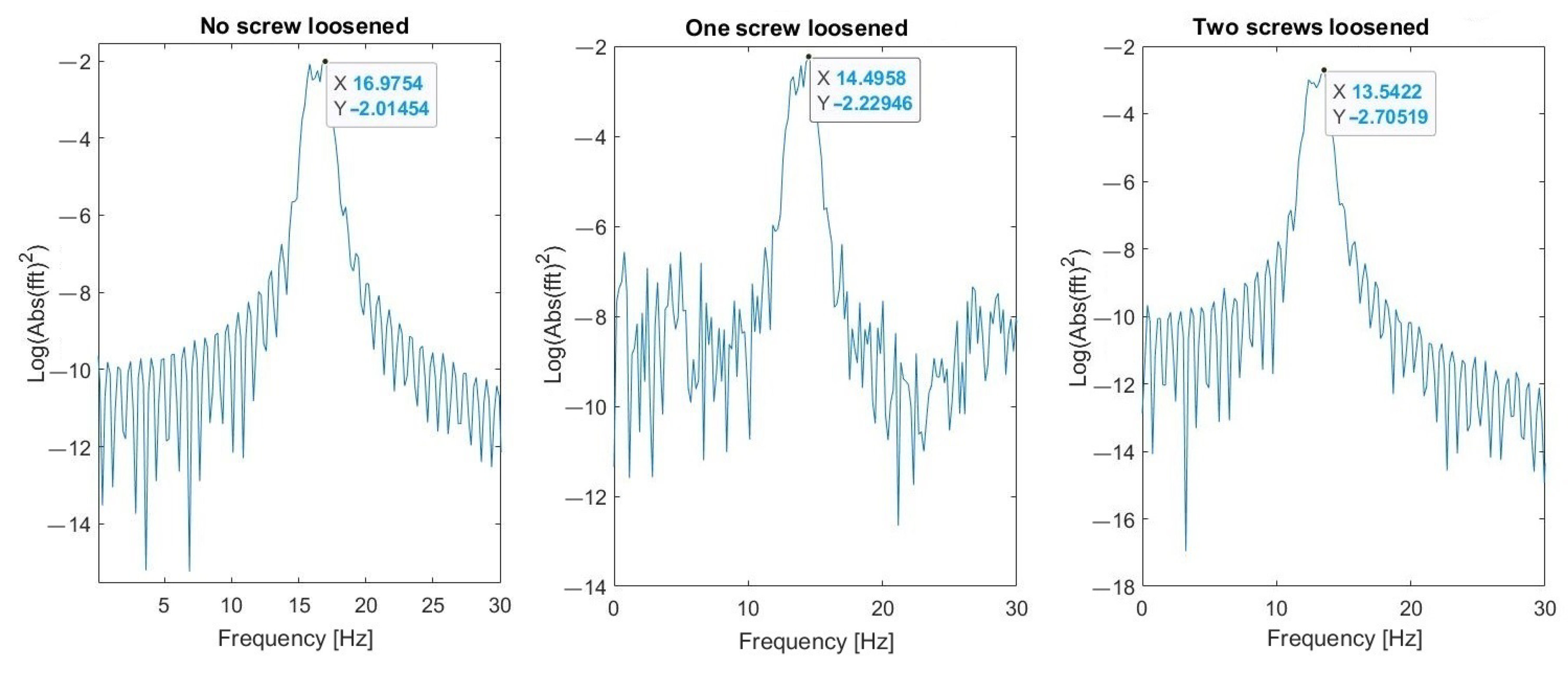
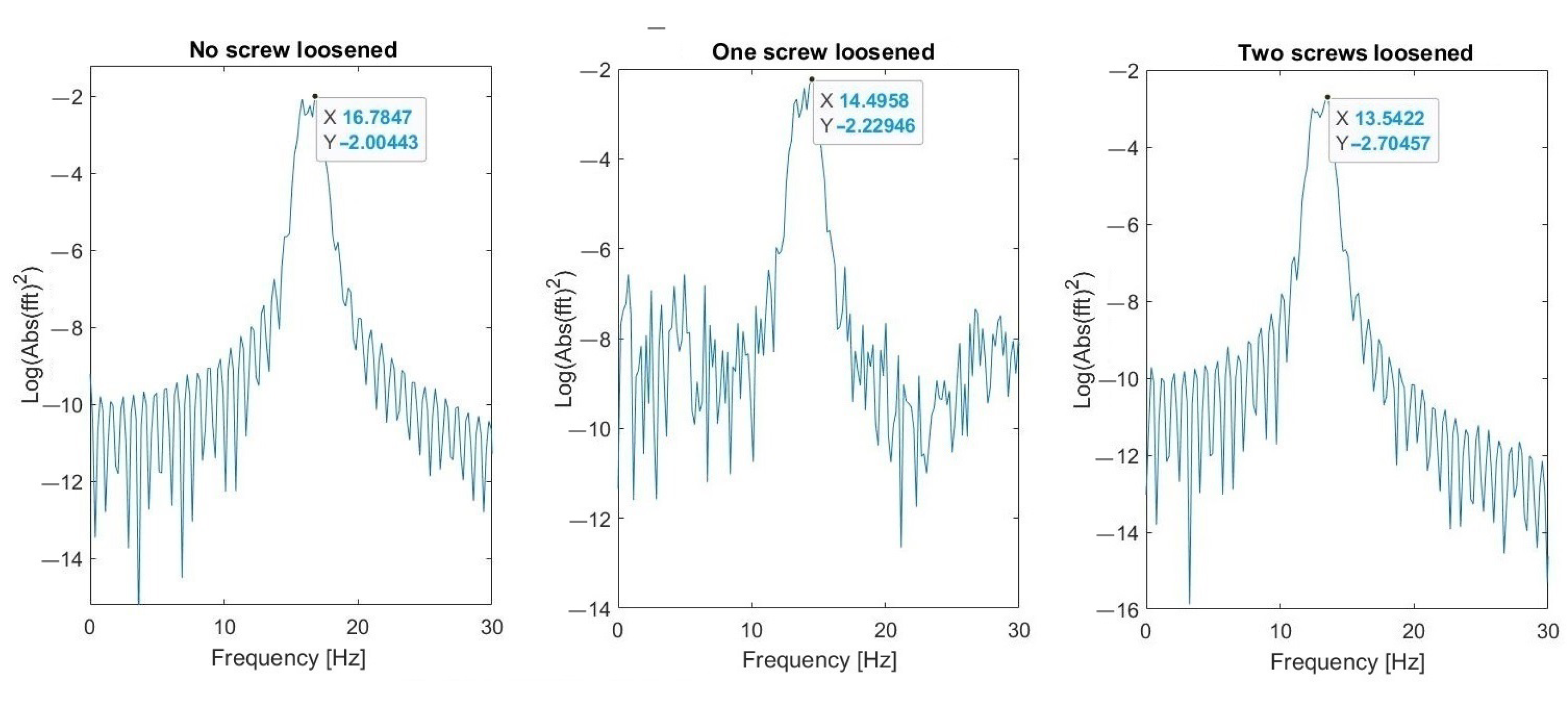
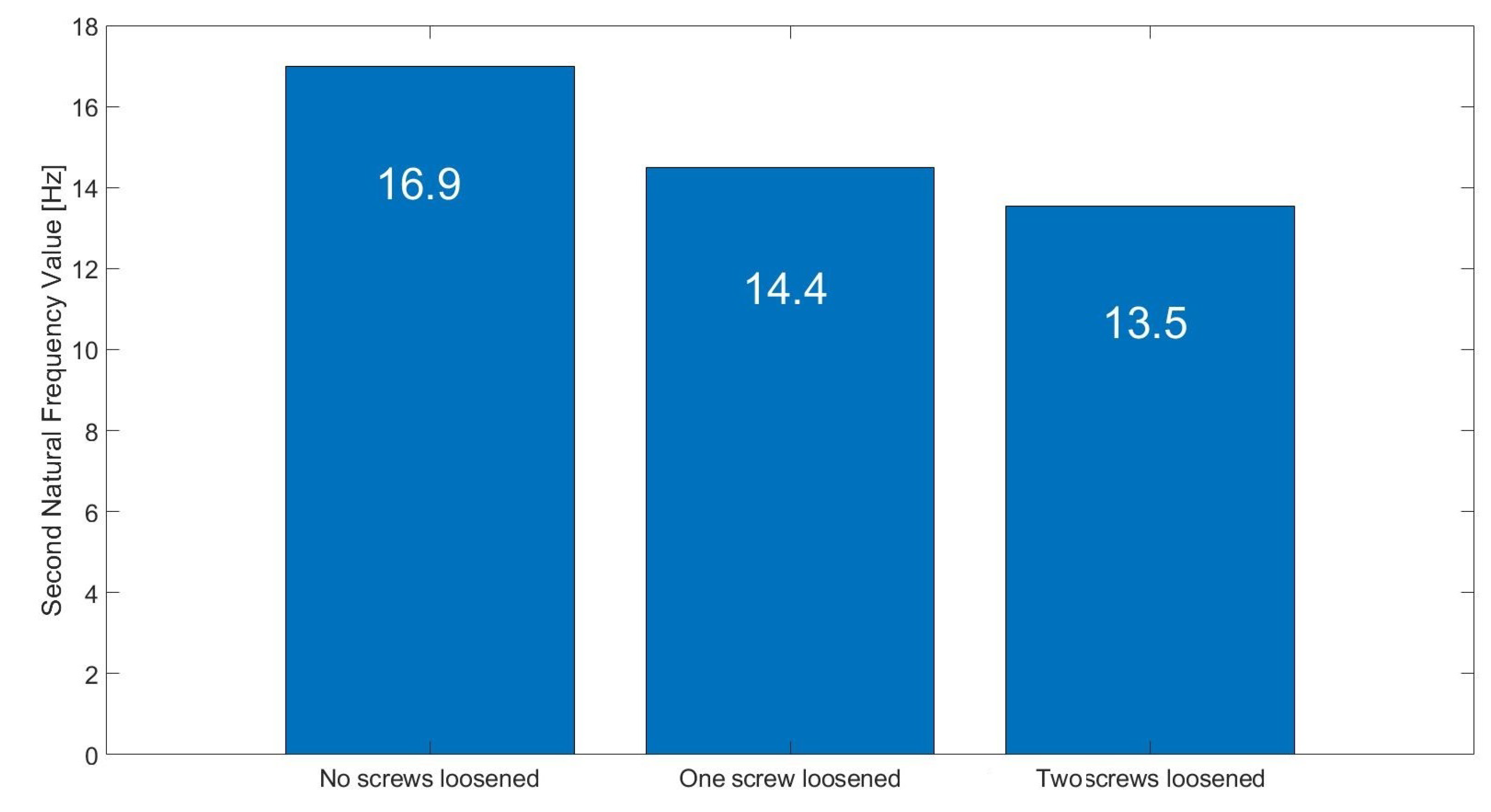
5.1. Results of Measurements
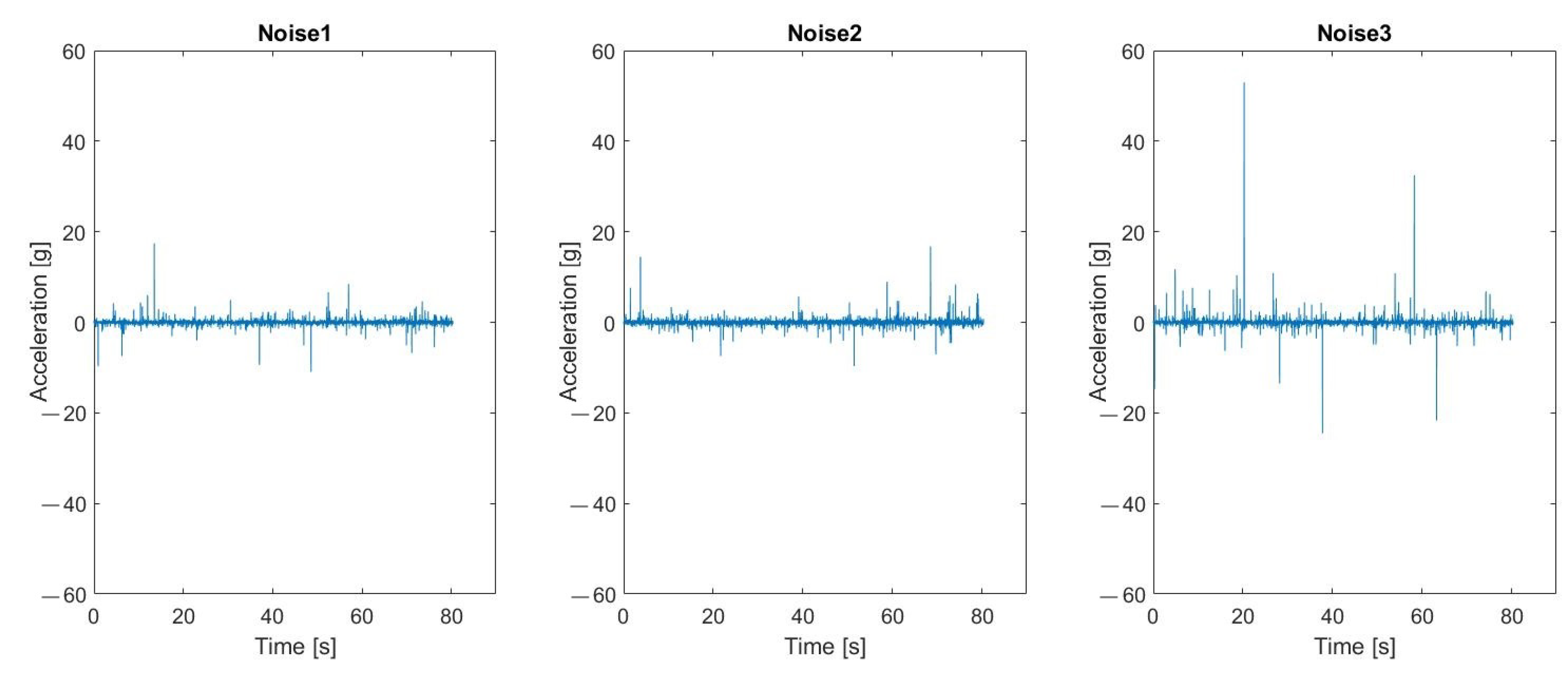
5.2. Verification of Robustness to Impulsive Noise
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krot, P.; Zimroz, R.; Michalak, A.; Wodecki, J.; Ogonowski, S.; Drozda, M.; Jach, M. Development and verification of the diagnostic model of the sieving screen. Shock Vib. 2020, 2020, 8015465. [Google Scholar] [CrossRef]
- Michalak, A.; Wodecki, J.; Drozda, M.; Wyłomańska, A.; Zimroz, R. Model of the Vibration Signal of the Vibrating Sieving Screen Suspension for Condition Monitoring Purposes. Sensors 2021, 21, 213. [Google Scholar] [CrossRef]
- Skoczylas, A.; Anufriiev, S.; Stefaniak, P. Oversized ore pieces detection method based on computer vision and sound processing for validation of vibrational signals in diagnostics of mining screen. In Proceedings of the SGEM International Multidisciplinary Scientific GeoConference EXPO Proceedings, STEF92 Technology, Albena, Bulgaria, 16–25 August 2020. [Google Scholar] [CrossRef]
- Krot, P.; Korennoi, V.; Zimroz, R. Vibration-Based Diagnostics of Radial Clearances and Bolts Loosening in the Bearing Supports of the Heavy-Duty Gearboxes. Sensors 2020, 20, 7284. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Wyłomańska, A.; Zimroz, R. Influence of non-Gaussian noise on the effectiveness of cyclostationary analysis—Simulations and real data analysis. Meas. J. Int. Meas. Confed. 2021, 171, 108814. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Zimroz, R. Local damage detection based on vibration data analysis in the presence of Gaussian and heavy-tailed impulsive noise. Measurement 2021, 169, 108400. [Google Scholar] [CrossRef]
- Wodecki, J. Time-Varying Spectral Kurtosis: Generalization of Spectral Kurtosis for Local Damage Detection in Rotating Machines under Time-Varying Operating Conditions. Sensors 2021, 21, 3590. [Google Scholar] [CrossRef]
- Hebda-Sobkowicz, J.; Zimroz, R.; Pitera, M.; Wyłomańska, A. Informative frequency band selection in the presence of non-Gaussian noise—A novel approach based on the conditional variance statistic with application to bearing fault diagnosis. Mech. Syst. Signal Process. 2020, 145, 106971. [Google Scholar] [CrossRef]
- Wyłomańska, A.; Zimroz, R.; Janczura, J.; Obuchowski, J. Impulsive noise cancellation method for copper ore crusher vibration signals enhancement. IEEE Trans. Ind. Electron. 2016, 63, 5612–5621. [Google Scholar] [CrossRef]
- Hebda-Sobkowicz, J.; Zimroz, R.; Wyłomańska, A. Selection of the Informative Frequency Band in a Bearing Fault Diagnosis in the Presence of Non-Gaussian Noise—Comparison of Recently Developed Methods. Appl. Sci. 2020, 10, 2657. [Google Scholar] [CrossRef]
- Aqueveque, P.; Radrigan, L.; Morales, A.S.; Willenbrinck, E. Development of a Cyber-Physical System to Monitor Early Failures Detection in Vibrating Screens. IEEE Access 2021, 9, 145866–145885. [Google Scholar] [CrossRef]
- Safranyik, F.; Csizmadia, B.M.; Hegedus, A.; Keppler, I. Optimal oscillation parameters of vibrating screens. J. Mech. Sci. Technol. 2019, 33, 2011–2017. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, L.; Zhang, C.; Qi, L.; Liu, C.; Zhao, Y. Research on impact characteristics of screening coals on vibrating screen based on discrete-finite element method. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 42, 1963–1976. [Google Scholar] [CrossRef]
- Li, Z.; Li, K.; Ge, X.; Tong, X. Performance optimization of banana vibrating screens based on PSO-SVR under DEM simulations. J. Vibroeng. 2019, 21, 28–39. [Google Scholar] [CrossRef]
- Wu, X.; Li, Z.; Xia, H.; Tong, X. Vibration Parameter Optimization of a Linear Vibrating Banana Screen Using DEM 3D Simulation. J. Eng. Technol. Sci. 2018, 50, 346–363. [Google Scholar] [CrossRef]
- Harzanagh, A.A.; Orhan, E.C.; Ergun, S.L. Discrete element modelling of vibrating screens. Miner. Eng. 2018, 121, 107–121. [Google Scholar] [CrossRef]
- Xiao, J.; Tong, X. Particle stratification and penetration of a linear vibrating screen by the discrete element method. Int. J. Min. Sci. Technol. 2012, 22, 357–362. [Google Scholar] [CrossRef]
- Baragetti, S.; Villa, F. A dynamic optimization theoretical method for heavy loaded vibrating screens. Nonlinear Dyn. 2014, 78, 609–627. [Google Scholar] [CrossRef]
- Chandravanshi, M.; Mukhopadhyay, A. Analysis of variations in vibration behavior of vibratory feeder due to change in stiffness of helical springs using FEM and EMA methods. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3343–3362. [Google Scholar] [CrossRef]
- Dang, T.N. Modeling and Dynamic Simulation of a Multi-slope Vibrating Screen to Determine the Basic Working Parameters. In Advances in Engineering Research and Application; Springer: Cham, Switzerland, 2022; pp. 671–684. [Google Scholar] [CrossRef]
- Song, B.C.; Liu, C.S.; Peng, L.P.; Li, J. Dynamic analysis of new type elastic screen surface with multi degree of freedom and experimental validation. J. Cent. South Univ. 2015, 22, 1334–1341. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Fan, Z. Similarity analysis between scale model and prototype of large vibrating screen. Shock Vib. 2015, 2015, 247193. [Google Scholar] [CrossRef]
- Yang, X.; Wu, J.; Jiang, H.; Qiu, W.; Liu, C. Dynamic modeling and parameters optimization of large vibrating screen with full degree of freedom. Shock Vib. 2019, 2019, 1915708. [Google Scholar] [CrossRef]
- Krot, P.; Zimroz, R. Methods of springs failures diagnostics in ore processing vibrating screens. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 362, p. 012147. [Google Scholar]
- Gursky, V.; Krot, P.; Dilay, I.; Zimroz, R. Optimization of the vibrating machines with adjustable frequency characteristics. In Proceedings of the Workshop on Nonstationary Systems and Their Applications; Springer: Cham, Switzerland, 2021; pp. 352–363. [Google Scholar]
- Gelman, L. Piecewise model and estimates of damping and natural frequency for a spur gear. Mech. Syst. Signal Process. 2007, 21, 1192–1196. [Google Scholar] [CrossRef]
- Gelman, L.; Gorpinich, S.; Thompson, C. Adaptive diagnosis of the bilinear mechanical systems. Mech. Syst. Signal Process. 2009, 23, 1548–1553. [Google Scholar] [CrossRef]
- Duda-Mróz, N.; Anufriiev, S.; Stefaniak, P. Application of Wavelet Filtering to Vibrational Signals from the Mining Screen for Spring Condition Monitoring. Minerals 2021, 11, 1076. [Google Scholar] [CrossRef]
- Gong, S.; Oberst, S.; Wang, X. An experimentally validated rubber shear spring model for vibrating flip-flow screens. Mech. Syst. Signal Process. 2020, 139, 106619. [Google Scholar] [CrossRef]
- Bulat, A.; Dyrda, V.; Lysytsya, M.; Grebenyuk, S. Numerical simulation of the stress-strain state of thin-layer rubber-metal vibration absorber elements under nonlinear deformation. Strength Mater. 2018, 50, 387–395. [Google Scholar] [CrossRef]
- Ene, G. Design of the elastic system of the vibrating screens. Chem. Mag. 2009, 60, 1123–1128. [Google Scholar]
- Ene, G.; Sporea, N. Approaches regarding the calculus of the elastic system of the initial vibrating screens. Rev. Chim. 2016, 67, 308–313. [Google Scholar]
- Slepyan, L.I.; Slepyan, V.I. Coupled mode parametric resonance in a vibrating screen model. Mech. Syst. Signal Process. 2014, 43, 295–304. [Google Scholar] [CrossRef]
- Wodecki, J.; Krot, P.; Wróblewski, A.; Chudy, K.; Zimroz, R. Condition Monitoring of Horizontal Sieving Screens—A Case Study of Inertial Vibrator Bearing Failure in Calcium Carbonate Production Plant. Materials 2023, 16, 1533. [Google Scholar] [CrossRef]
- Lyan, I.; Panovko, G.; Shokhin, A. Dynamic portrait calculation of the systems with spatial oscillations. In Proceedings of the International Conference of Young Scientists and Students Topical Problems of Mechanical Engineering ToPME 2021: Mechanical Engineering Research Institute of the Russian Academy of Sciences (IMASH RAN), Moscow, Russia, 30 November–2 December 2021; AIP Publishing: Melville, NY, USA, 2023. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, J.; Kou, Z.; Zhang, Y.; Liu, C. Dynamic characteristics analysis of a novel vibrating screen based on electromechanical coupling simulation. J. Vibroeng. 2023. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, C.; Yan, C.; Li, H. Design and Dynamic Analysis of a Four-Degree-of-Freedom Chaotic Vibrating Screen. Shock Vib. 2021, 2021, 8830428. [Google Scholar] [CrossRef]
- Wu, M.; Chen, F.; Li, A.; Chen, Z.; Sun, N. A novel vibration isolator for vibrating screen based on magnetorheological damper. J. Mech. Sci. Technol. 2021, 35, 4343–4352. [Google Scholar] [CrossRef]
- Ogonowski, S.; Krauze, P. Trajectory Control for Vibrating Screen with Magnetorheological Dampers. Sensors 2022, 22, 4225. [Google Scholar] [CrossRef] [PubMed]
- Nozhenko, V. The system of forming the control mode of the electric drive during the start-up of the vibration machine. World Sci. 2021, 7. [Google Scholar] [CrossRef]
- Bickford, J. Handbook of Bolts and Bolted Joints; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Pan, Q.; Pan, R.; Shao, C.; Chang, M.; Xu, X. Research review of principles and methods for ultrasonic measurement of axial stress in bolts. Chin. J. Mech. Eng. 2020, 33, 1–16. [Google Scholar] [CrossRef]
- Pan, Q.; Pan, R.; Chang, M.; Shao, C.; Liu, X.; Xu, X. Reliability evaluation of bolt fastening force based on ultrasonic measurement method. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 2212–2217. [Google Scholar]
- Mba, D. Applicability of acoustic emissions to monitoring the mechanical integrity of bolted structures in low speed rotating machinery: Case study. NDT E Int. 2002, 35, 293–300. [Google Scholar] [CrossRef]
- Argatov, I.; Sevostianov, I. Health monitoring of bolted joints via electrical conductivity measurements. Int. J. Eng. Sci. 2010, 48, 874–887. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Su, Z.; Xiao, Y. Continuous monitoring of residual torque of loose bolt in a bolted joint. Procedia Eng. 2017, 188, 278–285. [Google Scholar] [CrossRef]
- Wang, F.; Song, G. Monitoring of multi-bolt connection looseness using a novel vibro-acoustic method. Nonlinear Dyn. 2020, 100, 243–254. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, H.; Liao, Y.; Su, Z.; Xiao, Y. Vibro-acoustic modulation (VAM)-inspired structural integrity monitoring and its applications to bolted composite joints. Compos. Struct. 2017, 176, 505–515. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Liao, Y.; Su, Z.; Xiao, Y. Contact acoustic nonlinearity (CAN)-based continuous monitoring of bolt loosening: Hybrid use of high-order harmonics and spectral sidebands. Mech. Syst. Signal Process. 2018, 103, 280–294. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.; Wang, T.; Luo, Y. A piezoelectric active sensing method for detection of bolt load loss. Sens. Rev. 2014, 34, 337–342. [Google Scholar] [CrossRef]
- Shao, J.; Wang, T.; Yin, H.; Yang, D.; Li, Y. Bolt looseness detection based on piezoelectric impedance frequency shift. Appl. Sci. 2016, 6, 298. [Google Scholar] [CrossRef]
- Kedra, R.; Rucka, M. Bolted joint monitoring using the elastic wave propagation. In Proceedings of the 13th International Conference on Damage Assessment of Structures, Porto, Portugal, 9–10 July 2019; Springer: Singapore, 2020; pp. 234–243. [Google Scholar]
- Wang, F.; Chen, Z.; Song, G. Monitoring of multi-bolt connection looseness using entropy-based active sensing and genetic algorithm-based least square support vector machine. Mech. Syst. Signal Process. 2020, 136, 106507. [Google Scholar] [CrossRef]
- Chen, D.; Huo, L.; Song, G. EMI based multi-bolt looseness detection using series/parallel multi-sensing technique. Smart Struct. Syst. 2020, 25, 423–432. [Google Scholar]
- Huynh, T.C.; Dang, N.L.; Kim, J.T. Preload monitoring in bolted connection using piezoelectric-based smart interface. Sensors 2018, 18, 2766. [Google Scholar] [CrossRef]
- Huynh, T.C.; Ho, D.D.; Dang, N.L.; Kim, J.T. Sensitivity of piezoelectric-based smart interfaces to structural damage in bolted connections. Sensors 2019, 19, 3670. [Google Scholar] [CrossRef]
- Dravid, S.; Tripathi, K.; Chouksey, M. Role of washers in controlling loosening of full threaded bolted joints. Procedia Technol. 2014, 14, 543–552. [Google Scholar] [CrossRef]
- Kong, X.; Li, J. An image-based feature tracking approach for bolt loosening detection in steel connections. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2018, Denver, CO, USA, 5–8 March 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10598, p. 105980U. [Google Scholar]
- Kong, X.; Li, J. Image registration-based bolt loosening detection of steel joints. Sensors 2018, 18, 1000. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Huynh, T.C.; Choi, S.H.; Kim, J.T. Vision-based technique for bolt-loosening detection in wind turbine tower. Wind Struct. 2015, 21, 709–726. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Loh, K.J.; Su, W.; Xue, Z.; Zhao, X. Autonomous bolt loosening detection using deep learning. Struct. Health Monit. 2020, 19, 105–122. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Y.; Wang, N. Bolt loosening angle detection technology using deep learning. Struct. Control Health Monit. 2019, 26, e2292. [Google Scholar] [CrossRef]
- Pham, H.C.; Ta, Q.B.; Kim, J.T.; Ho, D.D.; Tran, X.L.; Huynh, T.C. Bolt-loosening monitoring framework using an image-based deep learning and graphical model. Sensors 2020, 20, 3382. [Google Scholar] [CrossRef]
- Cha, Y.J.; You, K.; Choi, W. Vision-based detection of loosened bolts using the Hough transform and support vector machines. Autom. Constr. 2016, 71, 181–188. [Google Scholar] [CrossRef]
- Xu, C.; Huang, C.C.; Zhu, W.D. Bolt loosening detection in a jointed beam using empirical mode decomposition–based nonlinear system identification method. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719875656. [Google Scholar] [CrossRef]
- Deka, A.; Rao, A.; Kamath, S.; Gaurav, A.; Gangadharan, K. Modeling and experimental studies on the dynamics of bolted joint structure: Comparison of three vibration-based techniques for structural health monitoring. In Advances in Rotor Dynamics, Control, and Structural Health Monitoring; Springer: Singapore, 2020; pp. 301–313. [Google Scholar]
- Todd, M.; Nichols, J.; Nichols, C.; Virgin, L. An assessment of modal property effectiveness in detecting bolted joint degradation: Theory and experiment. J. Sound Vib. 2004, 275, 1113–1126. [Google Scholar] [CrossRef]
- Čelič, D.; Boltežar, M. Identification of the dynamic properties of joints using frequency–response functions. J. Sound Vib. 2008, 317, 158–174. [Google Scholar] [CrossRef]
- Milanese, A.; Marzocca, P.; Nichols, J.; Seaver, M.; Trickey, S. Modeling and detection of joint loosening using output-only broad-band vibration data. Struct. Health Monit. 2008, 7, 309–328. [Google Scholar] [CrossRef]
- De Oliveira Teloli, R.; da Silva, S.; Ritto, T.G.; Chevallier, G. Bayesian model identification of higher-order frequency response functions for structures assembled by bolted joints. Mech. Syst. Signal Process. 2021, 151, 107333. [Google Scholar] [CrossRef]
- Tol, Ş.; Ozguven, H.N. Dynamic characterization of bolted joints using FRF decoupling and optimization. Mech. Syst. Signal Process. 2015, 54–55, 124–138. [Google Scholar] [CrossRef]
- He, X.; She, T. A new identification method for bolt looseness in wind turbine towers. Shock Vib. 2019, 2019, 6056181. [Google Scholar]
- Chen, G.; Chen, Y.; Chen, Y.; Ji, S. Dynamics modeling and experimental modal analysis of bolt loosening for lightning rod. J. Vibroeng. 2020, 22, 657–671. [Google Scholar] [CrossRef]
- Brøns, M.; Thomsen, J.; Sah, S.; Tcherniak, D.; Fidlin, A. Analysis of transient vibrations for estimating bolted joint tightness. In Nonlinear Structures and Systems, Volume 1; Springer: Cham, Switzerlands, 2020; pp. 21–24. [Google Scholar]
- Brøns, M.; Thomsen, J.J.; Sah, S.M.; Tcherniak, D.; Fidlin, A. Estimating bolt tension from vibrations: Transient features, nonlinearity, and signal processing. Mech. Syst. Signal Process. 2021, 150, 107224. [Google Scholar] [CrossRef]
- Sah, S.M.; Thomsen, J.J.; Fidlin, A. Transverse vibrations of tightened bolts: Simplified modeling of tension-dependent boundary stiffness and damping. Eng. Struct. 2020, 205, 110049. [Google Scholar] [CrossRef]
- PKiMSA Carboautomatyka S.A. Product Catalog. Mechanical Industry. Available online: https://carbo.com.pl/wp-content/uploads/2022/11/Katalog_A4_Carboautomatyka_Mechaniczny_PL_EN_RU.pdf (accessed on 10 August 2023).
- Kistler LabAmp Data Sheet, Type 5165A. Available online: https://kistler.cdn.celum.cloud/SAPCommerce_Download_original/003-146e.pdf (accessed on 16 November 2022).
- Rao, S.S. Vibration of Continuous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Fu, Z.F.; He, J. Modal Analysis; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Weron, R. On the Chambers-Mallows-Stuck method for simulating skewed stable random variables. Stat. Probab. Lett. 1996, 28, 165–171. [Google Scholar] [CrossRef]
- Zhang, W.; Xie, J.; Li, T.; Ding, Y. Tensile low-cycle fatigue performance and life prediction of high-strength bolts. J. Constr. Steel Res. 2022, 197, 107468. [Google Scholar] [CrossRef]
- Schenk, CONiQ Online. Condition Monitoring for Screening Machines and Vibrating Feeders. Available online: https://www.schenckprocess.com/products/coniq-condition-monitoring (accessed on 10 August 2023).
- Schaeffler; FAG SmartCheck. Machinery Monitoring for Every Machine. Available online: https://www.schaeffler.com/remotemedien/media/_shared_media/08_media_library/01_publications/schaeffler_2/tpi/downloads_8/tpi_214_en_us.pdf (accessed on 10 August 2023).
- Metso ScreenWatch. Screen Condition Monitoring. Enhancing Screen Availability. Available online: https://www.metso.com/globalassets/saleshub/documents—episerver/screenwatch_screen_monitoring_2014_lr.pdf (accessed on 10 August 2023).
- SKF Copperhead. Fault Detection for Mining and Mineral Processing Equipment. Available online: http://evolution.skf.com/fault-detection-for-mining-and-mineral-processing-equipment-2/ (accessed on 10 August 2023).
- Bobyr, S.; Krot, P.; Parusov, E.; Golubenko, T.; Baranovs’ka, O. Increasing the wear resistance of structural alloy steel 38CrNi3MoV subjected to isothermal hardening and deep cryogenic treatment. Appl. Sci. 2023, 13, 9143. [Google Scholar] [CrossRef]
- Krot, P.; Bobyr, S.; Zharkov, I.; Prykhodko, I.; Borkowski, P. Increasing the durability of critical parts in heavy-duty industrial machines by deep cryogenic treatment. In Structural Integrity; Springer: Cham, Switzerland, 2022; pp. 127–133. [Google Scholar]



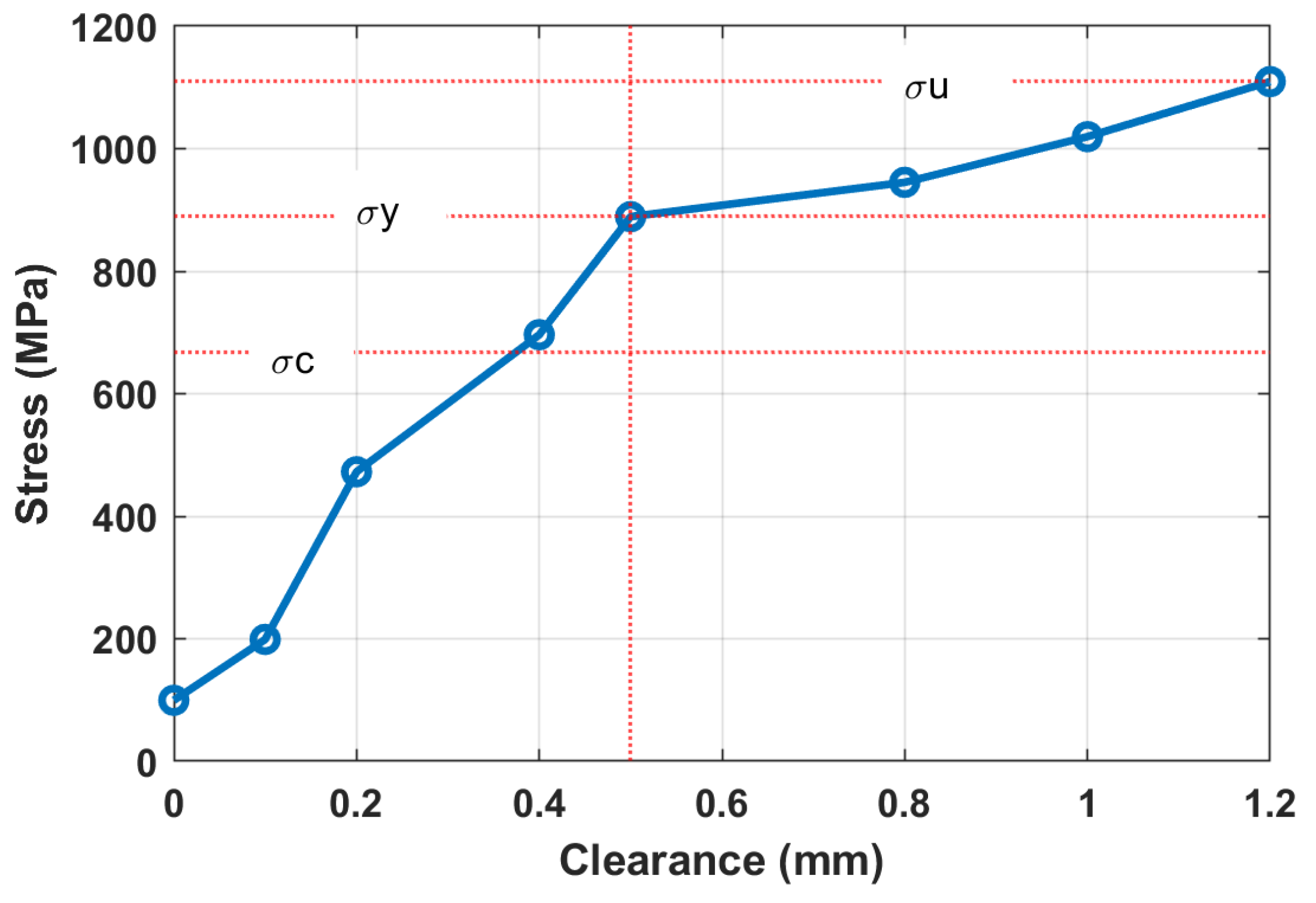

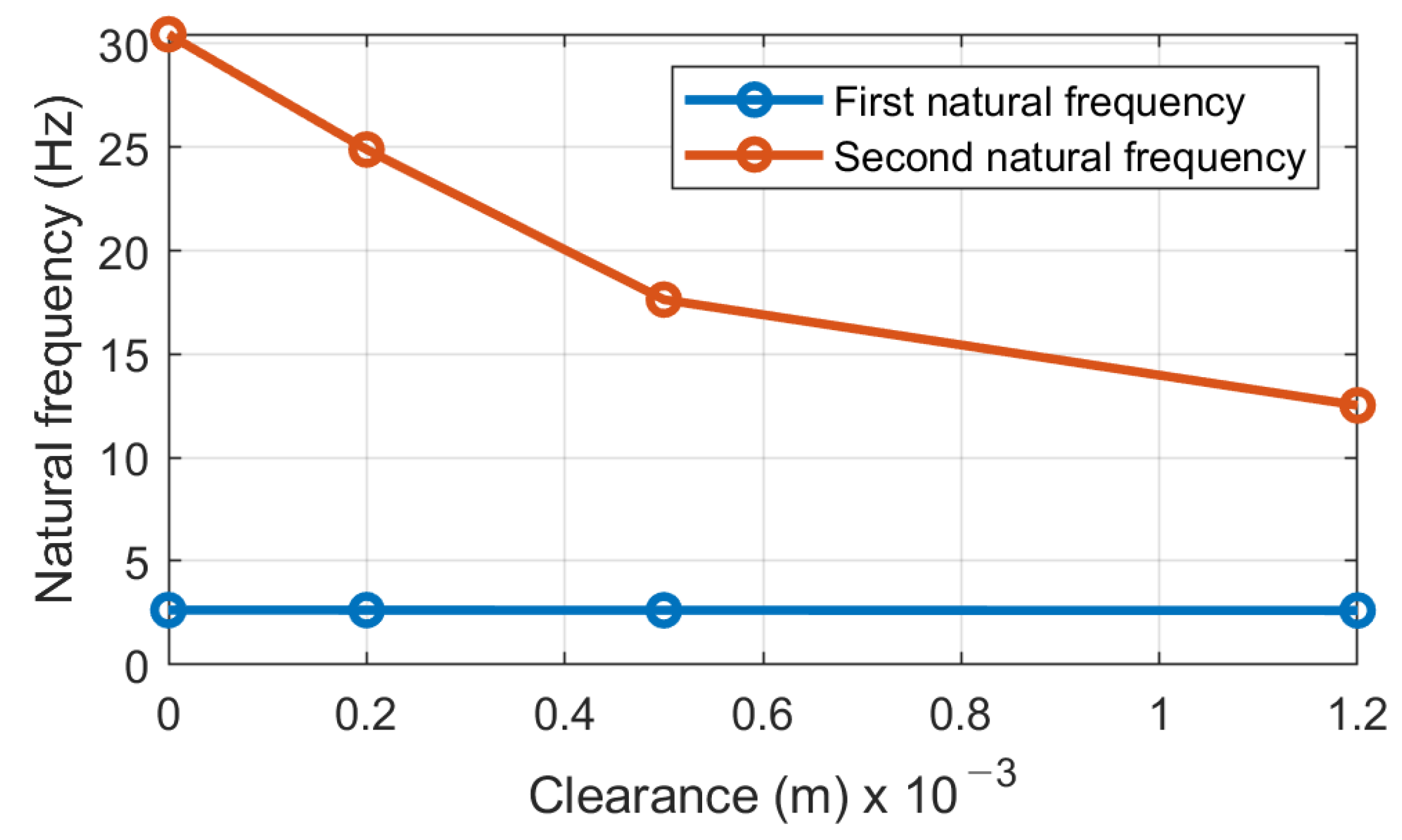
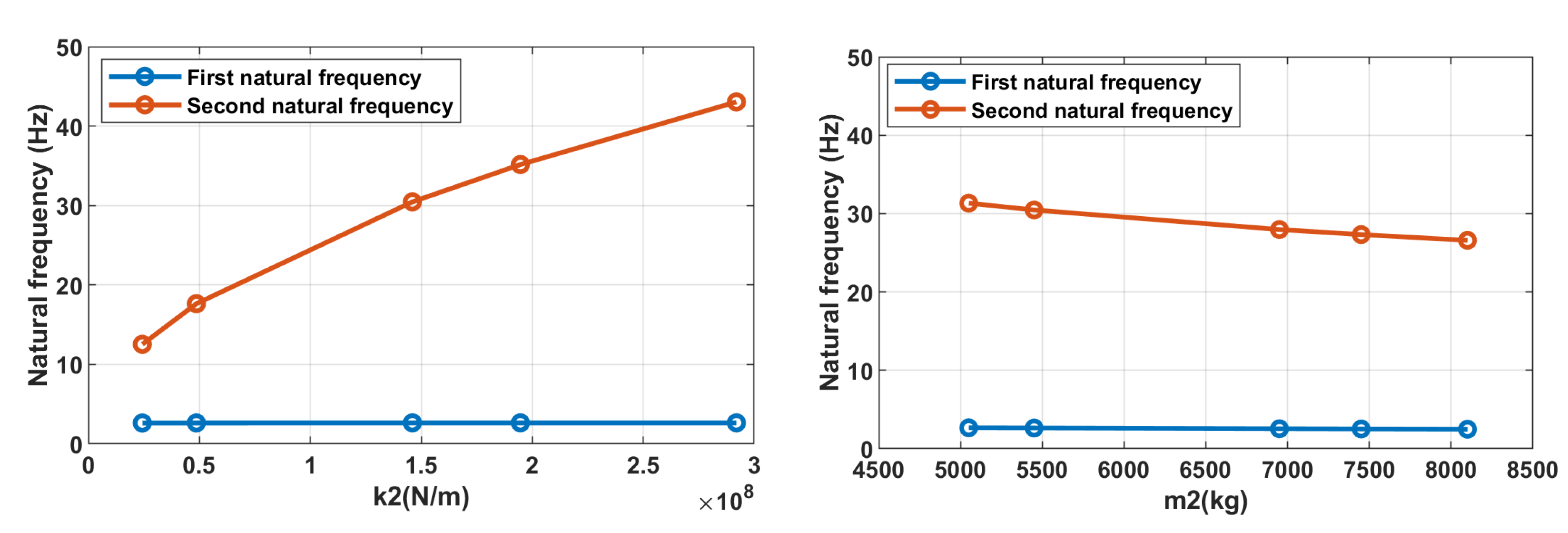
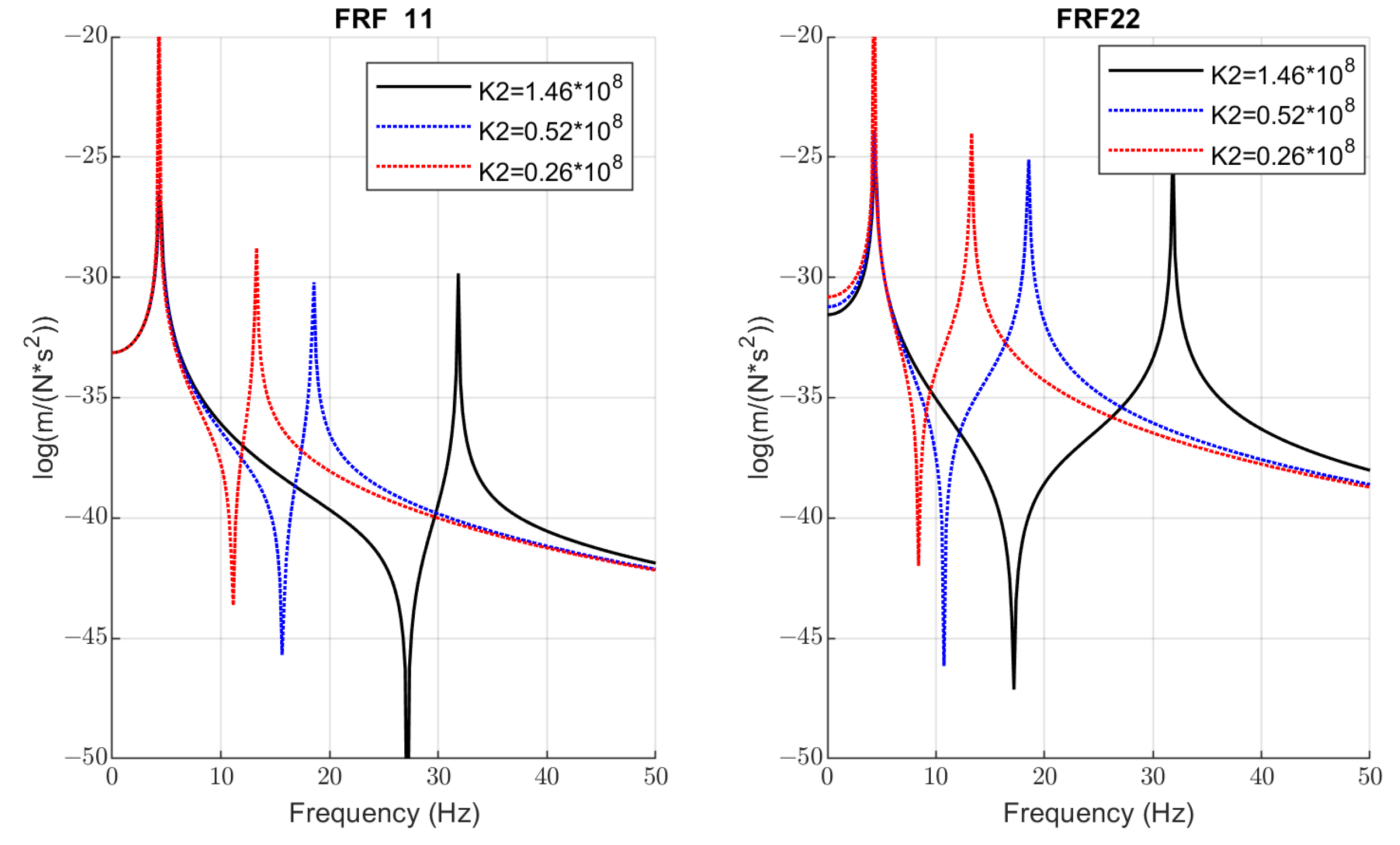






| Nr | Action | Maintenance Period | ||||
|---|---|---|---|---|---|---|
| 50 h | Week | Month | Year | 2 Years | ||
| 1 | Lubrication of vibrator bearings | |||||
| 2 | Control of sieve mounting | |||||
| 3 | Control of sieves and vibrators | |||||
| 4 | Control of springs | |||||
| 5 | Control of belt drives | |||||
| 6 | Inspection of sieve wear | |||||
| 7 | Inspection of drives | |||||
| 8 | Inspection of vibrators | |||||
| Parameter | Value | Units |
|---|---|---|
| Mass of screen body | 15,000 | kg |
| Mass of upper deck | 5450 | kg |
| Stiffness of supporting springs | N/m | |
| Stiffness of bolted joints | N/m | |
| Damping in supporting springs | 10 | s |
| Damping in bolted joints | 10 | s |
| Clearance in bolted joints | – | m |
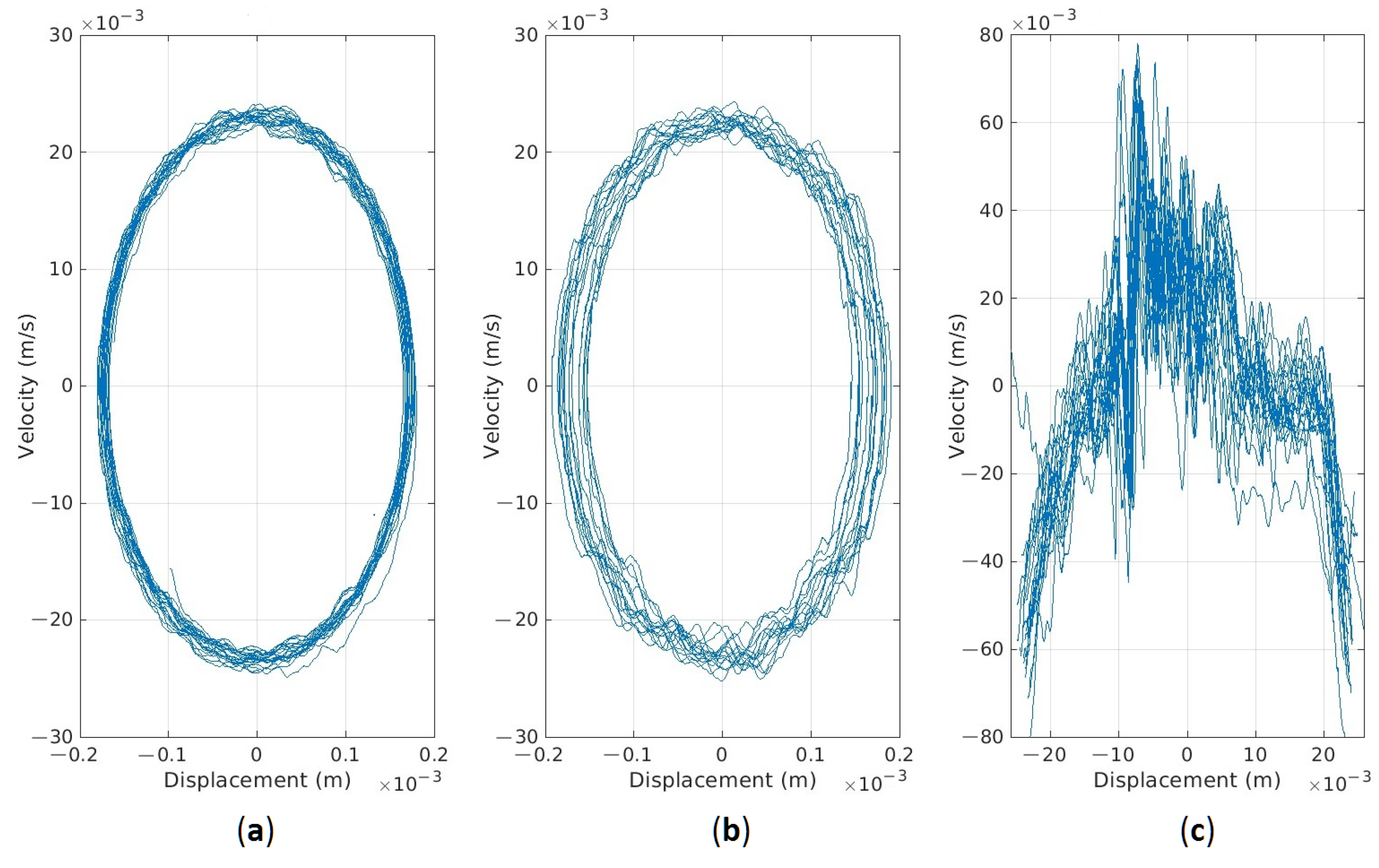
| Parameters | Case (a) | Case (b) | Case (c) |
|---|---|---|---|
| −0.18 | −0.19 | −25.68 | |
| 0.18 | 0.19 | 24.44 | |
| −24.60 | −25.14 | −79.57 | |
| 24.10 | 23.97 | 77.99 | |
| 0.36 | 0.38 | 50.12 | |
| 48.70 | 49.11 | 157.56 | |
| 17.51 | 18.82 | 7897.11 |
| Parameter | Noise1 | Noise2 | Noise3 |
|---|---|---|---|
| Alpha | 1.7 | 1.9 | 1.5 |
| Beta | 0.01 | 0.03 | 0.005 |
| Gamma | 0 | 0 | 0 |
| Delta | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krot, P.; Shiri, H.; Dąbek, P.; Zimroz, R. Diagnostics of Bolted Joints in Vibrating Screens Based on a Multi-Body Dynamical Model. Materials 2023, 16, 5794. https://doi.org/10.3390/ma16175794
Krot P, Shiri H, Dąbek P, Zimroz R. Diagnostics of Bolted Joints in Vibrating Screens Based on a Multi-Body Dynamical Model. Materials. 2023; 16(17):5794. https://doi.org/10.3390/ma16175794
Chicago/Turabian StyleKrot, Pavlo, Hamid Shiri, Przemysław Dąbek, and Radosław Zimroz. 2023. "Diagnostics of Bolted Joints in Vibrating Screens Based on a Multi-Body Dynamical Model" Materials 16, no. 17: 5794. https://doi.org/10.3390/ma16175794







