Enhanced Superconducting Critical Parameters in a New High-Entropy Alloy Nb0.34Ti0.33Zr0.14Ta0.11Hf0.08
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
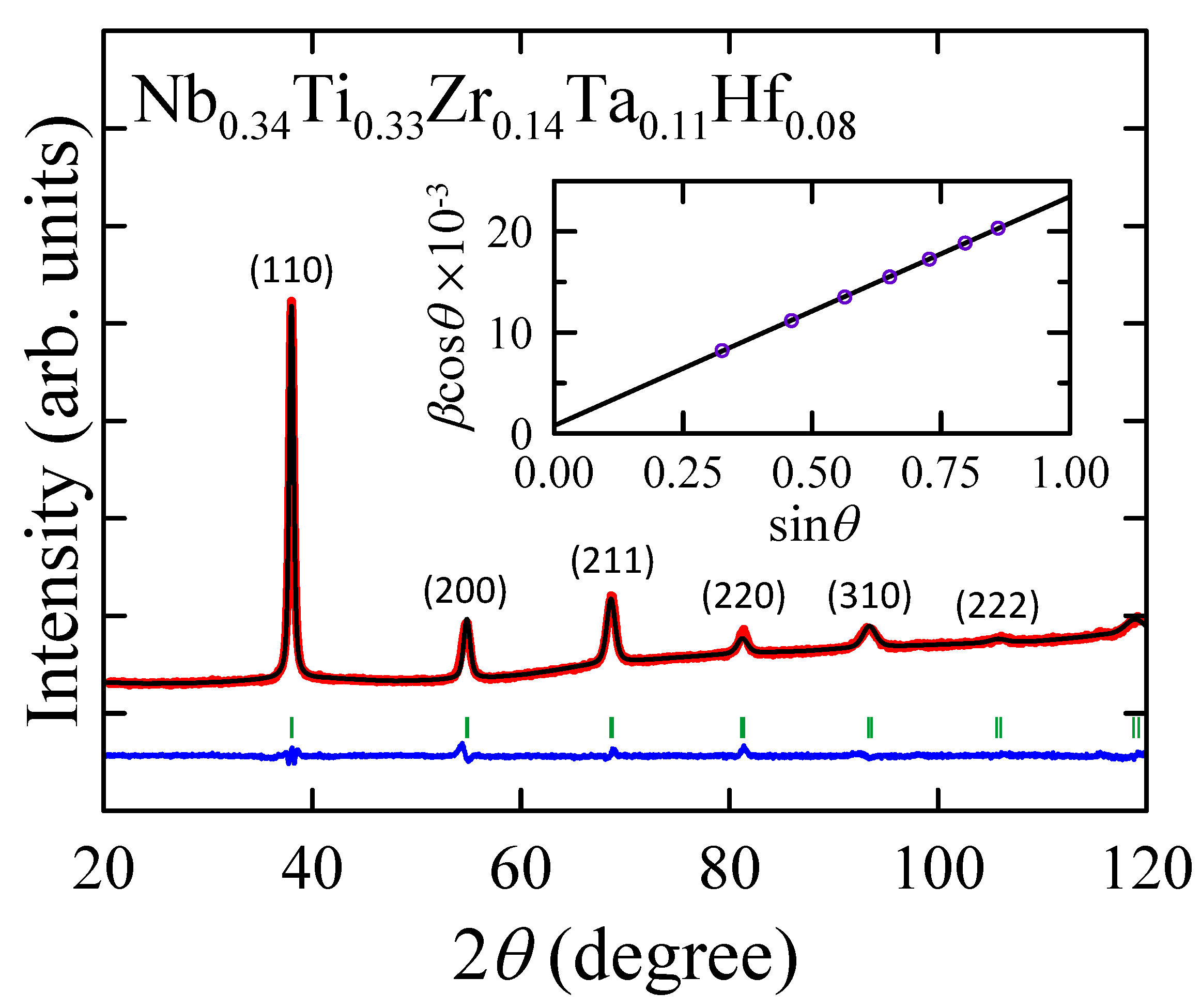
3.1. Phase Formation and Crystal Structure
3.2. Homogeneity and Chemical Composition
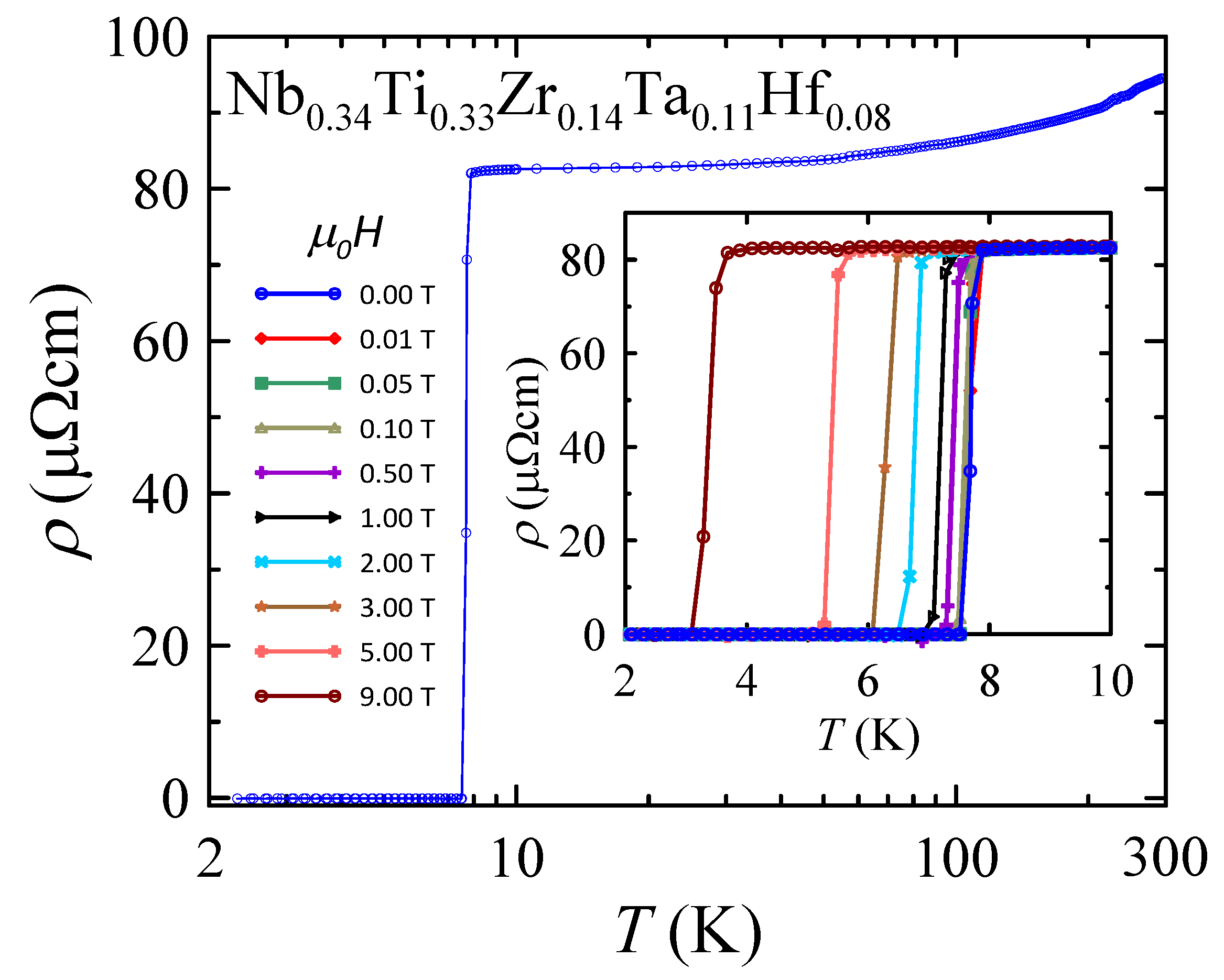
3.3. Electrical Resistivity
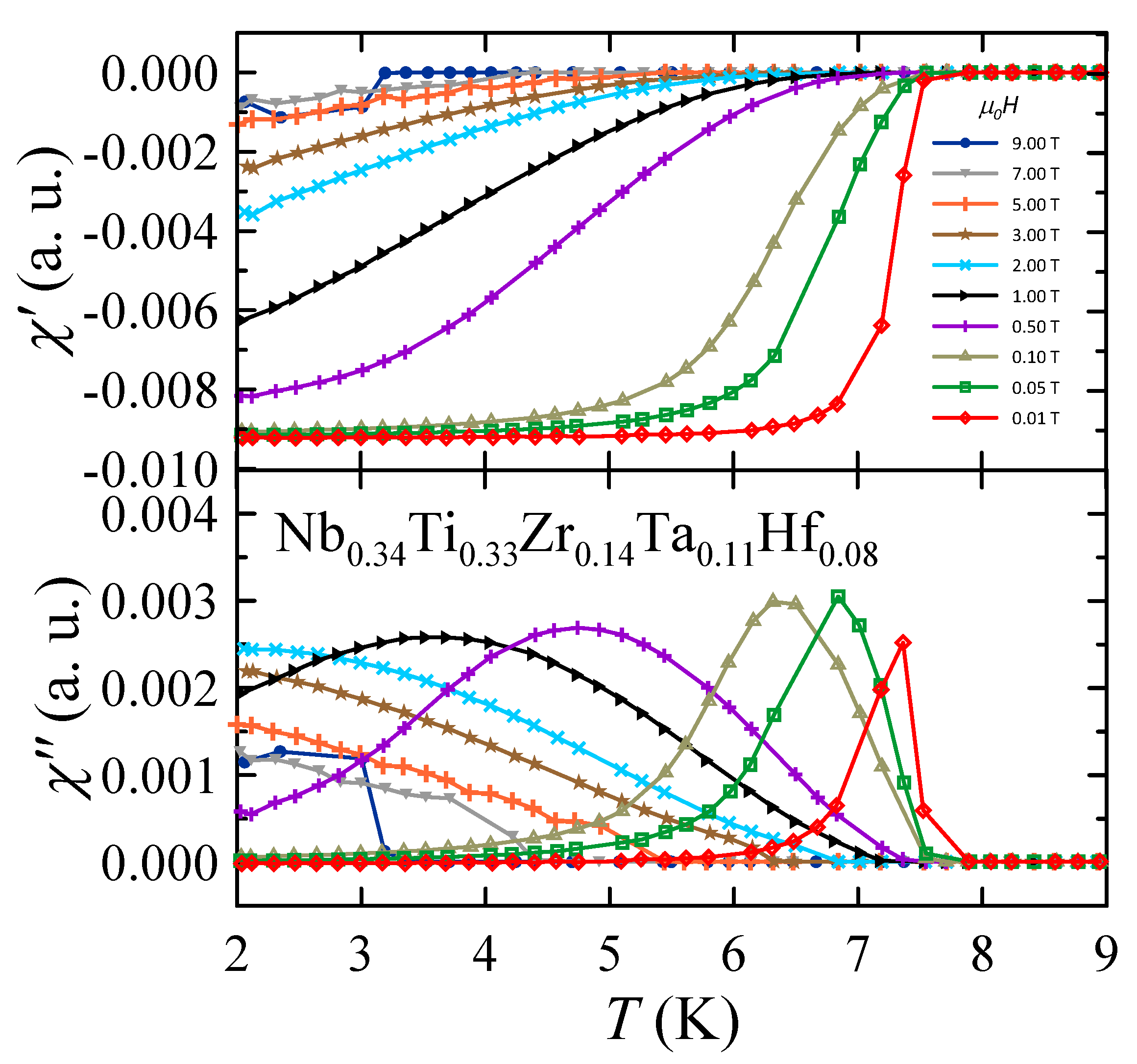
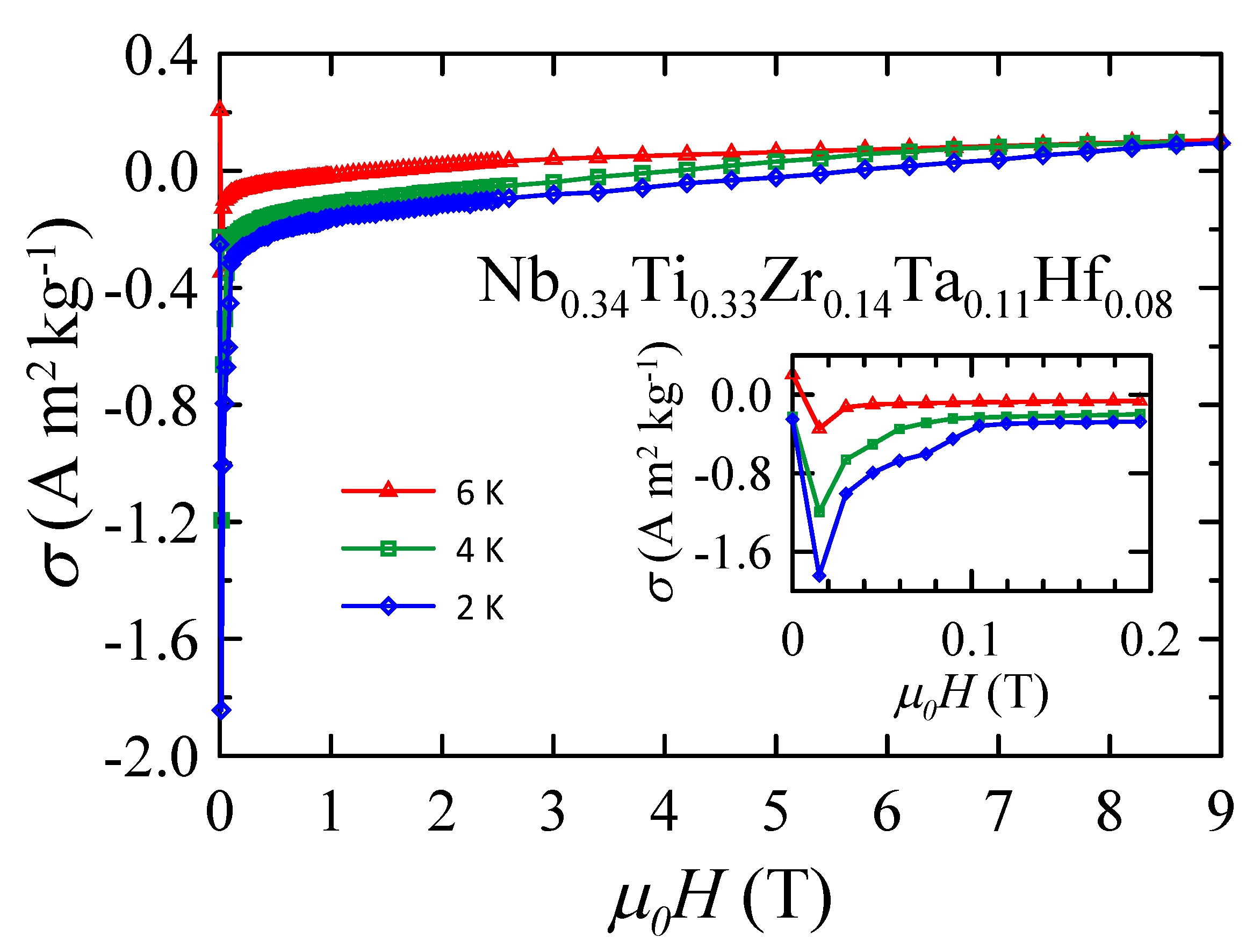
3.4. Magnetic Properties
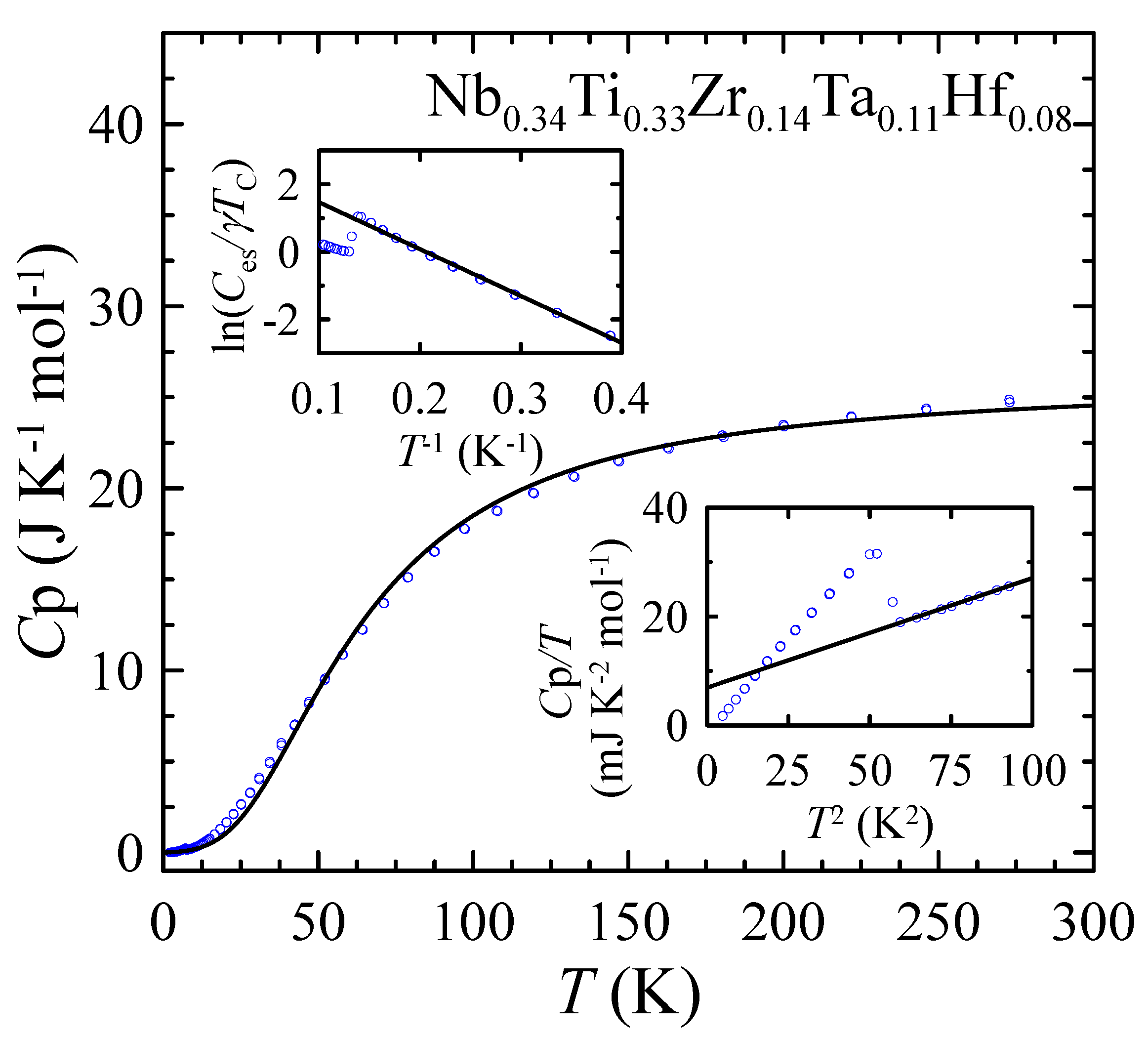
3.5. Thermodynamic Properties
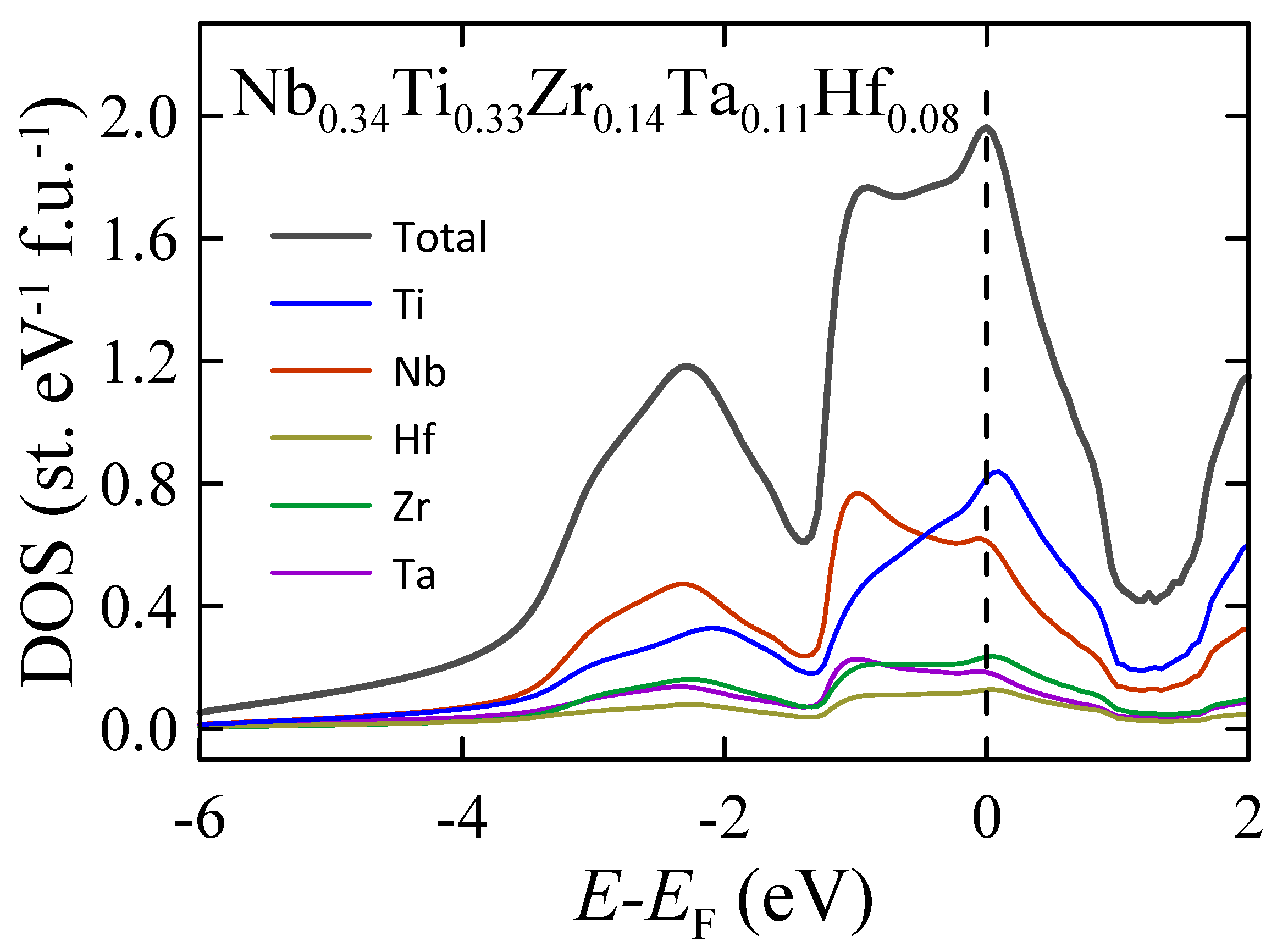
3.6. Electronic Structure Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.; Knight, P.; Vincent, A. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Pickering, E.J.; Jones, N.G. High-entropy alloys: A critical assessment of their founding principles and future prospects. Int. Mater. Rev. 2016, 61, 183–202. [Google Scholar] [CrossRef]
- Koželj, P.; Vrtnik, S.; Jelen, A.; Jazbec, S.; Jagličić, Z.; Maiti, S.; Feuerbacher, M.; Steurer, W.; Dolinšek, J. Discovery of a Superconducting High-Entropy Alloy. Phys. Rev. Lett. 2014, 113, 107001. [Google Scholar] [CrossRef]
- Sun, L.; Cava, R.J. High-entropy alloy superconductors: Status, opportunities, and challenges. Phys. Rev. Mater. 2019, 3, 090301. [Google Scholar] [CrossRef]
- Vrtnik, S.; Koželj, P.; Meden, A.; Maiti, S.; Steurer, W.; Feuerbacher, M.; Dolinšek, J. Superconductivity in thermally annealed Ta-Nb-Hf-Zr-Ti high-entropy alloys. J. Alloys Compd. 2017, 695, 3530–3540. [Google Scholar] [CrossRef]
- Yuan, Y.; Wu, Y.; Luo, H.; Wang, Z.; Liang, X.; Yang, Z.; Wang, H.; Liu, X.; Lu, Z. Superconducting Ti15Zr15Nb35Ta35 High-Entropy Alloy With Intermediate Electron-Phonon Coupling. Front. Mater. 2018, 5, 72. [Google Scholar] [CrossRef]
- von Rohr, F.O.; Cava, R.J. Isoelectronic substitutions and aluminium alloying in the Ta-Nb-Hf-Zr-Ti high-entropy alloy superconductor. Phys. Rev. Mater. 2018, 2, 034801. [Google Scholar] [CrossRef]
- Kim, G.; Lee, M.H.; Yun, J.H.; Rawat, P.; Jung, S.G.; Choi, W.; You, T.S.; Kim, S.J.; Rhyee, J.S. Strongly correlated and strongly coupled s-wave superconductivity of the high entropy alloy Ta1/6Nb2/6Hf1/6Zr1/6Ti1/6 compound. Acta Mater. 2020, 186, 250–256. [Google Scholar] [CrossRef]
- Ishizu, N.; Kitagawa, J. New high-entropy alloy superconductor Hf21Nb25Ti15V15Zr24. Results Phys. 2019, 13, 102275. [Google Scholar] [CrossRef]
- Sobota, P.; Topolnicki, R.; Ossowski, T.; Pikula, T.; Pikul, A.; Idczak, R. Superconductivity in the high-entropy alloy (NbTa)0.67(MoHfW)0.33. Phys. Rev. B 2022, 106, 184512. [Google Scholar] [CrossRef]
- Matthias, B.T.; Geballe, T.H.; Compton, V.B. Superconductivity. Rev. Mod. Phys. 1963, 35, 1–22. [Google Scholar] [CrossRef]
- Hawksworth, D.G.; Larbalestier, D.C. Enhanced Values of Hc2 in Nb-Ti Ternary and Quaternary Alloys. In Advances in Cryogenic Engineering Materials: Volume 26; Clark, A.F., Reed, R.P., Eds.; Springer: Boston, MA, USA, 1980; pp. 479–486. [Google Scholar] [CrossRef]
- Soven, P. Coherent-Potential Model of Substitutional Disordered Alloys. Phys. Rev. 1967, 156, 809–813. [Google Scholar] [CrossRef]
- Butler, W.H. Theory of electronic transport in random alloys: Korringa-Kohn-Rostoker coherent-potential approximation. Phys. Rev. B 1985, 31, 3260–3277. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Krnel, M.; Jelen, A.; Vrtnik, S.; Luzar, J.; Gačnik, D.; Koželj, P.; Wencka, M.; Meden, A.; Hu, Q.; Guo, S.; et al. The Effect of Scandium on the Structure, Microstructure and Superconductivity of Equimolar Sc-Hf-Nb-Ta-Ti-Zr Refractory High-Entropy Alloys. Materials 2022, 15, 1122. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Williamson, G.; Hall, W. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Prozorov, R.; Kogan, V.G. Effective Demagnetizing Factors of Diamagnetic Samples of Various Shapes. Phys. Rev. Appl. 2018, 10, 014030. [Google Scholar] [CrossRef]
- Gaspari, G.D.; Gyorffy, B.L. Electron-Phonon Interactions, d Resonances, and Superconductivity in Transition Metals. Phys. Rev. Lett. 1972, 28, 801–805. [Google Scholar] [CrossRef]
- Kaprzyk, S.; Bansil, A. Green’s function and a generalized Lloyd formula for the density of states in disordered muffin-tin alloys. Phys. Rev. B 1990, 42, 7358–7362. [Google Scholar] [CrossRef] [PubMed]
- Bansil, A.; Kaprzyk, S. First-principles treatment of disorder effects in complex alloys: A study of BaxK1-xBiO3 and BaPb1-xBixO3. Phys. Rev. B 1991, 43, 10335–10339. [Google Scholar] [CrossRef] [PubMed]
- Akai, H. Electronic Structure Ni–Pd Alloys Calculated by the Self-Consistent KKR-CPA Method. J. Phys. Soc. Jpn. 1982, 51, 468–474. [Google Scholar] [CrossRef]
- Akai, H. Fast Korringa-Kohn-Rostoker coherent potential approximation and its application to FCC Ni-Fe systems. J. Phys. Condens. Matter 1989, 1, 8045–8064. [Google Scholar] [CrossRef]
- Kotani, T.; Akai, H. KKR-ASA method in exact exchange-potential band-structure calculations. Phys. Rev. B 1996, 54, 16502–16514. [Google Scholar] [CrossRef]
- Perdew, J.P.; Yue, W. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800–8802. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Toby, B.H. R factors in Rietveld analysis: How good is good enough? Powder Diffr. 2006, 21, 67–70. [Google Scholar] [CrossRef]
- Vegard, L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Zeitschrift für Physik 1921, 5, 17–26. [Google Scholar] [CrossRef]
- Clem, J.R. Granular and superconducting-glass properties of the high-temperature superconductors. Phys. C Supercond. 1988, 153–155, 50–55. [Google Scholar] [CrossRef]
- Helfand, E.; Werthamer, N.R. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. II. Phys. Rev. 1966, 147, 288–294. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
- Maki, K. Effect of Pauli Paramagnetism on Magnetic Properties of High-Field Superconductors. Phys. Rev. 1966, 148, 362–369. [Google Scholar] [CrossRef]
- Godeke, A.; Cheng, D.; Dietderich, D.; Ferracin, P.; Prestemon, S.; Sabbi, G.; Scanlan, R. Limits of NbTi and Nb3Sn, and Development of W and R Bi–2212 High Field Accelerator Magnets. IEEE Trans. Appl. Supercond. 2007, 17, 1149–1152. [Google Scholar] [CrossRef]
- Clogston, A.M. Upper Limit for the Critical Field in Hard Superconductors. Phys. Rev. Lett. 1962, 9, 266–267. [Google Scholar] [CrossRef]
- Martin, C.A. Simple treatment of anharmonic effects on the specific heat. J. Phys. Condens. Matter 1991, 3, 5967. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition Temperature of Strong-Coupled Superconductors. Phys. Rev. 1968, 167, 331–344. [Google Scholar] [CrossRef]
- Parks, R. Superconductivity In Two Volumes; CRC Press: Boca Raton, FL, USA, 1969; Volume 1. [Google Scholar]
- Tinkham, M. Introduction to Superconductivity; Dover Books on Physics Series; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Orlando, T.P.; McNiff, E.J.; Foner, S.; Beasley, M.R. Critical fields, Pauli paramagnetic limiting, and material parameters of Nb3Sn and V3Si. Phys. Rev. B 1979, 19, 4545–4561. [Google Scholar] [CrossRef]
- Jasiewicz, K.; Wiendlocha, B.; Korbeń, P.; Kaprzyk, S.; Tobola, J. Superconductivity of Ta34Nb33Hf8Zr14Ti11 high entropy alloy from first principles calculations. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2016, 10, 415–419. [Google Scholar] [CrossRef]
- Jasiewicz, K.; Wiendlocha, B.; Górnicka, K.; Gofryk, K.; Gazda, M.; Klimczuk, T.; Tobola, J. Pressure effects on the electronic structure and superconductivity of (TaNb)0.67(HfZrTi)0.33 high entropy alloy. Phys. Rev. B 2019, 100, 184503. [Google Scholar] [CrossRef]
- Tari, A. The Specific Heat of Matter at Low Temperatures; Imperial College Press: London, UK, 2003. [Google Scholar]
- Carbotte, J.P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 1990, 62, 1027–1157. [Google Scholar] [CrossRef]
- Savrasov, S.Y.; Savrasov, D.Y. Electron-phonon interactions and related physical properties of metals from linear-response theory. Phys. Rev. B 1996, 54, 16487–16501. [Google Scholar] [CrossRef]
- Szcześniak, R.; Durajski, A.; Herok, L. Thermodynamic properties of antiperovskite MgCNi3 in superconducting phase. Solid State Commun. 2015, 203, 63–68. [Google Scholar] [CrossRef]
- Idczak, R.; Nowak, W.; Babij, M.; Tran, V. Type-II superconductivity in cold-rolled tantalum. Phys. Lett. A 2020, 384, 126750. [Google Scholar] [CrossRef]
- Idczak, R.; Nowak, W.; Babij, M.; Tran, V. Influence of severe plastic deformation on superconducting properties of Re and In. Phys. C Supercond. Its Appl. 2021, 590, 1353945. [Google Scholar] [CrossRef]
- Prozorov, R.; Zarea, M.; Sauls, J.A. Niobium in the clean limit: An intrinsic type-I superconductor. Phys. Rev. B 2022, 106, L180505. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Idczak, R.; Nowak, W.; Rusin, B.; Topolnicki, R.; Ossowski, T.; Babij, M.; Pikul, A. Enhanced Superconducting Critical Parameters in a New High-Entropy Alloy Nb0.34Ti0.33Zr0.14Ta0.11Hf0.08. Materials 2023, 16, 5814. https://doi.org/10.3390/ma16175814
Idczak R, Nowak W, Rusin B, Topolnicki R, Ossowski T, Babij M, Pikul A. Enhanced Superconducting Critical Parameters in a New High-Entropy Alloy Nb0.34Ti0.33Zr0.14Ta0.11Hf0.08. Materials. 2023; 16(17):5814. https://doi.org/10.3390/ma16175814
Chicago/Turabian StyleIdczak, Rafał, Wojciech Nowak, Bartosz Rusin, Rafał Topolnicki, Tomasz Ossowski, Michał Babij, and Adam Pikul. 2023. "Enhanced Superconducting Critical Parameters in a New High-Entropy Alloy Nb0.34Ti0.33Zr0.14Ta0.11Hf0.08" Materials 16, no. 17: 5814. https://doi.org/10.3390/ma16175814




