Optimal Design of Validation Experiment for Material Deterioration
Abstract
:1. Introduction
2. Validation Metric of the Degradation Model
2.1. Deterioration Modeling for Materials
2.2. Dimensionality Reduction in Deterioration Models
2.3. Normalized Area Metric
2.4. Kernel Density Estimation
3. Validation Experiment Design for Deterioration Models
3.1. Optimization Model of Validation Experiment for Deterioration Models
3.2. Design Process for Validation Experiments
- Step 1:
- Choose the minimum number of experimental samples , the number of observation instants and the observation moments .
- Step 2:
- Sampling a set of samples from the same experimental model, the number of experiments is m and .
- Step 3:
- Calculate the normalized area metric .
- Step 4:
- Repeat Steps 2–3 and calculate the credibility of the current scheme.
- Step 5:
- If , go optimize observation instants. If not, increase the number of experimental samples m = m + 1 and repeat Steps 2–5.
- Step 6:
- The number of experimental samples is obtained via Equation (15). Remove an observation moment under the current experimental sample size: .
- Step 7:
- Generate new observation moments by permutation and combination and calculate the credibility.
- Step 8:
- Calculate the credibility of each scheme.
- Step 9:
- If , continue to remove an observation moment and repeat Steps 7–9. If not, record the previous optimal scheme and go to Step 10.
- Step 10:
- Determine whether the current sample size is less than the maximum number of experimental samples . If Yes, increase the number of experimental samples m = m + 1 and go to Step 2. If No, go to Step 11.
- Step 11:
- Calculate the cost of each optimal experimental scheme and choose the best experimental scheme.
4. Results and Discussion
4.1. Mathematical Model
4.2. Cantilever Beam
4.2.1. Optimization of Validation Experiments
4.2.2. Impact of Dispersion and Observation Moments on Credibility
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |||
| degradation variable | degradation time | ||
| distance | mean value | ||
| standard deviation | normalized area metric | ||
| the area between function and x-axis | probability density function | ||
| interval number | vector of observation instants | ||
| o | number of observation instants | m | number of experimental samples |
| pre-set threshold | probability function | ||
| total cost of validation experiment | cost of an experimental sample | ||
| cost of an experimental observation | labor cost and public resource cost of a sample in a unit time | ||
| Subscript | |||
| e | experimental data | s | simulation model |
| lower bound of interval number | upper bound of interval number | ||
References
- Garnich, M.R.; Akula, V.M.K. Review of degradation models for progressive failure analysis of fiber reinforced polymer composites. Appl. Mech. Rev. 2009, 62, 010801. [Google Scholar]
- Li, S.; Chen, Z.; Liu, Q.; Shi, W.; Li, K. Modeling and Analysis of Performance Degradation Data for Reliability Assessment: A Review. IEEE Access. 2020, 8, 74648–74678. [Google Scholar]
- Iannacone, L.; Giordano, P.F.; Gardoni, P.; Limongelli, M.P. Quantifying the value of information from inspecting and monitoring engineering systems subject to gradual and shock deterioration. Struct. Health Monit. 2022, 21, 72–89. [Google Scholar]
- Huang, Q.; Gardoni, P.; Trejo, D.; Pagnotta, A. Probabilistic model for steel–concrete bond behavior in bridge columns affected by alkali silica reactions. Eng. Struct. 2014, 71, 1–11. [Google Scholar]
- Dong, W.; Liu, S.S.; Bae, J.; Cao, Y. Reliability modelling for multi-component systems subject to stochastic deterioration and generalized cumulative shock damages. Reliab. Eng. Syst. Saf. 2021, 205, 107260. [Google Scholar] [CrossRef]
- Sanchez-Silva, M.; Klutke, G.A.; Rosowsky, D.V. Life-cycle performance of structures subject to multiple deterioration mechanisms. Struct. Saf. 2011, 33, 206–217. [Google Scholar] [CrossRef]
- Jia, G.; Gardoni, P. State-dependent stochastic models: A general stochastic framework for modeling deteriorating engineering systems considering multiple deterioration processes and their interactions. Struct. Saf. 2018, 72, 99–110. [Google Scholar]
- Kumar, R.; Cline, D.; Gardoni, P. A stochastic framework to model deterioration in engineering systems. Struct. Saf. 2015, 53, 36–43. [Google Scholar] [CrossRef]
- Shen, L.; Wang, Y.; Zhai, Q.; Tang, Y. Degradation modeling using stochastic processes with random initial degradation. IEEE Trans. Reliab. 2019, 68, 1320–1329. [Google Scholar] [CrossRef]
- Peng, W.; Li, Y.; Yang, Y.; Mi, J.; Huang, H. Bayesian degradation analysis with inverse Gaussian process models under time-varying degradation rates. IEEE Trans. Reliab. 2017, 66, 84–96. [Google Scholar]
- Ni, G.; Chen, J.; Wang, H. Degradation assessment of rolling bearing towards safety based on random matrix single ring machine learning. Saf. Sci. 2019, 118, 403–408. [Google Scholar]
- Zheng, X.W.; Li, H.N.; Gardoni, P. Life-cycle probabilistic seismic risk assessment of high-rise buildings considering carbonation induced deterioration. Eng. Struct. 2021, 231, 111752. [Google Scholar]
- Li, Y.; Dong, Y.; Guo, H. Copula-based multivariate renewal model for life-cycle analysis of civil infrastructure considering multiple dependent deterioration processes. Reliab. Eng. Syst. Saf. 2023, 231, 108992. [Google Scholar]
- Moon, M.Y.; Kim, H.S.; Lee, K.; Park, B.; Choi, K.K. Uncertainty quantification and statistical model validation for an offshore jacket structure panel given limited test data and simulation model. Struct. Multidiscip. Optim. 2020, 61, 2305–2318. [Google Scholar]
- Moon, M.; Choi, K.K.; Lamb, D. Target output distribution and distribution of bias for statistical model validation given a limited number of test data. Struct. Multidiscip. Optim. 2019, 60, 1327–1353. [Google Scholar]
- Ling, Y.; Mahadevan, S. Quantitative model validation techniques: New insights. Reliab. Eng. Syst. Saf. 2013, 111, 217–231. [Google Scholar]
- Liu, Y.; Chen, W.; Arendt, P.; Huang, H.Z. Toward a better understanding of model validation metrics. J. Mech. Des. 2011, 133, 071005. [Google Scholar]
- Hernandez, W.P.; Castello, D.A.; Roitman, N.; Magluta, C. Thermorheologically simple materials: A bayesian framework for model calibration and validation. J. Sound. Vib. 2017, 402, 14–30. [Google Scholar]
- Ferson, S.; Oberkampf, W.L.; Ginzburg, L. Model validation and predictive capability for the thermal challenge problem. Comput. Method. Appl. M. 2008, 197, 2408–2430. [Google Scholar]
- Yang, C.B.; Zeng, S.K.; Guo, J.B. Validation metric of degradation model with dynamic performance. J. Shanghai Jiaotong Univ. 2015, 20, 302–306. [Google Scholar] [CrossRef]
- Zhan, Z.F.; Fu, Y.; Yang, R.J.; Peng, Y.H. An enhanced Bayesian based model validation method for dynamic systems. J. Mech. Des. 2011, 133, 041005. [Google Scholar]
- Xi, Z.M.; Pan, H.; Fu, Y.; Yang, R.J. Validation metric for dynamic system responses under uncertainty. SAE Int. J. Mater. Manuf. 2015, 8, 309–314. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Fu, Y.; Yang, R.J.; Barbat, S.; Chen, W. Validating dynamic engineering models under uncertainty. J. Mech. Des. 2016, 138, 111402. [Google Scholar]
- Atkinson, A.D.; Hill, R.R.; Pignatiello, J.; Vining, G.; White, T.; Chicken, E. Dynamic model validation metric based on wavelet thresholded signals. J. Verif. Valid. Uncertain. Quantif. 2017, 2, 021002. [Google Scholar]
- Lee, G.; Kim, W.; Oh, H.; Youn, B.D.; Kim, N.H. Review of statistical model calibration and validation-from the perspective of uncertainty structures. Struct. Multidiscip. Optim. 2019, 60, 1619–1644. [Google Scholar]
- Yondo, R.; Andrés, E.; Valero, E. A review on design of experiments and surrogate models in aircraft real-time and many-query aerodynamic analyses. Prog. Aerosp. Sci. 2018, 96, 23–61. [Google Scholar]
- Beng, W.C.; Rokiah, O.; Ramadhansyah, P.J.; Mohd, R.M.H.; Andrei, V.S.; Marcin, N.; Bartłomiej, J.; Paweł, P.; Dariusz, K.; Przemysław, P.; et al. Design of experiment on concrete mechanical properties prediction: A critical review. Materials. 2021, 14, 1866. [Google Scholar]
- Huan, X.; Marzouk, Y. Gradient-based stochastic optimization methods in Bayesian experimental design. Int. J. Uncertain. Quantif. 2014, 4, 479–510. [Google Scholar] [CrossRef]
- Jiang, X.; Mahadevan, S. Bayesian cross-entropy methodology for optimal design of validation experiments. Meas. Sci. Technol. 2006, 17, 1895–1908. [Google Scholar] [CrossRef]
- Ao, D.; Hu, Z.; Mahadevan, S. Design of validation experiments for life prediction models. Reliab. Eng. Syst. Saf. 2017, 165, 22–33. [Google Scholar]



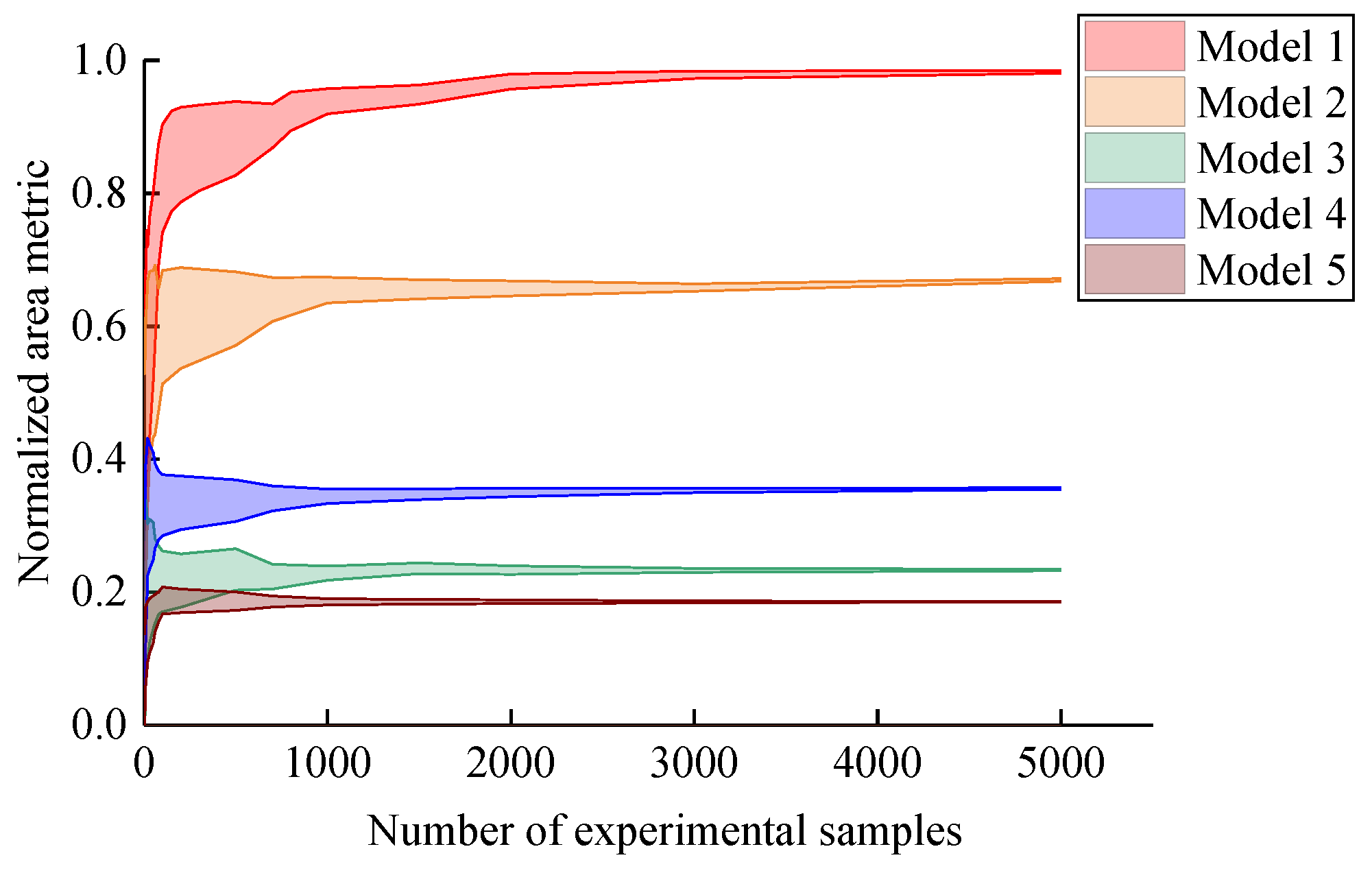




| Validation Metric | ||||
| validation result | worst | moderate | good | excellent |
| Model 1 | 1 | 1 | |
| Model 2 | 1.2 | 1 | |
| Model 3 | 1 | 1 | |
| Model 4 | 1 | 2 | |
| Model 5 | 1.2 | 2 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.75 | 80% | ||
| $16 | $2/year | ||
| $20.5 |
| Scheme | Number of Experimental Samples | Reduced Number of Observations | Total Cost | P |
|---|---|---|---|---|
| 1 | 65 | 0 | $59,540 | 80.4% |
| 2 | 66 | 0 | $60,456 | 80.9% |
| 3 | 66 | 1 (32nd year) | $59,103 | 80.1% |
| Reduced Number of Observation Moments | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 80.9% | 80.1% | 66.8% | 53.4% | 35.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Sun, D.; Liang, X. Optimal Design of Validation Experiment for Material Deterioration. Materials 2023, 16, 5854. https://doi.org/10.3390/ma16175854
Song X, Sun D, Liang X. Optimal Design of Validation Experiment for Material Deterioration. Materials. 2023; 16(17):5854. https://doi.org/10.3390/ma16175854
Chicago/Turabian StyleSong, Xiangrong, Dongyang Sun, and Xuefeng Liang. 2023. "Optimal Design of Validation Experiment for Material Deterioration" Materials 16, no. 17: 5854. https://doi.org/10.3390/ma16175854
APA StyleSong, X., Sun, D., & Liang, X. (2023). Optimal Design of Validation Experiment for Material Deterioration. Materials, 16(17), 5854. https://doi.org/10.3390/ma16175854





