Research on the Flexural Performance of Steel Pipe Steel Slag Powder Ultra-High-Performance Concrete Components
Abstract
:1. Introduction
2. Experiment Overview
2.1. Experimental Design
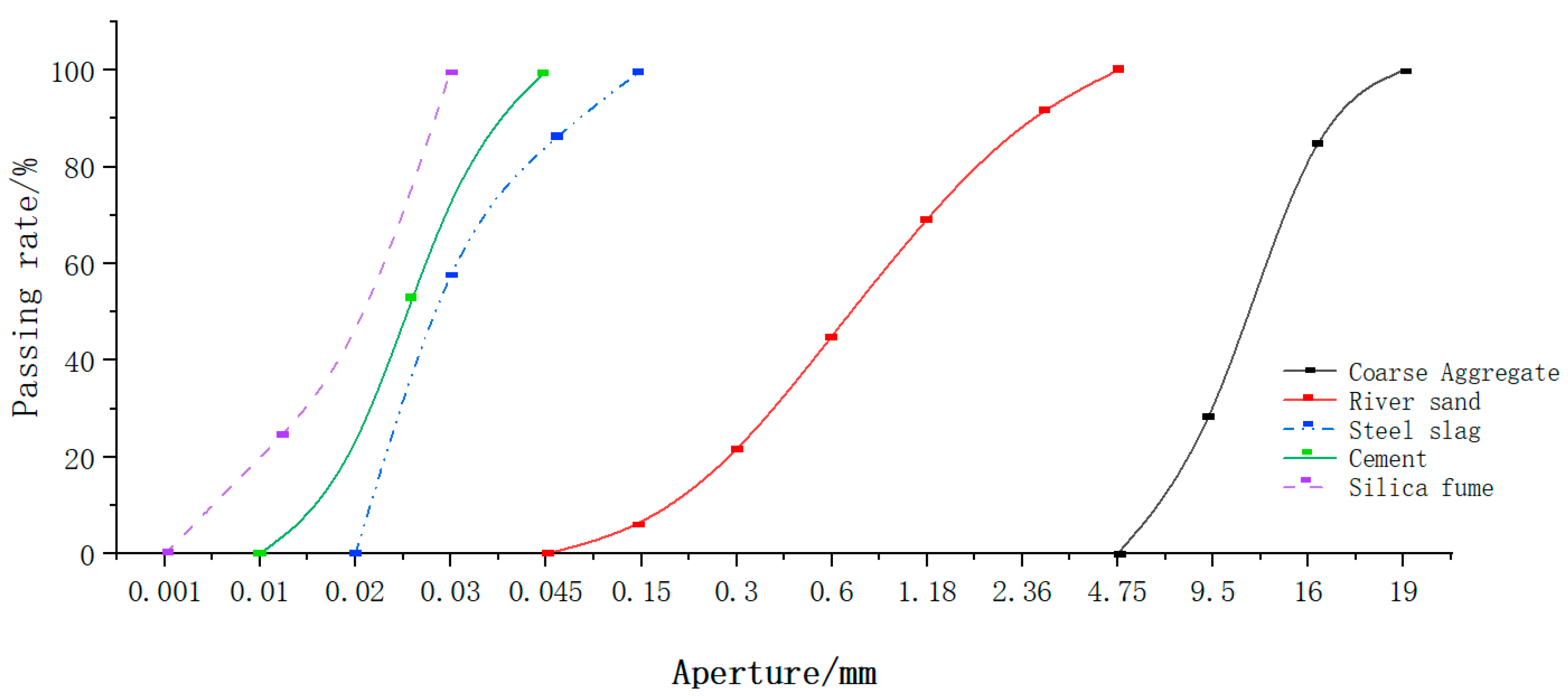
2.2. Test Piece Fabrication
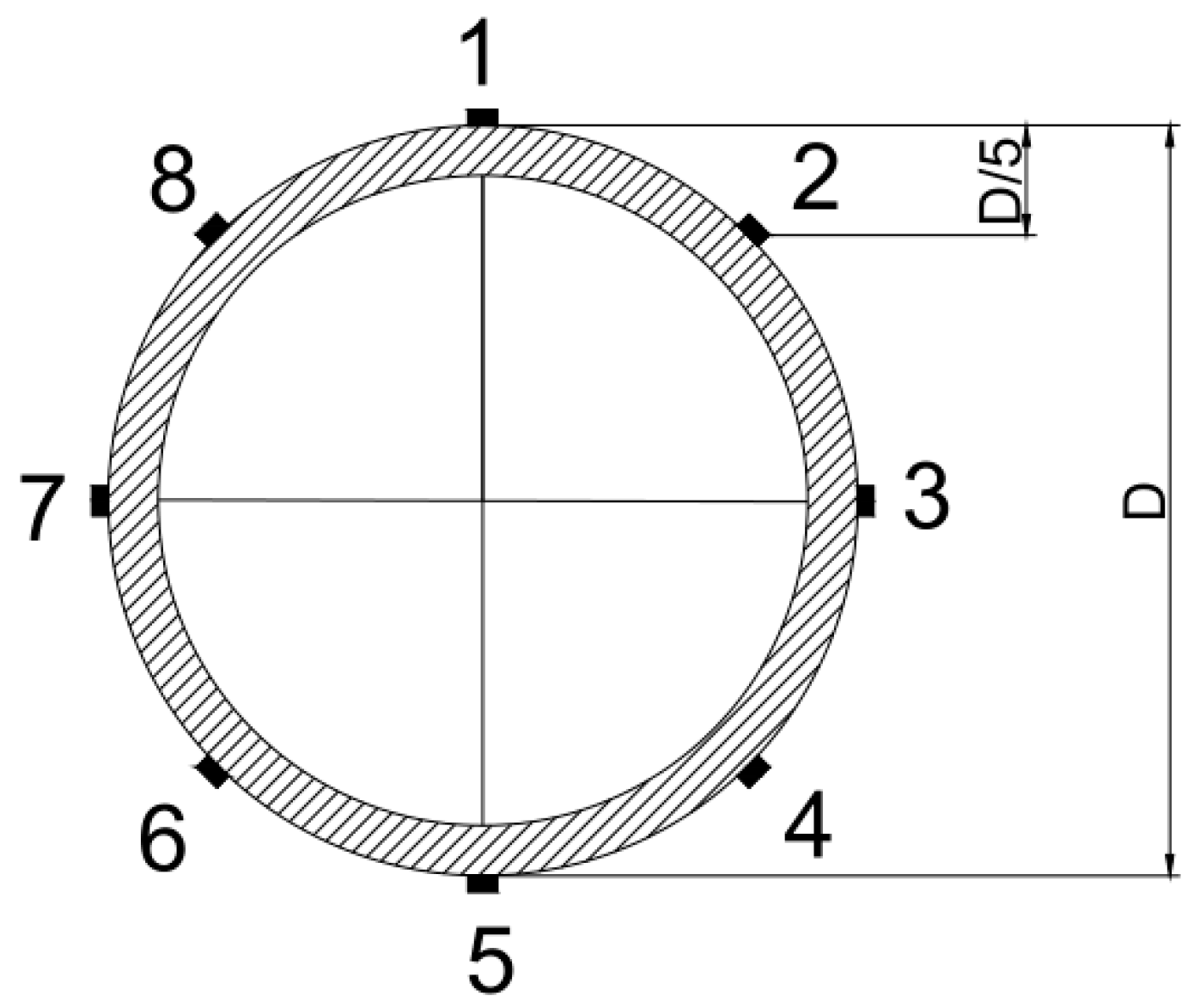
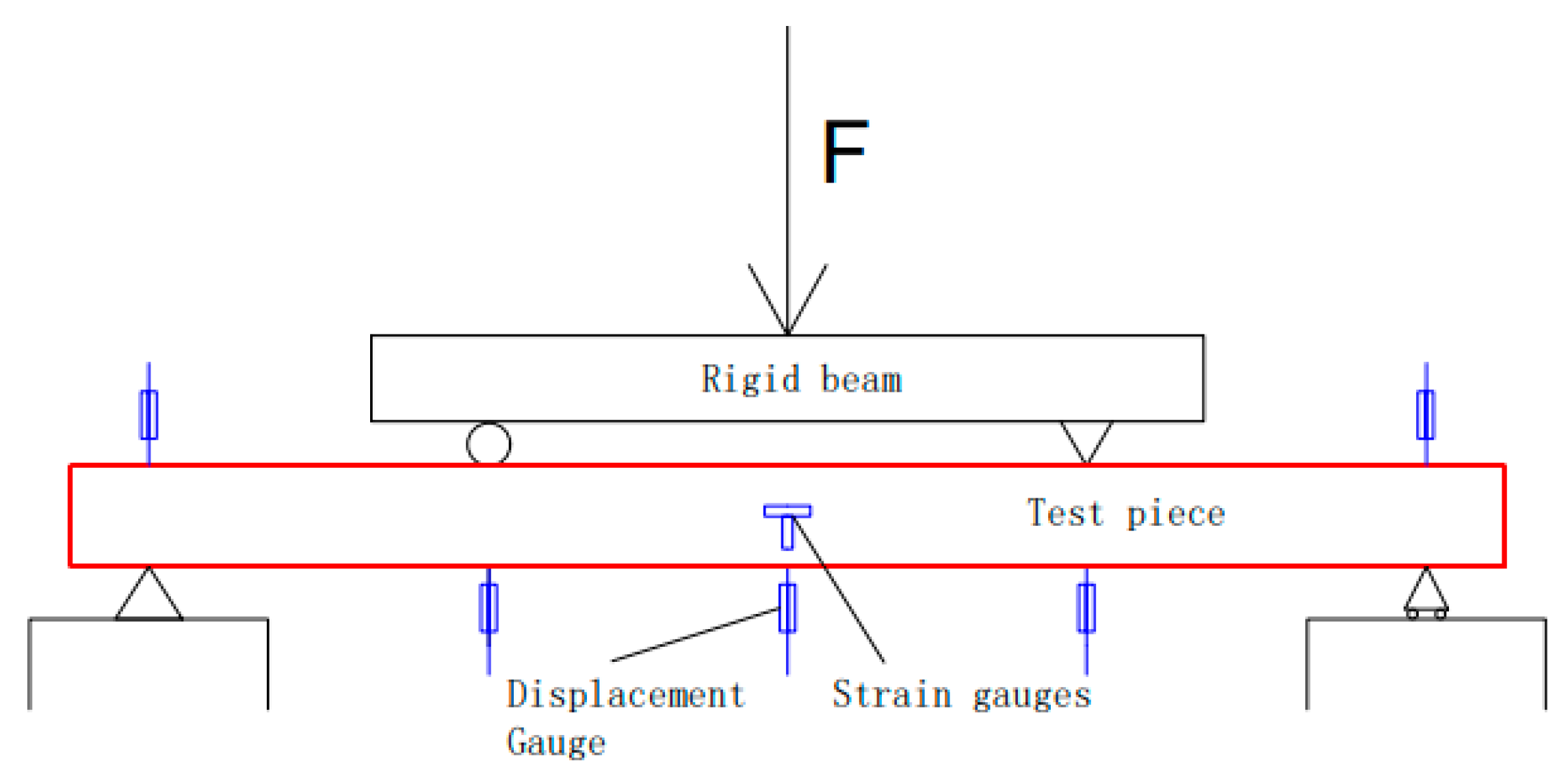
2.3. Measurement Point Arrangement and Loading System
3. Experimental Results and Analysis
3.1. Destruction Phenomenon
3.2. Load Deflection Curve
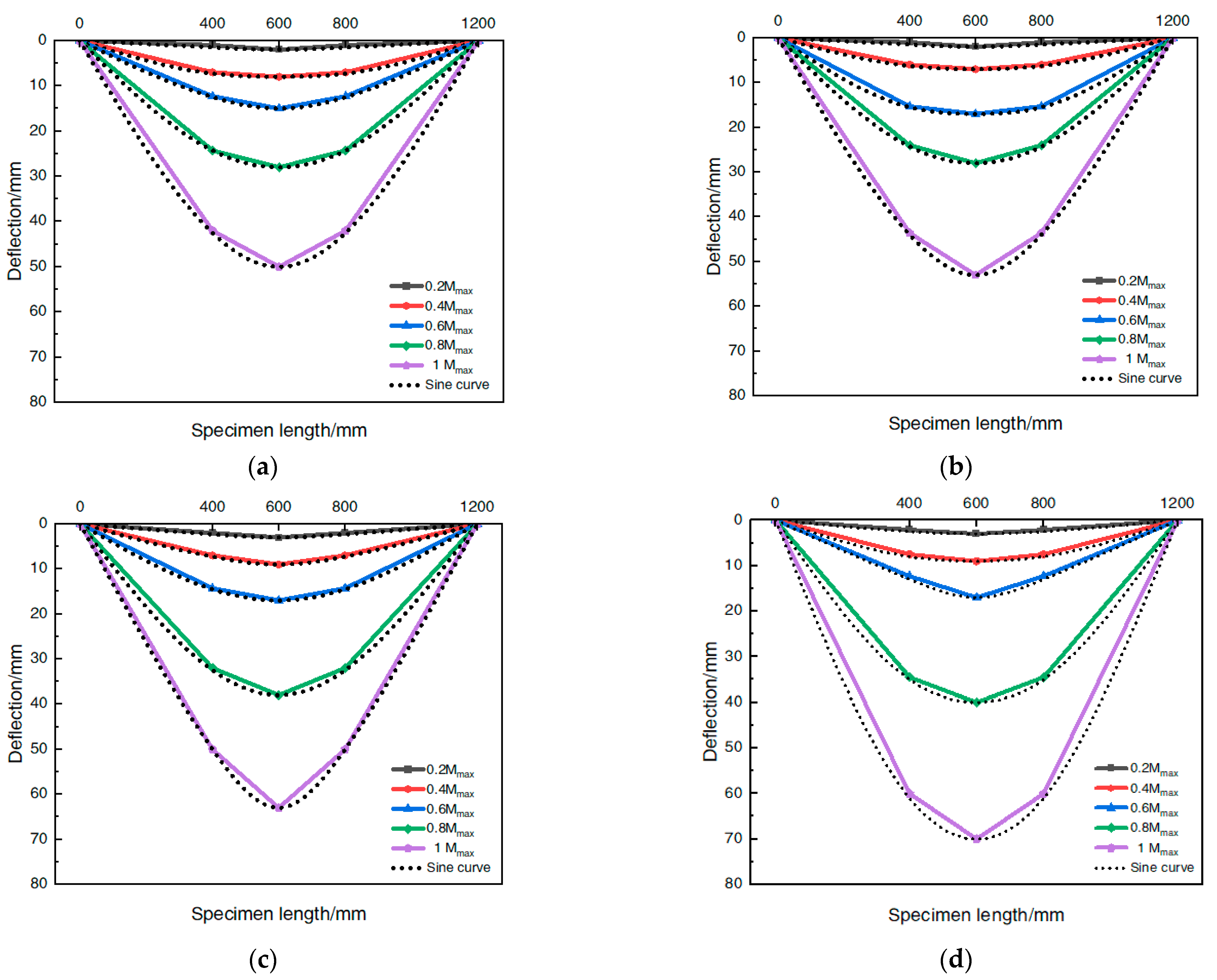
3.3. Deflection Distribution Curve
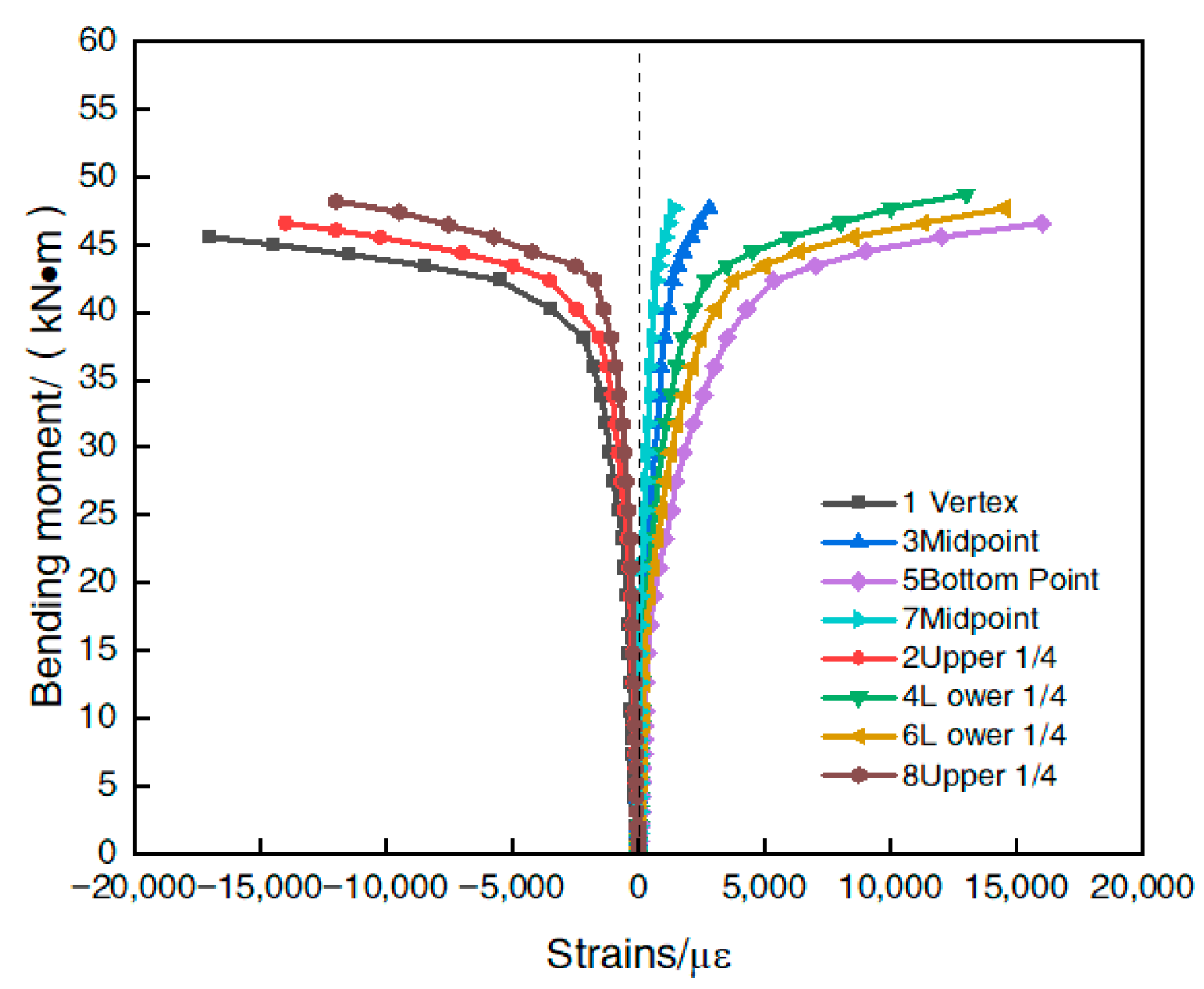
3.4. Bending Moment–Deflection Curve
4. Finite Element Analysis
4.1. Model Building
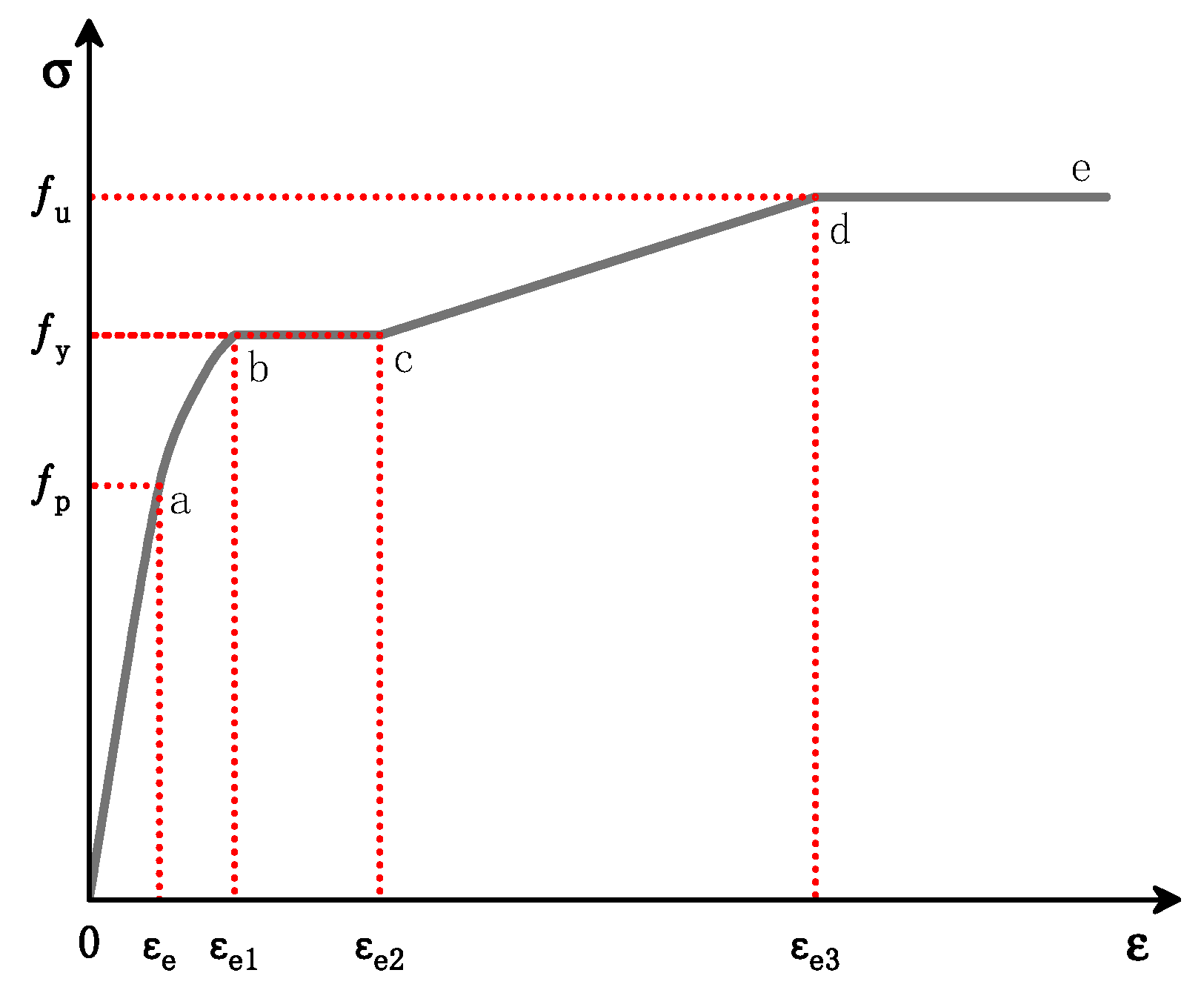
4.1.1. Steel Principal Structure Relationship Model
4.1.2. Steel-Pipe–Steel-Slag-Powder-UHPC Intrinsic Structure Relationship Model
4.2. Model Validation
4.2.1. Destruction Form
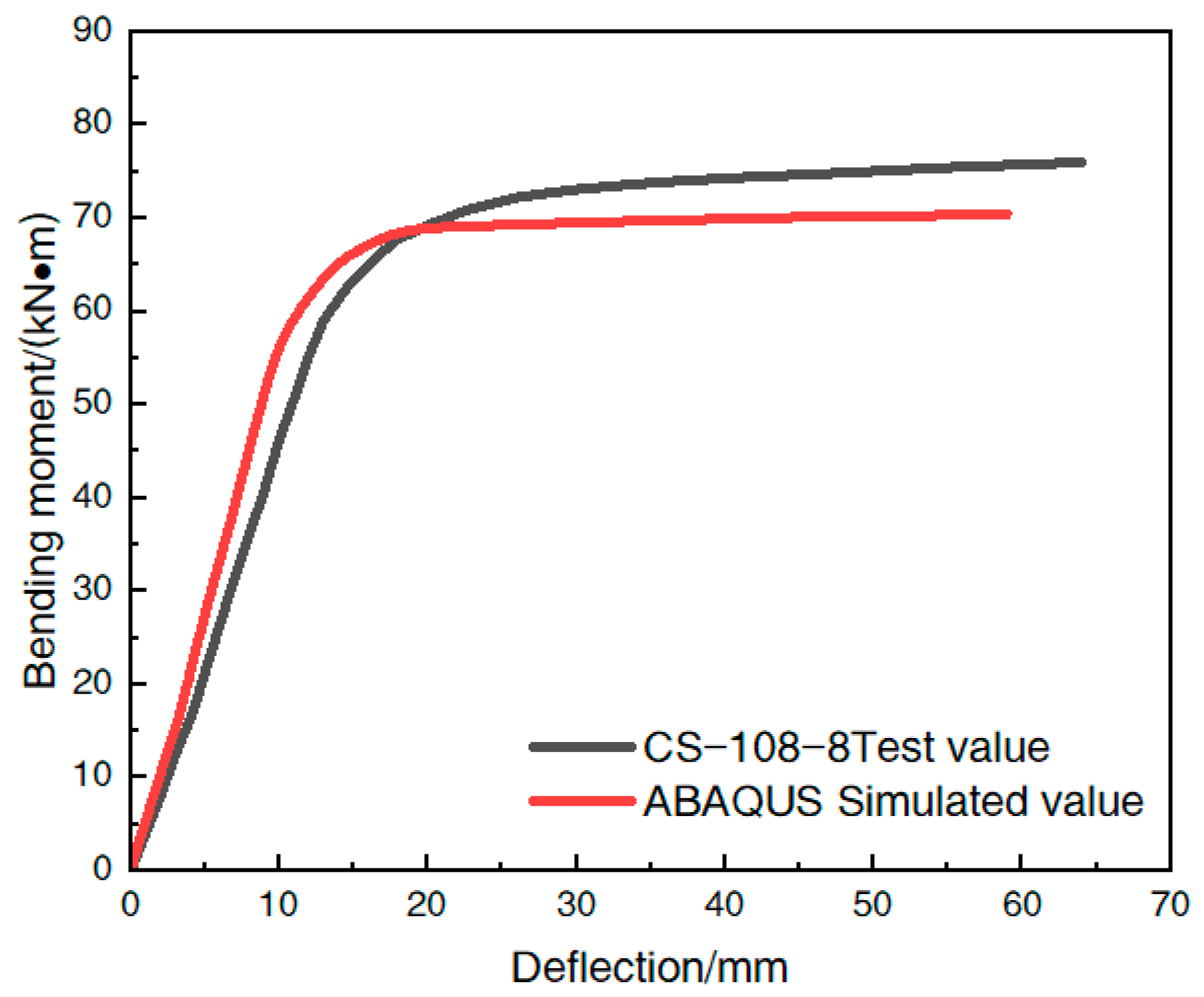
4.2.2. Bending Moment–Deflection Curve
4.2.3. Flexural Bearing Capacity
4.3. Analysis of the Simulation Parameters
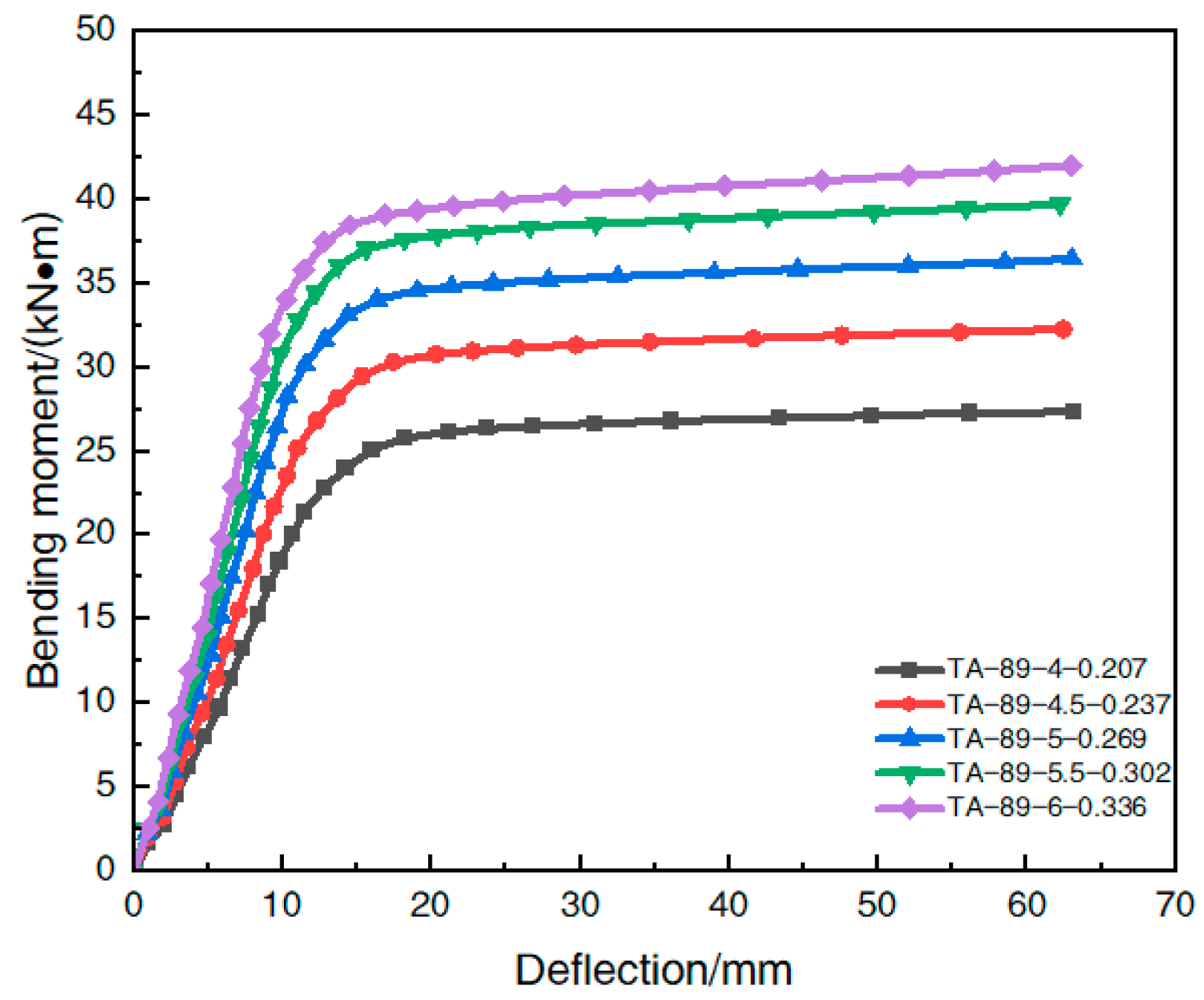
4.3.1. Change in the Steel Content
4.3.2. Change in the Yield Strength of Steel
4.3.3. Strength Variation in the UHPC with the Inside-Filling Steel-Slag Powder
5. Conclusions
- (1)
- All types of the steel-tube-steel-slag-powder-UHPC beams were subject to “bow damage” during loading, and the deflection distribution curve basically conformed to the variation law of the sinusoidal half-wave function, showing good ductility. The deflection distribution curves of the same cross-sectional members were basically the same, and there was no significant change due to the change of the in-fill steel-slag-powder–UHPC ratio, which indicates that the influence of the in-fill material type on the deflection distribution of the members is relatively small.
- (2)
- The shapes of the moment–deflection curves of the steel-tube-steel-slag-powder-UHPC beams were basically similar, and they could all be divided into an elastic phase, an elasto-plastic phase, and a strengthening phase. When the cross-sectional deflection reached L/30, the external load acting on the specimen continued to increase, indicating that the steel-tube-steel-slag-powder-UHPC beams had a good plastic deformation capacity with later flexural bearing capacity.
- (3)
- The type of steel pipe had a significant effect on the flexural bearing capacity of the steel-tube-steel-slag-powder-UHPC beams; the larger the diameter of the steel pipe section and the thicker the wall, the higher the flexural bearing capacity. The amount of steel fiber admixture also had a certain degree of influence on the flexural load-bearing capacity. The admixture of steel fiber played a role in hindering the cracking and crack development of the UHPC, which effectively improved the flexural load-bearing capacity of the steel-pipe–UHPC beam. The amount of coarse aggregate and the length of the high-temperature maintenance had less influence on the flexural load-bearing capacity of the steel-pipe–UHPC beams, and the ecological steel-pipe–UHPC with coarse aggregate can be prepared when the proportion of coarse aggregate dosing is low.
- (4)
- The steel-tube-steel-slag-powder-UHPC beams established by the finite element software matched well with the bending moment–deflection curves of the corresponding test members, and the calculated ultimate flexural bearing capacity and the test results had a stable error between 5.6% and 11.2%, which indicates that the model was reasonably established; so, the finite element method can be used for simulation analysis under the restricted test conditions.
- (5)
- The finite element calculation analysis showed that the change in the steel content rate had a significant effect on the initial flexural stiffness and ultimate flexural bearing capacity of the beam; when the steel content rate increased, the initial flexural stiffness and ultimate flexural bearing capacity of the member increased significantly; the yield strength of steel had a small effect on the flexural stiffness of the steel-tube–steel-slag powder-UHPC beams in the initial and use stages but had a significant effect on the ultimate flexural bearing capacity; and the change in the in-fill UHPC strength had a small effect on the flexural bearing capacity of the beam. The change in the UHPC strength had less effect on the flexural load-bearing capacity of the beam, and the appropriate reduction in the strength of the in-fill UHPC can be considered in an actual project to reduce the construction cost.
- (6)
- Compared with traditional steel pipe concrete, steel-tube-steel-slag-powder-UHPC beam has high toughness, high elasticity, low shrinkage, and other excellent performance, which can effectively reduce the impact of the difference between the performance of steel and concrete materials. At the same time, steel slag micronized powder UHPC for industrial solid waste reuse, adding coarse aggregate, can reduce its preparation costs, provide economic and environmental protection, and save green energy. The next step should be to deepen the steel-tube-steel-slag-powder-UHPC beam material’s structural integration research in order to promote the steel pipe concrete material’s lightweight, high performance, and green sustainable development and improve its application performance and use range.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, B.C.; Ji, T.; Huang, Q.W.; Wu, H.Z.; Ding, Q.J.; Zhan, Y.W. A review of ultra-high performance concrete research. J. Build. Sci. Eng. 2014, 31, 1–24. [Google Scholar]
- Shao, X.D.; Qiu, M.H.; Yan, B.F.; Luo, J. Progress of research and application of ultra-high performance concrete in bridge engineering at home and abroad. Mater. Guide 2017, 31, 33–43. [Google Scholar]
- Azreen, N.M.; Raizal, R.; Mugahed, A.; Voo, Y.L.; Haniza, M.; Hairie, M.; Rayed, A.; Hisham, A. Simulation of ultra-high-performance concrete mixed with hematite and barite aggregates using Monte Carlo for dry cask storage. Constr. Build. Mater. 2020, 263, 120161. [Google Scholar] [CrossRef]
- Mou, T.M.; Fan, B.K.; Zhao, Y.C.; Li, S. Application and development of steel pipe concrete bridges in China. Highway 2017, 62, 161–165. [Google Scholar]
- Chang, J.; Xu, Y.F.; Xiao, J.; Wang, L.; Jiang, J.Q.; Guo, J.X. Influence of acid rain climate environment on deterioration of shear strength parameters of Natural residual expansive soil. Transp. Geotech. 2023, 40, 101017. [Google Scholar] [CrossRef]
- Liu, Y.J.; Sun, L.P.; Zhou, X.H.; Peng, J.P.; Zhang, N.; Li, H. Advances in engineering applications and research of steel pipe concrete bridge towers. Chin. J. Highw. 2022, 35, 1–21. [Google Scholar]
- Tu, C.L.; Shi, Y.J.; Liu, D. Calculation method for axial compression load capacity of high-strength steel pipe concrete columns. Adv. Build. Steel Struct. 2020, 22, 99–107. [Google Scholar]
- Chen, B.C.; Wei, J.G.; Su, J.Z.; Huang, W.; Chen, Y.C.; Huang, Q.W.; Chen, Z.H. Advances in the application of ultra-high performance concrete. J. Build. Sci. Eng. 2019, 36, 10–20. [Google Scholar]
- Hu, H.W.; Vizzari, D.; Zha, X.D.; Mantalovas, K. A comparison of solar and conventional pavements via life cycle assessment. Transp. Res. Part D Transp. Environ. 2023, 119, 103750. [Google Scholar] [CrossRef]
- Chang, J.; Li, J.; Hu, H.W.; Qian, J.; Yu, M. Numerical investigation of aggregate segregation of superpave gyratory compaction and its influence on mechanical properties of asphalt mixtures. J. Mater. Civ. Eng. 2023, 35, 04022453. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Yang, X.; Zhang, A.; Yu, M. Monte Carlo simulations of deformation behaviour of unbound granular materials based on a real aggregate library. Int. J. Pavement Eng. 2023, 24, 2165650. [Google Scholar] [CrossRef]
- Fu, Z.D.; Lv, L.N.; Xiao, J.; He, Y.J.; Shen, P.L. The effect of CSA expansion agent on the properties of ultra-high performance concrete. J. Mater. Sci. Eng. 2019, 37, 559–564. [Google Scholar]
- Wang, Z.; Wang, J.Q.; Liu, T.X.; Xiu, H.L. Calculation model of axial compression bearing capacity and deformation capacity of short UHPC columns with round steel tubes. J. Cent. South Univ. 2019, 50, 428–436. [Google Scholar]
- Lu, Q.R.; Xu, L.H.; Ji, Y.; Yu, M.; Yang, Y.X. A compressive principal structure model for steel tube-confined ultra-high performance concrete. J. Silic. 2020, 48, 1201–1211. [Google Scholar]
- Tang, J.J.; Wang, T.; Li, J.Y. Orthogonal analysis of axial compression load capacity of short columns of round steel pipes with ultra-high performance concrete containing coarse aggregates. People’s Pearl River 2021, 42, 52–56. [Google Scholar]
- Zhou, X.J.; Mou, T.M.; Tang, H.Y.; Fan, B.K. Experimental Study on Ultrahigh Strength Concrete Filled Steel Tube Short Columns under Axial Load. Adv. Mater. Sci. Eng. 2017, 2017, 8410895. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Liu, A.R.; Zeng, X.B.; Fu, J.Y.; Huang, Y.H. Study on the load-bearing capacity of high-strength steel tube-ultra-high-performance concrete arch. J. Build. Struct. 2021, 42, 365–372. [Google Scholar]
- Wei, J.G.; Luo, X.; Chen, B.C.; Lv, J.Y. Study on the flexural performance of round high-strength steel tube UHPC beams. Eng. Mech. 2021, 38, 183–194. [Google Scholar]
- Deng, Z.C.; Sun, T.; Li, J.Y. Study on the flexural performance of high-strength steel tube restrained ultra-high performance concrete beams. J. Tianjin Univ. 2021, 54, 1111–1120. [Google Scholar]
- Huang, W.R.; Yang, Y.Z.; Cui, T.; Liu, Y.J. Study on shrinkage deformation performance of ultra-high performance concrete containing coarse aggregates. Concrete 2021, 8, 99–103. [Google Scholar]
- GB/T 228.1-2021; Tensile Test of Metallic Materials Part 1: Room Temperature Test Method. Standardization Administration of the People’s Republic of China: Beijing, China, 2021.
- Tang, X.Y.; Ma, J.L.; Luo, J.; He, B.B.; Lu, C.J. Analysis of factors influencing mechanical properties of steel slag powder ecological type ultra-high performance concrete. Silic. Bull. 2023, 42, 607–617. [Google Scholar]
- JTG/T 3650-2020; Technical Specification for Construction of Highway Bridges and Culverts. People’s Communication Press: Beijing, China, 2020.
- GB/T 50080-2016; Standard for Test Methods for the Performance of Ordinary Concrete Mixes. China Academy of Building Research: Beijing, China, 2016.
- GB/T 50081-2019; Standard for Test Methods of Physical and Mechanical Properties of Concrete. Ministry of Housing and Urban-Rural Development: Beijing, China, 2019.
- Hu, H.W.; Zha, X.D.; Li, Z.H.; Lv, R.D. Preparation and performance study of solar pavement panel based on transparent Resin-Concrete. Sustain. Energy Technol. Assess. 2022, 52, 102169. [Google Scholar] [CrossRef]
- Xiang, Y.; Leroy, G. Stress-strain curves for hot-rolled steels. J. Constr. Steel Res. 2017, 133, 36–46. [Google Scholar]
- Zhong, T.; Zhi, B.W.; Qing, Y. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Constr. Steel Res. 2013, 89, 121–131. [Google Scholar]
- Rao, Y.L.; Zhang, C.C.; Li, Y.; Huang, Y.S.; Li, D. Experimental study on the axial compression bearing capacity of high-strength cold-formed rectangular steel tube concrete short columns. J. Huaqiao Univ. 2019, 40, 338–343. [Google Scholar]




| Test Piece Number | Steel Pipe Type D × t /mm | Steel Content α | Yield Strength of Steel Pipe fy/MPa | Conservation Conditions | Hoop System Number ξ |
|---|---|---|---|---|---|
| S-50-1 | 50 × 4 | 0.417 | 278 | A | 1.18 |
| CS-50-2 | 50 × 4 | 0.417 | 278 | B | 1.02 |
| C-50-3 | 50 × 4 | 0.417 | 278 | C | 1.38 |
| S-89-4 | 89 × 6 | 0.336 | 275 | C | 0.86 |
| C-89-5 | 89 × 6 | 0.336 | 275 | A | 1.25 |
| CS-89-6 | 89 × 6 | 0.336 | 275 | B | 0.93 |
| T-108-7 | 108 × 8 | 0.378 | 273 | B | 1.13 |
| CS-108-8 | 108 × 8 | 0.378 | 273 | C | 1.02 |
| CS-108-9 | 108 × 8 | 0.378 | 273 | A | 0.93 |
| Matching Ratio Group | Working Performance/mm | 28 d Mechanical Properties/MPa | ||||
|---|---|---|---|---|---|---|
| Slump | Extensibility | Cubic Compressive Strength | Axial Compressive Strength | Flexural Strength | Modulus of Elasticity | |
| 1 | 265 | 610 | 117.4 | 98.1 | 16.26 | 46,400 |
| 2 | 245 | 590 | 137.1 | 112.7 | 15.32 | 55,200 |
| 3 | 230 | 420 | 112.4 | 83.9 | 10.47 | 50,300 |
| 4 | 260 | 610 | 133.6 | 107.8 | 20.83 | 48,800 |
| 5 | 260 | 690 | 108.1 | 73.8 | 9.01 | 49,500 |
| 6 | 235 | 410 | 128.4 | 99.5 | 14.83 | 47,200 |
| 7 | 270 | 640 | 120.1 | 91.1 | 8.61 | 43,100 |
| 8 | 255 | 580 | 139.2 | 102.4 | 15.38 | 53,700 |
| 9 | 210 | 320 | 139.7 | 110.5 | 14.21 | 56,800 |
| Specimen Number | Test Value/ | Analog Value/ | Error/ |
|---|---|---|---|
| (kN⋅m) | (kN⋅m) | % | |
| S-50-1 | 14.1 | 12.8 | 9.2 |
| CS-50-2 | 14.4 | 13.6 | 5.6 |
| C-50-3 | 13.3 | 12.1 | 9.0 |
| S-89-4 | 43.2 | 40.2 | 6.9 |
| C-89-5 | 40.4 | 38.0 | 5.9 |
| CS-89-6 | 42.4 | 39.7 | 6.4 |
| T-108-7 | 71.2 | 66.6 | 6.5 |
| CS-108-8 | 73.6 | 67.8 | 7.9 |
| CS-108-9 | 76.8 | 68.2 | 11.2 |
| Error Mean | 7.6 |
| Model Number | Steel Pipe Type D × t × L/mm | Steel Content α | Steel Tube Yielding Strength fy/MPa | Cubic Compressive Strength fcu/MPa | Axial Compression Resistance Strength fck/MPa |
|---|---|---|---|---|---|
| TA-89-4-0.207 | 89 × 4 × 1350 | 0.207 | 275 | 120 | 93 |
| TA-89-4.5-0.237 | 89 × 4.5 × 1350 | 0.237 | 275 | 120 | 93 |
| TA-89-5-0.269 | 89 × 5 × 1350 | 0.269 | 275 | 120 | 93 |
| TA-89-5.5-0.302 | 89 × 5.5 × 1350 | 0.302 | 275 | 120 | 93 |
| TA-89-6-0.336 | 89 × 6 × 1350 | 0.336 | 275 | 120 | 93 |
| Model Number | Ultimate Flexural Load Capacity /(kN⋅m) | Improvement Rate /(%) |
|---|---|---|
| TA-89-4-0.207 | 27.3 | - |
| TA-89-4.5-0.237 | 32.8 | 20.1 |
| TA-89-5-0.269 | 36.9 | 35.4 |
| TA-89-5.5-0.302 | 39.9 | 46.3 |
| TA-89-6-0.336 | 41.6 | 52.4 |
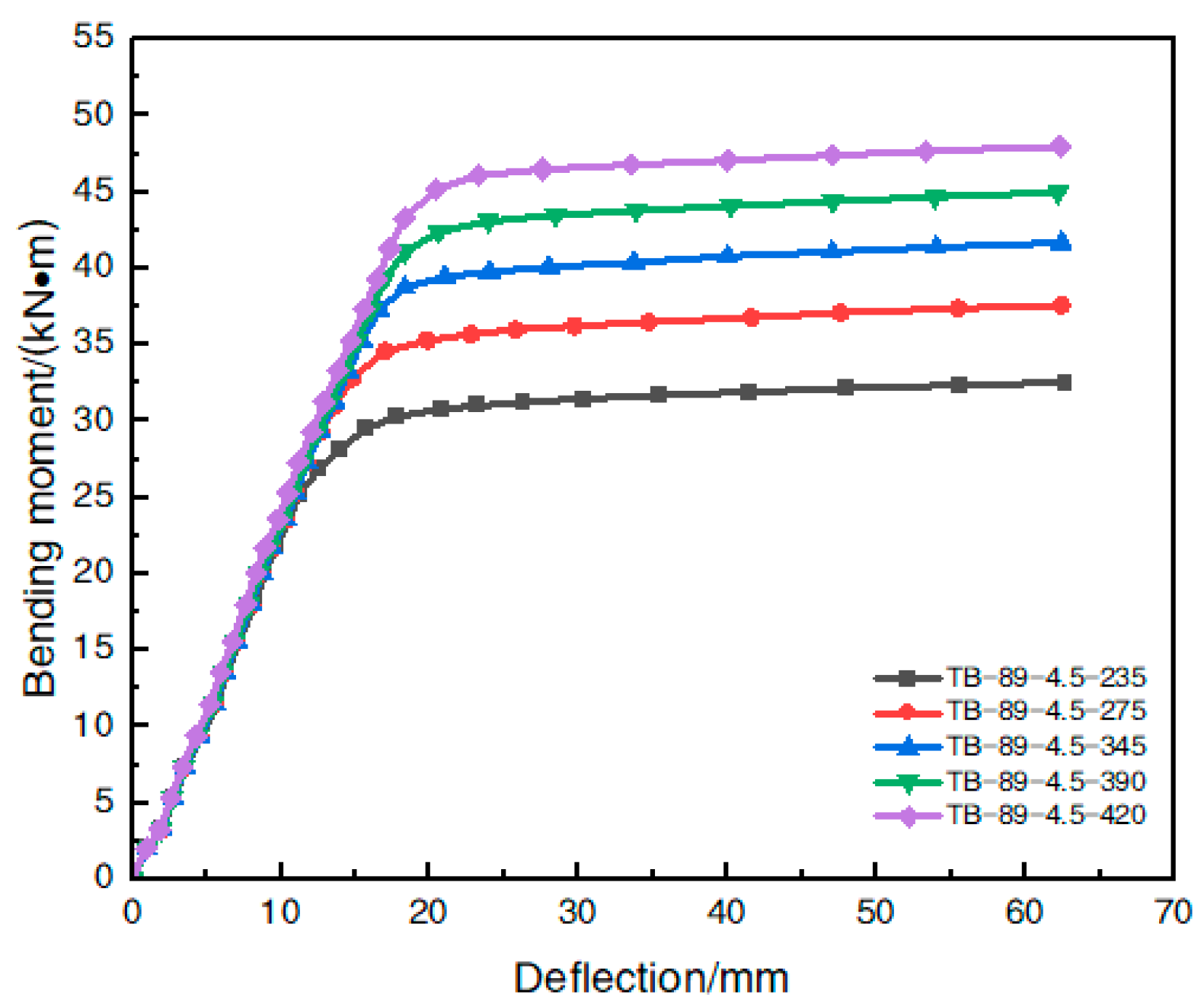
| Model Number | Steel Pipe Type D × t × L/mm | Steel Conten α | Steel Tube Yielding Strength fy/MPa | Cubic Compressive Strength fcy/MPa | Axial Compression Resistance Strength fck/MPa |
|---|---|---|---|---|---|
| TB-89-4.5-235 | 89 × 4.5 × 1350 | 0.237 | 235 | 120 | 93 |
| TB-89-4.5-275 | 89 × 4.5 × 1350 | 0.237 | 275 | 120 | 93 |
| TB-89-4.5-345 | 89 × 4.5 × 1350 | 0.237 | 345 | 120 | 93 |
| TB-89-4.5-390 | 89 × 4.5 × 1350 | 0.237 | 390 | 120 | 93 |
| TB-89-4.5-420 | 89 × 4.5 × 1350 | 0.237 | 420 | 120 | 93 |
| Model Number | Ultimate Flexural Bearing Capacity /(kN⋅m) | Improvement Rate /(%) |
|---|---|---|
| TB-89-4.5-235 | 32.8 | - |
| TB-89-4.5-275 | 37.4 | 14.1 |
| TB-89-4.5-345 | 41.2 | 25.8 |
| TB-89-4.5-390 | 44.5 | 36.0 |
| TB-89-4.5-420 | 47.2 | 44.0 |
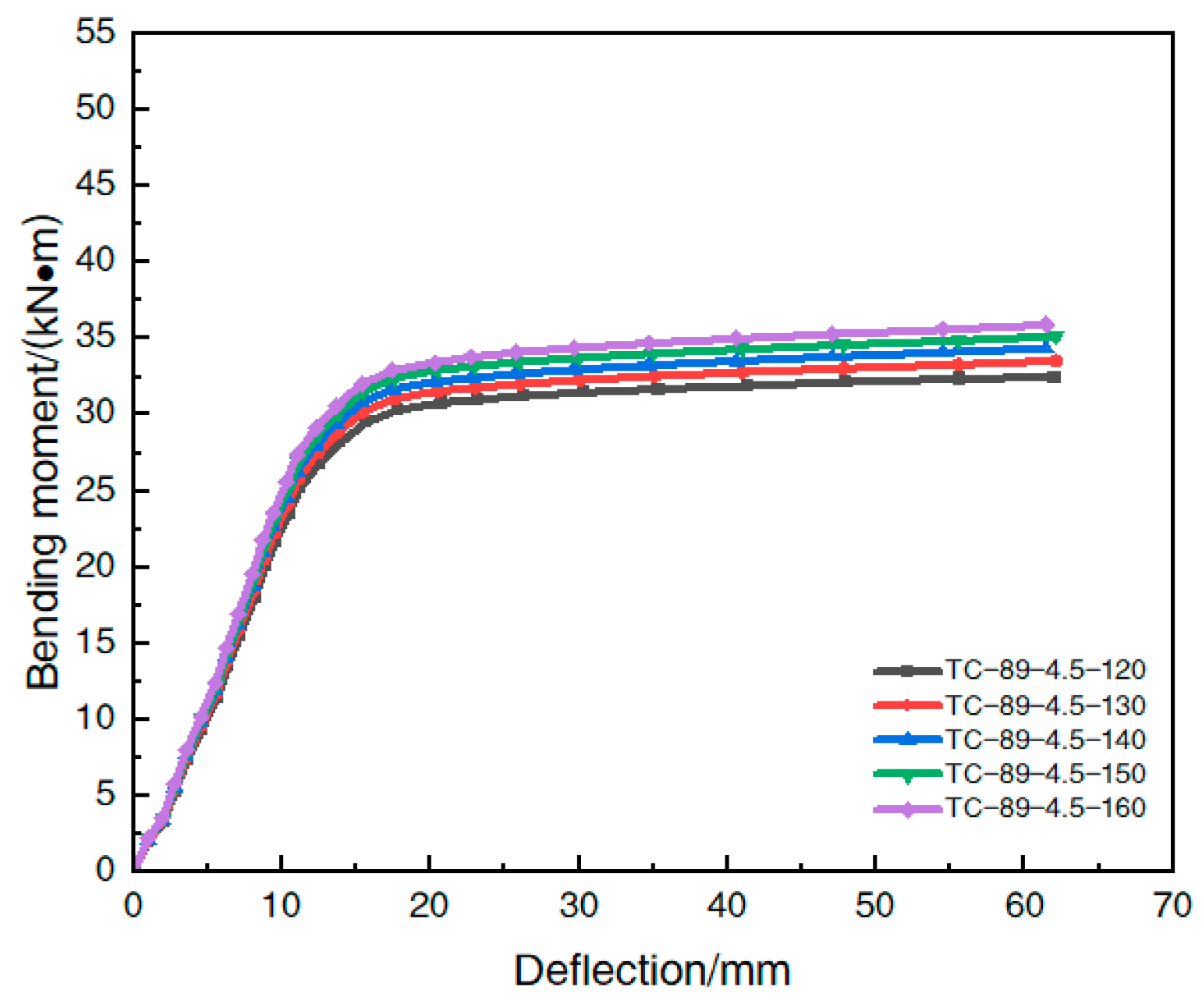
| Model Number | Steel Pipe Type D × t × L/mm | Steel Content α | Steel Tube Yielding Strength fy/MPa | Cubic Compressive Strength fcu/MPa | Axial Compression Resistance Strength fck/MPa |
|---|---|---|---|---|---|
| TC-89-4.5-120 | 89 × 4.5 × 1350 | 0.237 | 275 | 120 | 93 |
| TC-89-4.5-130 | 89 × 4.5 × 1350 | 0.237 | 275 | 130 | 101 |
| TC-89-4.5-140 | 89 × 4.5 × 1350 | 0.237 | 275 | 140 | 108 |
| TC-89-4.5-150 | 89 × 4.5 × 1350 | 0.237 | 275 | 150 | 116 |
| TC-89-4.5-160 | 89 × 4.5 × 1350 | 0.237 | 275 | 160 | 124 |
| Model Number | Ultimate Flexural Bearing /(kN⋅m) | Improvement Rate /(%) |
|---|---|---|
| TC-89-4.5-120 | 32.8 | - |
| TC-89-4.5-130 | 33.3 | 1.6 |
| TC-89-4.5-140 | 33.8 | 3.2 |
| TC-89-4.5-150 | 34.4 | 4.9 |
| TC-89-4.5-160 | 34.9 | 6.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Feng, C.; Chang, J.; Ma, J.; Hu, X. Research on the Flexural Performance of Steel Pipe Steel Slag Powder Ultra-High-Performance Concrete Components. Materials 2023, 16, 5960. https://doi.org/10.3390/ma16175960
Tang X, Feng C, Chang J, Ma J, Hu X. Research on the Flexural Performance of Steel Pipe Steel Slag Powder Ultra-High-Performance Concrete Components. Materials. 2023; 16(17):5960. https://doi.org/10.3390/ma16175960
Chicago/Turabian StyleTang, Xianyuan, Chenzhuo Feng, Jin Chang, Jieling Ma, and Xiansong Hu. 2023. "Research on the Flexural Performance of Steel Pipe Steel Slag Powder Ultra-High-Performance Concrete Components" Materials 16, no. 17: 5960. https://doi.org/10.3390/ma16175960
APA StyleTang, X., Feng, C., Chang, J., Ma, J., & Hu, X. (2023). Research on the Flexural Performance of Steel Pipe Steel Slag Powder Ultra-High-Performance Concrete Components. Materials, 16(17), 5960. https://doi.org/10.3390/ma16175960






