Study of Ultrasonic Guided Wave Propagation in Bone Composite Structures for Revealing Osteoporosis Diagnostic Indicators
Abstract
:1. Introduction
2. Bone Phantoms and Experimental Measurements
3. Guided Waves in Bone Phantoms
4. H-Function-Based Retrieval of Experimental Dispersion Curves
5. MPM-Based Retrieving of GW Parameters
6. Diagnostic Indicators
6.1. Effective Material Parameters
6.2. Resonance Response
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Laugier, P.; Haïat, G. (Eds.) Bone Quantitative Ultrasound; Springer: Dordrecht, The Netherlands, 2011; p. 468. [Google Scholar]
- Laugier, P.; Grimal, Q. (Eds.) Bone Quantitative Ultrasound; Springer: Cham, Switzerland, 2022; p. 429. [Google Scholar]
- Pisani, P.; Renna, M.D.; Conversano, F.; Casciaro, E.; Muratore, M.; Quarta, E.; Paola, M.D.; Casciaro, S. Screening and early diagnosis of osteoporosis through X-ray and ultrasound based techniques. World J. Radiol. 2013, 5, 398–410. [Google Scholar] [CrossRef]
- Hans, D.; Baim, S. Quantitative ultrasound (QUS) in the management of osteoporosis and assessment of fracture risk. J. Clin. Densitom. 2017, 20, 322–333. [Google Scholar] [PubMed]
- Bochud, N.; Laugier, P. Axial Transmission: Techniques, Devices and Clinical Results. In Bone Quantitative Ultrasound; Advances in Experimental Medicine and Biology, Volume 1364; Laugier, P., Grimal, Q., Eds.; Springer: Cham, Switzerland, 2022; pp. 55–94. [Google Scholar]
- Kilappa, V.; Xu, K.; Moilanen, P.; Heikkola, E.; Ta, D.; Timonen, J. Assessment of the Fundamental Flexural Guided Wave in Cortical Bone by an Ultrasonic Axial-Transmission Array Transducer. Ultrasound Med. Biol. 2013, 39, 1223–1232. [Google Scholar]
- Tatarinov, A.; Egorov, V.; Sarvazyan, N.; Sarvazyan, A. Multi-frequency axial transmission bone ultrasonometer. Ultrasonics 2014, 54, 1162–1169. [Google Scholar]
- Minonzio, J.G.; Foiret, J.; Moilanen, P.; Pirhonen, J.; Zhao, Z.; Talmant, M.; Timonen, J.; Laugier, P. A free plate model can predict guided modes propagating in tubular bone-mimicking phantoms. J. Acoust. Soc. Am. 2015, 137, EL98–EL104. [Google Scholar] [PubMed]
- Bochud, N.; Vallet, Q.; Minonzio, J.-G.; Laugier, P. Predicting bone strength with ultrasonic guided waves. Sci. Rep. 2017, 7, 43628. [Google Scholar] [PubMed]
- Kassou, K.; Remram, Y.; Laugier, P.; Minonzio, J.G. Dispersion characteristics of the flexural wave assessed using low frequency (50–150 kHz) point-contact transducers: A feasibility study on bone-mimicking phantoms. Ultrasonics 2017, 81, 1–9. [Google Scholar] [PubMed]
- Minonzio, J.G.; Bochud, N.; Vallet, Q.; Bala, Y.; Ramiandrisoa, D.; Follet, H.; Mitton, D.; Laugier, P. Bone cortical thickness and porosity assessment using ultrasound guided waves: An ex vivo validation study. Bone 2016, 116, 111–119. [Google Scholar]
- Chen, J.; Su, Z. On ultrasound waves guided by bones with coupled soft tissues: A mechanism study and in vitro calibration. Ultrasonics 2014, 54, 1186–1196. [Google Scholar]
- Lee, K.I.; Yoon, S.W. Relationships of the group velocity of the time-reversed Lamb wave with bone properties in cortical bone in vitro. J. Biomech. 2017, 55, 147–151. [Google Scholar] [PubMed]
- Pereira, D.; Haïat, G.; Fernandes, J.; Belanger, P. Effect of intracortical bone properties on the phase velocity and cut-off frequency of low-frequency guided wave modes (20–85 kHz). J. Acoust. Soc. Am. 2019, 145, 121–130. [Google Scholar] [PubMed]
- Tran, T.N.H.T.; Sacchi, M.D.; Ta, D.; Nguyen, V.-H.; Lou, E.; Le, L.H. Nonlinear Inversion of Ultrasonic Dispersion Curves for Cortical Bone Thickness and Elastic Velocities. Ann. Biomed. Eng. 2019, 47, 2178–2187. [Google Scholar] [PubMed]
- Schneider, J.; Iori, G.; Ramiandrisoa, D.; Hammami, M.; Gräsel, M.; Chappard, C.; Barkmann, R.; Laugier, P.; Grimal, Q.; Minonzio, J.-G.; et al. Ex vivo cortical porosity and thickness predictions at the tibia using full-spectrum ultrasonic guided-wave analysis. Arch. Osteoporos. 2019, 14, 21. [Google Scholar] [PubMed]
- Mazzotti, M.; Sugino, C.; Kohtanen, E.; Erturk, A.; Ruzzene, M. Experimental identification of high order Lamb waves and estimation of the mechanical properties of a dry human skull. Ultrasonics 2021, 113, 106343. [Google Scholar] [PubMed]
- Gu, M.; Li, Y.; Tran, T.N.H.T.; Song, X.; Shi, Q.; Xu, K.; Ta, D. Spectrogram decomposition of ultrasonic guided waves for cortical thickness assessment using basis learning. Ultrasonics 2022, 120, 106665. [Google Scholar]
- Talebi, M.; Abbasi-Rad, S.; Malekzadeh, M.; Shahgholi, M.; Ardakani, A.A.; Foudeh, K.; Rad, H.S. Cortical Bone Mechanical Assessment via Free Water Relaxometry at 3T. J. Magn. Reson. Imaging 2021, 54, 1744–1751. [Google Scholar]
- Abbasi-Rad, S.; Akbari, A.; Malekzadeh, M.; Shahgholi, M.; Arabalibeik, H.; Saligheh Rad, H. Quantifying cortical bone free water using short echo time (STE-MRI) at 1.5T. Magn. Reson. Imaging 2020, 71, 17–24. [Google Scholar]
- Karjalainen, J.P.; Riekkinen, O.; Töyräs, J.; Jurvelin, J.S.; Kröger, H. New method for point-of-care osteoporosis screening and diagnostics. Osteoporos. Int. 2016, 27, 971–977. [Google Scholar]
- Karbalaeisadegh, Y.; Yousefian, O.; Iori, G.; Raum, K.; Muller, M. Acoustic diffusion constant of cortical bone: Numerical simulation study of the effect of pore size and pore density on multiple scattering. J. Acoust. Soc. Am. 2019, 146, 1015–1023. [Google Scholar]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors, 2nd ed.; Academic Press/Elsevier: Cambridge, MA, USA, 2014. [Google Scholar]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar]
- Osterhoff, G.; Morgan, E.F.; Shefelbine, S.J.; Karim, L.; McNamara, L.M.; Augat, P. Bone mechanical properties and changes with osteoporosis. Injury 2016, 47, 11–20. [Google Scholar] [CrossRef]
- Nirody, J.A.; Cheng, K.P.; Parrish, R.M.; Burghardt, A.J.; Majumdar, S.; Link, N.M.; Kazakia, G.J. Spatial distribution of intracortical porosity varies across age and sex. Bone 2015, 75, 88–95. [Google Scholar] [CrossRef]
- Glushkov, Y.V.; Glushkova, N.V.; Krivonos, A.S. The excitation and propagation of elastic waves in multilayered anisotropic composites. J. Appl. Math. Mech. 2010, 74, 297–305. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Eremin, A. Forced wave propagation and energy distribution in anisotropic laminate composites. J. Acoust. Soc. Am. 2011, 129, 2923–2934. [Google Scholar] [CrossRef] [PubMed]
- Glushkov, E.V.; Glushkova, N.V.; Fomenko, S.I.; Zhang, C. Surface waves in materials with functionally gradient coatings. Acoust. Phys. 2012, 58, 339–353. [Google Scholar] [CrossRef]
- Glushkov, E.V.; Glushkova, N.V.; Fomenko, S.I. Influence of porosity on characteristics of Rayleigh type waves in multilayered half-space. Acoust. Phys. 2011, 57, 230–240. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Ekhlakov, A.; Shapar, E. An analytically based computer model for surface measurements in ultrasonic crack detection. Wave Motion 2006, 43, 458–473. [Google Scholar] [CrossRef]
- Eremin, A.; Glushkov, E.; Glushkova, N.; Lammering, R. Guided wave time-reversal imaging of macroscopic localized inhomogeneities in anisotropic composites. Struct. Health Monit. 2019, 18, 1803–1819. [Google Scholar] [CrossRef]
- Eremin, A.A.; Glushkov, E.V.; Glushkova, N.V.; Lammering, R. Evaluation of effective elastic properties of layered composite fiber-reinforced plastic plates by piezoelectrically induced guided waves and laser Doppler vibrometry. Compos. Struct. 2015, 125, 449–458. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Bonello, B.; Lu, L.; Charron, E.; Gogneau, N.; Julien, F.; Tchernycheva, M.; Boyko, O. Evaluation of Effective Elastic Properties of Nitride NWs/Polymer Composite Materials Using Laser-Generated Surface Acoustic Waves. Appl. Sci. 2018, 8, 2319. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Eremin, A.; Lammering, R. Trapped mode effects in notched plate-like structures. J. Sound Vib. 2015, 358, 142–151. [Google Scholar] [CrossRef]
- Eremin, A.; Golub, M.; Glushkov, E.; Glushkova, N. Identification of delamination based on the Lamb wave scattering resonance frequencies. NDT E Int. 2019, 103, 145–153. [Google Scholar] [CrossRef]
- Alleyne, D.; Cawley, P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals. J. Acoust. Soc. Am. 1991, 37, 1159–1168. [Google Scholar] [CrossRef]
- Hua, Y.; Sarkar, T.K. Matrix Pencil Method for Estimating Parameters of Exponentially Damped/Undamped Sinusoids in Noise. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 814–824. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef]
- Ibryaeva, O.L.; Salov, D.D. Modification of the Matrix Pencil Method using a combined evaluation of signal poles and their inverses. Bull. South Ural. State Univ. Ser. Comput. Math. Softw. Eng. 2017, 6, 26–37. (In Russian) [Google Scholar]
- Glushkov, E.V.; Glushkova, N.V.; Ermolenko, O.A.; Tatarinov, A.M. Extracting guided wave characteristics of bone phantoms from ultrasonometric data for osteoporosis diagnosis. In Proceedings of the International Conference “2022 Days on Diffraction”, St. Petersburg, Russia, 30 May–3 June 2022; pp. 35–40. [Google Scholar]
- Bochud, N.; Laurent, J.; Bruno, F.; Royer, D.; Prada, C. Towards real-time assessment of anisotropic plate properties using elastic guided waves. J. Acoust. Soc. Am. 2018, 143, 1138–1147. [Google Scholar] [CrossRef] [PubMed]
- Janson, E.; Tatarinov, A.; Dzenis, V.; Kregers, A. Constructional peculiarities of the human tibia defined by reference to ultrasound measurement data. Biomaterials 1984, 5, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Tatarinov, A.M.; Dubonos, S.L.; Ianson, K.A.; Oganov, V.S.; Dzenis, V.V.; Rakhmanov, A.S. Ultrasonic diagnostics of human bone state during 370-day antiortostatic hypokinesia. Kosm. Biol. Aviakosm. Med. (Space Biol. Aerosp. Med.) 1990, 24, 29–31. (In Russian) [Google Scholar]
- Sarvazyan, A.; Tatarinov, A.; Egorov, V.; Airapetian, S.; Kurtenok, V.; Gatt Jr., C.J. Application of the dual-frequency ultrasonometer for osteoporosis detection. Ultrasonics 2009, 49, 331–337. [Google Scholar] [CrossRef]
- Tatarinov, A.; Panov, V. Physical models of cortical bone conditions, fabricated by a 3D printer to test for sensitivity of axial transmission technique. In Proceedings of the 6th European Symposium on Characterization of Bone, Corfu, Greece, 10–12 June 2015; pp. 1–4. [Google Scholar]
- Ermolenko, O.A.; Fomenko, S.I.; Glushkov, E.V.; Glushkova, N.V.; Tatarinov, A.M. Accounting for modal excitability and bone porosity in ultrasonometric osteoporosis diagnostics. In Proceedings of the International Conference “2021 Days on Diffraction”, St. Petersburg, Russia, 31 May–4 June 2021; pp. 36–41. [Google Scholar]
- Glushkov, E.; Glushkova, N.; Ermolenko, O.; Tatarinov, A. Analysis of the Ultrasonic Guided Wave Sensitivity to the Bone Structure for Osteoporosis Diagnostics. In Proceedings of the 2020 International Conference on “Physics and Mechanics of New Materials and Their Applications” (PHENMA 2020), Kitakyushu, Japan, 26–29 March 2021; Volume 10, pp. 409–424. [Google Scholar]
- Lowe, M.J.S.; Cawley, P.; Kao, J.-Y.; Diligent, O. The low frequency reflection characteristics of the fundamental antisymmetric Lamb wave A0 from a rectangular notch in a plate. J. Acoust. Soc. Am. 2002, 112, 2612–2622. [Google Scholar] [CrossRef]
- Bernard, S. Resonant Ultrasound Spectroscopy for the Viscoelastic Characterization of Cortical Bone. Ph.D. Thesis, Université Pierre et Marie Curie (Paris 6), Paris, France, 2014. [Google Scholar]
- Minonzio, J.-G.; Foiret, J.; Talmant, M.; Laugier, P. Impact of attenuation on guided mode wavenumber measurement in axial transmission on bone mimicking plates. J. Acoust. Soc. Am. 2011, 130, 3574–3582. [Google Scholar] [CrossRef] [PubMed]
- Nguyen Minh, H.; Du, J.; Raum, K. Estimation of Thickness and Speed of Sound in Cortical Bone Using Multifocus Pulse-Echo Ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 568–579. [Google Scholar] [CrossRef]
- Liu, G.; Ma, W.; Han, X. An inverse procedure for determination of material constants of composite laminates using elastic waves. Comput. Methods Appl. Mech. Eng. 2002, 191, 3543–3554. [Google Scholar] [CrossRef]
- Penrose, R. On Best Approximate Solutions of Linear Matrix Equations. Math. Camb. Philos. Soc. 1956, 52, 17–19. [Google Scholar] [CrossRef]
- Prada, C.; Balogun, O.; Murray, T.W. Laser-based ultrasonic generation and detection of zero-group velocity Lamb waves in thin plates. Appl. Phys. Lett. 2005, 87, 194109. [Google Scholar] [CrossRef]
- Prada, C.; Clorennec, D.; Royer, D. Local vibration of an elastic plate and zero group velocity Lamb modes. J. Acoust. Soc. Am. 2008, 124, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Tolstoy, I.; Usdin, E. Wave propagation in elastic plates: Low and high mode dispersion. J. Acoust. Soc. Am. 1957, 29, 37–42. [Google Scholar] [CrossRef]
- Grünsteidl, C.; Veres, I.A.; Murray, T.W. Experimental and numerical study of the excitability of zero group velocity lamb waves by laser-ultrasound. J. Acoust. Soc. Am. 2015, 138, 242–249. [Google Scholar] [CrossRef]
- Grünsteidl, C.; Murray, T.W.; Berer, T.; Veres, I.A. Inverse characterization of plates using zero group velocity Lamb modes. Ultrasonics 2016, 65, 1–4. [Google Scholar] [CrossRef]
- Glushkov, E.V.; Glushkova, N.V. Multiple zero-group velocity resonances in elastic layered structures. J. Sound Vib. 2021, 500, 116023. [Google Scholar] [CrossRef]

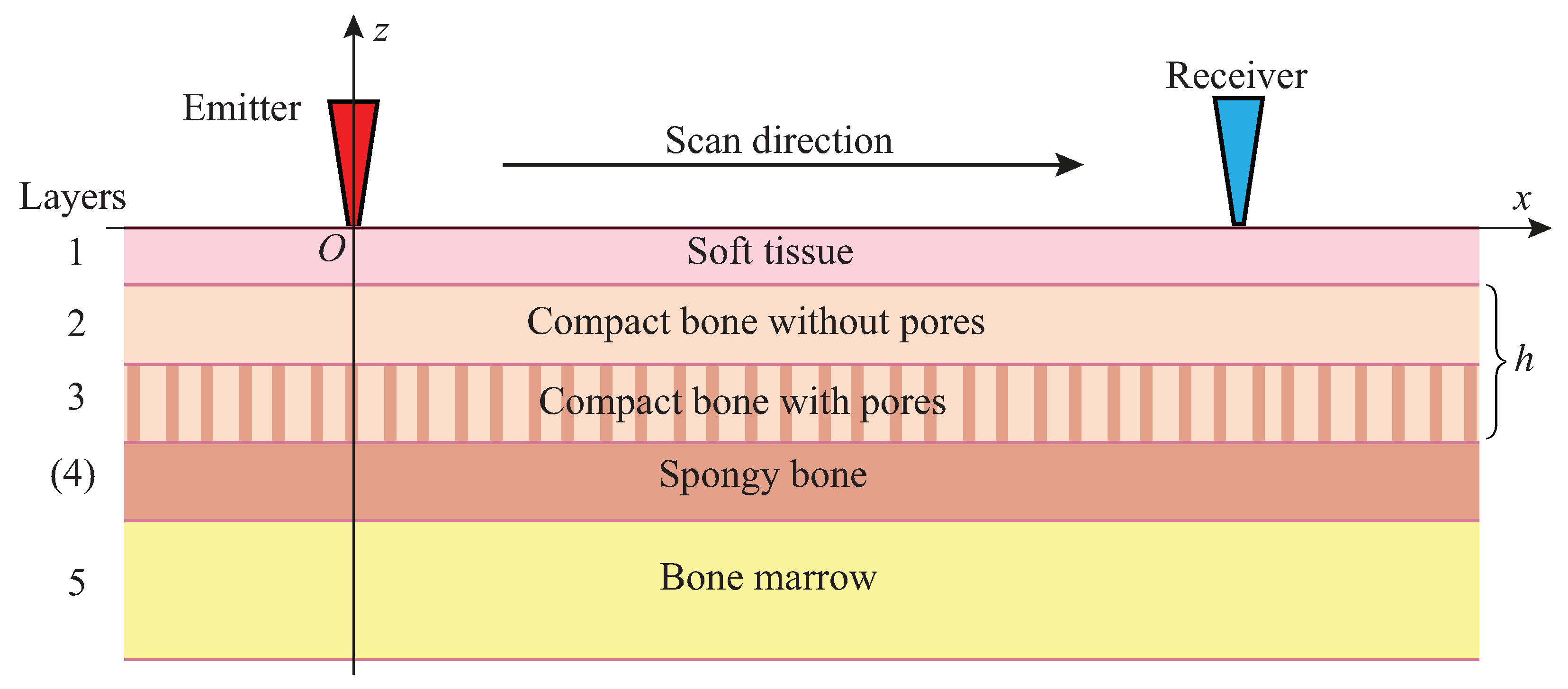
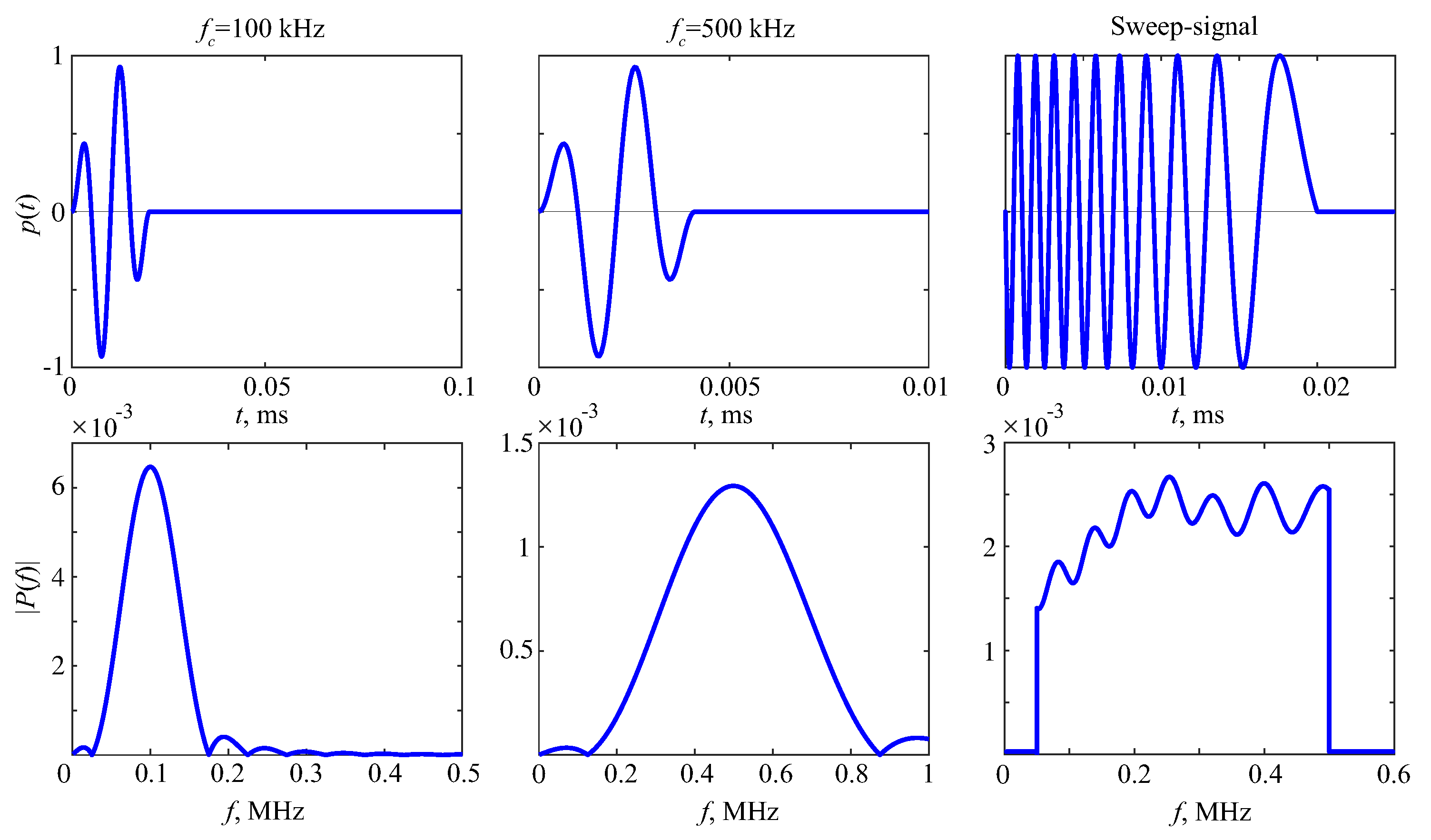

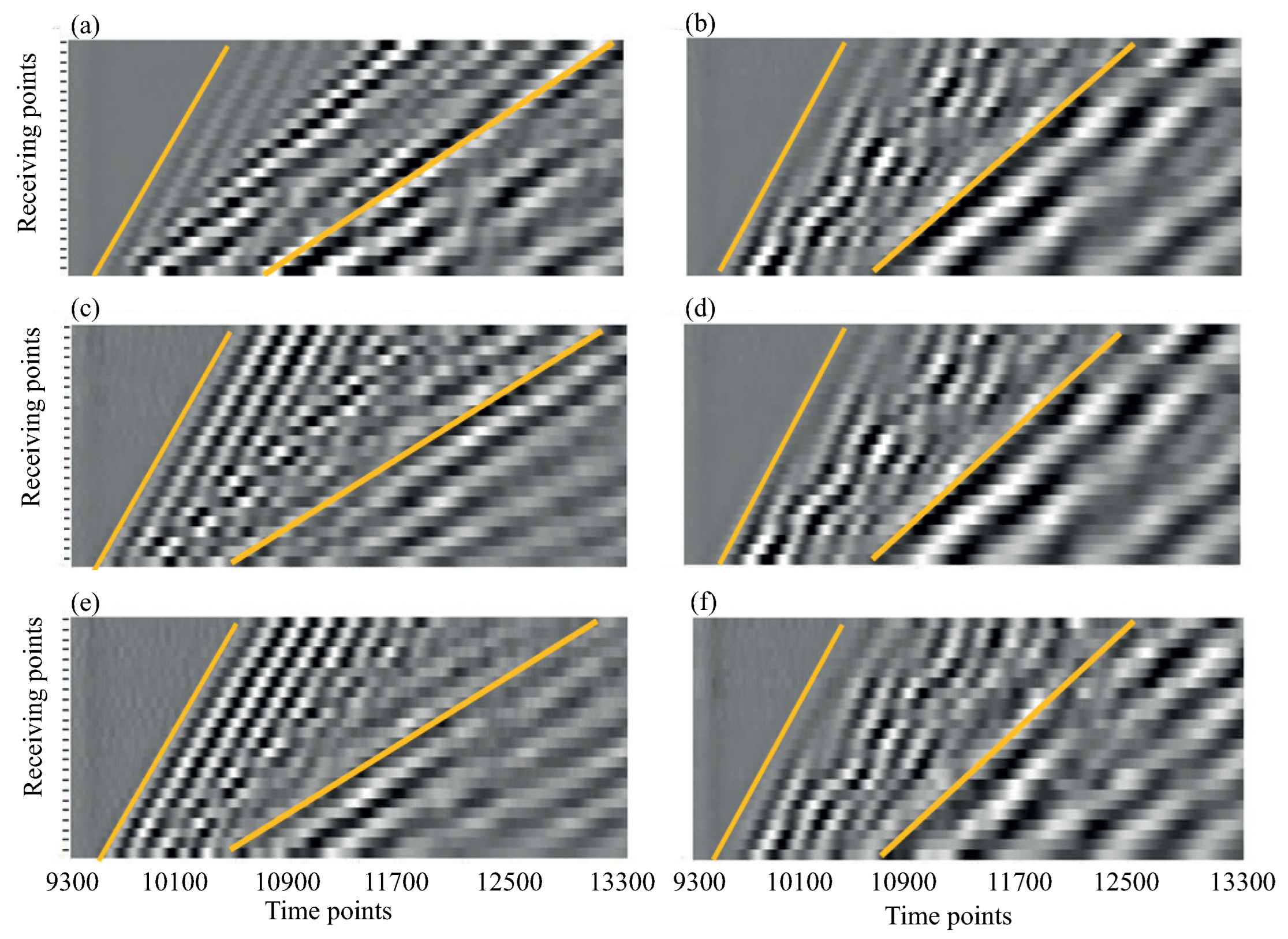


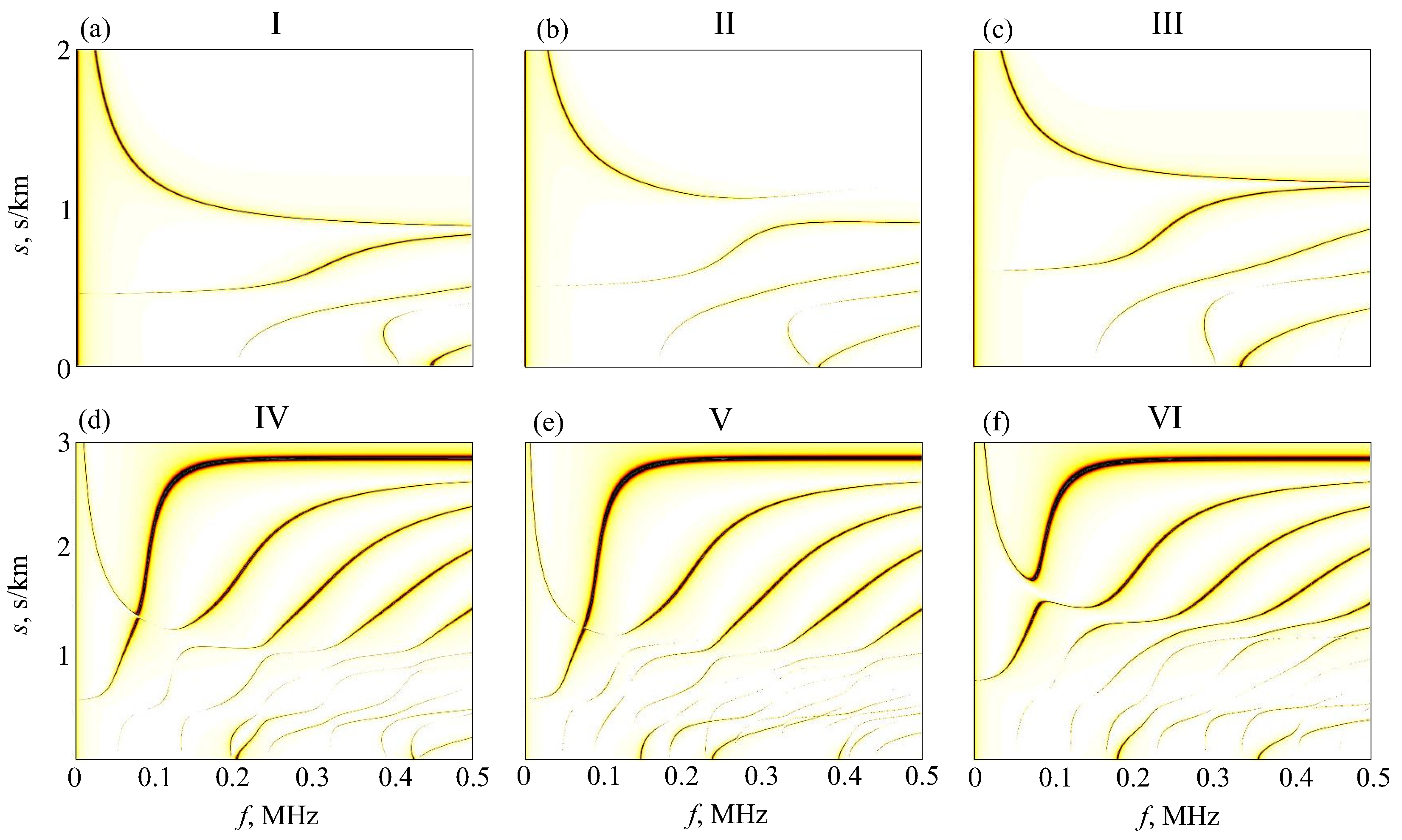
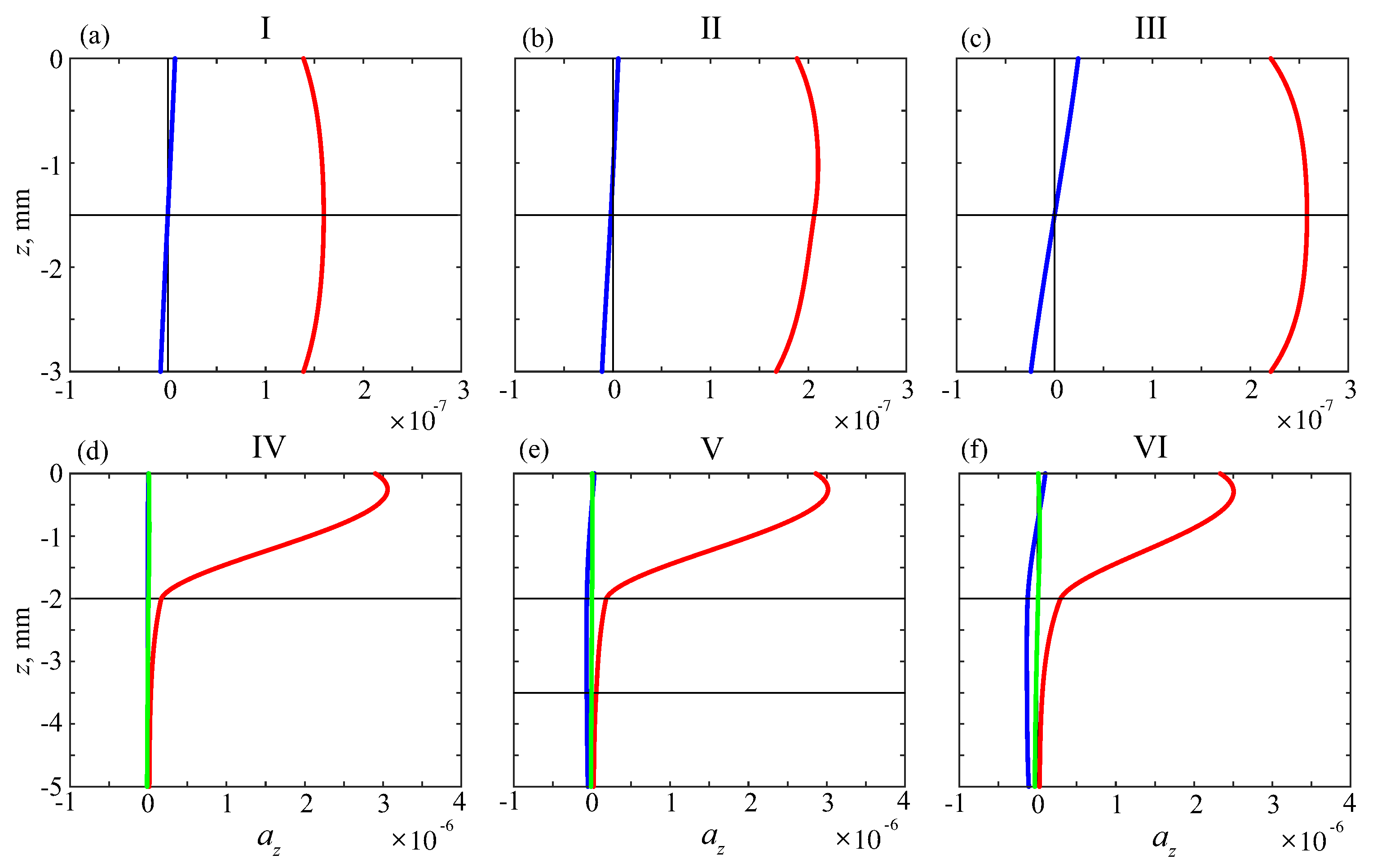
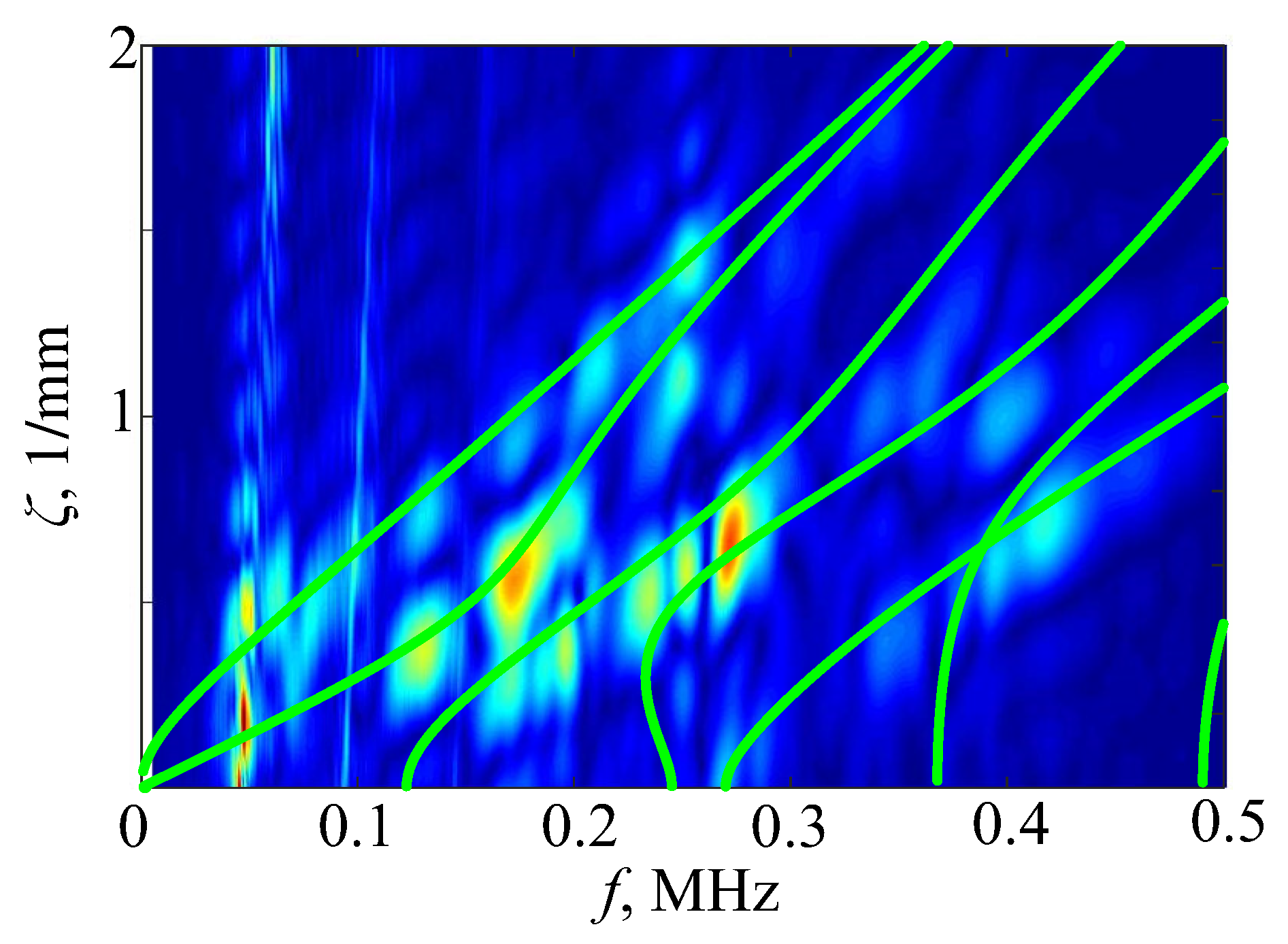
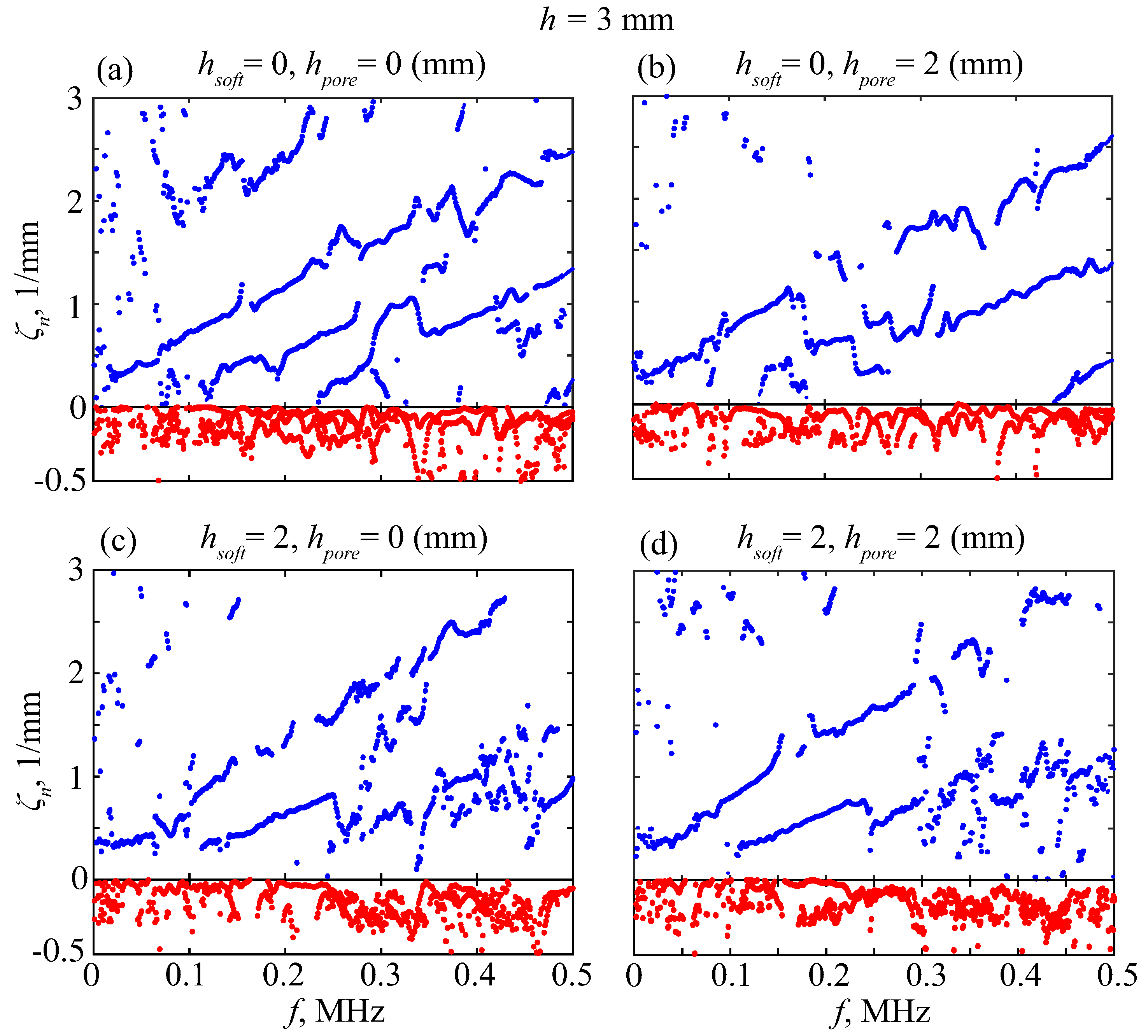


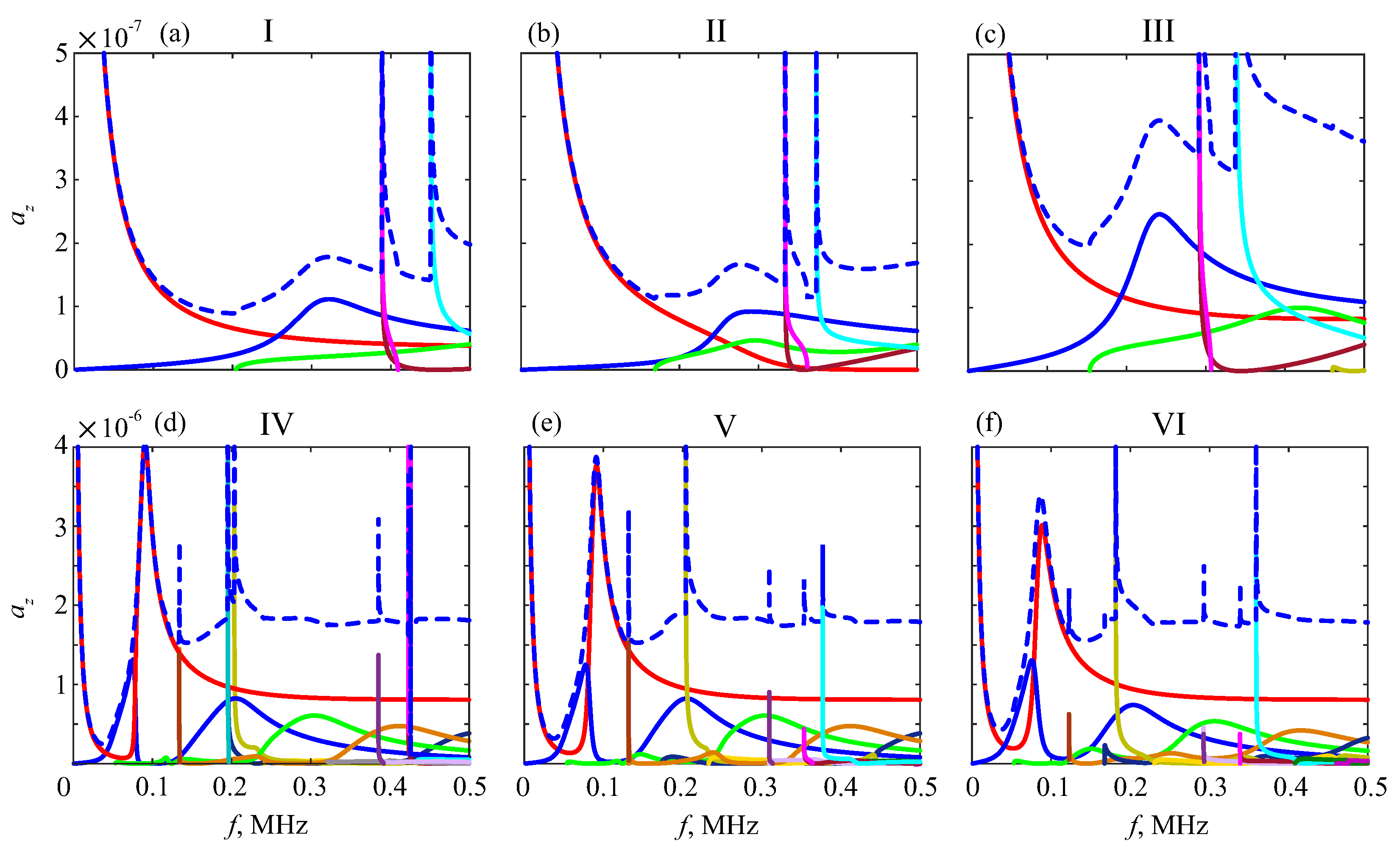
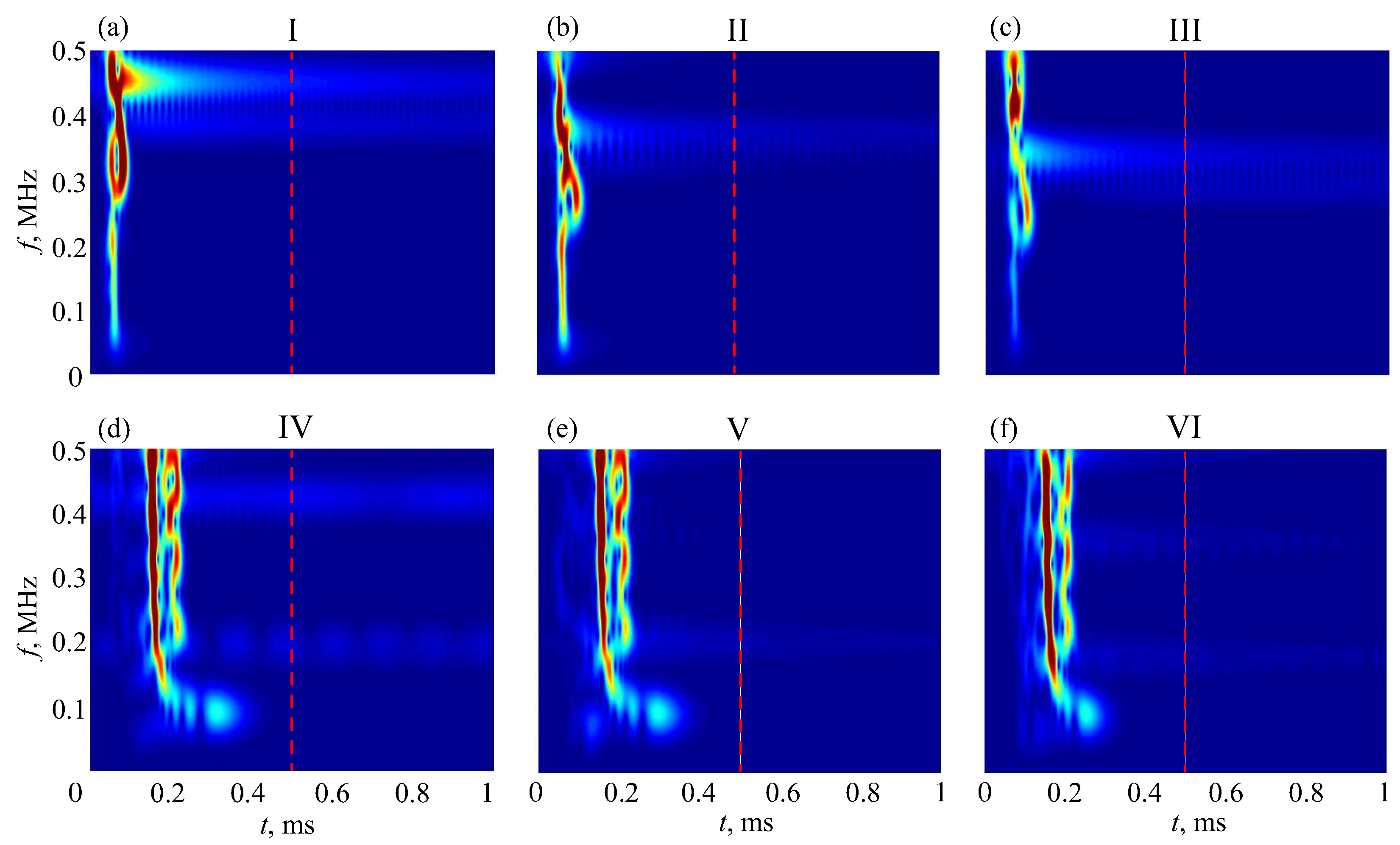
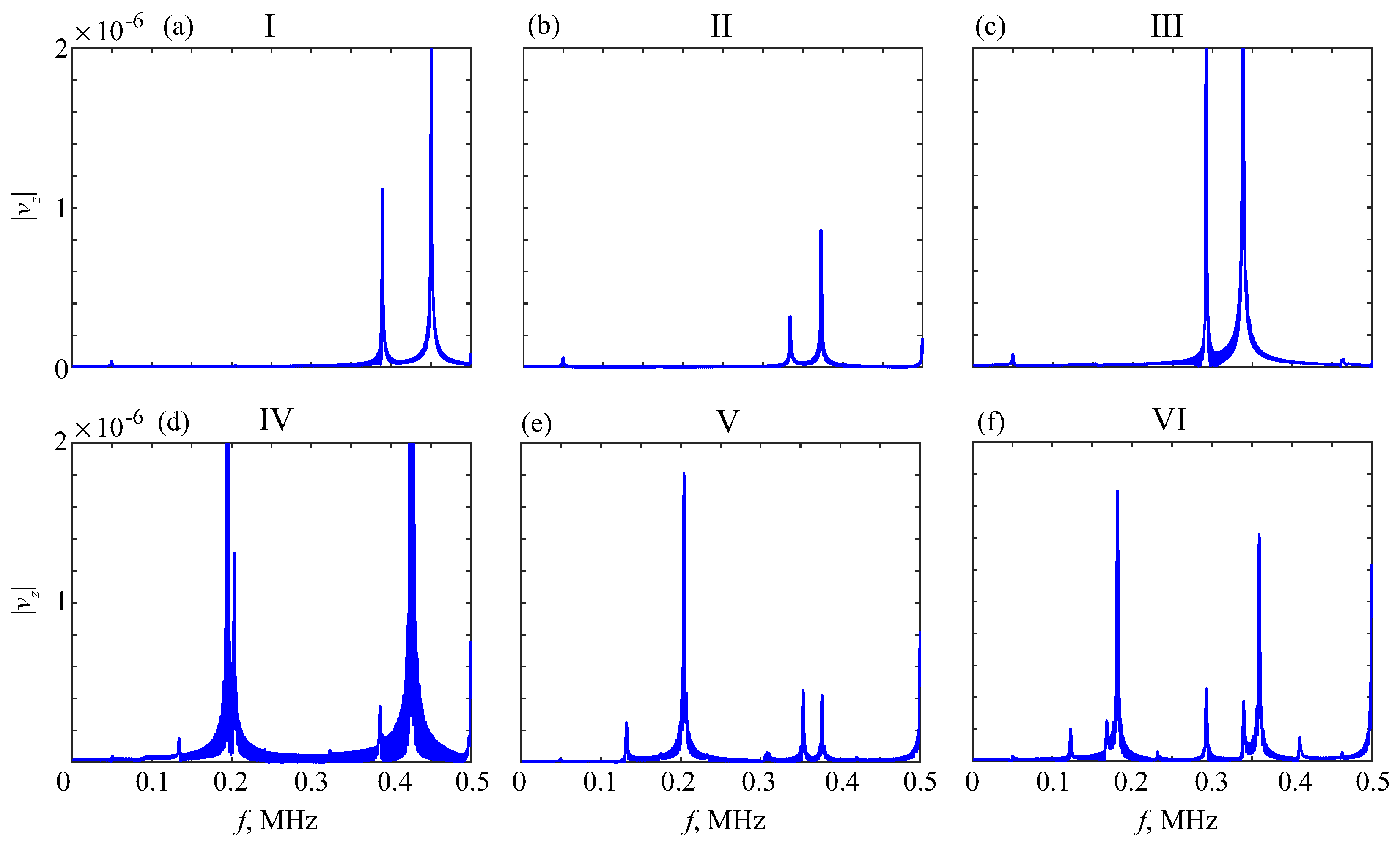

| Material | (m/s) | (m/s) | (kg/m3) | |
|---|---|---|---|---|
| Soft plastic | 1550 | 369 | 1060 | 0.47 |
| Plexiglass (PMMA) | 2700 | 1226 | 1190 | 0.37 |
| Its drilled part | 2025 | 920 | 952 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glushkov, E.V.; Glushkova, N.V.; Ermolenko, O.A.; Tatarinov, A.M. Study of Ultrasonic Guided Wave Propagation in Bone Composite Structures for Revealing Osteoporosis Diagnostic Indicators. Materials 2023, 16, 6179. https://doi.org/10.3390/ma16186179
Glushkov EV, Glushkova NV, Ermolenko OA, Tatarinov AM. Study of Ultrasonic Guided Wave Propagation in Bone Composite Structures for Revealing Osteoporosis Diagnostic Indicators. Materials. 2023; 16(18):6179. https://doi.org/10.3390/ma16186179
Chicago/Turabian StyleGlushkov, Evgeny V., Natalia V. Glushkova, Olga A. Ermolenko, and Alexey M. Tatarinov. 2023. "Study of Ultrasonic Guided Wave Propagation in Bone Composite Structures for Revealing Osteoporosis Diagnostic Indicators" Materials 16, no. 18: 6179. https://doi.org/10.3390/ma16186179
APA StyleGlushkov, E. V., Glushkova, N. V., Ermolenko, O. A., & Tatarinov, A. M. (2023). Study of Ultrasonic Guided Wave Propagation in Bone Composite Structures for Revealing Osteoporosis Diagnostic Indicators. Materials, 16(18), 6179. https://doi.org/10.3390/ma16186179






