Author Contributions
Y.H.: conceptualization, methodology, modelization, investigation, validation, and writing—original draft. D.L. (Dehong Lu): conceptualization, methodology, advising, supervision, writing—review, and editing. Z.L.: experimental support, reviewing, supervision, and project administration. D.L. (Donghui Lu): empirical data collection and review, supervision, project administration. All authors have read and agreed to the published version of the manuscript.
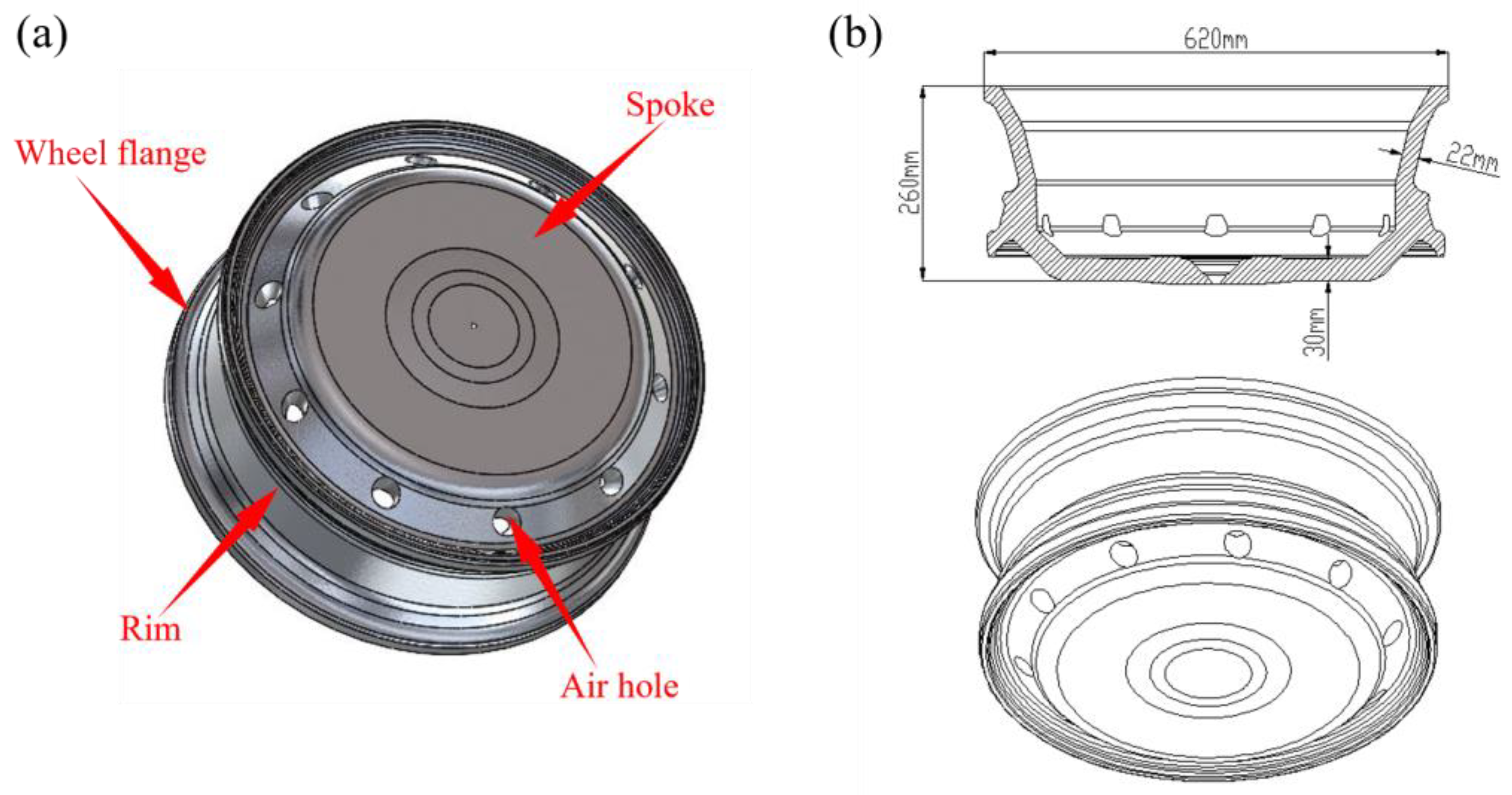
Figure 1.
Schematic diagram of the wheel: (a) Schematic diagram of wheel casting, (b) CAD dimensions of the wheel.
Figure 1.
Schematic diagram of the wheel: (a) Schematic diagram of wheel casting, (b) CAD dimensions of the wheel.
Figure 2.
Experimental flow chart.
Figure 2.
Experimental flow chart.
Figure 3.
Cracks location map: (a) Hub crack, (b) Crack development diagram.
Figure 3.
Cracks location map: (a) Hub crack, (b) Crack development diagram.
Figure 4.
Three-dimensional cross-sectional view of the wheel mold cooling system of the mold.
Figure 4.
Three-dimensional cross-sectional view of the wheel mold cooling system of the mold.
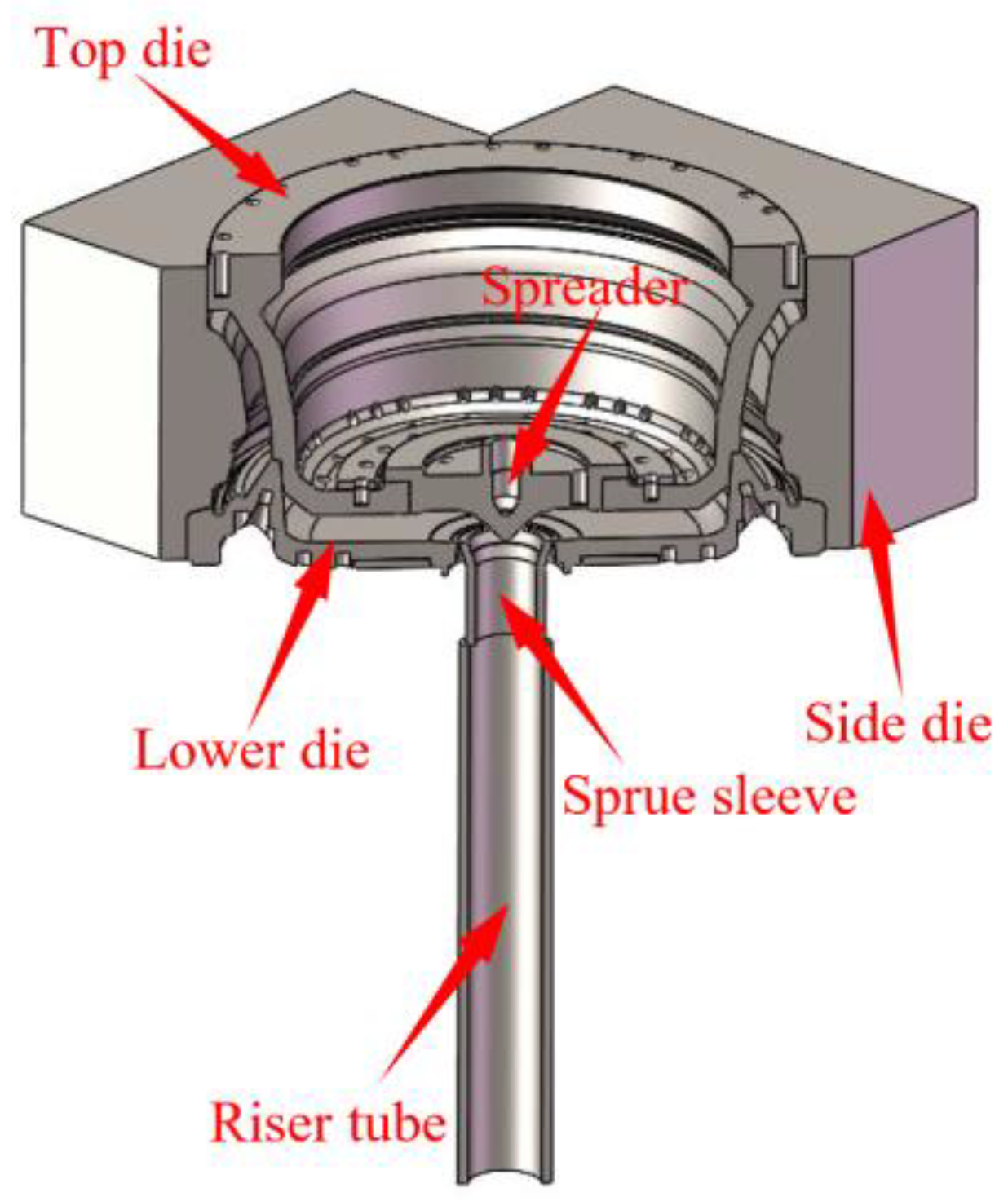
Figure 5.
Schematic diagram of the overall.
Figure 5.
Schematic diagram of the overall.
Figure 6.
Schematic diagram of each mold cooling: (a) Top die, (b) Lower die, (c) Side die.
Figure 6.
Schematic diagram of each mold cooling: (a) Top die, (b) Lower die, (c) Side die.
Figure 7.
Heat transfer coefficient between metal fluid and mold.
Figure 7.
Heat transfer coefficient between metal fluid and mold.
Figure 8.
Response diagnostic chart: (a) Residual normal probability chart, (b) Predicted and actual distribution chart.
Figure 8.
Response diagnostic chart: (a) Residual normal probability chart, (b) Predicted and actual distribution chart.
Figure 9.
Defect volume fraction response surface plot: (a) X1 − X2, (b) X1 − X3, (c) X1 − X4, (d) X2 − X3, (e) X2 − X4, (f) X3 − X4.
Figure 9.
Defect volume fraction response surface plot: (a) X1 − X2, (b) X1 − X3, (c) X1 − X4, (d) X2 − X3, (e) X2 − X4, (f) X3 − X4.
Figure 10.
Response diagnostic chart: (a) Residual normal probability chart, (b) Predicted and actual distribution chart.
Figure 10.
Response diagnostic chart: (a) Residual normal probability chart, (b) Predicted and actual distribution chart.
Figure 11.
Spoke large plane average SDAS response surface plot: (a) X1 − X2, (b) X1 − X3, (c) X1 − X4, (d) X2 − X3, (e) X2 − X4, (f) X3 − X4.
Figure 11.
Spoke large plane average SDAS response surface plot: (a) X1 − X2, (b) X1 − X3, (c) X1 − X4, (d) X2 − X3, (e) X2 − X4, (f) X3 − X4.
Figure 12.
Optimization flow chart.
Figure 12.
Optimization flow chart.
Figure 13.
Variable mapping relationship chart.
Figure 13.
Variable mapping relationship chart.
Figure 14.
Distribution of Pareto solution scattering points.
Figure 14.
Distribution of Pareto solution scattering points.
Figure 15.
Optimized process simulation diagram: (a) Defect distribution map, (b) Secondary dendrite spacing map.
Figure 15.
Optimized process simulation diagram: (a) Defect distribution map, (b) Secondary dendrite spacing map.
Figure 16.
Solidification rate test point distribution map.
Figure 16.
Solidification rate test point distribution map.
Figure 17.
Variation curve of solidification fraction under different processes: (a) Solidification fraction curve under the original cooling process, (b) Solidification fraction curve after correction of the cooling process.
Figure 17.
Variation curve of solidification fraction under different processes: (a) Solidification fraction curve under the original cooling process, (b) Solidification fraction curve after correction of the cooling process.
Figure 18.
X-ray inspection location map.
Figure 18.
X-ray inspection location map.
Figure 19.
X-ray inspection diagram of different positions: (a) Spoke, (b) Intersection of spoke and rim, (c) Rim.
Figure 19.
X-ray inspection diagram of different positions: (a) Spoke, (b) Intersection of spoke and rim, (c) Rim.
Figure 20.
Sampling location diagram under different processes: (a) Original process hub sampling location map, (b) Optimized process sampling location map.
Figure 20.
Sampling location diagram under different processes: (a) Original process hub sampling location map, (b) Optimized process sampling location map.
Figure 21.
Comparison of the stress–strain curve.
Figure 21.
Comparison of the stress–strain curve.
Figure 22.
Comparative graph of mechanical performance tests.
Figure 22.
Comparative graph of mechanical performance tests.
Figure 23.
Local metallographic organization of the spoke surface under different processes: (a) Local metallographic view of the spoke surface of the original process wheel, (b) Local metallographic view of the spoke surface of the optimized process wheel.
Figure 23.
Local metallographic organization of the spoke surface under different processes: (a) Local metallographic view of the spoke surface of the original process wheel, (b) Local metallographic view of the spoke surface of the optimized process wheel.
Table 1.
A356 material composition table.
Table 1.
A356 material composition table.
| Element | Si | Fe | Cu | Mn | Mg | Ti | Sn | Ni |
| Mass Fraction (%) | 6.64 | 0.150 | 0.0018 | 0.0046 | 0.346 | 0.127 | 0.0100 | 0.0060 |
| Element | P | Zn | Pb | Sb | Sr | Ca | Cr | Al |
| Mass Fraction (%) | 0.0011 | 0.0101 | 0.0032 | <0.0030 | 0.0126 | 0.00068 | 0.0035 | 93.19 |
Table 2.
Experimental variables and levels.
Table 2.
Experimental variables and levels.
| Process Parameters | ID | Level 1 | Level 2 | Level 3 |
|---|
| Pouring temperature (°C) | X1 | 690 | 700 | 710 |
| Mold temperature (°C) | X2 | 350 | 400 | 450 |
| Holding pressure (mb) | X3 | 700 | 950 | 1200 |
| Holding time (s) | X4 | 220 | 240 | 260 |
Table 3.
BBD experimental design scheme.
Table 3.
BBD experimental design scheme.
| Run | Factor 1 | Factor 2 | Factor 3 | Factor 4 |
|---|
| X1: Pouring Temperature (°C) | X2: Mold Temperature (°C) | X3: Holding Pressure (mb) | X4: Holding Time (s) |
|---|
| 1st | 700 | 450 | 1200 | 240 |
| 2nd | 690 | 400 | 1200 | 240 |
| 3rd | 710 | 450 | 950 | 240 |
| 4th | 710 | 400 | 950 | 260 |
| 5th | 710 | 400 | 700 | 240 |
| 6th | 700 | 400 | 950 | 240 |
| 7th | 710 | 400 | 1200 | 240 |
| 8th | 710 | 400 | 950 | 220 |
| 9th | 700 | 400 | 700 | 220 |
| 10th | 700 | 450 | 950 | 220 |
| 11th | 700 | 450 | 950 | 260 |
| 12th | 710 | 350 | 950 | 240 |
| 13th | 700 | 400 | 950 | 240 |
| 14th | 700 | 400 | 700 | 260 |
| 15th | 690 | 350 | 950 | 240 |
| 16th | 690 | 450 | 950 | 240 |
| 17th | 700 | 400 | 950 | 240 |
| 18th | 700 | 450 | 700 | 240 |
| 19th | 690 | 400 | 700 | 240 |
| 20th | 700 | 400 | 1200 | 260 |
| 21st | 700 | 400 | 950 | 240 |
| 22nd | 700 | 350 | 700 | 240 |
| 23rd | 700 | 350 | 950 | 260 |
| 24th | 690 | 400 | 950 | 260 |
| 25th | 700 | 350 | 950 | 220 |
| 26th | 700 | 350 | 1200 | 240 |
| 27th | 700 | 400 | 950 | 240 |
| 28th | 700 | 400 | 1200 | 220 |
| 29th | 690 | 400 | 950 | 220 |
Table 4.
Opening and closing time of each cooling point and the value of HTC.
Table 4.
Opening and closing time of each cooling point and the value of HTC.
| Location | Cooling Process | Open Time | Close Time | HTC(W/m2∙K) |
|---|
| L1 | Air cooling | 170 | 290 | 600 |
| L2 | Air cooling | 160 | 290 | 600 |
| L3 | Air cooling | 155 | 290 | 600 |
| L4 | Air cooling | 140 | 260 | 600 |
| L5 | Air cooling | 105 | 220 | 1500 |
| L6 | Water cooling | 105 | 220 | 5000 |
| L7 | Air cooling | 100 | 200 | 1500 |
| T1 | Water cooling | 280 | 320 | 6000 |
| T2 | Air cooling | 240 | 320 | 600 |
| T3 (Close) | Air cooling | 180 | 320 | 600 |
| T4 | Air cooling | 125 | 160 | 600 |
| T5 | Air cooling | 120 | 160 | 600 |
| T6 | Air cooling | 40 | 240 | 600 |
| A Channel | Air cooling | 50 | 120 | 600 |
| C Channel | Air cooling | 80 | 160 | 600 |
| S1 | Air cooling | 55 | 160 | 600 |
| S2 | Water cooling | 80 | 160 | 5000 |
Table 5.
Simulation-based estimates.
Table 5.
Simulation-based estimates.
| Run | Y1: Defect Volume (%) | Y2: Spoke Large Plane Average SDAS (µm) |
|---|
| 1st | 0.449 | 58.14 ± 1.37 |
| 2nd | 1.057 | 52.46 ± 1.01 |
| 3rd | 0.585 | 57.05 ± 0.83 |
| 4th | 0.997 | 50.74 ± 1.24 |
| 5th | 1.455 | 50.33 ± 1.57 |
| 6th | 0.793 | 50.75 ± 0.96 |
| 7th | 0.679 | 50.36 ± 1.44 |
| 8th | 0.754 | 49.86 ± 1.25 |
| 9th | 1.843 | 49.94 ± 1.13 |
| 10th | 0.603 | 57.94 ± 1.03 |
| 11th | 0.599 | 55.34 ± 0.87 |
| 12th | 1.987 | 45.41 ± 1.36 |
| 13th | 0.873 | 50.41 ± 1.15 |
| 14th | 1.879 | 49.85 ± 1.16 |
| 15th | 2.572 | 45.05 ± 1.44 |
| 16th | 0.671 | 57.94 ± 1.03 |
| 17th | 0.766 | 50.27 ± 0.98 |
| 18th | 0.996 | 58.23 ± 1.25 |
| 19th | 2.34 | 50.01 ± 1.13 |
| 20th | 0.659 | 50.72 ± 1.01 |
| 21st | 0.771 | 50.59 ± 1.32 |
| 22nd | 2.906 | 45.18 ± 0.99 |
| 23rd | 2.133 | 46.37 ± 1.24 |
| 24th | 1.114 | 49.93 ± 1.51 |
| 25th | 2.159 | 45.04 ± 1.25 |
| 26th | 1.547 | 46.26 ± 1.12 |
| 27th | 0.898 | 49.19 ± 1.06 |
| 28th | 0.689 | 52.66 ± 1.26 |
| 29th | 1.452 | 52.34 ± 0.87 |
Table 6.
Defect volume fraction response model analysis of variance.
Table 6.
Defect volume fraction response model analysis of variance.
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|
| Model | 13.22 | 14 | 0.9439 | 87.62 | <0.0001 | significant |
| X1 | 0.6298 | 1 | 0.6298 | 58.45 | <0.0001 | |
| X2 | 7.36 | 1 | 7.36 | 683.61 | <0.0001 | |
| X3 | 3.35 | 1 | 3.35 | 310.81 | <0.0001 | |
| X4 | 0.0012 | 1 | 0.0012 | 0.1095 | 0.7456 | |
| X1X2 | 0.0623 | 1 | 0.0623 | 5.78 | 0.0306 | |
| X1X3 | 0.0643 | 1 | 0.0643 | 5.96 | 0.0285 | |
| X1X4 | 0.0844 | 1 | 0.0844 | 7.83 | 0.0142 | |
| X2X3 | 0.1648 | 1 | 0.1648 | 15.30 | 0.0016 | |
| X2X4 | 0.0001 | 1 | 0.0001 | 0.0112 | 0.9171 | |
| X3X4 | 0.0011 | 1 | 0.0011 | 0.1011 | 0.7552 | |
| X12 | 0.2840 | 1 | 0.2840 | 26.36 | 0.0002 | |
| X22 | 1.05 | 1 | 1.05 | 97.41 | <0.0001 | |
| X32 | 0.6385 | 1 | 0.6385 | 59.26 | <0.0001 | |
| X42 | 0.0806 | 1 | 0.0806 | 7.48 | 0.0161 | |
| Residual | 0.1508 | 14 | 0.0108 | | | |
| Lack of Fit | 0.1359 | 10 | 0.0136 | 3.64 | 0.1124 | not significant |
| Pure Error | 0.0149 | 4 | 0.0037 | | | |
| Cor Total | 13.37 | 28 | | | | |
Table 7.
Summary of defect volume fraction model fitting.
Table 7.
Summary of defect volume fraction model fitting.
| Std.Dev | Mean | R2 | Adjusted R2 | C.V.% | Precision AP |
|---|
| 0.1038 | 1.25 | 0.9887 | 0.9774 | 8.31 | 35.1420 |
Table 8.
Analysis of variance for the secondary dendrite spacing response model.
Table 8.
Analysis of variance for the secondary dendrite spacing response model.
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|
| Model | 448.30 | 14 | 32.02 | 97.49 | <0.0001 | significant |
| X1 | 1.32 | 1 | 1.32 | 4.02 | 0.0647 | |
| X2 | 424.00 | 1 | 424.00 | 1290.85 | <0.0001 | |
| X3 | 4.15 | 1 | 4.15 | 12.65 | 0.0032 | |
| X4 | 1.94 | 1 | 1.94 | 5.92 | 0.0290 | |
| X1X2 | 0.3906 | 1 | 0.3906 | 1.19 | 0.2939 | |
| X1X3 | 1.46 | 1 | 1.46 | 4.46 | 0.0532 | |
| X1X4 | 2.71 | 1 | 2.71 | 8.24 | 0.0123 | |
| X2X3 | 0.3422 | 1 | 0.3422 | 1.04 | 0.3247 | |
| X2X4 | 3.86 | 1 | 3.86 | 11.76 | 0.0041 | |
| X3X4 | 0.8556 | 1 | 0.8556 | 2.60 | 0.1288 | |
| X12 | 0.2166 | 1 | 0.2166 | 0.6595 | 0.4303 | |
| X22 | 6.38 | 1 | 6.38 | 19.41 | 0.0006 | |
| X32 | 1.78 | 1 | 1.72 | 5.24 | 0.0381 | |
| X42 | 0.0514 | 1 | 0.0514 | 0.1564 | 0.6984 | |
| Residual | 4.60 | 14 | 0.3285 | | | |
| Lack of Fit | 3.08 | 10 | 0.3084 | 0.8142 | 0.6411 | not significant |
| Pure Error | 1.51 | 4 | 0.3787 | | | |
| Cor Total | 452.90 | 28 | | | | |
Table 9.
Summary of secondary dendrite spacing model fits.
Table 9.
Summary of secondary dendrite spacing model fits.
| Std.Dev | Mean | R2 | Adjusted R2 | C.V.% | Precision AP |
|---|
| 0.5731 | 50.98 | 0.9898 | 0.9556 | 1.12 | 33.6096 |
Table 10.
Genetic algorithm parameter settings.
Table 10.
Genetic algorithm parameter settings.
| Population Size | Number of Generations | Crossover Probability | Crossover Distribution Index | Mutation Distribution Index |
|---|
| 200 | 20 | 0.9 | 10.0 | 20.0 |
Table 11.
Part Pareto-optimized solution set table.
Table 11.
Part Pareto-optimized solution set table.
| No. | X1 (°C) | X2 (°C) | X3 (mb) | X4 (s) | Y1 (%) | Y2 (µm) | Comment |
|---|
| 1 | 703.18 | 408.96 | 1085.8 | 248.21 | 0.456 | 52.42 | Optimal solution |
| 2 | 702.86 | 421.52 | 1102.3 | 243.05 | 0.500 | 53.40 | |
| 3 | 709.97 | 371.96 | 1047.8 | 220.41 | 1.126 | 46.64 | |
| 4 | 703.54 | 409.21 | 1092.7 | 242.41 | 0.496 | 51.80 | |
| 5 | 707.99 | 397.21 | 1068.3 | 228.02 | 0.654 | 50.07 | |
| 6 | 702.53 | 415.28 | 1115.2 | 244.11 | 0.441 | 53.64 | |
| 7 | 709.72 | 384.97 | 1054.3 | 221.21 | 0.874 | 48.23 | |
| 8 | 702.53 | 405.89 | 1082.4 | 241.73 | 0.533 | 51.41 | |
Table 12.
Cooling process calibration table.
Table 12.
Cooling process calibration table.
| Location | Cooling Process | Open Time (s) | Close Time (s) | HTC (W/m2∙K) |
|---|
| T4 | Air cooling | 125→127 | 160 | 600 |
| T5 | Air cooling | 120→117 | 160 | 600 |
Table 13.
Comparison table of different process properties.
Table 13.
Comparison table of different process properties.
| Original Process | Optimized Process |
|---|
| | Rm | Rp 0.2 | A | | Rm | Rp 0.2 | A |
|---|
| No. | ≥MPa | ≥MPa | ≥% | No | ≥MPa | ≥MPa | ≥% |
|---|
| 1 | 151.7 | 111.3 | 2.1 | 4 | 172.9 | 111.7 | 3.7 |
| 2 | 165.6 | 109.9 | 3.4 | 5 | 177.9 | 111.6 | 4.2 |
| 3 | 168.9 | 107.8 | 3.6 | 6 | 179.8 | 107.9 | 4.9 |