In Situ, Real-Time Temperature Mapping and Thermal FE Simulations of Large-Format 3D Printed PETG/CF Vertical Wall
Abstract
:1. Introduction
2. Materials and Methods
2.1. Printing Process Information
2.2. Interlayer Thermocouples—Final Position Measurement
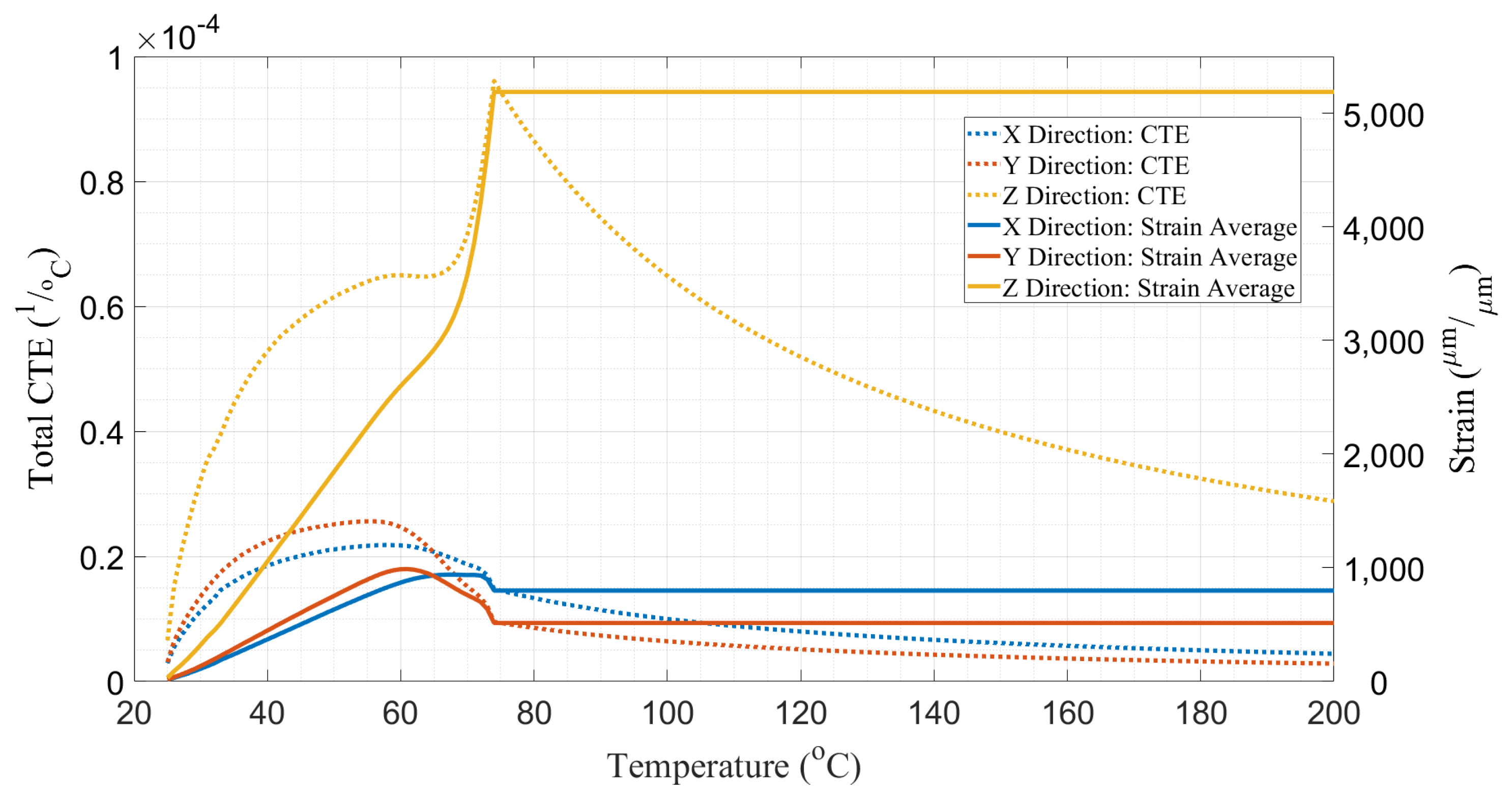
2.3. PETG/CF Material Characterization
2.4. Thermal FE Model of the PETG/CF Wall
3. Results and Discussion
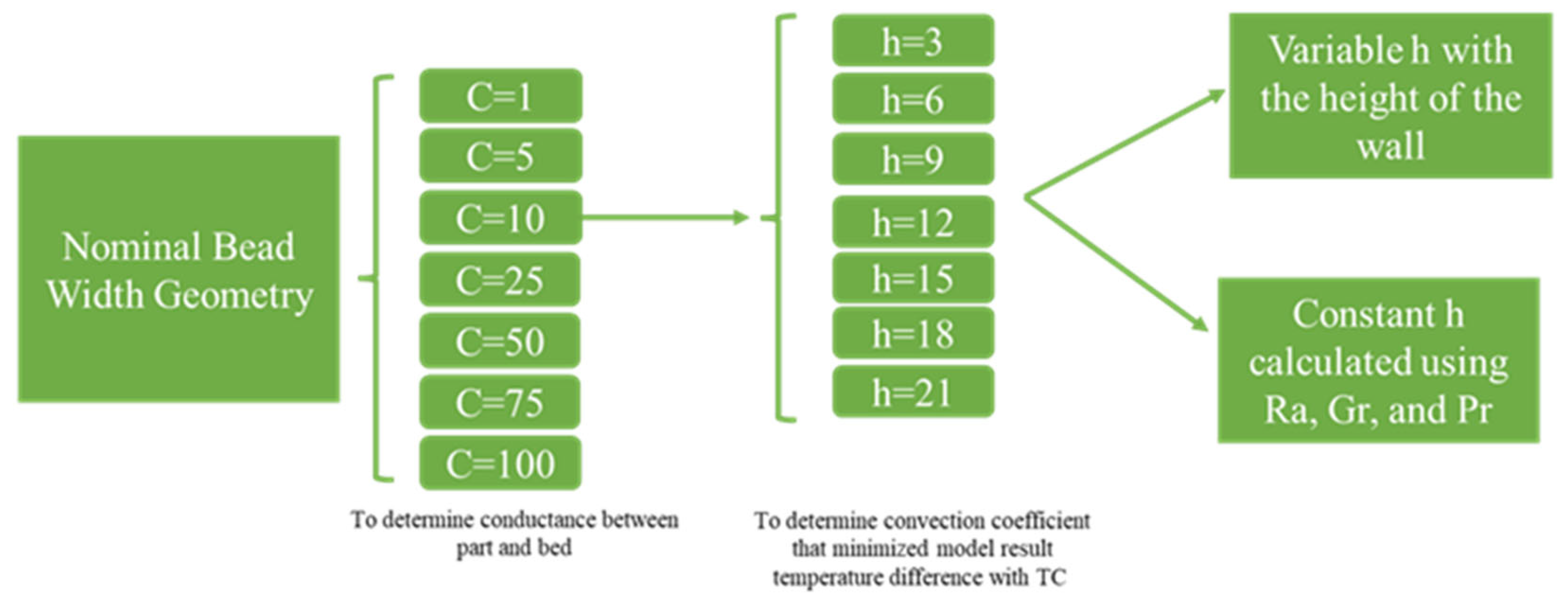
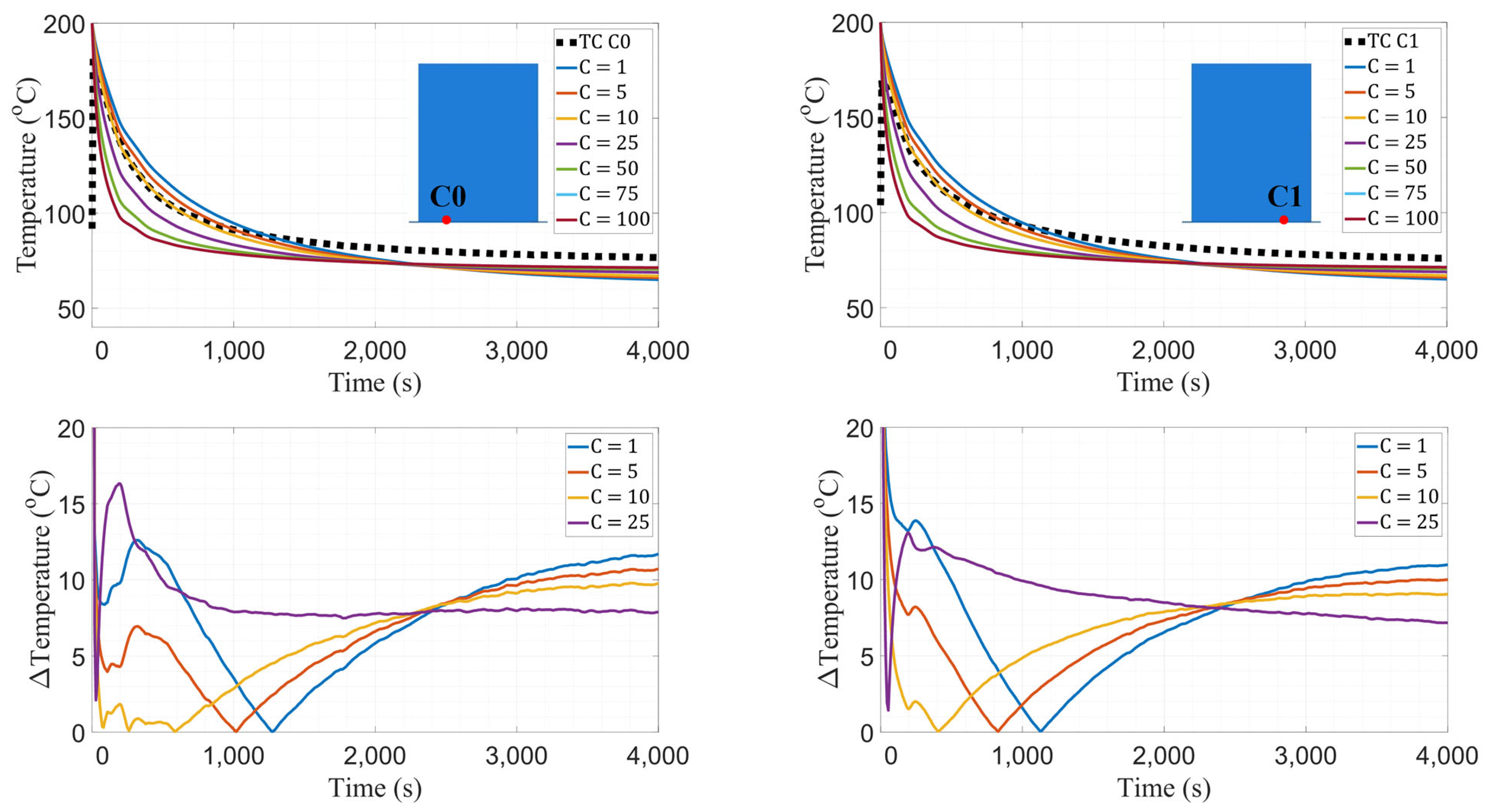
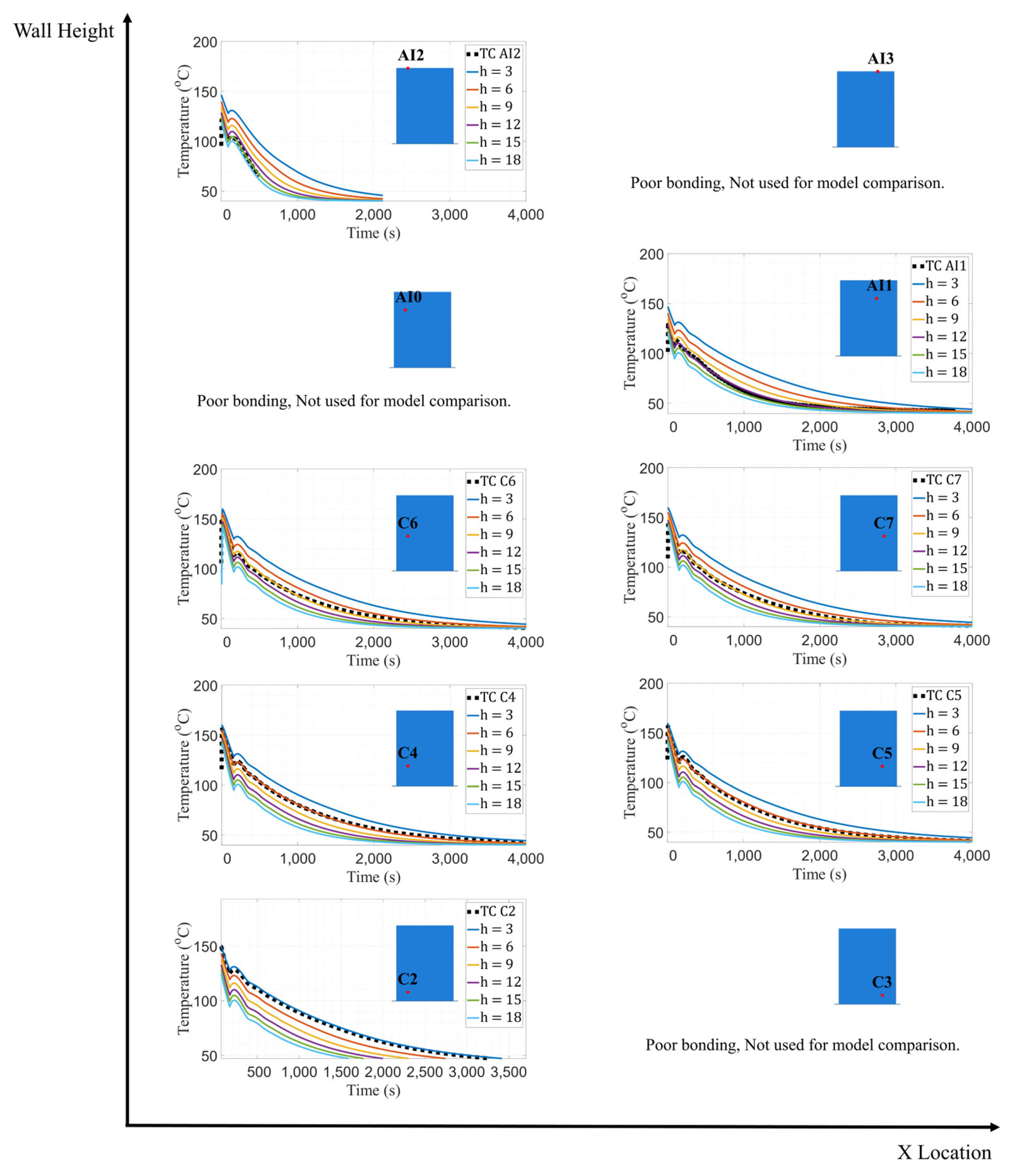
3.1. Wall/Bed Thermal Conductance Study
3.2. Wall Convection Study
3.3. Wall Residual Stress Study
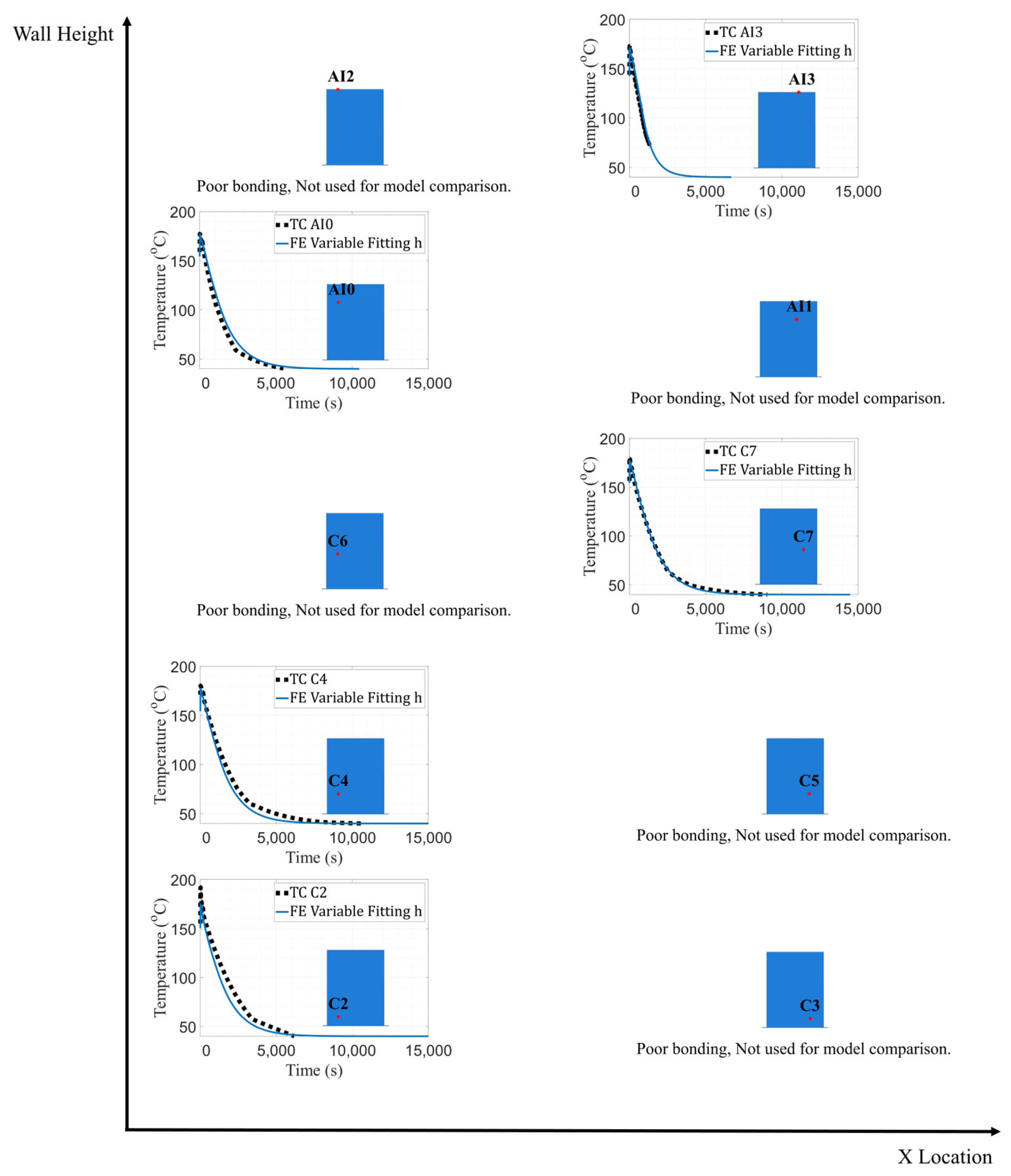
3.4. Extension to Other Vertical Walls Printed on BAAM
4. Conclusions
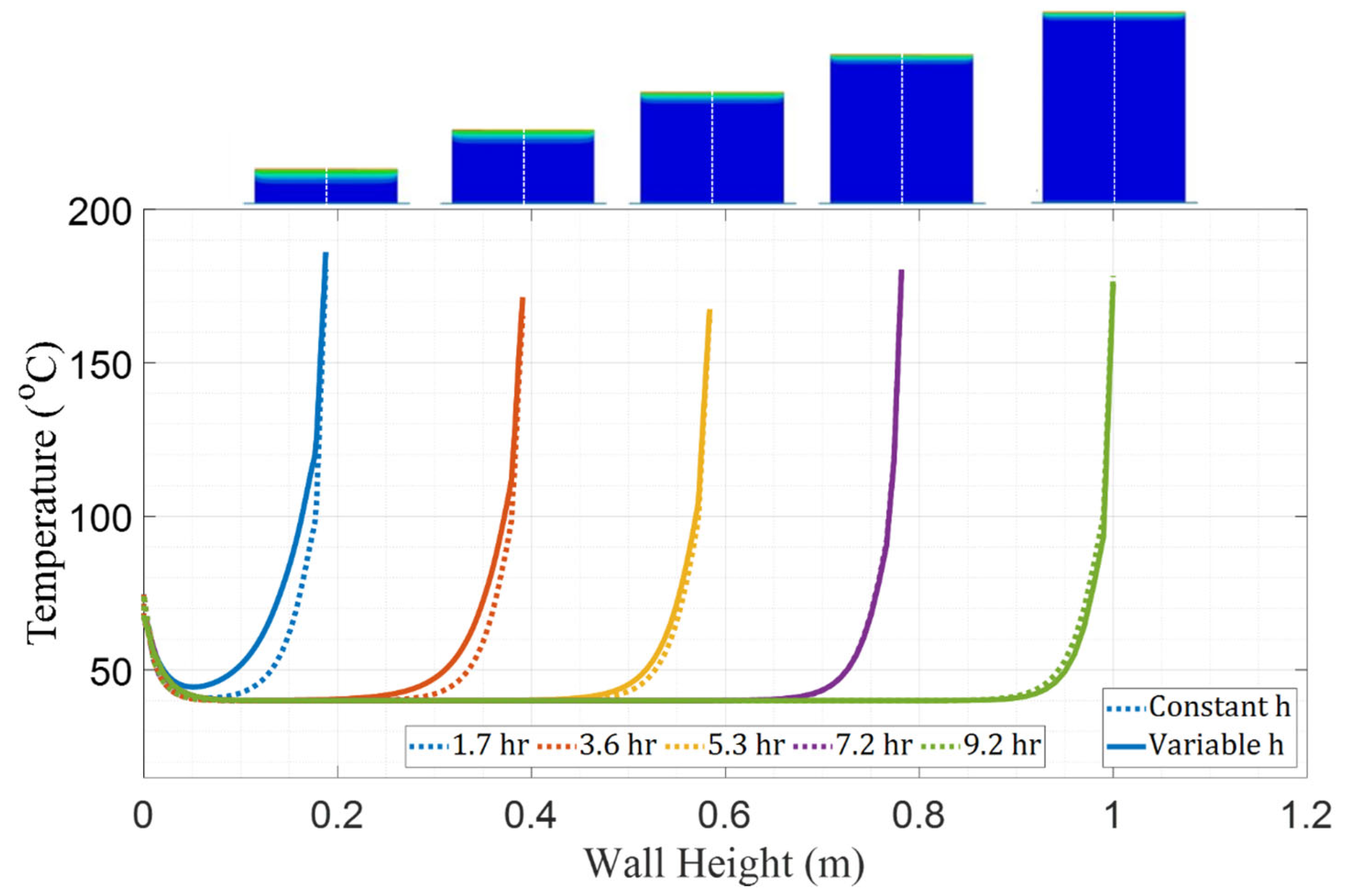
- There were significant differences in temperature predictions between FE models that applied constant or variable convection coefficients. During the early stages of manufacturing, the model with a constant convection coefficient over-predicts cooling and gradually transitions to an under-prediction of cooling rate.
- The progression of convection coefficients which minimized error in comparison with experimental data increased with the height of the wall. This may be due to the difference in air flow at regions of the wall at increasing heights above the BAAM print bed. The linearity of the increase of convection coefficient is a compelling result. However, this linear behavior cannot be extended as a rule, which is demonstrated by independent predictions of the thermal history from the ABS/CF wall manufactured with similar process conditions.
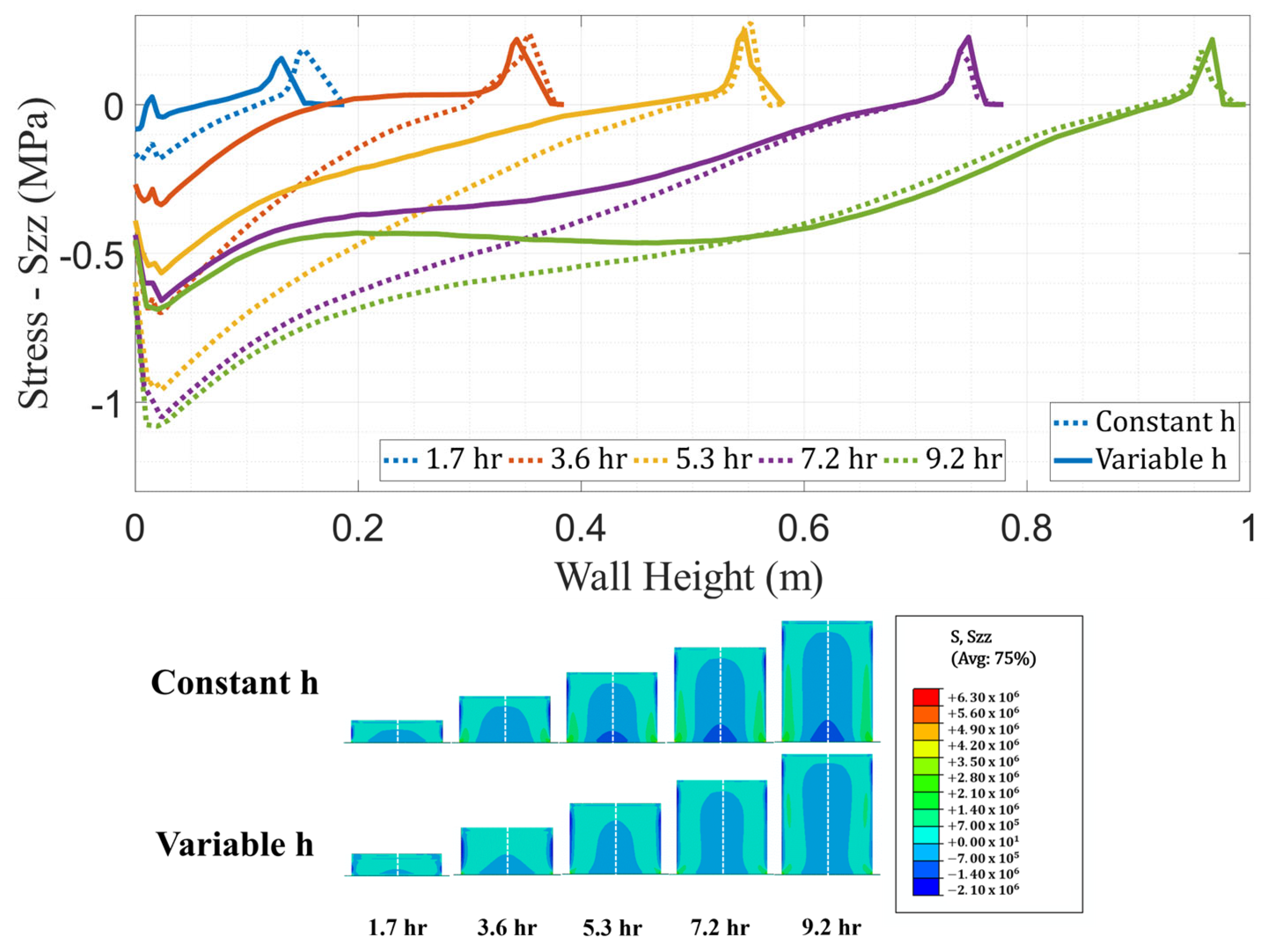
- Significant differences were found in stress predictions between both models. The model that used a constant convection coefficient predicted normal stresses in the vertical direction at locations closest to the bed and during all stages of manufacturing that were nearly double those predicted with the variable convection coefficient model. Although cracks were not observed in the part and both models predicted stresses below the material strength, these results suggest that accurate thermal modeling is crucial for the prediction of residual stresses and, consequently, part integrity during and immediately after the manufacturing process.
- Regarding material characterization, adding thermal conductivity data as a function of temperature to the FE thermal model may further improve model predictions.
- The analysis of data generated by the PETG/CF wall experiment enabled the derivation of a correlation equation between convection coefficient and air properties that can be applied to other vertical surfaces manufactured with the BAAM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Post, B.K.; Chesser, P.C.; Lind, R.F.; Roschli, A.; Love, L.J.; Gaul, K.T.; Sallas, M.; Blue, F.; Wu, S. Using Big Area Additive Manufacturing to Directly Manufacture a Boat Hull Mould. Virtual Phys. Prototyp. 2019, 14, 123–129. [Google Scholar] [CrossRef]
- Hassen, A.A.; Springfield, R.; Lindahl, J.; Post, B.; Love, L.; Duty, C.; Vaidya, U.; Pipes, R.B.; Kunc, V. The Durability of Large-Scale Additive Manufacturing Composite Molds. In Proceedings of the CAMX Conference Proceedings, Anaheim, CA, USA, 27–29 September 2016. [Google Scholar]
- Al Jassmi, H.; Al Najjar, F.; Mourad, A.-H.I. Large-Scale 3D Printing: The Way Forward. IOP Conf. Ser. Mater. Sci. Eng. 2018, 324, 012088. [Google Scholar] [CrossRef]
- Holshouser, C.; Newell, C.; Palas, S.; Love, L.J.; Kunc, V.; Lind, R.F.; Lloyd, P.D.; Rowe, J.C.; Blue, C.A.; Duty, C.E.; et al. Out of Bounds Additive Manufacturing. Adv. Mater. Process. 2013, 171, 15–17. [Google Scholar] [CrossRef]
- Love, L.J.; Kunc, V.; Rios, O.; Duty, C.E.; Elliott, A.M.; Post, B.K.; Smith, R.J.; Blue, C.A. The Importance of Carbon Fiber to Polymer Additive Manufacturing. J. Mater. Res. 2014, 29, 1893–1898. [Google Scholar] [CrossRef]
- Love, L.J. Utility of Big Area Additive Manufacturing (BAAM) for the Rapid Manufacture of Customized Electric Vehicles; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2015. [Google Scholar]
- Duty, C.E.; Kunc, V.; Compton, B.; Post, B.; Erdman, D.; Smith, R.; Lind, R.; Lloyd, P.; Love, L. Structure and Mechanical Behavior of Big Area Additive Manufacturing (BAAM) Materials. Rapid Prototyp. J. 2017, 23, 181–189. [Google Scholar] [CrossRef]
- Ferrini-Mundy, J.; Varahramyan, K. 2022 Research Report: R1 Global Impact—Local Relevance; University of Maine: Orono, ME, USA, 2023. [Google Scholar]
- Lee, J.-Y.; An, J.; Chua, C.K. Fundamentals and Applications of 3D Printing for Novel Materials. Appl. Mater. Today 2017, 7, 120–133. [Google Scholar] [CrossRef]
- Shofner, M.L.; Lozano, K.; Rodríguez-Macías, F.J.; Barrera, E.V. Nanofiber-reinforced Polymers Prepared by Fused Deposition Modeling. J. Appl. Polym. Sci. 2003, 89, 3081–3090. [Google Scholar] [CrossRef]
- Ahn, S.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic Material Properties of Fused Deposition Modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef]
- Hoskins, D.; Kunc, V.; Hassen, A.; Lindahl, J.; Duty, C. Characterizing Thermal Expansion of Large-Scale 3D Printed Parts. In Proceedings of the SAMPE 2019, Charlotte, NC, USA, 11 April 2019. [Google Scholar]
- Advani, S.G.; Tucker, C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Compton, B.G.; Post, B.K.; Duty, C.E.; Love, L.; Kunc, V. Thermal Analysis of Additive Manufacturing of Large-Scale Thermoplastic Polymer Composites. Addit. Manuf. 2017, 17, 77–86. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Development and Validation of Extrusion Deposition Additive Manufacturing Process Simulations. Addit. Manuf. 2019, 25, 218–226. [Google Scholar] [CrossRef]
- Brenken, B. Extrusion Deposition Additive Manufacturing of Fiber Reinforced Semi-Crystalline Polymers; Purdue University: West Lafayette, IN, USA, 2017. [Google Scholar]
- Zhang, Y.; Chou, Y.K. Three-Dimensional Finite Element Analysis Simulations of the Fused Deposition Modelling Process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2006, 220, 1663–1671. [Google Scholar] [CrossRef]
- Lieneke, T.; Denzer, V.; Adam, G.A.O.; Zimmer, D. Dimensional Tolerances for Additive Manufacturing: Experimental Investigation for Fused Deposition Modeling. Procedia CIRP 2016, 43, 286–291. [Google Scholar] [CrossRef]
- Alaimo, G.; Marconi, S.; Costato, L.; Auricchio, F. Influence of Meso-Structure and Chemical Composition on FDM 3D-Printed Parts. Compos. Part B Eng. 2017, 113, 371–380. [Google Scholar] [CrossRef]
- Ziemian, C.; Sharma, M.; Ziemian, S. Anisotropic Mechanical Properties of ABS Parts Fabricated by Fused Deposition Modelling. Mech. Eng. 2012, 23, 159–180. [Google Scholar]
- Soleyman, E.; Aberoumand, M.; Soltanmohammadi, K.; Rahmatabadi, D.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Baghani, M. 4D Printing of PET-G via FDM Including Tailormade Excess Third Shape. Manuf. Lett. 2022, 33, 1–4. [Google Scholar] [CrossRef]
- Soleyman, E.; Rahmatabadi, D.; Soltanmohammadi, K.; Aberoumand, M.; Ghasemi, I.; Abrinia, K.; Baniassadi, M.; Wang, K.; Baghani, M. Shape Memory Performance of PETG 4D Printed Parts under Compression in Cold, Warm, and Hot Programming. Smart Mater. Struct. 2022, 31, 085002. [Google Scholar] [CrossRef]
- Dinwiddie, R.B.; Love, L.J.; Rowe, J.C. Real-Time Process Monitoring and Temperature Mapping of a 3D Polymer Printing. In Proceedings of the SPIE 8705, Thermosense: Thermal Infrared Applications XXXV, Baltimore, MD, USA, 22 May 2013; Stockton, G.R., Colbert, F.P., Eds.; SPIE: Bellingham, WA, USA, 2013; Volume 8705, pp. 165–173. [Google Scholar]
- Dinwiddie, R.B.; Kunc, V.; Lindal, J.M.; Post, B.; Smith, R.J.; Love, L.; Duty, C.E. Infrared Imaging of the Polymer 3D-Printing Process. In Proceedings of the SPIE 9105, Thermosense: Thermal Infrared Applications XXXVI, Baltimore, MD, USA, 12 June 2014; Colbert, F.P., Hsieh, S.-J., Eds.; SPIE: Bellingham, WA, USA, 2014; p. 910502. [Google Scholar]
- Meraz Trejo, E.; Jimenez, X.; Billah, K.M.M.; Seppala, J.; Wicker, R.; Espalin, D. Compressive Deformation Analysis of Large Area Pellet-Fed Material Extrusion 3D Printed Parts in Relation to in Situ Thermal Imaging. Addit. Manuf. 2020, 33, 101099. [Google Scholar] [CrossRef]
- Planinsic, G. Infrared Thermal Imaging: Fundamentals, Research and Applications. Eur. J. Phys. 2011, 32, 1431. [Google Scholar] [CrossRef]
- Kousiatza, C.; Tzetzis, D.; Karalekas, D. In-Situ Characterization of 3D Printed Continuous Fiber Reinforced Composites: A Methodological Study Using Fiber Bragg Grating Sensors. Compos. Sci. Technol. 2019, 174, 134–141. [Google Scholar] [CrossRef]
- Kousiatza, C.; Chatzidai, N.; Karalekas, D. Temperature Mapping of 3D Printed Polymer Plates: Experimental and Numerical Study. Sensors 2017, 17, 456. [Google Scholar] [CrossRef] [PubMed]
- Chin, R.K.; Beuth, J.L.; Amon, C.H. Thermomechanical Modeling of Molten Metal Droplet Solidification Applied to Layered Manufacturing. Mech. Mater. 1996, 24, 257–271. [Google Scholar] [CrossRef]
- Talagani, M.; DorMohammadi, S.; Dutton, R.; Godines, C.; Kumar Baid, H.; Abdi, F.; Kunc, V.; Compton, B.G.; Simunovic, S.; Duty, C.; et al. Numerical Simulation of Big Area Additive Manufacturing (3D Printing) of a Full Size Car. SAMPE J. 2015, 51, 27–36. [Google Scholar]
- Bhandari, S.; Lopez-Anido, R. Finite Element Analysis of Thermoplastic Polymer Extrusion 3D Printed Material for Mechanical Property Prediction. Addit. Manuf. 2018, 22, 187–196. [Google Scholar] [CrossRef]
- Bhandari, S.; Lopez-Anido, R.A. Discrete-Event Simulation Thermal Model for Extrusion-Based Additive Manufacturing of PLA and ABS. Materials 2020, 13, 4985. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, X.Z.; Yu, W.W.; Deng, Y.H. Numerical Investigation of the Influence of Process Conditions on the Temperature Variation in Fused Deposition Modeling. Mater. Des. 2017, 130, 59–68. [Google Scholar] [CrossRef]
- Stockman, T.; Schneider, J.A.; Walker, B.; Carpenter, J.S. A 3D Finite Difference Thermal Model Tailored for Additive Manufacturing. JOM 2019, 71, 1117–1126. [Google Scholar] [CrossRef]
- Bhandari, S.; Lopez-Anido, R.A. Coupled Thermo-Mechanical Numerical Model to Minimize Risk in Large-Format Additive Manufacturing of Thermoplastic Composite Designs. Prog. Addit. Manuf. 2023, 8, 393–407. [Google Scholar] [CrossRef]
- Zhou, Y.; Nyberg, T.; Xiong, G.; Liu, D. Temperature Analysis in the Fused Deposition Modeling Process. In Proceedings of the 2016 3rd International Conference on Information Science and Control Engineering (ICISCE), Beijing, China, 8–10 July 2016; pp. 678–682. [Google Scholar]
- Ji, L.B.; Zhou, T.R. Finite Element Simulation of Temperature Field in Fused Deposition Modeling. Adv. Mater. Res. 2010, 97–101, 2585–2588. [Google Scholar] [CrossRef]
- D’Amico, A.; Peterson, A.M. An Adaptable FEA Simulation of Material Extrusion Additive Manufacturing Heat Transfer in 3D. Addit. Manuf. 2018, 21, 422–430. [Google Scholar] [CrossRef]
- Bhandari, S.; Lopez-Anido, R. Finite Element Modeling of 3D-Printed Part with Cellular Internal Structure Using Homogenized Properties. Prog. Addit. Manuf. 2019, 4, 143–154. [Google Scholar] [CrossRef]
- Deering, R.A. Additive Manufacturing Part Level Distortion Sensitivity Analysis within Abaqus on a Thin Walled, Tubular Structure. 2018. Available online: https://www.3ds.com/fileadmin/PRODUCTS-SERVICES/SIMULIA/Resources-center/PDF/2018-SaoE-Additive_Manufacturing_Part_Level_Distortion_Sensitivity_Analysis_within_Abaqus_on_a_Thin-walled__Tubular_Structure.pdf (accessed on 28 September 2023).
- Cattenone, A.; Morganti, S.; Alaimo, G.; Auricchio, F. Finite Element Analysis of Additive Manufacturing Based on Fused Deposition Modeling: Distortions Prediction and Comparison with Experimental Data. J. Manuf. Sci. Eng. 2019, 141, 011010. [Google Scholar] [CrossRef]
- Courter, B.; Savane, V.; Bi, J.; Dev, S.; Hansen, C.J. Finite Element Simulation of the Fused Deposition Modelling Process. In Proceedings of the NAFEMS World Congress, Stockholm, Sweden, 11–13 June 2017; pp. 11–14. [Google Scholar]
- Favaloro, A.J.; Brenken, B.; Barocio, E.; Pipes, R.B. Simulation of Polymeric Composites Additive Manufacturing Using Abaqus. In Proceedings of the Science in the Age of Experience, Chicago, IL, USA, 15–18 May 2017; pp. 103–114. [Google Scholar]
- Vaca, E.B. Fusion Bonding of Fiber Reinforced Semi-Crystalline Polymers in Extrusion Deposition Additive Manufacturing; Purdue University: West Lafayette, IN, USA, 2018. [Google Scholar]
- Nycz, A.; Lee, Y.; Noakes, M.; Ankit, D.; Masuo, C.; Simunovic, S.; Bunn, J.; Love, L.; Oancea, V.; Payzant, A.; et al. Effective Residual Stress Prediction Validated with Neutron Diffraction Method for Metal Large-Scale Additive Manufacturing. Mater. Des. 2021, 205, 109751. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S.; Nouri, H. Printability and Tensile Performance of 3D Printed Polyethylene Terephthalate Glycol Using Fused Deposition Modelling. Polymers 2019, 11, 1220. [Google Scholar] [CrossRef]
- Dolzyk, G.; Jung, S. Tensile and Fatigue Analysis of 3D-Printed Polyethylene Terephthalate Glycol. J. Fail. Anal. Prev. 2019, 19, 511–518. [Google Scholar] [CrossRef]
- Billah, K.M.M.; Lorenzana, F.A.R.; Martinez, N.L.; Wicker, R.B.; Espalin, D. Thermomechanical Characterization of Short Carbon Fiber and Short Glass Fiber-Reinforced ABS Used in Large Format Additive Manufacturing. Addit. Manuf. 2020, 35, 101299. [Google Scholar] [CrossRef]
- Rios, O.; Carter, W.; Post, B.; Lloyd, P.; Fenn, D.; Kutchko, C.; Rock, R.; Olson, K.; Compton, B. 3D Printing via Ambient Reactive Extrusion. Mater. Today Commun. 2018, 15, 333–336. [Google Scholar] [CrossRef]
- Huang, H.; Ma, N.; Chen, J.; Feng, Z.; Murakawa, H. Toward Large-Scale Simulation of Residual Stress and Distortion in Wire and Arc Additive Manufacturing. Addit. Manuf. 2020, 34, 101248. [Google Scholar] [CrossRef]
- Nycz, A.; Kishore, V.; Lindahl, J.; Duty, C.; Carnal, C.; Kunc, V. Controlling Substrate Temperature with Infrared Heating to Improve Mechanical Properties of Large-Scale Printed Parts. Addit. Manuf. 2020, 33, 101068. [Google Scholar] [CrossRef]
- Colón Quintana, J.L.; Slattery, L.; Pinkham, J.; Keaton, J.; Lopez-Anido, R.A.; Sharp, K. Effects of Fiber Orientation on the Coefficient of Thermal Expansion of Fiber-Filled Polymer Systems in Large Format Polymer Extrusion-Based Additive Manufacturing. Materials 2022, 15, 2764. [Google Scholar] [CrossRef] [PubMed]
- ASTM D792–20; Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement. West ASTM: Conshohocken, PA, USA, 2020.
- ASTM D3418–21; Standard Test Method for Transition Temperatures and Enthalpies of Fusion and Crystallization of Polymers by Differential Scanning Calorimetry. ASTM: Conshohocken, PA, USA, 2021.
- ISO/DIS 22007-2; Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 2: Transient Plane Source Method. ISO: Geneva, Switzerland, 2022.
- ASTM E831-19; Standard Test Method for Linear Thermal Expansion of Solid Materials by Thermomechanical Analysis. ASTM: Conshohocken, PA, USA, 2019.
- ASTM D7028-07; Standard Test Method for Glass Transition Temperature (DMA Tg) of Polymer Matrix Composites by Dy-Namic Mechanical Analysis (DMA). ASTM: Conshohocken, PA, USA, 2015.
- ASTM D5023-15; Standard Test Method for Plastics: Dynamic Mechanical Properties: In Flexure (Three-Point Bending). ASTM: Conshohocken, PA, USA, 2016.
- Steva, B.; Warren, K.; Seigars, C.; Helten, B. Evaluation of the Shear Behavior of CF-PETG and CF-PC Coupons Manufactured Using Large-Scale Additive Manufacturing Processes. In Proceedings of the ECCM20—The 20th European Conference on Composite Materials, Lausanne, Switzerland, 26–30 June 2022. [Google Scholar]
- Seigars, C.; Warren, K.; Steva, B.; Murphy, C.; Helten, B. Characterizing the Tensile and Compressive Behavior of PETG/CF and PC/CF Manufactured Using Large Scale Additive Processes. In Proceedings of the ECCM20—The 20th European Conference on Composite Materials, Lausanne, Switzerland, 26–30 June 2022. [Google Scholar]
- Kim, P.; Baid, H.; Hassen, A.; Kumar, A.; Lindahl, J.; Hoskins, D.; Ajinjeru, C.; Duty, C.; Yeole, P.; Vaidya, U.; et al. Analysis on Part Distortion and Residual Stress in Big Area Additive Manufacturing with Carbon Fiber-Reinforced Thermoplastic Using Dehomogenization Technique. In Proceedings of the Composites and Advanced Materials Expo (CAMX 2019), Anaheim, CA, USA, 23–26 September 2019. [Google Scholar]
- Choo, K.; Friedrich, B.; Daugherty, T.; Schmidt, A.; Patterson, C.; Abraham, M.A.; Conner, B.; Rogers, K.; Cortes, P.; MacDonald, E. Heat Retention Modeling of Large Area Additive Manufacturing. Addit. Manuf. 2019, 28, 325–332. [Google Scholar] [CrossRef]
- Morgan, R.V.; Stowers Reid, R.; Baker, A.M.; Lucero, B.; Bernardin, J.D. Emissivity Measurements of Additively Manufactured Materials; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2017. [Google Scholar]
- Na, T.Y. Numerical Solution of Natural Convection Flow Past a Non-Isothermal Vertical Flat Plate. Appl. Sci. Res. 1977, 33, 519–543. [Google Scholar] [CrossRef]
- Chen, T.Y.W.; Wollersheim, D.E. Free Convection at a Vertical Plate with Uniform Flux Condition in Non-Newtonian Power-Law Fluids. J. Heat Transf. 1973, 95, 123–124. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Gregg, J.L. Laminar Free Convection from a Vertical Plate with Uniform Surface Heat Flux. J. Fluids Eng. 1956, 78, 435–440. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Hawkins, G.A.; Jakob, M. Heat Transfer by Free Convection from Heated Vertical Surfaces to Liquids. J. Fluids Eng. 1948, 70, 13–17. [Google Scholar] [CrossRef]
- Cheesewright, R. Turbulent Natural Convection from a Vertical Plane Surface. J. Heat Transf. 1968, 90, 1–6. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H.S. Correlating Equations for Laminar and Turbulent Free Convection from a Vertical Plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals and Applications; McGraw-Hill Education: New York, NY, USA, 2020. [Google Scholar]
- Properties of Air at 1 Atm Pressure. Engineers Edge. Available online: https://www.engineersedge.com/physics/properties_of_air_at_1_atm_pressure_13828.htm (accessed on 28 September 2023).
- ASTM D638-22; Standard Test Method for Tensile Properties of Plastics. ASTM: Conshohocken, PA, USA, 2022.
- Havet, M.; Blay, D. Natural Convection over a Non-Isothermal Vertical Plate. Int. J. Heat Mass Transf. 1999, 42, 3103–3112. [Google Scholar] [CrossRef]
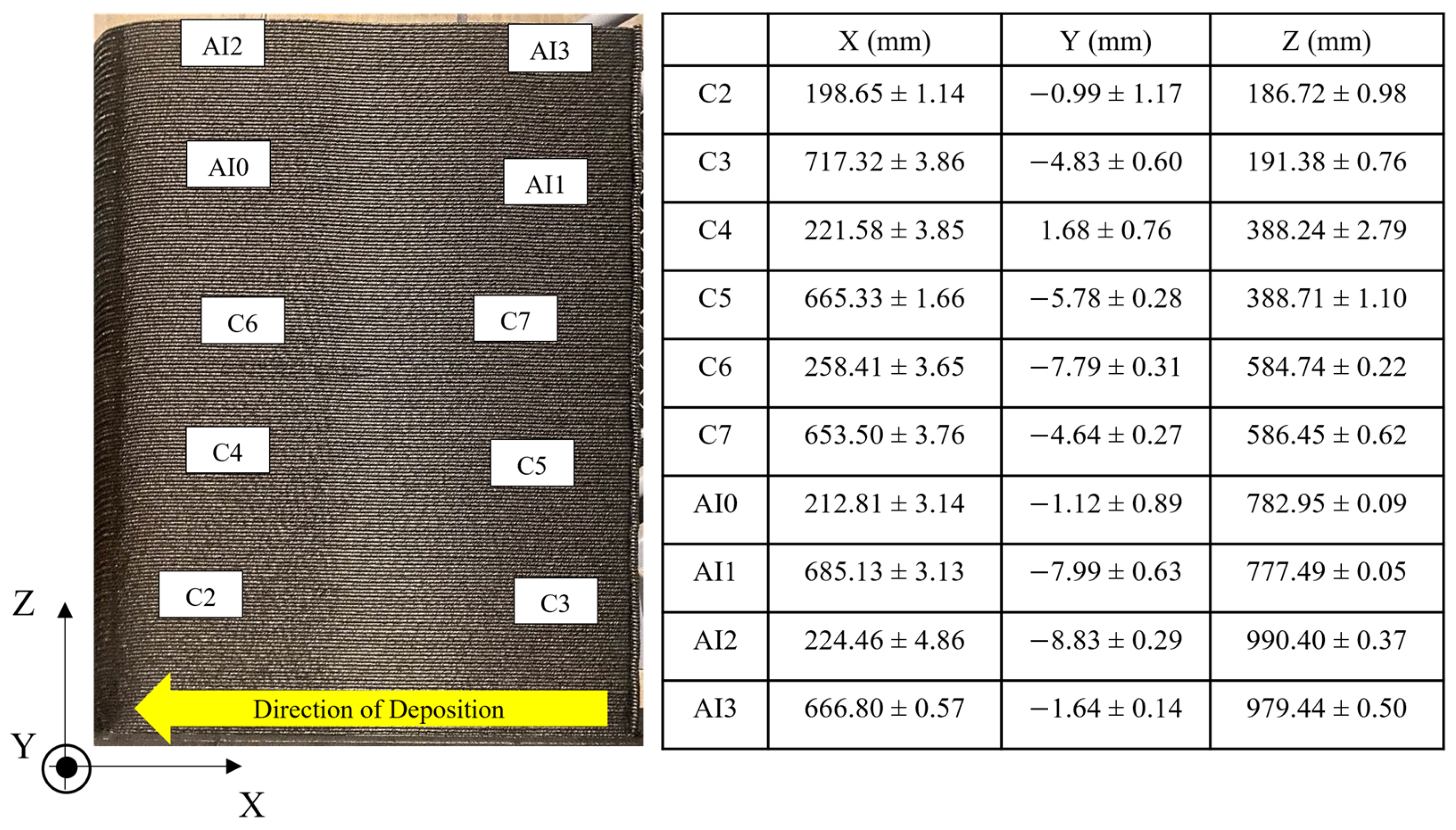

| Dimensions | Value | Printing Process Information | Value |
|---|---|---|---|
| Wall Height (m) | 1 | Deposition Temperature (°C) | 200 |
| Wall Length (m) | 0.75 | Bed Set Temperature (°C) | 90 |
| Bead Width (mm) | 15.875 | Dryer Temperature (°C) | 60 |
| Bead Height (mm) | 5.08 | Feed Rate (m/min) | 3.24 |
| Bead Count | 1 | Deposition/Layer Time (s) | <168/13.9 |
| Layer Count | 197 | Manufacturing Time (hours) | <10 |
| Temperature (°C) | 25 | 60 | 75 | 90 | 125 | 200 | 225 |
| Cp (J/kg°C) | 763.8 | 903.2 | 1154.4 | 1181.6 | 1268.8 | 1442.4 | 1496.6 |
| Temperature (°C) | Exx (MPa) | Eyy (MPa) | Ezz (MPa) | Gxy (MPa) | Gxz (MPa) | Gyz (MPa) | νxy | νyz | νxz |
|---|---|---|---|---|---|---|---|---|---|
| 20 | 12,100 ± 15 | 2720 | 2720 ± 10 | 1110 | 1110 | 1134 | 0.38 | 0.39 | 0.38 |
| 32.8 | 6876 ± 18 | 2612 | 2612 ± 12 | 2509 | 2509 | 972 | 0.32 | 0.34 | 0.32 |
| 44.3 | 6761 ± 19 | 2569 | 2569 ± 12 | 2467 | 2467 | 955 | 0.32 | 0.34 | 0.32 |
| 54.2 | 6640 ± 24 | 2523 | 2523 ± 13 | 2423 | 2423 | 938 | 0.32 | 0.34 | 0.32 |
| 64.5 | 6389 ± 25 | 2427 | 2427 ± 13 | 2332 | 2332 | 903 | 0.32 | 0.34 | 0.32 |
| 74.2 | 4289 ± 25 | 1630 | 1630 ± 13 | 1565 | 1565 | 606 | 0.32 | 0.34 | 0.32 |
| Wall Height (m) | Convection Coefficient—h (W/m2K) |
|---|---|
| 0.19 | 3 |
| 0.39 | 6 |
| 0.58 | 9 |
| 0.78 | 12 |
| 0.98 | 15 |
| Properties | Value |
|---|---|
| Ambient Temperature (°C) | 40 |
| Deposition Temperature (°C) | 200 |
| Wall Height (m) | 1 |
| Air Density (kg/m3) | 1.127 |
| Air Thermal Diffusivity (m2/s) | 2.346 × 10−5 |
| Air Kinetic Viscosity (m2/s) | 1.702 × 10−5 |
| Air Thermal Conductivity (W/mK) | 0.02662 |
| Gravitational Constant (m/s2) | 9.81 |
| Wall Height (m) | Convection Coefficient—h (W/m2K) |
|---|---|
| 0.19 | 3 |
| 0.39 | 3 |
| 0.58 | 6 |
| 0.78 | 9 |
| 0.98 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robles Poblete, F.; Ireland, M.; Slattery, L.; Davids, W.G.; Lopez-Anido, R.A. In Situ, Real-Time Temperature Mapping and Thermal FE Simulations of Large-Format 3D Printed PETG/CF Vertical Wall. Materials 2023, 16, 6486. https://doi.org/10.3390/ma16196486
Robles Poblete F, Ireland M, Slattery L, Davids WG, Lopez-Anido RA. In Situ, Real-Time Temperature Mapping and Thermal FE Simulations of Large-Format 3D Printed PETG/CF Vertical Wall. Materials. 2023; 16(19):6486. https://doi.org/10.3390/ma16196486
Chicago/Turabian StyleRobles Poblete, Felipe, Matthew Ireland, Lucinda Slattery, William G. Davids, and Roberto A. Lopez-Anido. 2023. "In Situ, Real-Time Temperature Mapping and Thermal FE Simulations of Large-Format 3D Printed PETG/CF Vertical Wall" Materials 16, no. 19: 6486. https://doi.org/10.3390/ma16196486
APA StyleRobles Poblete, F., Ireland, M., Slattery, L., Davids, W. G., & Lopez-Anido, R. A. (2023). In Situ, Real-Time Temperature Mapping and Thermal FE Simulations of Large-Format 3D Printed PETG/CF Vertical Wall. Materials, 16(19), 6486. https://doi.org/10.3390/ma16196486








