Numerical Simulation Analysis of Fracture Propagation in Rock Based on Smooth Particle Hydrodynamics
Abstract
:1. Introduction
2. The Basic Theory of SPH
2.1. Basic Ideas of SPH
2.2. SPH Basic Formula
2.3. Smooth Function
3. Implementation Method
3.1. Particle Search Method
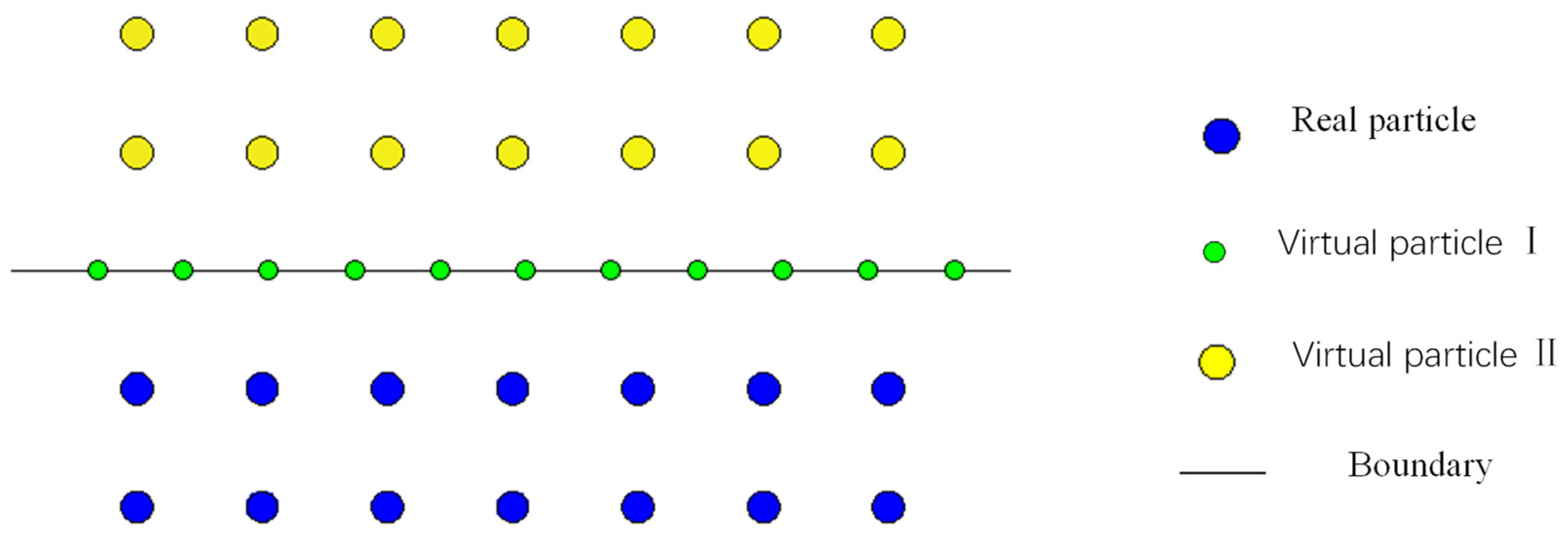
3.2. Boundary Condition
3.3. Time Integral
3.4. Realization of Solid Mechanics Constitutive Equation in SPH
3.5. Brittle Damage Fracture Model
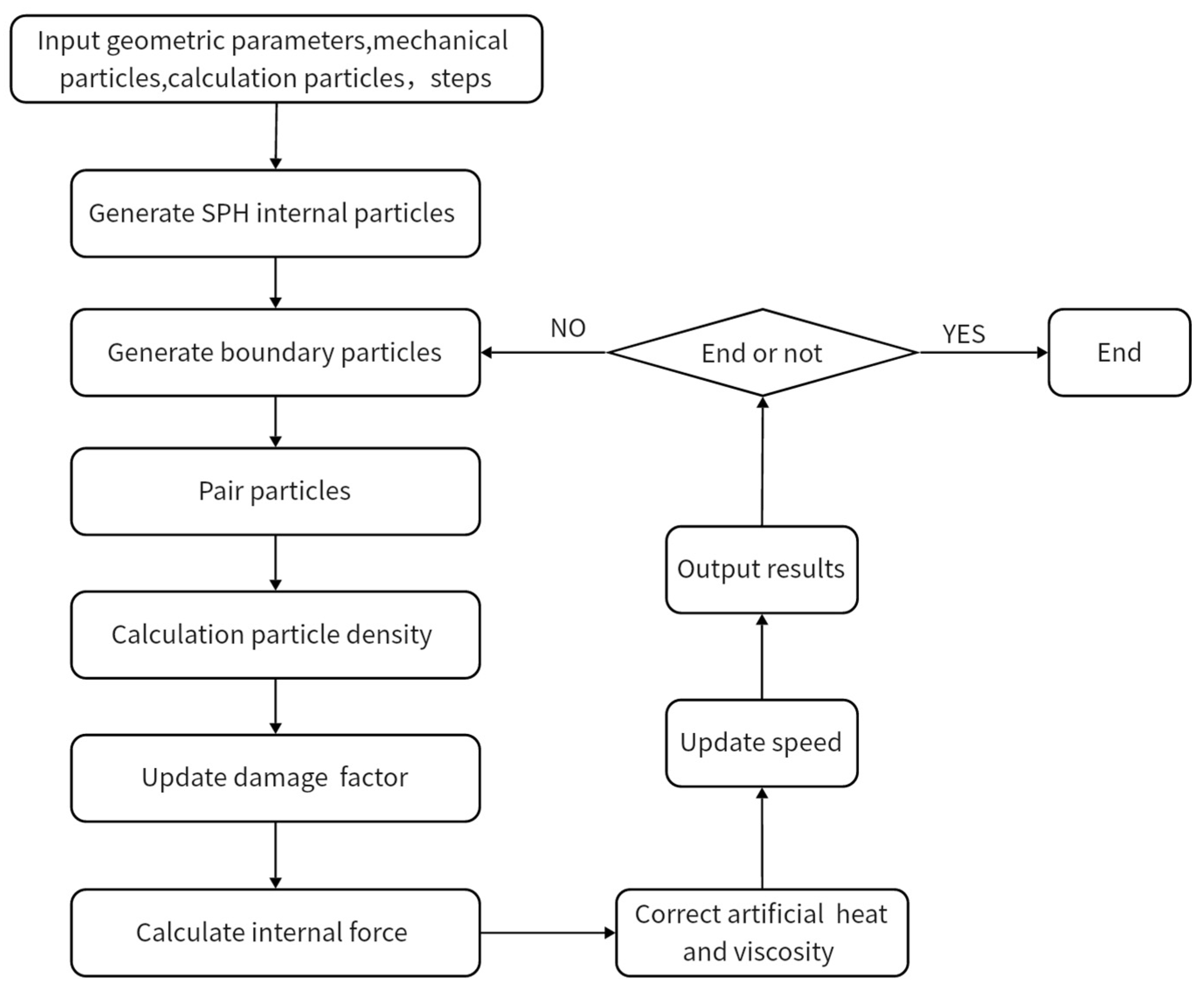
3.6. Programming Architecture
4. Example Analysis
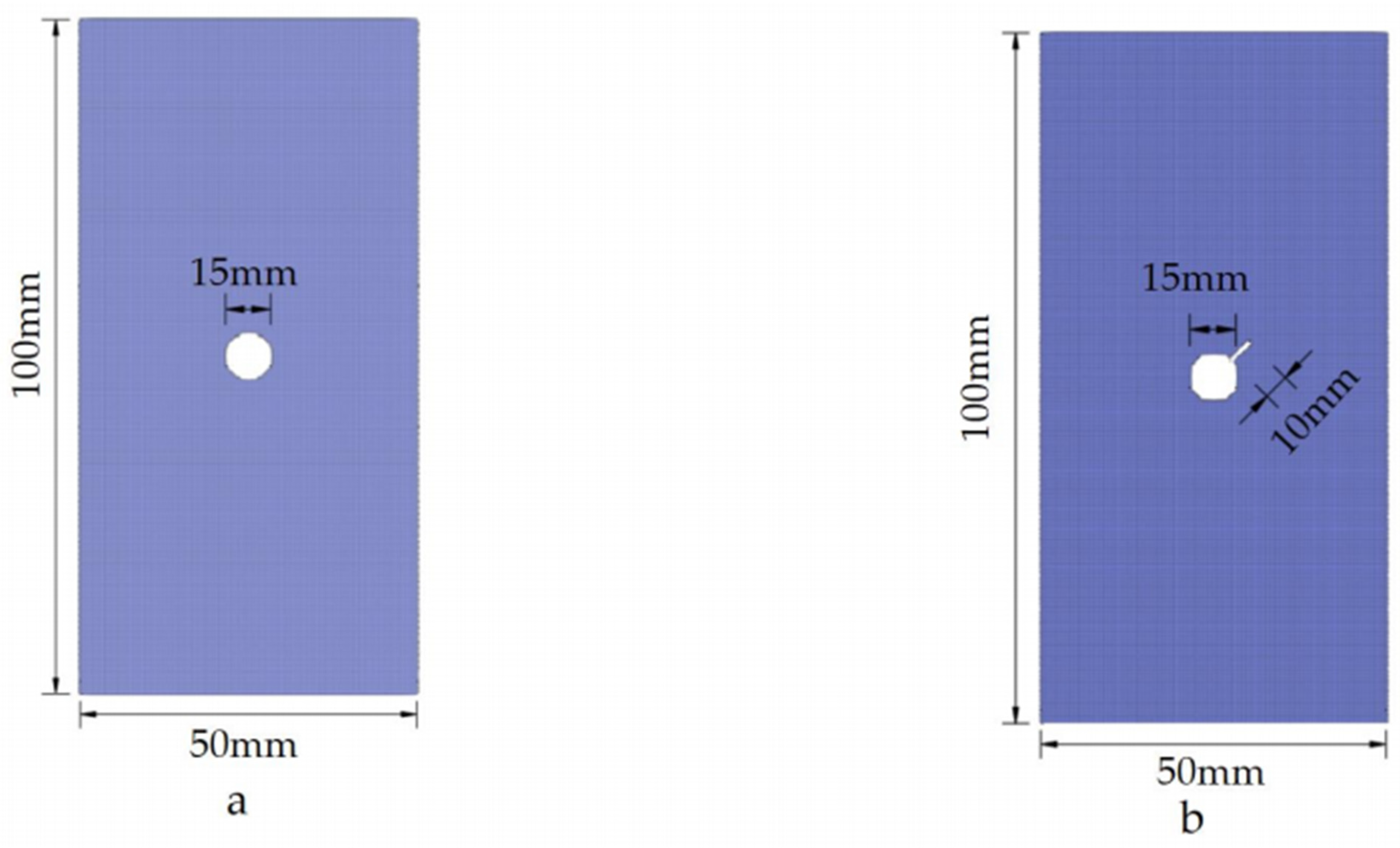
4.1. Example Size
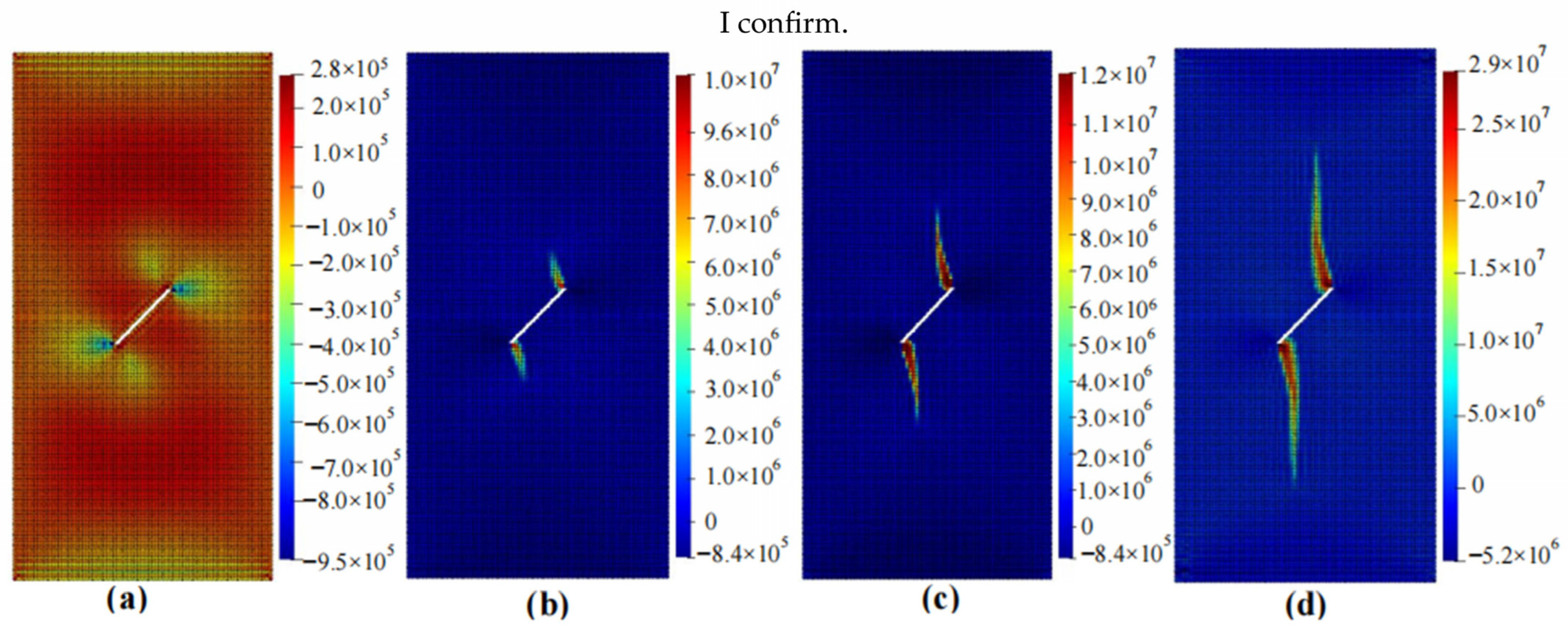
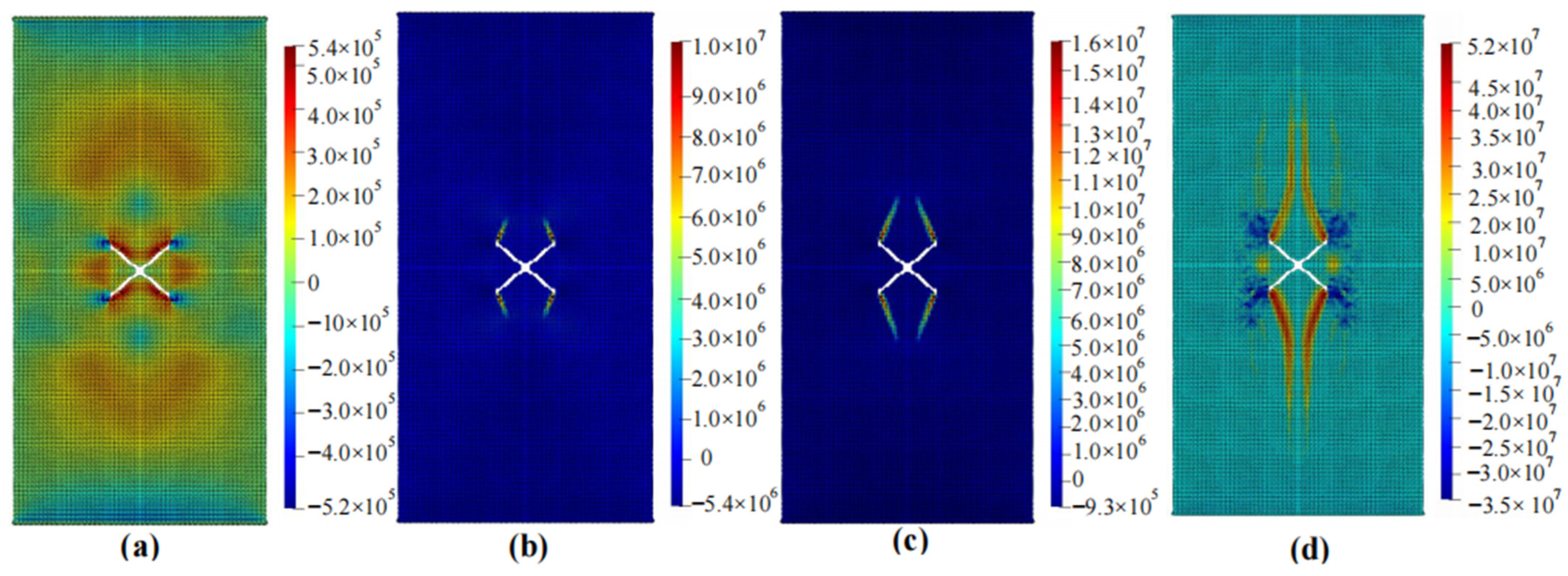
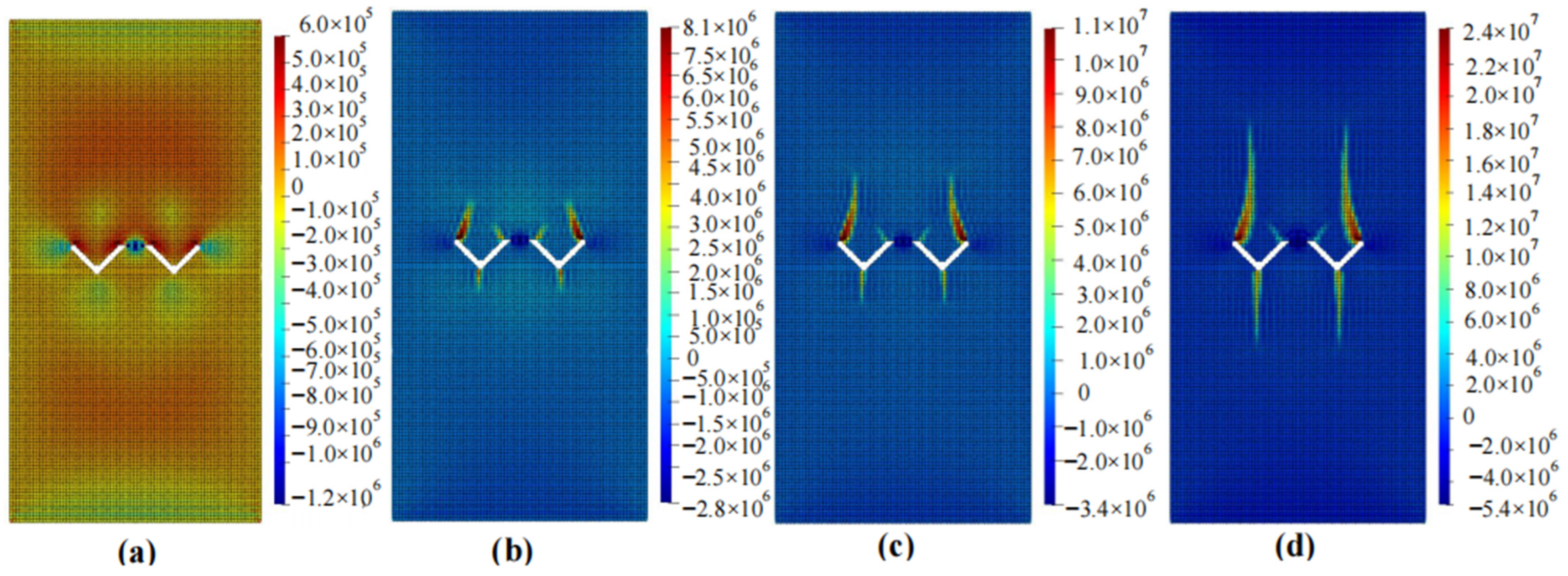
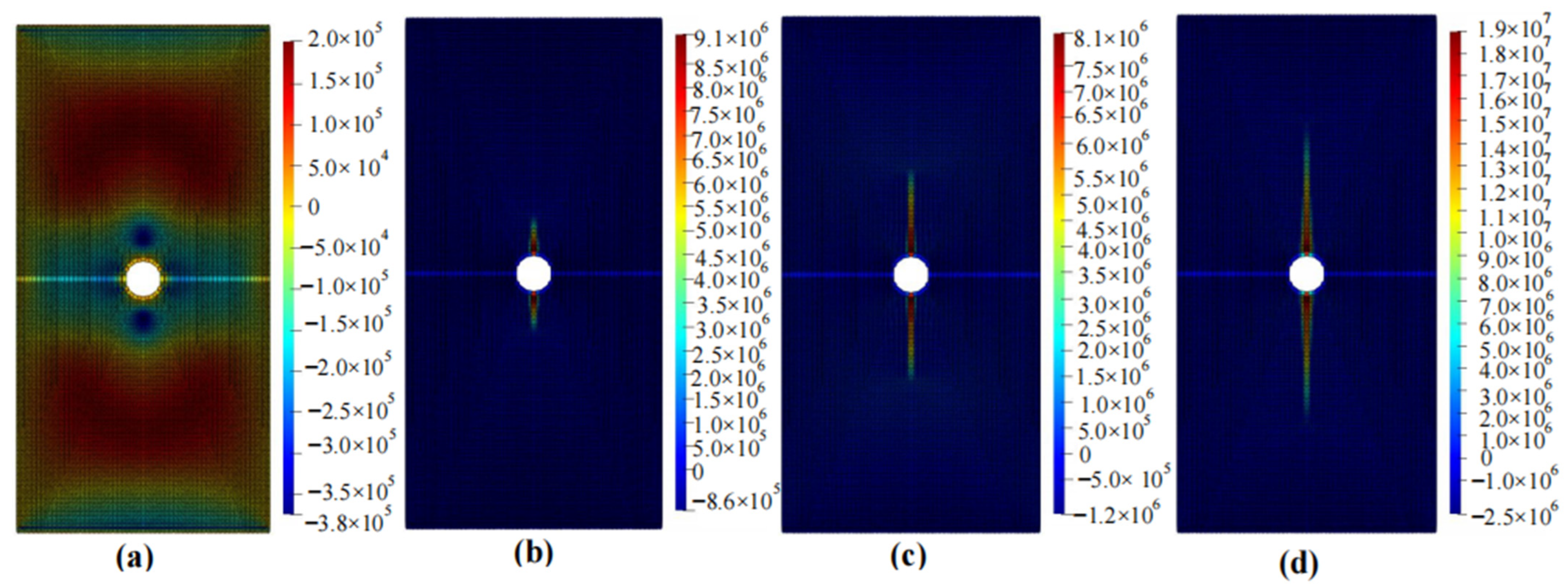
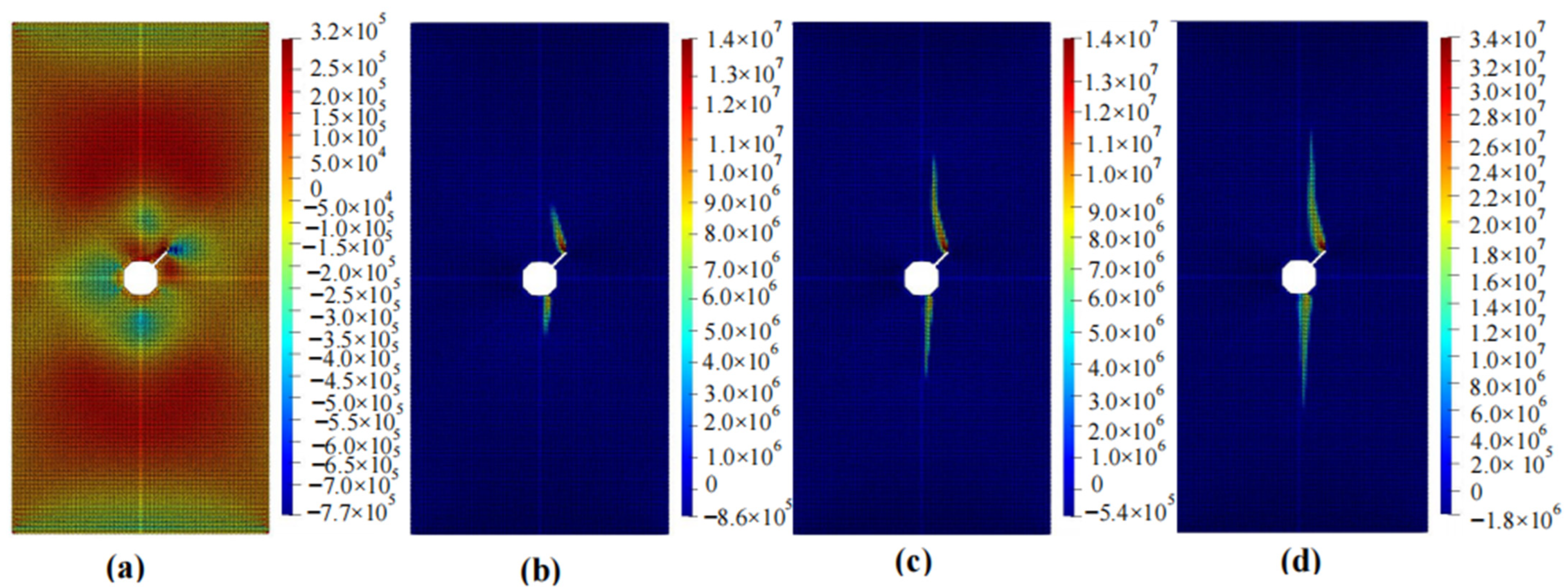
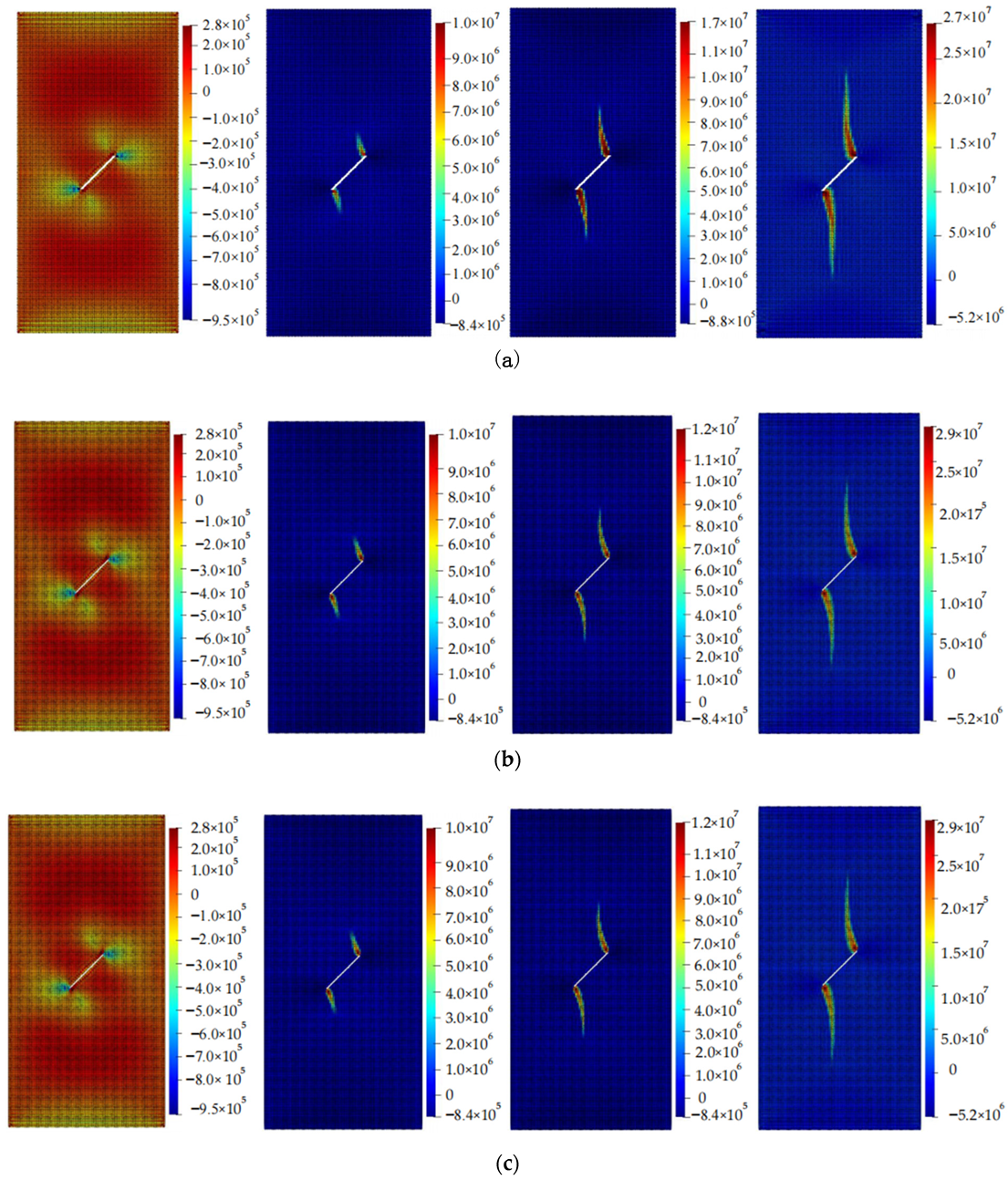
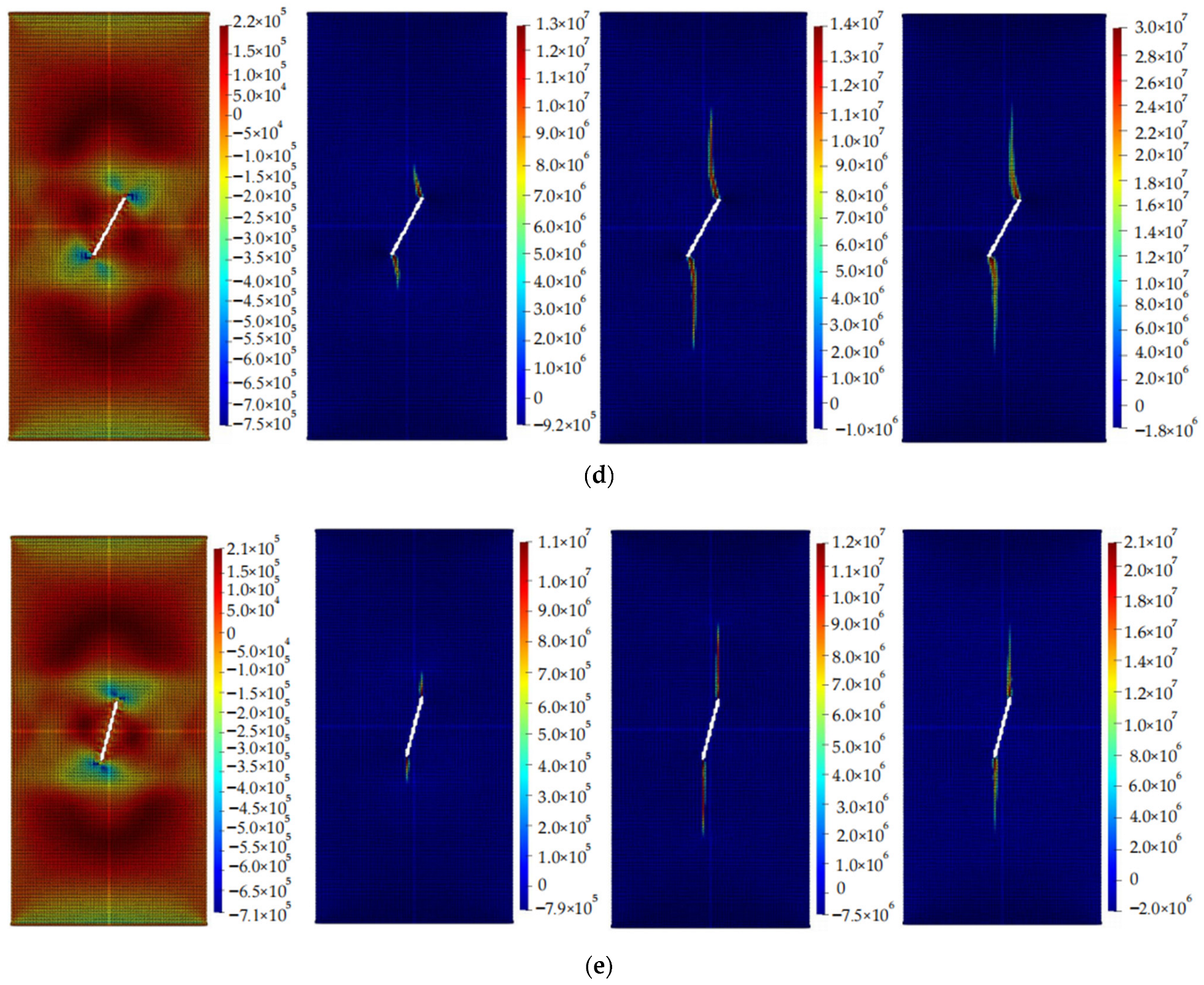
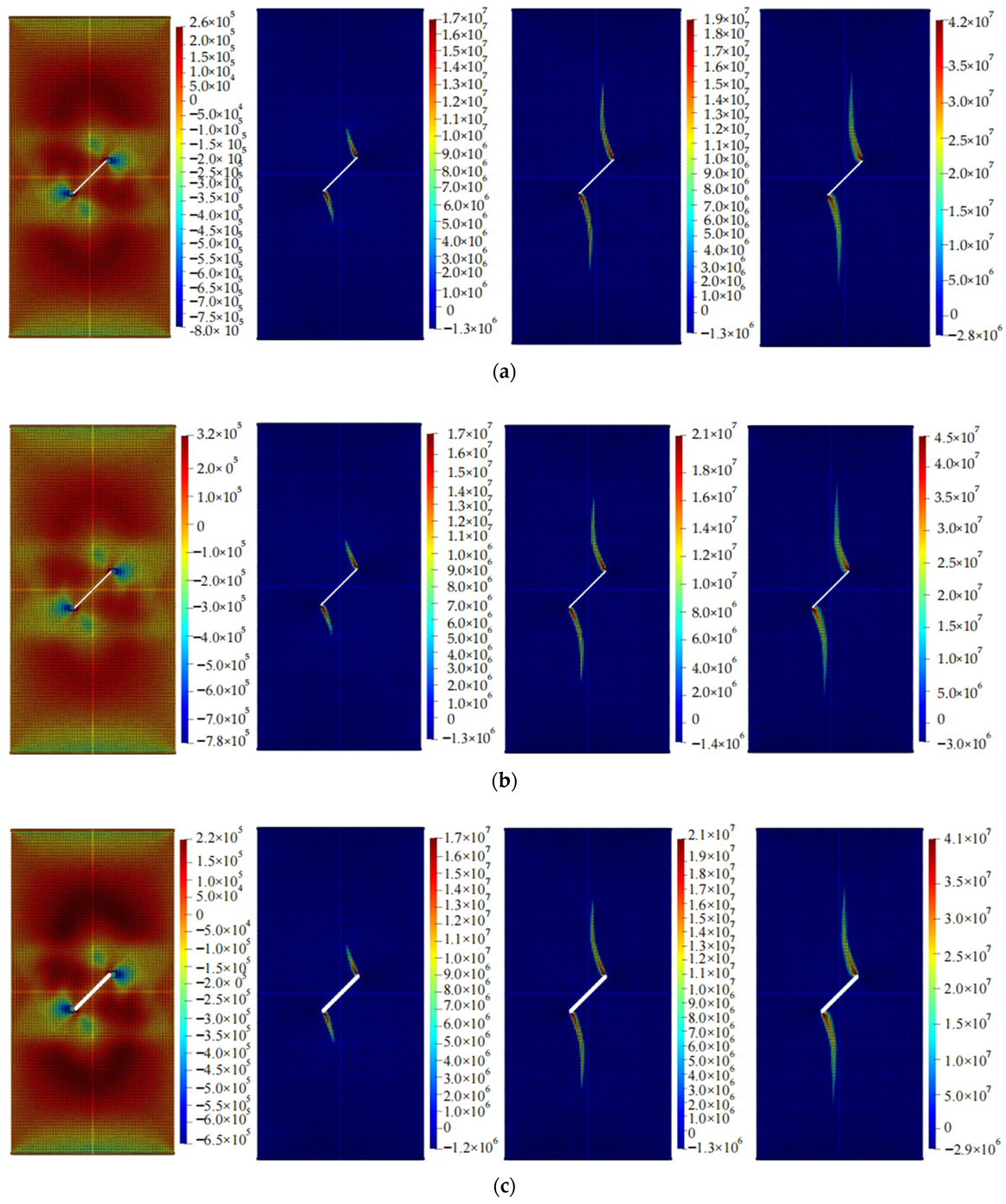
4.2. Calculation Results
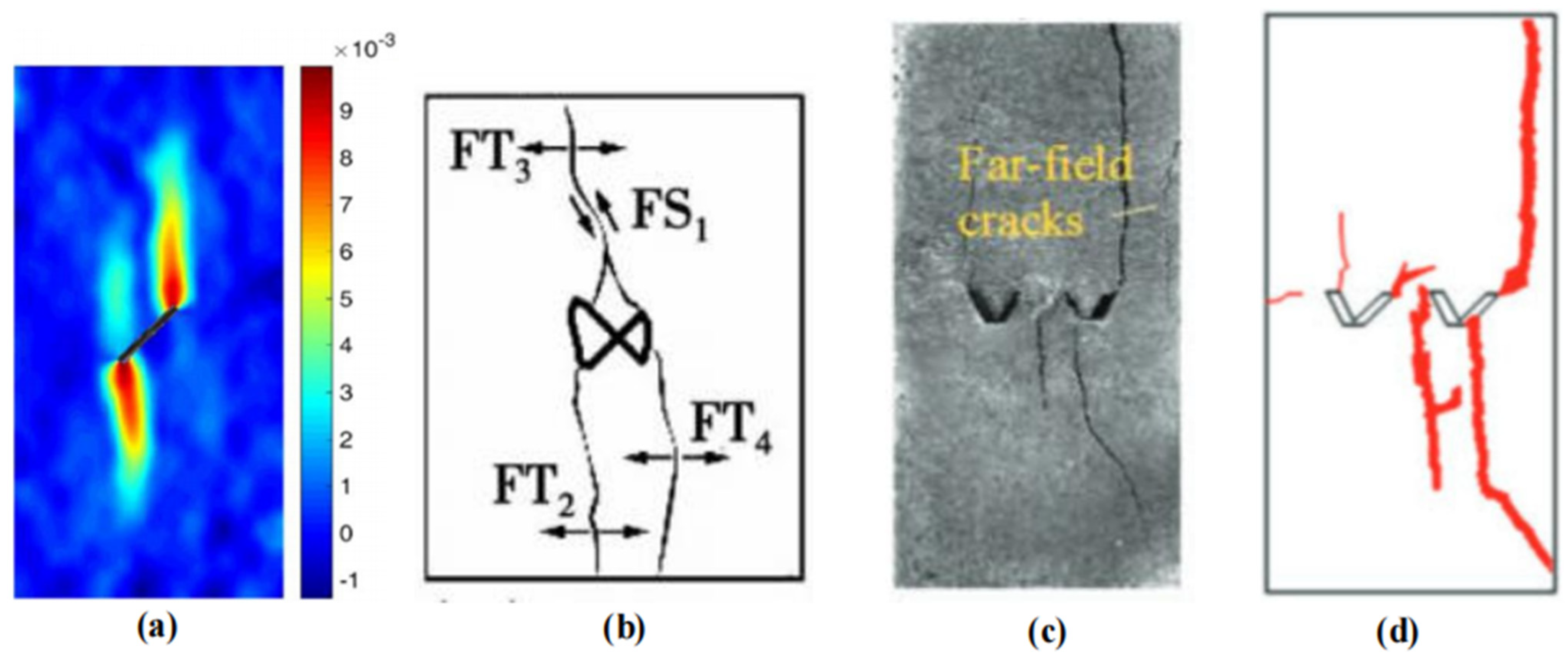
4.3. Comparison with Existing Experimental or Numerical Simulation Results and Validation
4.4. Influence of Particle Number
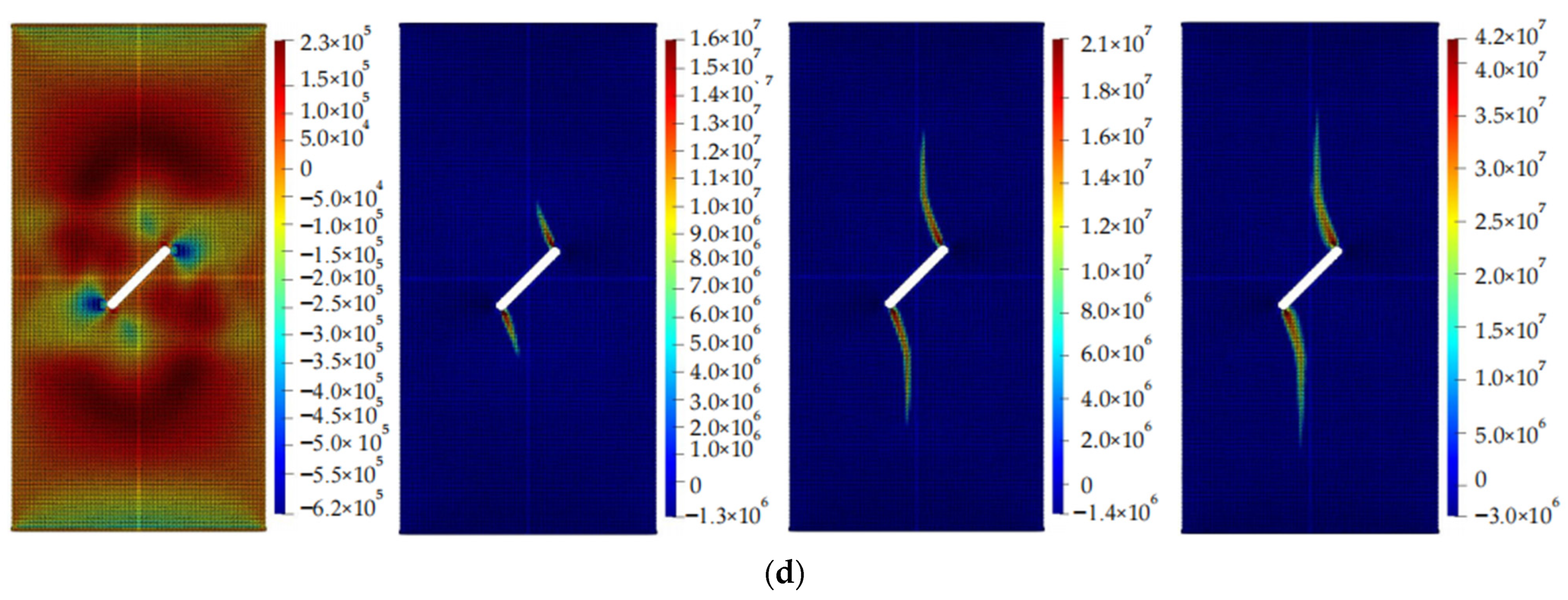
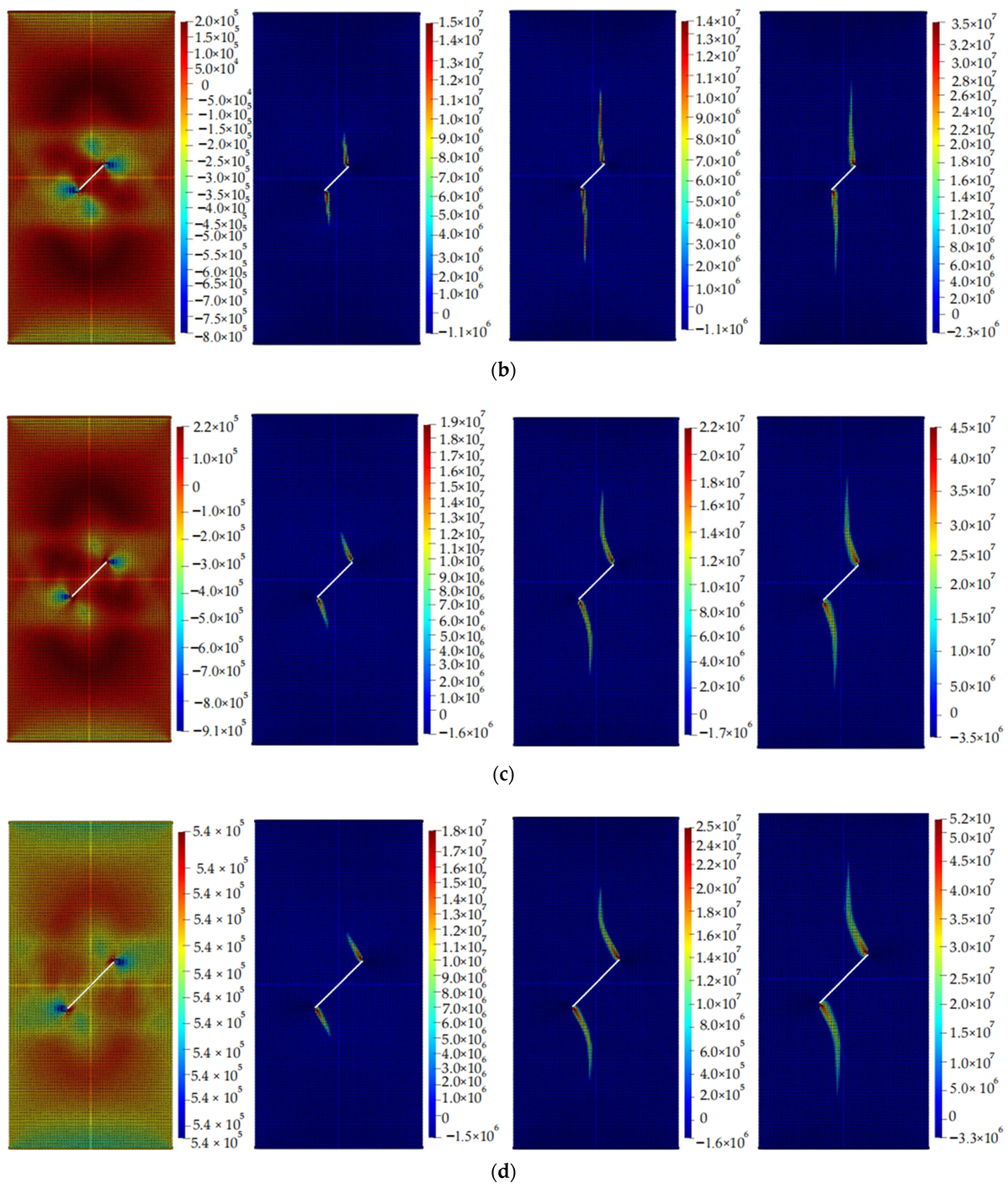
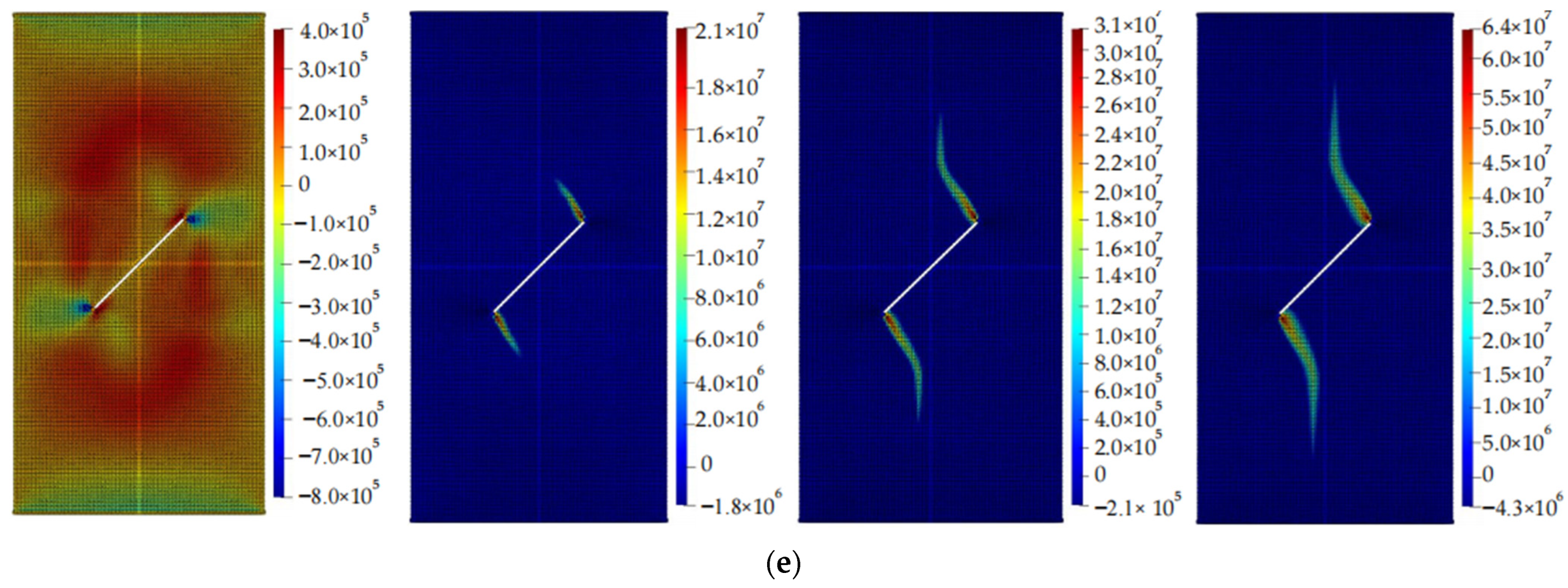
5. The Relationship between Crack Propagation and Geometric Parameters of Cracks
5.1. The Relationship between Crack Propagation and Inclination Angle
5.2. Relationship with Crack Width
5.3. Relationship with Crack Length
6. Conclusions
- a.
- This study applies the SPH method with a fifth-order smoothing function to solid mechanics. This method is relatively simple in regard to programming and can effectively simulate the crack propagation and failure processes of rock materials. Our numerical simulation results are in good agreement with previous experimental and numerical simulation results, demonstrating the method’s efficacy in studying crack propagation and providing guidance for rock mechanics research. The number of particles has a minor influence on the calculation results.
- b.
- Stress concentration often originates at the tip of a crack and tends to propagate longitudinally. For specimens with circular holes, crack propagation mainly occurs at the top and bottom of the hole. If there are cracks around the hole, the failure will preferentially occur at the crack rather than the top or bottom of the hole. The specimen starts to fail at a displacement of approximately 0.01 mm to 0.02 mm, and complete failure occurs at a displacement of around 0.06 mm. Different shapes of defects have a significant impact on the failure mode of rocks, while they have a minimal effect on the time it takes for the rock to fail.
- c.
- The lengths of pre-existing cracks and the angles between them and the horizontal direction have a significant impact on the crack propagation path and the size of the stress concentration area, while the width of reserved cracks has a relatively small effect on crack propagation. The larger the length of the crack and the smaller the angle between it and the horizontal direction, the larger the stress concentration area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Swoboda, G.; Shen, X.; Rosas, L. Damage model for jointed rock mass and its application to tunnelling. Comput. Geotech. 1998, 22, 183–203. [Google Scholar] [CrossRef]
- Tian, J.J.; Xu, D.J.; Liu, T.H. An experimental investigation of the fracturing behaviour of rock-like materials containing two V-shaped parallelogram flaws. Int. J. Min. Sci. Technol. 2020, 30, 777–783. [Google Scholar] [CrossRef]
- Wang, T.T.; Huang, T.H. Anisotropic Deformation of a Circular Tunnel Excavated in a Rock Mass Containing Sets of Ubiquitous Joints: Theory Analysis and Numerical Modeling. Rock Mech. Rock Eng. 2013, 47, 643–657. [Google Scholar] [CrossRef]
- Tang, H.; Zhang, J.H.; Chen, H. Laboratory tests on failure mechanism of fractured rock under compression. J. Eng. Geol. 2016, 24, 363–368. [Google Scholar]
- Yang, S.Q.; Yang, D.S.; Jing, H.W.; Li, Y.H.; Wang, S.Y. An Experimental Study of the Fracture Coalescence Behaviour of Brittle Sandstone Specimens Containing Three Fissures. Rock Mech. Rock Eng. 2011, 45, 563–582. [Google Scholar] [CrossRef]
- Sun, D.; Rao, Q.; Wang, S.; Yi, W.; Zhao, C. A new prediction method for multi-crack initiation of anisotropic rock. Theor. Appl. Fract. Mech. 2022, 118, 103269. [Google Scholar] [CrossRef]
- Zhou, X.P.; Zhao, Y.; Qian, Q.H. A novel meshless numerical method for modeling progressive failure processes of slopes. Eng. Geol. 2015, 192, 139–153. [Google Scholar] [CrossRef]
- Yang, S.; Cao, M.; Ren, X.; Ma, G.; Zhang, J.; Wang, H. 3D crack propagation by the numerical manifold method. Comput. Struct. 2018, 194, 116–129. [Google Scholar] [CrossRef]
- Branco, R.; Antunes, F.V.; Costa, J.D. A review on 3D-FE adaptive remeshing techniques for crack growth modelling. Eng. Fract. Mech. 2015, 141, 170–195. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Pathak, H.; Singh, A.; Singh, I.V.; Yadav, S.K. A simple and efficient XFEM approach for 3-D cracks simulations. Int. J. Fract. 2013, 181, 189–208. [Google Scholar] [CrossRef]
- Daux, C.; Moës, N.; Dolbow, J.; Sukumar, N.; Belytschko, T. Arbitrary branched and intersecting cracks with the extended finite element method. Int. J. Numer. Methods Eng. 2000, 48, 1741–1760. [Google Scholar] [CrossRef]
- Marazzato, F.; Ern, A.; Monasse, L. Quasi-static crack propagation with a Griffith criterion using a variational discrete element method. Comput. Mech. 2021, 69, 527–539. [Google Scholar] [CrossRef]
- Yu, T.T.; Xia, S.X. DEM for Modeling Cracks Propagation in Rocks under Uniaxial Compression Tests. In Proceedings of the International Conference on Materials Science and Information Technology (MSIT 2011), Singapore, 16–18 September 2012; pp. 4788–4793. [Google Scholar]
- Thuan, H.N.T.; Kim, H.G. Numerical simulation of crack propagation in shell structures using interface shell elements. Comput. Mech. 2020, 66, 537–557. [Google Scholar]
- Lim, H.H.; Kim, H.G. Finite element analysis of three-dimensional cracks by connecting global and local meshes. Eng. Fract. Mech. 2023, 286, 109304. [Google Scholar] [CrossRef]
- Zhou, J.; Lan, H.; Zhang, L.; Yang, D.; Song, J.; Wang, S. Novel grain-based model for simulation of brittle failure of Alxa porphyritic granite. Eng. Geol. 2019, 251, 100–114. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, S.; Zhu, Z.; Yu, S.; Xie, X. Improved peridynamic model and its application to crack propagation in rocks. R. Soc. Open Sci. 2022, 9, 221013. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Sun, G.; Zheng, H. Modeling complex crack problems using the three-node triangular element fitted to numerical manifold method with continuous nodal stress. Sci. China Technol. Sci. 2017, 60, 1537–1547. [Google Scholar] [CrossRef]
- Li, G.; Wang, K.; Qian, X. An NMM-based fluid-solid coupling model for simulating rock hydraulic fracturing process. Eng. Fract. Mech. 2020, 235, 107193. [Google Scholar] [CrossRef]
- Sun, C.; Song, E.; Zhang, L.; Nan, F. SPH Model for Numerical Test of Heterogeneous Rock-like Material. In MATEC Web of Conferences; EDP Sciences: Les Ulis, French, 2020; p. 319. [Google Scholar]
- Bi, J.; Zhou, X.P. Numerical Simulation of Zonal Disintegration of the Surrounding Rock Masses Around a Deep Circular Tunnel Under Dynamic Unloading. Int. J. Comput. Methods 2015, 12, 1550020. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, X.P.; Qian, Q.H. Progressive failure processes of reinforced slopes based on general particle dynamic method. J. Cent. South Univ. 2015, 22, 4049–4055. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, X.P. A Novel Numerical Algorithm for Simulation of Initiation, Propagation and Coalescence of Flaws Subject to Internal Fluid Pressure and Vertical Stress in the Framework of General Particle Dynamics. Rock Mech. Rock Eng. 2017, 50, 1833–1849. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, X. Numerical simulation of kinetic friction in the fracture process of rocks in the framework of General Particle Dynamics. Comput. Geotech. 2017, 83, 1–15. [Google Scholar] [CrossRef]
- Yao, W.W.; Zhou, X.P.; Berto, F. Continuous smoothed particle hydrodynamics for cracked nonconvex bodies by diffraction criterion. Theor. Appl. Fract. Mech. 2020, 108, 102584. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Zhou, X.P. Analysis of the numerical stability of soil slope using virtual-bond general particle dynamics. Eng. Geol. 2018, 243, 101–110. [Google Scholar] [CrossRef]
- Yu, S.; Ren, X.; Zhang, J.; Wang, H.; Sun, Z. An improved form of smoothed particle hydrodynamics method for crack propagation simulation applied in rock mechanics. Int. J. Min. Sci. Technol. 2021, 31, 421–428. [Google Scholar] [CrossRef]
- Ren, X.; Yu, S.; Zhang, J.; Wang, H.; Sun, Z. An Improved Form of 2D SPH Method for Modeling the Excavation Damage of Tunnels Containing Random Fissures. Geofluids 2021, 2021, 5719171. [Google Scholar] [CrossRef]
- Yu, S.; Ren, X.; Zhang, J.; Wang, H.; Sun, Z. An Improved Smoothed Particle Hydrodynamics Method and Its Application in Rock Hydraulic Fracture Modelling. Rock Mech. Rock Eng. 2021, 54, 6039–6055. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R.; Zong, Z. An overview on smoothed particle hydrodynamics. Int. J. Comput. Methods 2008, 5, 135–188. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R.; Lam, K.Y. Adaptive smoothed particle hydrodynamics for high strain hydrodynamics with material strength. Shock. Waves 2006, 15, 2–129. [Google Scholar] [CrossRef]
- Mu, D.; Tang, A.; Qu, H.; Wang, J. An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads. Materials 2023, 16, 1572. [Google Scholar] [CrossRef] [PubMed]
- Irfan, M.; Shah, I.; Niazi, U.M.; Ali, M.; Ali, S.; Jalalah, M.S.; Khan, M.K.A.; Almawgani, A.H.M.; Rahman, S. Numerical analysis of non-aligned inputs M-type micromixers with different shaped obstacles for biomedical applications. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2021, 236, 870–880. [Google Scholar] [CrossRef]
- Liu, L.; Li, H.; Li, X.; Wu, R. Full-field strain evolution and characteristic stress levels of rocks containing a single pre-existing flaw under uniaxial compression. Bull. Eng. Geol. Environ. 2020, 79, 3145–3161. [Google Scholar] [CrossRef]
- Tang, S.C.; Feng, P.; Zhao, J.C. Uniaxial Mechanical Properties and Failure Mechanism of Rock Specimens Containing Cross Fissures. Chin. J. Undergr. Space Eng. 2021, 17, 1376–1383,1407. [Google Scholar]
- Yang, S.; Liu, X.; Li, Y. Experimental analysis of mechanical behavior of sandstone containing hole and fissure under uniaxial compression. Chin. J. Rock Mech. Eng. 2022, 31, 3534–3546. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Zhang, H.; Zhang, J.; Yu, S.; Maimaitiyusupu, S. Numerical Simulation Analysis of Fracture Propagation in Rock Based on Smooth Particle Hydrodynamics. Materials 2023, 16, 6560. https://doi.org/10.3390/ma16196560
Ren X, Zhang H, Zhang J, Yu S, Maimaitiyusupu S. Numerical Simulation Analysis of Fracture Propagation in Rock Based on Smooth Particle Hydrodynamics. Materials. 2023; 16(19):6560. https://doi.org/10.3390/ma16196560
Chicago/Turabian StyleRen, Xuhua, Hui Zhang, Jixun Zhang, Shuyang Yu, and Semaierjiang Maimaitiyusupu. 2023. "Numerical Simulation Analysis of Fracture Propagation in Rock Based on Smooth Particle Hydrodynamics" Materials 16, no. 19: 6560. https://doi.org/10.3390/ma16196560
APA StyleRen, X., Zhang, H., Zhang, J., Yu, S., & Maimaitiyusupu, S. (2023). Numerical Simulation Analysis of Fracture Propagation in Rock Based on Smooth Particle Hydrodynamics. Materials, 16(19), 6560. https://doi.org/10.3390/ma16196560






