Effects of Printing Layer Orientation on the High-Frequency Bending-Fatigue Life and Tensile Strength of Additively Manufactured 17-4 PH Stainless Steel
Abstract
:1. Introduction
2. Test Specimen Preparation
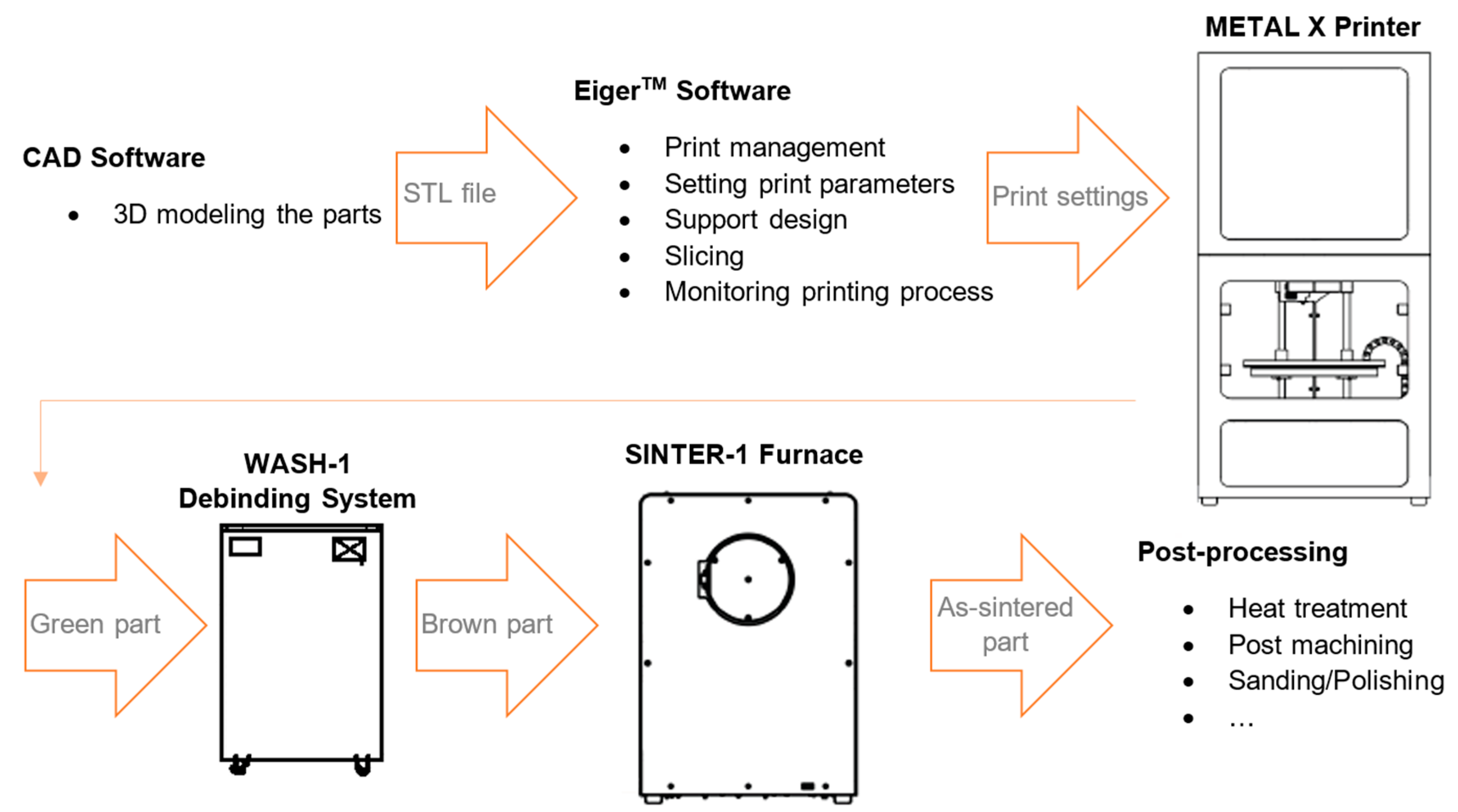
2.1. Bound Powder Extrusion (BPE)/Atomic Diffusion Additive Manufacturing (ADAM)
2.2. Material’s Composition and Expected Properties
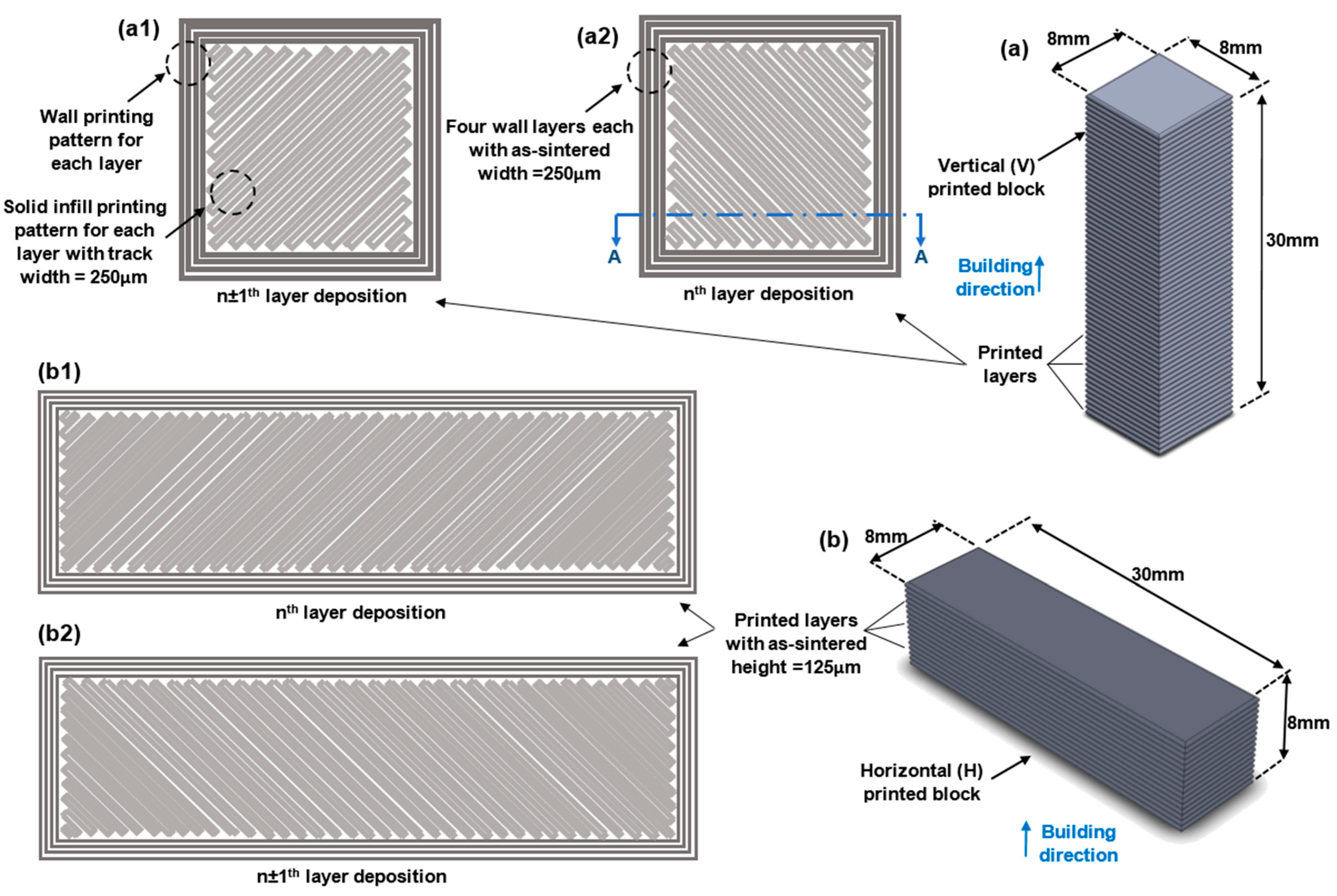
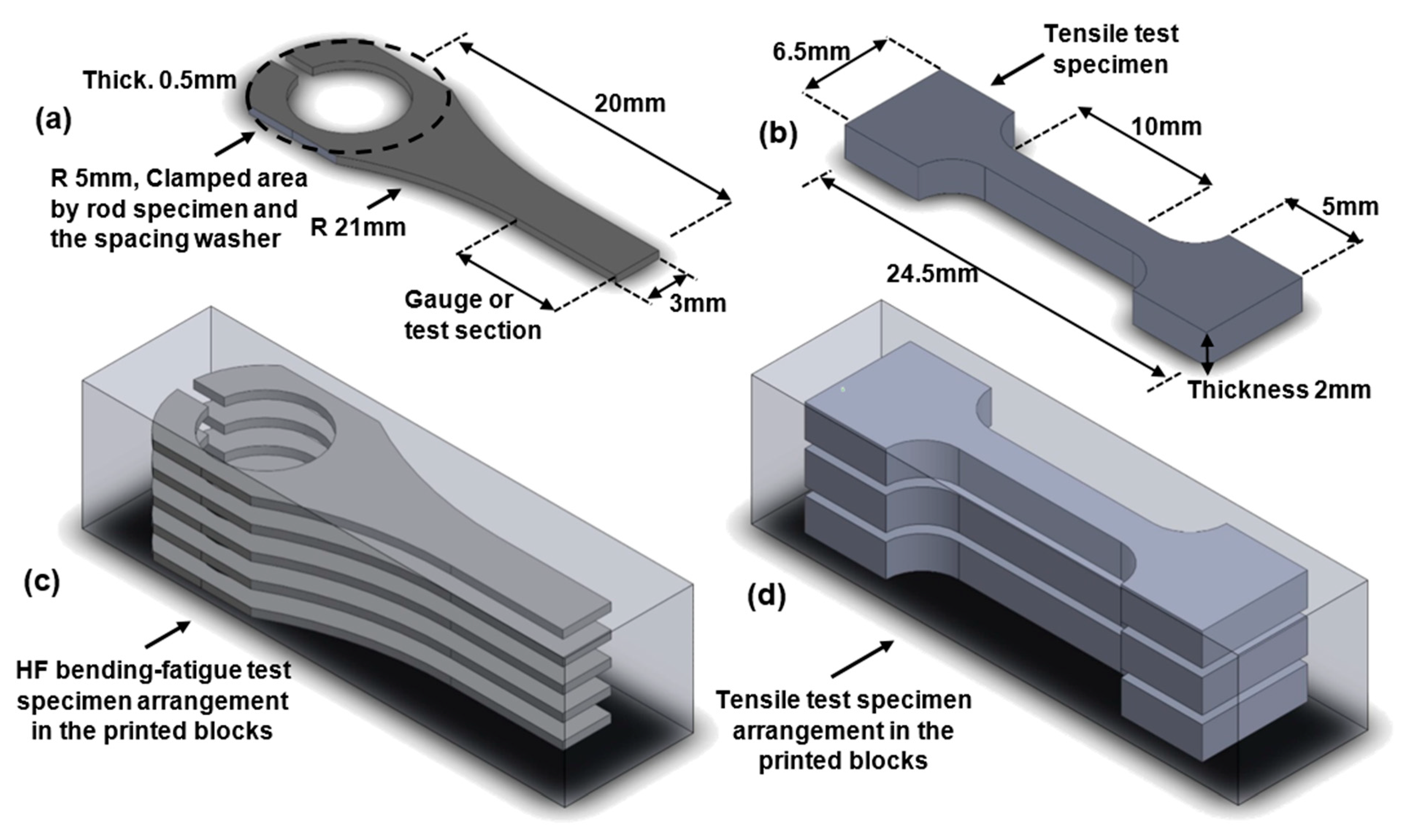
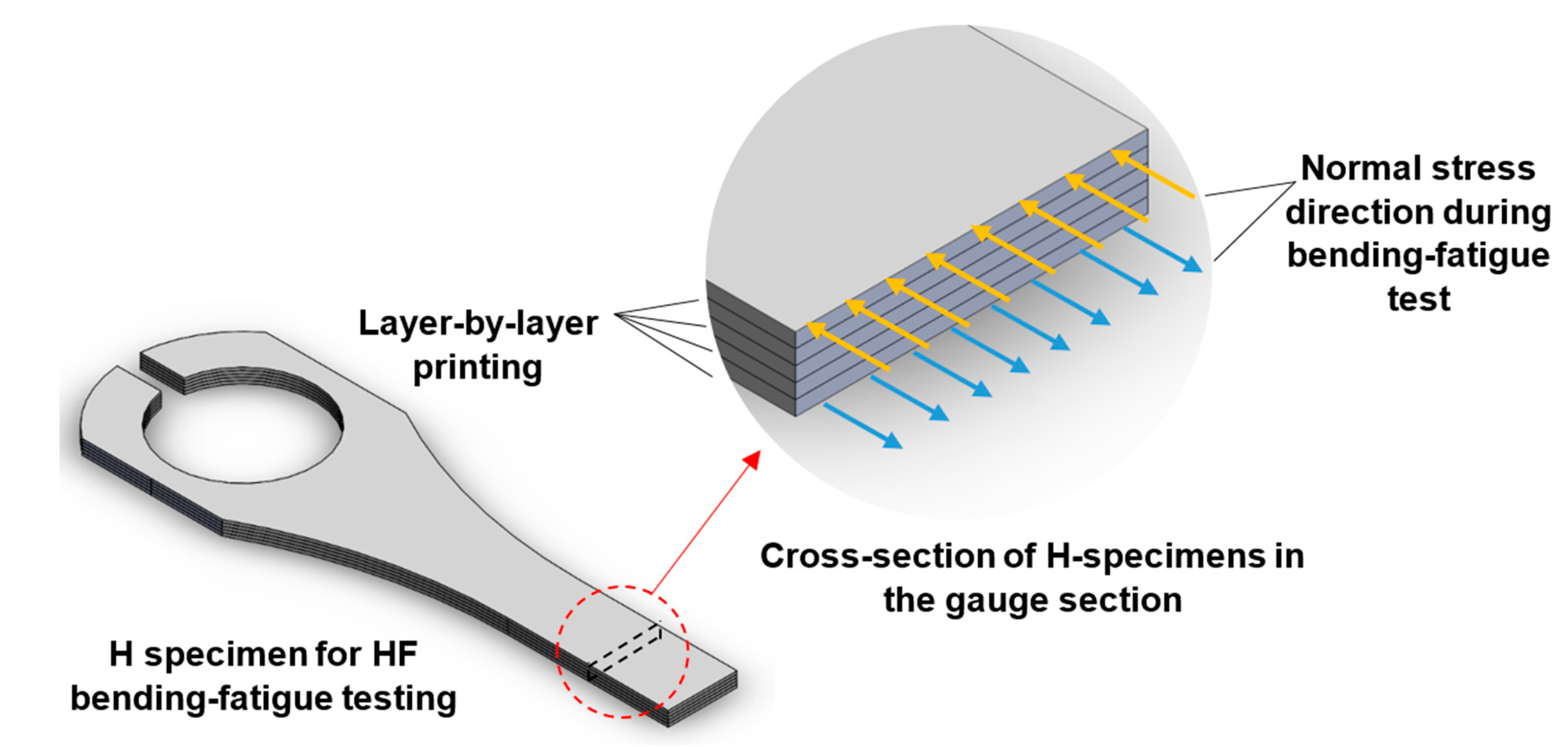
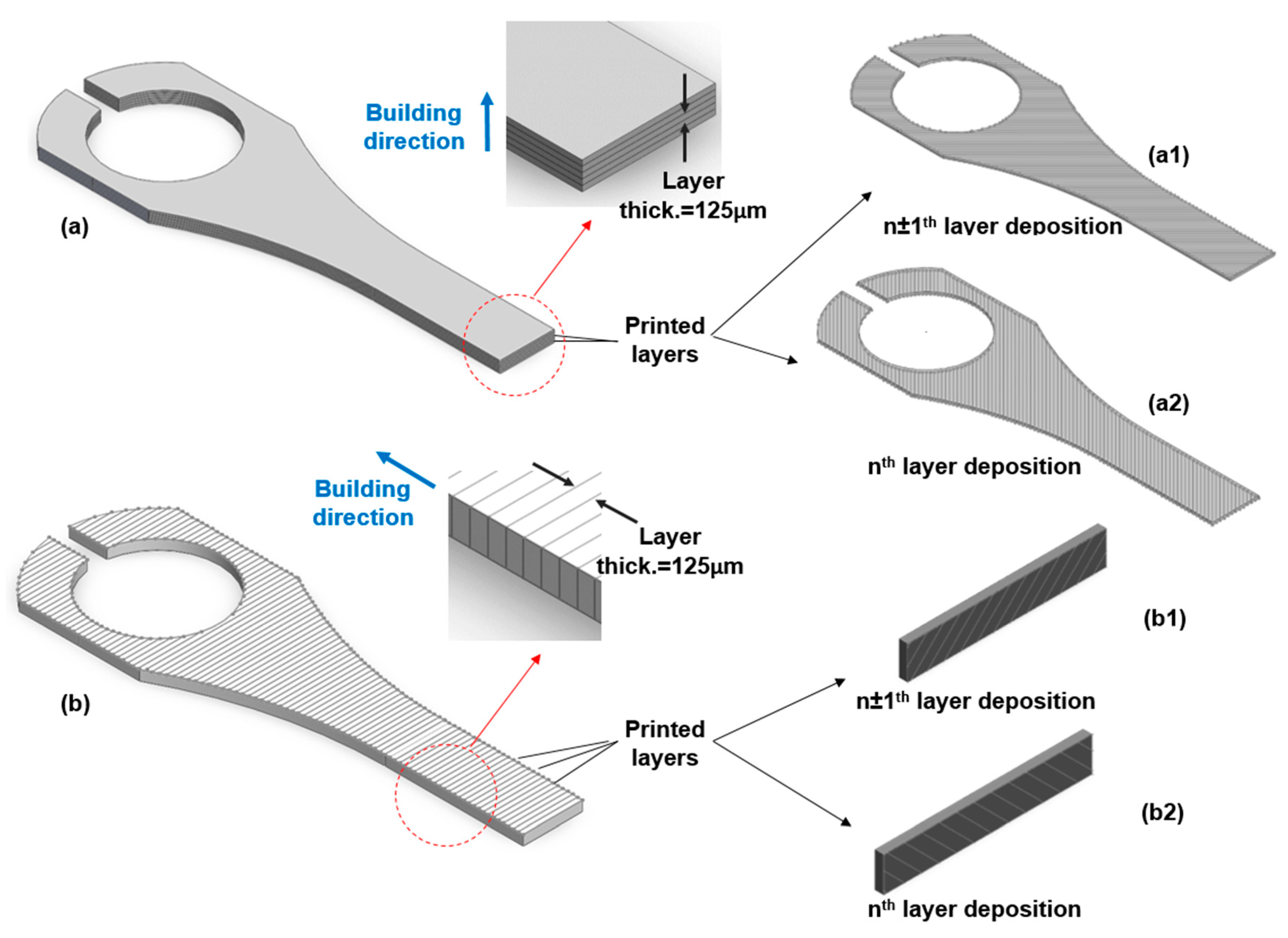
2.3. Test Specimen Preparation with Two Different Printing Orientations
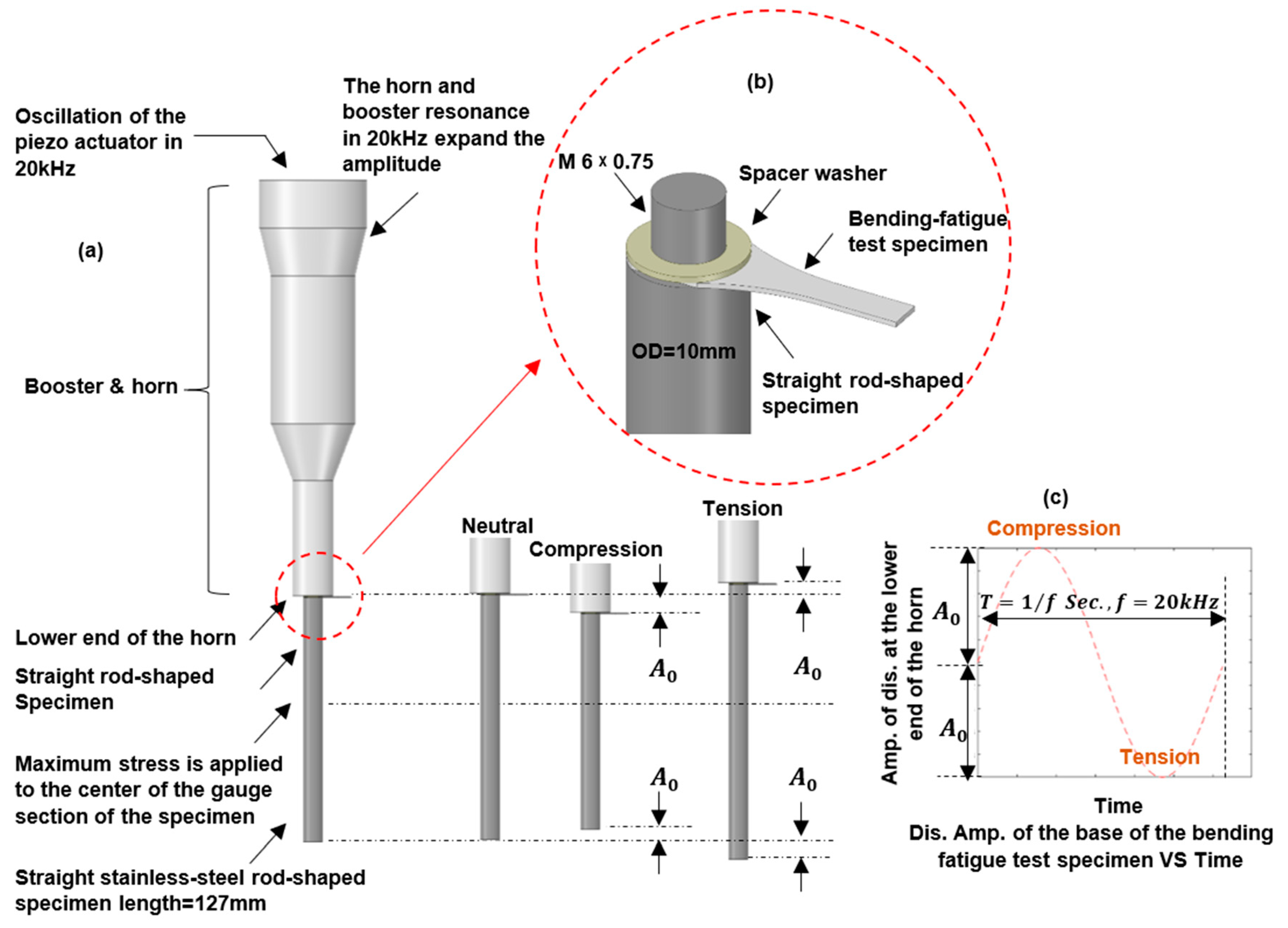
2.4. Ultrasonic Bending-Fatigue Test
2.5. Tensile Test
3. Ultrasonic Bending-Fatigue Test Specimen Design
3.1. Vibration Response Theoretical Analysis
3.2. Finite Element Analysis (FEA)
4. Results and Discussion
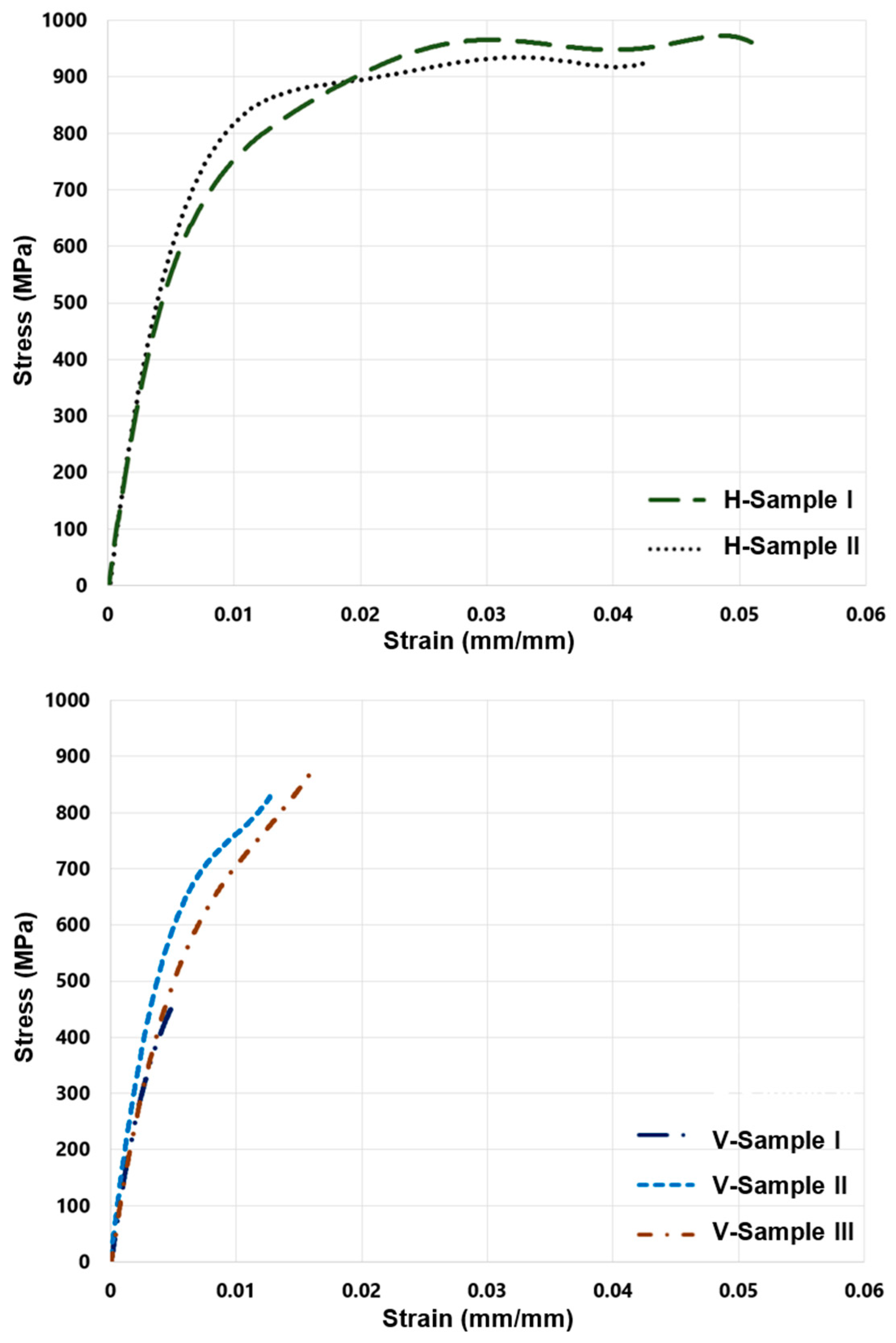
4.1. Tensile Test Results
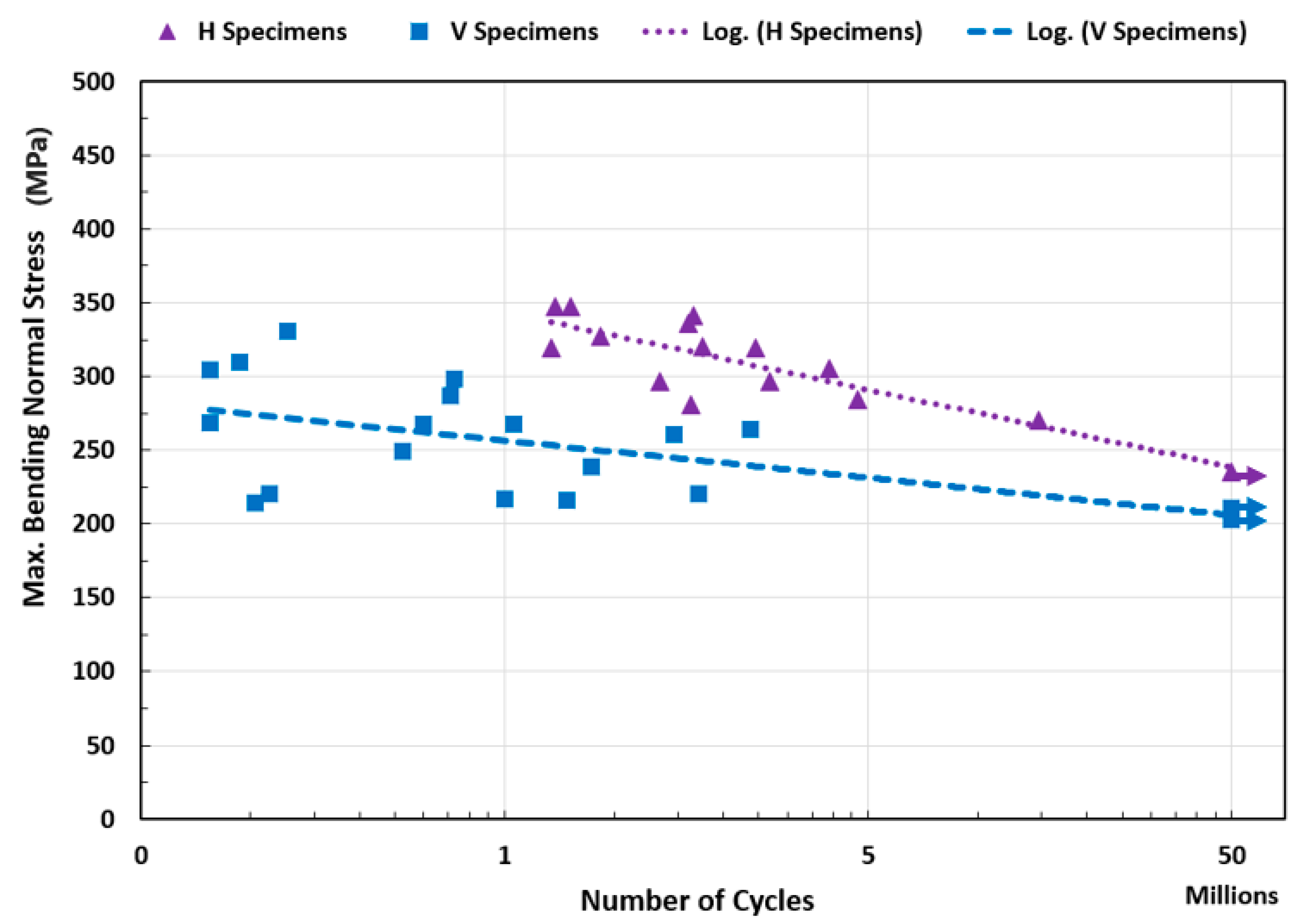
4.2. Ultrasonic Bending-Fatigue Test Results
4.3. Discussions and Fractography
4.4. In Comparison with the Literature Data
5. Summary and Conclusions
- (1)
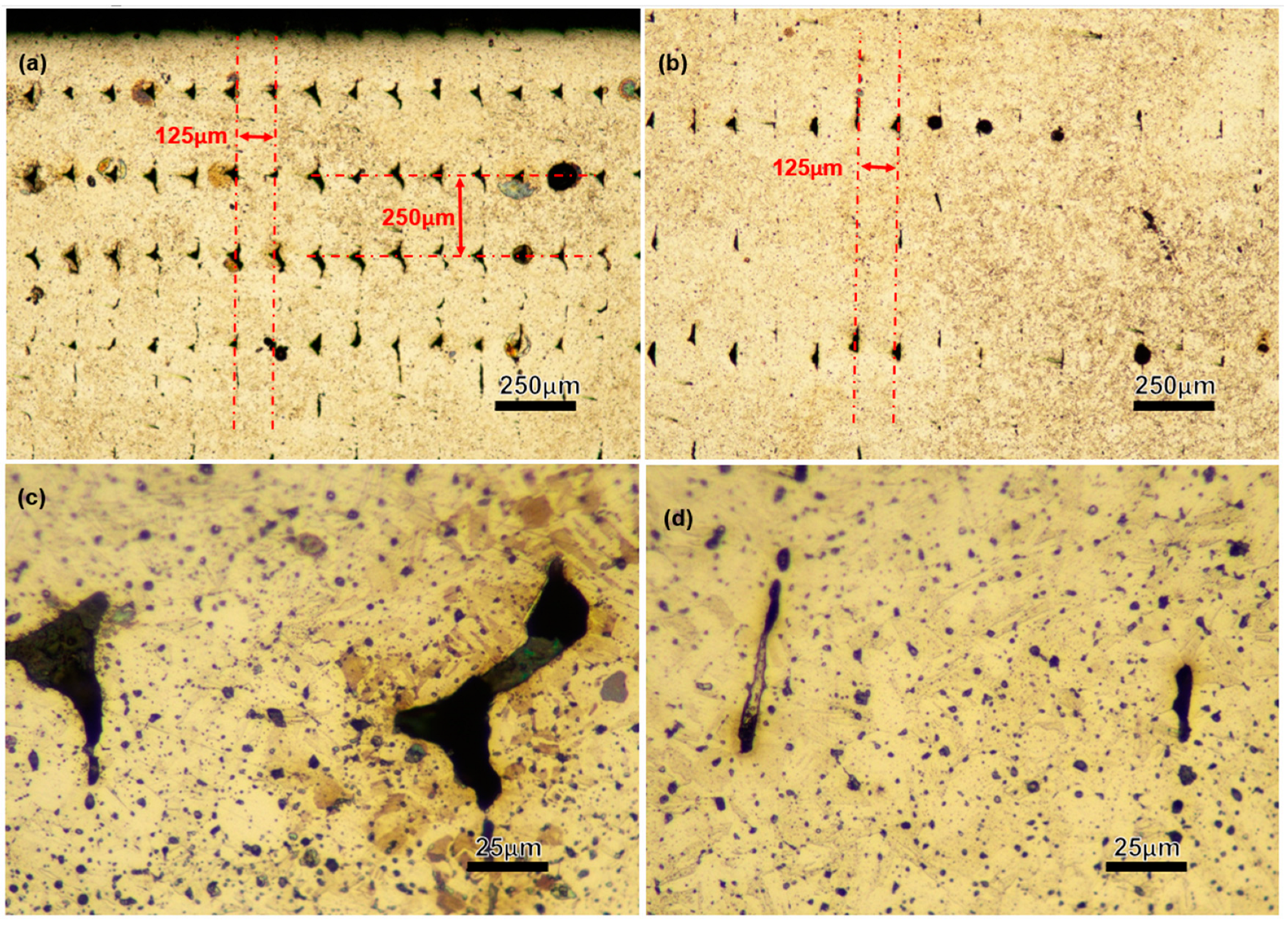
- Two types of defects were observed inside the samples after sintering. First, large-sized pores originated from a lack of sintering mainly extended along the fabrication layer boundaries and slightly went to the track boundaries within the same fabrication layer. Second, the small-sized pores stemmed from trapped gas and residual binders that show shapes close to spherical or un-densified metal powders. Overall, the large defects show a more significant effect on the mechanical property of the specimens;
- (2)
- The vertically-oriented specimens show inferior ductility and toughness than that of the horizontally-oriented counterparts, which is ascribed to the large pores (strip-shaped) extending along the fabrication tracks/layer boundaries;
- (3)
- Similarly, vertically-oriented specimens have a lower fatigue life than the horizontally-oriented parts, which also stemmed from the large defects. Compared with wrought 17-4 PH alloy, lower ductility was observed in the horizontally-oriented specimens in this study, which is due to the existence of both small defects and large defects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| AB | As-built |
| AC | Air cooling |
| ADAM | Atomic diffusion additive manufacturing |
| AM | Additive manufacturing |
| BPE | Bound powder extrusion |
| EDM | Electrical discharge machining |
| HCF | High-cycle fatigue |
| HT | Heat-treated |
| LCF | Low-cycle fatigue |
| L-PBF | Laser-powder bed fusion |
| PH | Precipitation hardening |
| SEM | Scanning electron microscopy |
| SLM | Selective laser melting |
| SS | Stainless steel |
References
- ASTM ISO/ASTM52900-21; Additive Manufacturing—General Principles—Fundamentals and Vocabulary. ASTM: West Conshohocken, PA, USA, 2021.
- ASTM ISO/ASTM52921-13(2019); Standard Terminology for Additive Manufacturing—Coordinate Systems and Test Methodologies. ASTM: West Conshohocken, PA, USA, 2019.
- Nezhadfar, P.D.; Burford, E.; Anderson-Wedge, K.; Zhang, B.; Shao, S.; Daniewicz, S.R.; Shamsaei, N. Fatigue crack growth behavior of additively manufactured 17-4 PH stainless steel: Effects of build orientation and microstructure. Int. J. Fatigue 2019, 123, 168–179. [Google Scholar] [CrossRef]
- Soltani-Tehrani, A.; Pegues, J.; Shamsaei, N. Fatigue behavior of additively manufactured 17-4 PH stainless steel: The effects of part location and powder re-use. Addit. Manuf. 2020, 36, 101398. [Google Scholar] [CrossRef]
- Jirandehi, A.P.; Hajshirmohammadi, B.; Carrion, P.; Khonsari, M.M.; Shamsaei, N.; Shao, S. Strain energy-based fatigue failure analyses of LB-PBF Inconel 718: Effect of build orientation. Addit. Manuf. 2022, 52, 102661. [Google Scholar] [CrossRef]
- Mostafaei, A.; Zhao, C.; He, Y.; Ghiaasiaan, S.R.; Shi, B.; Shao, S.; Shamsaei, N.; Wu, Z.; Kouraytem, N.; Sun, T.; et al. Defects and anomalies in powder bed fusion metal additive manufacturing. Curr. Opin. Solid State Mater. Sci. 2022, 26, 100974. [Google Scholar]
- Gonzalez-Gutierrez, J.; Cano, S.; Schuschnigg, S.; Kukla, C.; Sapkota, J.; Holzer, C. Additive Manufacturing of Metallic and Ceramic Components by the Material Extrusion of Highly-Filled Polymers: A Review and Future Perspectives. Materials 2018, 11, 840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramazani, H.; Kami, A. Metal FDM, a new extrusion-based additive manufacturing technology for manufacturing of metallic parts: A review. Prog. Addit. Manuf. 2022, 7, 609–626. [Google Scholar] [CrossRef]
- Sehhat, M.H.; Behdani, B.; Hung, C.H.; Mahdianikhotbesara, A. Development of an empirical model on melt pool variation in laser foil printing additive manufacturing process using statistical analysis. Metallogr. Microstruct. Anal. 2021, 10, 684–691. [Google Scholar] [CrossRef]
- Sehhat, M.H.; Mahdianikhotbesara, A.; Yadegari, F. Verification of stress transformation in anisotropic material additively manufactured by fused deposition modeling (FDM). Int. J. Adv. Manuf. Technol. 2022, 123, 1777–1783. [Google Scholar] [CrossRef]
- Zeng, C.; Ghadimi, H.; Ding, H.; Nemati, S.; Garbie, A.; Raush, J.; Guo, S. Microstructure Evolution of Al6061 Alloy Made by Additive Friction Stir Deposition. Materials 2022, 15, 3676. [Google Scholar] [CrossRef] [PubMed]
- Markforged. What Is Atomic Diffusion Additive Manufacturing (ADAM)? Available online: https://markforged.com/resources/learn/3d-printing-basics/3d-printing-processes/what-is-atomic-diffusion-additive-manufacturing-adam (accessed on 5 December 2022).
- Markforged. 3D Printer Types & Technologies. Available online: https://markforged.com/resources/learn/3d-printing-basics/3d-printing-introduction/3d-printer-types-technologies (accessed on 5 December 2022).
- Yadollahi, A.; Shamsaei, N.; Thompson, S.M.; Elwany, A.; Bian, L. Effects of building orientation and heat treatment on fatigue behavior of selective laser melted 17-4 PH stainless steel. Int. J. Fatigue 2017, 94, 218–235. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Khonsari, M. Investigation of metal fatigue using a coupled entropy-kinetic model. Int. J. Fatigue 2022, 161, 106907. [Google Scholar] [CrossRef]
- Moghanlou, M.R.; Khonsari, M. On the kinetic formulation of fracture fatigue entropy of metals. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 565–577. [Google Scholar] [CrossRef]
- Amooie, M.A.; Khonsari, M.M. On the effect of environmental temperature on fracture fatigue entropy. Int. J. Fatigue 2022, 168, 107411. [Google Scholar] [CrossRef]
- Nezhadfar, P.D.; Johnson, A.; Shamsaei, N. Fatigue behavior and microstructural evolution of additively manufactured Inconel 718 under cyclic loading at elevated temperature. Int. J. Fatigue 2020, 136, 105598. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Cai, L.; Hu, T.; Wang, P.; Li, X.; Sun, R.; Li, W. A fatigue life prediction approach to interior cracking induced high cycle and very high cycle fatigue for surface-carburized steels. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 865–881. [Google Scholar] [CrossRef]
- Romano, S.; Nezhadfar, P.D.; Shamsaei, N.; Seifi, M.; Beretta, S. High cycle fatigue behavior and life prediction for additively manufactured 17-4 PH stainless steel: Effect of sub-surface porosity and surface roughness. Theor. Appl. Fract. Mech. 2020, 106, 102477. [Google Scholar] [CrossRef]
- Henry, T.C.; Morales, M.A.; Cole, D.P.; Shumeyko, C.M.; Riddick, J.C. Mechanical behavior of 17-4 PH stainless steel processed by atomic diffusion additive manufacturing. Int. J. Adv. Manuf. Technol. 2021, 114, 2103–2114. [Google Scholar] [CrossRef]
- Suwanpreecha, C.; Seensattayawong, P.; Vadhanakovint, V.; Manonukul, A. Influence of Specimen Layout on 17-4PH (AISI 630) Alloys Fabricated by Low-Cost Additive Manufacturing. Metall. Mater. Trans. A 2021, 52, 1999–2009. [Google Scholar] [CrossRef]
- Suwanpreecha, C.; Manonukul, A. On the build orientation effect in as-printed and as-sintered bending properties of 17-4PH alloy fabricated by metal fused filament fabrication. Rapid Prototyp. J. 2022, 28, 1076–1085. [Google Scholar] [CrossRef]
- Porro, M.; Zhang, B.; Parmar, A.; Shin, Y.C. Data-Driven Modeling of Mechanical Properties for 17-4 PH Stainless Steel Built by Additive Manufacturing. Integr. Mater. Manuf. Innov. 2022, 11, 241–255. [Google Scholar] [CrossRef]
- Markforged. The Markforged Metal Additive Manufacturing Process. Available online: https://markforged.com/resources/learn/design-for-additive-manufacturing-metals/metal-additive-manufacturing-introduction/metal-additive-manufacturing-process (accessed on 5 December 2022).
- Markforged. What is Fused Deposition Modeling (FDM)? Available online: https://markforged.com/resources/learn/3d-printing-basics/3d-printing-processes/what-is-fused-deposition-modeling-fdm (accessed on 5 December 2022).
- Markforged. Metal X Facilities Guide 3.0.2. Available online: https://s3.amazonaws.com/mf.product.doc.images/InternalKnowledgeBase/MetalX_Facilities_Guide.pdf (accessed on 5 December 2022).
- German, R. Thinking about metal binder jetting or FFF? Here is (almost) everything you need to know about sintering. Metal Addit. Manuf. 2019, 5, 127–139. [Google Scholar]
- Markforged. 17-4PH Stainless Steel. Available online: https://markforged.com/materials/metals/17-4-ph-stainless-steel (accessed on 5 December 2022).
- Ghadimi, H.; Jirandehi, A.P.; Nemati, S.; Guo, S. Small-sized specimen design with the provision for high-frequency bending-fatigue testing. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 3517–3537. [Google Scholar] [CrossRef]
- Solav, D.; Moerman, K.M.; Jaeger, A.M.; Genovese, K.; Herr, H.M. MultiDIC: An Open-Source Toolbox for Multi-View 3D Digital Image Correlation. IEEE Access 2018, 6, 30520–30535. [Google Scholar] [CrossRef]
- Dutton, B.; Vesga, W.; Waller, J.; James, S.; Seifi, M. Metal Additive Manufacturing Defect Formation and Nondestructive Evaluation Detectability. In Structural Integrity of Additive Manufactured Parts; ASTM International: West Conshohocken, PA, USA, 2020; pp. 1–50. [Google Scholar]
- Zhang, Y.; Yu, L.; Wang, J.; Mao, H.; Cui, K. Microstructure and mechanical properties of high strength porous ceramics with high sewage sludge content. J. Clean. Prod. 2022, 380, 135084. [Google Scholar] [CrossRef]
- Metallic Materials Properties Development and Standardization (MMPDS-17); Battelle Memorial Institute: Columbus, OI, USA, 2022.
- Raefsky, M. Fatigue Properties of 17-4 PH and 15-5 PH Steel in the H-900 and H-1050 Condition; Defense Technical Information Center: Fort Belvoir, VA, USA, 1968.
- Kedziora, S.; Decker, T.; Museyibov, E.; Morbach, J.; Hohmann, S.; Huwer, A.; Wahl, M. Strength Properties of 316L and 17-4 PH Stainless Steel Produced with Additive Manufacturing. Materials 2022, 15, 6278. [Google Scholar] [CrossRef] [PubMed]
- Yadollahi, A. Fatigue Behavior of 17-4 PH Stainless Steel Fabricated Using Selective Laser Melting; University of Texas at Austin: Austin, TX, USA, 2015. [Google Scholar]


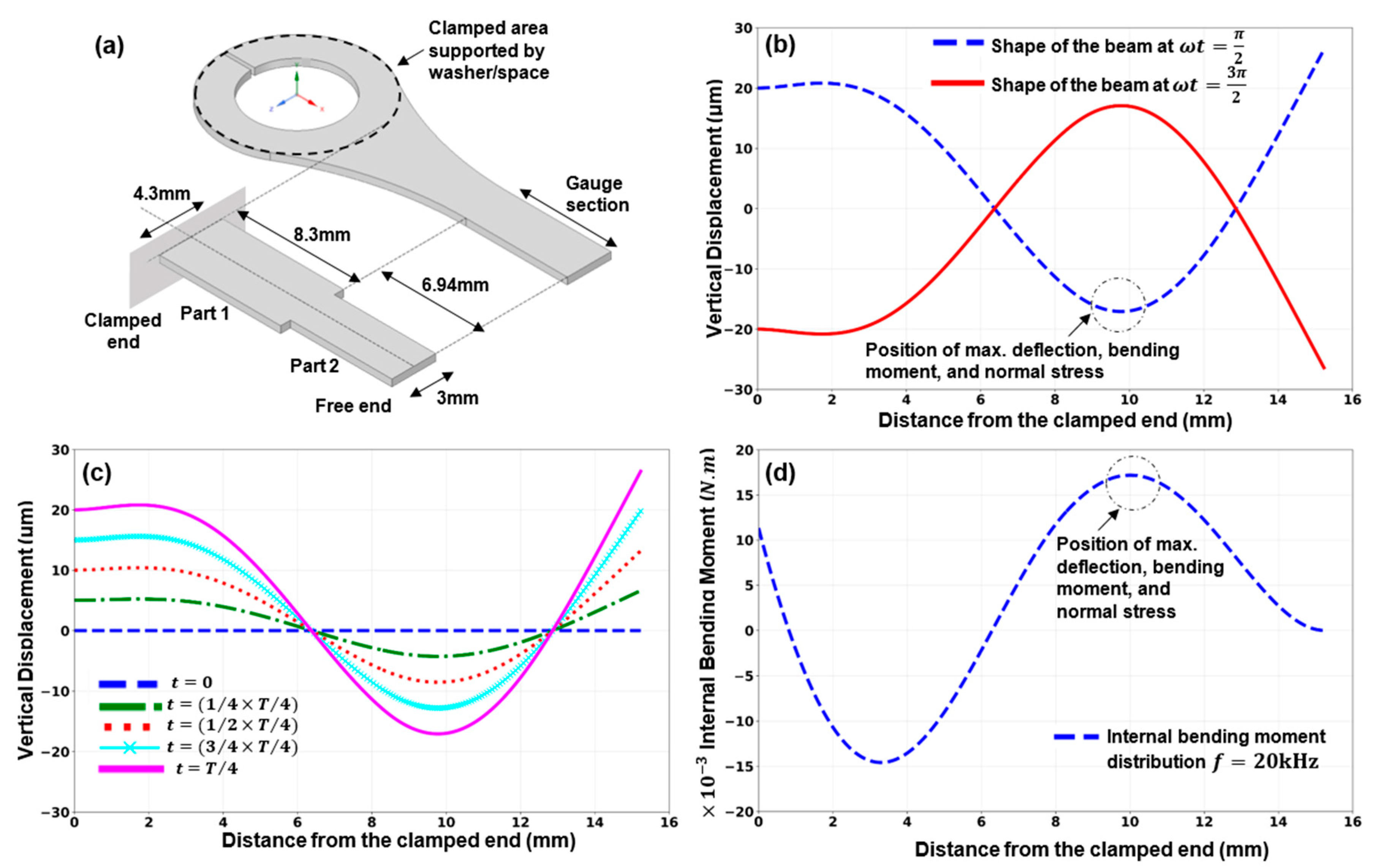






| Cross-Section Area () | Period () | ||
| Horn tip’s displacement amplitude () | Internal shear force () | ||
| Modulus of elasticity () | Deflection of the beam in y direction () | ||
| Frequency () | Global x coordinate () | ||
| Applied external distributed force () | X coordinate for beam Part1 () | ||
| Second moment of inertia of the cross-section area () | X coordinate for beam Part2 () | ||
| Total length of the beam () | Global y coordinate () | ||
| Length of Part1 () | Global z coordinate () | ||
| Length of Part2 () | Density () | ||
| Internal bending moment () | Normal stress () | ||
| Time () | Angular frequency () |
| Composition | Chromium | Nickel | Copper | Silicon | Manganese | Niobium | Carbon | Phosphorous | Sulfur | Iron |
|---|---|---|---|---|---|---|---|---|---|---|
| Amount | 15–17.5% | 3–5% | 3–5% | 1% max | 1% max | 0.15–0.45% | 0.07% max | 0.04% max | 0.03% max | bal. |
| Mechanical Property | Standard | Values for As-Sintered Parts | Unit |
|---|---|---|---|
| Ultimate Tensile Strength | ASTM E8 | 1050 | MPa |
| 0.2% Yield Strength | ASTM E8 | 800 | MPa |
| Elongation at Break | ASTM E8 | 5% | - |
| Tensile Modulus | ASTM E8 | 140 | GPa |
| Hardness | ASTM E18 | 30 | HRC |
| Relative Density | ASTM B923 | 96% | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghadimi, H.; Jirandehi, A.P.; Nemati, S.; Ding, H.; Garbie, A.; Raush, J.; Zeng, C.; Guo, S. Effects of Printing Layer Orientation on the High-Frequency Bending-Fatigue Life and Tensile Strength of Additively Manufactured 17-4 PH Stainless Steel. Materials 2023, 16, 469. https://doi.org/10.3390/ma16020469
Ghadimi H, Jirandehi AP, Nemati S, Ding H, Garbie A, Raush J, Zeng C, Guo S. Effects of Printing Layer Orientation on the High-Frequency Bending-Fatigue Life and Tensile Strength of Additively Manufactured 17-4 PH Stainless Steel. Materials. 2023; 16(2):469. https://doi.org/10.3390/ma16020469
Chicago/Turabian StyleGhadimi, Hamed, Arash P. Jirandehi, Saber Nemati, Huan Ding, Abdelrahman Garbie, Jonathan Raush, Congyuan Zeng, and Shengmin Guo. 2023. "Effects of Printing Layer Orientation on the High-Frequency Bending-Fatigue Life and Tensile Strength of Additively Manufactured 17-4 PH Stainless Steel" Materials 16, no. 2: 469. https://doi.org/10.3390/ma16020469
APA StyleGhadimi, H., Jirandehi, A. P., Nemati, S., Ding, H., Garbie, A., Raush, J., Zeng, C., & Guo, S. (2023). Effects of Printing Layer Orientation on the High-Frequency Bending-Fatigue Life and Tensile Strength of Additively Manufactured 17-4 PH Stainless Steel. Materials, 16(2), 469. https://doi.org/10.3390/ma16020469









