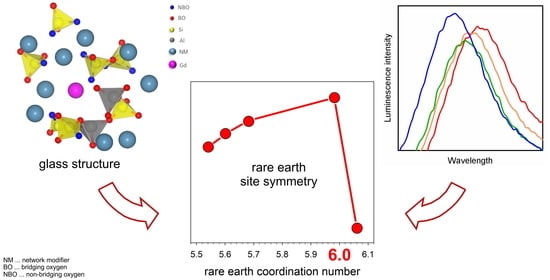
The Effect of Glass Structure on the Luminescence Spectra of Sm3+-Doped Aluminosilicate Glasses
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
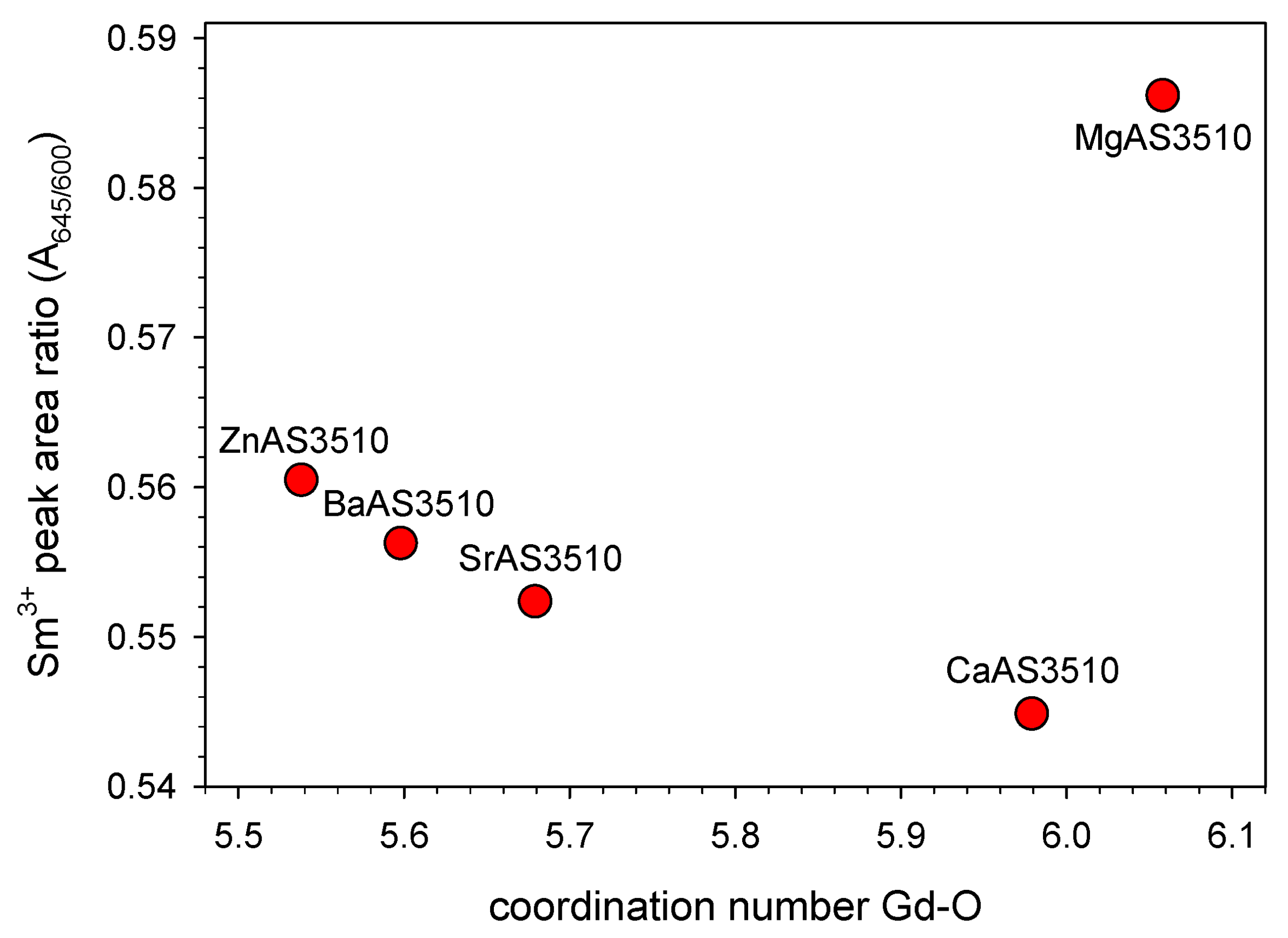
3.1. Peak Area Ratio and Sm3+ Site Symmetry
3.2. Peak Position, Optical Basicity, and Peak Broadening
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Herrmann, A.; Tewelde, M.; Kuhn, S.; Tiegel, M.; Rüssel, C. The Effect of Glass Composition on the Luminescence Properties of Sm3+ doped Alumino Silicate Glasses. J. Non-Cryst. Solids 2018, 502, 190–197. [Google Scholar] [CrossRef]
- Herrmann, A.; Assadi, A.A.; Lachheb, R.; Zekri, M.; Erlebach, A.; Damak, K.; Maâlej, R.; Sierka, M.; Rüssel, C. The effect of glass structure and local rare earth site symmetry on the optical properties of rare earth doped alkaline earth aluminosilicate glasses. Acta Mater. (under review).
- Tiegel, M.; Hosseinabhadi, R.; Kuhn, S.; Herrmann, A.; Rüssel, C. Young’s modulus, Vickers hardness and indentation fracture toughness of alumino silicate glasses. Ceram. Int. 2015, 41, 7267–7275. [Google Scholar] [CrossRef]
- Herrmann, A.; Rüssel, C. New Aluminosilicate Glasses as High-power Laser Materials. Int. J. Appl. Glass Sci. 2015, 6, 210–219. [Google Scholar] [CrossRef]
- Zekri, M.; Erlebach, A.; Herrmann, A.; Damak, K.; Rüssel, C.; Sierka, M.; Maâlej, R. The Structure of Gd3+-Doped Li2O and K2O Containing Aluminosilicate Glasses from Molecular Dynamics Simulations. Materials 2021, 14, 3265. [Google Scholar] [CrossRef]
- Assadi, A.A.; Herrmann, A.; Tewelde, M.; Damak, K.; Maalej, R.; Rüssel, C. Tb3+ as a probe for the molecular structure of mixed barium magnesium alumino silicate glasses. J. Lumin. 2018, 199, 384–390. [Google Scholar] [CrossRef]
- Blasse, G.; Grabmaier, B.C. Luminescent Materials; Springer: Berlin/Heidelberg, Germany, 1994; pp. 41–44. [Google Scholar] [CrossRef]
- Henrie, D.E.; Fellows, R.L.; Choppin, G.R. Hypersensitivity in the electronic transitions of lanthanide and actinide transitions. Coord. Chem. Rev. 1976, 18, 199–224. [Google Scholar] [CrossRef]
- Cormier, L. Glasses: Aluminosilicates. Encycl. Mater. Tech. Ceram. Glasses 2021, 2, 496–518. [Google Scholar] [CrossRef]
- Duffy, J.A. A review of optical basicity and its applications to oxidic systems. Geochim. Cosmochim. Acta 1993, 57, 3961–3970. [Google Scholar] [CrossRef]
- Dimitrov, V.; Komatsu, T.J. An interpretation of optical properties of oxides and oxide glasses in terms of the electronic ion polarizability and average single bond strength. J. Univ. Chem. Technol. Metall. 2010, 45, 219–250. [Google Scholar]
- Zekri, M.; Erlebach, A.; Herrmann, A.; Damak, K.; Rüssel, C.; Sierka, M.; Maâlej, R. Structure prediction of rare earth doped BaO and MgO containing aluminosilicate glasses—The model case of Gd2O3. Materials 2018, 11, 1790. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Pedone, A.; Malavasi, G.; Menziani, M.C.; Cormack, A.N.; Segre, U. A new self-consistent empirical interatomic potential model for oxides, silicates, and silica-based glasses. J. Phys. Chem. B 2006, 110, 11780–11795. [Google Scholar] [CrossRef] [PubMed]
- Pedone, A.; Malavasi, G.; Menziani, M.C.; Segre, U.; Cormack, A.N. Role of Magnesium in Soda-Lime Glasses: Insight into Structural, Transport, and Mechanical Properties through Computer Simulations. J. Phys. Chem. C 2008, 112, 11034–11041. [Google Scholar] [CrossRef]
- Linati, L.; Lusvardi, G.; Malavasi, G.; Menabue, L.; Menziani, M.C.; Mustarelli, P.; Pedone, A.; Segre, U. Medium-range order in phospho-silicate bioactive glasses: Insights from MAS-NMR spectra, chemical durability experiments and molecular dynamics simulations. J. Non-Cryst. Solids 2008, 354, 84–89. [Google Scholar] [CrossRef]
- Pedone, A.; Malavasi, G.; Cormack, A.N.; Segre, U.; Menziani, M.C. Insight into Elastic Properties of Binary Alkali Silicate Glasses; Prediction and Interpretation through Atomistic Simulation Techniques. Chem. Mater. 2007, 19, 3144–3154. [Google Scholar] [CrossRef]
- Afify, N.D.; Mountjoy, G. Molecular-dynamics modeling of Eu3+-ion clustering in SiO2 glass. Phys. Rev. B 2009, 79, 024202. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles, 1st ed.; CRC Press: Boca Raton, FL, USA, 1988; pp. 22–23. ISBN 978-1-138-41337-5. [Google Scholar]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Shinoda, W.; Shiga, M.; Mikami, M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B 2004, 69, 134103. [Google Scholar] [CrossRef]
- Haynes, W.M.; Lide, D.R. CRC Handbook of Chemistry and Physics: A Ready Reference Book of Chemical and Physical Data, 91st ed.; CRC Press: Boca Raton, FL, USA, 2010; ISBN 978-1439820773. [Google Scholar]
- Carnall, W.T.; Fields, P.R.; Rajnak, K. Electronic energy levels of the trivalent lanthanide aquo ions. I. Pr3+, Nd3+, Pm3+, Sm3+, Dy3+, Ho3+, Er3+, and Tm3+. J. Phys. Chem. 1968, 49, 4424–4442. [Google Scholar] [CrossRef]
- May, P.S.; Metcalf, D.H.; Richardson, F.S.; Carter, R.C.; Miller, C.E.; Palmer, R.A. Measurement and analysis of excited-state decay kinetics and chiroptical activity in the 6Hj←4G5/2 transitions of Sm3+ in trigonal Na3[Sm(C4H4O5)3]·2NaClO4·6H2O. J. Lumin. 1992, 51, 249–268. [Google Scholar] [CrossRef]
- Farries, M.C.; Morkel, P.R.; Townsend, J.E. Spectroscopic and lasing characteristics of samarium-doped glass fibre. IEE Proc. J (Optoelectron.) 1990, 137, 318–322. [Google Scholar] [CrossRef]
- Ratnakaram, Y.C.; Thirupathi Naidu, D.; Chakradhar, R.P.S. Spectral studies of Sm3+ and Dy3+ doped lithium cesium mixed alkali borate glasses. J. Non-Cryst. Solids 2006, 352, 3914–3922. [Google Scholar] [CrossRef]
- Kuhn, S.; Herrmann, A.; Rüssel, C. Judd-Ofelt analysis of Sm3+-doped lanthanum-aluminosilicate glasses. J. Lumin. 2015, 157, 390–397. [Google Scholar] [CrossRef]
- Herrmann, A.; Friedrich, D.; Zscheckel, T.; Rüssel, C. Luminescence properties of Sm3+ doped alkali/earth alkali orthoborates of the type XZBO3 with X = Li, Na, Cs and Z = Ca, Sr, Ba. J. Lumin. 2019, 214, 116550. [Google Scholar] [CrossRef]
- Cormier, L.; Delbes, L.; Baptiste, B.; Montouillout, V. Vitrification, crystallization behavior and structure of zinc aluminosilicate glasses. J. Non-Cryst. Solids 2021, 555, 120609. [Google Scholar] [CrossRef]
- Assadi, A.A.; Herrmann, A.; Lachheb, R.; Damak, K.; Rüssel, C.; Maalej, R. Experimental and Theoretical Study of Erbium Doped Aluminosilicate Glasses. J. Lumin. 2016, 176, 212–219. [Google Scholar] [CrossRef]
- Reisfeld, R.; Panczer, G.; Patra, A.; Gaft, M. Time-resolved spectroscopy of Sm3+ in silica and silica-Al sol-gel glasses. Mater. Lett. 1999, 38, 413–417. [Google Scholar] [CrossRef]
- Tanabe, S. Optical transitions of rare earth ions for amplifers: How the local structure works in glass. J. Non-Cryst. Solids 1999, 259, 1–9. [Google Scholar] [CrossRef]
- Berneschi, S.; Bettinelli, M.; Brenci, M.; Nunzi Conti, G.; Pelli, S.; Sebastiani, S.; Siligardi, C.; Speghini, A.; Righini, G.C. Aluminum co-doping of soda-lime silicate glasses: Effect on optical and spectroscopic properties. J. Non-Cryst. Solids 2005, 351, 1747–1753. [Google Scholar] [CrossRef]


| Sample Name | MgAS3510 | ZnAS3510 | CaAS3510 | SrAS3510 | BaAS3510 |
|---|---|---|---|---|---|
| Network modifier oxide (mol%) | (MgO) 35 | (ZnO) 35 | (CaO) 35 | (SrO) 35 | (BaO) 35 |
| Al2O3 (mol%) | 10 | 10 | 10 | 10 | 10 |
| SiO2 (mol%) | 55 | 55 | 55 | 55 | 55 |
| density(g/cm3) | 2.62 | 3.24 | 2.80 | 3.28 | 3.75 |
| transition temperature Tg (°C) | 811 | 705 | 812 | 795 | 771 |
| refractive index ne | 1.562 | 1.614 | 1.594 | 1.599 | 1.621 |
| theoretical optical basicity Λ | 0.561 | 0.592 | 0.605 | 0.625 | 0.635 |
| peak area A600 (cm−1) | 404.140 | 417.650 | 404.985 | 414.462 | 424.554 |
| peak area A645 (cm−1) | 236.895 | 234.086 | 220.666 | 228.934 | 236.162 |
| peak area ratioA645/A600 | 0.586 | 0.560 | 0.545 | 0.552 | 0.556 |
| Gd3+ Coordination Number (Percentage) Distance | MgAS3510 | ZnAS3510 | CaAS3510 | SrAS3510 | BaAS3510 |
|---|---|---|---|---|---|
| Gd-NBO | 4.047 (66.8%) | 3.805 (68.7%) | 4.209 (70.4%) | 4.123 (72.6%) | 4.275 (76.4%) |
| Gd-BO | 1.979 (32.7%) | 1.712 (30.9%) | 1.746 (29.2%) | 1.539 (27.1%) | 1.310 (23.4%) |
| Gd-Tri | 0.031 (0.5%) | 0.020 (0.4%) | 0.024 (0.4%) | 0.017 (0.3%) | 0.012 (0.2%) |
| Σ (Gd-O) | 6.058 2.25 Å | 5.538 2.25 Å | 5.979 2.25 Å | 5.679 2.25 Å | 5.598 2.25 Å |
| Gd-Al | 1.906 (16.4%) 3.51 Å | 1.883 (17.0%) 3.51 Å | 1.749 (14.9%) 3.57 Å | 1.779 (15.5%) 3.45 Å | 1.715 (14.6%) 3.57 Å |
| Gd-Si | 5.487 (47.2%) 3.57 Å | 5.177 (46.7%) 3.57 Å | 5.231 (44.7%) 3.57 Å | 5.008 (43.6%) 3.57 Å | 4.674 (39.9%) 3.57 Å |
| Gd-NM | (Mg) 4.223 (36.4%) 3.33 Å | (Zn) 4.030 (36.3%) 3.27Å | (Ca) 4.732 (40.4%) 3.51 Å | (Sr) 4.703 (40.9%) 3.75 Å | (Ba) 5.329 (45.5%) 3.87Å |
| NM Coordination Number (Percentage) Distance | MgAS3510 | ZnAS3510 | CaAS3510 | SrAS3510 | BaAS3510 |
|---|---|---|---|---|---|
| NM-O | (Mg) 4.635 2.01 Å | (Zn) 4.225 1.95 Å | (Ca) 6.230 2.37 Å | (Sr) 7.404 2.55 Å | (Ba) 9.108 2.73 Å |
| NM-Al | 1.740 (18.4%) 3.21 Å | 1.586 (18.7%) 3.15 Å | 2.020 (16.4%) 3.21 Å | 2.172 (15.6%) 3.39 Å | 2.314 (15.2%) 3.51 Å |
| NM-Si | 4.381 (46.5%) 3.27 Å | 3.919 (46.1%) 3.21 Å | 5.808 (47.1%) 3.57 Å | 6.379 (45.8%) 3.63 Å | 7.244 (47.7%) 3.57 Å |
| NM-NM | 3.306 (35.1%) 2.97 Å | 2.995 (35.2%) 2.79 Å | 4.500 (36.5%) 3.39 Å | 5.376 (38.6%) 3.75 Å | 5.641 (37.1%) 3.99 Å |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrmann, A.; Zekri, M.; Maalej, R.; Rüssel, C. The Effect of Glass Structure on the Luminescence Spectra of Sm3+-Doped Aluminosilicate Glasses. Materials 2023, 16, 564. https://doi.org/10.3390/ma16020564
Herrmann A, Zekri M, Maalej R, Rüssel C. The Effect of Glass Structure on the Luminescence Spectra of Sm3+-Doped Aluminosilicate Glasses. Materials. 2023; 16(2):564. https://doi.org/10.3390/ma16020564
Chicago/Turabian StyleHerrmann, Andreas, Mohamed Zekri, Ramzi Maalej, and Christian Rüssel. 2023. "The Effect of Glass Structure on the Luminescence Spectra of Sm3+-Doped Aluminosilicate Glasses" Materials 16, no. 2: 564. https://doi.org/10.3390/ma16020564
APA StyleHerrmann, A., Zekri, M., Maalej, R., & Rüssel, C. (2023). The Effect of Glass Structure on the Luminescence Spectra of Sm3+-Doped Aluminosilicate Glasses. Materials, 16(2), 564. https://doi.org/10.3390/ma16020564