Predicting Compressive Strength and Hydration Products of Calcium Aluminate Cement Using Data-Driven Approach
Abstract
:1. Introduction
2. Modeling Methods
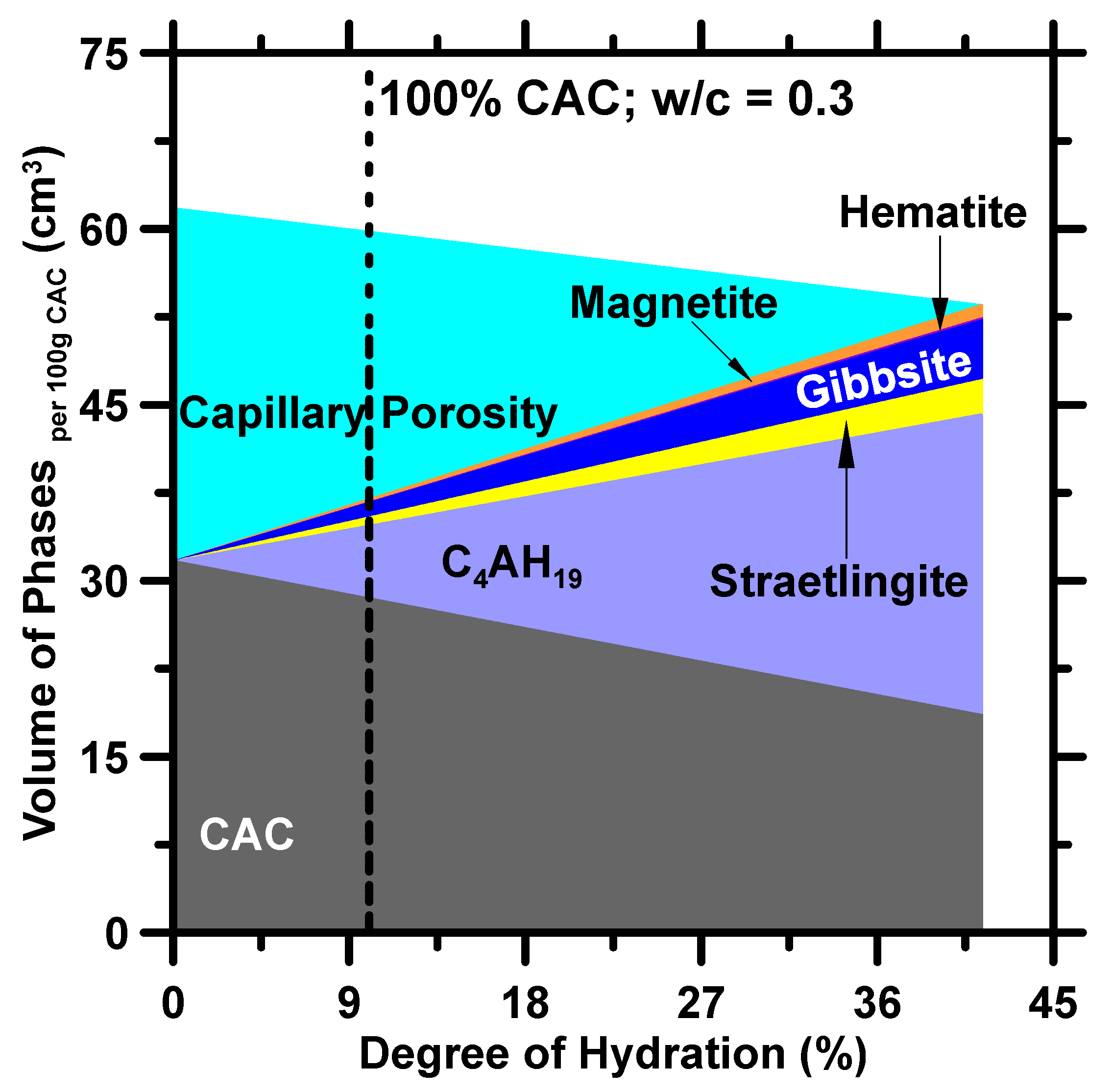
2.1. Thermodynamic Model
2.2. XGboost Model
3. Database
4. Results and Discussion
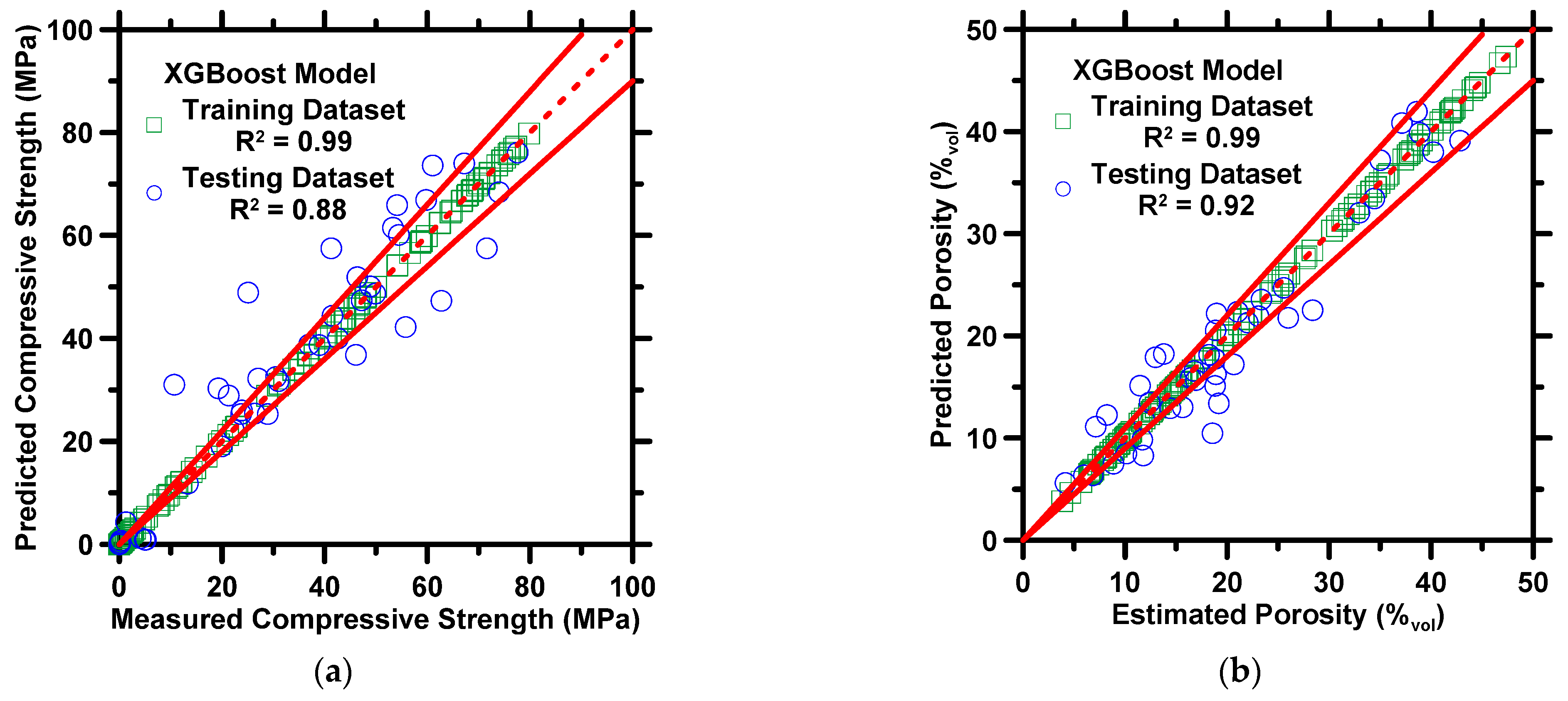
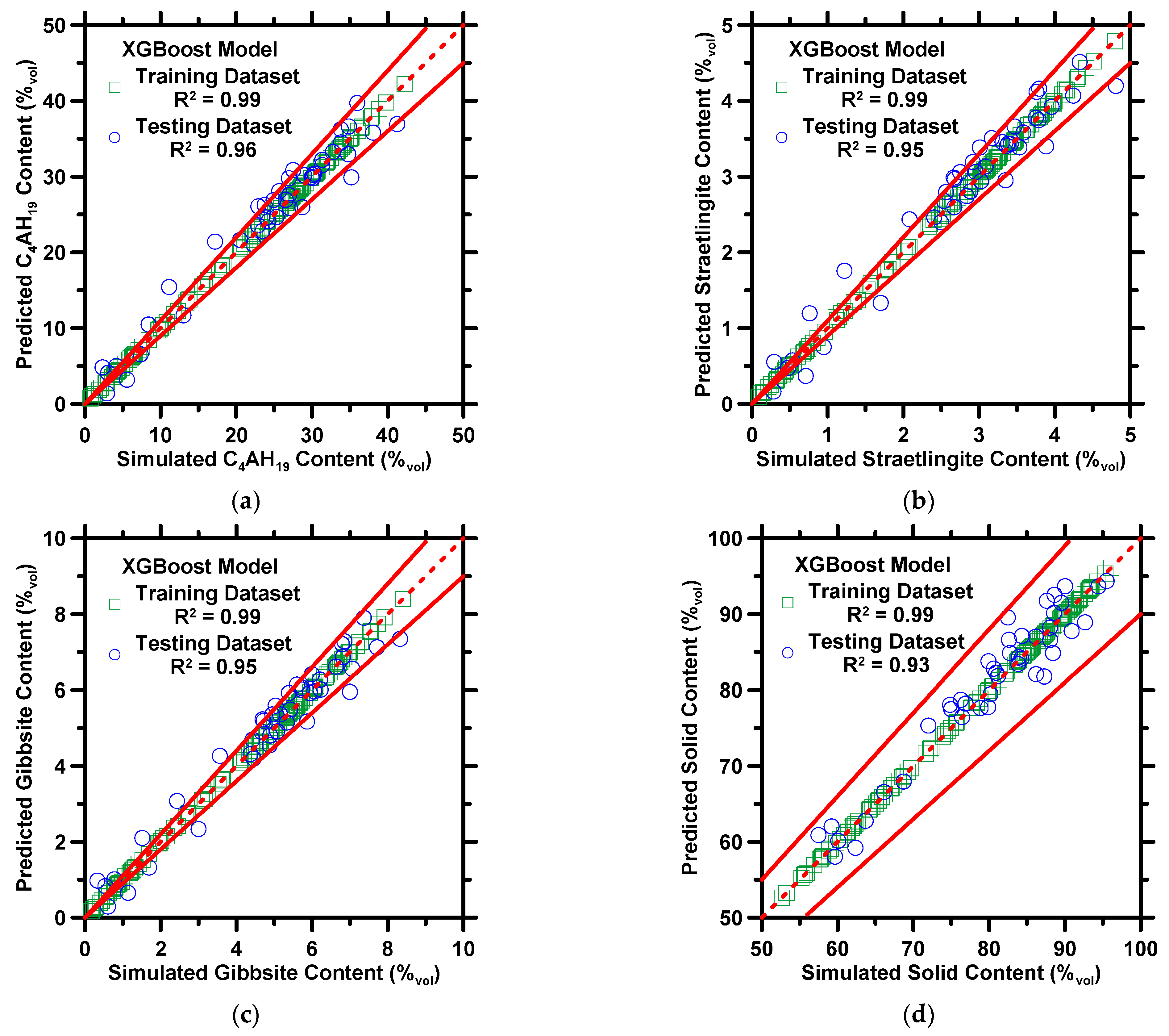
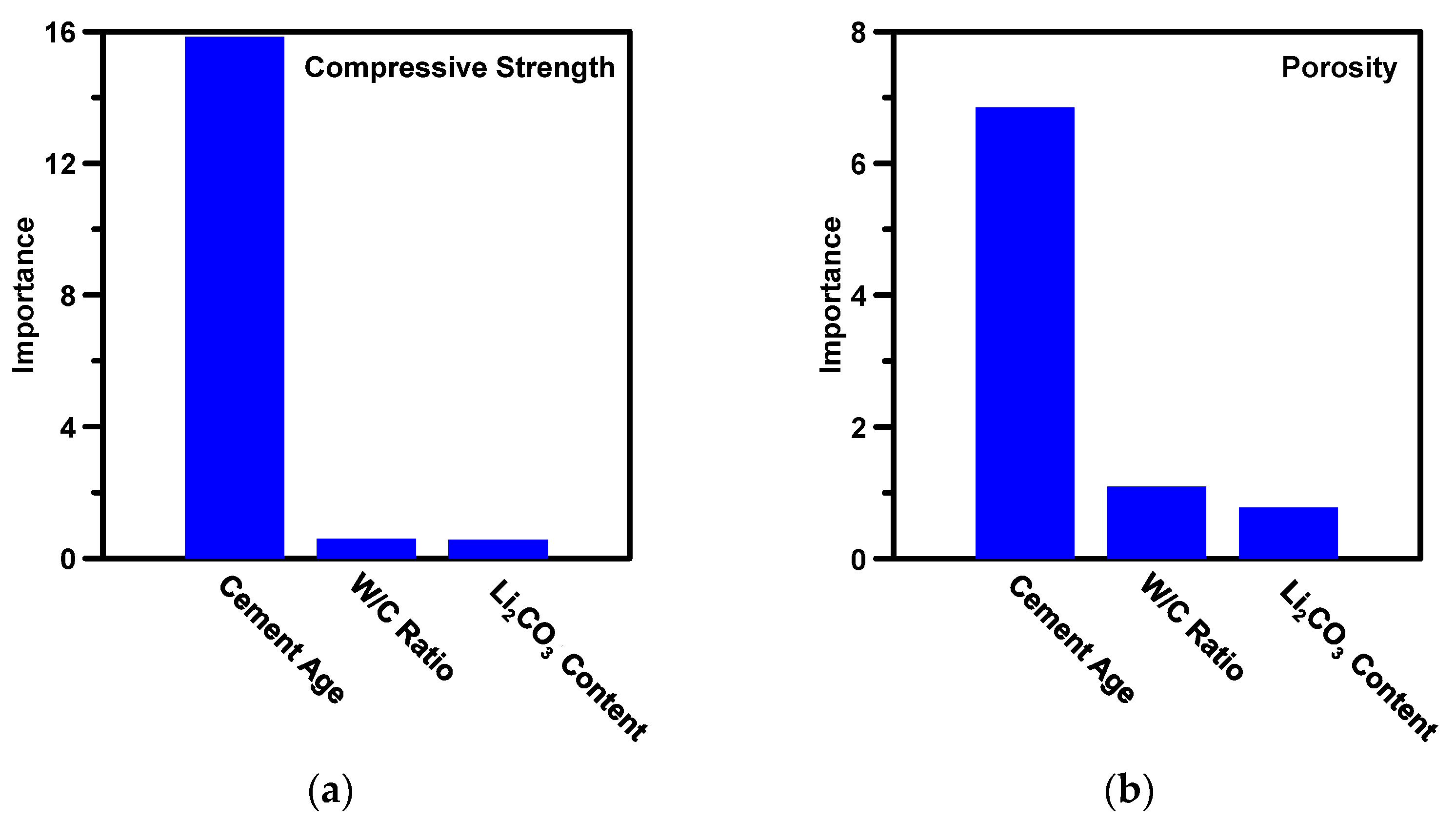
4.1. Machine Learning Prediction
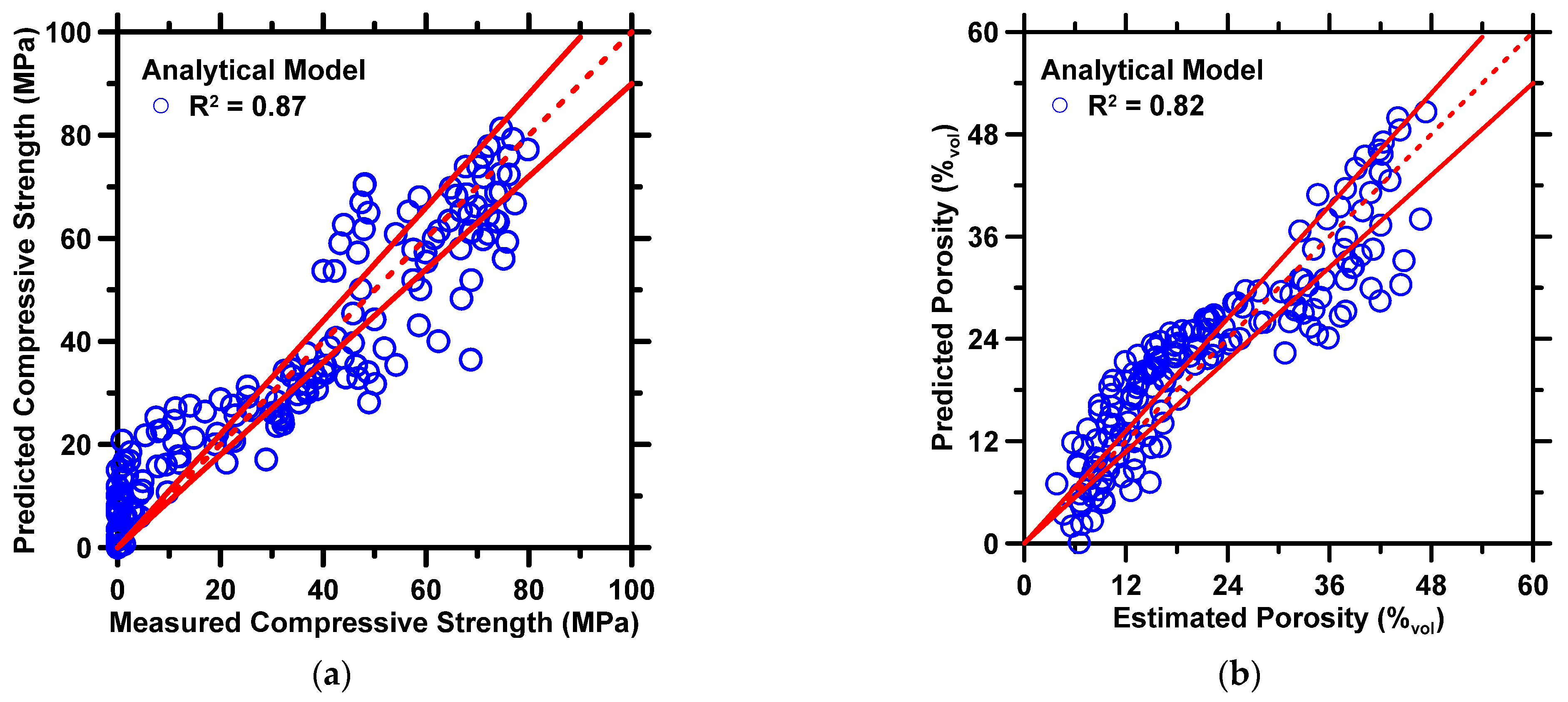
4.2. Analytical Model Development
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chatterjee, A.; Sui, T. Alternative Fuels—Effects on Clinker Process and Properties. Cem. Concr. Res. 2019, 123, 105777. [Google Scholar] [CrossRef]
- Gartner, E.; Hirao, H. A Review of Alternative Approaches to the Reduction of CO2 Emissions Associated with the Manufacture of the Binder Phase in Concrete. Cem. Concr. Res. 2015, 78, 126–142. [Google Scholar] [CrossRef] [Green Version]
- Schneider, M. Process Technology for Efficient and Sustainable Cement Production. Cem. Concr. Res. 2015, 78, 14–23. [Google Scholar] [CrossRef]
- Ludwig, H.-M.; Zhang, W. Research Review of Cement Clinker Chemistry. Cem. Concr. Res. 2015, 78, 24–37. [Google Scholar] [CrossRef]
- Zapata, J.F.; Azevedo, A.; Fontes, C.; Monteiro, S.N.; Colorado, H.A. Environmental Impact and Sustainability of Calcium Aluminate Cements. Sustainability 2022, 14, 2751. [Google Scholar] [CrossRef]
- Gevaudan, J.P.; Osio-Norgaard, J.; Srubar, W.V. Alternative Cements: Recent Developments and Future Directions. AEI 2019, 294–308. [Google Scholar] [CrossRef]
- Justnes, H. Alternative Low-CO2 “Green” Clinkering Processes. Rev. Mineral. Geochem. 2012, 74, 83–99. [Google Scholar] [CrossRef]
- Taylor, H.F.W. Cement Chemistry, 2nd ed.; Academic Pres Inc.: San Diego, CA, USA, 1992; Volume 1, ISBN 0-12-683900-X. [Google Scholar]
- Pöllmann, H. Calcium Aluminate Cements—Raw Materials, Differences, Hydration and Properties. Rev. Mineral. Geochem. 2012, 74, 1–82. [Google Scholar] [CrossRef]
- Kurtis, K.E. Innovations in Cement-Based Materials: Addressing Sustainability in Structural and Infrastructure Applications. MRS Bull. 2015, 40, 1102–1109. [Google Scholar] [CrossRef] [Green Version]
- Andrew, R. Global CO2 Emissions from Cement Production. Earth Syst. Sci. Data 2017, 10, 195–217. [Google Scholar] [CrossRef]
- Mangabhai, R.J. Calcium Aluminate Cements: Proceedings of a Symposium Dedicated to H G Midgley, London, July 1990; CRC Press: London, UK, 2014; ISBN 978-0-429-07850-7. [Google Scholar]
- Kırca, Ö.; Özgür Yaman, İ.; Tokyay, M. Compressive Strength Development of Calcium Aluminate Cement–GGBFS Blends. Cem. Concr. Compos. 2013, 35, 163–170. [Google Scholar] [CrossRef]
- Sakai, E.; Sugiyama, T.; Saito, T.; Daimon, M. Mechanical Properties and Micro-Structures of Calcium Aluminate Based Ultra High Strength Cement. Cem. Concr. Res. 2010, 40, 966–970. [Google Scholar] [CrossRef]
- Scrivener, K.L.; Cabiron, J.-L.; Letourneux, R. High-Performance Concretes from Calcium Aluminate Cements. Cem. Concr. Res. 1999, 29, 1215–1223. [Google Scholar] [CrossRef]
- Lothenbach, B.; Pelletier-Chaignat, L.; Winnefeld, F. Stability in the System CaO–Al2O3–H2O. Cem. Concr. Res. 2012, 42, 1621–1634. [Google Scholar] [CrossRef]
- Falzone, G.; Balonis, M.; Sant, G. X-AFm Stabilization as a Mechanism of Bypassing Conversion Phenomena in Calcium Aluminate Cements. Cem. Concr. Res. 2015, 72, 54–68. [Google Scholar] [CrossRef]
- Bensted, J.; Barnes, P. Structure and Performance of Cements; Spon Press: London, UK, 2002; ISBN 978-0-203-47778-6. [Google Scholar]
- Pacewska, B.; Nowacka, M.; Aleknevičius, M.; Antonovič, V. Early Hydration of Calcium Aluminate Cement Blended with Spent FCC Catalyst at Two Temperatures. Procedia Eng. 2013, 57, 844–850. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A.J.; Singh, B. Properties of Some Blended High-Alumina Cements. Cem. Concr. Res. 1992, 22, 1101–1114. [Google Scholar] [CrossRef]
- Roy, D.M. Relationships Between Permeability, Porosity, Diffusion and Microstructure Of Cement Pastes, Mortar, And Concrete At Different Temperatures. MRS Online Proc. Libr. 1988, 137, 179–189. [Google Scholar] [CrossRef]
- Powers, T.C. Structure and Physical Properties of Hardened Portland Cement Paste. J. Am. Ceram. Soc. 1958, 41, 1–6. [Google Scholar] [CrossRef]
- Bradbury, C.; Callaway, P.M.; Double, D.D. The Conversion of High Alumina Cement/Concrete. Mater. Sci. Eng. 1976, 23, 43–53. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials; McGraw-Hill Publishing: New York, NY, USA, 2006; ISBN 0-07-158919-8. [Google Scholar]
- Matusinović, T.; Vrbos, N. Alkali Metal Salts as Set Accelerators for High Alumina Cement. Cem. Concr. Res. 1993, 23, 177–186. [Google Scholar] [CrossRef]
- Hovasse, C. Setting and Hardening of Aluminous Cement. 1974. Available online: https://patentimages.storage.googleapis.com/f0/66/b5/1c5e06e341fc4f/US3826665.pdf (accessed on 28 October 2020).
- Aldera, A. Fluidized Molding Material for Manufacturing Cores and Molds and a Method Therefor. 1971. Available online: https://patentimages.storage.googleapis.com/49/b2/b5/abd1ed29fd1cb7/US3600203.pdf (accessed on 28 October 2020).
- Ebsworth, E.A.V.; Connor, J.A.; Turner, J.J.; Ebsworth, E.A.V. The Chemistry of Oxygen. In Comprehensive Inorganic Chemistry, 1st ed.; Pergamon Press: Oxford, UK, 1975; ISBN 978-0-08-018858-4. [Google Scholar]
- Luong, T.; Mayer, H.; Eckert, H.; Novinson, T.I. In Situ 27Al NMR Studies of Cement Hydration: The Effect of Lithium-Containing Setting Accelerators. J. Am. Ceram. Soc. 1989, 72, 2136–2141. [Google Scholar] [CrossRef]
- Rodger, S.A.; Double, D.D. The Chemistry of Hydration of High Alumina Cement in the Presence of Accelerating and Retarding Admixtures. Cem. Concr. Res. 1984, 14, 73–82. [Google Scholar] [CrossRef]
- Powers, T.C.; Brownyard, T.L. Studies of the Physical Properties of Hardened Portland Cement Paste. J. Proc. 1946, 43, 249–336. [Google Scholar] [CrossRef]
- Karni, J. Prediction of Compressive Strength of Concrete. Mat. Constr. 1974, 7, 197–200. [Google Scholar] [CrossRef]
- Tango, C.E.S. Time-Generalisation of Abrams’ Model for High Performance Concrete and Practical Application Examples. In Proceedings of the International Symposium on High Performance Concrete, Hong Kong, China, 10–15 December 2000. [Google Scholar]
- Popovics, S. History of a Mathematical Model for Strength Development of Portland Cement Concrete. ACI Mater. J. 1998, 95, 593–600. [Google Scholar] [CrossRef]
- AL-Shukaili, S.M.; Latif, Q.B.; Alias, I. Multi Variable Empirical Formula for SFRC Compressive, Tensile, and Shear Strength. In Proceedings of the International Conference on Civil, Disaster Management and Environmental Sciences, Bali, Indonesia, 2–3 February 2017. [Google Scholar]
- Gavela, S.; Nikoloutsopoulos, N.; Papadakos, G.; Passa, D.; Sotiropoulou, A. Multifactorial Experimental Analysis of Concrete Compressive Strength as a Function of Time and Water-to-Cement Ratio. Procedia Struct. Integr. 2018, 10, 135–140. [Google Scholar] [CrossRef]
- Feret, R. Sur la Compacité des Mortiers Hydrauliques; C. Dunod: Paris, France, 1892. [Google Scholar]
- Abrams, D.A. Design of Concrete Mixtures; Structural Materials Research Laboratory, Lewis Institute: Chicago, IL, USA, 1919; Volume 1. [Google Scholar]
- Popovics, S. New Formulas for the Prediction of the Effect of Porosity on Concrete Strength. J. Proc. 1985, 82, 136–146. [Google Scholar] [CrossRef]
- Feng, D.-C.; Liu, Z.-T.; Wang, X.-D.; Chen, Y.; Chang, J.-Q.; Wei, D.-F.; Jiang, Z.-M. Machine Learning-Based Compressive Strength Prediction for Concrete: An Adaptive Boosting Approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Uysal, M.; Tanyildizi, H. Estimation of Compressive Strength of Self Compacting Concrete Containing Polypropylene Fiber and Mineral Additives Exposed to High Temperature Using Artificial Neural Network. Constr. Build. Mater. 2012, 27, 404–414. [Google Scholar] [CrossRef]
- Dantas, A.T.A.; Batista Leite, M.; De Jesus Nagahama, K. Prediction of Compressive Strength of Concrete Containing Construction and Demolition Waste Using Artificial Neural Networks. Constr. Build. Mater. 2013, 38, 717–722. [Google Scholar] [CrossRef]
- Duan, Z.H.; Kou, S.C.; Poon, C.S. Prediction of Compressive Strength of Recycled Aggregate Concrete Using Artificial Neural Networks. Constr. Build. Mater. 2013, 40, 1200–1206. [Google Scholar] [CrossRef]
- Dao, D.V.; Trinh, S.H.; Ly, H.-B.; Pham, B.T. Prediction of Compressive Strength of Geopolymer Concrete Using Entirely Steel Slag Aggregates: Novel Hybrid Artificial Intelligence Approaches. Appl. Sci. 2019, 9, 1113. [Google Scholar] [CrossRef] [Green Version]
- Quaranta, G.; De Domenico, D.; Monti, G. Machine-Learning-Aided Improvement of Mechanics-Based Code-Conforming Shear Capacity Equation for RC Elements with Stirrups. Eng. Struct. 2022, 267, 114665. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jang, H.; Hwang, S.-H.; Jeon, J.-S. Data-Driven Machine-Learning-Based Seismic Failure Mode Identification of Reinforced Concrete Shear Walls. Eng. Struct. 2020, 208, 110331. [Google Scholar] [CrossRef]
- Bhat, R.; Han, T.; Akshay Ponduru, S.; Reka, A.; Huang, J.; Sant, G.; Kumar, A. Predicting Compressive Strength of Alkali-Activated Systems Based on the Network Topology and Phase Assemblages Using Tree-Structure Computing Algorithms. Constr. Build. Mater. 2022, 336, 127557. [Google Scholar] [CrossRef]
- Han, T.; Gomaa, E.; Gheni, A.; Huang, J.; ElGawady, M.; Kumar, A. Machine Learning Enabled Closed-Form Models to Predict Strength of Alkali-Activated Systems. J. Am. Ceram. Soc. 2022, 105, 4414–4425. [Google Scholar] [CrossRef]
- Han, T.; Siddique, A.; Khayat, K.; Huang, J.; Kumar, A. An Ensemble Machine Learning Approach for Prediction and Optimization of Modulus of Elasticity of Recycled Aggregate Concrete. Constr. Build. Mater. 2020, 244, 118271. [Google Scholar] [CrossRef]
- Cook, R.; Lapeyre, J.; Ma, H.; Kumar, A. Prediction of Compressive Strength of Concrete: A Critical Comparison of Performance of a Hybrid Machine Learning Model with Standalone Models. ASCE J. Mater. Civ. Eng. 2019, 31, 04019255. [Google Scholar] [CrossRef]
- Matschei, T.; Lothenbach, B.; Glasser, F.P. The AFm Phase in Portland Cement. Cem. Concr. Res. 2007, 37, 118–130. [Google Scholar] [CrossRef]
- Balonis, M. The Influence of Inorganic Chemical Accelerators and Corrosion Inhibitors on the Mineralogy of Hydrated Portland Cement Systems. Ph.D. Thesis, University of Aberdeen, Aberdeen, UK, 2010. [Google Scholar]
- Lothenbach, B.; Kulik, D.A.; Matschei, T.; Balonis, M.; Baquerizo, L.; Dilnesa, B.; Miron, G.D.; Myers, R.J. Cemdata18: A Chemical Thermodynamic Database for Hydrated Portland Cements and Alkali-Activated Materials. Cem. Concr. Res. 2019, 115, 472–506. [Google Scholar] [CrossRef] [Green Version]
- Kulik, D.A.; Wagner, T.; Dmytrieva, S.V.; Kosakowski, G.; Hingerl, F.F.; Chudnenko, K.V.; Berner, U.R. GEM-Selektor Geochemical Modeling Package: Revised Algorithm and GEMS3K Numerical Kernel for Coupled Simulation Codes. Comput. Geosci. 2012, 17, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Lothenbach, B.; Matschei, T.; Möschner, G.; Glasser, F.P. Thermodynamic Modelling of the Effect of Temperature on the Hydration and Porosity of Portland Cement. Cem. Concr. Res. 2008, 38, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Matschei, T.; Lothenbach, B.; Glasser, F.P. Thermodynamic Properties of Portland Cement Hydrates in the System CaO–Al2O3–SiO2–CaSO4–CaCO3–H2O. Cem. Concr. Res. 2007, 37, 1379–1410. [Google Scholar] [CrossRef]
- Outhwaite, C.W. Extension of the Debye–Hückel Theory of Electrolyte Solutions. J. Chem. Phys. 1969, 50, 2277–2288. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive Logistic Regression: A Statistical View of Boosting. Ann. Statist. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost Algorithm-Based Prediction of Concrete Electrical Resistivity for Structural Health Monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- Matusinović, T.; Šipušić, J.; Vrbos, N. Porosity–Strength Relation in Calcium Aluminate Cement Pastes. Cem. Concr. Res. 2003, 33, 1801–1806. [Google Scholar] [CrossRef]
- C01 Committee C349-02; Test Method for Compressive Strength of Hydraulic-Cement Mortars (Using Portions of Prisms Broken in Flexure). ASTM International: West Conshohocken, PA, USA, 2010.
- C109/C109M-20b; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars (Using 2-in. or [50-Mm] Cube Specimens). ASTM International: West Conshohocken, PA, USA, 2020.
- Röβler, M.; Odler, I. Investigations on the Relationship between Porosity, Structure and Strength of Hydrated Portland Cement Pastes, I. Effect of Porosity. Cem. Concr. Res. 1985, 15, 320–330. [Google Scholar] [CrossRef]
- Schaffer, C. Selecting a Classification Method by Cross-Validation. Mach. Learn. 1993, 13, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Eitrich, T.; Lang, B. Efficient Optimization of Support Vector Machine Learning Parameters for Unbalanced Datasets. J. Comput. Appl. Math. 2006, 196, 425–436. [Google Scholar] [CrossRef] [Green Version]
- ACI (American Concrete Institute) Committee 214. Guide to Evaluation of Strength Test Results of Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2011; ISBN 978-0-87031-423-0. [Google Scholar]
- Li, Y.; Gou, J.; Fan, Z. Particle Swarm Optimization-Based Extreme Gradient Boosting for Concrete Strength Prediction. In Proceedings of the 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu, China, 20–22 December 2019; pp. 982–986. [Google Scholar]
- Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.-N.; Moayedi, H. A Novel Artificial Intelligence Technique to Predict Compressive Strength of Recycled Aggregate Concrete Using ICA-XGBoost Model. Eng. Comput. 2020, 37, 3329–3346. [Google Scholar] [CrossRef]
- Han, T.; Stone-Weiss, N.; Huang, J.; Goel, A.; Kumar, A. Machine Learning as a Tool to Design Glasses with Controlled Dissolution for Application in Healthcare Industry. Acta Biomater. 2020, 107, 286–298. [Google Scholar] [CrossRef] [PubMed]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- McKinnon, K.I.M. Convergence of the Nelder--Mead Simplex Method to a Nonstationary Point. SIAM J. Optim. 1998, 9, 148–158. [Google Scholar] [CrossRef]
| Analytical Model | Reference |
|---|---|
| Feret et al. [37] | |
| Abrams et al. [38] | |
| Powers et al. [31] | |
| Gavela et al. [36] |
| Attribute | Unit | Min. | Max. | Mean | Std.Dev. |
|---|---|---|---|---|---|
| Water-to-Cement Ratio | Unitless | 0.20 | 0.30 | 0.25 | 0.04 |
| Li2CO3 Content | %mass | 2.55 | 10.91 | 3.89 | 1.17 |
| Cement Age | Hour | 1 | 168 | 30.42 | 51.62 |
| Compressive Strength | MPa | 0 | 79.80 | 33.08 | 26.65 |
| Porosity | %Vol | 3.84 | 47.34 | 21.35 | 11.96 |
| C4AH19 Content | %Vol | 0.74 | 42.23 | 21.78 | 11.44 |
| Straetlingite Content | %Vol | 0.09 | 4.80 | 2.48 | 1.30 |
| Gibbsite Content | %Vol | 0.16 | 8.40 | 4.34 | 2.27 |
| Solid Content | %Vol | 52.64 | 96.13 | 78.65 | 11.96 |
| R | R2 | MAE | RMSE | |
|---|---|---|---|---|
| Compressive Strength | Unitless | Unitless | MPa | MPa |
| 0.9386 | 0.8809 | 5.577 | 8.088 | |
| Porosity | Unitless | Unitless | %Vol | %Vol |
| 0.9578 | 0.9173 | 2.353 | 2.967 | |
| C4AH19 Content | Unitless | Unitless | %Vol | %Vol |
| 0.9789 | 0.9582 | 1.693 | 2.155 | |
| Straetlingite Content | Unitless | Unitless | %Vol | %Vol |
| 0.9757 | 0.9520 | 0.2060 | 0.2598 | |
| Gibbsite Content | Unitless | Unitless | %Vol | %Vol |
| 0.9757 | 0.9520 | 0.3839 | 0.4553 | |
| Solid Content | Unitless | Unitless | %Vol | %Vol |
| 0.9655 | 0.9322 | 2.205 | 2.716 |
| Compressive Strength | C1 | 82.159 | C2 | −41.801 | C3 | 3.632 |
| C4 | 1788 | C5 | 1.631 | C6 | 0.274 | |
| C7 | −15.422 | |||||
| Porosity | C1 | 2.610 | C2 | 55.324 | C3 | −0.488 |
| C4 | −710 | C5 | 35.542 | C6 | −0.258 | |
| C7 | −16.192 |
| R | R2 | MAE | RMSE | |
|---|---|---|---|---|
| Compressive Strength | Unitless | Unitless | MPa | MPa |
| 0.9351 | 0.8745 | 7.666 | 9.673 | |
| Porosity | Unitless | Unitless | %Vol | %Vol |
| 0.9075 | 0.8236 | 4.244 | 5.065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponduru, S.A.; Han, T.; Huang, J.; Kumar, A. Predicting Compressive Strength and Hydration Products of Calcium Aluminate Cement Using Data-Driven Approach. Materials 2023, 16, 654. https://doi.org/10.3390/ma16020654
Ponduru SA, Han T, Huang J, Kumar A. Predicting Compressive Strength and Hydration Products of Calcium Aluminate Cement Using Data-Driven Approach. Materials. 2023; 16(2):654. https://doi.org/10.3390/ma16020654
Chicago/Turabian StylePonduru, Sai Akshay, Taihao Han, Jie Huang, and Aditya Kumar. 2023. "Predicting Compressive Strength and Hydration Products of Calcium Aluminate Cement Using Data-Driven Approach" Materials 16, no. 2: 654. https://doi.org/10.3390/ma16020654
APA StylePonduru, S. A., Han, T., Huang, J., & Kumar, A. (2023). Predicting Compressive Strength and Hydration Products of Calcium Aluminate Cement Using Data-Driven Approach. Materials, 16(2), 654. https://doi.org/10.3390/ma16020654







