Identification of Differential Drive Robot Dynamic Model Parameters
Abstract
:1. Introduction
- three-wheeled systems (two independent driven wheels, one non-driven castor wheel);
- four-wheeled systems:
- –
- two independent driven standard wheels mounted on the front of the robot and two castor wheels mounted on the rear of the robot;
- –
- four independently controlled Swedish wheels;
- six-wheeled systems (two independent driven standard wheels mounted in the center of the robot frame and four castor wheels mounted on the corners of the robot frame).
2. Related Works
3. Materials and Methods
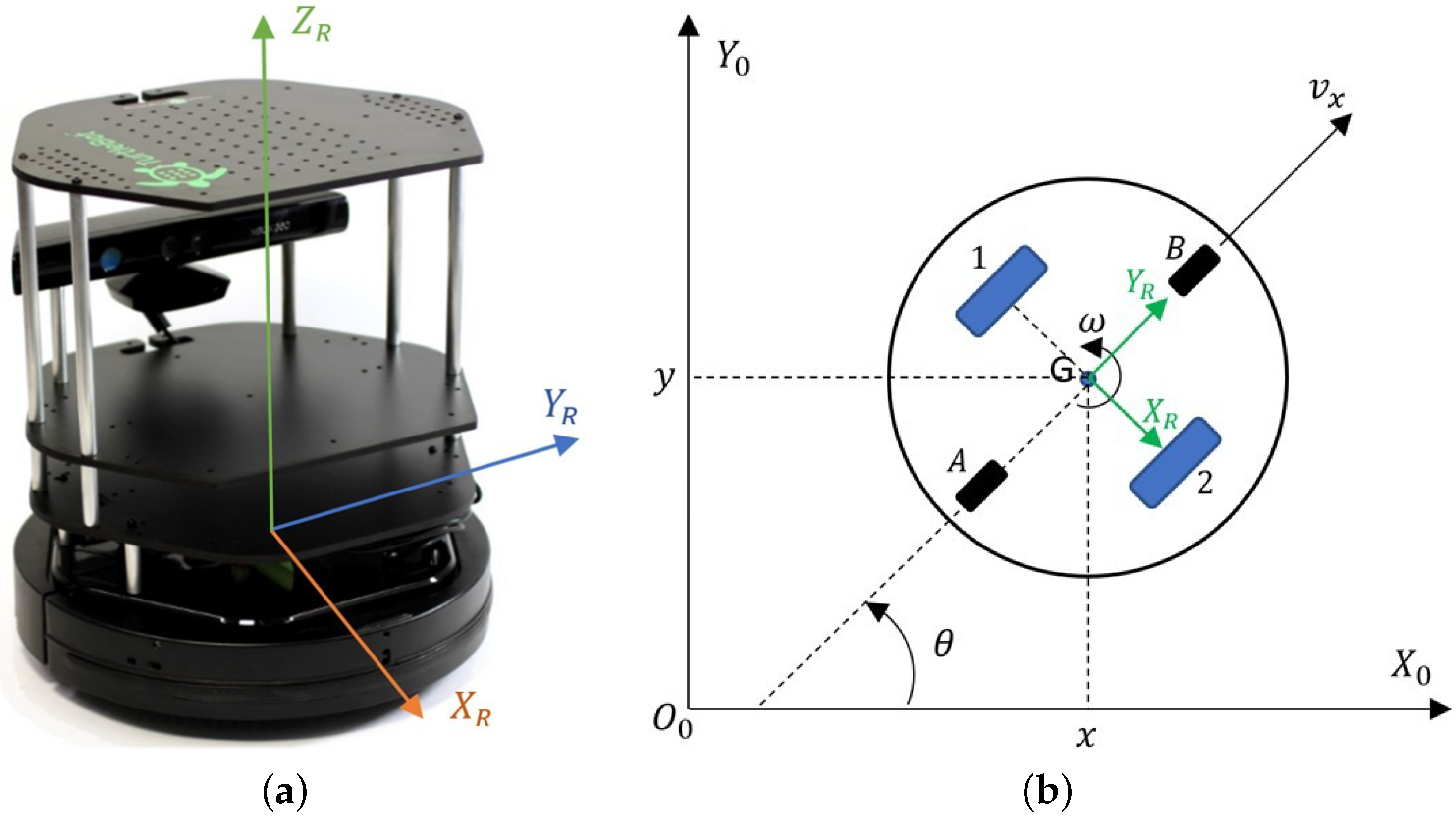
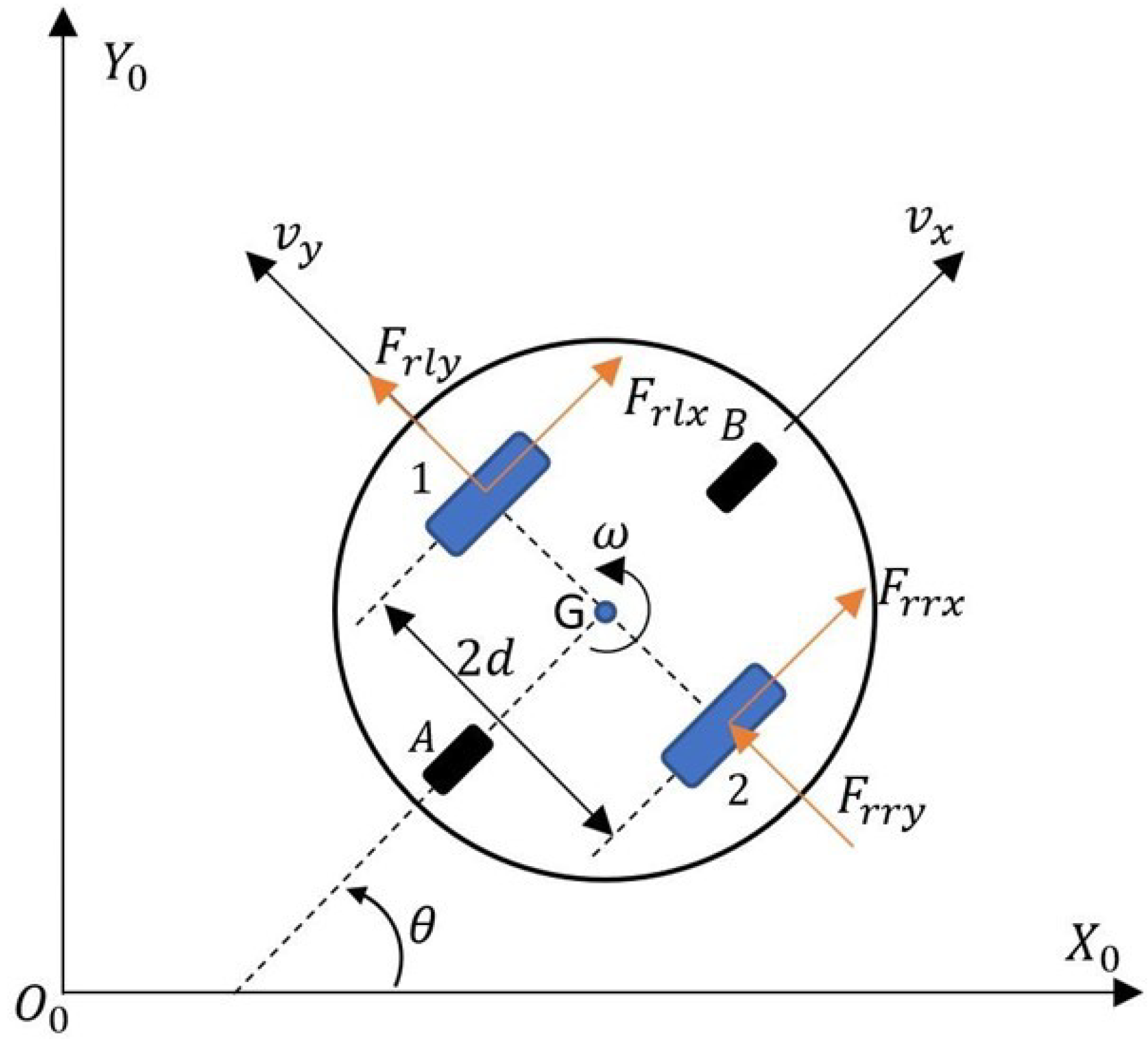
3.1. Kinematic and Dynamic Robot Model
3.2. Offline Identification of Robot Dynamic Model Parameters
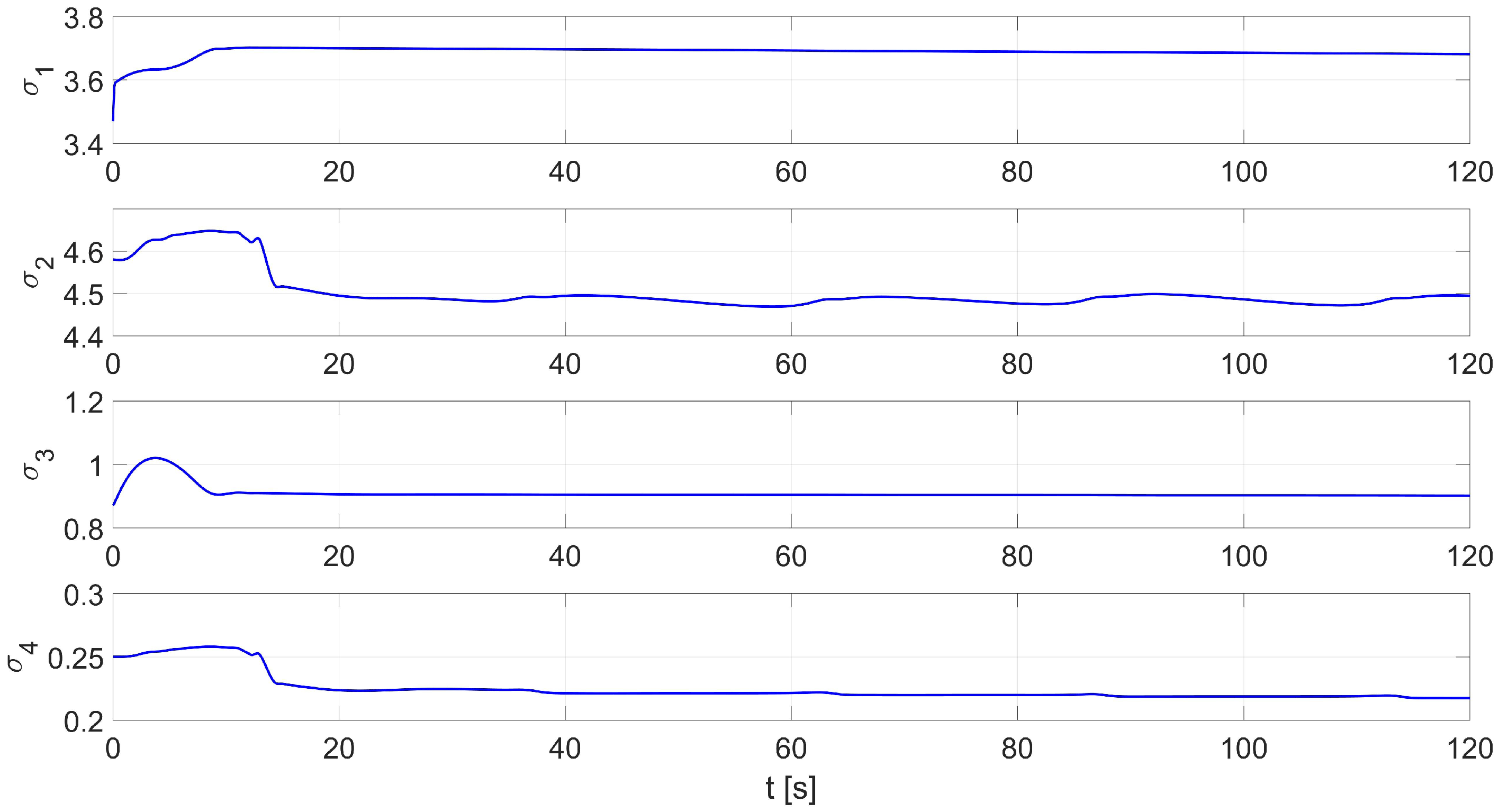
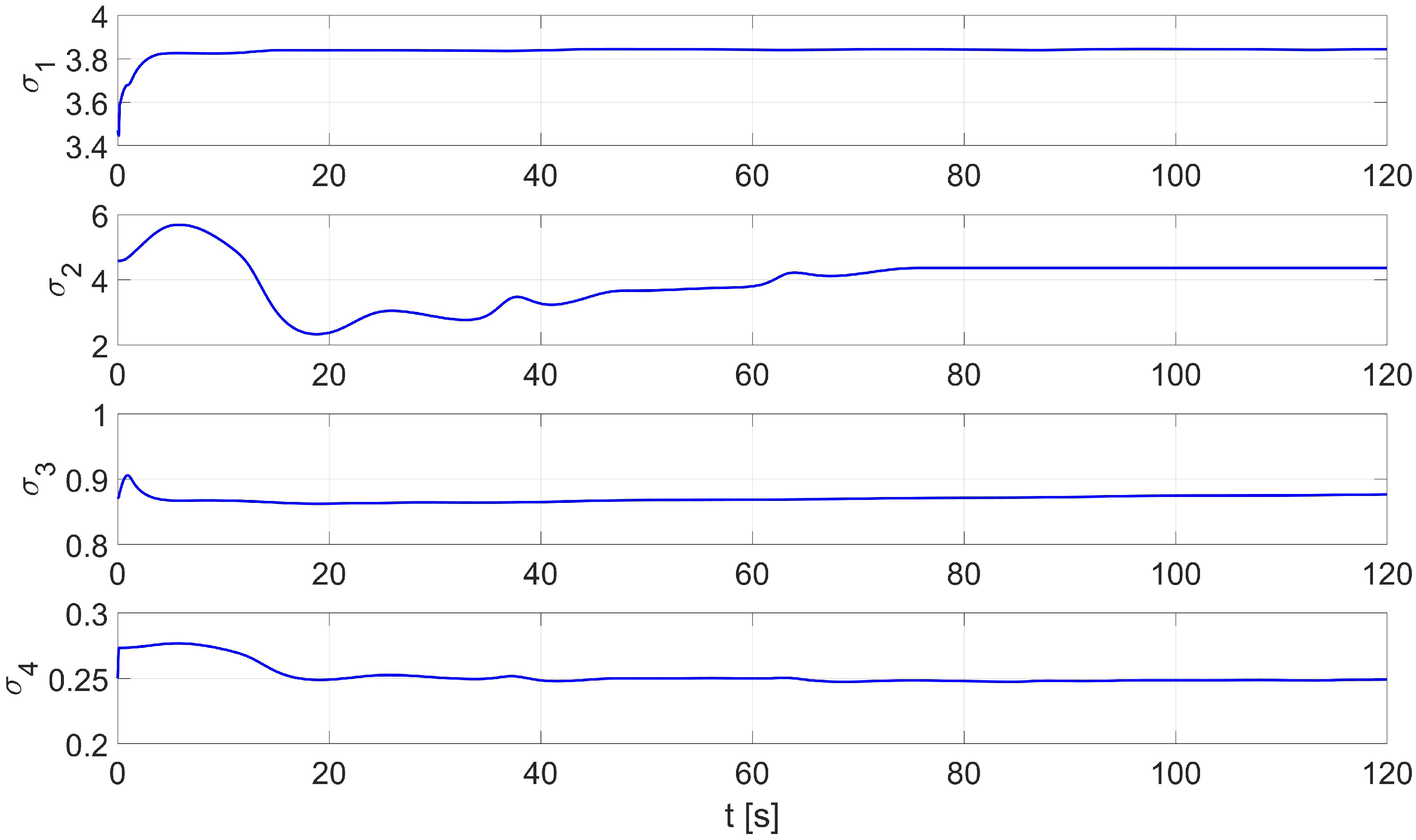
3.3. Online Identification of Robot Model Parameters
4. Results
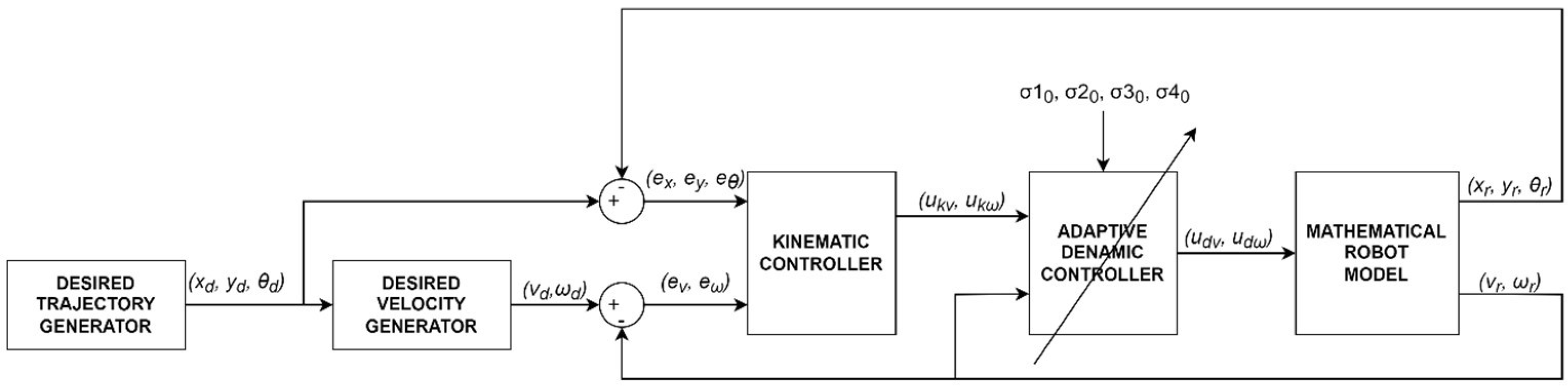
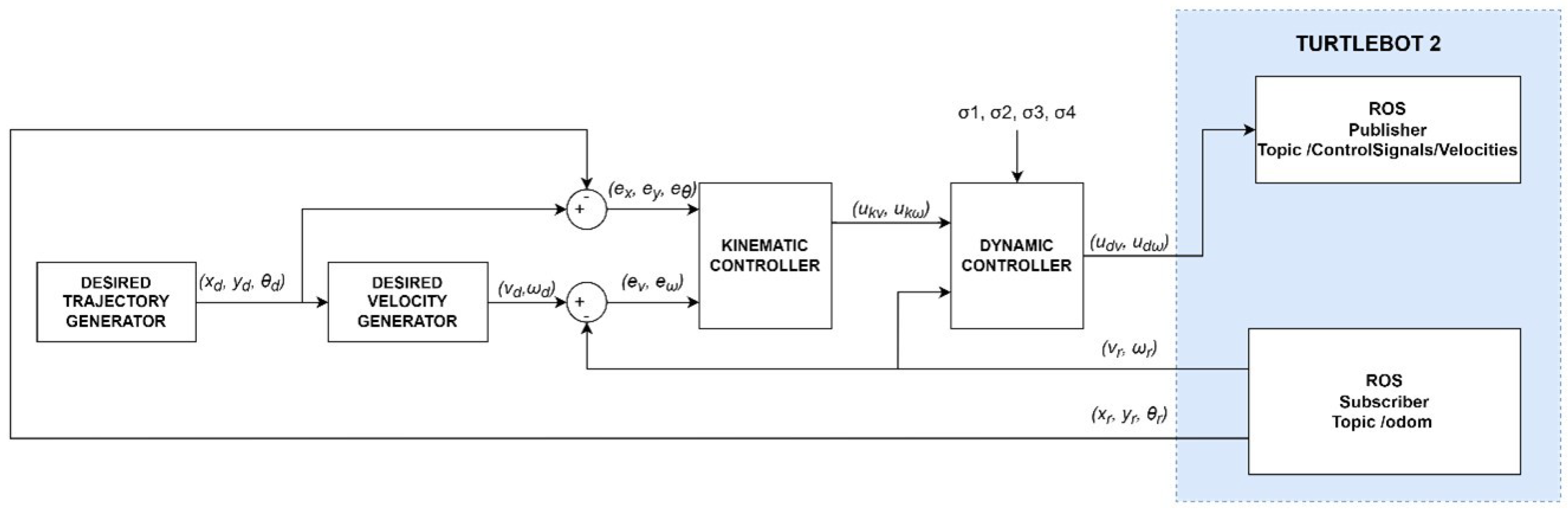
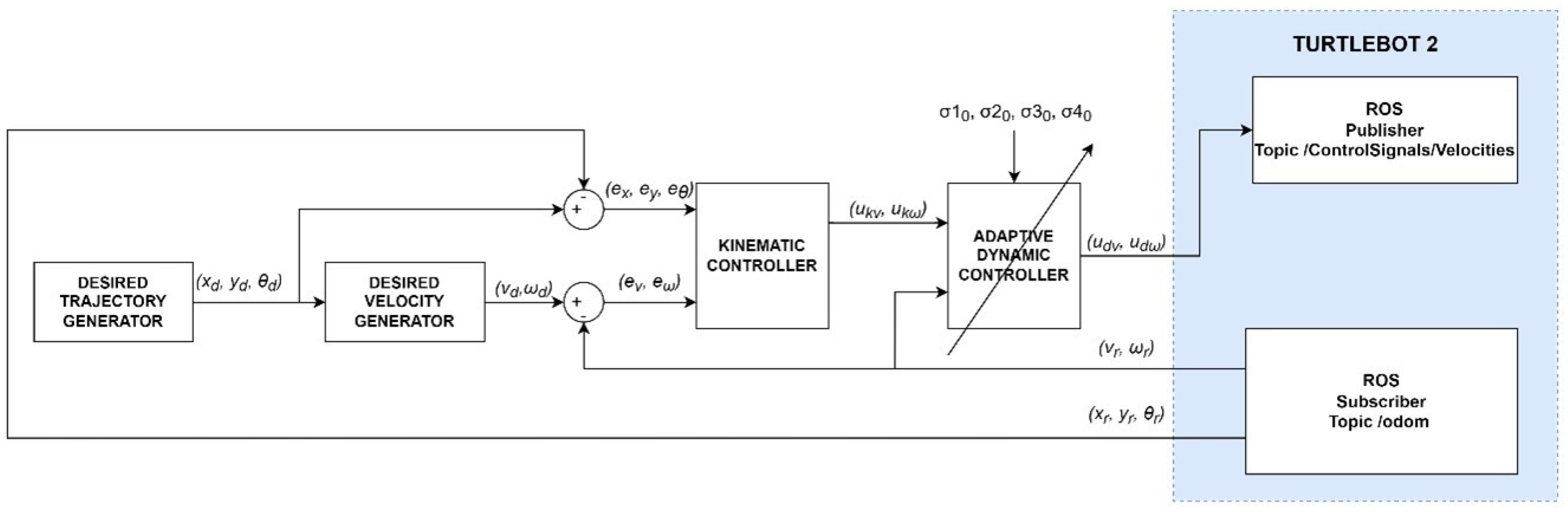
4.1. Kinematic and Dynamic Controller
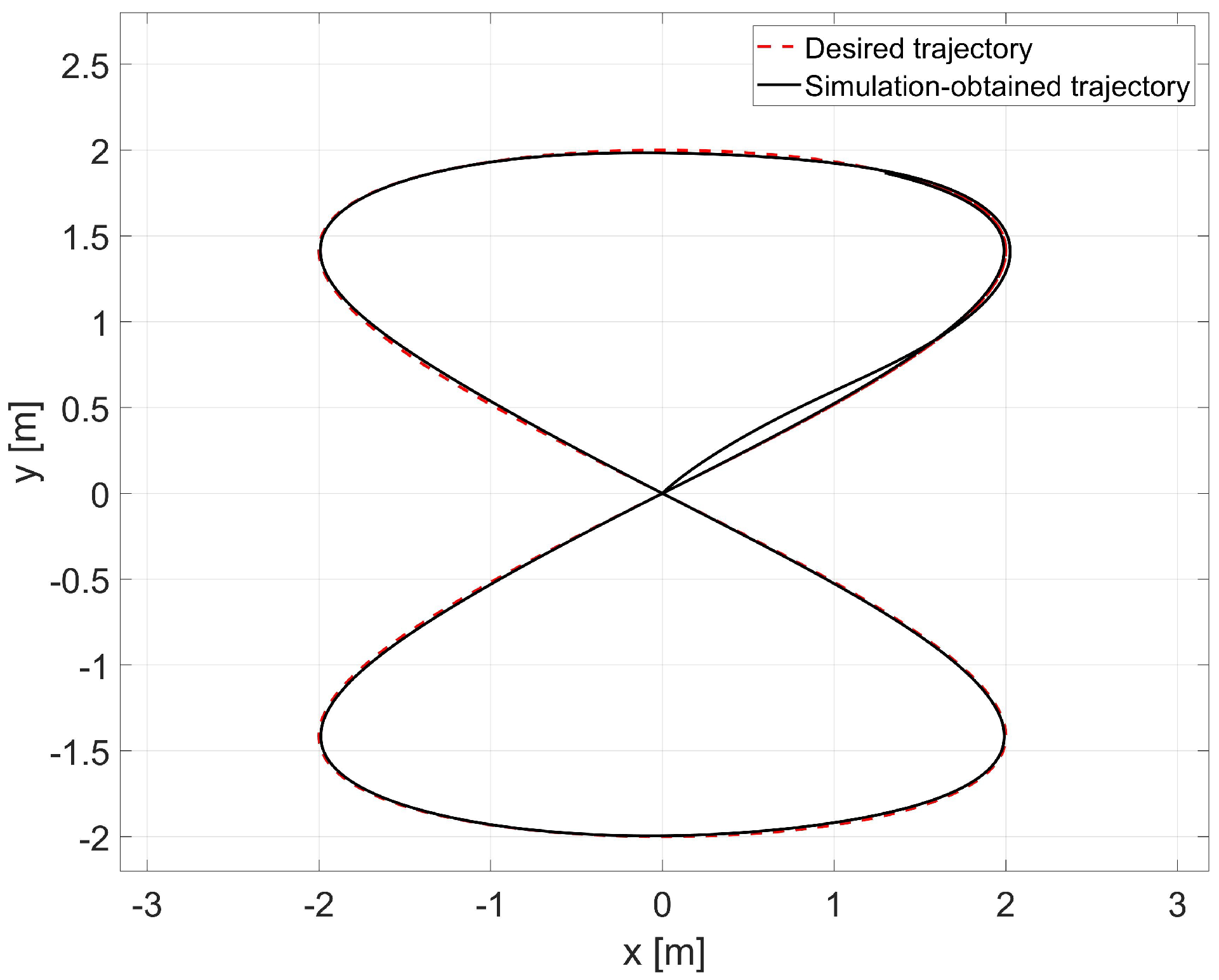
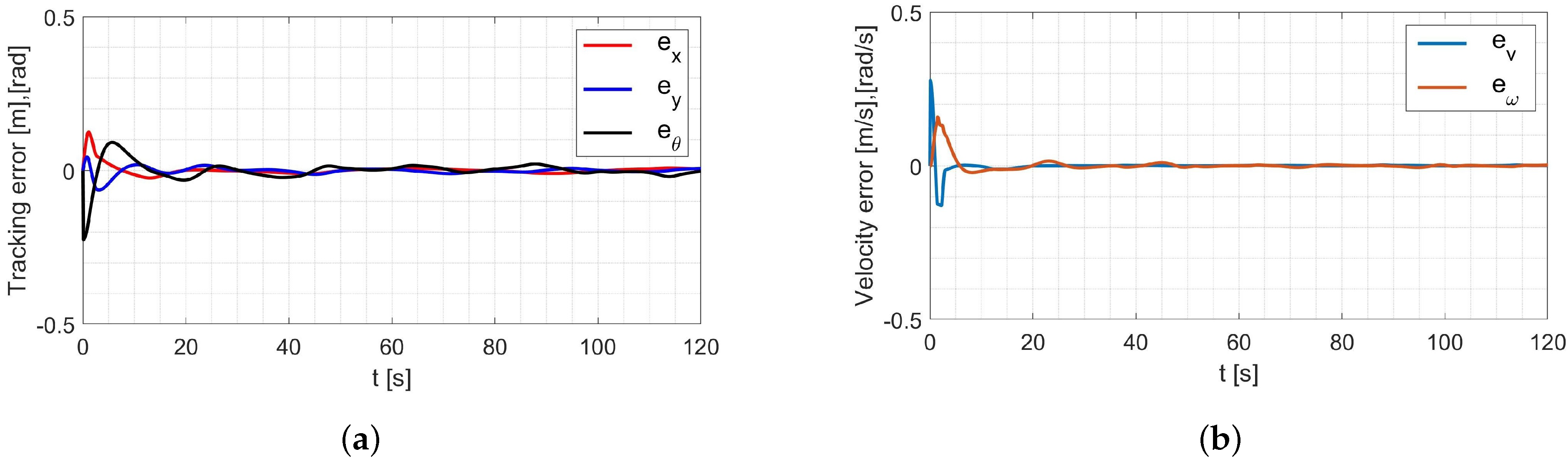
4.2. Simulation Tests of the Control System Considering Parameters Identified Offline
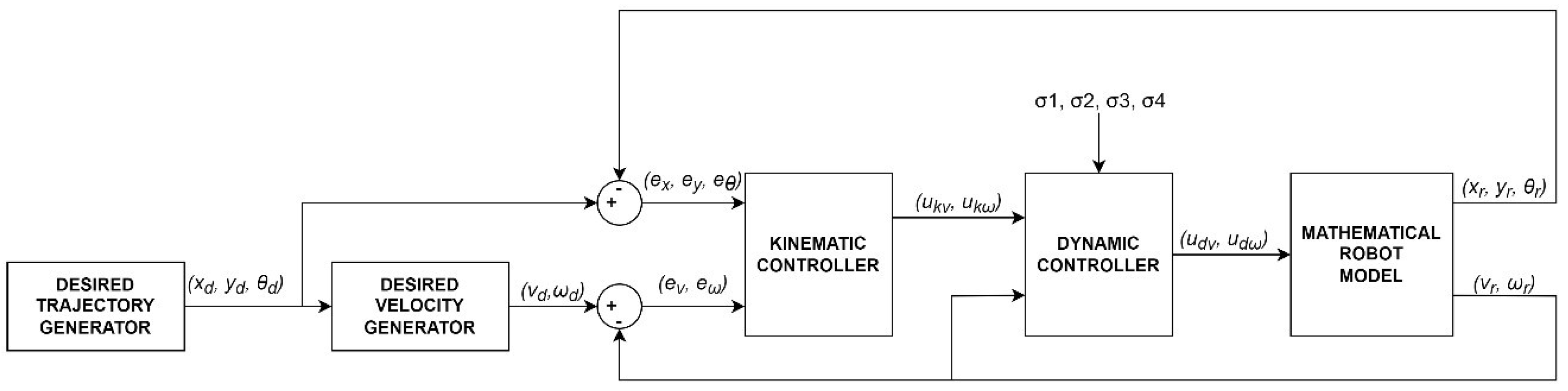
- desired trajectory generator module that determines the position , and orientation ,
- a generator of the desired linear velocity and angular velocity ,
- a kinematic controller described by Equation (10),
- a dynamic controller described by Equation (12),
- and a mathematical model of the robot described by Equations (1) and (3).
- in the x-axis direction: ,
- in the y-axis direction: ,
- orientation: ,
- linear velocity ,
- angular velocity .
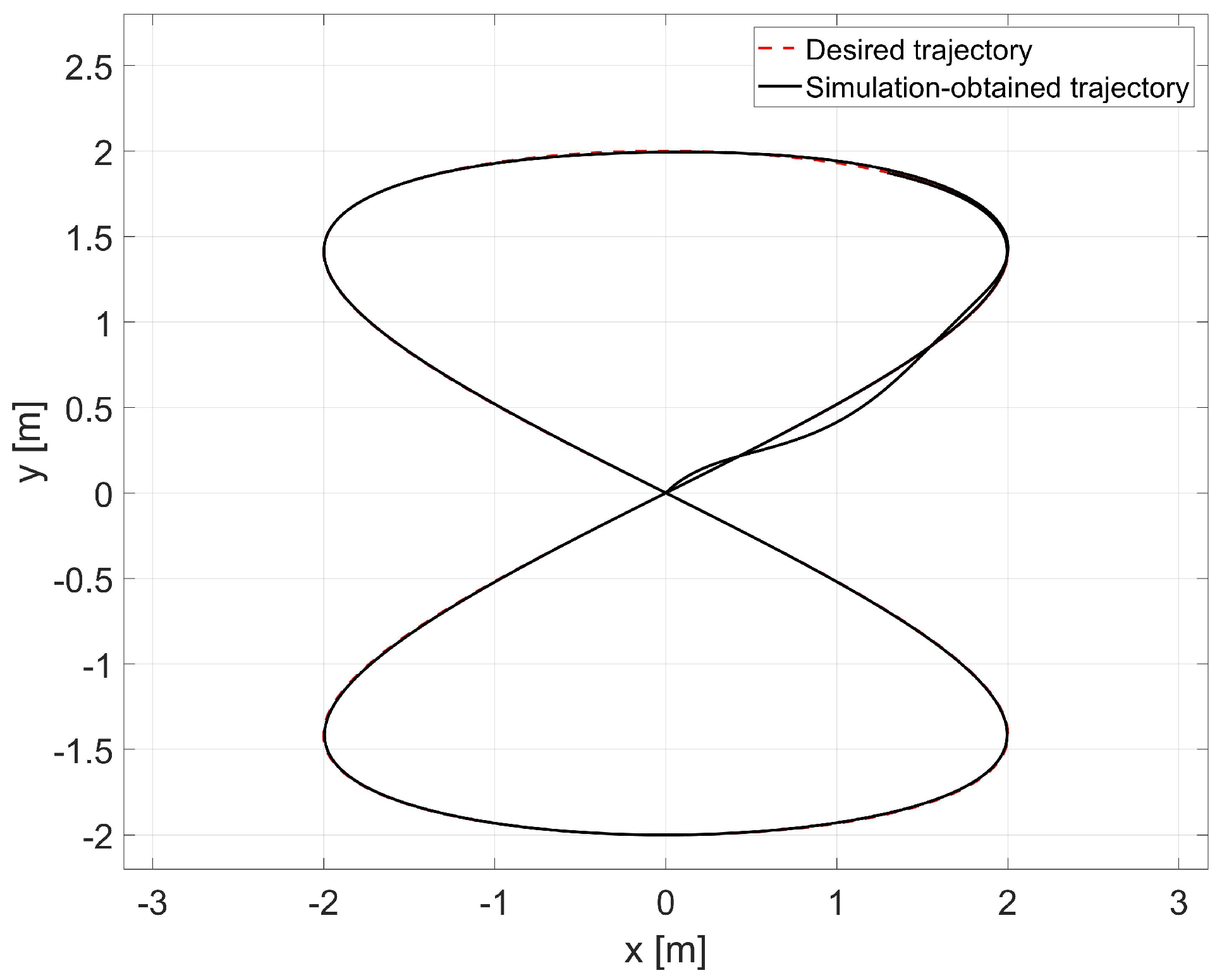
4.3. Simulation Studies of the Control System with Online Identification
- in the x-axis direction: ,
- in the y-axis direction: ,
- orientation: ,
- linear velocity ,
- angular velocity .
- in the x-axis direction: ,
- in the y-axis direction: ,
- orientation: ,
- linear velocity ,
- angular velocity .
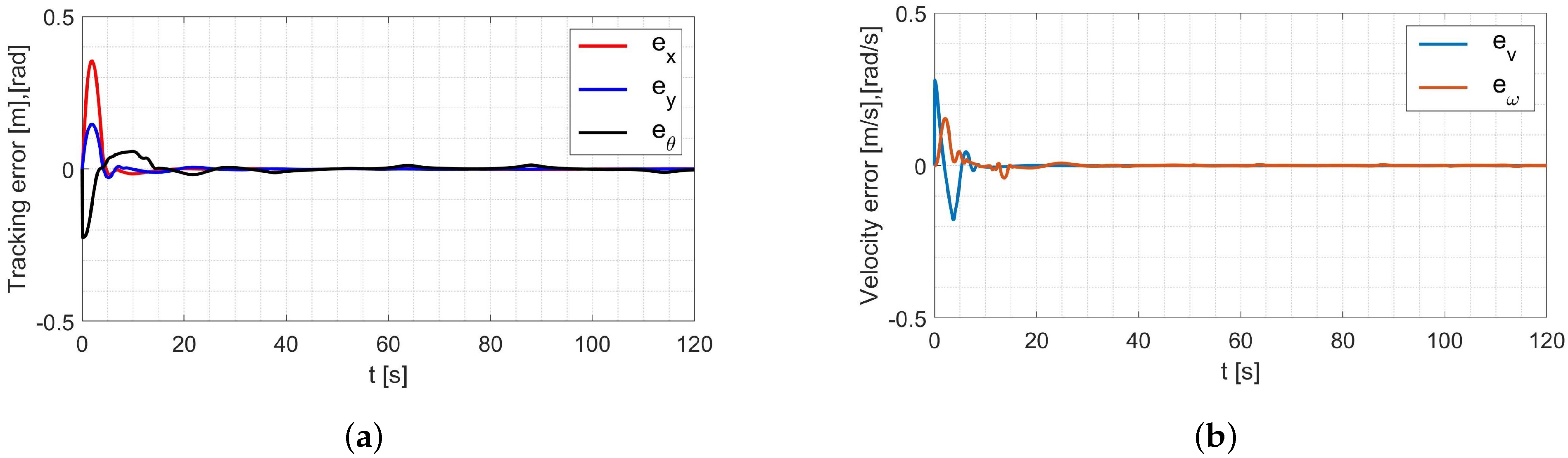
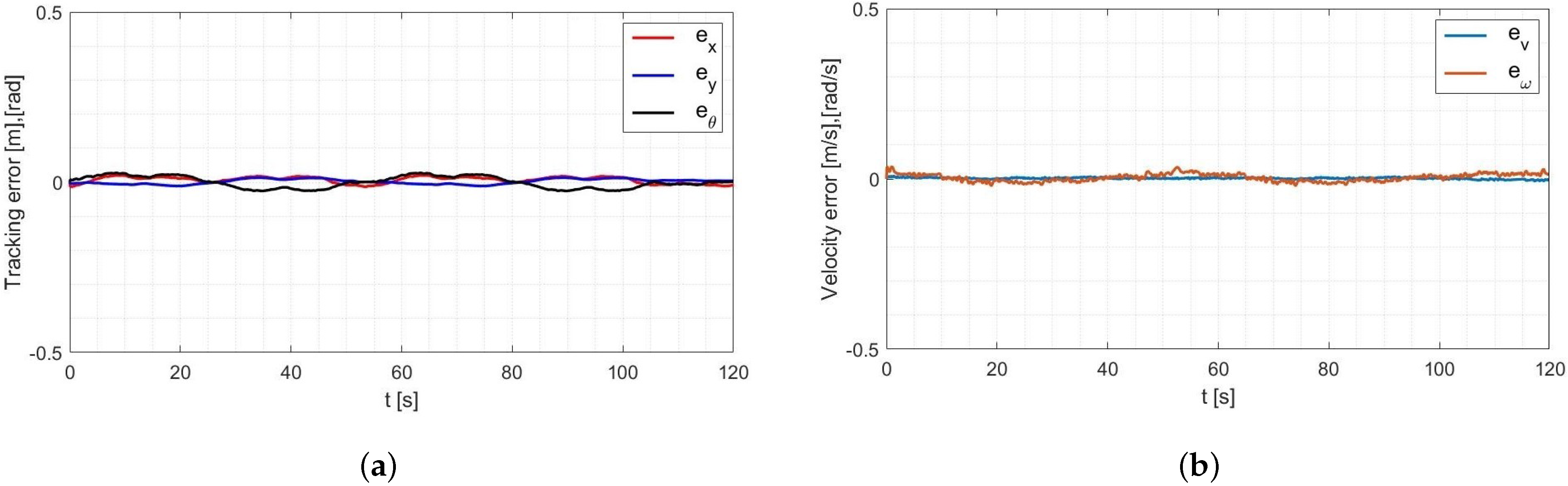
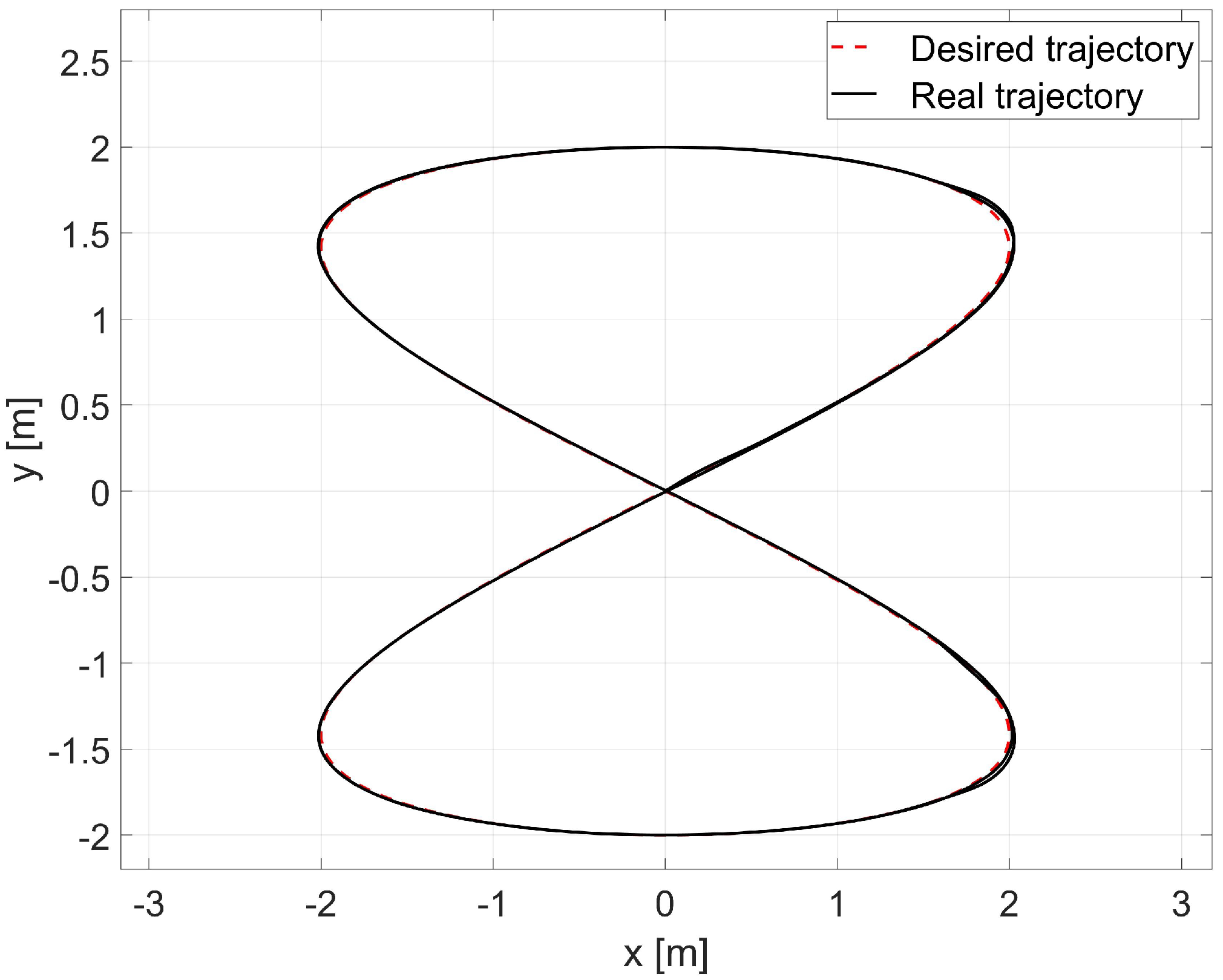
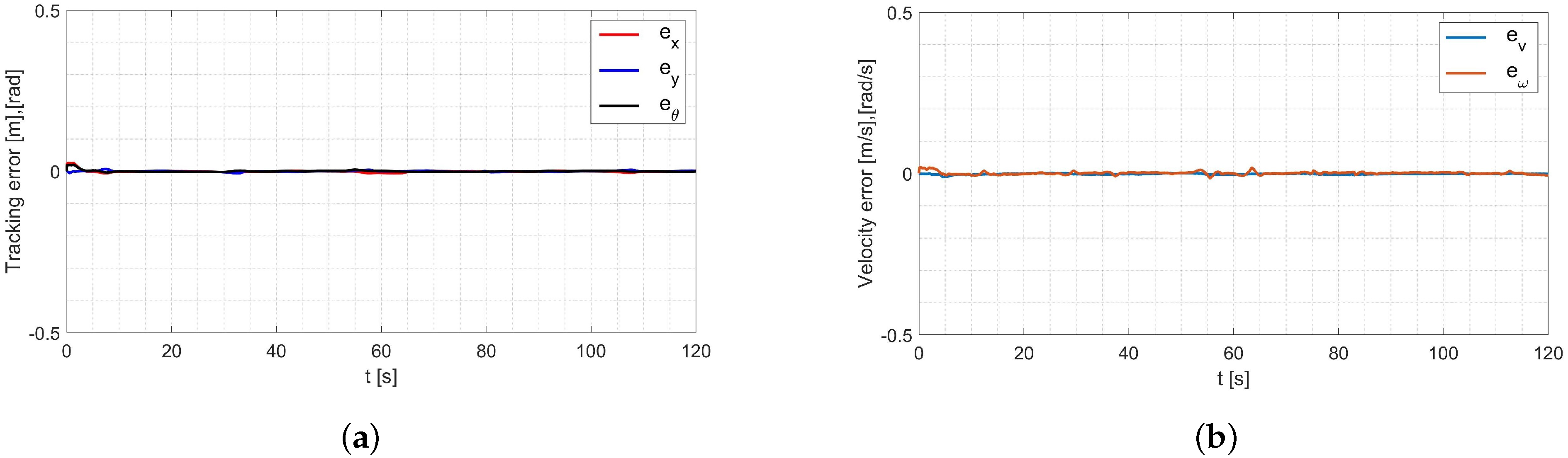
4.4. Laboratory Tests of the Control System with Parameters Identified Offline
- in the x-axis direction: ,
- in the y-axis direction: ,
- orientation: ,
- linear velocity ,
- angular velocity .
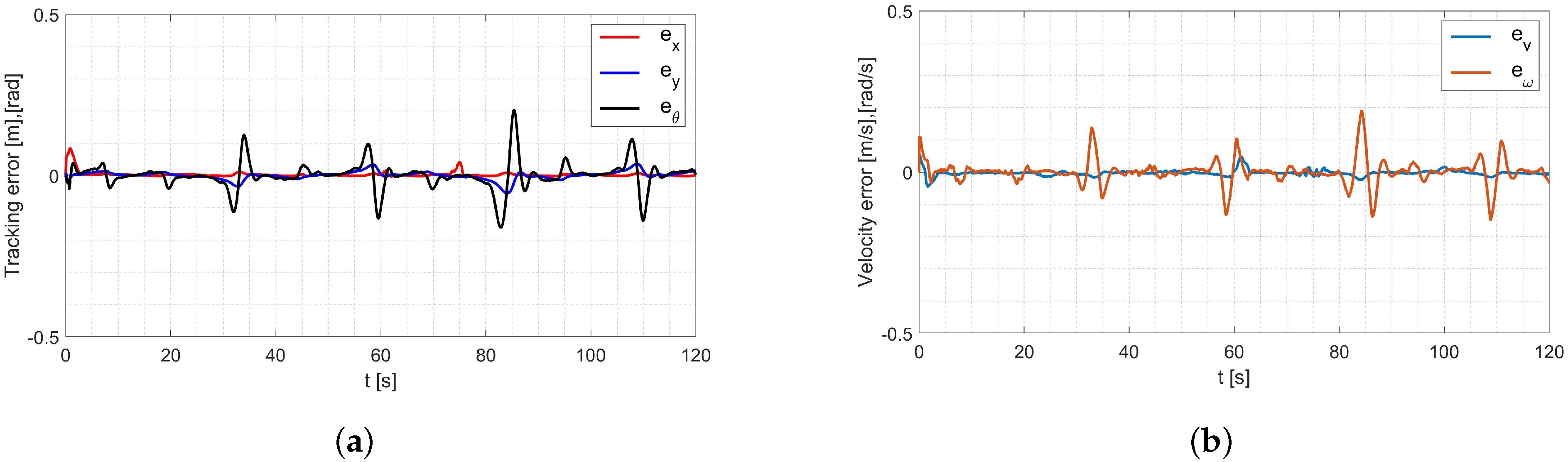
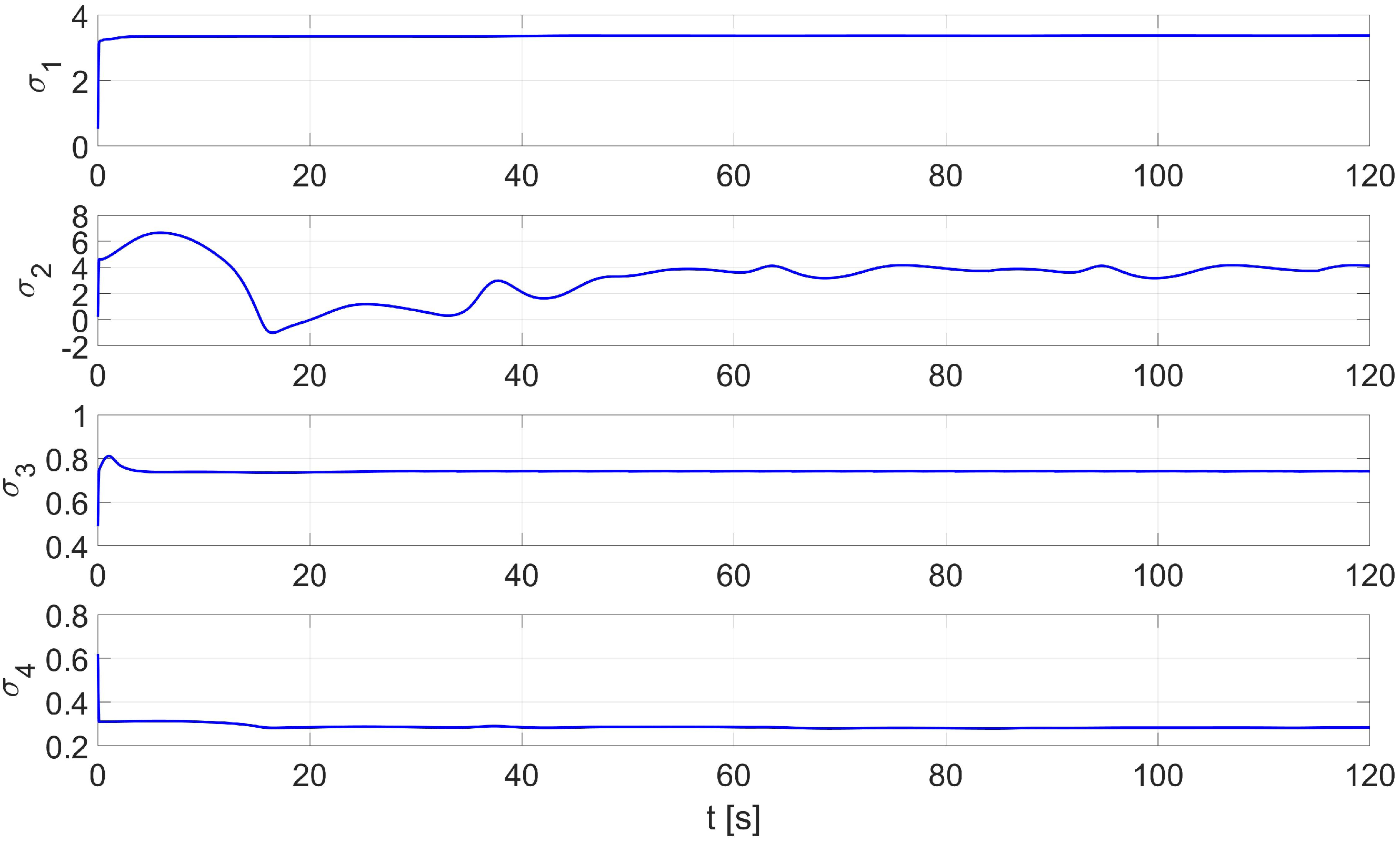
4.5. Laboratory Tests of Control System with Online Identification
- in the x-axis direction: ,
- in the y-axis direction: ,
- orientation: ,
- linear velocity ,
- angular velocity .
- in the x-axis direction: ,
- in the y-axis direction: ,
- orientation: ,
- linear velocity ,
- angular velocity .
5. Conclusions
- all the values of the parameters identified by the selected methods are correct, and their implementation in the control system gives satisfactory results of tracking the desired trajectory;
- parameters identified by the Levenberg-Marguardt method allow trajectory tracking with a tracking error of about 30–40 [mm] and a regulation time of about 2.9 [s];
- the use of online identification by the RLS method with random initial parameters made it possible to achieve a tracking accuracy of the set trajectory of about 10–20 [mm] and a control time of 7.5 [s]; the use of adaptive technology in the control system made it possible to improve the tracking accuracy compared to the control system with constant values of the parameters of the robot model;
- The best tracking accuracy of the desired trajectory (a tracking error of about 2–5 [mm] and a regulation time of 1.6 [s]) was achieved using the RLS method with the initial parameters determined by the Levenberg-Marguardt method.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RLS | Recursive Least Squares method |
| L-M | Levenberg-Marguardt method |
| desired robot position and orientation | |
| desired robot position and orientation | |
| desired robot velocities (linear and angular) | |
| real robot velocities (linear and angular) | |
| forward and lateral robot velocities | |
| longitudal and lateral force of right wheel | |
| longitudal and lateral force of left wheel | |
| m | mass of the robot |
| moment of inertia of the robot with respect to the axis passing through the point G | |
| G | robot center of mass and center of rotation |
| parameters of the robot dynamic model | |
| position and orientation tracking errors | |
| velocity errors | |
| control signals from kinematic controller | |
| gains of the kinematic kontrollers | |
| oscillation damping coefficient | |
| characteristic frequency | |
| b | additional control coefficient |
| control signals from dynamic controller | |
| gains of the dynamic controller | |
| regulation time |
Appendix A
Appendix B
References
- Szrek, J.; Jakubiak, J.; Zimroz, R. A Mobile Robot-Based System for Automatic Inspection of Belt Conveyors in Mining Industry. Energies 2022, 15, 327. [Google Scholar] [CrossRef]
- Pia̧tek, Z. Mobile Industrial Robots Enters Polish Mobile Robot Market (In Polish). 2018. Available online: https://przemysl-40.pl/index.php/2018/01/11/mobile-industrial-robots-wchodzi-na-polski-rynek/ (accessed on 5 December 2022).
- AGV, AIV, AMR, SGV—So What’s the Deal with the Nomenclature? (In Polish). Available online: http://www.mobot.pl/artykul/5095/agv-aiv-amr-sgv-czyli-o-co-chodzi-z-tym-nazewnictwem/ (accessed on 5 December 2022).
- Jahn, U.; Heß, D.; Stampa, M.; Sutorma, A.; Röhrig, C.; Schulz, P.; Wolff, C. A Taxonomy for Mobile Robots: Types, Applications, Capabilities, Implementations, Requirements, and Challenges. Robotics 2020, 9, 109. [Google Scholar] [CrossRef]
- SFS-EN ISO 3691-4:2020; Industrial Trucks. Safety Requirements and Verification. Part 4: Driverless Industrial Trucks and Their Systems. SFS: Singapore, 2020.
- Vasconcelos, J.V.R.; Brandão, A.S.; Sarcinelli-Filho, M. Real-Time Path Planning for Strategic Missions. Appl. Sci. 2020, 10, 7773. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, P.; Zeng, Z.; Xiao, J.; Lu, H.; Zhou, Z. Robot navigation in a crowd by integrating deep reinforcement learning and online planning. Appl. Intell. 2022, 52, 15600–15616. [Google Scholar] [CrossRef]
- Wróblewski, P. Analysis of Torque Waveforms in Two-Cylinder Engines for Ultralight Aircraft Propulsion Operating on 0W-8 and 0W-16 Oils at High Thermal Loads Using the Diamond-like Carbon Composite Coating. SAE Int. J. Engines 2021, 15, 2022. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, B.; Long, J.; Kuang, Y.; Chen, X.; Hou, M.; Gao, J.; Zhou, S.; Fan, B.; He, Y.; et al. Interfacial Laser-Induced Graphene Enabling High-Performance Liquid-Solid Triboelectric Nanogenerator. Adv. Mater. 2021, 33, 2104290. [Google Scholar] [CrossRef]
- Siwek, M.; Besseghieur, K.; Baranowski, L. The effects of the swarm configuration and the obstacles placement on control signals transmission delays in decentralized ROS-embedded group of mobile robots. AIP Conf. Proc. 2018, 2029, 20069. [Google Scholar] [CrossRef]
- Timofeev, A.; Daeef, F. Control of a transport robot in extreme weather based on computer vision systems. J. Phys. Conf. Ser. 2021, 2131, 32027. [Google Scholar] [CrossRef]
- Javed, M.A.; Muram, F.U.; Punnekkat, S.; Hansson, H. Safe and secure platooning of Automated Guided Vehicles in Industry 4.0. J. Syst. Archit. 2021, 121, 102309. [Google Scholar] [CrossRef]
- Falcó, A.; Hilario, L.; Montés, N.; Mora, M.C.; Nadal, E. A Path Planning Algorithm for a Dynamic Environment Based on Proper Generalized Decomposition. Mathematics 2020, 8, 2245. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-Del-pulgar, C.J.; García-Cerezo, A. Path planning for autonomous mobile robots: A review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path planning for the mobile robot: A review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, W.; Borys, S.; Panasiuk, J.; Siwek, M.; Prusaczyk, P. Experimental Study of the Vibrations of a Roller Shutter Gripper. Appl. Sci. 2022, 12, 9996. [Google Scholar] [CrossRef]
- Borys, S.; Kaczmarek, W.; Laskowski, D.; Polak, R. Experimental Study of the Vibration of the Spot Welding Gun at a Robotic Station. Appl. Sci. 2022, 12, 12209. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.C. Path smoothing techniques in robot navigation: State-of-the-art, current and future challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Dai, S.L.; Yang, C. Mixed reality enhanced user interactive path planning for omnidirectional mobile robot. Appl. Sci. 2020, 10, 1135. [Google Scholar] [CrossRef] [Green Version]
- Andreasson, H.; Saarinen, J.; Cirillo, M.; Stoyanov, T.; Lilienthal, A.J. Drive the drive: From discrete motion plans to smooth drivable trajectories. Robotics 2014, 3, 400–416. [Google Scholar] [CrossRef] [Green Version]
- Siwek, M.; Baranowski, L.; Panasiuk, J.; Kaczmarek, W. Modeling and simulation of movement of dispersed group of mobile robots using Simscape multibody software. AIP Conf. Proc. 2019, 2078, 020045. [Google Scholar] [CrossRef]
- Baranowski, L.; Siwek, M. Use of 3D Simulation to Design Theoretical and Real Pipe Inspection Mobile Robot Model. Acta Mech. Autom. 2018, 12, 232–236. [Google Scholar] [CrossRef] [Green Version]
- Noh, S.; Park, J.; Park, J. Autonomous Mobile Robot Navigation in Indoor Environments: Mapping, Localization, and Planning. In Proceedings of the International Conference on Information and Communication Technology Convergence, Jeju, Republic of Korea, 21–23 October 2020; pp. 908–913. [Google Scholar] [CrossRef]
- Besseghieur, K.L.; Trebinski, R.; Kaczmarek, W.; Panasiuk, J. Trajectory tracking control for a nonholonomic mobile robot under ROS. J. Phys. Conf. Ser. 2018, 1016, 12008. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, F.; Ribeiro, T.; Ribeiro, A.F.; Lopes, G.; Flores, P. A Recursive Algorithm for the Forward Kinematic Analysis of Robotic Systems Using Euler Angles. Robotics 2022, 11, 15. [Google Scholar] [CrossRef]
- Groves, K.; Hernandez, E.; West, A.; Wright, T.; Lennox, B. Robotic exploration of an unknown nuclear environment using radiation informed autonomous navigation. Robotics 2021, 10, 78. [Google Scholar] [CrossRef]
- Wróblewski, P. Investigation of energy losses of the internal combustion engine taking into account the correlation of the hydrophobic and hydrophilic. Energy 2023, 264, 126002. [Google Scholar] [CrossRef]
- Panasiuk, J.; Siwek, M.; Kaczmarek, W.; Borys, S.; Prusaczyk, P. The concept of using the mobile robot for telemechanical wires installation in pipelines. AIP Conf. Proc. 2018, 2029, 020054. [Google Scholar] [CrossRef]
- Khosla, P.K.; Kanade, T. Parameter Identification of Robot Dynamics. In Proceedings of the 24th IEEE Conference on Decision and Control, Fort Lauderdale, FL, USA, 11–13 December 1985; pp. 1754–1760. [Google Scholar] [CrossRef]
- Gautier, M.; Janot, A.; Vandanjon, P.O. A new closed-loop output error method for parameter identification of robot dynamics. IEEE Trans. Control Syst. Technol. 2013, 21, 428–444. [Google Scholar] [CrossRef] [Green Version]
- Briot, S.; Krut, S.; Gautier, M. Dynamic Parameter Identification of Overactuated Parallel Robots. J. Dyn. Syst. Meas. Control. Trans. ASME 2015, 137, 111002. [Google Scholar] [CrossRef]
- Lomakin, A.; Deutscher, J. Identification of dynamic parameters for rigid robots based on polynomial approximation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 7271–7278. [Google Scholar] [CrossRef]
- Uddin, N. Adaptive control system design for two-wheeled robot stabilization. In Proceedings of the 12th South East Asian Technical University Consortium, Yogyakarta, Indonesia, 12–13 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Al-Jlailaty, H.; Jomaa, H.; Daher, N.; Asmar, D. Balancing a Two-Wheeled Mobile Robot using Adaptive Control. In Proceedings of the 2018 IEEE International Multidisciplinary Conference on Engineering Technology, Beirut, Lebanon, 14–16 November 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Zhai, J.; Song, Z. Adaptive sliding mode trajectory tracking control for wheeled mobile robots. Int. J. Control 2019, 92, 2255–2262. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Kong, H.; Ke, F. Model predictive tracking control of nonholonomic mobile robots with coupled input constraints and unknown dynamics. IEEE Trans. Ind. Inform. 2019, 15, 3196–3205. [Google Scholar] [CrossRef]
- Al-Mayyahi, A.; Wang, W.; Birch, P. Adaptive neuro-fuzzy technique for autonomous ground vehicle navigation. Robotics 2014, 3, 349–370. [Google Scholar] [CrossRef] [Green Version]
- Bouzoualegh, S.; Guechi, E.H.; Kelaiaia, R. Model Predictive Control of a Differential-Drive Mobile Robot. Acta Univ. Sapientiae Electr. Mech. Eng. 2018, 10, 20–41. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Sun, Q.; Shi, Y. Trajectory Tracking Control of Autonomous Ground Vehicles Using Adaptive Learning MPC. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5554–5564. [Google Scholar] [CrossRef]
- Wu, W.; You, J.; Zhang, Y.; Li, M.; Su, K. Parameter Identification of Spatial-Temporal Varying Processes by a Multi-Robot System in Realistic Diffusion Fields. Robotica 2021, 39, 842–861. [Google Scholar] [CrossRef]
- Xu, X.; Liu, X.; Zhao, B.; Yang, B. An extensible positioning system for locating mobile robots in unfamiliar environments. Sensors 2019, 19, 4025. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Liu, Y.H.; Jiang, T.; Wang, K.; Fang, M. Adaptive Trajectory Tracking of Nonholonomic Mobile Robots Using Vision-Based Position and Velocity Estimation. IEEE Trans. Cybern. 2018, 48, 571–582. [Google Scholar] [CrossRef] [PubMed]
- Alatise, M.; Hancke, G. Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors 2017, 17, 2164. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, C.; Ren, M. An Enhanced Hybrid Visual–Inertial Odometry System for Indoor Mobile Robot. Sensors 2022, 22, 2930. [Google Scholar] [CrossRef]
- Robot Operating System. Available online: https://www.roscomponents.com/en/mobile-robots/9-turtlebot-2.html (accessed on 5 December 2022).
- Rivera, Z.B.; De Simone, M.C.; Guida, D. Unmanned Ground Vehicle Modelling in Gazebo/ROS-Based Environments. Machines 2019, 7, 42. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Liu, S.; Li, J. Research and Implementation of Autonomous Navigation for Mobile Robots Based on SLAM Algorithm under ROS. Sensors 2022, 22, 4172. [Google Scholar] [CrossRef]
- Chen, C.S.; Lin, C.J.; Lai, C.C.; Lin, S.Y. Velocity Estimation and Cost Map Generation for Dynamic Obstacle Avoidance of ROS Based AMR. Machines 2022, 10, 501. [Google Scholar] [CrossRef]
- Giergiel, M.; Malka, P. Modelowanie Kinematyki I Dynamiki Mobilnego Minirobota. Model. Inżynierskie 2006, 157–162. [Google Scholar]
- Giergiel, M.J.; Hendzel, Z.; Żylski, W. Modelowanie i Sterowanie Mobilnych Robotów Kołowych; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2013; p. 257. [Google Scholar]
- Malka, P. Pozycjonowanie i Nada̧żanie Minirobota Kołowego; AGH: Kraków, Poland, 2007. [Google Scholar]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots; The MIT Press: Cambridge, MA, USA, 2011; Volume 49, pp. 49–1492. [Google Scholar] [CrossRef] [Green Version]
- Nascimento Martins, F.; Santos Brandão, A. Motion Control and Velocity-Based Dynamic Compensation for Mobile Robots. In Applications of Mobile Robots; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Das, T.; Kar, I.N. Design and implementation of an adaptive fuzzy logic-based controller for wheeled mobile robots. IEEE Trans. Control Syst. Technol. 2006, 14, 501–510. [Google Scholar] [CrossRef]
- Hendzel, Z.; Rykała, Ł. Modelling of dynamics of a wheeled mobile robot with mecanum wheels with the use of lagrange equations of the second kind. Int. J. Appl. Mech. Eng. 2017, 22, 81–99. [Google Scholar] [CrossRef] [Green Version]
- Ahmad Abu Hatab, R.D. Dynamic Modelling of Differential-Drive Mobile Robots using Lagrange and Newton-Euler Methodologies: A Unified Framework. Adv. Robot. Autom. 2013, 2, 1–7. [Google Scholar] [CrossRef] [Green Version]
- De La Cruz, C.; Carelli, R. Dynamic model based formation control and obstacle avoidance of multi-robot systems. Robotica 2008, 26, 345–356. [Google Scholar] [CrossRef]
- Martins, F.N.; Sarcinelli-Filho, M.; Carelli, R. A Velocity-Based Dynamic Model and Its Properties for Differential Drive Mobile Robots. J. Intell. Robot. Syst. Theory Appl. 2017, 85, 277–292. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, D.; Chung, J.H.; Velinsky, S.A. Dynamic model based robust tracking control of a differentially steered wheeled mobile robot. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 26–26 June 1998; Volume 2, pp. 850–855. [Google Scholar] [CrossRef]
- Gratton, S.; Lawless, A.S.; Nichols, N.K. Approximate Gauss-newton methods for nonlinear least squares problems. SIAM J. Optim. 2007, 18, 106–132. [Google Scholar] [CrossRef] [Green Version]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar] [CrossRef] [Green Version]
- Palacín, J.; Rubies, E.; Clotet, E. Systematic Odometry Error Evaluation and Correction in a Human-Sized Three-Wheeled Omnidirectional Mobile Robot Using Flower-Shaped Calibration Trajectories. Appl. Sci. 2022, 12, 2606. [Google Scholar] [CrossRef]
- Klančar, G.; Matko, D.; Blažič, S. Mobile robot control on a reference path. In Proceedings of the 2005 IEEE International Symposium on, Mediterrean Conference on Control and Automation Intelligent Control, Limassol, Cyprus, 27–29 June 2005; Volume 2005, pp. 1343–1348. [Google Scholar] [CrossRef]

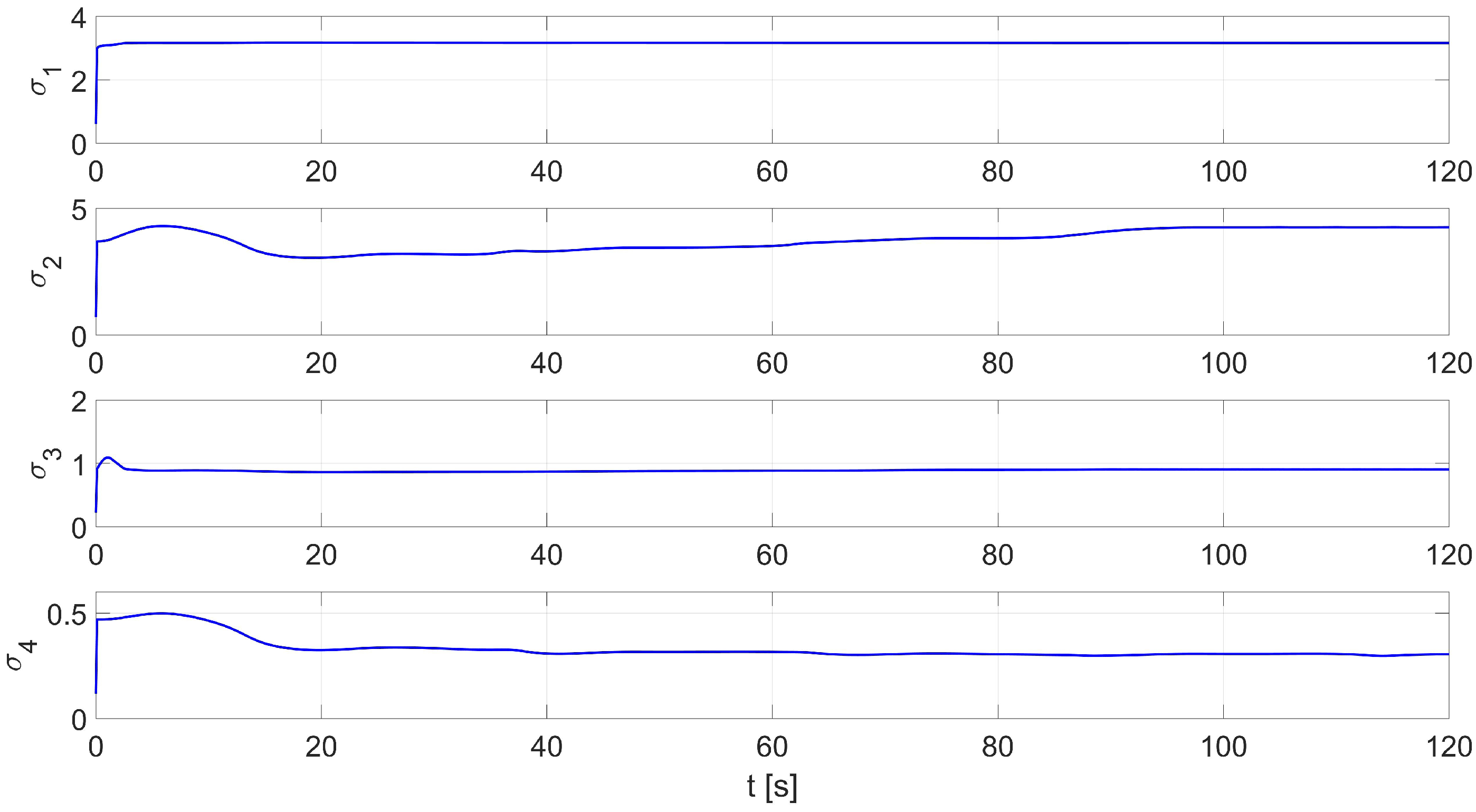




| Test No. | Identification Time [s] | |||||
|---|---|---|---|---|---|---|
| 1 | Initial values | 0.16 | 0.52 | 0.96 | 0.37 | |
| Identified values | 4.09 | 5.46 | 0.97 | 0.29 | 6.65 | |
| 2 | Initial values | 0.61 | 0.26 | 0.76 | 0.29 | |
| Identified values | 3.14 | 4.06 | 0.81 | 0.24 | 6.01 | |
| 3 | Initial values | 0.59 | 0.55 | 0.92 | 0.29 | |
| Identified values | 3.14 | 4.17 | 0.83 | 0.24 | 6.40 | |
| 4 | Initial values | 0.65 | 0.45 | 0.55 | 0.30 | |
| Identified values | 3.49 | 4.63 | 0.85 | 0.24 | 5.92 | |
| 5 | Initial values | 0.38 | 0.56 | 0.08 | 0.05 | |
| Identified values | 3.37 | 4.56 | 0.84 | 0.26 | 5.65 | |
| Average | 3.47 | 4.58 | 0.87 | 0.25 | 6.13 | |
| Variance | 0.15 | 0.30 | 0.00 | 0.00 | ||
| Standard deviation | 0.35 | 0.49 | 0.06 | 0.02 |
| Test No. | |||||
|---|---|---|---|---|---|
| 1 | Initial values | 0.6 | 0.71 | 0.22 | 0.12 |
| Identified values | 3.16 | 4.15 | 0.92 | 0.3 | |
| 2 | Initial values | 0.93 | 0.73 | 0.49 | 0.58 |
| Identified values | 3.26 | 4.51 | 0.89 | 0.22 | |
| 3 | Initial values | 0.24 | 0.46 | 0.96 | 0.55 |
| Identified values | 3.84 | 4.34 | 0.86 | 0.25 | |
| 4 | Initial values | 0.52 | 0.23 | 0.49 | 0.62 |
| Identified values | 3.37 | 3.87 | 0.78 | 0.28 | |
| 5 | Initial values | 0.68 | 0.39 | 0.37 | 0.99 |
| Identified values | 3.32 | 4.16 | 0.76 | 0.24 | |
| Average | 3.39 | 4.21 | 0.84 | 0.26 | |
| Variance | 0.06 | 0.05 | 0.00 | 0.00 | |
| Standard deviation | 0.24 | 0.21 | 0.06 | 0.03 |
| Test No. | Initial values | 3.47 | 4.58 | 0.87 | 0.25 |
| 1 | RLS + offline | 3.68 | 4.49 | 0.90 | 0.22 |
| 2 | RLS + offline | 3.66 | 4.50 | 0.80 | 0.22 |
| 3 | RLS + offline | 3.62 | 4.51 | 0.85 | 0.23 |
| 4 | RLS + offline | 3.67 | 4.52 | 0.89 | 0.20 |
| 5 | RLS + offline | 3.62 | 4.54 | 0.83 | 0.24 |
| Average | 3.65 | 4.51 | 0.85 | 0.22 | |
| Variance | 0.00 | 0.00 | 0.00 | 0.00 | |
| Standard deviation | 0.03 | 0.02 | 0.04 | 0.01 |
| Errors | Simulation Tests | Laboratory Tests | ||||
|---|---|---|---|---|---|---|
| L-M | RLS | RLS + L-M | L-M | RLS | RLS − L-M | |
| 0.007 | 0.009 | 0.005 | 0.033 | 0.021 | 0.009 | |
| 0.007 | 0.016 | 0.002 | 0.046 | 0.013 | 0.008 | |
| 0.021 | 0.022 | 0.001 | 0.2 | 0.025 | 0.012 | |
| 0.001 | 0.001 | 0.001 | 0.023 | 0.011 | 0.001 | |
| 0.007 | 0.015 | 0.017 | 0.18 | 0.033 | 0.033 | |
| 8.2 | 7.8 | 4.8 | 2.9 | 7.5 | 1.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siwek, M.; Panasiuk, J.; Baranowski, L.; Kaczmarek, W.; Prusaczyk, P.; Borys, S. Identification of Differential Drive Robot Dynamic Model Parameters. Materials 2023, 16, 683. https://doi.org/10.3390/ma16020683
Siwek M, Panasiuk J, Baranowski L, Kaczmarek W, Prusaczyk P, Borys S. Identification of Differential Drive Robot Dynamic Model Parameters. Materials. 2023; 16(2):683. https://doi.org/10.3390/ma16020683
Chicago/Turabian StyleSiwek, Michał, Jarosław Panasiuk, Leszek Baranowski, Wojciech Kaczmarek, Piotr Prusaczyk, and Szymon Borys. 2023. "Identification of Differential Drive Robot Dynamic Model Parameters" Materials 16, no. 2: 683. https://doi.org/10.3390/ma16020683
APA StyleSiwek, M., Panasiuk, J., Baranowski, L., Kaczmarek, W., Prusaczyk, P., & Borys, S. (2023). Identification of Differential Drive Robot Dynamic Model Parameters. Materials, 16(2), 683. https://doi.org/10.3390/ma16020683







