Design and Optimization of Thermal Field for PVT Method 8-Inch SiC Crystal Growth
Abstract
:1. Introduction
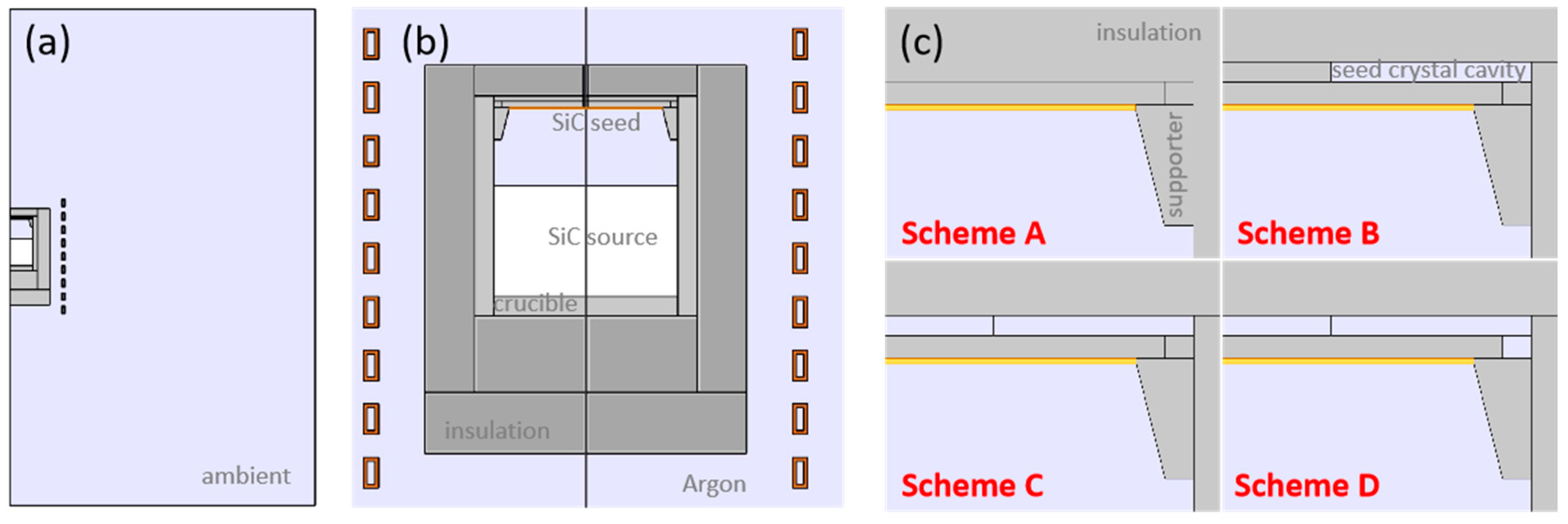
2. Modeling and Experiment
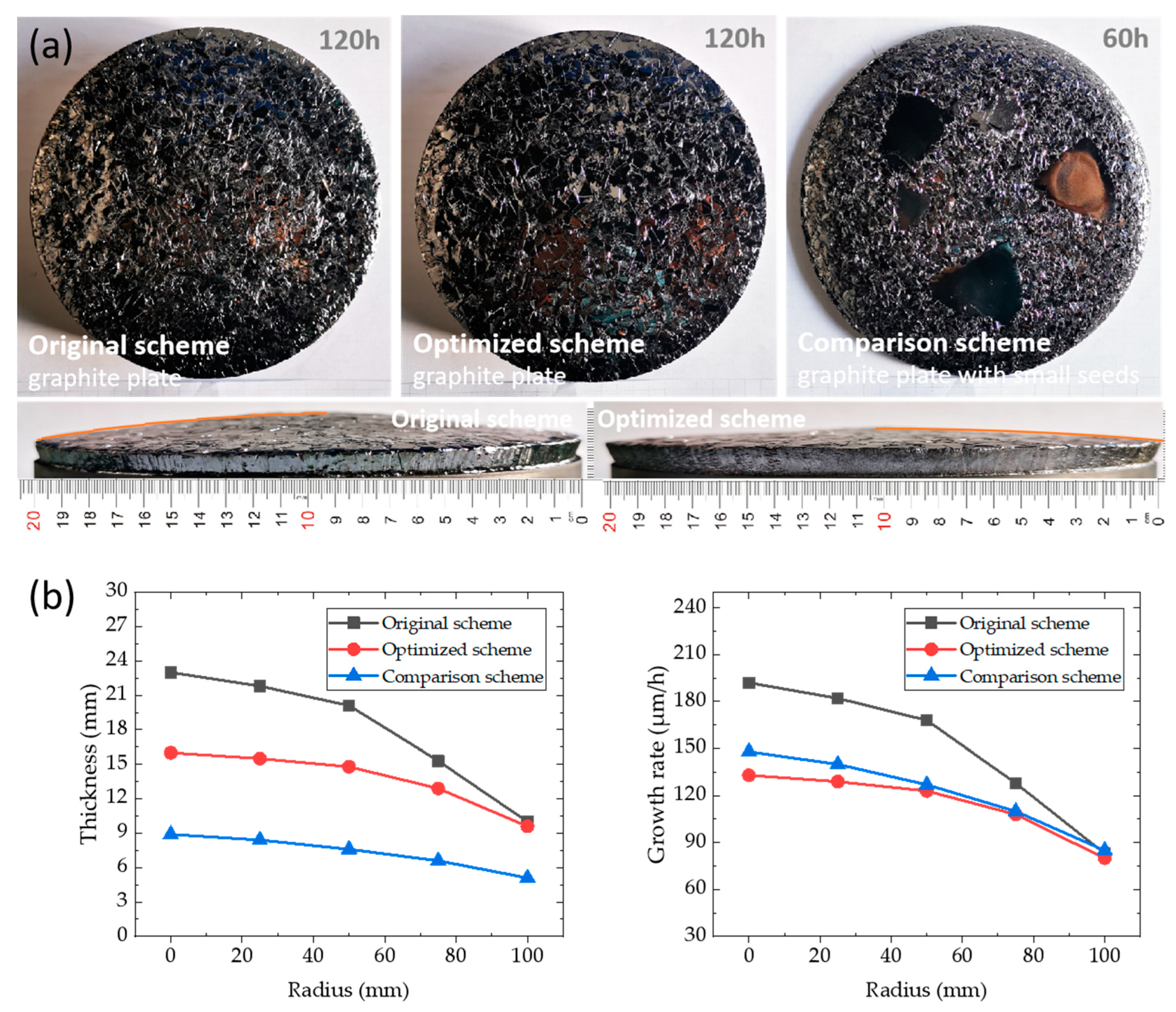
3. Results and Discussion
3.1. Optimization of Seed Crystal Interface Temperature
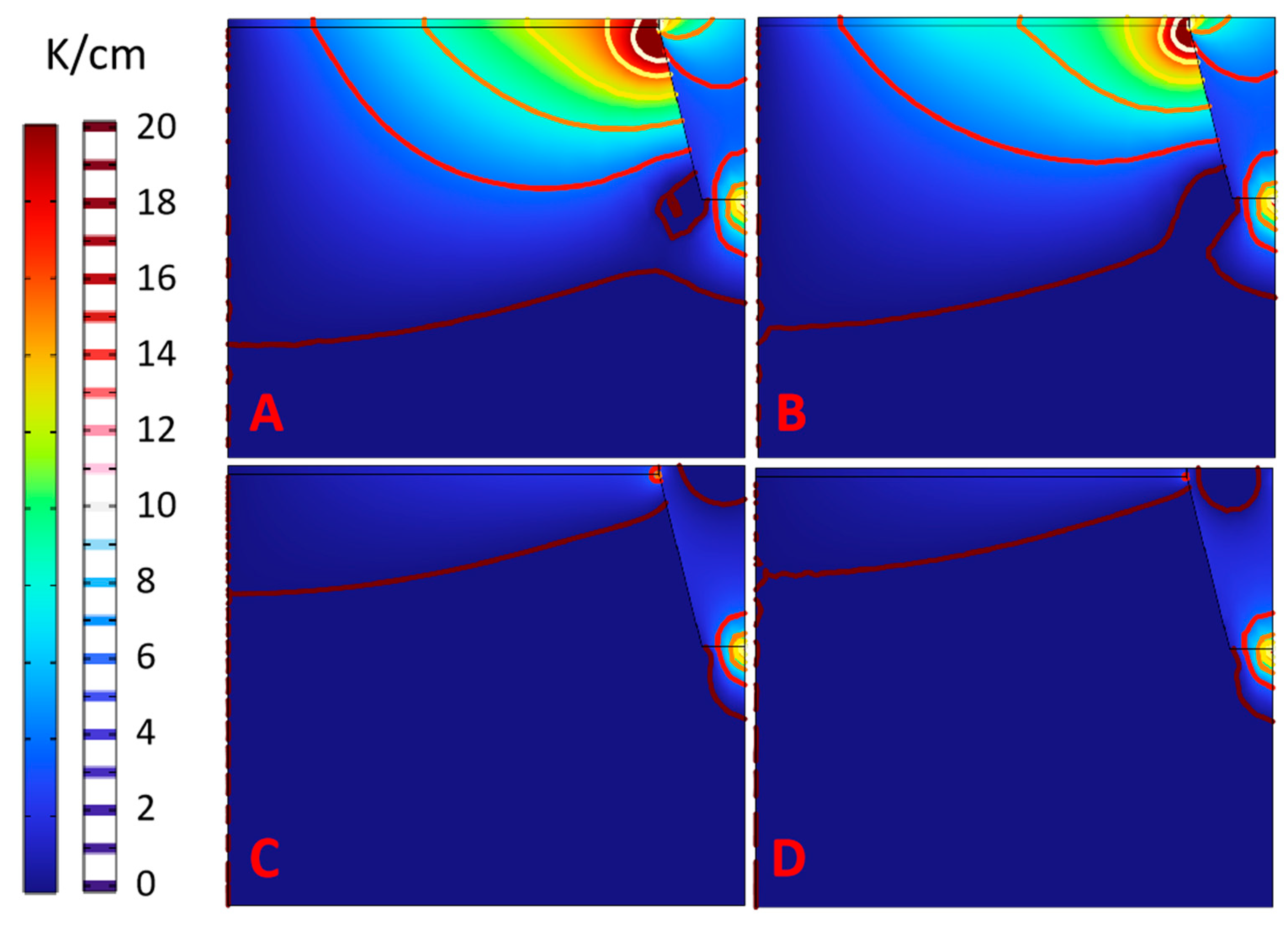
3.1.1. Temperature Distribution Inside Crucible
3.1.2. Temperature Distribution in SiC Seeds
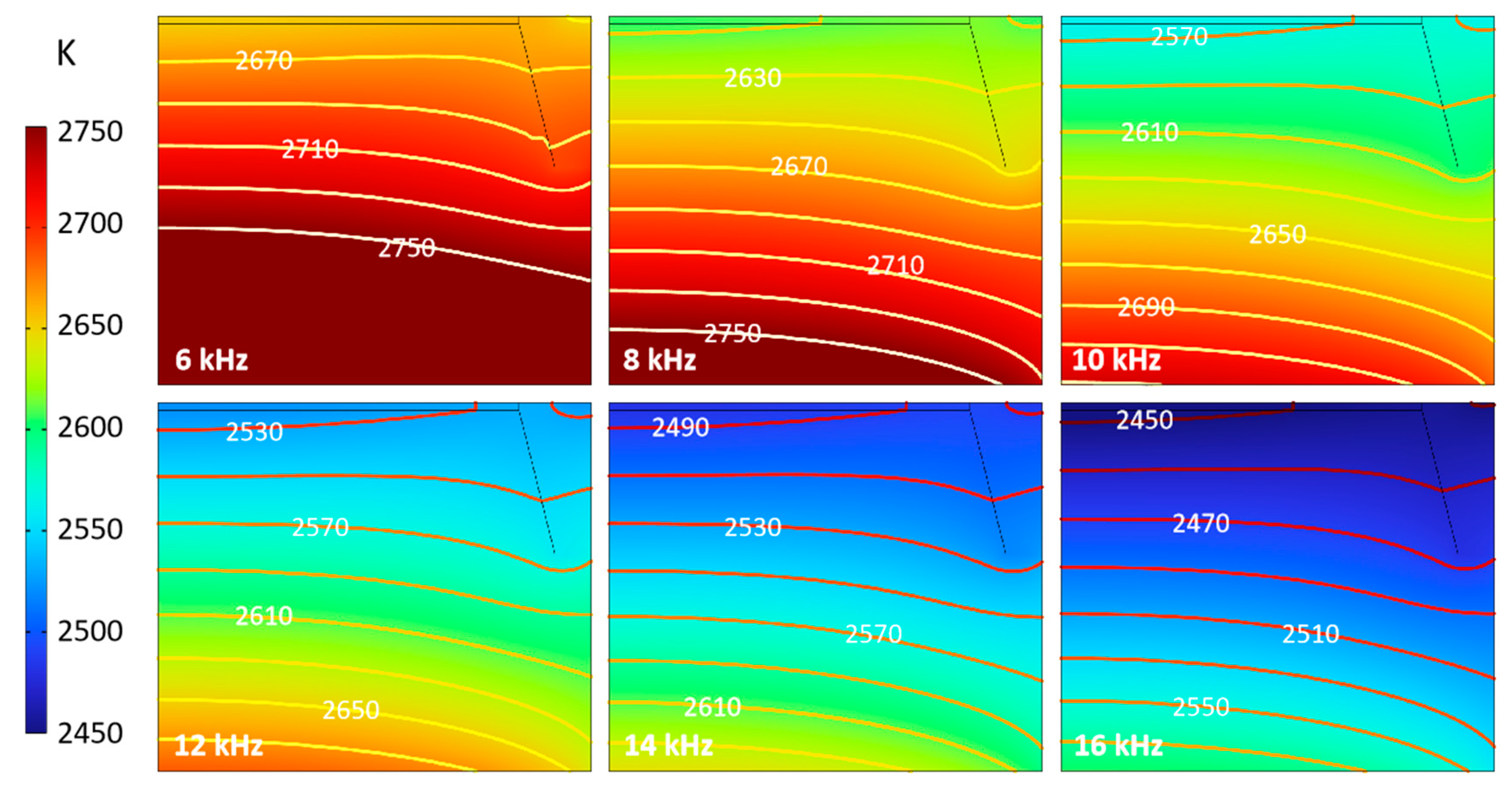
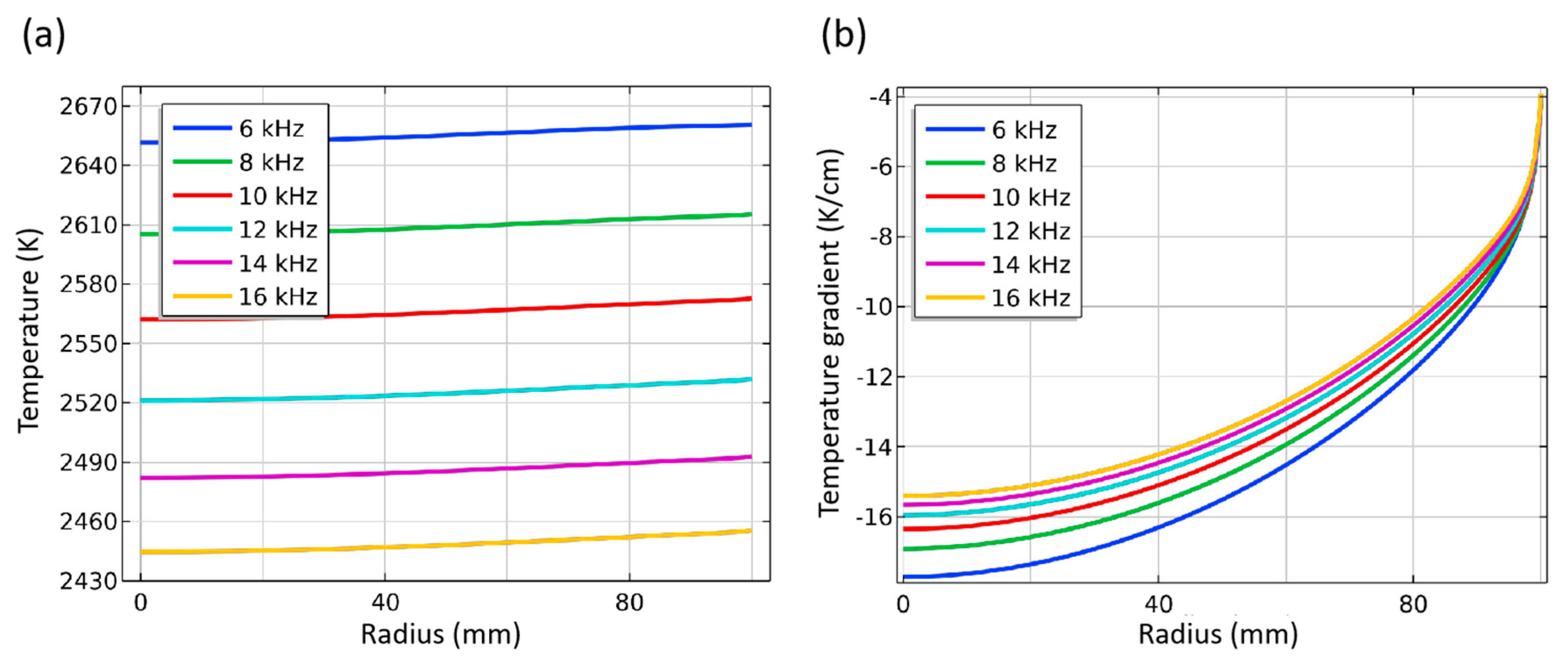
3.2. Influence of Induction Coils Characteristics
3.2.1. Heating Frequency
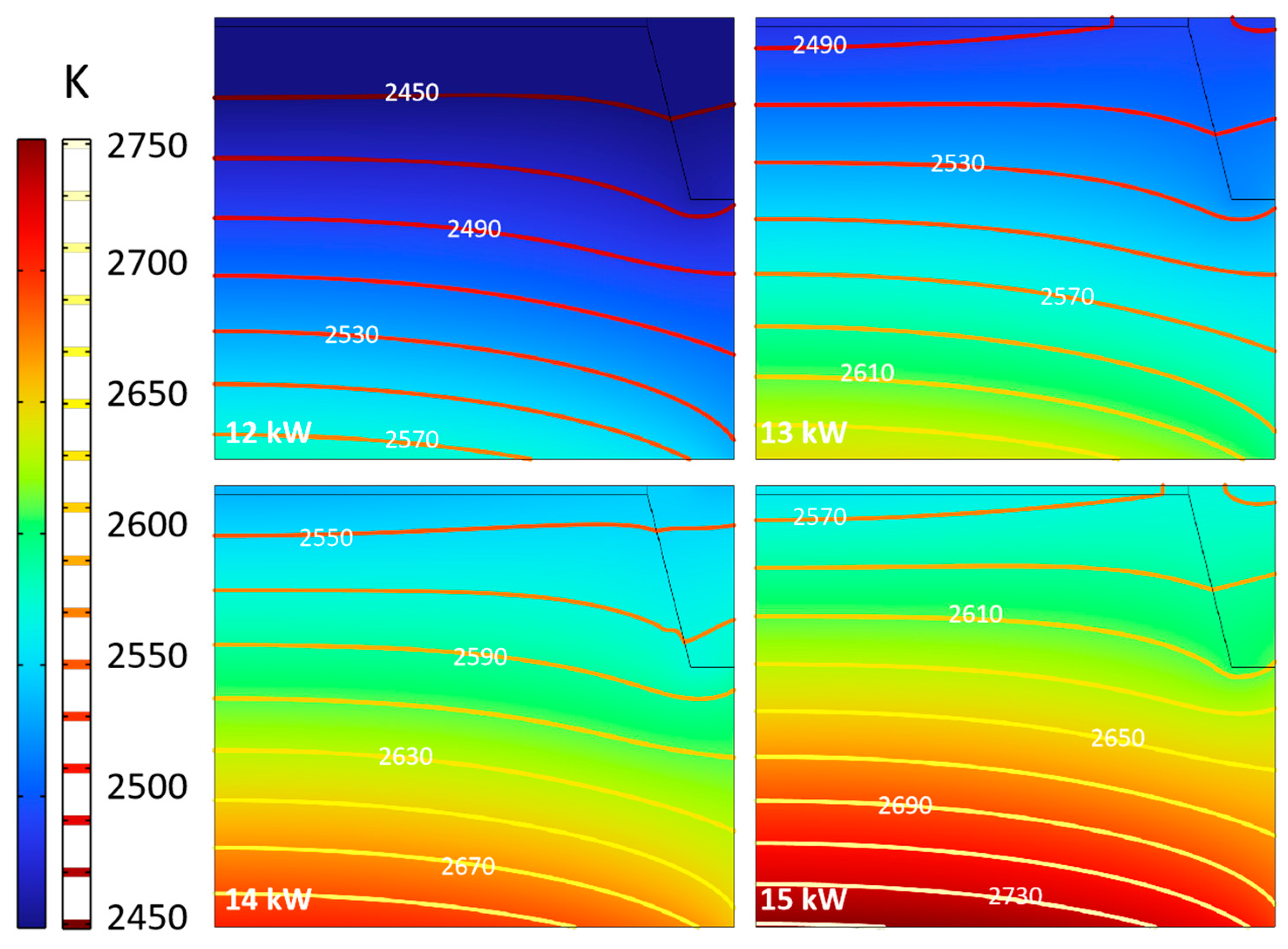
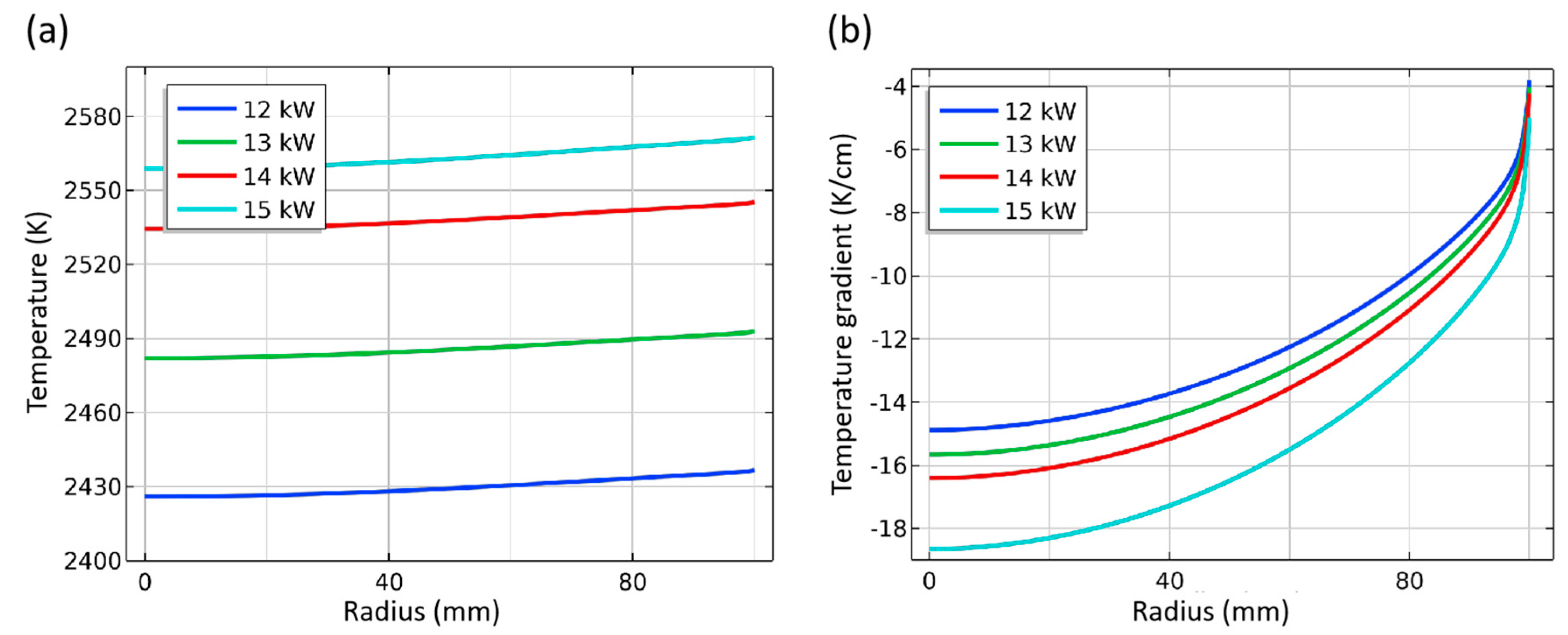
3.2.2. Heating Power
3.3. Relative Position of Coil and Raw Material
3.3.1. Diameter of Induction Coils
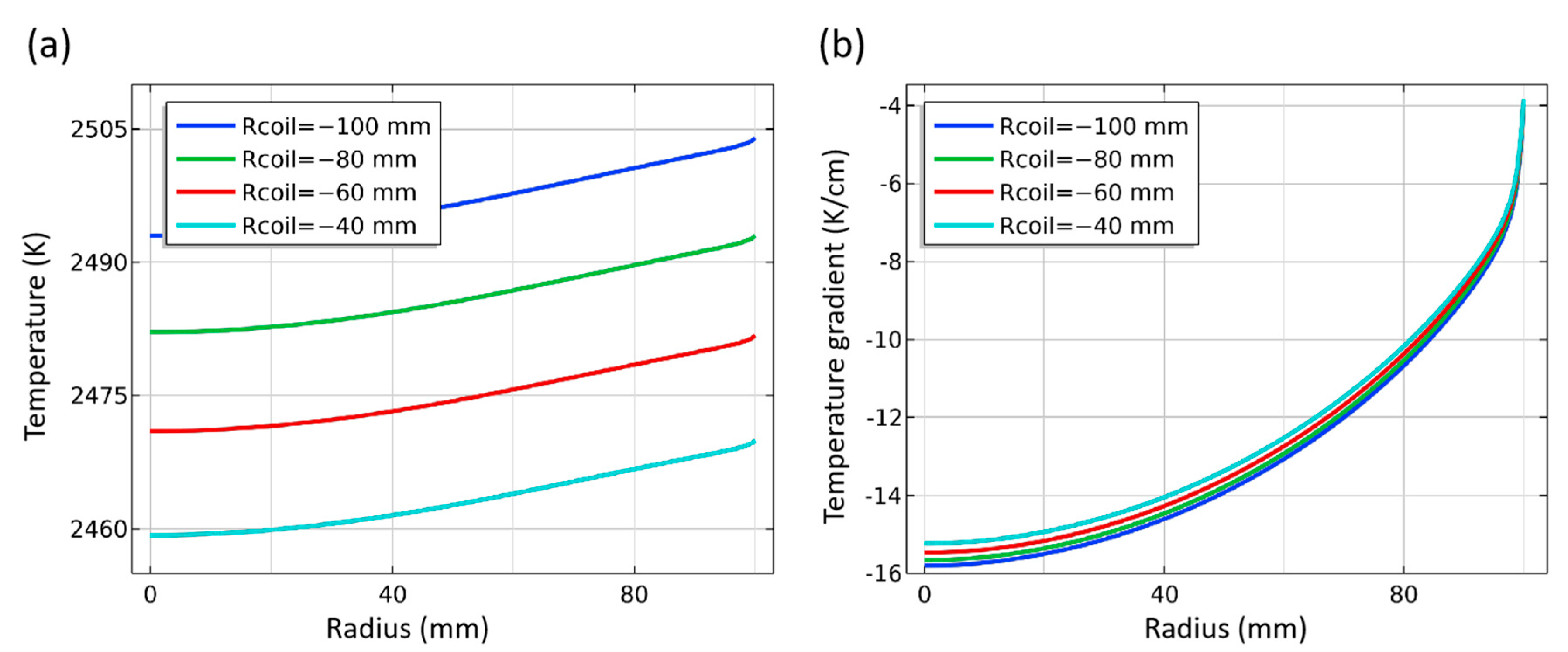
3.3.2. Position of Induction Coils
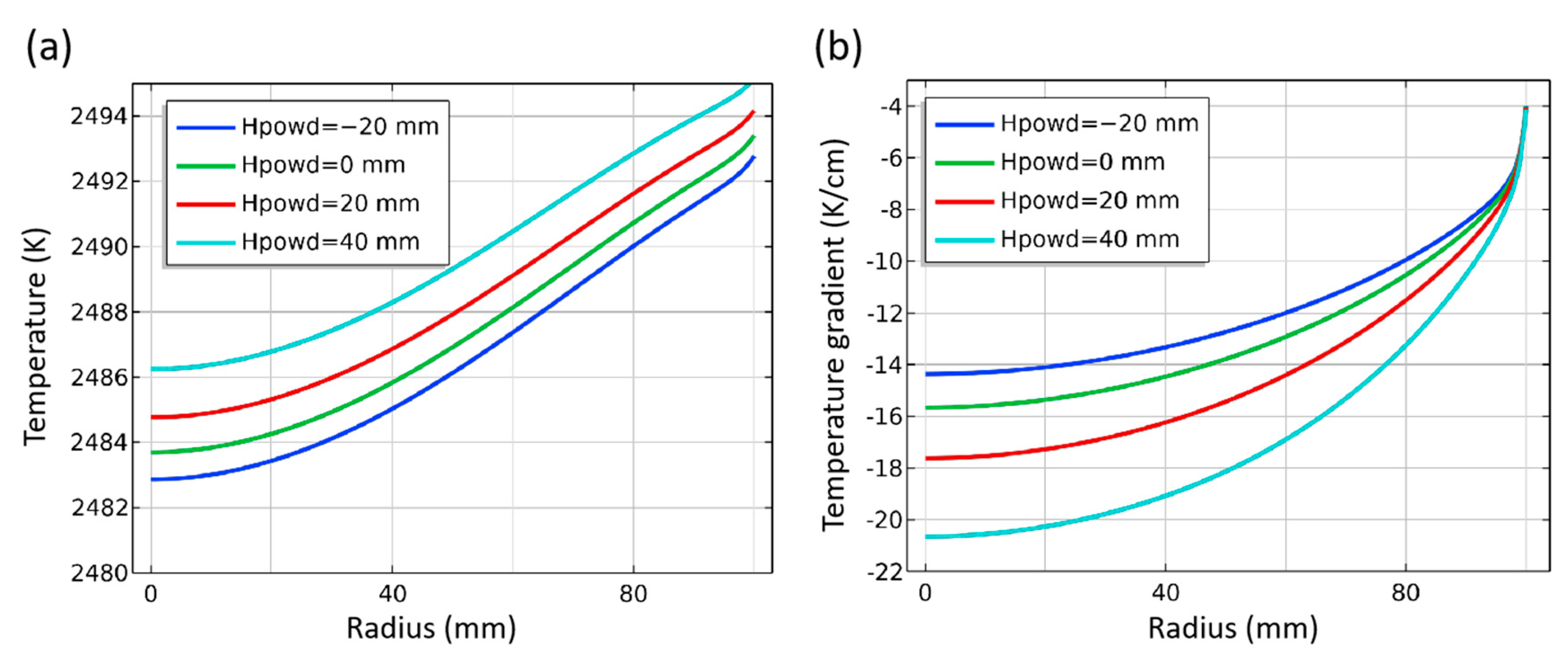
3.3.3. Position of SiC Source Surface
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tairov, Y.M. Growth of Bulk SiC. Mater. Sci. Eng. B 1995, 29, 83–89. [Google Scholar] [CrossRef]
- Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. Properties of Advanced Semiconductor Materials; Wiley-Interscience: New York, NY, USA, 2001. [Google Scholar]
- Masri, P. Silicon Carbide and Silicon Carbide Based Structures. Surf. Sci. Rep. 2002, 48, 1–51. [Google Scholar] [CrossRef]
- Shi, S.; Yu, Y.; Wang, N.; Zhang, Y.; Shi, W.; Liao, X.; Duan, N. Investigation of the Anisotropy of 4H-SiC Materials in Nanoindentation and Scratch Experiments. Materials 2022, 15, 2496. [Google Scholar] [CrossRef]
- Gao, P.; Xin, J.; Yan, C.F.; Kong, H.K.; Chen, J.J.; Liu, X.C.; Shi, E.W. Research on the Key Problems in the Industrialization of SiC Substrate Materials. Mater. Sci. Forum 2019, 963, 56–59. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Y.; Tang, X.; Gao, B. Optimization of Crucible and Heating Model for Large-Sized Silicon Carbide Ingot Growth in Top-Seeded Solution Growth. J. Cryst. Growth 2020, 533, 125406. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Y.; Tang, X.; Gao, B. Improvement of Growth Interface Stability for 4-Inch Silicon Carbide Crystal Growth in TSSG. Crystals 2019, 9, 653. [Google Scholar] [CrossRef] [Green Version]
- Horiuchi, T.; Wang, L.; Sekimoto, A.; Okano, Y.; Ujihara, T.; Dost, S. Adjoint-Based Sensitivity Analysis for the Optimal Crucible Temperature Profile in the RF-Heating TSSG-SiC Crystal Growth Process. J. Cryst. Growth 2019, 517, 59–63. [Google Scholar] [CrossRef]
- Luo, H.; Han, X.; Huang, Y.; Yang, D.; Pi, X. Numerical Simulation of a Novel Method for PVT Growth of SiC by Adding a Graphite Block. Crystals 2021, 11, 1581. [Google Scholar] [CrossRef]
- Ellefsen, O.M.; Arzig, M.; Steiner, J.; Wellmann, P.; Runde, P. Optimization of the SiC Powder Source Material for Improved Process Conditions During PVT Growth of SiC Boules. Materials 2019, 12, 3272. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, Y.; Mitani, T.; Komatsu, N.; Kato, T.; Okumura, H. Control of Temperature Distribution to Suppress Macro-Defects in Solution Growth of 4H-SiC Crystals. J. Cryst. Growth 2019, 523, 125151. [Google Scholar] [CrossRef]
- Hoshino, N.; Kamata, I.; Tokuda, Y.; Makino, E.; Kanda, T.; Sugiyama, N.; Kuno, H.; Kojima, J.; Tsuchida, H. Fast Growth of N-Type 4H-SiC Bulk Crystal by Gas-Source Method. J. Cryst. Growth 2017, 478, 9–16. [Google Scholar] [CrossRef]
- Herro, Z.G.; Epelbaum, B.M.; Bickermann, M.; Masri, P.; Winnacker, A. Effective Increase of Single-Crystalline Yield During PVT Growth of SiC by Tailoring of Temperature Gradient. J. Cryst. Growth 2004, 262, 105–112. [Google Scholar] [CrossRef]
- Kim, J.; Ku, K.; Kim, D.; Kim, S.P.; Lee, W.J.; Shin, B.C.; Lee, G.H.; Kim, I.S. SiC Crystal Growth by Sublimation Method with Modification of Crucible and Insulation Felt Design. Mater. Sci. Forum 2005, 483–485, 47–52. [Google Scholar] [CrossRef]
- Yan, J.Y.; Chen, Q.S.; Jiang, Y.N.; Zhang, H. Improvement of the Thermal Design in the SiC PVT Growth Process. J. Cryst. Growth 2014, 385, 34–37. [Google Scholar] [CrossRef] [Green Version]
- Pezoldt, J.; Cimalla, V. Imprinting the Polytype Structure of Silicon Carbide by Rapid Thermal Processing. Crystals 2020, 10, 523. [Google Scholar] [CrossRef]
- Steiner, J.; Wellmann, P.J. Impact of Mechanical Stress and Nitrogen Doping on the Defect Distribution in the Initial Stage of the 4H-SiC PVT Growth Process. Materials 2022, 15, 1897. [Google Scholar] [CrossRef]
- Masumoto, K.; Kojima, K.; Okumura, H. Study of Spiral Growth On 4H-silicon Carbide On-Axis Substrates. J. Cryst. Growth 2017, 475, 251–255. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Z.; Chen, Q. Numerical Simulation of the Flow Field and Concentration Distribution in the Bulk Growth of Silicon Carbide Crystals. J. Cryst. Growth 2006, 292, 519–522. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Liu, G.; Chen, C.; Hou, Y.; Xu, M.; Zhang, Y. Numerical Simulation of Temperature Fields in a Three-Dimensional SiC Crystal Growth Furnace with Axisymmetric and Spiral Coils. Appl. Sci. 2018, 8, 705. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Kim, J.; Jang, B.; Ko, S.K.; Kyun, M.O.; Seo, J.D.; Ku, K.R.; Choi, J.M.; Lee, W.J. Modified Hot-Zone Design for Large Diameter 4H-SiC Single Crystal Growth. Mater. Sci. Forum 2018, 963, 18–21. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wang, J.; Wang, Y.M. Thermal Stress Simulation of Optimized SiC Single Crystal Growth Crucible Structure. J. Cryst. Growth 2018, 504, 31–36. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, G.; Li, T.; Zhao, L. Optimization of Thermal Field of 150 Mm SiC Crystal Growth by PVT Method. RSC Adv. 2022, 12, 19936–19945. [Google Scholar] [CrossRef] [PubMed]
- Steiner, J.; Arzig, M.; Denisov, A.; Wellmann, P.J. Impact of Varying Parameters on the Temperature Gradients in 100 Mm Silicon Carbide Bulk Growth in a Computer Simulation Validated by Experimental Results. Cryst. Res. Technol. 2020, 55, 1900121. [Google Scholar] [CrossRef]
- Tan, P.; Kang, W.; Yin, J.; Kang, J. 200 Mm Silicon Carbide Bulk Growth Optimisation: Mass Transport Controlled by a Designed Gas Deflector. Phys. Scr. 2022, 97, 105708. [Google Scholar] [CrossRef]
- Iatcheva, I.I.; Stancheva, R.; Tahrilov, H.; Lilianova, I. Coupled Electromagnetic-Thermal Field Investigation in Induction Heating Device. In Magnetism and Magnetic Materials; Trans Tech Publications: Zurich, Switzerland, 2009. [Google Scholar]
- Bouabdallah, S.; Bessah, R. Magnetohydrodynamics Stability of Natural Convection During Phase Change of Molten Gallium in a Three-Dimensional Enclosure. Fluid Dyn. Mater. Process. 2010, 6, 251–276. [Google Scholar]
- Bouabdallah, S.; Bessaïh, R. Effect of Magnetic Field On 3D Flow and Heat Transfer During Solidification from a Melt. Int. J. Heat Fluid Flow 2012, 37, 154–166. [Google Scholar] [CrossRef]








| Structure | Diameter (mm) | Height (mm) |
|---|---|---|
| Ambient | 3200 | 2600 |
| Insulation | 420 | 507 |
| Crucible | 290 | 287 |
| SiC seed | 200 | 2 |
| SiC source | 200 | 145 |
| Coils | 40 × 20 mm (with cavity 30 × 10 mm) | |
| Parameter | Unit | Graphite Felt | Graphite | SiC | Argon [gas] |
|---|---|---|---|---|---|
| Conductivity | S/m | 200 | sigGR(T) | 1000 | 0 |
| Heat capacity (P) | J/(kg·K) | 1000 | 2260 | 1200 | C_gas_2(T) |
| Density | kg/m3 | 100 | 1950 | 3200 | rho_gas_3(T) |
| Thermal conductivity | W/(m·K) | kGF(T) | kGR(T) | kSiC(T) | k_gas_3(T) |
| Domains | Mesh Type | Maximum Cell Size (mm) | Grid Cell Number | Mesh Element Quality |
|---|---|---|---|---|
| Gas domain | Triangular | 44 | 25,926 | 0.8968 |
| Gas inside crucible | Triangular | 10 | ||
| Coils | Quadrilateral | 5 | 4144 | 0.9966 |
| Side and bottom insulation | Quadrilateral | 5 | ||
| Crucible wall, bottom and powder | Quadrilateral | 5 | ||
| SiC seed and view tube | Quadrilateral | 1 |
| Parameter | Unit | Structure | Value |
|---|---|---|---|
| Temperature | K | Surface of coils | 300 |
| Ambient | 300 | ||
| Pressure | Pa | Fluid domains | 1000 |
| Default power | kW | Coils | 13 |
| Default frequency | kHz | Coils | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Fu, G.; Cai, H.; Yang, J.; Fan, G.; Chen, Y.; Li, T.; Zhao, L. Design and Optimization of Thermal Field for PVT Method 8-Inch SiC Crystal Growth. Materials 2023, 16, 767. https://doi.org/10.3390/ma16020767
Zhang S, Fu G, Cai H, Yang J, Fan G, Chen Y, Li T, Zhao L. Design and Optimization of Thermal Field for PVT Method 8-Inch SiC Crystal Growth. Materials. 2023; 16(2):767. https://doi.org/10.3390/ma16020767
Chicago/Turabian StyleZhang, Shengtao, Guoqing Fu, Hongda Cai, Junzhi Yang, Guofeng Fan, Yanyu Chen, Tie Li, and Lili Zhao. 2023. "Design and Optimization of Thermal Field for PVT Method 8-Inch SiC Crystal Growth" Materials 16, no. 2: 767. https://doi.org/10.3390/ma16020767




