Hot Workability of the Multi-Size SiC Particle-Reinforced 6013 Aluminum Matrix Composites
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Initial Microstructure of the Composites
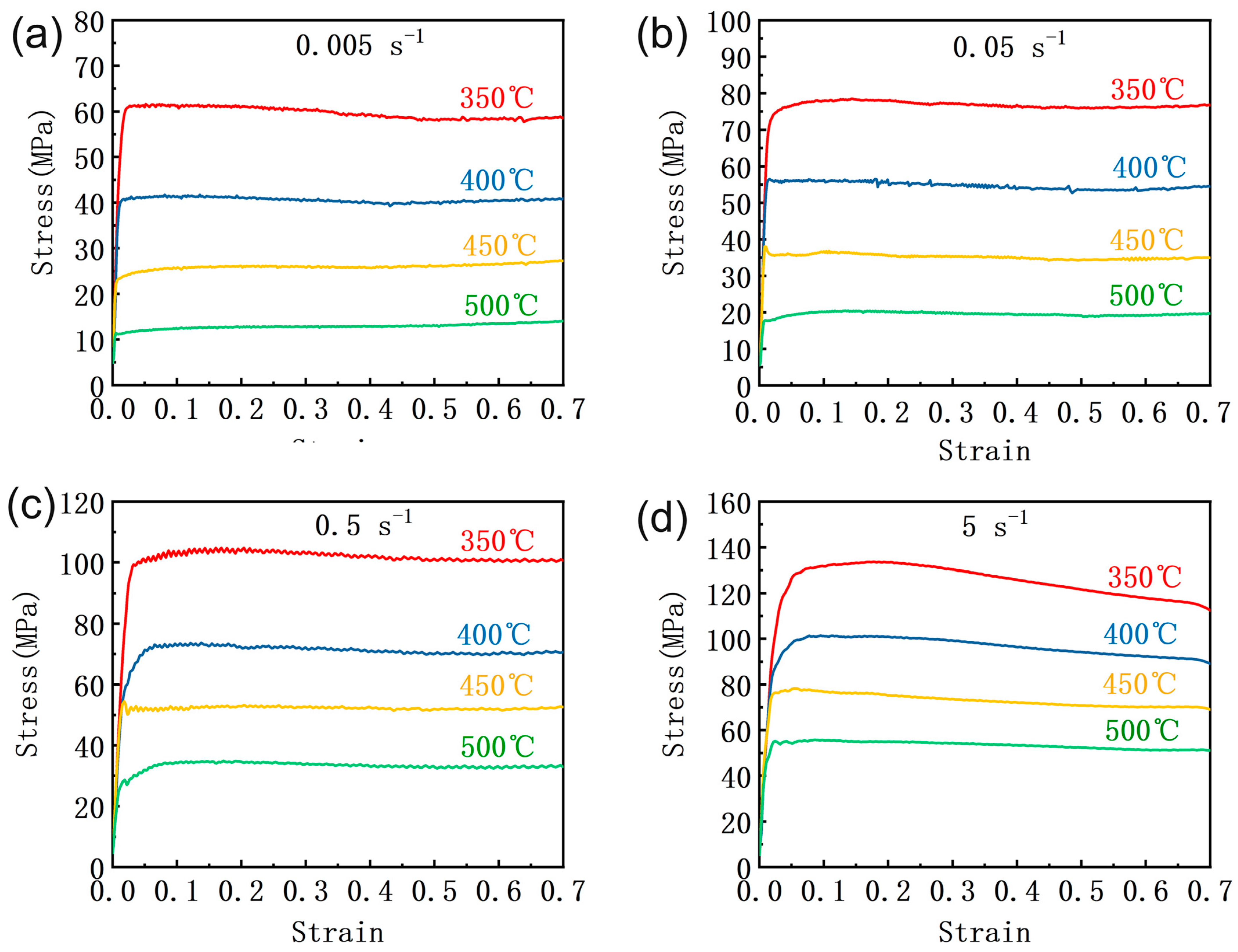
3.2. Flow Stress Characteristics
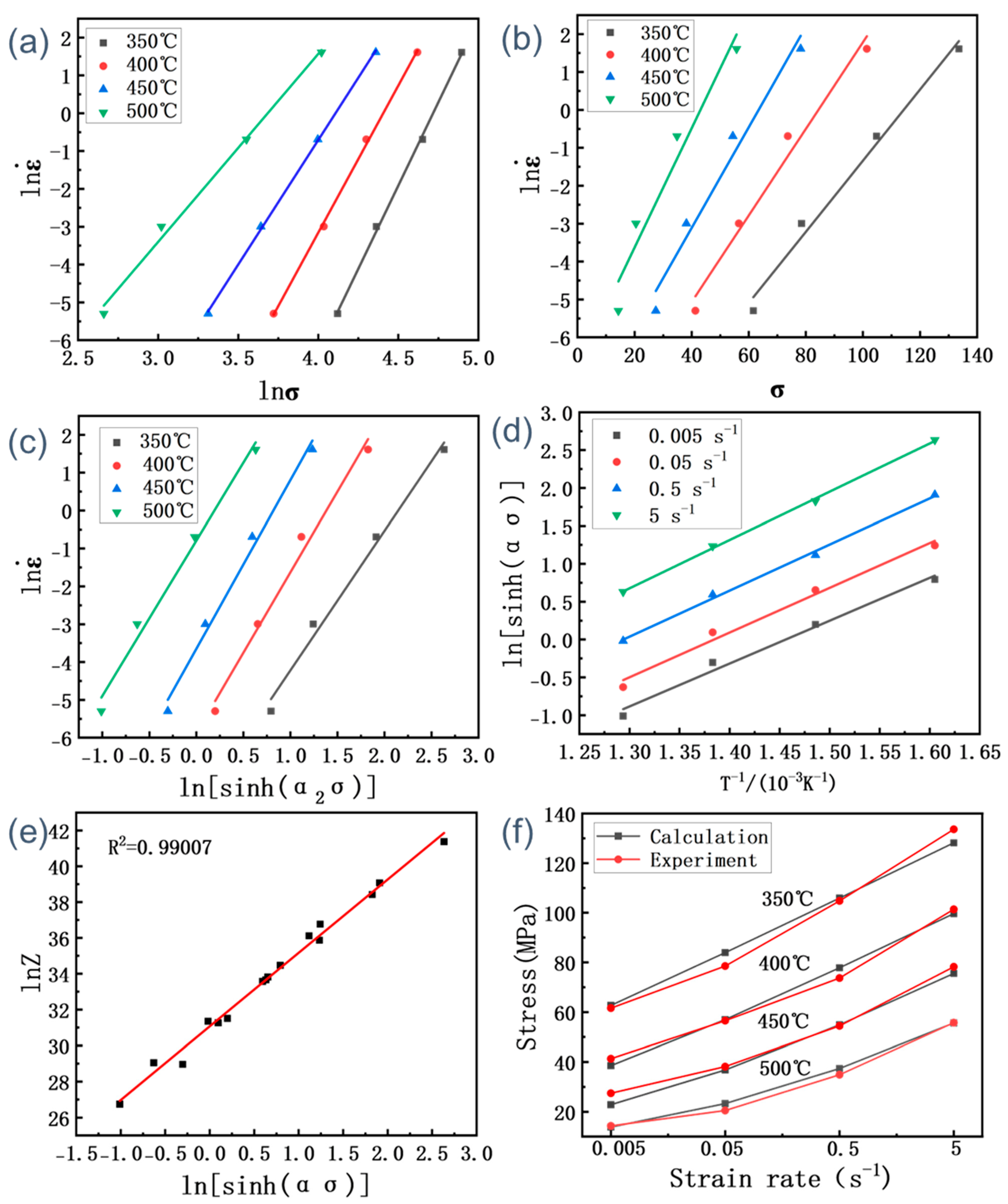
3.3. Constitutive Model
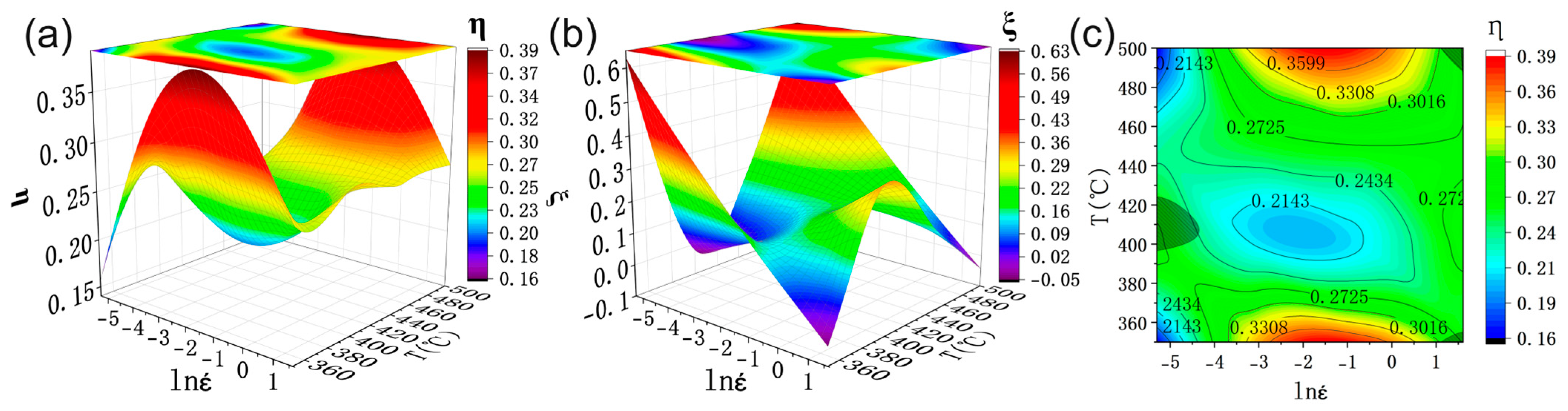
3.4. Processing Map
3.5. Microstructural Characterization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Garg, P.; Jamwal, A.; Kumar, D.; Sadasivuni, K.K.; Hussain, C.M.; Gupta, P. Advance research progresses in aluminium matrix composites: Manufacturing & applications. J. Mater. Res. Technol. 2019, 8, 4924–4939. [Google Scholar] [CrossRef]
- Samal, P.; Vundavilli, P.R.; Meher, A.; Mahapatra, M.M. Recent progress in aluminum metal matrix composites: A review on processing, mechanical and wear properties. J. Manuf. Process. 2020, 59, 131–152. [Google Scholar] [CrossRef]
- Mula, S.; Pabi, S.; Koch, C.C.; Padhi, P.; Ghosh, S. Workability and mechanical properties of ultrasonically cast Al–Al2O3 nanocomposites. Mater. Sci. Eng. A 2012, 558, 485–491. [Google Scholar] [CrossRef]
- Shi, Q.; Wang, C.; Deng, K.; Nie, K.; Liang, W. Recrystallization Behavior of a Mg-5Zn Alloy Influenced by Minor SiC(p) during Hot Compression. Materials 2022, 15, 8498. [Google Scholar] [CrossRef]
- Gao, Y.Y.; Liu, Y.; Li, Y.L.; Zhang, A.; Teng, H.; Dong, Z.H.; Li, T.; Jiang, B. Preparation and Characterization of In Situ (TiC-TiB(2))/Al-Cu-Mg-Si Composites with High Strength and Wear Resistance. Materials 2022, 15, 8750. [Google Scholar] [CrossRef] [PubMed]
- Hashiguchi, D.; Tricker, D.; Tarrant, A.; Campbell, J.; Pokross, C. Discontinuously reinforced aluminum MMC extrusions. Met. Powder Rep. 2017, 72, 252–258. [Google Scholar] [CrossRef]
- Wang, Z.; Song, M.; Sun, C.; He, Y. Effects of particle size and distribution on the mechanical properties of SiC reinforced Al–Cu alloy composites. Mater. Sci. Eng. A 2011, 528, 1131–1137. [Google Scholar] [CrossRef]
- Song, M.; Huang, B. Effects of particle size on the fracture toughness of SiCp/Al alloy metal matrix composites. Mater. Sci. Eng. A 2008, 488, 601–607. [Google Scholar] [CrossRef]
- Song, M. Effects of volume fraction of SiC particles on mechanical properties of SiC/Al composites. Trans. Nonferrous Met. Soc. China 2009, 19, 1400–1404. [Google Scholar] [CrossRef]
- Du, A.; Lattanzi, L.; Jarfors, A.E.W.; Zhou, J.; Zheng, J.; Wang, K.; Yu, G. The Influence of Ce, La, and SiC Particles Addition on the Formability of an Al-Si-Cu-Mg-Fe SiCp-MMC. Materials 2022, 15, 3789. [Google Scholar] [CrossRef]
- Ko, B.-C.; Park, G.-S.; Yoo, Y.-C. The effects of SiC particle volume fraction on the microstructure and hot workability of SiCp/AA 2024 composites. J. Mater. Process. Technol. 1999, 95, 210–215. [Google Scholar] [CrossRef]
- Li, Q.; Qiu, F.; Dong, B.-X.; Gao, X.; Shu, S.-L.; Yang, H.-Y.; Jiang, Q.-C. Processing, multiscale microstructure refinement and mechanical property enhancement of hypoeutectic Al–Si alloys via in situ bimodal-sized TiB2 particles. Mater. Sci. Eng. A 2020, 777, 139081. [Google Scholar] [CrossRef]
- Zhang, J.; Ouyang, Q.; Guo, Q.; Li, Z.; Fan, G.; Su, Y.; Jiang, L.; Lavernia, E.J.; Schoenung, J.M.; Zhang, D. 3D Microstructure-based finite element modeling of deformation and fracture of SiCp/Al composites. Compos. Sci. Technol. 2016, 123, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.-X.; Li, Q.; Wang, Z.-F.; Liu, T.-S.; Yang, H.-Y.; Shu, S.-L.; Chen, L.-Y.; Qiu, F.; Jiang, Q.-C.; Zhang, L.-C. Enhancing strength-ductility synergy and mechanisms of Al-based composites by size-tunable in-situ TiB2 particles with specific spatial distribution. Compos. Part B Eng. 2021, 217, 108912. [Google Scholar] [CrossRef]
- Shen, M.; Wang, X.; Zhang, M.; Hu, X.; Zheng, M.; Wu, K. Fabrication of bimodal size SiCp reinforced AZ31B magnesium matrix composites. Mater. Sci. Eng. A 2014, 601, 58–64. [Google Scholar] [CrossRef]
- Chen, S.; Teng, J.; Luo, H.; Wang, Y.; Zhang, H. Hot deformation characteristics and mechanism of PM 8009Al/SiC particle reinforced composites. Mater. Sci. Eng. A 2017, 697, 194–202. [Google Scholar] [CrossRef]
- Chen, X.; Fu, D.; Teng, J.; Zhang, H. Hot deformation behavior and mechanism of hybrid aluminum-matrix composites reinforced with micro-SiC and nano-TiB2. J. Alloy. Compd. 2018, 753, 566–575. [Google Scholar] [CrossRef]
- Gangolu, S.; Rao, A.G.; Sabirov, I.; Kashyap, B.; Prabhu, N.; Deshmukh, V. Development of constitutive relationship and processing map for Al-6.65Si-0.44Mg alloy and its composite with B4C particulates. Mater. Sci. Eng. A 2016, 655, 256–264. [Google Scholar] [CrossRef]
- Kai, X.; Zhao, Y.; Wang, A.; Wang, C.; Mao, Z. Hot deformation behavior of in situ nano ZrB2 reinforced 2024Al matrix composite. Compos. Sci. Technol. 2015, 116, 1–8. [Google Scholar] [CrossRef]
- Liu, K.; Su, Y.; Wang, X.; Cai, Y.; Cao, H.; Ouyang, Q.; Zhang, D. Achieving simultaneous enhancement of strength and ductility in Al matrix composites by employing the synergetic strengthening effect of micro- and nano-SiCps. Compos. Part B Eng. 2023, 248, 110350. [Google Scholar] [CrossRef]
- Sun, Y.; Xie, J.; Hao, S.; Wang, A.; Liu, P.; Li, M. Dynamic recrystallization model of 30%SiCp/Al composite. J. Alloy. Compd. 2015, 649, 865–871. [Google Scholar] [CrossRef]
- Tang, S.; Shao, S.; Liu, H.; Jiang, F.; Fu, D.; Zhang, H.; Teng, J. Microstructure and mechanical behaviors of 6061 Al matrix hybrid composites reinforced with SiC and stainless steel particles. Mater. Sci. Eng. A 2021, 804, 140732. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, X.; Yue, H.; Liu, S.; Ren, L.; Xin, Y.; Lyu, L.; Zhao, Y.; Quan, G.; Gupta, M. Hot deformation behavior and processing maps of hybrid SiC and CNTs reinforced AZ61 alloy composite. J. Alloy. Compd. 2021, 868, 159098. [Google Scholar] [CrossRef]
- Shao, J.; Xiao, B.; Wang, Q.; Ma, Z.; Liu, Y.; Yang, K. Constitutive flow behavior and hot workability of powder metallurgy processed 20vol.%SiCP/2024Al composite. Mater. Sci. Eng. A 2010, 527, 7865–7872. [Google Scholar] [CrossRef]
- Zhang, L.-J.; Qiu, F.; Wang, J.-G.; Wang, H.-Y.; Jiang, Q.-C. Microstructures and mechanical properties of the Al2014 composites reinforced with bimodal sized SiC particles. Mater. Sci. Eng. A 2015, 637, 70–74. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Z.; Fu, D.; Zhang, H.; Teng, J.; Jiang, F. Comparative Hot Workability Characteristics of an Al–Si/SiCp Aluminium Matrix Composite Hybrid Reinforced with Various TiB2 Additions. Met. Mater. Int. 2020, 27, 1880–1891. [Google Scholar] [CrossRef]
- Diler, E.A.; Ipek, R. An experimental and statistical study of interaction effects of matrix particle size, reinforcement particle size and volume fraction on the flexural strength of Al–SiCp composites by P/M using central composite design. Mater. Sci. Eng. A 2012, 548, 43–55. [Google Scholar] [CrossRef]
- Slipenyuk, A.; Kuprin, V.; Milman, Y.; Goncharuk, V.; Eckert, J. Properties of P/M processed particle reinforced metal matrix composites specified by reinforcement concentration and matrix-to-reinforcement particle size ratio. Acta Mater. 2006, 54, 157–166. [Google Scholar] [CrossRef]
- Sellars, C.; McTegart, W. On the mechanism of hot deformation. Acta Met. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- McQueen, H.J.; Bourell, D.L. Hot Workability of Metals and Alloys. Jom 1987, 39, 28–35. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Liao, H.; Wu, Y.; Zhou, K.; Yang, J. Hot deformation behavior and processing map of Al–Si–Mg alloys containing different amount of silicon based on Gleebe-3500 hot compression simulation. Mater. Des. 2015, 65, 1091–1099. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K. Processing maps: A status report. J. Mater. Eng. Perform. 2003, 12, 638–645. [Google Scholar] [CrossRef]
- Murty, S.N.; Rao, B.N.; Kashyap, B. Instability criteria for hot deformation of materials. Int. Mater. Rev. 2013, 45, 15–26. [Google Scholar] [CrossRef]



| Powder | Purity (%) | Dimension (μm) |
|---|---|---|
| 6013Al | 99.2 | 7 |
| SiC | 99.5 | 0.7 |
| SiC | 99.5 | 2 |
| SiC | 99.5 | 5 |
| Strain ε | A (MPa−1) | n | A (s−1) | Q (kJ/mol) |
|---|---|---|---|---|
| 0.1 | 0.035486657 | 3.15642 | 6.67 × 1012 | 205.1840524 |
| 0.3 | 0.036103 | 3.229925 | 1.69 × 1013 | 211.1135983 |
| 0.5 | 0.036829023 | 3.3890925 | 3.83 × 1013 | 216.6694489 |
| 0.7 | 0.036537749 | 3.672925 | 1.67 × 1014 | 226.9465338 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Chen, S.; Tang, J.; Fu, D.; Teng, J.; Jiang, F. Hot Workability of the Multi-Size SiC Particle-Reinforced 6013 Aluminum Matrix Composites. Materials 2023, 16, 796. https://doi.org/10.3390/ma16020796
Wu C, Chen S, Tang J, Fu D, Teng J, Jiang F. Hot Workability of the Multi-Size SiC Particle-Reinforced 6013 Aluminum Matrix Composites. Materials. 2023; 16(2):796. https://doi.org/10.3390/ma16020796
Chicago/Turabian StyleWu, Changlong, Shuang Chen, Jie Tang, Dingfa Fu, Jie Teng, and Fulin Jiang. 2023. "Hot Workability of the Multi-Size SiC Particle-Reinforced 6013 Aluminum Matrix Composites" Materials 16, no. 2: 796. https://doi.org/10.3390/ma16020796
APA StyleWu, C., Chen, S., Tang, J., Fu, D., Teng, J., & Jiang, F. (2023). Hot Workability of the Multi-Size SiC Particle-Reinforced 6013 Aluminum Matrix Composites. Materials, 16(2), 796. https://doi.org/10.3390/ma16020796







