Combined Influences of Water Content and Coarse Grain Content on Shear Strength of Unsaturated Soil Mixture
Abstract
:1. Introduction
2. Materials and Methods
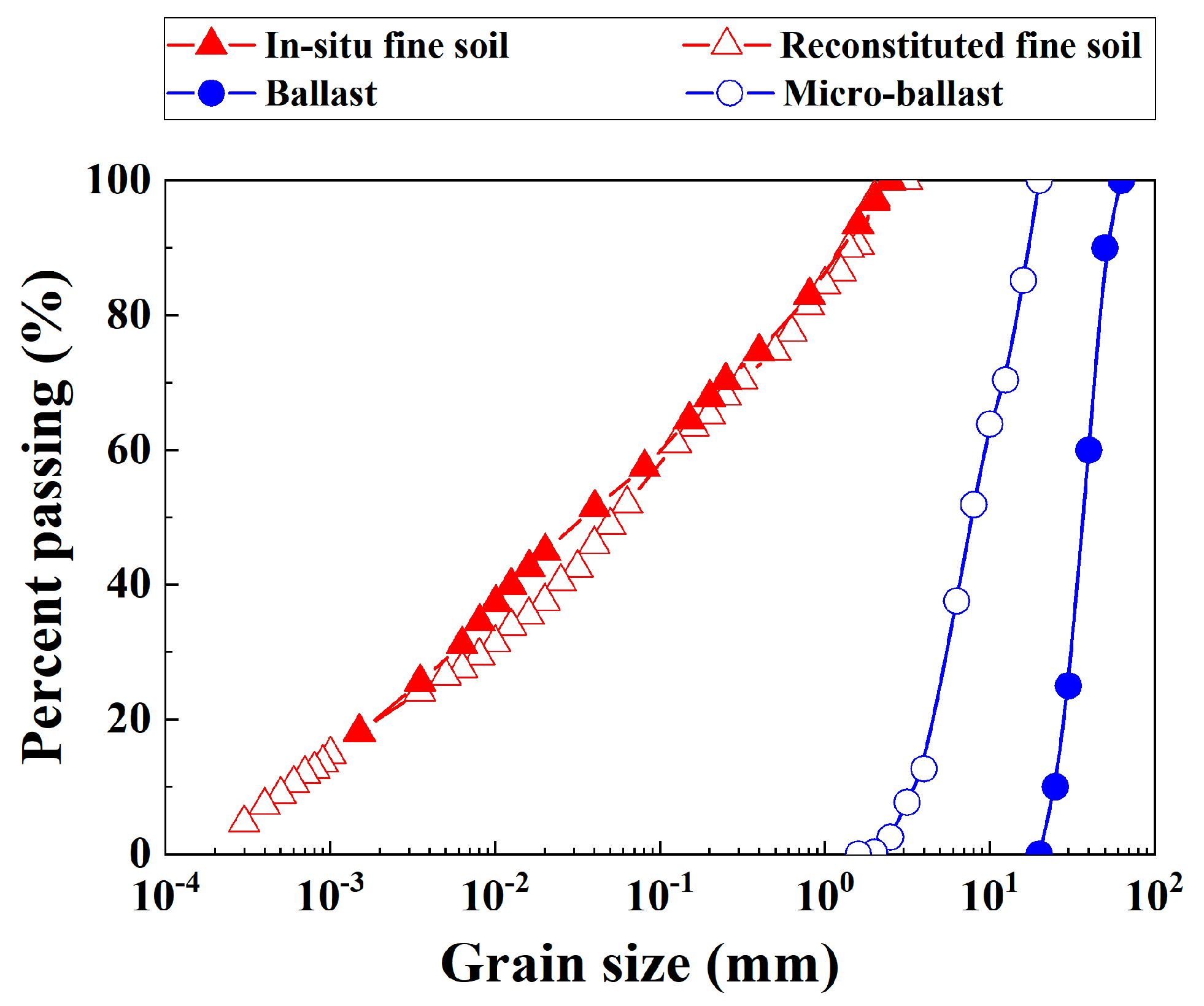
2.1. Reconstituted Fine Soil and Micro-Ballast
2.2. Monotonic Triaxial Tests
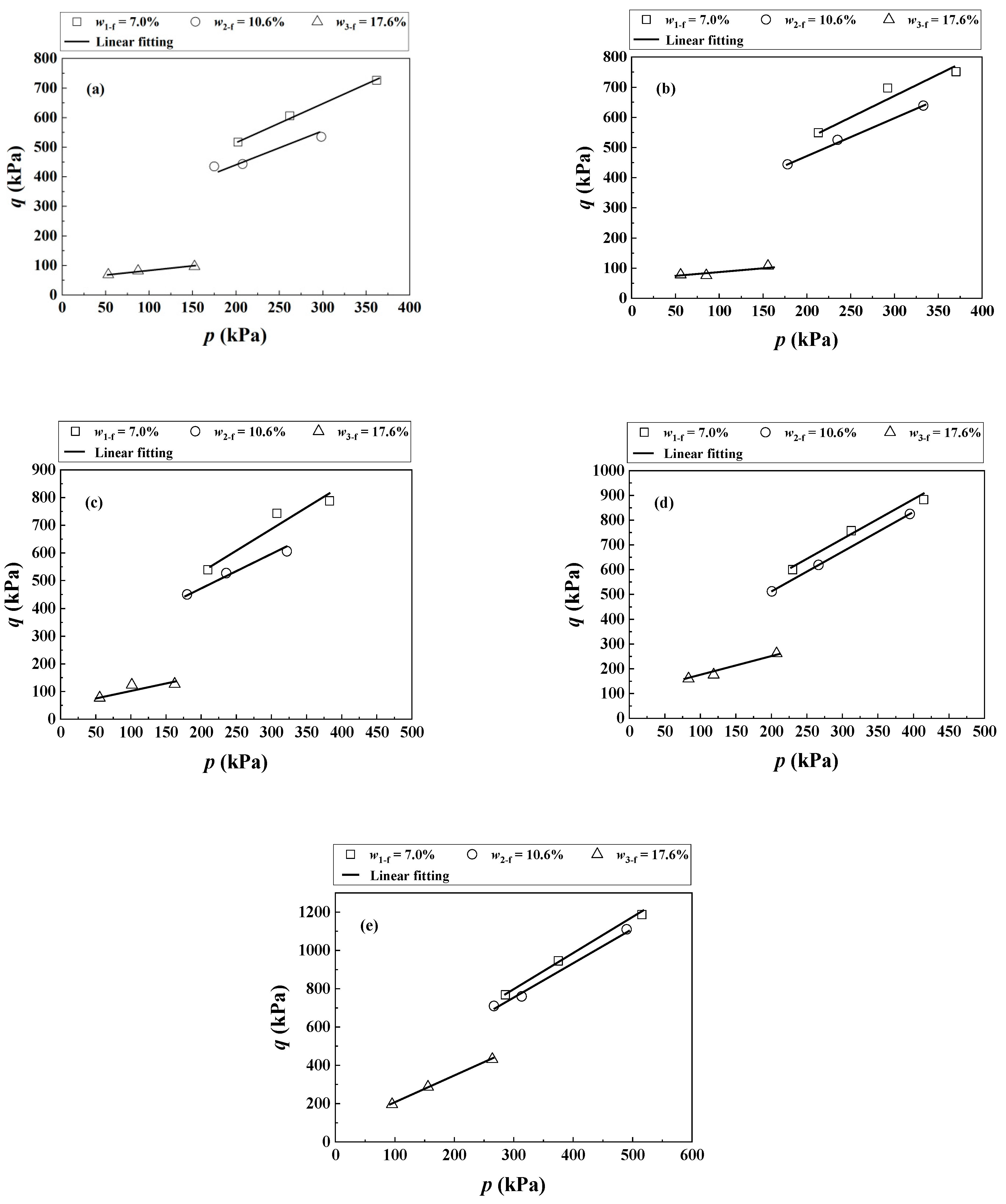
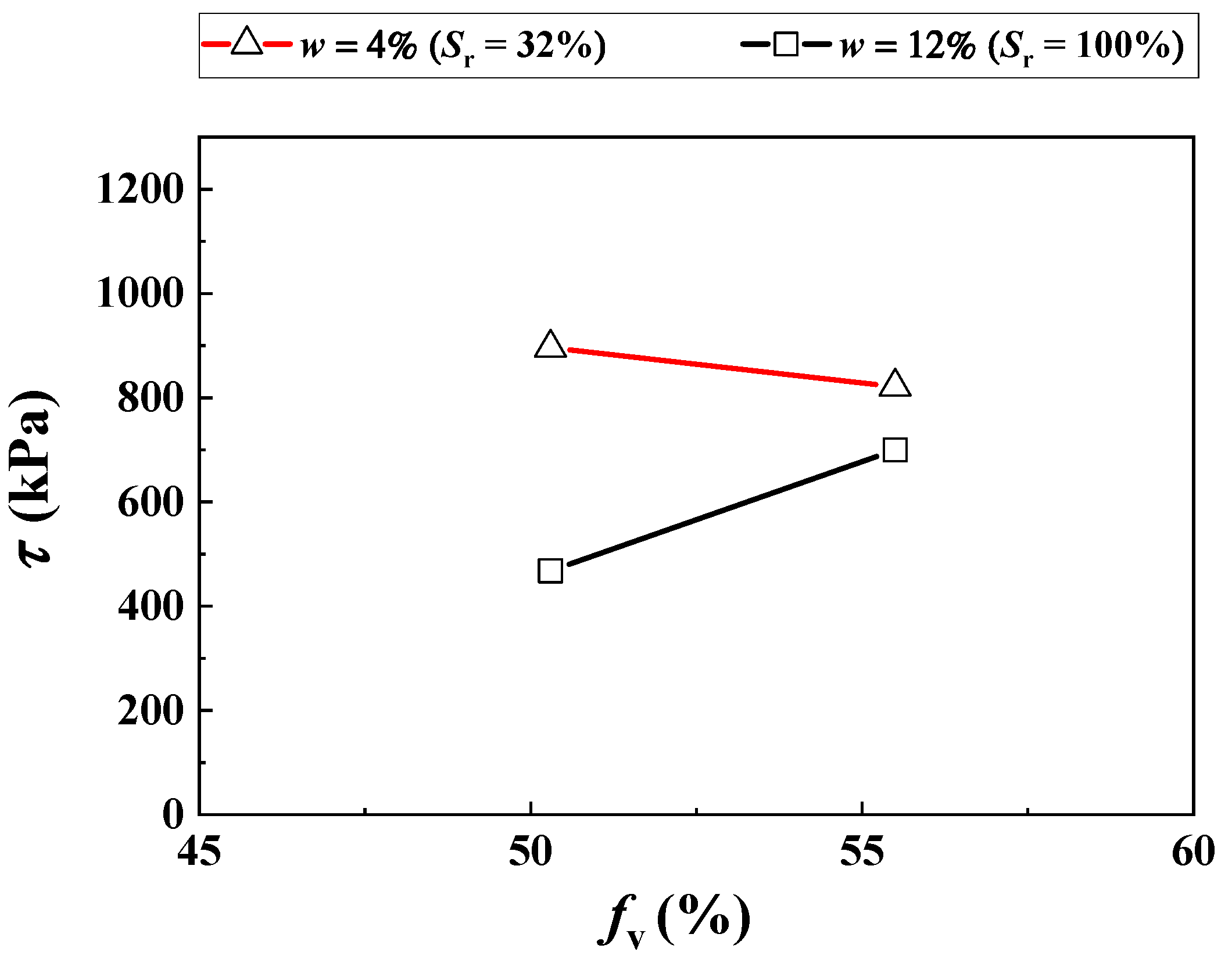
3. Experimental Results
4. Modelling of Shear Strength
| Reference | Equation | |
|---|---|---|
| Abramento and Carvalho [11] | (1) | |
| Vanapalli et al. [12] | (2) | |
| Öberg and Sallfors [25] | (3) | |
| Xu and Sun [26] | (4) | |
| Vilar [13] | (5) | |
| Han and Vanapalli [14] | (6) |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| c | apparent cohesion |
| effective cohesion | |
| axial strain | |
| volumetric strain | |
| fv | volumetric coarse grain content |
| fv-cha | characteristic volumetric coarse grain content |
| Gs | specific gravity |
| Ip | plasticity index |
| ρd | dry density of sample |
| ρd–f | dry density of fine soil |
| ρdmax-f | maximum dry density of fine soil |
| q | deviator stress |
| τ | shear stress |
| τsat | shear stress under saturated condition |
| τref | shear stress under referenced condition |
| Sr | degree of saturation |
| Sr-r | residual degree of saturation |
| effective degree of saturation | |
| effective degree of saturation under a referenced state | |
| w | water content of soil mixture |
| wf | water content of fine soil |
| wopt-f | optimum water content of fine soil |
| wL | liquid limit |
| χ | effective stress parameter |
| confining pressure | |
| φ | friction angle |
| effective friction angle | |
| suction | |
| ref | suction under referenced state |
References
- Trinh, V.N. Comportement Hydromecanique des Materiaux Constitutifs de Plateformes Ferroviaires Anciennes. Ph.D. Thesis, Ecole Nationale des Ponts et Chaussées, Université Paris-Est, Paris, France, 2011. [Google Scholar]
- Trinh, V.N.; Tang, A.M.; Cui, Y.J.; Dupla, J.C.; Canou, J.; Calon, N.; Lambert, L.; Robinet, A.; Schoen, O. Mechanical characterisation of the fouled ballast in ancient railway track substructure by large-scale triaxial tests. Soils Found. 2012, 52, 511–523. [Google Scholar] [CrossRef]
- Duong, T.V.; Tang, A.M.; Cui, Y.J.; Trinh, V.N.; Dupla, J.C.; Calon, N.; Canou, J.; Robinet, A. Effects of fines and water contents on the mechanical behavior of interlayer soil in ancient railway sub-structure. Soils Found. 2013, 53, 868–878. [Google Scholar] [CrossRef]
- Qi, S.; Cui, Y.J.; Chen, R.P.; Wang, H.L.; Lamas-Lopez, F.; Aimedieu, P.; Dupla, J.C.; Canou, J.; Saussine, G. Influence of grain size distribution of inclusions on the mechanical behaviours of track-bed materials. Géotechnique 2020, 70, 238–247. [Google Scholar] [CrossRef]
- Qi, S.; Cui, Y.J.; Dupla, J.C.; Chen, R.P.; Wang, H.L.; Su, Y.; Lamas-Lopez, F.; Canou, J. Investigation of the parallel gradation method based on the response of track-bed materials under cyclic loadings. Transp. Geotech. 2020, 24, 100360. [Google Scholar] [CrossRef]
- Wan, Z.; Bian, X.; Li, S.; Chen, Y.; Cui, Y. Remediation of mud pumping in ballastless high-speed railway using polyurethane chemical injection. Constr. Build. Mater. 2020, 259, 120401. [Google Scholar] [CrossRef]
- Bian, X.; Wan, Z.; Zhao, C.; Cui, Y.; Chen, Y. Mud pumping in the roadbed of ballastless high-speed railway. Géotechnique 2021, 73, 614–628. [Google Scholar] [CrossRef]
- Vallejo, L.E. Interpretation of the limits in shear strength in binary granular mixtures. Can. Geotech. J. 2001, 38, 1097–1104. [Google Scholar] [CrossRef]
- Seif El Dine, B.; Dupla, J.C.; Frank, R.; Canou, J.; Kazan, Y. Mechanical characterization of matrix coarse-grained soils with a large-sized triaxial device. Can. Geotech. J. 2010, 47, 425–438. [Google Scholar] [CrossRef]
- Wang, H.L.; Cui, Y.J.; Lamas-Lopez, F.; Calon, N.; Saussine, G.; Dupla, J.C.; Canou, J.; Aimedieu, P.; Chen, R.P. Investigation on the mechanical behavior of track-bed materials at various contents of coarse grains. Constr. Build. Mater. 2018, 164, 228–237. [Google Scholar] [CrossRef]
- Abramento, M.; Carvalho, C.S. Geotechnical parameters for the study of natural slopes instabilization at ‘Serra do Mar’, Brazil. In Congrès Intrnational de Mécanique des Sols et des Travaux de Fondations; A.A. Balkema: Rotterdam, The Netherlands, 1989; Volume 12, pp. 1599–1602. [Google Scholar]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Vilar, O.M. A simplified procedure to estimate the shear strength envelope of unsaturated soils. Can. Geotech. J. 2006, 43, 1088–1095. [Google Scholar] [CrossRef]
- Han, Z.; Vanapalli, S.K. Stiffness and shear strength of unsaturated soils in relation to soil-water characteristic curve. Géotechnique 2016, 66, 627–647. [Google Scholar] [CrossRef]
- Wang, H.L.; Cui, Y.J.; Lamas-Lopez, F.; Dupla, J.C.; Canou, J.; Calon, N.; Saussine, G.; Aimedieu, P.; Chen, R.P. Permanent deformation of track-bed materials at various inclusion contents under large number of loading cycles. J. Geotech. Geoenviron. Eng. 2018, 144, 04018044. [Google Scholar] [CrossRef]
- Su, Y.; Cui, Y.J.; Dupla, J.C.; Canou, J.; Qi, S. Developing a Sample Preparation Approach to Study the Mechanical Behavior of Unsaturated Fine/Coarse Soil Mixture. Geotech. Test. J. 2021, 44, 20190450. [Google Scholar] [CrossRef]
- Han, Z.; Vanapalli, S.K. Relationship between resilient modulus and suction for compacted subgrade soils. Eng. Geol. 2016, 211, 85–97. [Google Scholar] [CrossRef]
- Yang, S.R.; Huang, W.H.; Tai, Y.T. Variation of resilient modulus with soil suction for compacted subgrade soils. Transp. Res. Rec. 2005, 1913, 99–106. [Google Scholar] [CrossRef]
- Yang, S.R.; Lin, H.D.; Kung, J.H.; Huang, W.H. Suction-controlled laboratory test on resilient modulus of unsaturated compacted subgrade soils. J. Geotech. Geoenviron. Eng. 2008, 134, 1375–1384. [Google Scholar] [CrossRef]
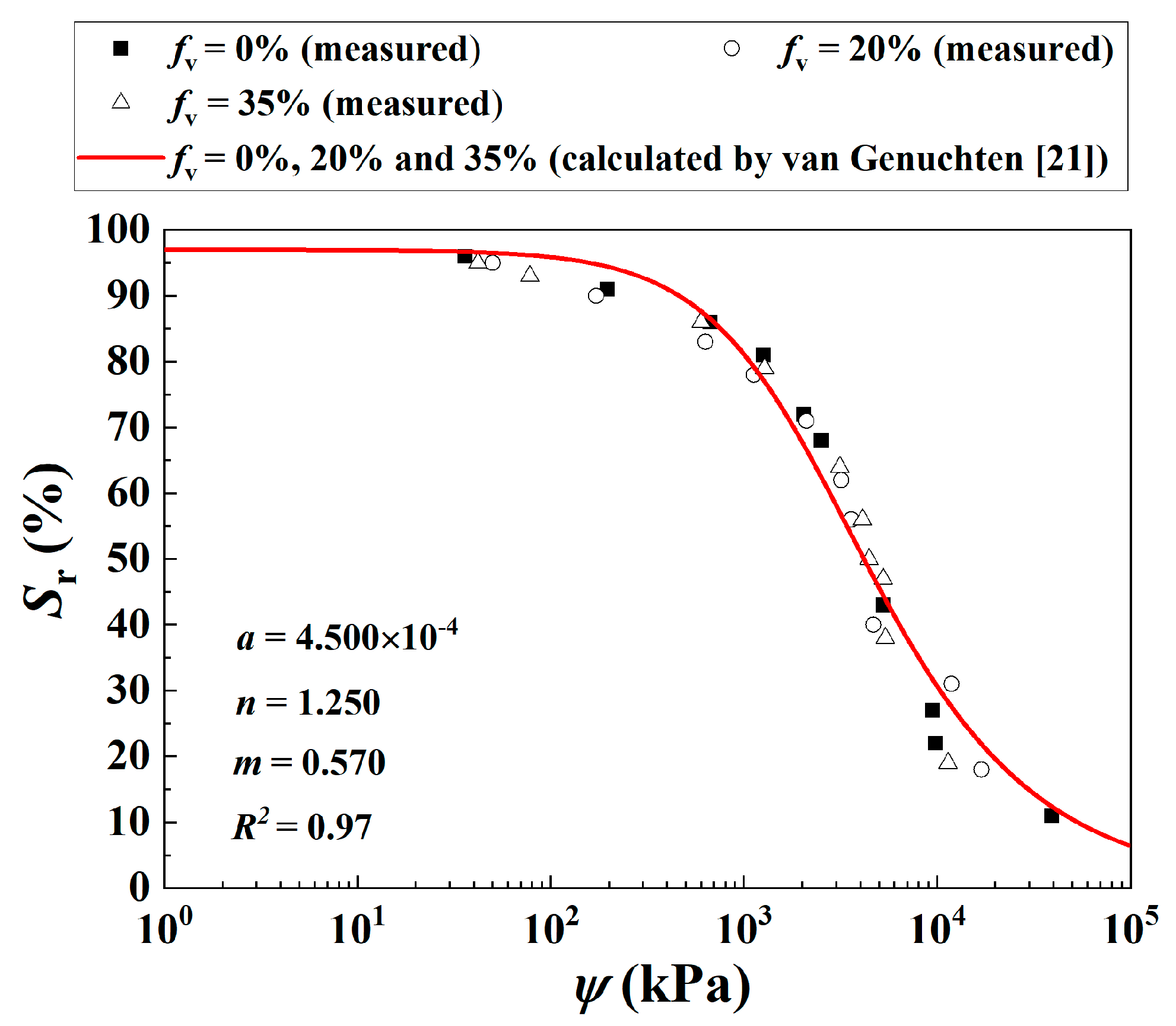
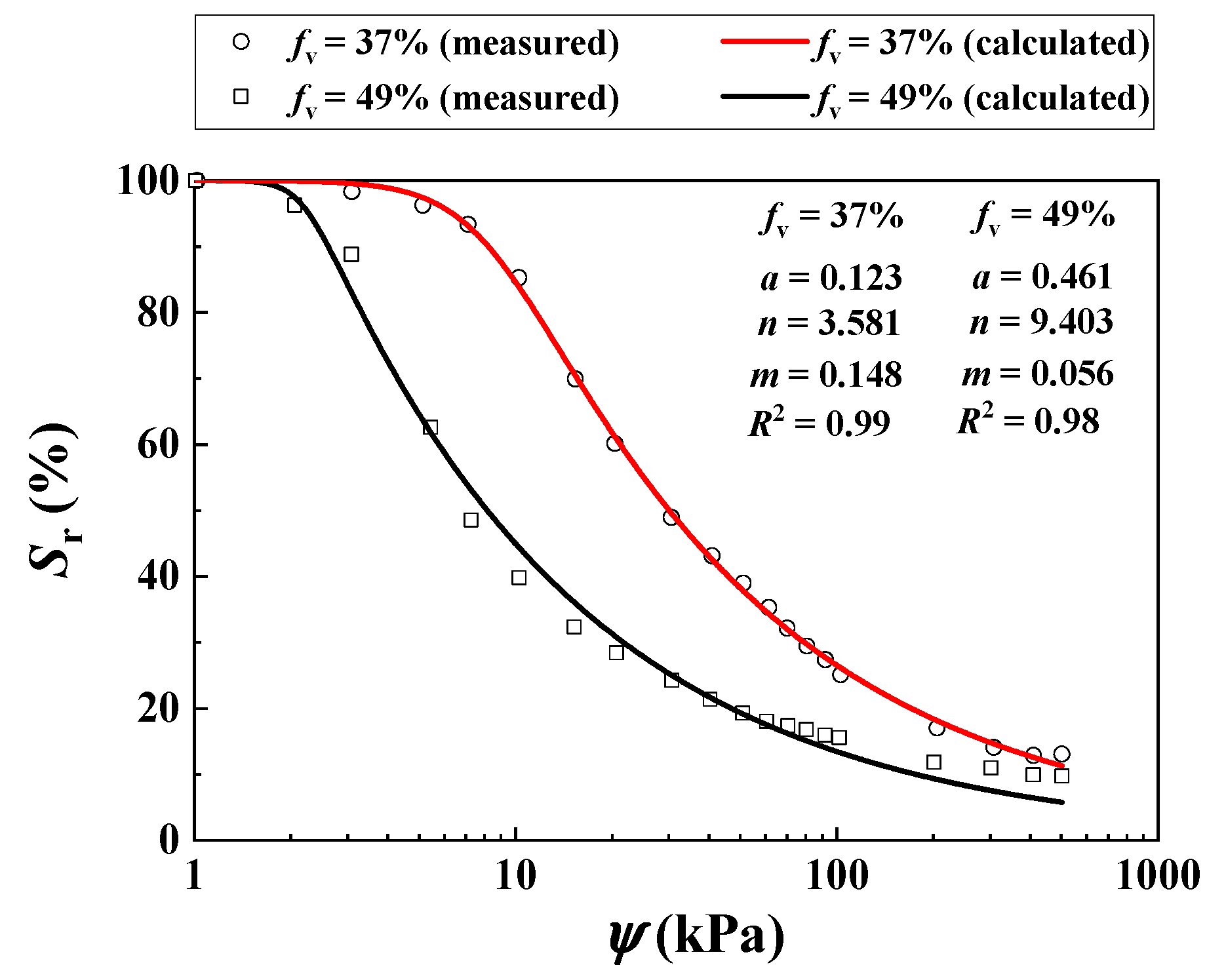
- Su, Y.; Cui, Y.J.; Dupla, J.C.; Canou, J. Soil-water retention behaviour of fine/coarse soil mixture with varying coarse grain contents and fine soil dry densities. Can. Geotech. J. 2022, 59, 291–299. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- ASTM D7181-11; Standard Test Method for Consolidated Drained Triaxial Compression Test for Soils (Superseded). ASTM International: West Conshohocken, PA, USA, 2011. [CrossRef]
- Delage, P.; Audiguier, M.; Cui, Y.J.; Howat, M.D. Microstructure of a compacted silt. Can. Geotech. J. 1996, 33, 150–158. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Baghbanrezvan, S.; Sadeghi, H.; Zhou, C.; Jafarzadeh, F. Effect of specimen preparation techniques on dynamic properties of unsaturated fine-grained soil at high suctions. Can. Geotech. J. 2017, 54, 1310–1319. [Google Scholar] [CrossRef]
- Öberg, A.L.; Sallfors, G. Determination of shear strength parameters of unsaturated silts and sands based on the water retention curve. Geotech. Test. J. 1997, 20, 40–48. [Google Scholar]
- Xu, Y.F.; Sun, D.A. A fractal model for soil pores and its application to determination of water permeability. Phys. A Stat. Mech. Appl. 2002, 316, 56–64. [Google Scholar] [CrossRef]
- Alonso, E.E.; Pereira, J.M.; Vaunat, J.; Olivella, S. A microstructurally based effective stress for unsaturated soils. Géotechnique 2010, 60, 913–925. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Rassam, D.W.; Williams, D.J. A relationship describing the shear strength of unsaturated soils. Can. Geotech. J. 1999, 36, 363–368. [Google Scholar] [CrossRef]
- Khalili, N.G.F.A.; Geiser, F.; Blight, G.E. Effective stress in unsaturated soils: Review with new evidence. Int. J. Geomech. 2004, 4, 115–126. [Google Scholar] [CrossRef]
- Khalili, N.; Zargarbashi, S. Influence of hydraulic hysteresis on effective stress in unsaturated soils. Géotechnique 2010, 60, 729–734. [Google Scholar] [CrossRef]

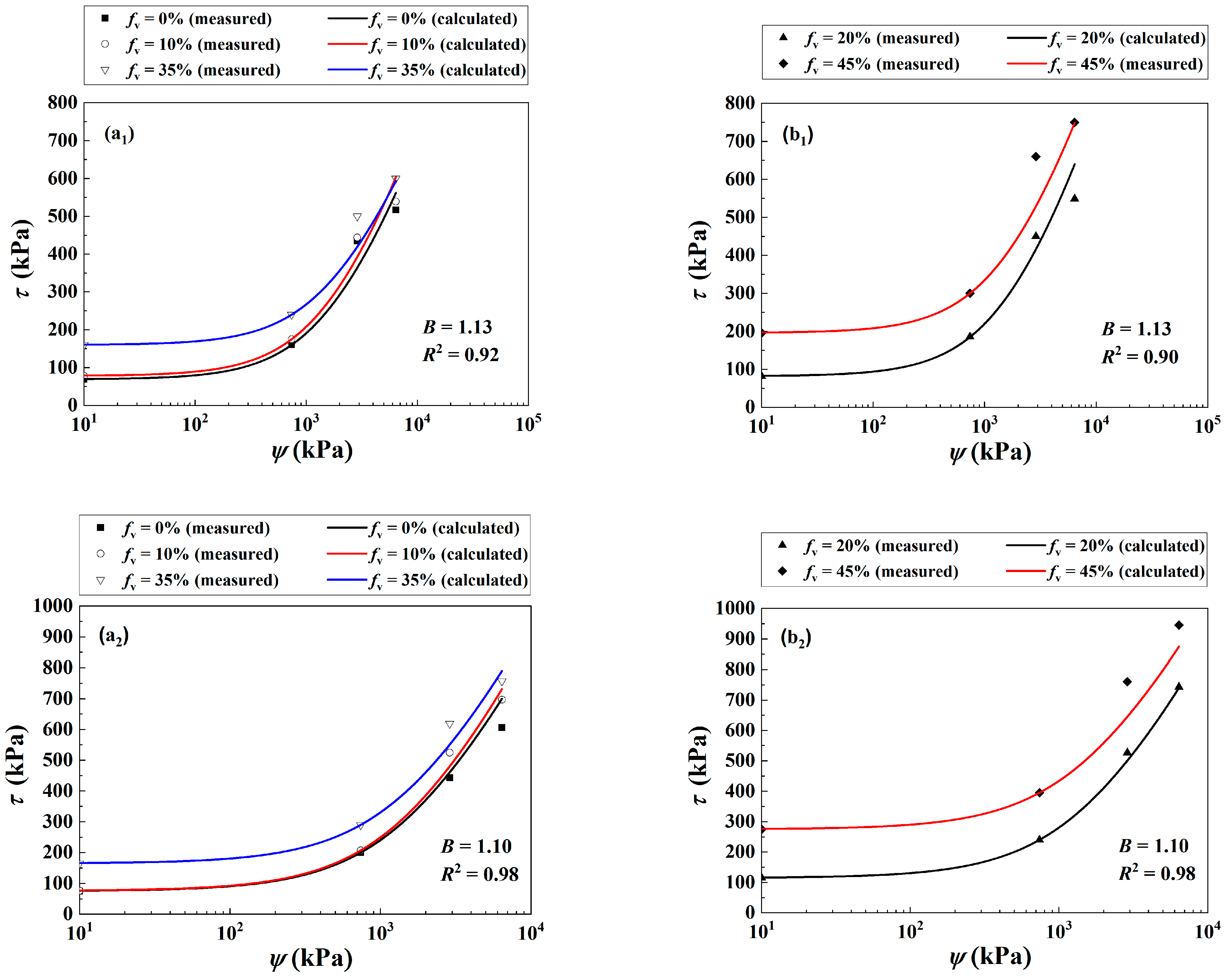
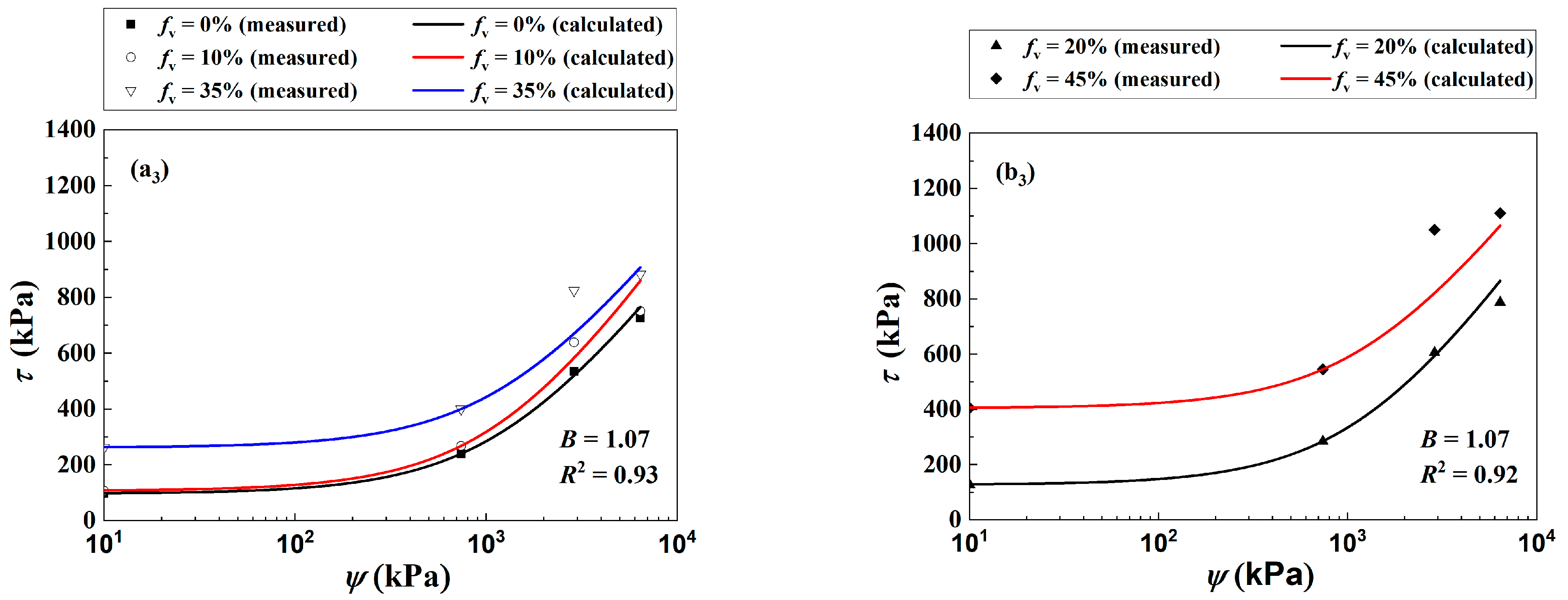
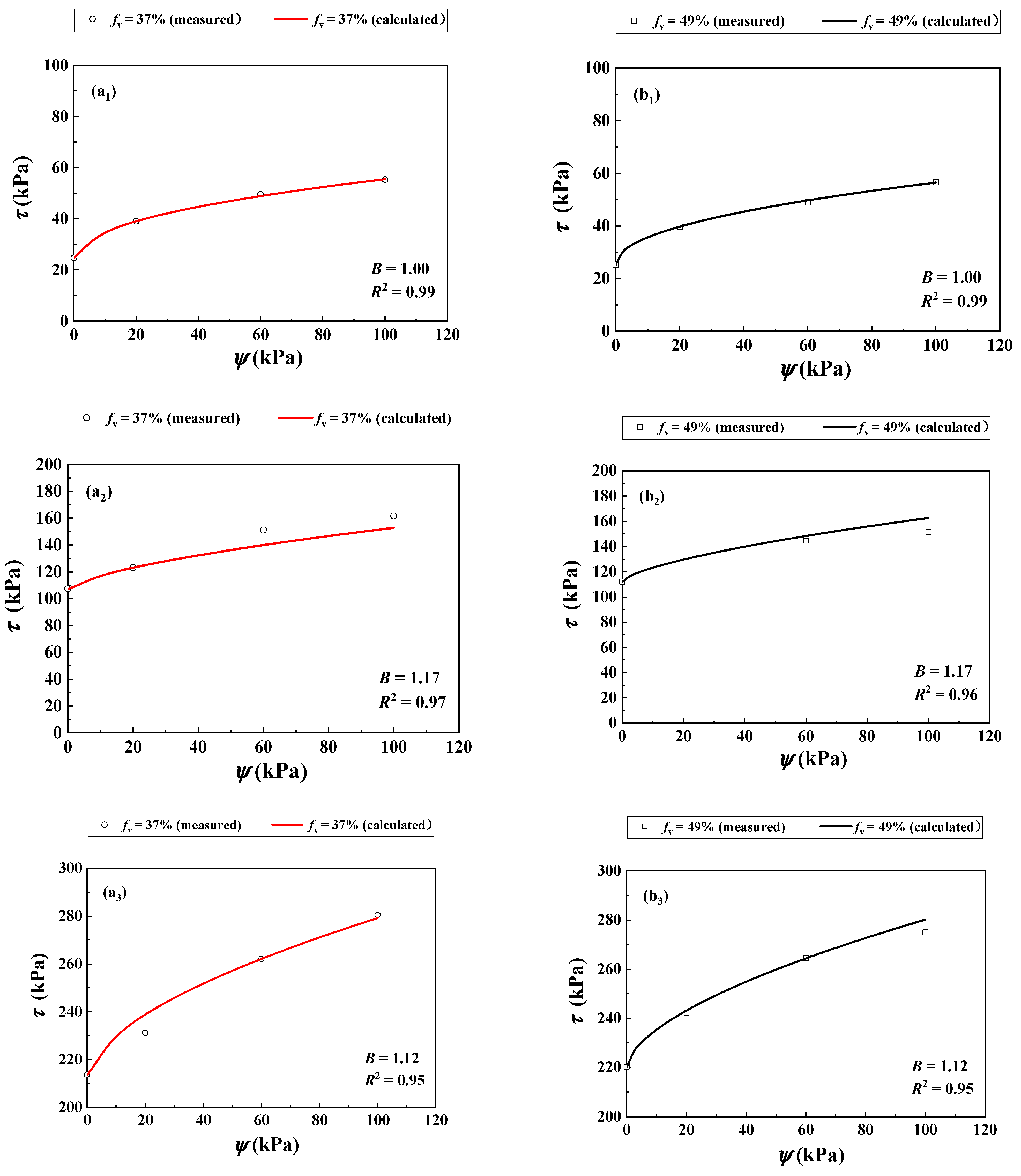
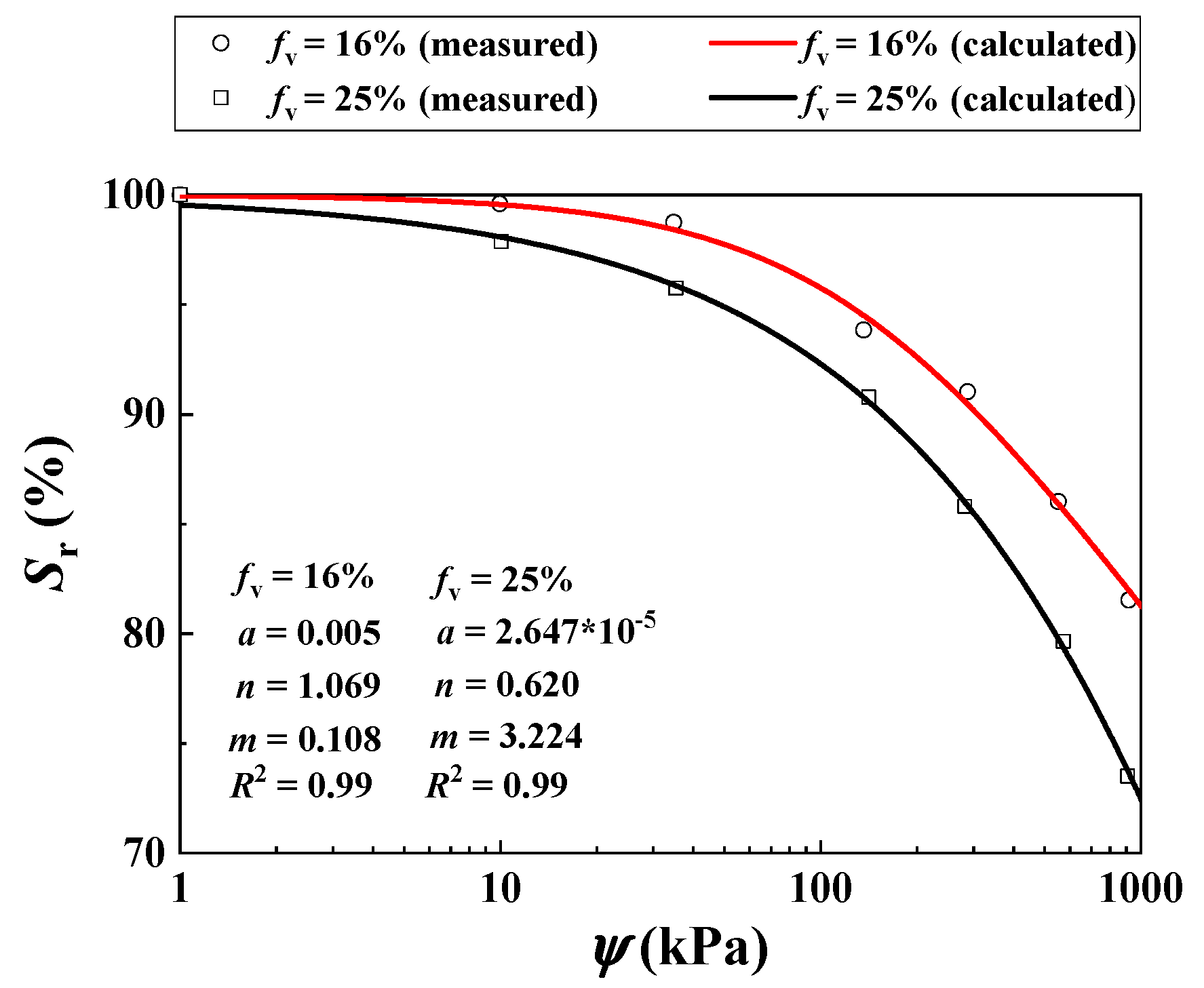
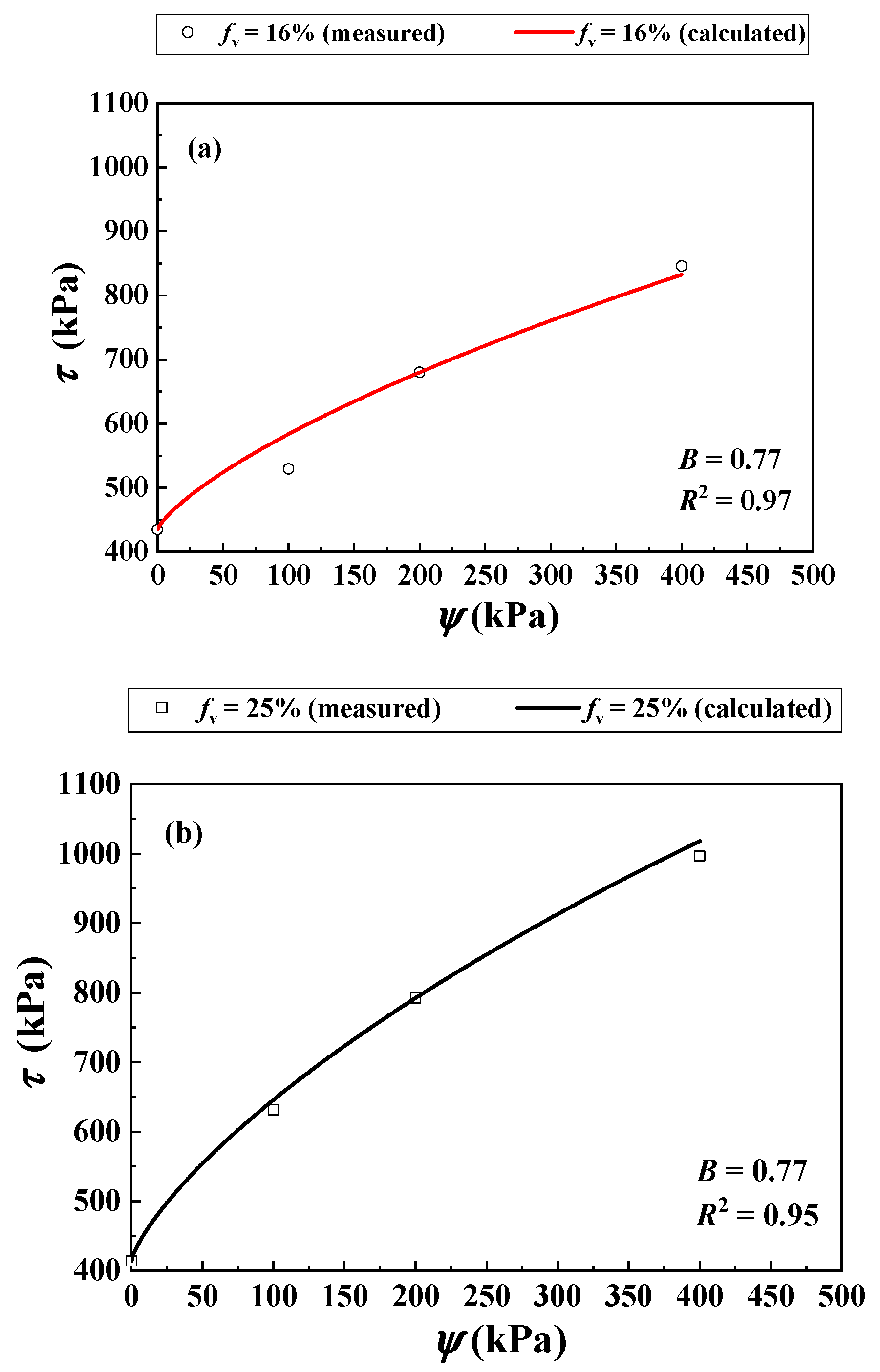
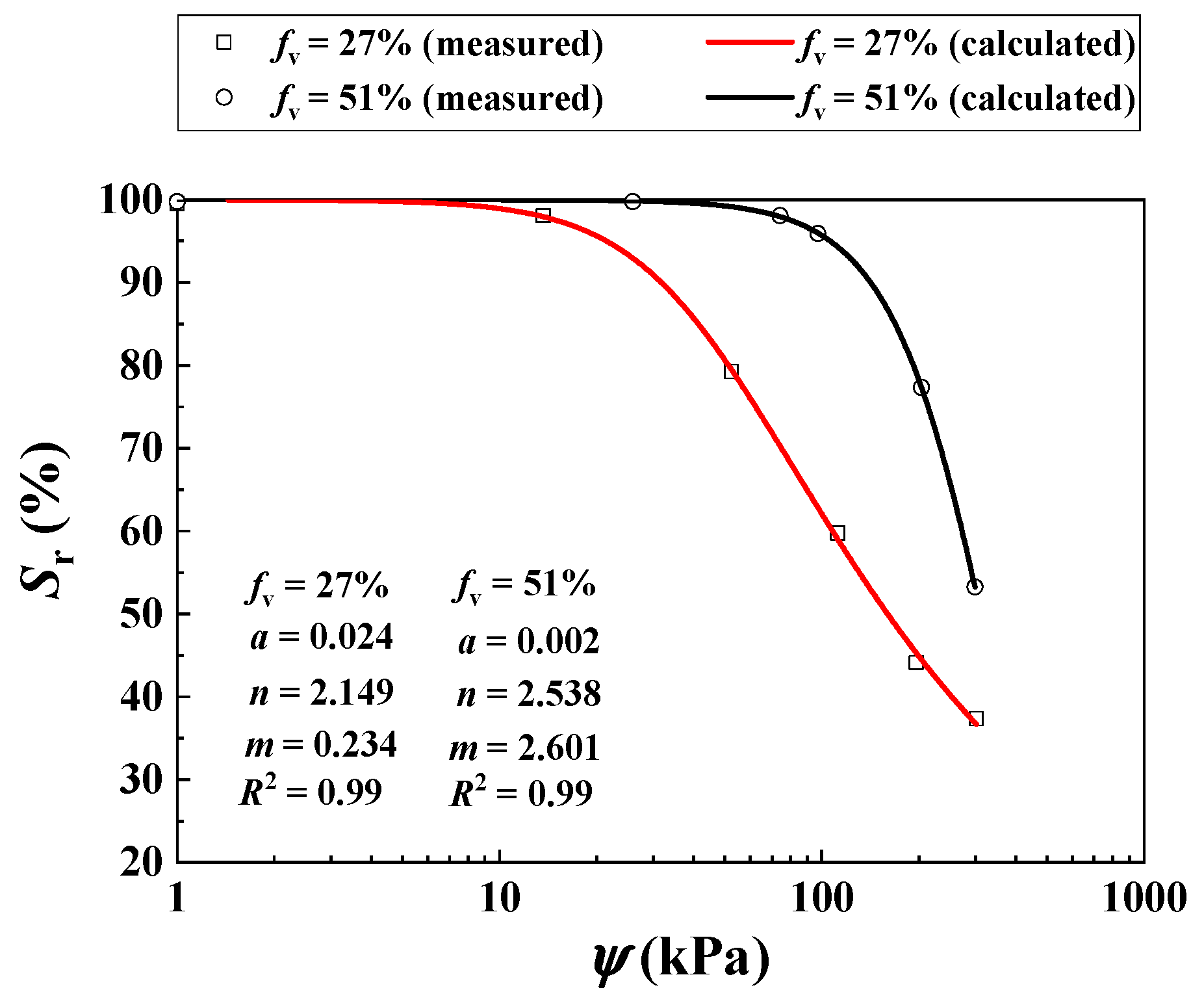


| Wf (%) | fv = 0% | fv = 10% | fv = 20% | fv = 35% | fv = 45% | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| c | φ | c | φ | c | φ | c | φ | c | φ | |
| 7 | 146 | 29 | 141 | 32 | 124 | 36 | 113 | 40 | 99 | 48 |
| 11 | 137 | 21 | 129 | 27 | 125 | 27 | 102 | 38 | 98 | 46 |
| 18 | 32 | 8 | 32 | 9 | 29 | 12 | 27 | 22 | 26 | 34 |
| Reference | fv (%) | Fine Soil Fraction | Soil Mixture | SWRC Fitted by van Genuchten [21] Model | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Gs | wL (%) | Ip (%) | wopt-f (%) | ρdmax-f (Mg/m3) | ψ (kPa) | ρd (Mg/m3) | a | n | m | ||
| Rassam and Williams [29] | 37 | N/A | 0, 20, 60 and 100 | N/A | 0.123 | 3.581 | 0.149 | ||||
| 49 | 0.461 | 9.403 | 0.056 | ||||||||
| Khalili et al. [30] | 16 | N/A | 33 | 12 | N/A | 0, 100, 200 and 400 | 1.69 | 0.005 | 1.069 | 0.108 | |
| 25 | 1.91 | 2.647 × 10−5 | 0.620 | 3.224 | |||||||
| Khalili and Zargarbashi [31] | 27 | N/A | 0, 30, 70, 100, 200 and 300 | 1.53 | 0.024 | 2.149 | 0.234 | ||||
| 51 | 0, 15, 50, 110, 200 and 300 | 1.63 | 0.002 | 2.538 | 2.601 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Han, B.; Duan, J.; Zhao, F. Combined Influences of Water Content and Coarse Grain Content on Shear Strength of Unsaturated Soil Mixture. Materials 2023, 16, 6657. https://doi.org/10.3390/ma16206657
Su Y, Han B, Duan J, Zhao F. Combined Influences of Water Content and Coarse Grain Content on Shear Strength of Unsaturated Soil Mixture. Materials. 2023; 16(20):6657. https://doi.org/10.3390/ma16206657
Chicago/Turabian StyleSu, Yu, Bo Han, Junyi Duan, and Fumin Zhao. 2023. "Combined Influences of Water Content and Coarse Grain Content on Shear Strength of Unsaturated Soil Mixture" Materials 16, no. 20: 6657. https://doi.org/10.3390/ma16206657





