Design of Variable Stiffness Trajectories with Cubic Ferguson Curve
Abstract
:1. Introduction
2. Definition of Variable Stiffness Laminates
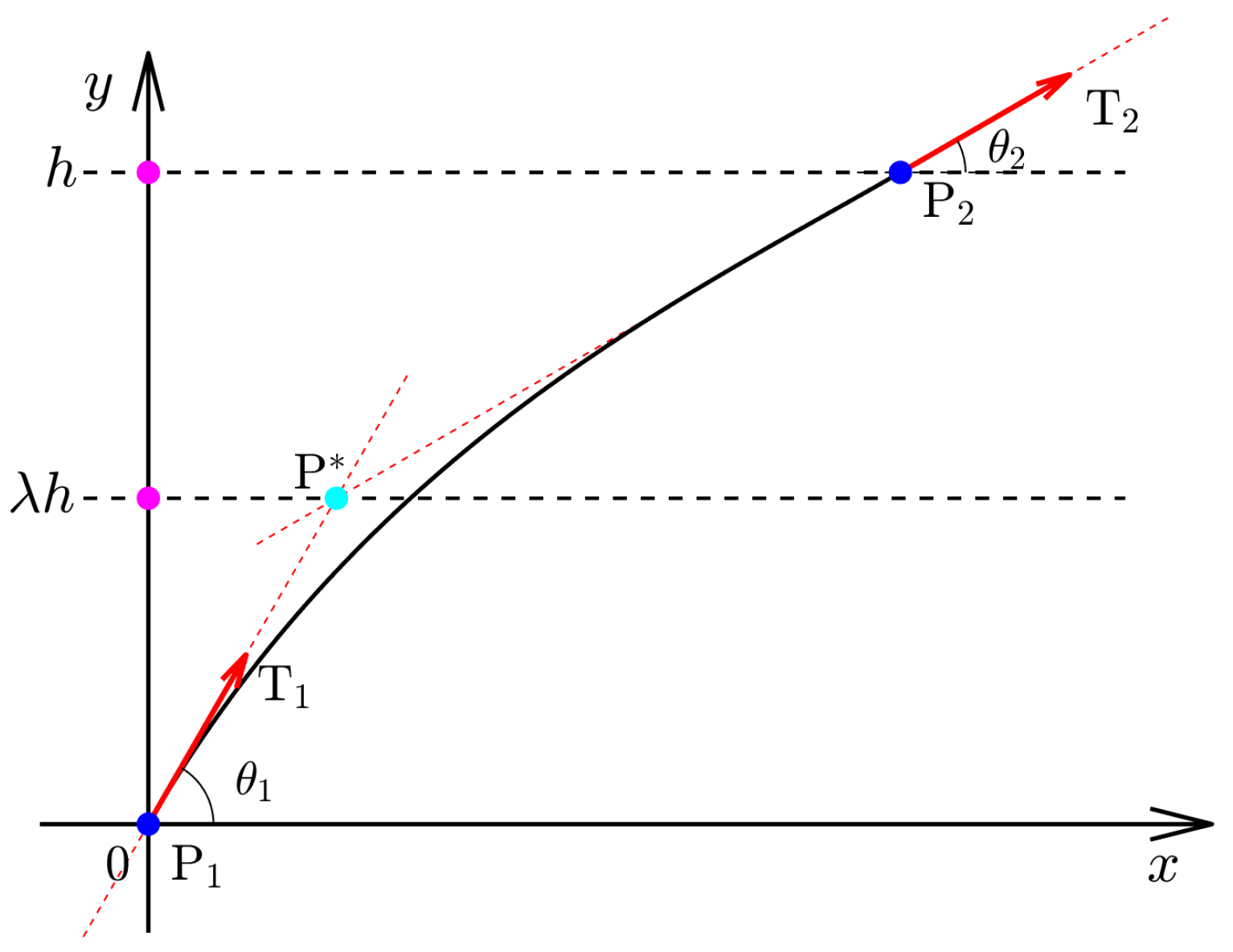
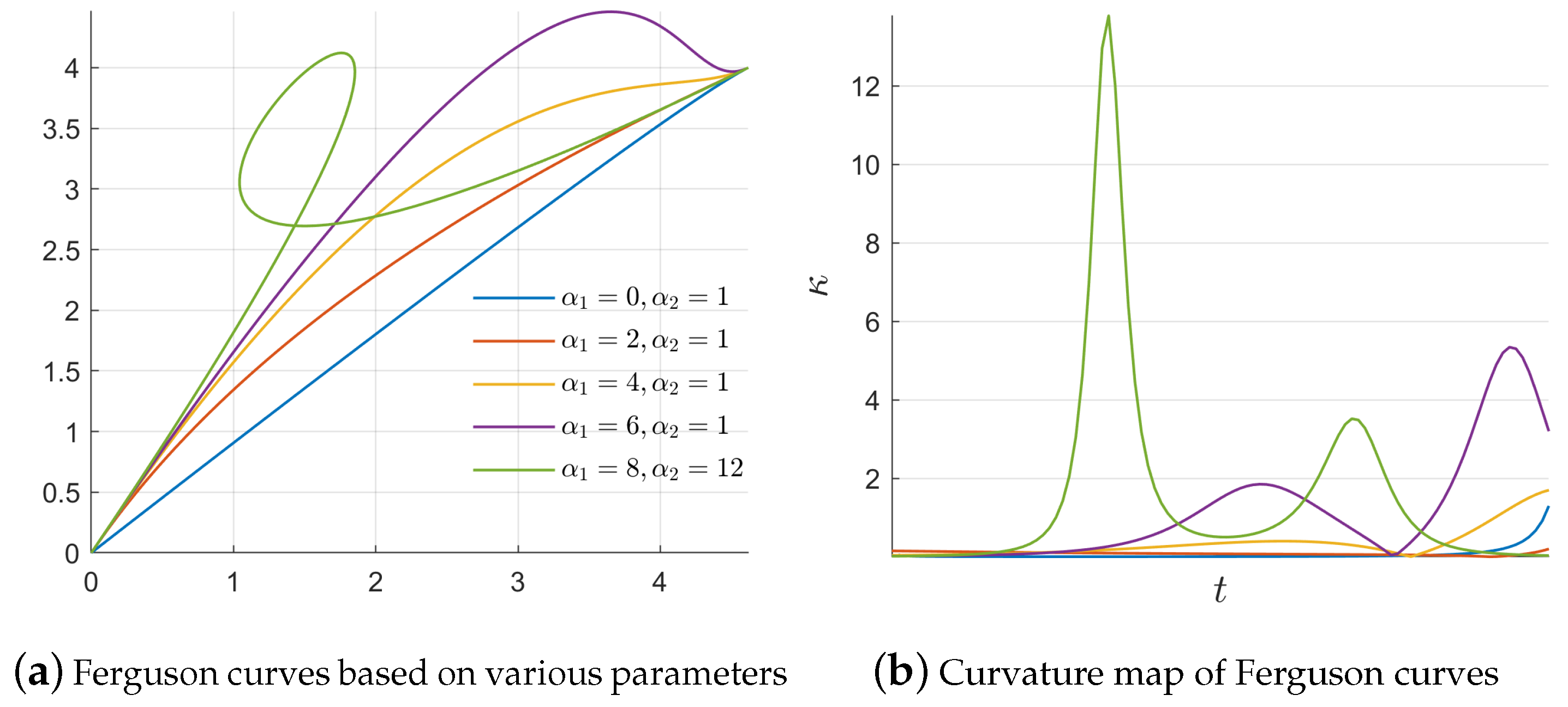
2.1. Cubic Ferguson Curve
2.2. Local Adjustable Property
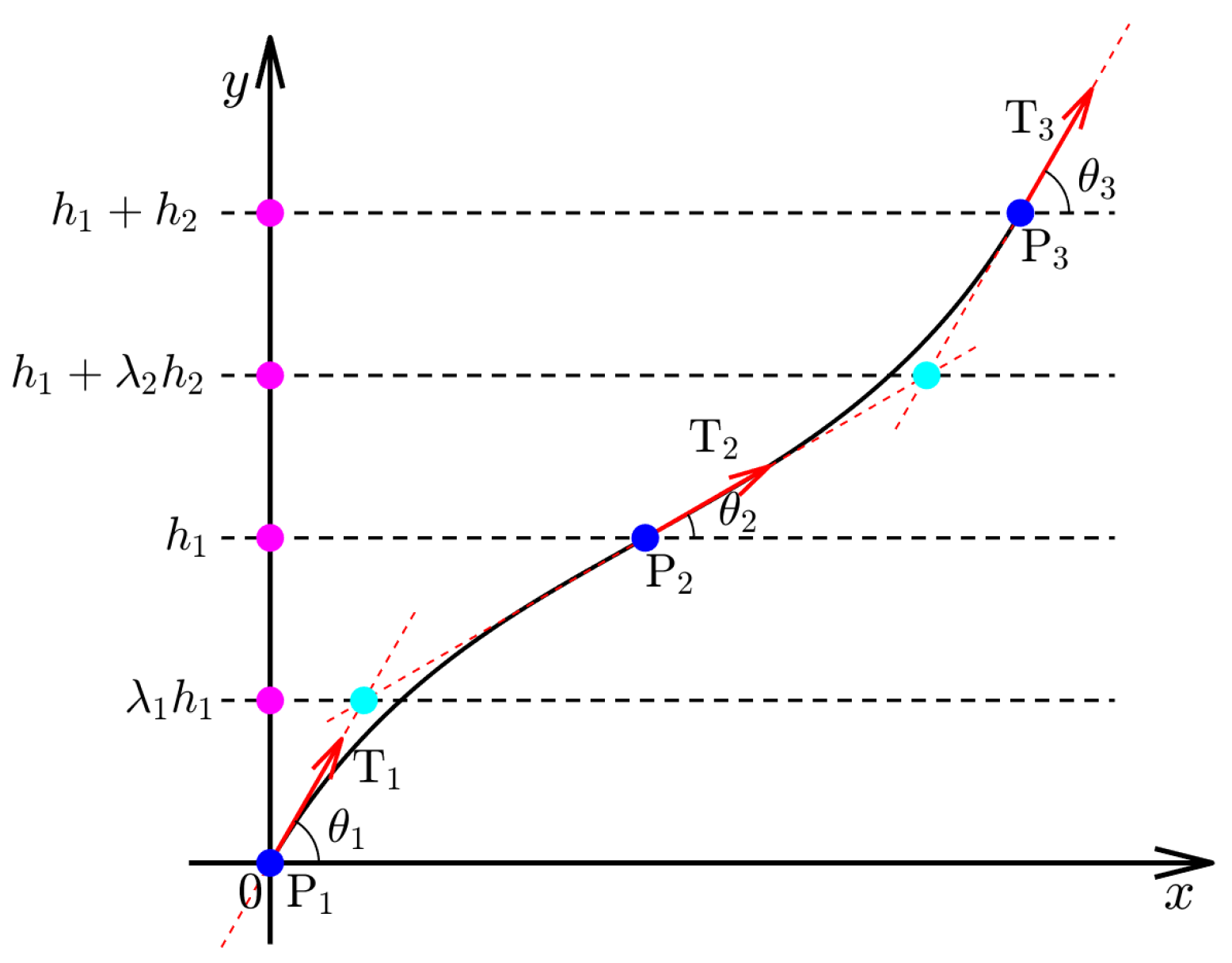
2.3. Connection of AFP Trajectories
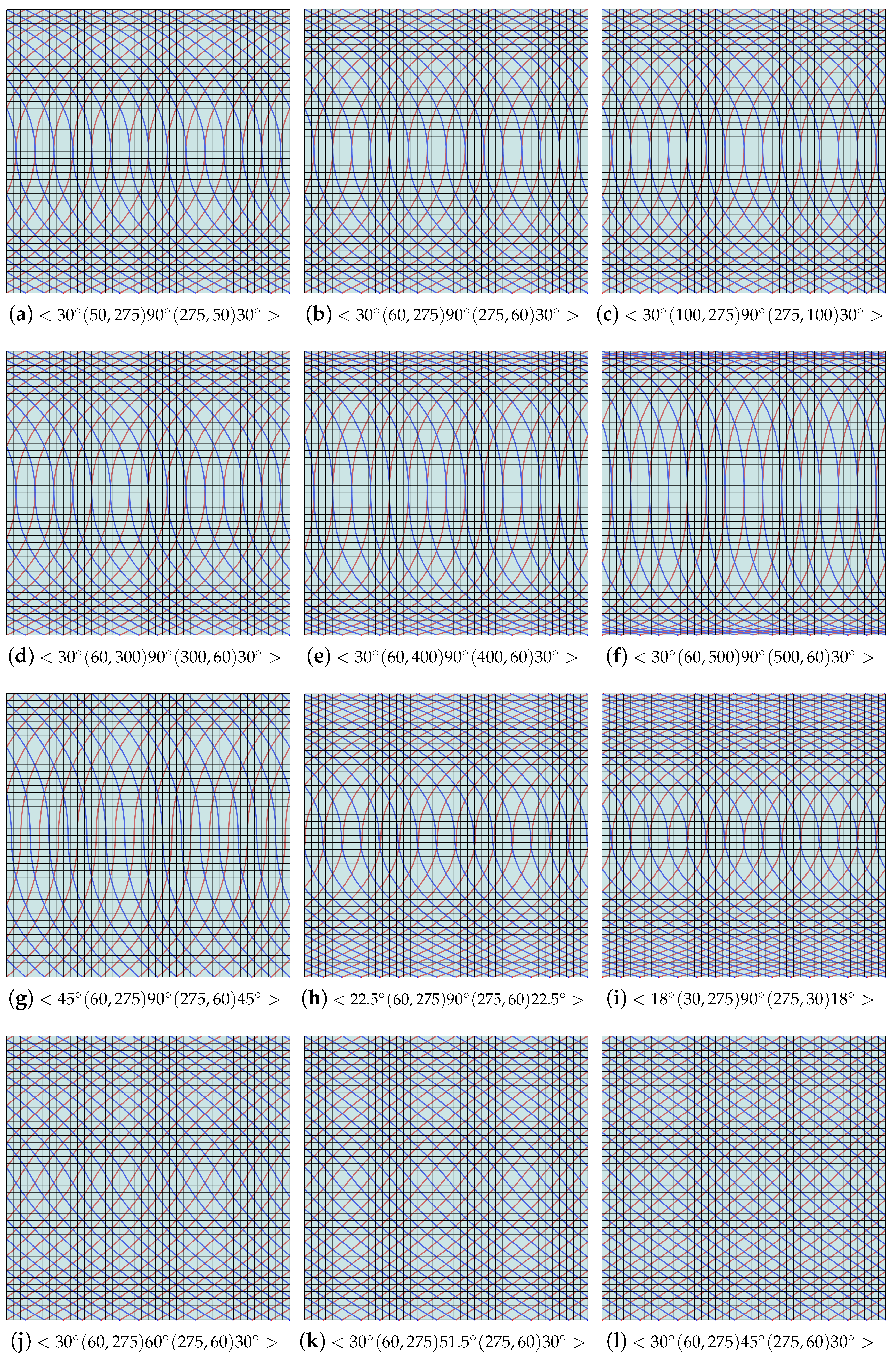
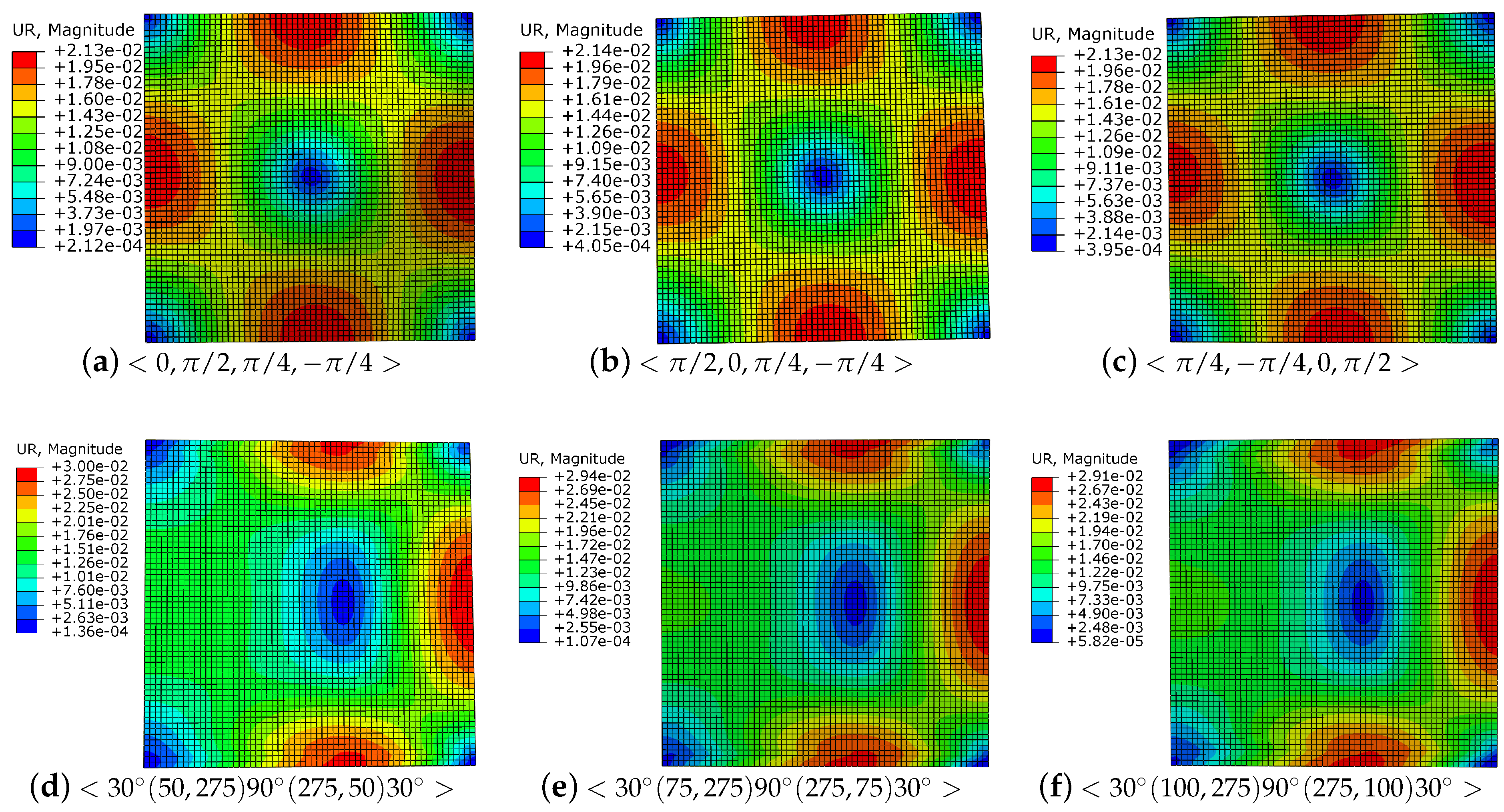
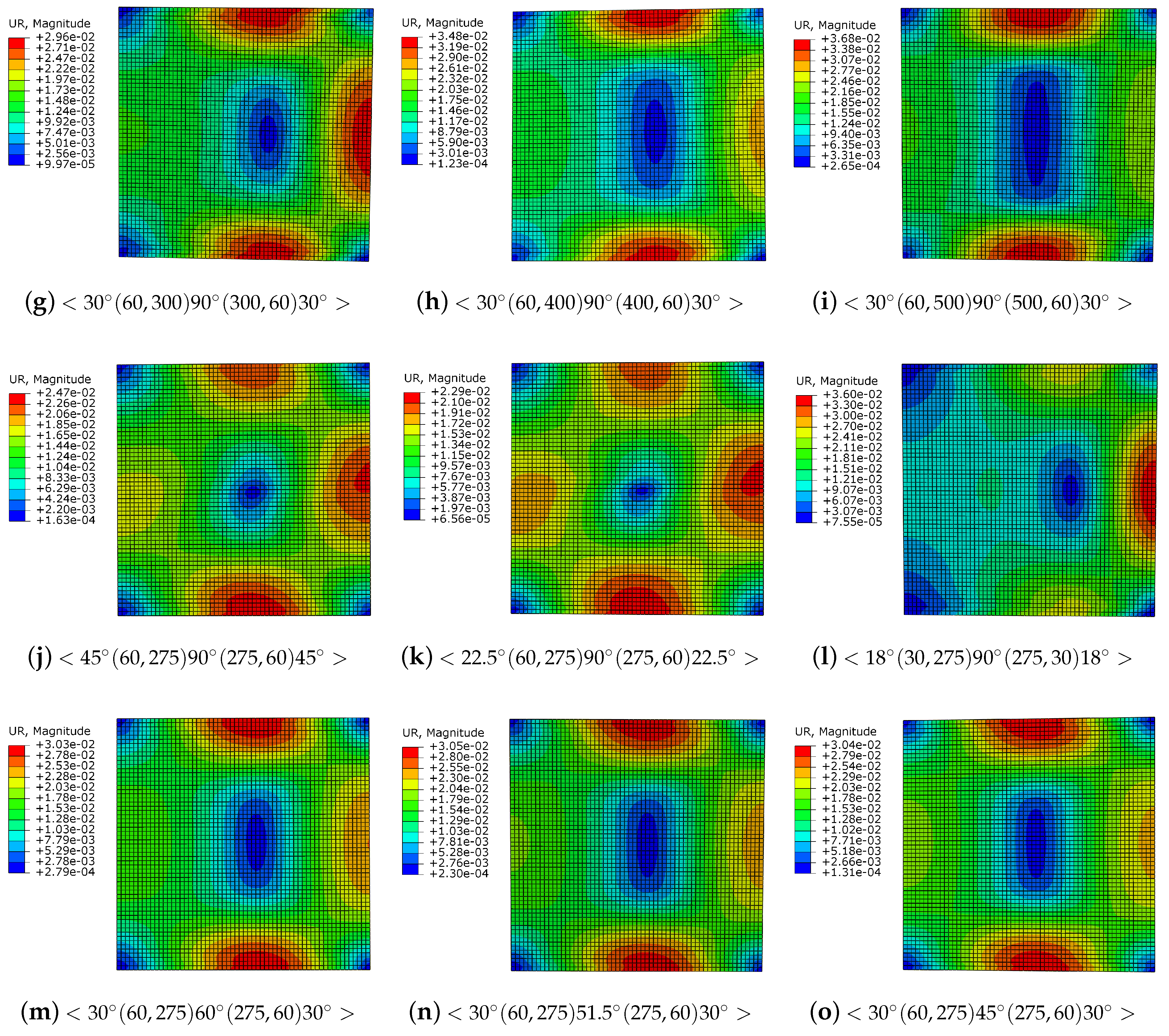
3. Analyses and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akbarzadeh, A.; Arian Nik, M.; Pasini, D. The role of shear deformation in laminated plates with curvilinear fiber paths and embedded defects. Compos. Struct. 2014, 118, 217–227. [Google Scholar] [CrossRef]
- Wang, X.; An, L.; Zhang, L.; Zhou, L. Uniform Coverage of Fibres over Open-contoured Freeform Structure Based on Arc-length Parameter. Chin. J. Aeronaut. 2008, 21, 571–577. [Google Scholar]
- Zhang, L.; Wang, X.; Pei, J.; Nian, C. Adaptive Path Planning of Fiber Placement Based on Improved Method of Mesh Dynamic Representation. Appl. Compos. Mater. 2019, 26, 785–803. [Google Scholar] [CrossRef]
- Shirinzadeh, B.; Foong, C.W.; Tan, B.H. Robotic fibre placement process planning and control. Assem. Autom. 2000, 20, 313–320. [Google Scholar] [CrossRef]
- Shirinzadeh, B.; Alici, G.; Foong, C.W.; Cassidy, G. Fabrication process of open surfaces by robotic fibre placement. Robot. Comput.-Integr. Manuf. 2004, 20, 17–28. [Google Scholar] [CrossRef]
- Shirinzadeh, B.; Cassidy, G.; Oetomo, D.; Alici, G.; Ang, M.H., Jr. Trajectory generation for open-contoured structures in robotic fibre placement. Robot. Comput.-Integr. Manuf. 2007, 23, 380–394. [Google Scholar] [CrossRef]
- Wang, K.; Wang, X.; Gan, J.; Jiang, S. A general method of trajectory generation based on point-cloud structures in automatic fibre placement. Compos. Struct. 2023, 314, 116976. [Google Scholar] [CrossRef]
- Gürdal, Z.; Tatting, B.; Wu, C. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response. Compos. Part A Appl. Sci. Manuf. 2008, 39, 911–922. [Google Scholar] [CrossRef]
- Falcó, O.; Mayugo, J.; Lopes, C.; Gascons, N.; Turon, A.; Costa, J. Variable-stiffness composite panels: As-manufactured modeling and its influence on the failure behavior. Compos. Part B Eng. 2014, 56, 660–669. [Google Scholar] [CrossRef]
- Khani, A.; IJsselmuiden, S.; Abdalla, M.; Gürdal, Z. Design of variable stiffness panels for maximum strength using lamination parameters. Compos. Part B Eng. 2011, 42, 546–552. [Google Scholar] [CrossRef]
- Hyer, M.; Lee, H. The use of curvilinear fiber format to improve buckling resistance of composite plates with central circular holes. Compos. Struct. 1991, 18, 239–261. [Google Scholar] [CrossRef]
- Biggers, S.; Srinivasan, S. Compression Buckling Response of Tailored Rectangular Composite Plates. AIAA J. 1993, 31. [Google Scholar] [CrossRef]
- Olmedo, R.; Gurdal, Z. Buckling Response of Laminates with Spatially Varying Fiber Orientations. In Proceedings of the 34th Structures, Structural Dynamics and Materials Conference, La Jolla, CA, USA, 19–22 April 1993. [Google Scholar]
- Jegley, D.; Tatting, B.; Gurdal, Z. Tow-Steered Panels with Holes Subjected to Compression or Shear Loading. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005. [Google Scholar]
- Sun, M.; Hyer, M.W. Use of Material Tailoring to Improve Buckling Capacity of Elliptical Composite Cylinders. AIAA J. 2008, 46, 770–782. [Google Scholar] [CrossRef]
- Abdalla, M.M.; Setoodeh, S.; Gürdal, Z. Design of variable stiffness composite panels for maximum fundamental frequency using lamination parameters. Compos. Struct. 2007, 81, 283–291. [Google Scholar] [CrossRef]
- Cho, H.; Rowlands, R. Optimizing Fiber Direction in Perforated Orthotropic Media to Reduce Stress Concentration. J. Compos. Mater. 2009, 43, 1177–1198. [Google Scholar] [CrossRef]
- Bruyneel, M. A general and effective approach for the optimal design of fiber reinforced composite structures. Compos. Sci. Technol. 2006, 66, 1303–1314. [Google Scholar] [CrossRef]
- Setoodeh, S.; Abdalla, M.M.; Gürdal, Z. Design of variable–stiffness laminates using lamination parameters. Compos. Part B Eng. 2006, 37, 301–309. [Google Scholar] [CrossRef]
- Blom, A.W.; Setoodeh, S.; Hol, J.M.; Gürdal, Z. Design of variable-stiffness conical shells for maximum fundamental eigenfrequency. Comput. Struct. 2008, 86, 870–878. [Google Scholar] [CrossRef]
- Blom, A.W.; Tatting, B.F.; Hol, J.M.; Gürdal, Z. Fiber path definitions for elastically tailored conical shells. Compos. Part B Eng. 2009, 40, 77–84. [Google Scholar] [CrossRef]
- Fayazbakhsh, K.; Arian Nik, M.; Pasini, D.; Lessard, L. Defect layer method to capture effect of gaps and overlaps in variable stiffness laminates made by Automated Fiber Placement. Compos. Struct. 2013, 97, 245–251. [Google Scholar] [CrossRef]
- Arian Nik, M.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Optimization of variable stiffness composites with embedded defects induced by Automated Fiber Placement. Compos. Struct. 2014, 107, 160–166. [Google Scholar] [CrossRef]
- Rouhi, M.; Ghayoor, H.; Fortin-Simpson, J.; Zacchia, T.T.; Hoa, S.V.; Hojjati, M. Design, manufacturing, and testing of a variable stiffness composite cylinder. Compos. Struct. 2018, 184, 146–152. [Google Scholar] [CrossRef]
- Alhajahmad, A.; Abdalla, M.M.; Gürdal, Z. Design Tailoring for Pressure Pillowing Using Tow-Placed Steered Fibers. J. Aircr. 2008, 45, 630–640. [Google Scholar] [CrossRef]
- Wu, Z.; Weaver, P.M.; Raju, G.; Chul Kim, B. Buckling analysis and optimisation of variable angle tow composite plates. Thin-Walled Struct. 2012, 60, 163–172. [Google Scholar] [CrossRef]
- Kim, B.C.; Potter, K.; Weaver, P.M. Continuous tow shearing for manufacturing variable angle tow composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1347–1356. [Google Scholar] [CrossRef]
- Niu, X.; Liu, Y.; Wu, J.; Yang, T. Curvature-controlled trajectory planning for variable stiffness composite laminates. Compos. Struct. 2020, 238, 111986. [Google Scholar] [CrossRef]
- Hao, P.; Liu, C.; Liu, X.; Yuan, X.; Wang, B.; Li, G.; Dong, M.; Chen, L. Isogeometric analysis and design of variable-stiffness aircraft panels with multiple cutouts by level set method. Compos. Struct. 2018, 206, 888–902. [Google Scholar] [CrossRef]
- Mori, Y.; Matsuzaki, R.; Kumekawa, N. Variable thickness design for composite materials using curvilinear fiber paths. Compos. Struct. 2021, 263, 113723. [Google Scholar] [CrossRef]
- Qu, W.; Pan, H.; Yang, D.; Li, J.; Ke, Y. As-built FE thermal analysis for complex curved structures in automated fiber placement. Simul. Model. Pract. Theory 2022, 118, 102561. [Google Scholar] [CrossRef]
- Wehbe, R.; Tatting, B.; Rajan, S.; Harik, R.; Sutton, M.; Gürdal, Z. Geometrical modeling of tow wrinkles in automated fiber placement. Compos. Struct. 2020, 246, 112394. [Google Scholar] [CrossRef]
- Zhu, Y.; Qin, Y.; Qi, S.; Xu, H.; Liu, D.; Yan, C. Variable Angle Tow reinforcement design for locally reinforcing an open-hole composite plate. Compos. Struct. 2018, 202, 162–169. [Google Scholar] [CrossRef]
- Shi, F. Computer Aided Geometry Design and Non Uniform Rational B Spline, 2nd ed.; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 1994. [Google Scholar]
- Wang, X.; Meng, Y.; Wang, Z.; Zhang, L. Constructing up to G2 continuous curve on freeform surface. Vis. Comput. 2010, 26, 813–822. [Google Scholar] [CrossRef]




| 120.45 | 9.51 | 5.10 | 5.10 | 3.63 | 0.32 |
| Laminate Types | Parameter Settings/ | Eigenvalues | Buckling Load/N | Maximum Curvature |
|---|---|---|---|---|
| Constant | > | 8.1055 | 1215.8 | 0 |
| <> | 8.0545 | 1208.2 | 0 | |
| <> | 8.0545 | 1208.2 | 0 | |
| <> | 8.1055 | 1215.8 | 0 | |
| <> | 7.6601 | 1149.0 | 0 | |
| <> | 7.6601 | 1149.0 | 0 | |
| <> | 7.2466 | 1087.0 | 0 | |
| <> | 7.2466 | 1087.0 | 0 | |
| <> | 6.4266 | 963.9 | 0 | |
| <> | 8.1781 | 1226.7 | 0 | |
| <> | 6.4266 | 963.9 | 0 | |
| <> | 8.1781 | 1226.7 | 0 | |
| Variable | <> | 10.563 | 1584.5 | 0.0344 |
| <> | 10.452 | 1567.8 | 0.0269 | |
| <> | 10.297 | 1544.6 | 0.0194 | |
| <> | 10.088 | 1513.2 | 0.0174 | |
| <> | 9.8124 | 1471.9 | 0.0171 | |
| <> | 10.435 | 1565.3 | 0.0422 | |
| <> | 9.6106 | 1441.3 | 0.1082 | |
| <> | 7.6440 | 1146.6 | 0.1819 | |
| <> | 9.1404 | 1371.1 | 0.0155 | |
| <> | 8.8989 | 1334.8 | 0.0103 | |
| <> | 8.6832 | 1302.5 | 0.0075 | |
| <> | 8.5022 | 1275.3 | 0.0078 | |
| <> | 9.9857 | 1497.9 | 0.0268 | |
| <> | 10.865 | 1628.8 | 0.0277 | |
| <> | 9.7859 | 1467.9 | 0.0253 | |
| <> | 9.1795 | 1376.9 | 0.0260 | |
| <> | 8.7090 | 1309.4 | 0.0260 | |
| <> | 8.3296 | 1249.4 | 0.0299 | |
| <> | 6.5797 | 1140.1 | 0.1644 | |
| <> | 7.6204 | 1143.1 | 0.1179 | |
| <> | 7.6121 | 1141.8 | 0.0911 | |
| <> | 7.6028 | 1140.4 | 0.0628 | |
| <> | 7.6111 | 1141.7 | 0.0345 | |
| <> | 7.6477 | 1147.2 | 0.0101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wang, K.; Wang, X. Design of Variable Stiffness Trajectories with Cubic Ferguson Curve. Materials 2023, 16, 6866. https://doi.org/10.3390/ma16216866
Zhang D, Wang K, Wang X. Design of Variable Stiffness Trajectories with Cubic Ferguson Curve. Materials. 2023; 16(21):6866. https://doi.org/10.3390/ma16216866
Chicago/Turabian StyleZhang, Deli, Kai Wang, and Xiaoping Wang. 2023. "Design of Variable Stiffness Trajectories with Cubic Ferguson Curve" Materials 16, no. 21: 6866. https://doi.org/10.3390/ma16216866





