Mechanical Properties and Cushioning Effectiveness of FPUF-EPS Combination Materials
Abstract
:1. Introduction
2. Materials and Methods
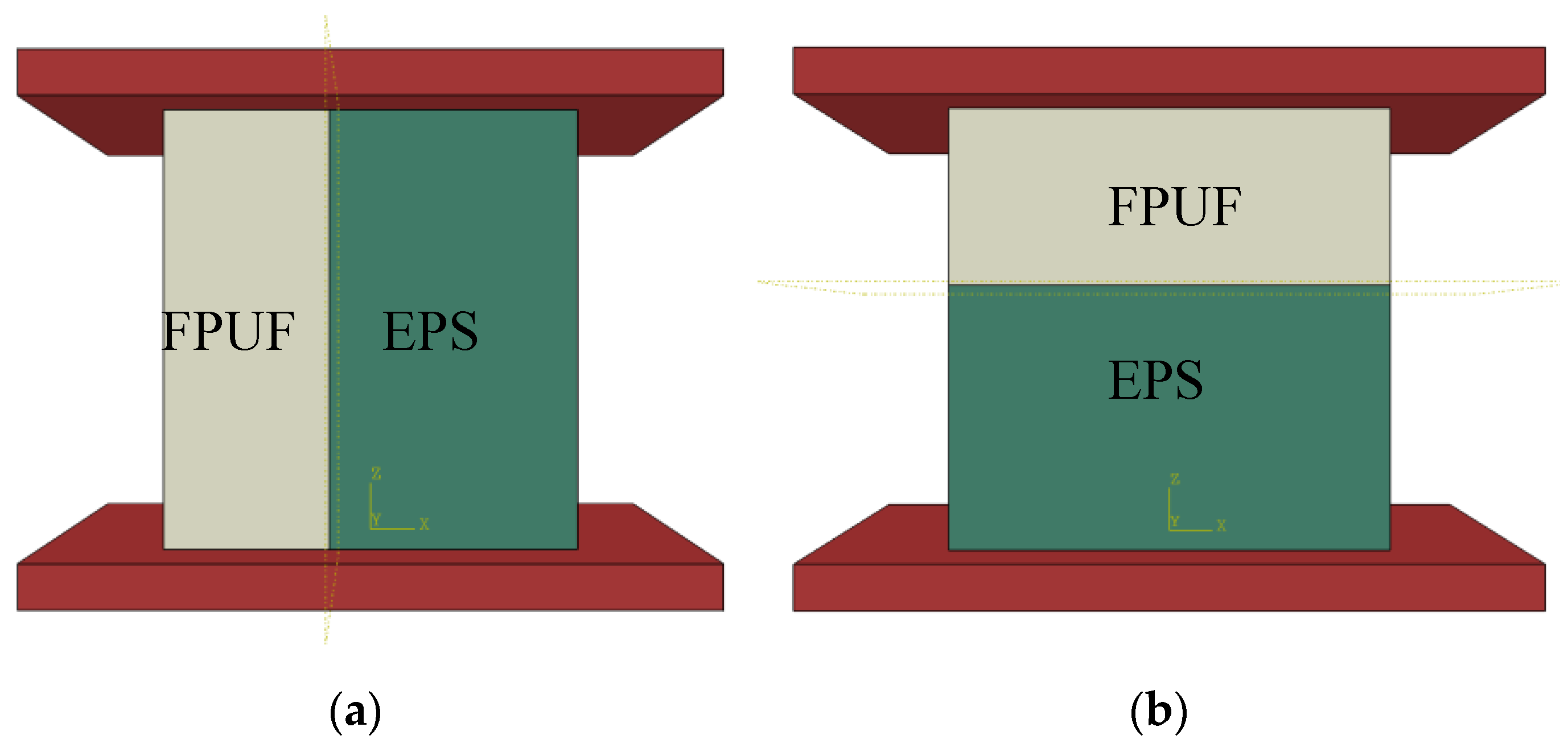
2.1. Model Analysis
2.2. Numerical Simulation
2.2.1. Finite Element Model
2.2.2. Material Model
2.2.3. Boundary Conditions
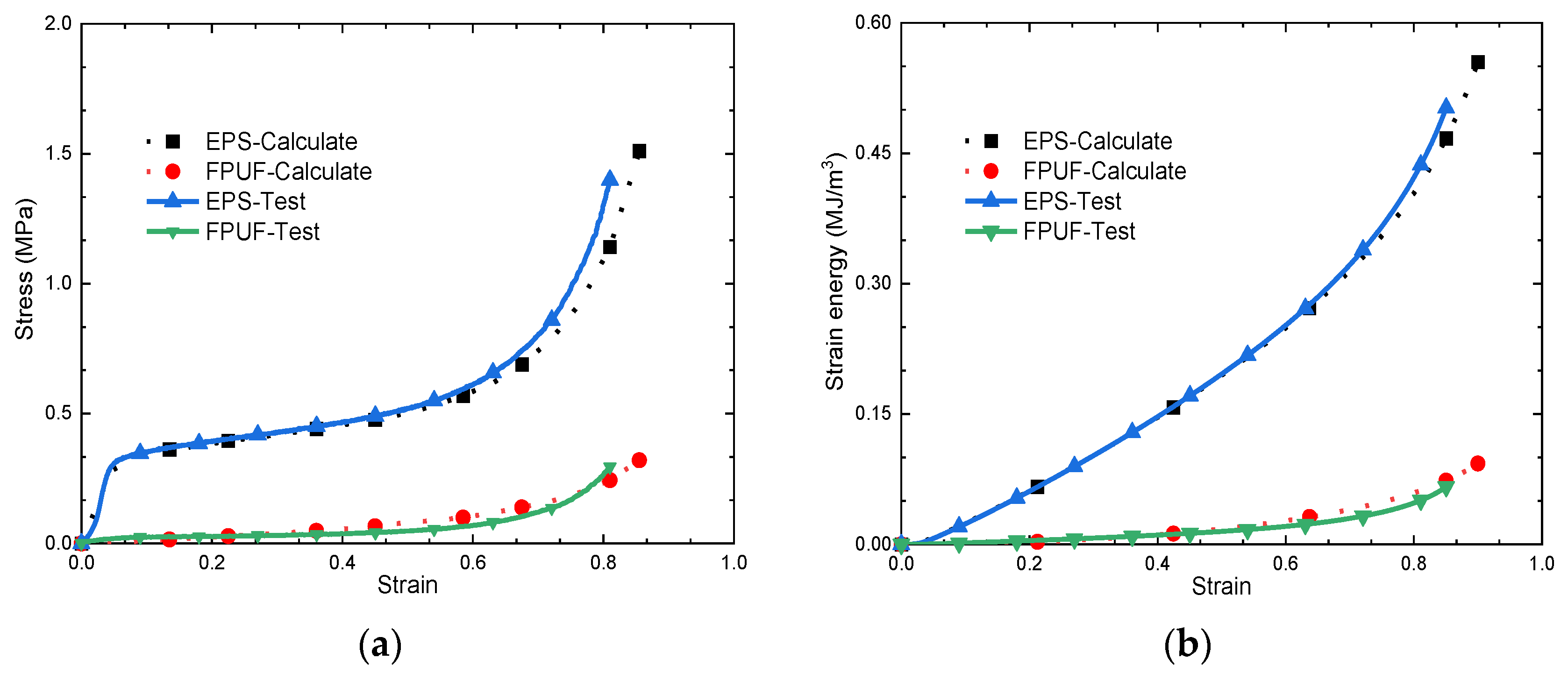
2.2.4. Model Validation
3. Cushioning Effectiveness of FPUF-EPS under Single Quasi-Static Compression Loading
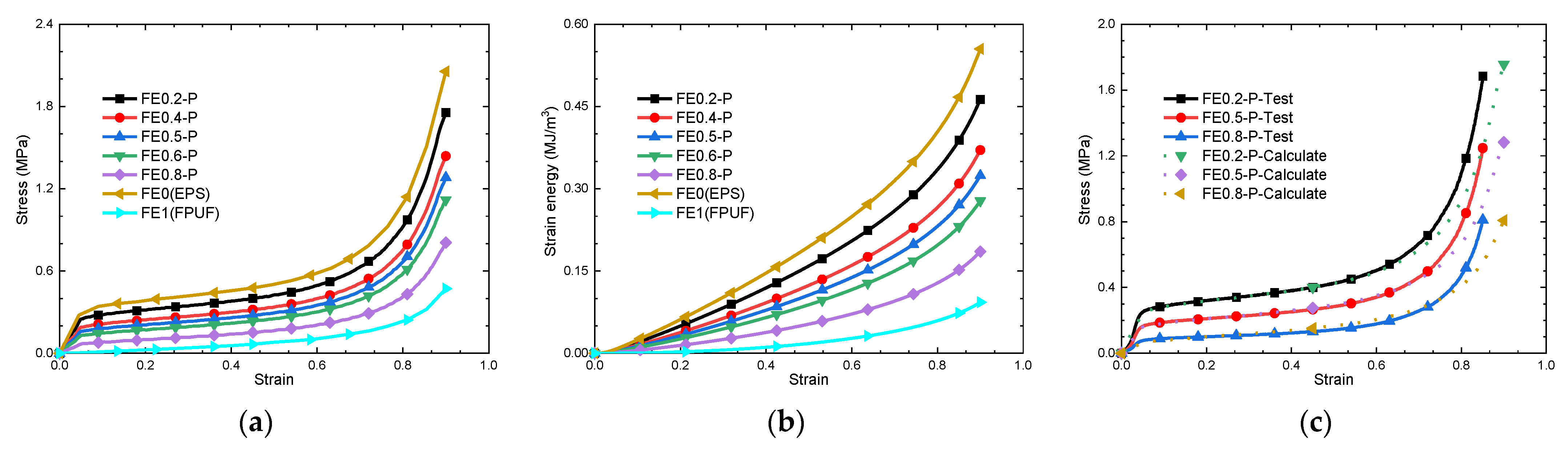
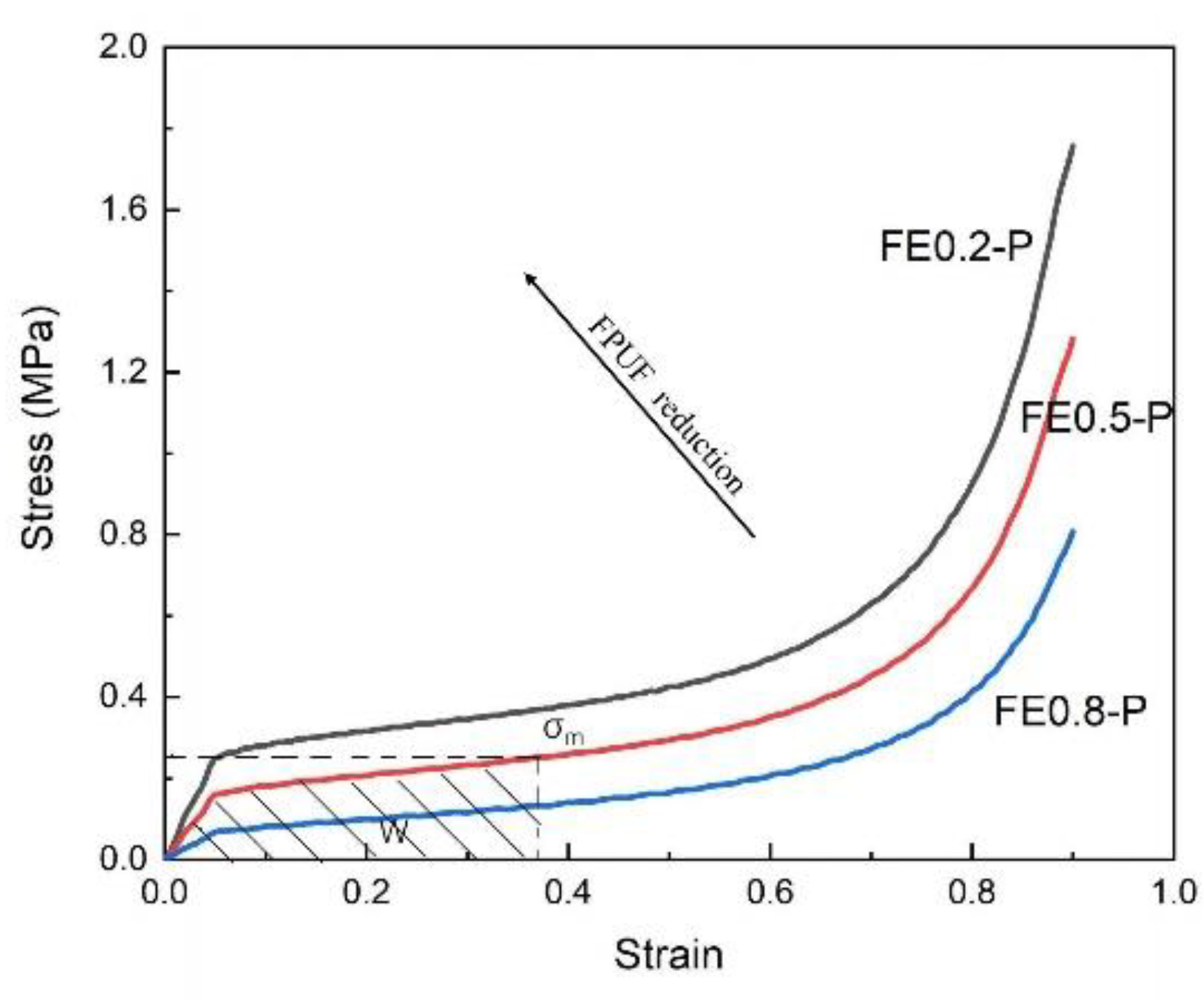
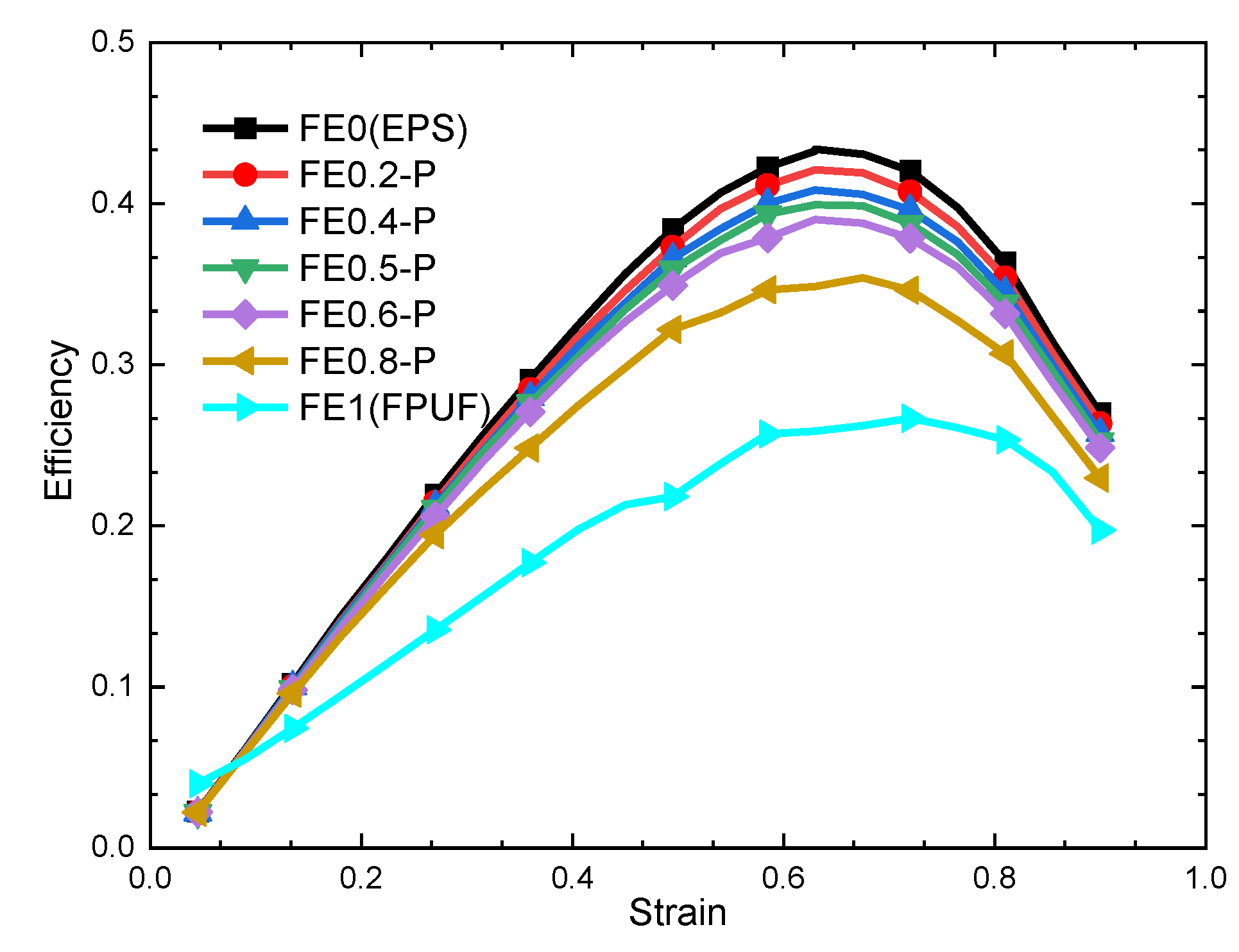
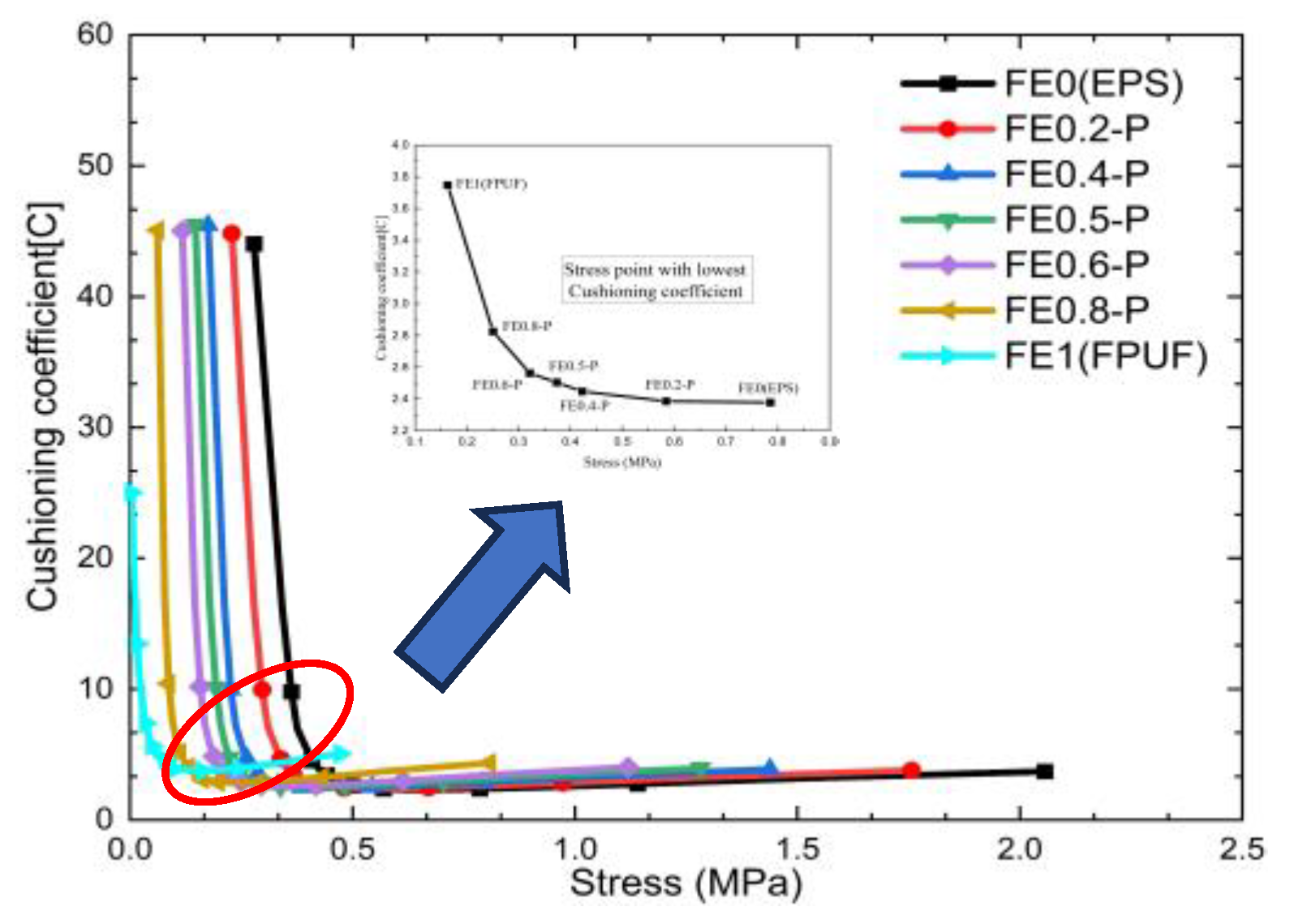
3.1. Cushioning Effectiveness of FE-P
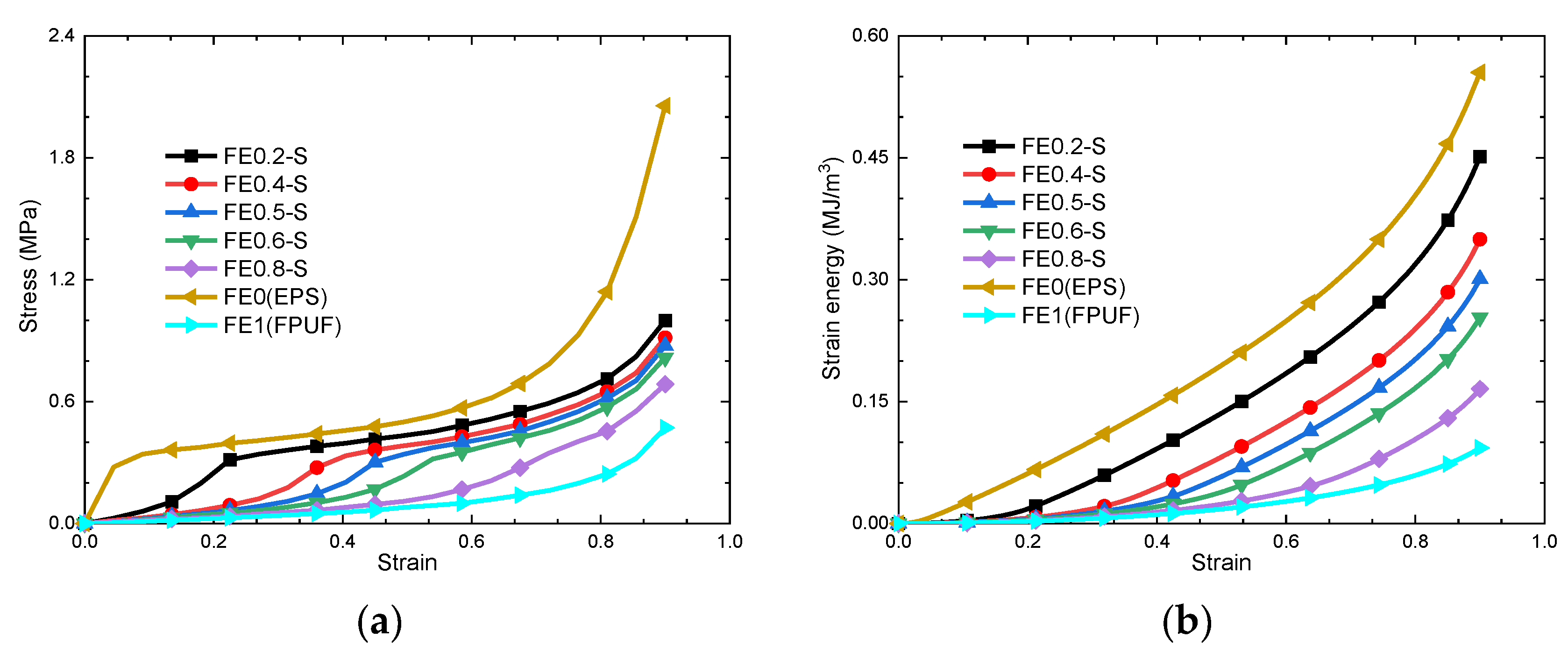
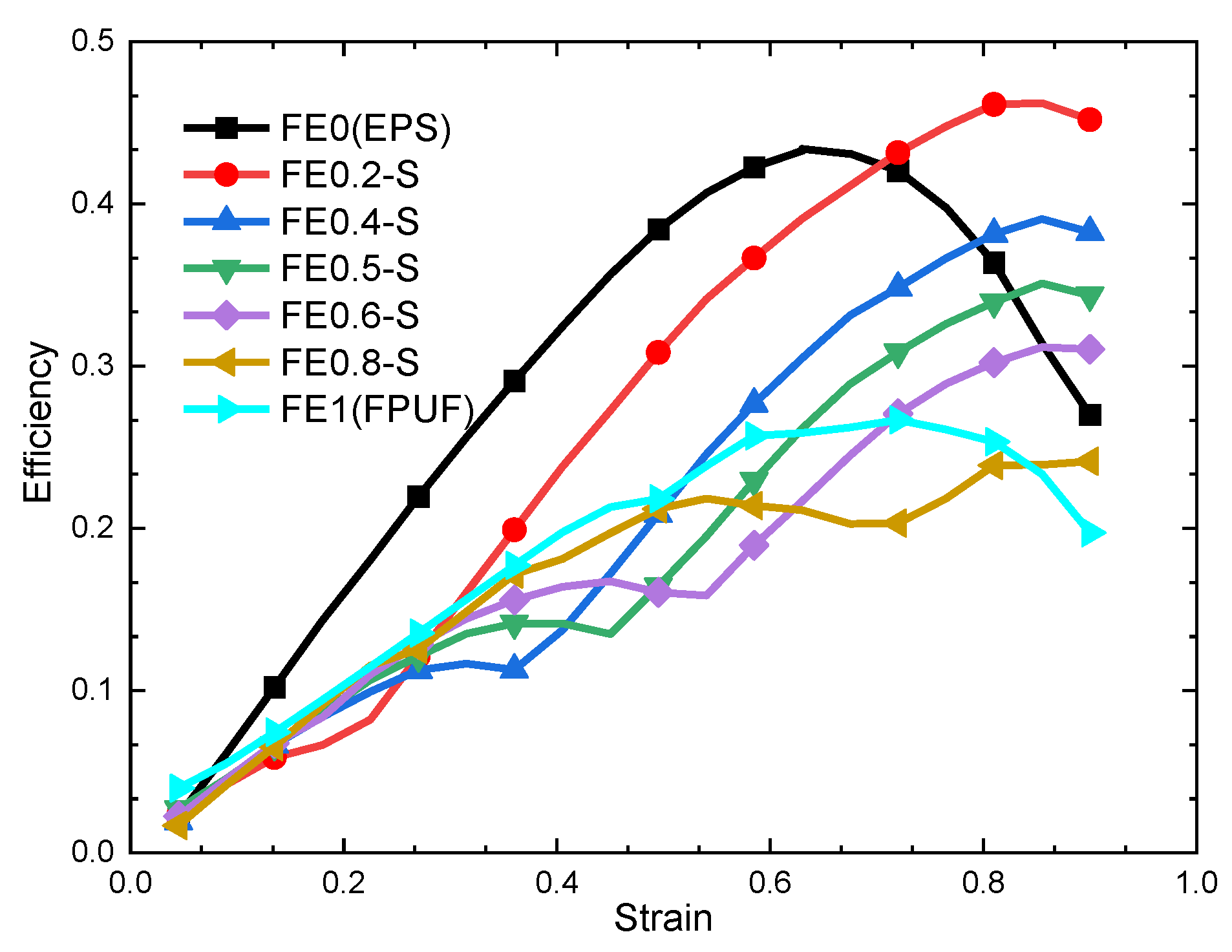
3.2. Cushioning Effectiveness of FE-S
4. Cushioning Effectiveness of FPUF-EPS under Single-Impact Loading
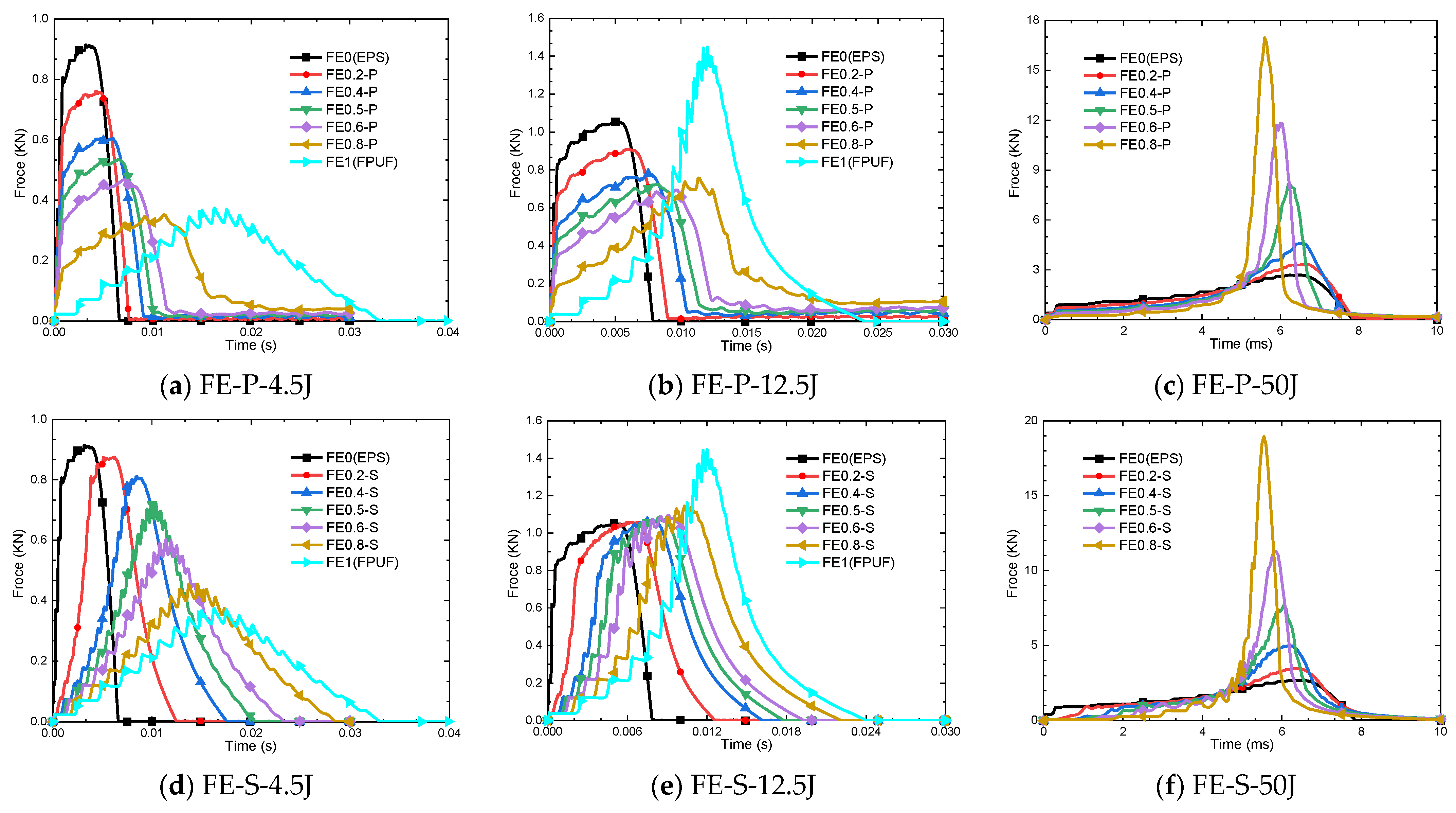
4.1. Force–Time Response Characteristics of FPUF-EPS
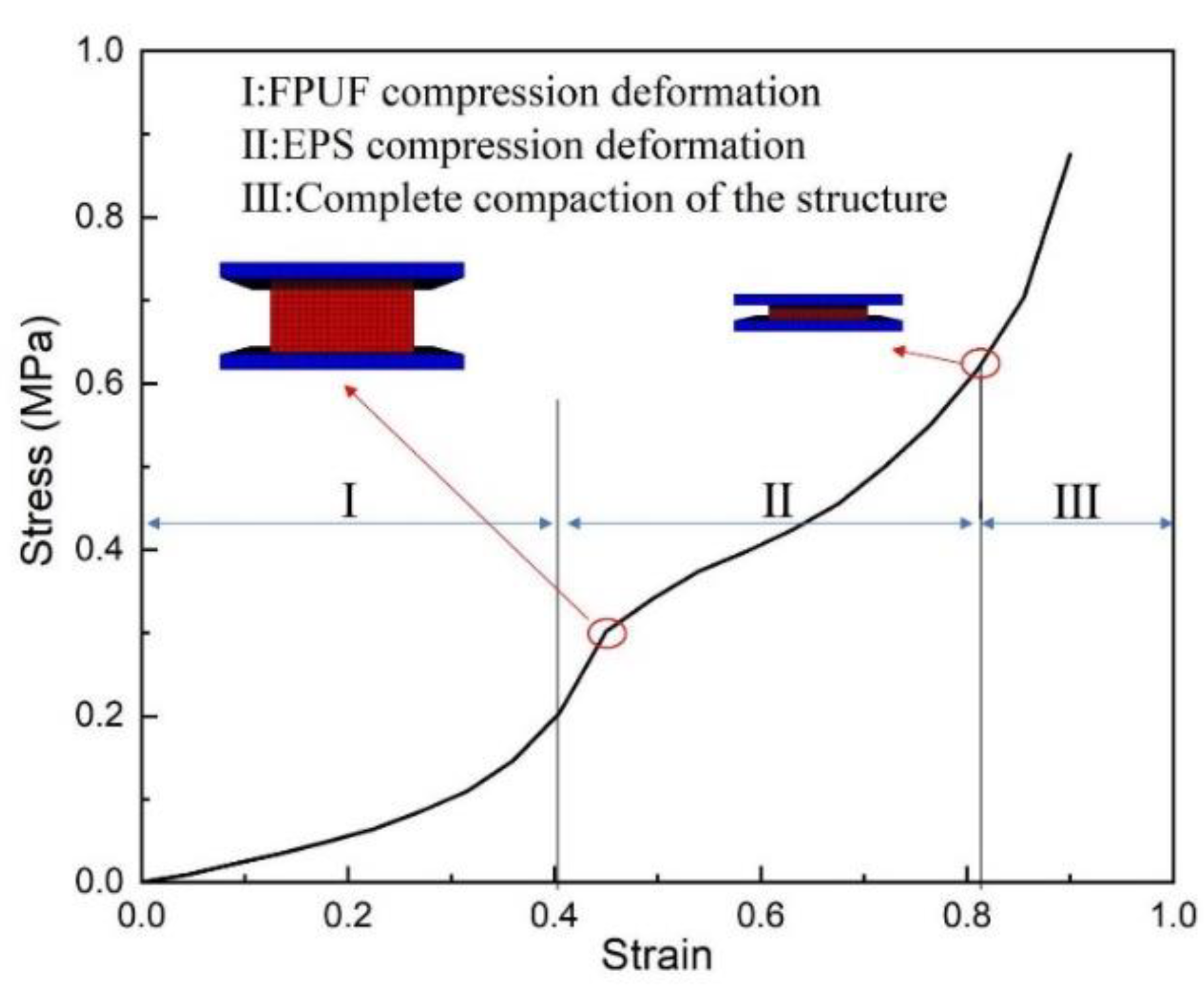
4.2. Mechanical Response Characteristics of FPUF-EPS
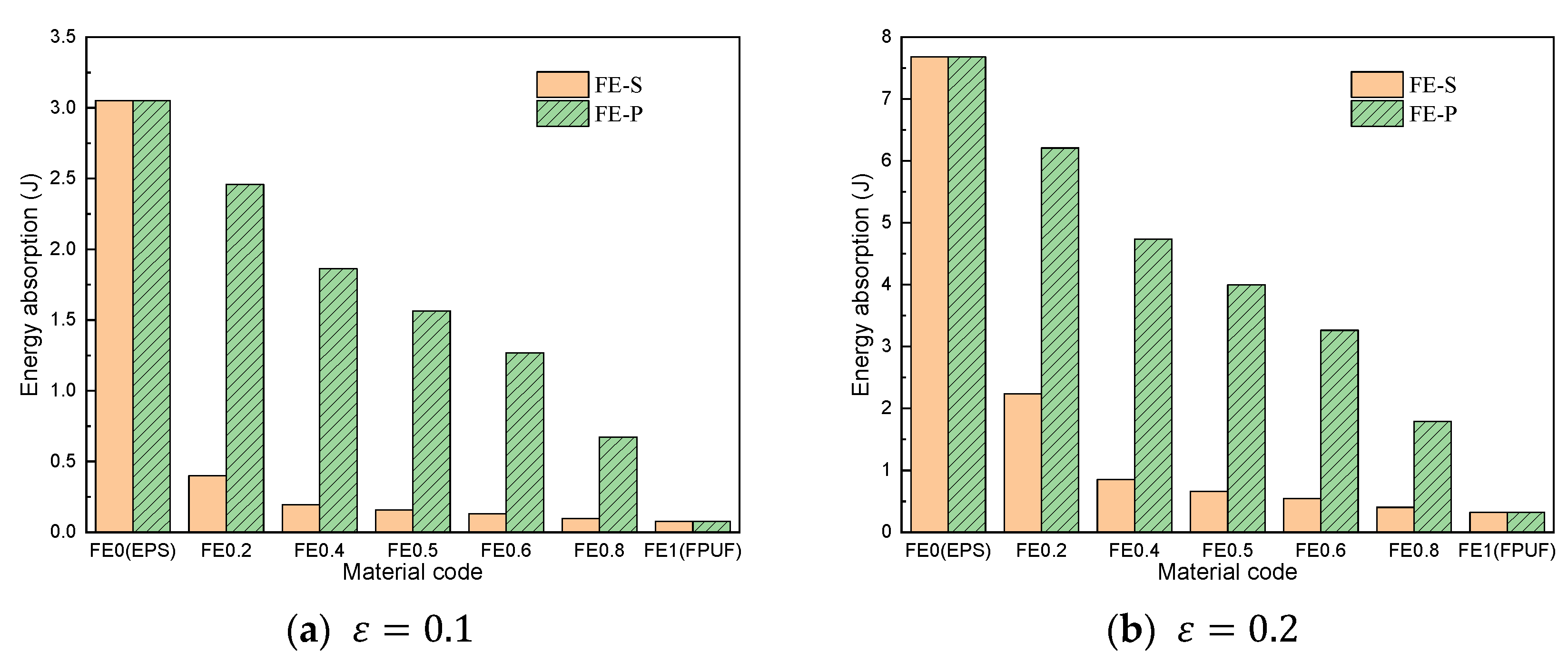
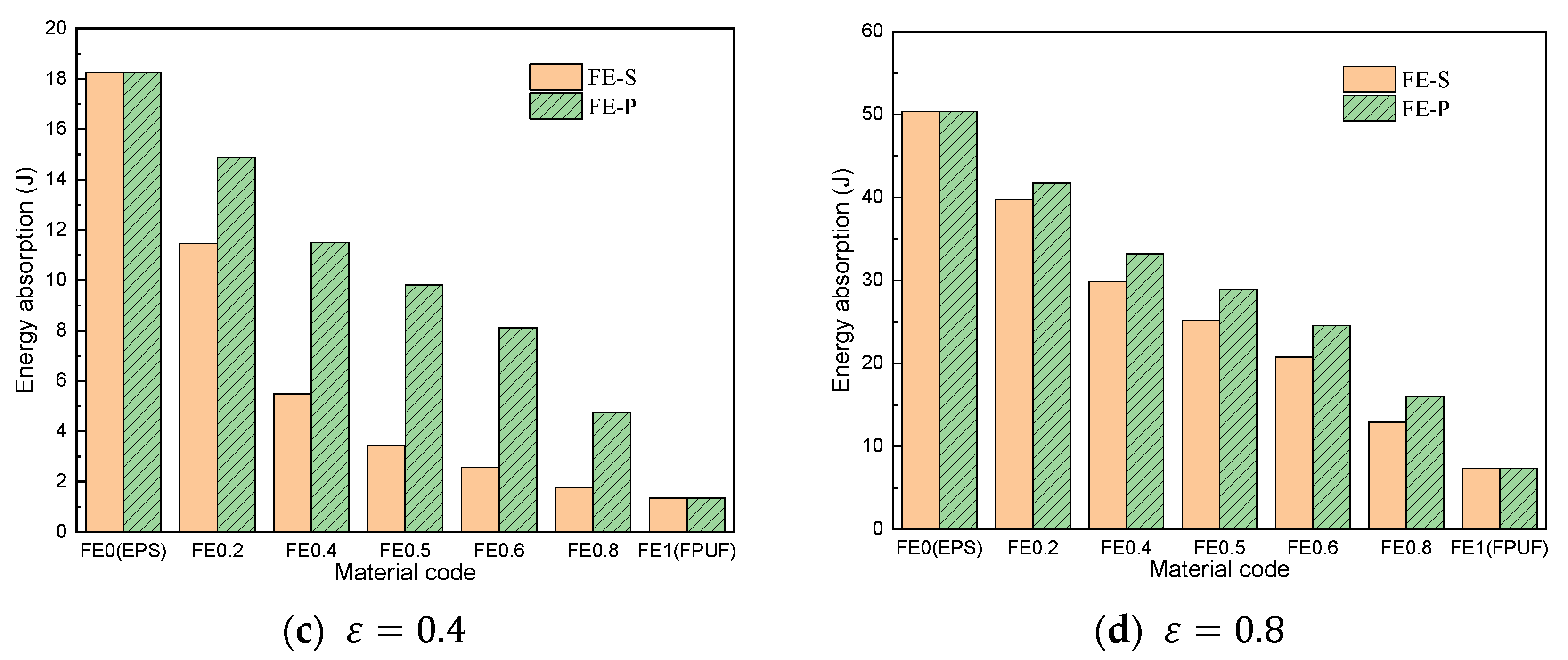
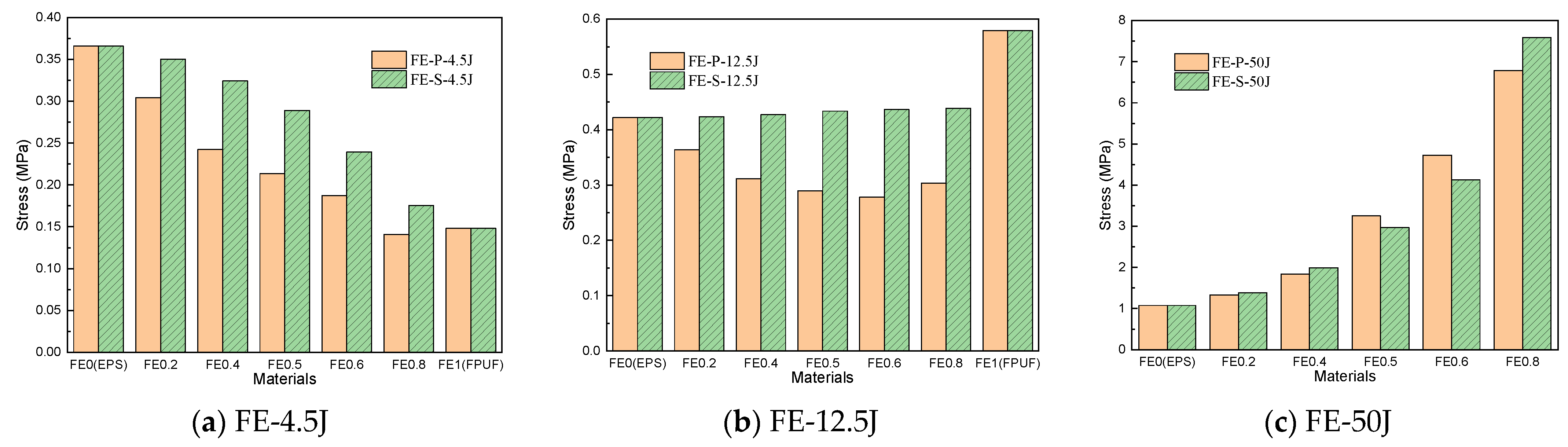
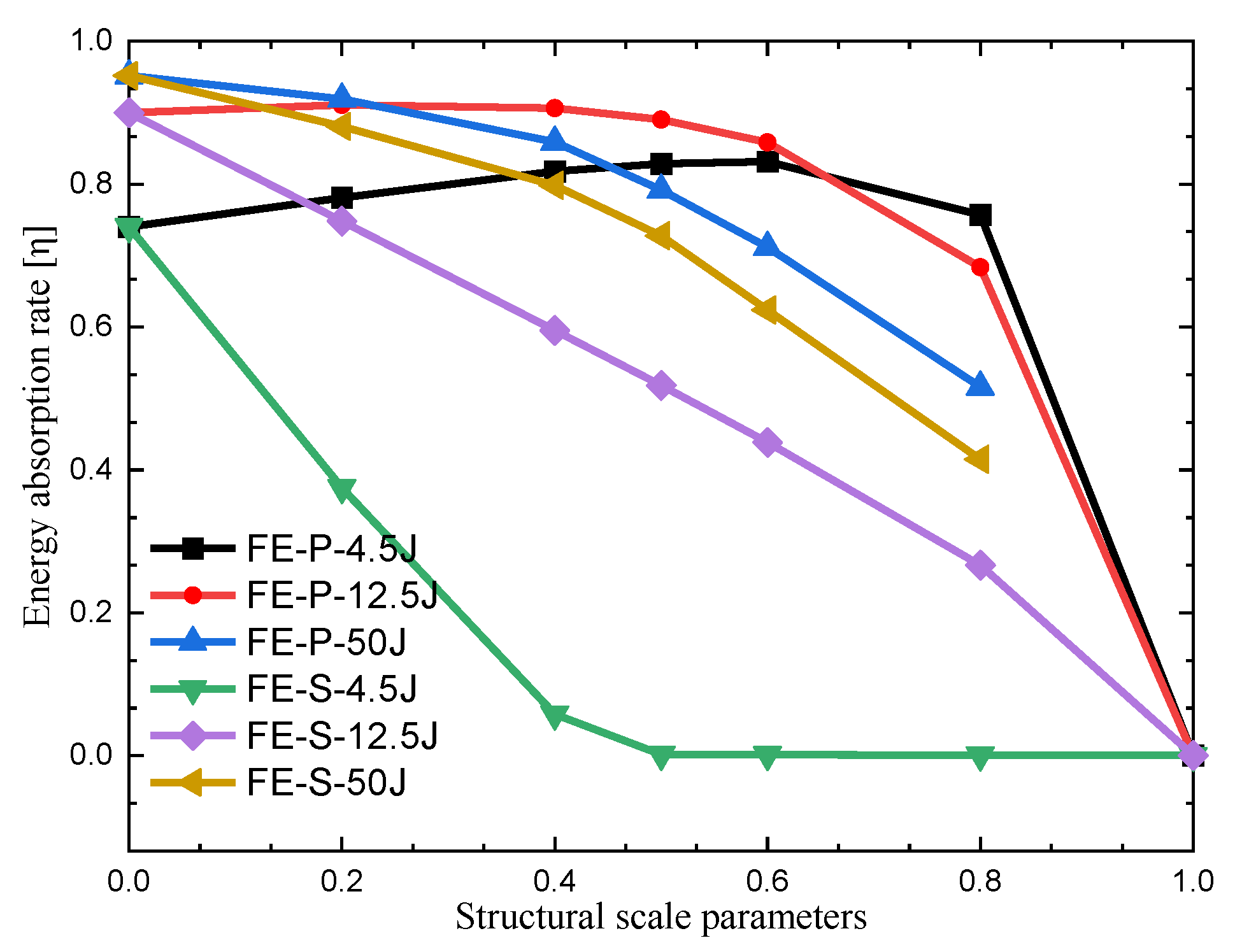
4.3. Energy Absorption and Influencing Factor of FPUF-EPS under Single-Impact Loading
5. Cushioning Effectiveness of FPUF-EPS under Multiple Compression Loadings
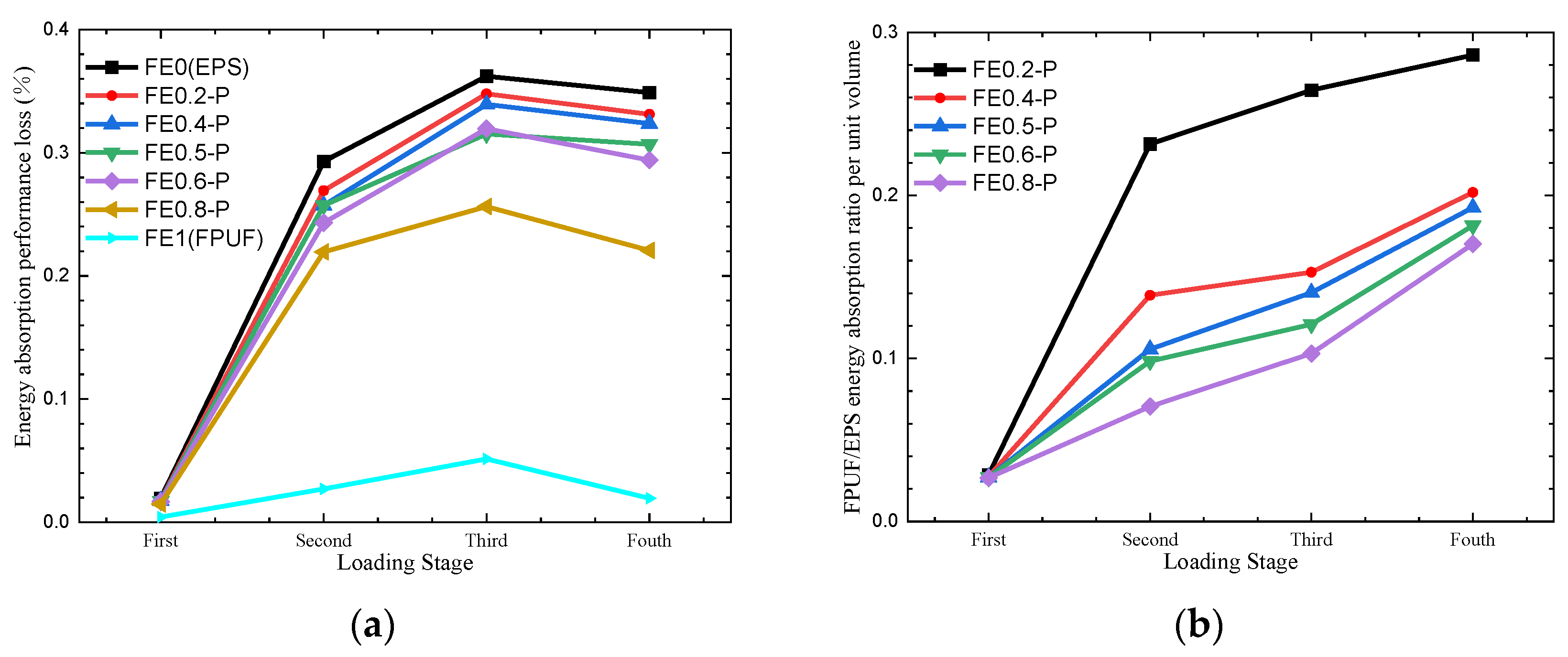
5.1. Cushioning Effectiveness of FE-P under Multiple Compression Loadings
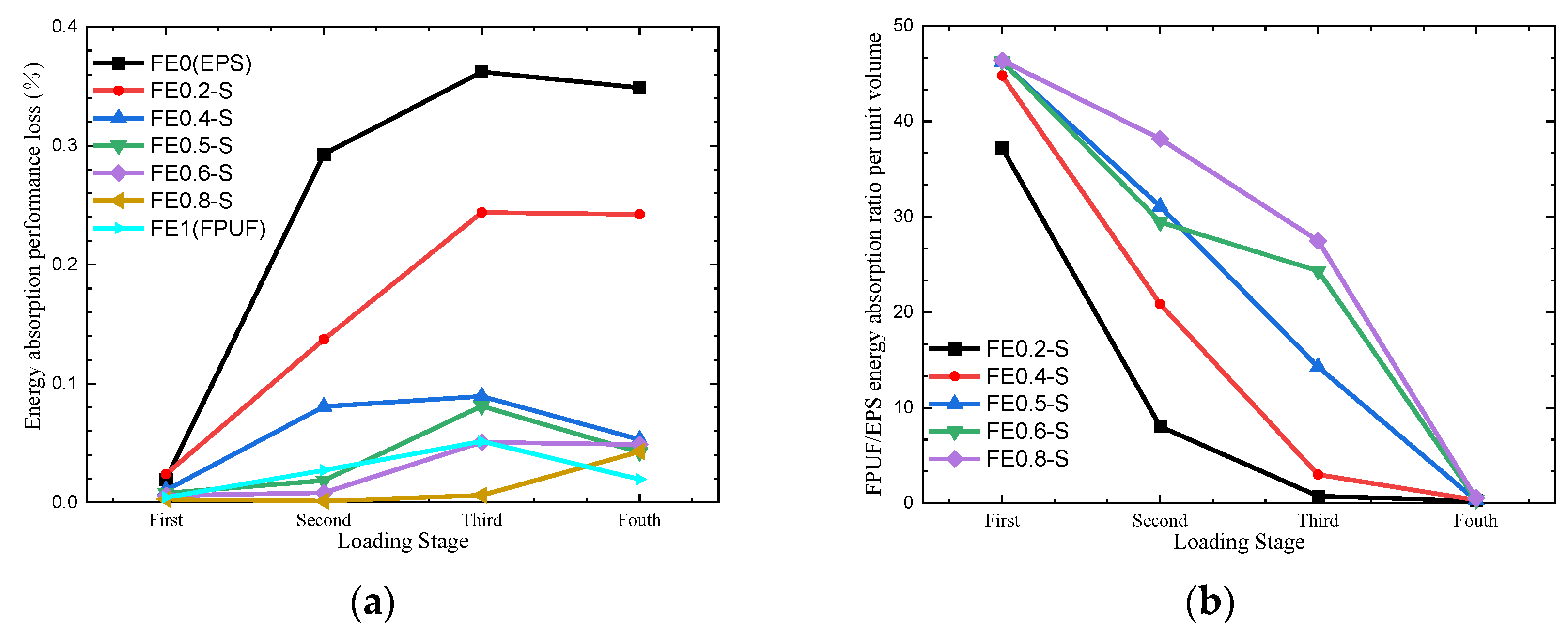
5.2. Cushioning Effectiveness of FE-S under Multiple Compression Loadings
6. Conclusions
- (1)
- The mechanical behavior and cushioning performance of FE-P and FE-S under single quasi-static compression loading are different. The plateau stress cushioning energy absorption of material combination changes linearly with the FPUF ratio. It means the cushioning energy absorption and the stress transmitted to the protection products can be adjusted by the structural scale parameters of the material combination.
- (2)
- FE-P and FE-S have different mechanical response behavior under impact conditions; the cushioning energy absorption of FE-S is lower than that of FE-P for the same deformation. The cushioning energy absorption rate of FE-S is positively related to the EPS ratio and the impact energy. The cushioning energy absorption rate of FE-P first increase and then decrease with the structural scale parameter increasing under the same impact condition. FE-P material is suitable for stress-sensitive protection products, and FE-S is suitable for acceleration-sensitive protection products.
- (3)
- FPUF is with small energy absorption but without cushioning energy absorption capacity loss in multiple compression loading conditions. EPS has high cushioning energy absorption but cannot maintain cushioning properties after multiple impact loading. For the FE-P and FE-S combination, the larger the proportion of FPUF, the smaller the cushioning energy absorption loss of FPUF-EPS. The proportion of EPS increases brings the stronger cushioning energy absorption of FPUF-EPS. So, the FE-P combination is superior for high-strength impact protection, and the FE-S combination is superior for low-strength impact conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols and Acronyms | Explanations |
| FPUF | Flexible polyurethane foam |
| EPS | Expanded polystyrene foam |
| FE-P | FPUF-EPS parallel combination material |
| FE-S | FPUF-EPS series combination material |
| FE0 | Neat EPS material (Thickness of EPS is 50 mm) |
| FE0.2-P | FPUF-EPS parallel combination material (Thickness of FPUF is 10 mm, EPS is 40 mm) |
| FE0.2-S | FPUF-EPS series combination material (Thickness of FPUF is 10 mm, EPS is 40 mm) |
| FE0.4-P | FPUF-EPS parallel combination material (Thickness of FPUF is 20 mm, EPS is 30 mm) |
| FE0.4-S | FPUF-EPS series combination material (Thickness of FPUF is 20 mm, EPS is 30 mm) |
| FE0.5-P | FPUF-EPS parallel combination material (Thickness of FPUF is 25 mm, EPS is 25 mm) |
| FE0.5-S | FPUF-EPS series combination material (Thickness of FPUF is 25 mm, EPS is 25 mm) |
| FE0.6-P | FPUF-EPS parallel combination material (Thickness of FPUF is 30 mm, EPS is 20 mm) |
| FE0.6-S | FPUF-EPS series combination material (Thickness of FPUF is 30 mm, EPS is 20 mm) |
| FE0.8-P | FPUF-EPS parallel combination material (Thickness of FPUF is 40 mm, EPS is 10 mm) |
| FE0.8-S | FPUF-EPS series combination material (Thickness of FPUF is 40 mm, EPS is 10 mm) |
| FE1 | Neat FPUF material (Thickness of FPUF is 50 mm) |
References
- Sun, Y.; Li, Q.M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef]
- Mills, N. Polymer Foams Handbook: Engineering and Biomechanics Applications and Design Guide; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Cronin, D.S.; Ouellet, S. Low density polyethylene, expanded polystyrene and expanded polypropylene: Strain rate and size effects on mechanical properties. Polym. Test. 2016, 53, 40–50. [Google Scholar] [CrossRef]
- Wadley, H.N. Cellular metals manufacturing. Adv. Eng. Mater. 2002, 4, 726–733. [Google Scholar] [CrossRef]
- Cady, C.M.; Gray, G.T.; Liu, C.; Lovato, M.L.; Mukai, T. Compressive properties of a closed-cell aluminum foam as a function of strain rate and temperature. Mater. Sci. Eng. A 2009, 525, 1–6. [Google Scholar] [CrossRef]
- Banhart, J.; Baumeister, J.; Weber, M. Damping properties of aluminium foams. Mater. Sci. Eng. A 1996, 205, 221–228. [Google Scholar] [CrossRef]
- Hanssen, A.G.; Hopperstad, O.S.; Langseth, M.; Ilstad, H. Validation of constitutive models applicable to aluminium foams. Int. J. Mech. Sci. 2002, 44, 359–406. [Google Scholar] [CrossRef]
- Queheillalt, D.T.; Wadley, H.N.; Choi, B.W.; Schwartz, D.S. Creep expansion of porous Ti-6Al-4V sandwich structures. Metall. Mater. Trans. A 2000, 31, 261–273. [Google Scholar] [CrossRef]
- Elzey, D.M.; Wadley, H.N.G. The limits of solid state foaming. Acta Mater. 2001, 49, 849–859. [Google Scholar] [CrossRef]
- Bisagni, C. Experimental investigation of the collapse modes and energy absorption characteristics of composite tubes. Int. J. Crashworthiness 2009, 14, 365–378. [Google Scholar] [CrossRef]
- Yuen, S.C.K.; Nurick, G.N. The energy-absorbing characteristics of tubular structures with geometric and material modifications: An overview. Appl. Mech. Rev. 2008, 61, 020802. [Google Scholar] [CrossRef]
- Kim, D.K.; Lee, S. Impact energy absorption of 6061 aluminum extruded tubes with different cross-sectional shapes. Mater. Des. 1999, 20, 41–49. [Google Scholar] [CrossRef]
- Ochelski, S.; Gotowicki, S. Experimental assessment of energy absorption capability of carbon-epoxy and glass-epoxy composites. Compos. Struct. 2009, 87, 215–224. [Google Scholar] [CrossRef]
- Hwang, B.K.; Kim, S.K.; Kim, J.H.; Kim, J.D.; Lee, J.M. Dynamic compressive behavior of rigid polyurethane foam with various densities under different temperatures. Int. J. Mech. Sci. 2020, 180, 105657. [Google Scholar] [CrossRef]
- Song, B.L.; Chen, W.W.; Dou, S.; Winfree, N.A.; Kang, J.H. Strain-rate effects on elastic and early cell-collapse responses of a polystyrene foam. Int. J. Impact Eng. 2005, 31, 509–521. [Google Scholar] [CrossRef]
- Chen, W.; Hao, H.; Hughes, D.; Shi, Y.; Cui, J.; Li, Z.X. Static and dynamic mechanical properties of expanded polystyrene. Mater. Des. 2015, 69, 170–180. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, X.; Liu, X.; Guan, X.; Zhang, C.; Niu, Y. Flexible and stretchable polyurethane/waterglass grouting material. Constr. Build. Mater. 2017, 138, 240–246. [Google Scholar] [CrossRef]
- Scarfato, P.; Di Maio, L.; Incarnato, L. Structure and physical-mechanical properties related to comfort of flexible polyurethane foams for mattress and effects of artificial weathering. Compos. Part B Eng. 2017, 109, 45–52. [Google Scholar] [CrossRef]
- Gholami, M.S.; Doutres, O.; Atalla, N. Effect of microstructure closed-pore content on the mechanical properties of flexible polyurethane foam. Int. J. Solids Struct. 2017, 112, 97–105. [Google Scholar] [CrossRef]
- Guo, A.; Li, H.; Xu, J.; Li, J.; Li, F. Effect of microstructure on the properties of polystyrene microporous foaming material. e-Polymers 2020, 20, 103–110. [Google Scholar] [CrossRef]
- Chuda-Kowalska, M.; Gajewski, T.; Garbowski, T. Mechanical characterization of orthotropic elastic parameters of a foam by the mixed experimental-numerical analysis. J. Theor. Appl. Mech. 2015, 53, 383–394. [Google Scholar] [CrossRef]
- Malcom, A.J.; Aronson, M.T.; Deshpande, V.S.; Wadley, H.N.G. Compressive response of glass fiber composite sandwich structures. Compos. Part A Appl. Sci. Manuf. 2013, 54, 88–97. [Google Scholar] [CrossRef]
- Jung, A.; Lach, E.; Diebels, S. New hybrid foam materials for impact protection. Int. J. Impact Eng. 2014, 64, 30–38. [Google Scholar] [CrossRef]
- Zhao, H.; Elnasri, I.; Girard, Y. Perforation of aluminium foam core sandwich panels under impact loading—An experimental study. Int. J. Impact Eng. 2007, 34, 1246–1257. [Google Scholar] [CrossRef]
- Cantwell, W.J.; Kiratisaevee, H.; Hazizan, M.A. The low velocity impact response of highperformance sandwich structures. Impact Load. Lightweight Struct. 2005, 49, 135. [Google Scholar]
- Zenkert, D.; Burman, M. Failure mode shifts during constant amplitude fatigue loading of GFRP/foam core sandwich beams. Int. J. Fatigue 2011, 33, 217–222. [Google Scholar] [CrossRef]
- Radford, D.D.; Deshpande, V.S.; Fleck, N.A. The use of metal foam projectiles to simulate shock loading on a structure. Int. J. Impact Eng. 2005, 31, 1152–1171. [Google Scholar] [CrossRef]
- Miltz, J.; Gruenbaum, G. Evaluation of cushioning properties of plastic foams from compressive measurements. Polym. Eng. Sci. 1981, 21, 1010–1014. [Google Scholar] [CrossRef]
- Schulze, C.; Vogel, D.; Sander, M.; Bader, R. Calibration of crushable foam plasticity models for synthetic bone material for use in finite element analysis of acetabular cup deformation and primary stability. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 25–37. [Google Scholar] [CrossRef]



| Materials Type | FE0 (EPS) | FE0.2 | FE0.4 | FE0.5 | FE0.6 | FE0.8 | FE1 (FPUF) |
|---|---|---|---|---|---|---|---|
| FPUF size (mm) | 0 | 50 × 50 × 10 | 50 × 50 × 20 | 50 × 50 × 25 | 50 × 50 × 30 | 50 × 50 × 40 | 50 × 50 × 50 |
| EPS size (mm) | 50 × 50 × 50 | 50 × 50 × 40 | 50 × 50 × 30 | 50 × 50 × 25 | 50 × 50 × 20 | 50 × 50 × 10 | 0 |
| Equivalent density (kg/m3) | 43.5 | 50.4 | 57.2 | 60.7 | 64.1 | 70.9 | 77.8 |
| Material | FE0 (EPS) | FE0.2-P | FE0.4-P | FE0.5-P | FE0.6-P | FE0.8-P |
|---|---|---|---|---|---|---|
| Equivalent Elastic Modulus | 6.19 | 5 | 3.79 | 3.18 | 2.57 | 1.34 |
| Material | FE0.2-S | FE0.4-S | FE0.5-S | FE0.6-S | FE0.8-S | FE1 (FPUF) |
| Equivalent Elastic Modulus | 0.65 | 0.34 | 0.27 | 0.22 | 0.16 | 0.11 |
| Materials | Structural Scale Parameters (Energy Absorption/J) | ||||||
|---|---|---|---|---|---|---|---|
| FE0 (EPS) | FE0.2 | FE0.4 | FE0.5 | FE0.6 | FE0.8 | FE1 (FPUF) | |
| FE-P-4.5J | 3.3 | 3.5 | 3.7 | 3.7 | 3.7 | 3.4 | 1.7 × 10−3 |
| FE-S-4.5J | 3.3 | 1.7 | 0.3 | 7.5 × 10−3 | 6.0 × 10−3 | 3.8 × 10−3 | 1.7 × 10−3 |
| FE-P-12.5J | 11.2 | 11.4 | 11.3 | 11.1 | 10.7 | 8.5 | 7.8 × 10−3 |
| FE-S-12.5J | 11.2 | 9.4 | 7.4 | 6.5 | 5.5 | 3.3 | 7.8 × 10−3 |
| FE-P-50J | 47.6 | 46.0 | 42.9 | 39.6 | 35.6 | 25.8 | --- |
| FE-S-50J | 47.6 | 44.0 | 39.9 | 36.4 | 31.2 | 20.7 | --- |
| Materials | FE0.2-P | FE0.4-P | FE0.5-P | FE0.6-P | FE0.8-P | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strain | Multiple (N) | Single (N) | Multiple (N) | Single (N) | Multiple (N) | Single (N) | Multiple (N) | Single (N) | Multiple (N) | Single (N) |
| 0.1 | 703.4 | 703.4 | 536.5 | 536.5 | 454.6 | 454.6 | 371.3 | 371.3 | 204.3 | 204.3 |
| 0.2 | 808.5 | 790.4 | 569.5 | 610.1 | 504.5 | 516.2 | 452.0 | 425.9 | 247.4 | 250.3 |
| 0.4 | 967.5 | 951.1 | 708.0 | 749.6 | 633.0 | 648.4 | 550.5 | 547.6 | 340.5 | 350.2 |
| 0.8 | 2302.3 | 2311.5 | 1910.2 | 1883.2 | 1651.6 | 1669.6 | 1476.0 | 1455.3 | 1031.8 | 1035.5 |
| Loading Stage | Structural Scale Parameters (Energy Absorption/J) | ||||||
|---|---|---|---|---|---|---|---|
| FE0 (EPS) | FE0.2-P | FE0.4-P | FE0.5-P | FE0.6-P | FE0.8-P | FE1 (FPUF) | |
| Strain 0.1 | 3.0 | 2.4 | 1.8 | 1.5 | 1.2 | 0.7 | 8.0 × 10−2 |
| Strain 0.2 | 5.4 | 4.5 | 3.5 | 3.0 | 2.5 | 1.4 | 0.3 |
| Strain 0.4 | 11.6 | 9.7 | 7.6 | 6.7 | 5.5 | 3.5 | 1.4 |
| Strain 0.8 | 32.8 | 27.9 | 22.4 | 20.0 | 17.4 | 12.5 | 7.2 |
| Multiple sum | 52.8 | 44.6 | 35.4 | 31.2 | 26.6 | 18.0 | 9.0 |
| Single | 50.4 | 41.8 | 33.2 | 28.9 | 24.6 | 16.0 | 7.4 |
| Materials | FE0.2-S | FE0.4-S | FE0.5-S | FE0.6-S | FE0.8-S | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strain | Multiple (N) | Single (N) | Multiple (N) | Single (N) | Multiple (N) | Single (N) | Multiple (N) | Single (N) | Multiple (N) | Single (N) |
| 0.1 | 177.1 | 176.6 | 79.8 | 79.4 | 63.8 | 62.4 | 54.8 | 52.1 | 39.4 | 41.9 |
| 0.2 | 622.0 | 623.2 | 179.1 | 189.1 | 126.6 | 139.3 | 78.6 | 114.7 | 83.3 | 79.2 |
| 0.4 | 1038 | 983.9 | 869.5 | 817.8 | 504.3 | 493.6 | 314.8 | 317.1 | 149.9 | 196.4 |
| 0.8 | 2242 | 1743.9 | 1875 | 1586.8 | 1677 | 1505.1 | 1480 | 1396.1 | 1115 | 1106.5 |
| Loading Stage | Structural Scale Parameters (Energy Absorption/J) | ||||||
|---|---|---|---|---|---|---|---|
| FE0 (EPS) | FE0.2-S | FE0.4-S | FE0.5-S | FE0.6-S | FE0.8-S | FE1 (FPUF) | |
| Strain 0.1 | 3.0 | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 | 8.0 × 10−2 |
| Strain 0.2 | 5.4 | 1.9 | 0.8 | 0.7 | 0.5 | 0.4 | 0.3 |
| Strain 0.4 | 11.6 | 11.0 | 5.0 | 3.2 | 2.4 | 1.8 | 1.4 |
| Strain 0.8 | 32.8 | 30.1 | 28.3 | 24.1 | 19.8 | 12.4 | 7.2 |
| Multiple sum | 52.8 | 43.5 | 34.2 | 28.1 | 22.9 | 14.6 | 9.0 |
| Single | 50.4 | 39.8 | 29.9 | 25.2 | 20.8 | 12.9 | 7.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhong, W.; Li, J.; Luo, J. Mechanical Properties and Cushioning Effectiveness of FPUF-EPS Combination Materials. Materials 2023, 16, 6886. https://doi.org/10.3390/ma16216886
Zhang Z, Zhong W, Li J, Luo J. Mechanical Properties and Cushioning Effectiveness of FPUF-EPS Combination Materials. Materials. 2023; 16(21):6886. https://doi.org/10.3390/ma16216886
Chicago/Turabian StyleZhang, Zexiong, Weizhou Zhong, Jiaxing Li, and Jingrun Luo. 2023. "Mechanical Properties and Cushioning Effectiveness of FPUF-EPS Combination Materials" Materials 16, no. 21: 6886. https://doi.org/10.3390/ma16216886
APA StyleZhang, Z., Zhong, W., Li, J., & Luo, J. (2023). Mechanical Properties and Cushioning Effectiveness of FPUF-EPS Combination Materials. Materials, 16(21), 6886. https://doi.org/10.3390/ma16216886





