A Theoretical Study on the Spatiotemporal Variation in the Temperature Field in Linings of High-Water-Temperature Tunnels
Abstract
:1. Introduction
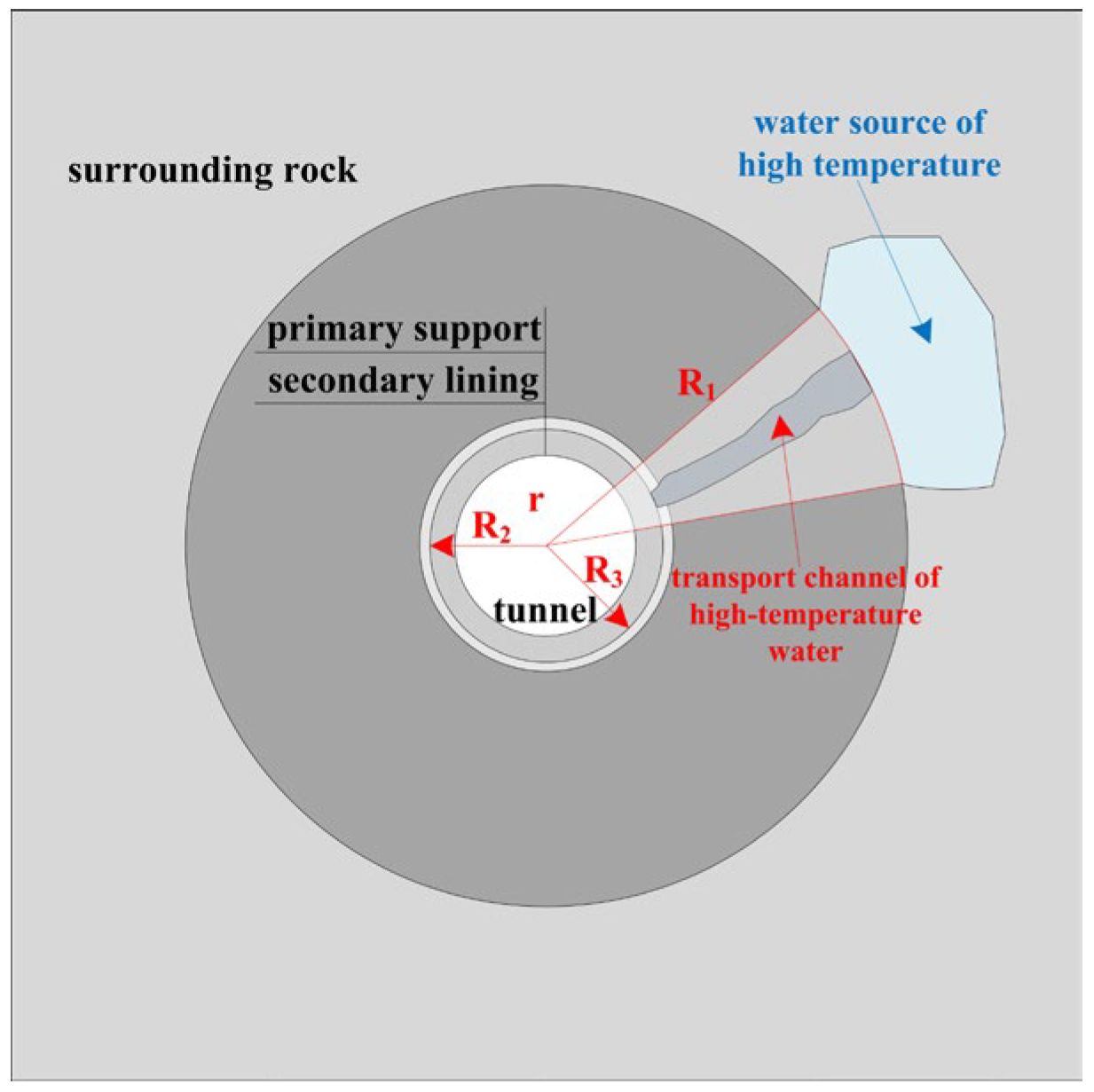
2. Analysis of the Lining Temperature Field of High-Water-Temperature Tunnels
2.1. The Theory of Unsteady Heat Conduction
2.1.1. The Conduction Differential Equation in the Unsteady State
2.1.2. Boundary Conditions for Theoretical Derivation
- (1)
- The first boundary condition: the temperature distribution on the boundary is known. For heat conduction in the unsteady state, it is expressed as Equation (5).
- (2)
- The second boundary condition: heat flux at the boundary is known. For heat conduction in the unsteady state, it is expressed as Equation (6), where n is the vector on the outer surface (the same below).
- (3)
- The third boundary condition: the coefficient of convectional heat transfer h and fluid temperature Tf are known. For heat conduction in the unsteady state, it is expressed as Equation (7).
2.2. Calculation of the Lining Temperature Field of High-Water-Temperature Tunnels
2.2.1. Basic Assumptions
- (1)
- The tunnel lining is simplified to circular lining, and heat only radially transfers along the tunnel.
- (2)
- The medium in each layer of tunnel linings meets the conditions of homogeneity and isotropy.
- (3)
- The thermal parameters of tunnel linings (density, specific heat and heat conductivity, etc.) and air temperature inside the tunnel remain constant.
- (4)
- Adjacent layers of tunnel linings are in close contact, and their heat flux and temperature have consecutive characteristics.
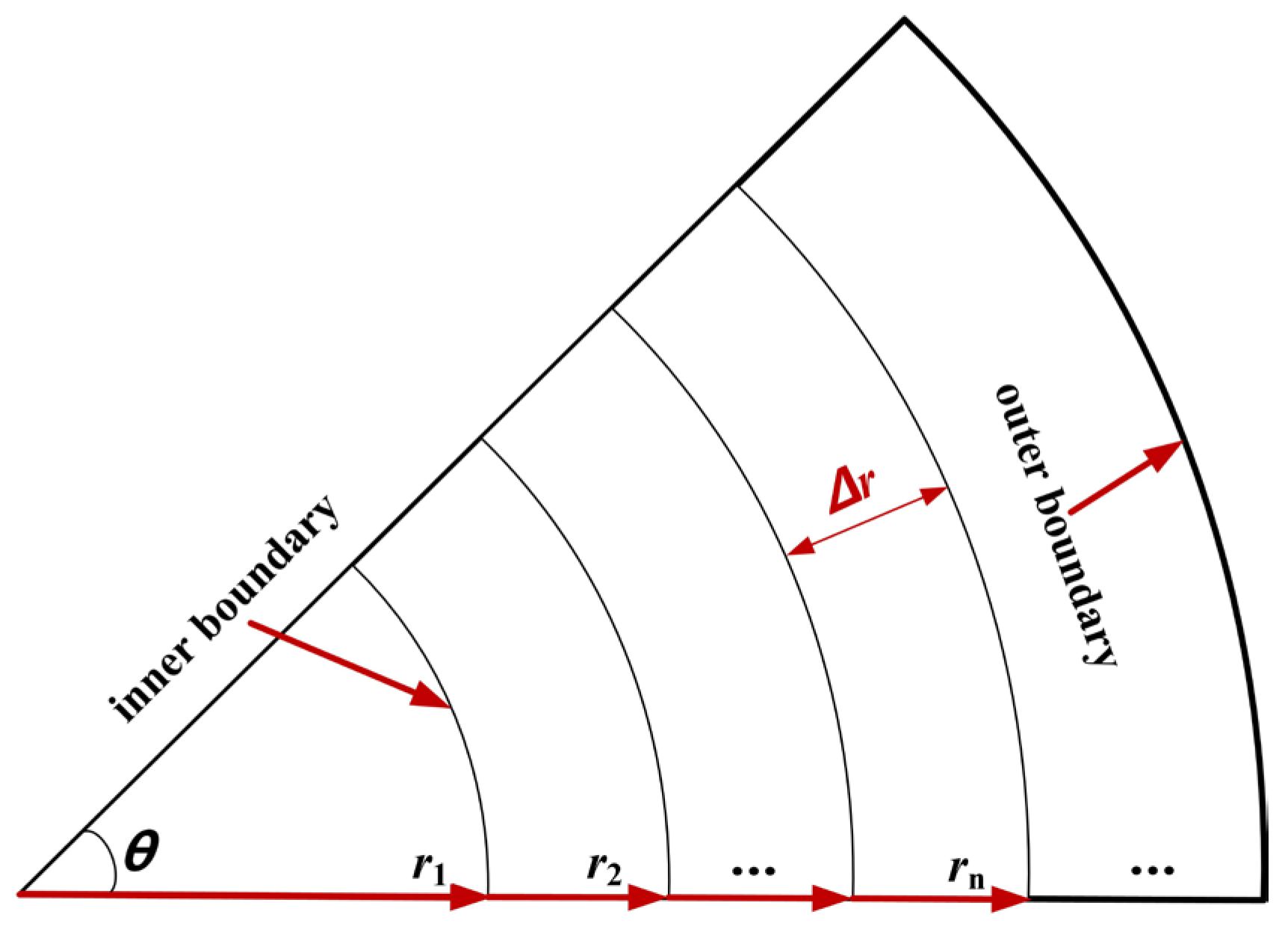
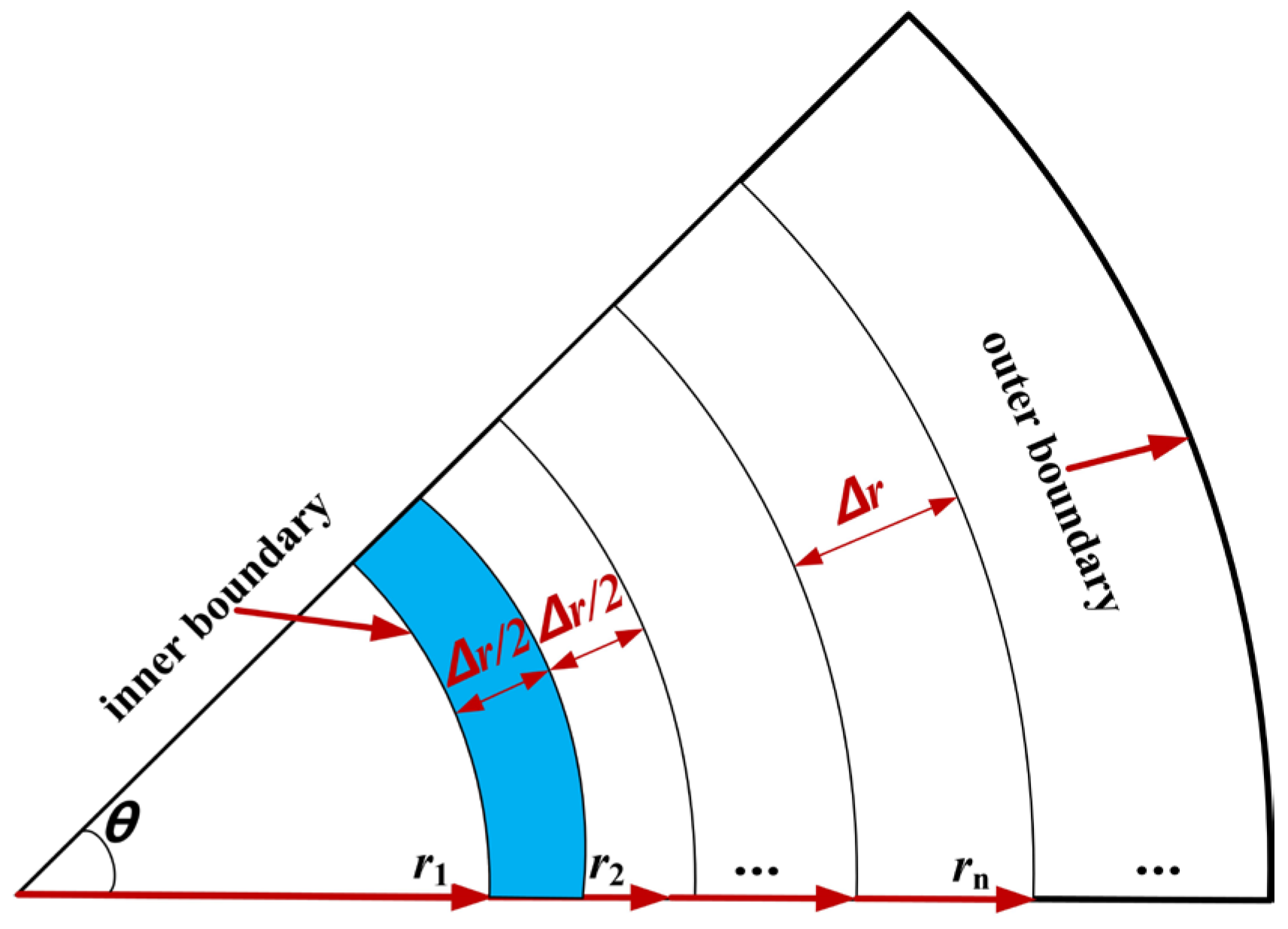
2.2.2. Discrete Equation for the Unsteady Temperature Field in the Tunnel Lining
- Establishment of internal node equations
- (1)
- Write Taylor expansions (8) and (9) of the function t for the point (n, i), respectively.
- (2)
- Discretization of the unsteady state term
- (3)
- Discretization of the internal heat source term
- (4)
- Discrete equation for internal nodes
- 2.
- Establishment of boundary node equations
- (1)
- Discrete equation for internal boundary nodes
- (2)
- Discrete equation for the outer boundary nodes
2.2.3. Solution Method for the Temperature Field in the Unsteady State
- (1)
- Set the basic assumptions, equate the tunnel to the circular tunnel, and establish heat conduction equations in the unsteady state as polar coordinates.
- (2)
- Establish discrete equations for internal nodes, internal and external boundary nodes, and the internal heat source term.
- (3)
- Select calculation parameters for secondary lining, including its dimensions, physical parameters, thermal parameters, boundary conditions for solving discrete equations for internal nodes, internal and external boundary nodes, and the internal heat source term, the spatial and temporal steps of the calculation and the calculation period.
- (4)
- Use mathematical calculation software and language programming to iteratively solve the discrete equations for the internal nodes, internal and external boundary nodes. The new value at any time is solved based on the initial value of node temperature, which can be obtained through iterative calculation until the result converges. To ensure the stability and convergence of iterative computation, both the temporal and spatial steps need to satisfy Equations (21) and (22).
3. Example Analysis
3.1. Calculation Conditions and Parameters
3.1.1. Setting of Working Conditions
- (1)
- Size of the calculation model: the excavation radius and secondary lining thickness of the circular tunnel are taken as 3.3 m and 0.35 m, respectively; the material of the lining concrete: C30 concrete; temperature on the lining’s inner boundary: 28 °C.
- (2)
- Temperature on the lining’s outer boundary: assuming that the hot water with a high temperature from a certain heat source around the tunnel reaches the lining’s outer surface (near surrounding rock side). The high temperature directly acts on the secondary lining and has a direct impact on its temperature field. This is an extreme condition, and calculating the spatiotemporal evolution of the lining’s temperature field under this extreme condition is of great significance for the exploration and development of high-temperature curing techniques for tunnel linings. The working conditions are shown in Table 2.
3.1.2. Calculation Parameters
3.2. Calculation Results
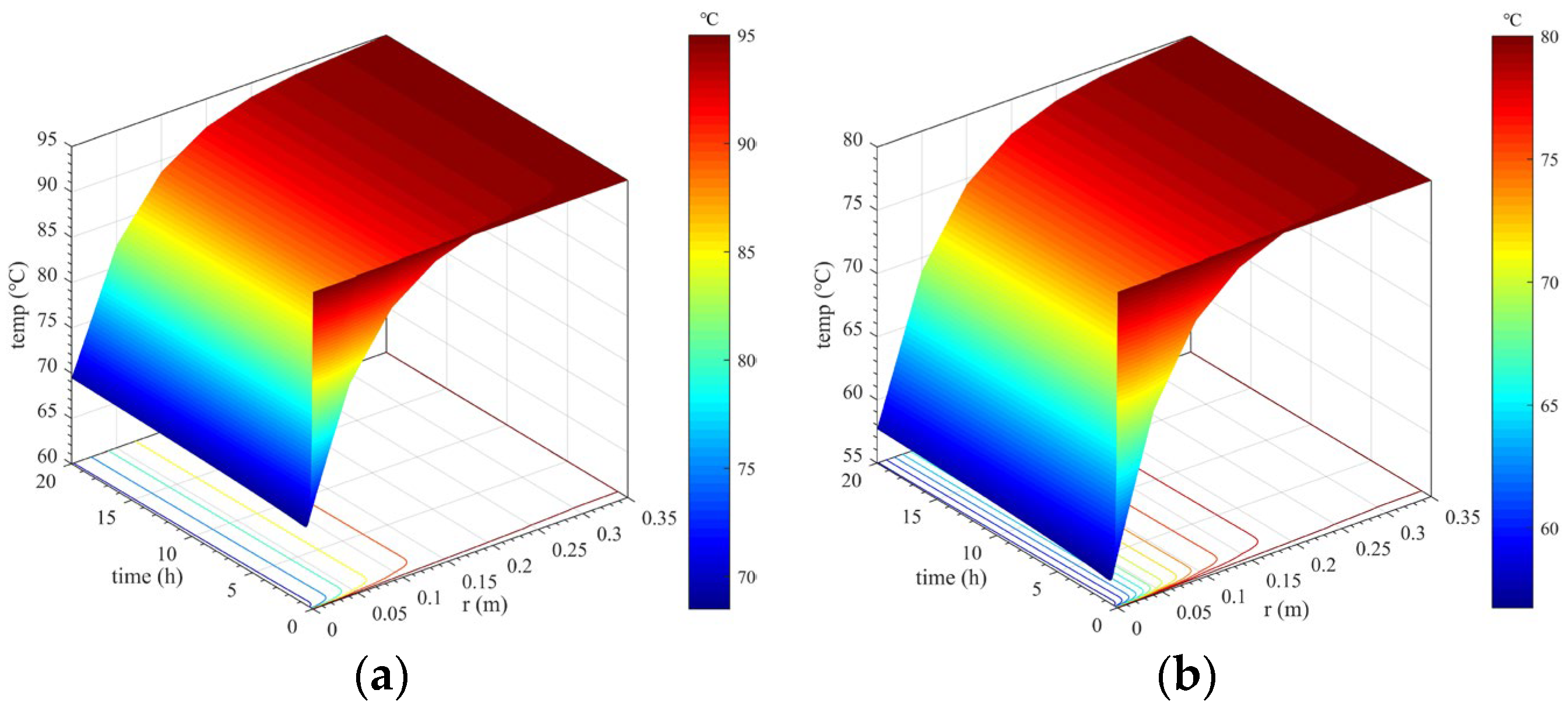
3.2.1. Calculation Results Considering Concrete Hydration Heat
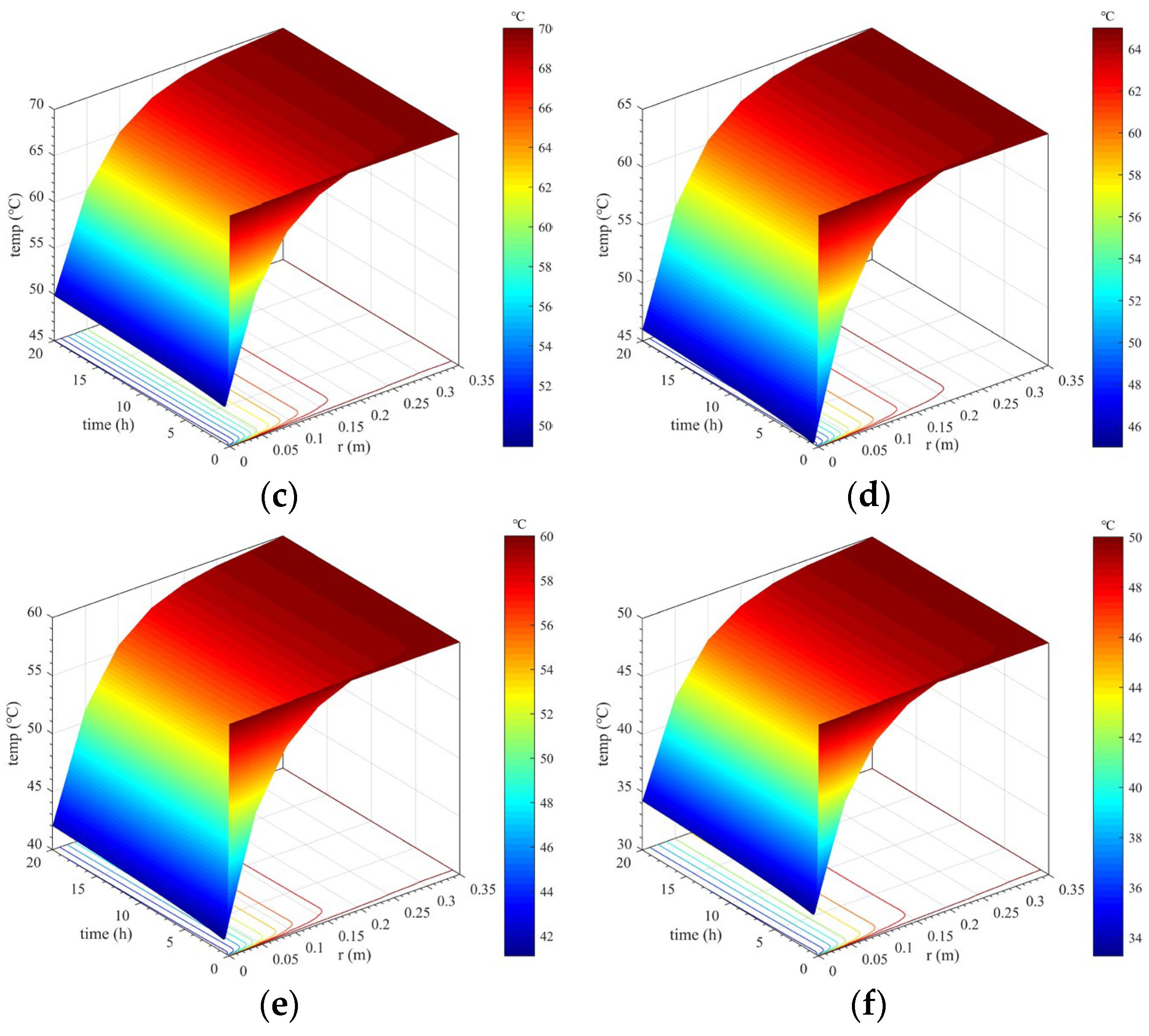
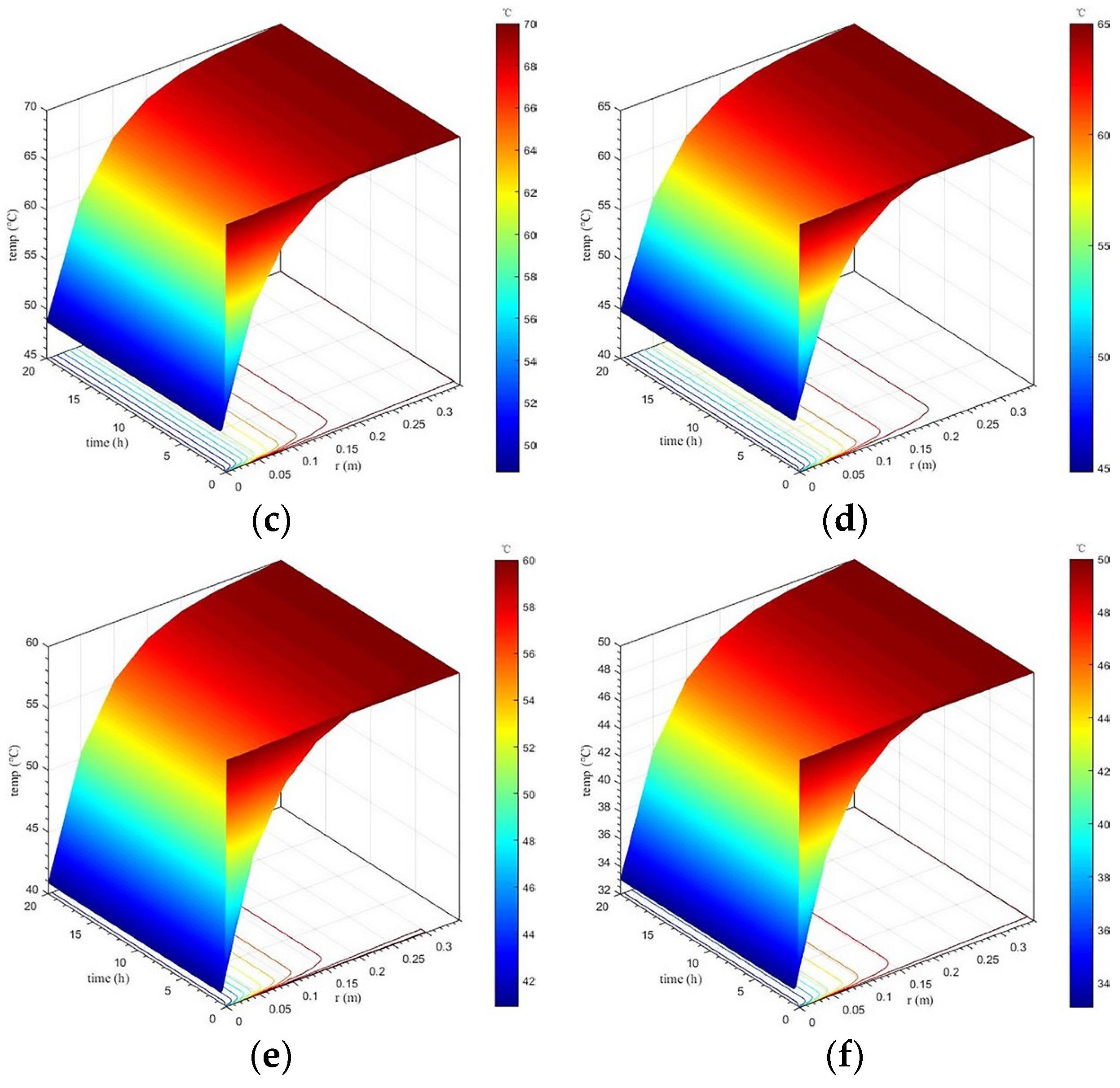
- Spatiotemporal variation in the lining’s temperature field
- 2.
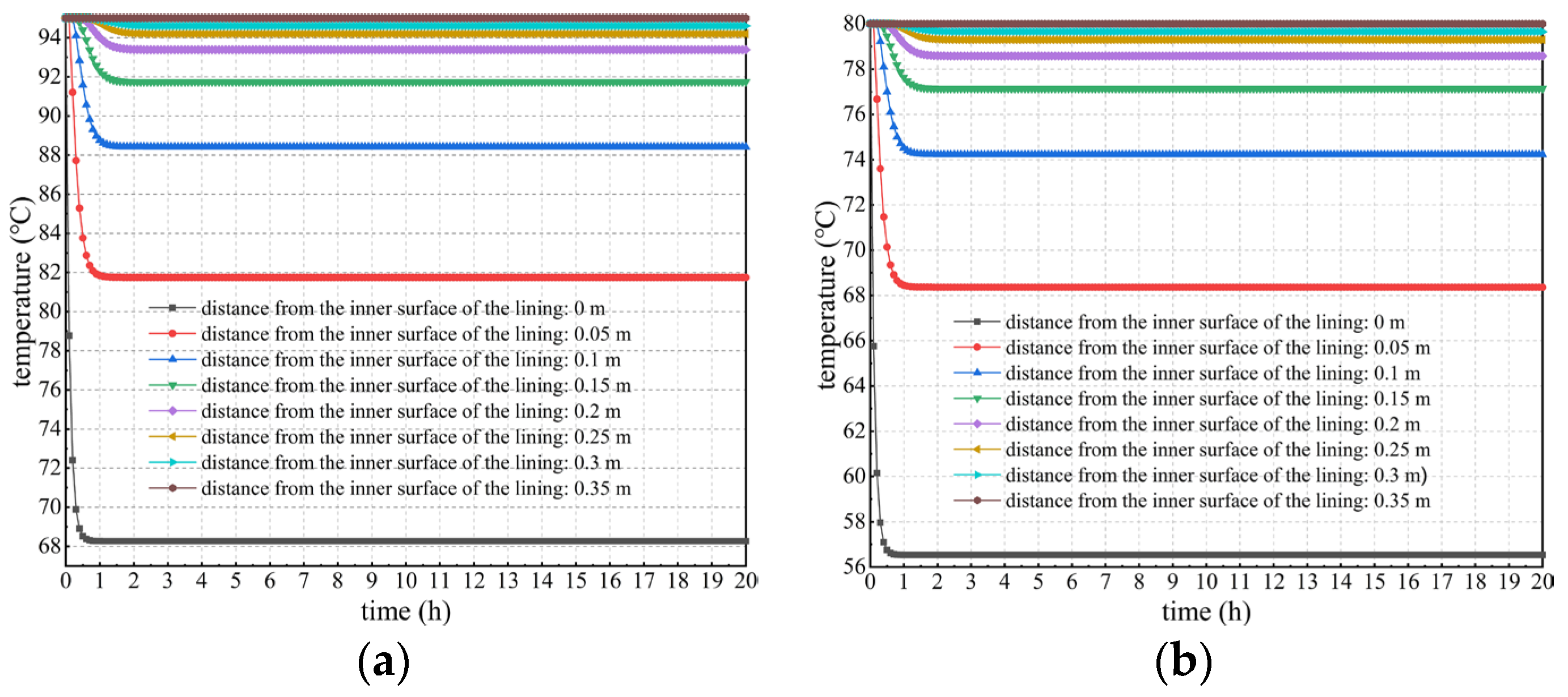
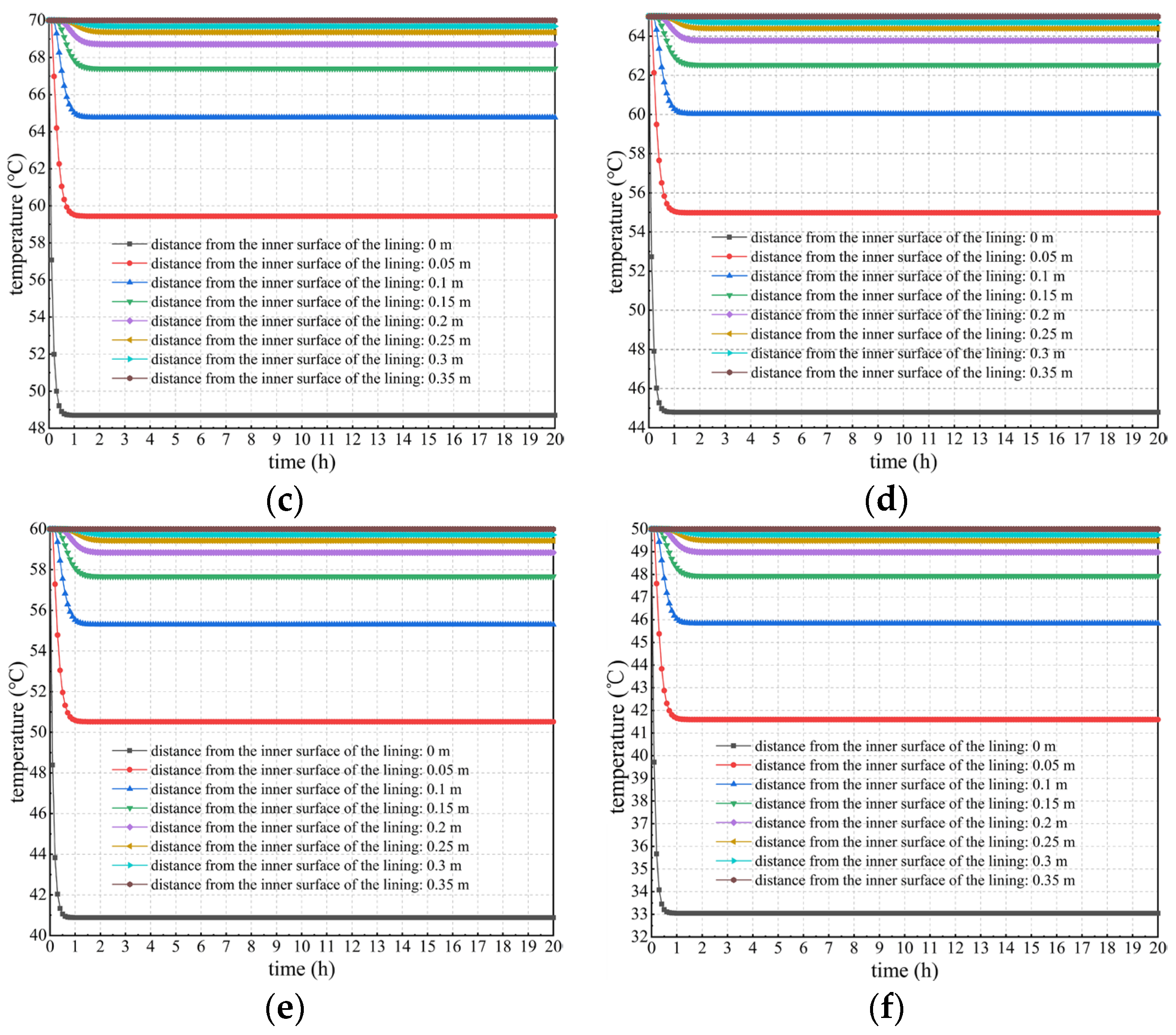
- Variation in the lining temperature under different temperatures and locations
- 3.
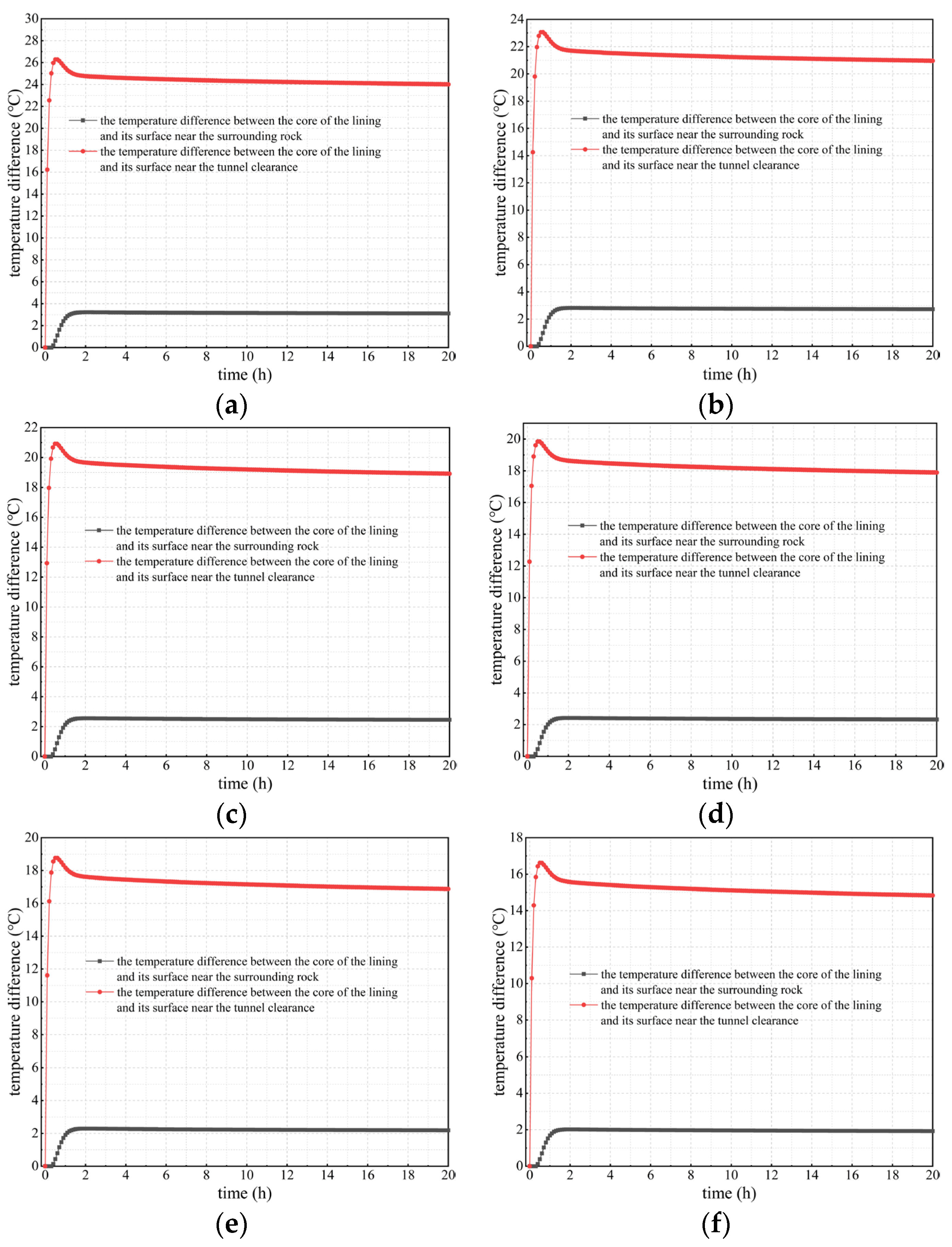
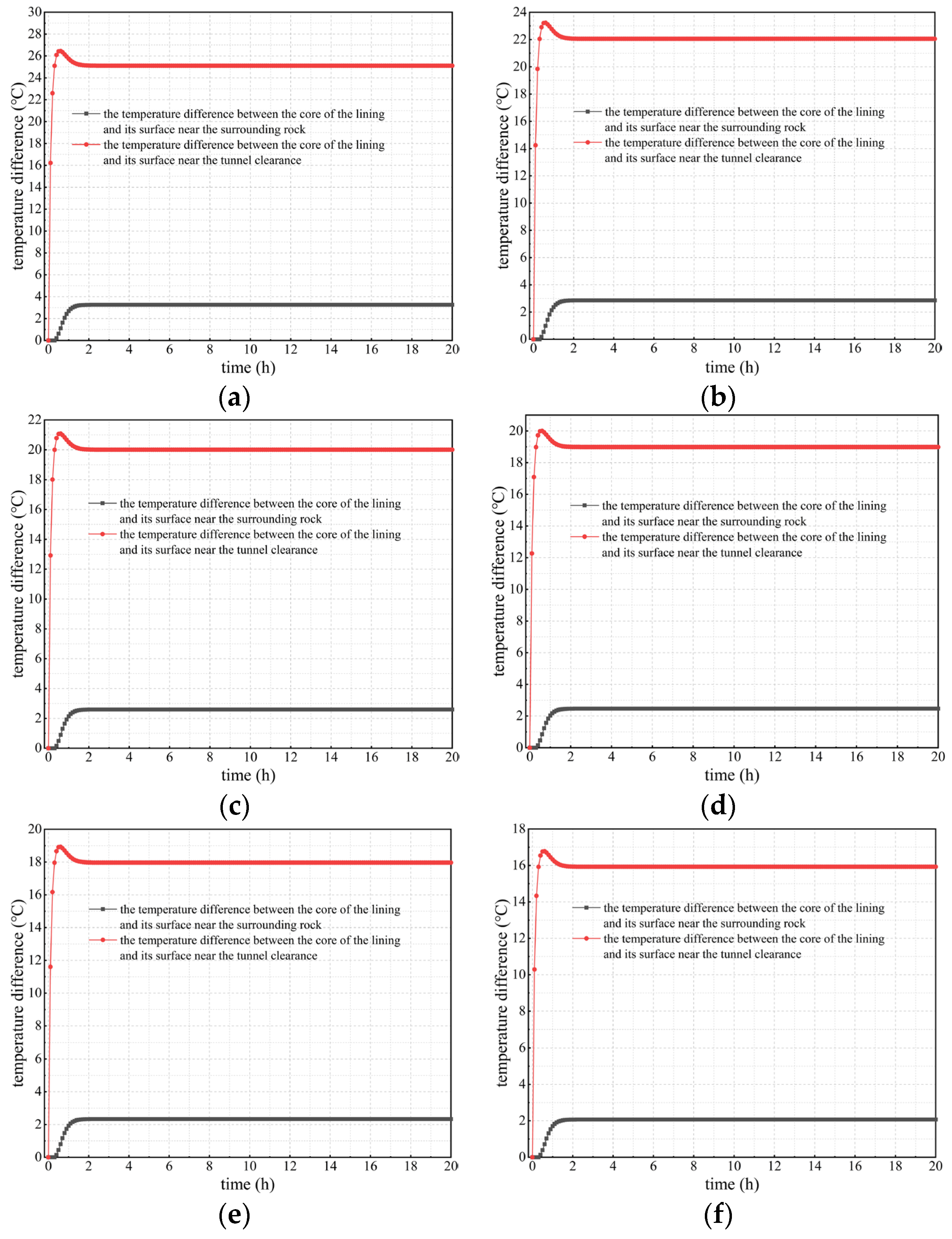
- The temperature difference variation between the lining’s core and surfaces
3.2.2. Calculation Results When Not Considering Concrete Hydration Heat
- Spatiotemporal variation in the lining’s temperature field
- 2.
- Temperature variation in secondary lining under different temperatures and locations
- 3.
- Variation in the temperature difference between the lining’s core and surfaces
4. Conclusions
- (1)
- Discrete equations for the temperature field in the unsteady state of secondary lining considering concrete hydration heat were finally established by deducing the discrete equations for the internal nodes and the boundary nodes of secondary linings. Moreover, the solution method for discrete equations was given. The results can lay a theoretical foundation for revealing the spatiotemporal evolution law of the lining’s temperature field considering concrete hydration heat. Additionally, the results also provide certain theoretical support for the reasonable curing of the lining concrete.
- (2)
- Results show that the temperature of secondary lining within a thickness range of approximately 15 cm adjacent to the tunnel clearance decreases most sharply. The higher the outer surface temperature of secondary lining, the more drastically the temperature decreases. The large temperature change can cause a drastic change in the temperature difference in tunnel linings, which is extremely detrimental to the lining concrete’s growth. Additionally, when considering concrete hydration heat, overall, the lining temperature after the temperature field reaches stability is approximately 1–2 °C higher than that when not considering concrete hydration heat.
- (3)
- When considering concrete hydration heat, the lining temperature basically stabilizes within 2 h after dropping, and the temperature change curve after stabilization is a horizontal line. However, when considering concrete hydration heat, the temperature of secondary lining rises to a certain extent after a sudden drop and reaches stability after approximately 20 h. The reason for this is that the heat of the lining near the tunnel clearance is rapidly lost under the action of the cooling measures such as ventilation, and the contribution of hydration heat to the changes in the lining temperature gradually becomes prominent.
- (4)
- The temperature difference between the lining’s core and outer and inner surfaces is negatively and positively correlated with its outer surface temperature, respectively. When the outer surface temperature of tunnel linings is 95, 80, or 70 °C, the temperature difference between the lining’s core and inner surface wholly or partially exceeds 20 °C. However, when the outer surface temperature does not exceed 65 °C, the temperature difference is less than 20 °C. Thus, insulation measures should be taken to control it so as not to exceed 65 °C, preventing problems such as lining cracks caused by an excessive temperature difference.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, W.; Choi, H.; Lee, T. Residual Compressive Strength Prediction Model for Concrete Subject to High Temperatures Using Ultrasonic Pulse Velocity. Materials 2023, 16, 515. [Google Scholar] [CrossRef]
- Kanagaraj, B.; Anand, N.; Alengaram, U.J.; Praveen, B.; Tattukolla, K. Performance evaluation on engineering properties and sustainability analysis of high strength geopolymer concrete. J. Build. Eng. 2022, 60, 105147. [Google Scholar] [CrossRef]
- Kang, F.C.; Li, Y.C. Numerical study on airflow temperature field in a hightemperature tunnel with insulation layer. Appl. Therm. Eng. 2020, 179, 115654. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Cao, Z.M.; Wang, W.; Mei, X.S.; Zhao, X.; Shen, S.W.; Na, T.X. Field test and numerical investigation on thermal environment of tunnel with air layer structure. Build. Environ. 2021, 203, 108105. [Google Scholar] [CrossRef]
- Lin, M.; Zhou, P.; Jiang, Y.F.; Zhou, F.C.; Lin, J.Y.; Wang, Z.J. Numerical investigation on comprehensive control system of cooling and heat insulation for high geothermal tunnel: A case study on the highway tunnel with the highest temperature in China. Int. J. Therm. Sci. 2022, 173, 107385. [Google Scholar] [CrossRef]
- Wang, M.N.; Hu, Y.P.; Liu, D.G.; Jiang, C.; Wang, Q.L.; Wang, Y.C. A study on the heat transfer of surrounding rock-supporting structures in high-geothermal tunnels. Appl. Sci. 2020, 10, 2307. [Google Scholar] [CrossRef]
- Hu, Y.P.; Wang, M.N.; Wang, Q.L.; Liu, D.G.; Tong, J.J. Field test of thermal environment and thermal adaptation of workers in high geothermal tunnel. Build. Environ. 2019, 160, 106174. [Google Scholar] [CrossRef]
- Wang, J.K.; Li, Y.; Yuan, H.; Sun, Y.C.; Mei, N. Studies on active thermal insulation technology based on heat sink principle. Appl. Therm. Eng. 2020, 167, 114758. [Google Scholar] [CrossRef]
- Sinno, N.; Shehata, M.H. Role of temperature on Alkali-Silica reaction and the efficacy of supplementary cementitious materials. Constr. Build. Mater. 2021, 313, 125427. [Google Scholar] [CrossRef]
- Kim, S.; Lee, N.; Lee, H.K.; Park, S. Experimental and theoretical studies of hydration of ultra-high performance concrete cured under various curing conditions. Constr. Build. Mater. 2021, 278, 122352. [Google Scholar] [CrossRef]
- Shirani, S.; Cuesta, A.; Morales-Cantero, A.; De la Torre, A.G.; Olbinado, M.P.; Aranda, M.A.G. Influence of curing temperature on belite cement hydration: A comparative study with Portland cement. Cem. Concr. Res. 2021, 147, 106499. [Google Scholar] [CrossRef]
- Zajac, M.; Hilbig, H.; Bullerjahn, F.; Ben Haha, M. Reactions involved in carbonation hardening of Portland cement: Effect of curing temperature. J. Sustain. Cem.-Based Mater. 2022, 12, 1107–1125. [Google Scholar] [CrossRef]
- Strangfeld, C.; Klewe, T. Comparison of the Calcium Carbide Method and Darr Drying to Quantify the Amount of Chemically Bound Water in Early Age Concrete. Materials 2022, 15, 8422. [Google Scholar] [CrossRef] [PubMed]
- Farqad, Y.; Wei, X.S. Early strength development and hydration of cement pastes at different temperatures or with superplasticiser characterised by electrical resistivity. Case Stud. Constr. Mater. 2022, 16, e00911. [Google Scholar] [CrossRef]
- Tran, V.N.; Nguyen, L.T.; Nguyen, T.H.Y. Enhancing the effectiveness of steam curing for cement paste incorporating fly ash based on long-term compressive strength and reaction degree of fly ash. Case Studies Constr. Mater. 2022, 16, e01146. [Google Scholar] [CrossRef]
- Leklou, N.; Das, S.K. Effect of curing temperatures on hydration, mechanical and microstructural properties of metakaolin-blended cement mortars. J. Therm. Anal. Calorim. 2023, 148, 6747–6760. [Google Scholar] [CrossRef]
- Ghasabeh, M.; Göktepe, S. Phase-field modeling of thermal cracking in hardening mass concrete. Eng. Fract. Mech. 2023, 289, 109398. [Google Scholar] [CrossRef]
- Lai, Y.M.; Liu, S.Y.; Wu, Z.W.; Yu, W.B. Approximate analytical solution for temperature fields in cold regions circular tunnels. Cold Reg. Sci. Technol. 2002, 34, 43–49. [Google Scholar] [CrossRef]
- Lu, X.S.; Tervola, P.; Viljanen, M. Transient analytical solution to heat conduction in multi-dimensional composite cylinder slab. Int. J. Heat Mass Transf. 2006, 49, 1107–1114. [Google Scholar] [CrossRef]
- Lu, X.S.; Viljanen, M. An analytical method to solve heat conduction in layered spheres with time-dependent boundary conditions. Phys. Lett. A 2006, 351, 274–282. [Google Scholar] [CrossRef]
- Singh, S.; Jain, P.K.; Rizwan, U. Analytical solution to transient heat conduction in polar coordinates with multiple layers in radial direction. Int. J. Therm. Sci. 2008, 47, 261–273. [Google Scholar] [CrossRef]
- Jain, P.K.; Singh, S.; Rizwan, U. Analytical solution to transient asymmetric heat conduction in a multilayer annulus. J. Heat Transf. 2009, 131, 011304. [Google Scholar] [CrossRef]
- Toutain, J.; Battaglia, J.L.; Pradere, C.; Pailhes, J.; Kusiak, A.; Aregba, W.; Batsale, J.C. Numerical inversion of Laplace transform for time resolved thermal characterization experiment. J. Heat Transf. 2011, 133, 044504. [Google Scholar] [CrossRef]
- Li, M.; Chen, W.H.; Jia, W. Calculation and analysis of the tunnel lining′ s thermal stress field under high temperature. Appl. Mech. Mater. 2011, 90–93, 2157–2162. [Google Scholar] [CrossRef]
- Liang, B.; Zhao, N.Y. A study on temperature distribution of surrounding rock and mechanical characteristics of lining of Monglian Tunnel under high geothermal. Adv. Mater. Res. 2011, 1279, 2594–2600. [Google Scholar] [CrossRef]
- Shao, Z.S.; Qiao, R.J.; Wang, X.Y. Elasticity solution for temperature and stress fields of tunnels with high geothermal temperature. Rock Soil Mech. 2013, 34, 1–8. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, X.H.; Zeng, Y.H.; Yang, Z.X.; Zhou, X.J. Numerical solution of the heat transfer between tunnels and rocks in high-temperature geothermal region. J. Railw. Sci. Eng. 2015, 12, 1406–1411. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, X.H.; Zeng, Y.H.; Fan, L. Temperature field analysis of a cold-region railway tunnel considering mechanical and train-induced ventilation effects. Appl. Therm. Eng. 2016, 100, 114–124. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, B.; Zubin, A.I.; Bu, X.; Pan, H.; Chen, S. Spatial-temporal evolution principle of temperature field in a high-temperature geothermal highway tunnel. Ain Shams Eng. J. 2023, 14, 101965. [Google Scholar] [CrossRef]
- Alhawat, H.; Hamid, R.; Baharom, S.; Azmi, M.R.; Kaish, A.B.M.A. Thermal behaviour of unloaded concrete tunnel lining through an innovative large-scale tunnel fire experimental testing setup. Constr. Build. Mater. 2021, 283, 122718. [Google Scholar] [CrossRef]
- Zhu, B.F. A method for computing the adiabatic temperature rise of concrete considering the effect of the temperature of concrete. J. Hydroelectr. Eng. 2003, 20, 69–73. (In Chinese) [Google Scholar]
- TB 10003-2016; Code for Design of Railway Tunnel. China Railway Publishing House: Beijing, China, 2016.
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- TB 10005-2010; Code for Durability Design on Concrete Structure of Railway. China Railway Publishing House: Beijing, China, 2010.



| Symbols | The Meaning of Symbols in the Equations |
|---|---|
| T | The object temperature (°C), which is a function with variables x, y, z and τ. |
| τ | Time of heat conduction (s). |
| α | Thermal diffusivity (m2/s), . |
| λ | Thermal conductivity (W/m·°C). |
| ρ | Medium density (kg/m3). |
| c | Specific heat of the medium (J/kg·°C). |
| Internal heat source (source term), which refers to the energy released in unit time of the microelement. | |
| Tk | Temperature of the k-th layer of the lining (°C). |
| αk | Thermal diffusivity of the k-th layer of the lining (m2/s), . |
| λk | Thermal conductivity of the k-th layer of the lining (W/m·°C). |
| ρk | Density of the k-th layer of the lining (kg/m3). |
| ck | Specific heat of the k-th layer of the lining (J/kg·°C). |
| Internal heat source of the k-th layer of the lining. | |
| r | Radius of the k-th layer of the medium (m). |
| n | Vector on the outer surface. |
| Tf | Fluid temperature (air temperature in the tunnel clearance) (°C). |
| h | Convective conversion coefficient (w/(m2·k)). |
| Δr | Spatial steps (m). |
| Δτ | Temporal steps (°C). |
| FO | Fourier number of grid. It is a dimensionless quantity used to describe the unsteady heat conduction and molecular diffusion, . |
| rn | Vertical length from node (n, i) to the longitudinal axis of the tunnel (unit: m), rn = (n − 1)Δr. |
| Temperature at node (n, i), K. | |
| Bi | Resistance to the heat conduction ratio (Biot number), . |
| r1 | Vertical length from the inner boundary to the tunnel’s longitudinal axis (unit: m). |
| Touter | The temperature field of the lining’s outer boundary (°C). |
| Position | Thickness (cm) | Computing Time (h) | Whether Concrete Hydration Heat Is Considered | Temperature on the Lining’s Outer Boundary (°C) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Secondary lining | 35 cm | 20 | No | 95 | 80 | 70 | 65 | 60 | 50 |
| 35 cm | 20 | Yes | 95 | 80 | 70 | 65 | 60 | 50 | |
| Parameters | Density (ρ, kg/m3) | Specific Heat (c, j/(kg·k)) | Heat Conductivity (λ, w/(m·k)) | Convective Conversion Coefficient (h, w/(m2·k)) | Thermal Diffusivity (α, 10−6 m2/s) |
|---|---|---|---|---|---|
| Secondary lining | 2000 | 960 | 2.944 | 35 | 1.636 |
| Air | 1.134 | / | 0.023 | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Huang, M.; Li, J.; Qian, Y. A Theoretical Study on the Spatiotemporal Variation in the Temperature Field in Linings of High-Water-Temperature Tunnels. Materials 2023, 16, 7139. https://doi.org/10.3390/ma16227139
Huang M, Huang M, Li J, Qian Y. A Theoretical Study on the Spatiotemporal Variation in the Temperature Field in Linings of High-Water-Temperature Tunnels. Materials. 2023; 16(22):7139. https://doi.org/10.3390/ma16227139
Chicago/Turabian StyleHuang, Mingli, Meng Huang, Jiacheng Li, and Yuan Qian. 2023. "A Theoretical Study on the Spatiotemporal Variation in the Temperature Field in Linings of High-Water-Temperature Tunnels" Materials 16, no. 22: 7139. https://doi.org/10.3390/ma16227139
APA StyleHuang, M., Huang, M., Li, J., & Qian, Y. (2023). A Theoretical Study on the Spatiotemporal Variation in the Temperature Field in Linings of High-Water-Temperature Tunnels. Materials, 16(22), 7139. https://doi.org/10.3390/ma16227139





