Research on Surface Integrity and Fatigue Properties in the Turning of TC17 Titanium Alloy Based on the Response Surface Method
Abstract
:1. Introduction
2. Materials and Methods
3. Results
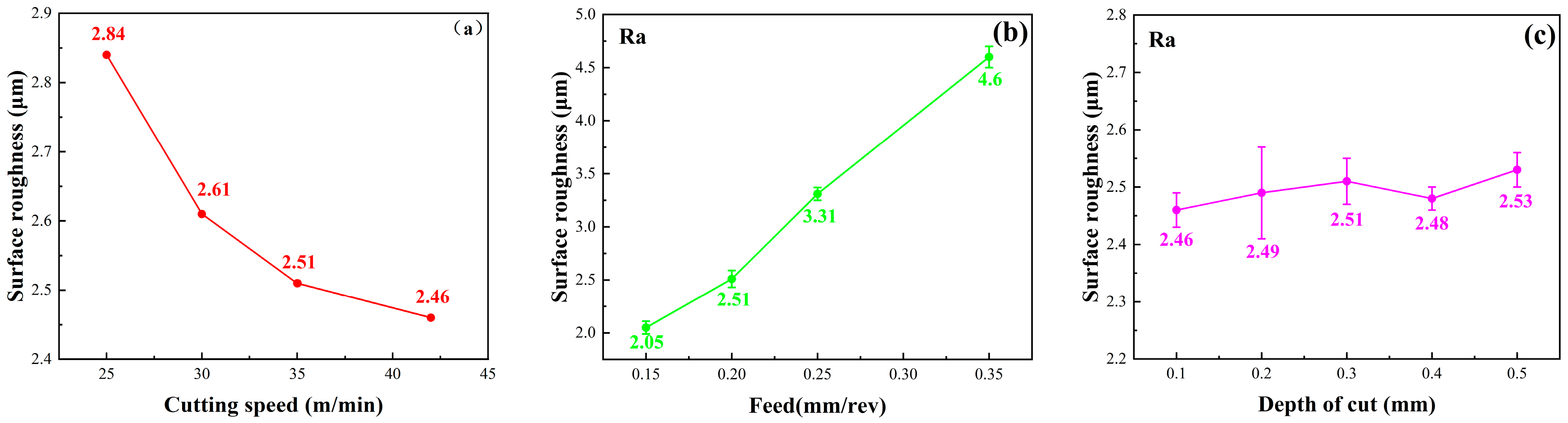
3.1. Single Factor Test Results
3.2. Analysis and Modeling Based on Response Surface Method
3.2.1. Response Surface Method Test Results
3.2.2. Analysis of Variance (ANOVA) of Experimental Results
3.2.3. The Establishment of the Response Mathematical Model
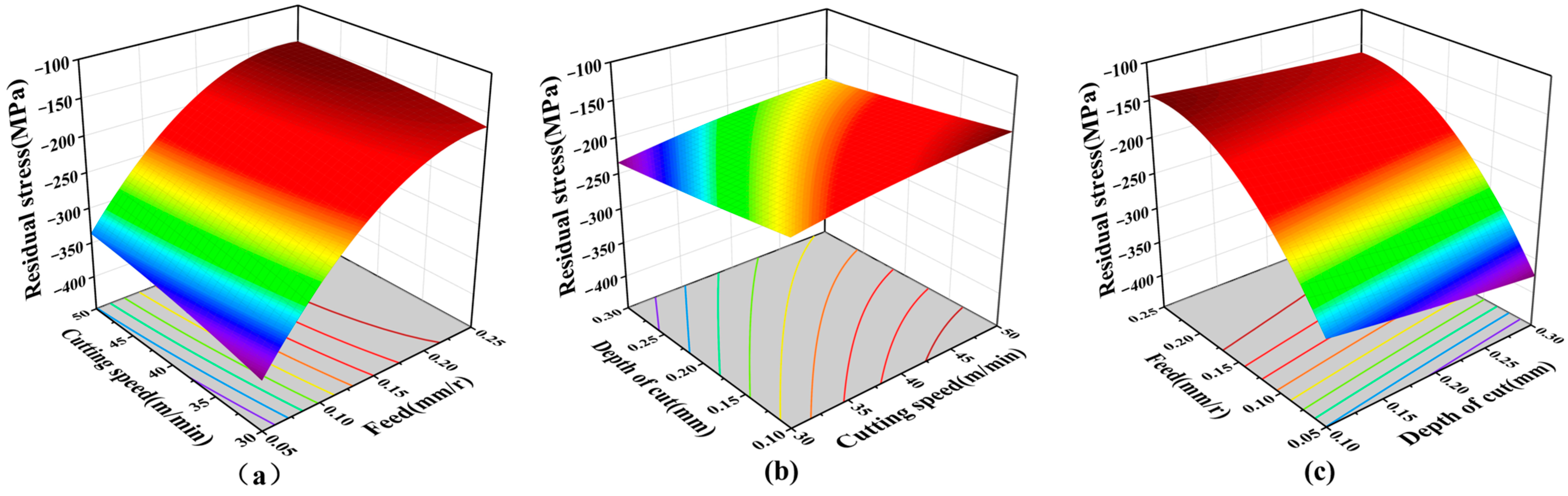
3.3. TC17 Turning Parameter Interaction Response Surface Graph Analysis
3.4. TC17 Fatigue Life Model
3.5. Analysis of Fatigue Fracture
4. Conclusions
- 1.
- A response model of turning parameters, surface residual stress, and surface roughness was constructed using the design–expert v10.0 software. According to the response surface graph and variance analysis table, it was found that the sequence of significance of the turning parameters affecting surface residual stress was as follows: > > ; the order of significance of turning parameters that affect surface roughness is > > . Under the processing conditions of this paper, the range of residual stress was −148 MPa to −384 MPa, and the range of surface roughness was 0.42 μm to 5.3 μm. When is 40 m/min, is 0.05 mm/rev and is 0.3 mm, and the surface roughness is the minimum. When is 30 m/min, is 0.05 mm/rev and is 0.2 mm, and residual compressive stress is the maximum.
- 2.
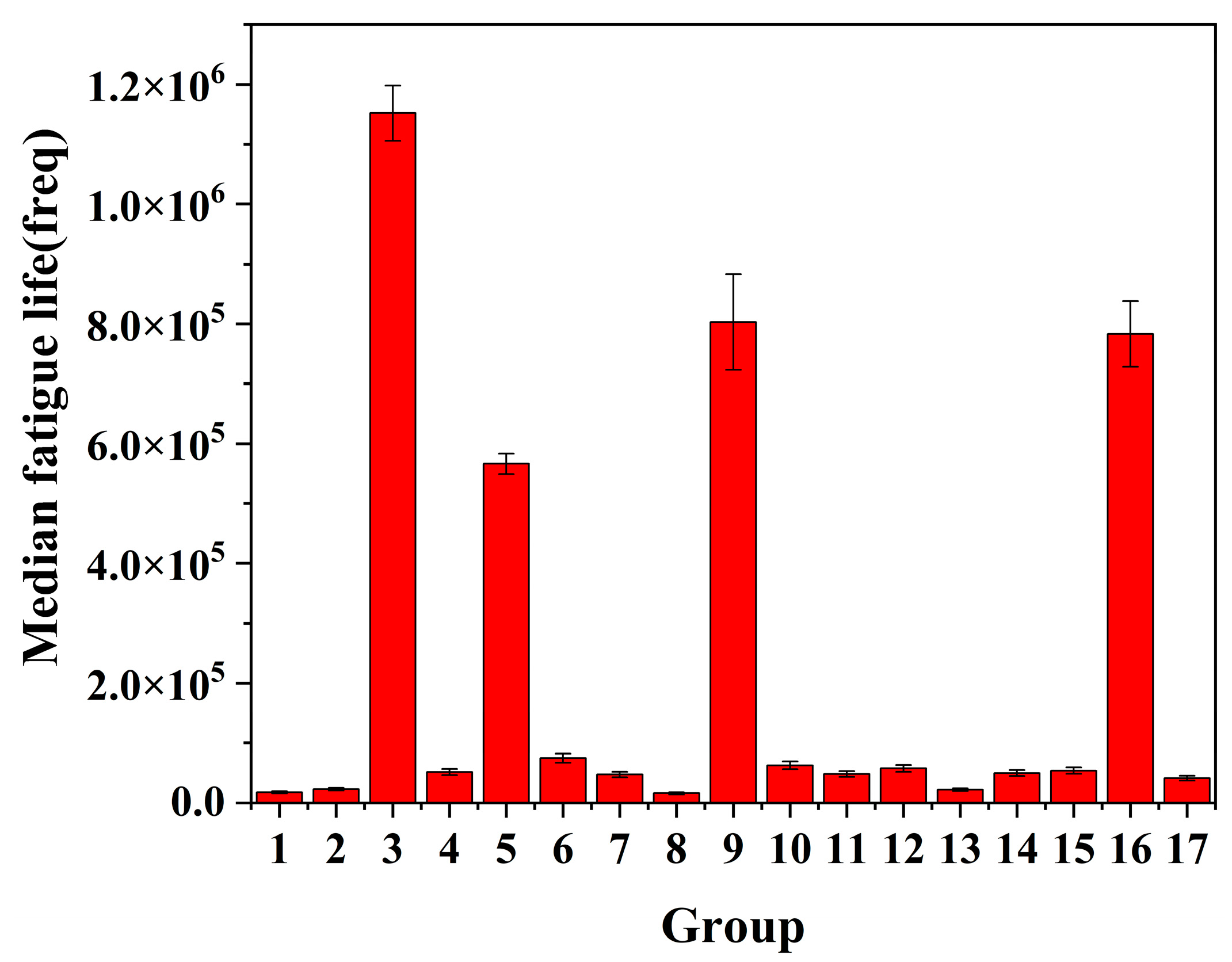
- Based on the fatigue life test results of specimens, the residual stress and surface roughness of the machined surface has a significant influence on the fatigue life of the sample, and the fatigue life decreases linearly with the increase in surface roughness. When the machining of residual compressive stress is introduced into the machined surface, the fatigue life can be significantly improved. The most extended fatigue life is 1,198,070 times, while the shortest fatigue life is only 14,470 times, and the span of fatigue life is large.
- 3.
- The influence of the law between various elements of surface integrity and fatigue life was studied, and the mathematical equation between the two was fitted using the least square method. It was concluded that the surface residual compressive stress had the greatest influence on fatigue life, followed by surface roughness. Therefore, the selection of turning parameters should be combined with the changing trend of residual compressive stress and surface roughness, and should be increased appropriately while ensuring surface roughness. When 30 m/min ≤≤ 50 m/min, 0.1 mm ≤≤ 0.3 mm, should not exceed 0.15 mm/rev.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiang, Q.; He, Y.; Hou, T. An Exploration of Surface Integrity Remanufacturing for Aeroengine Components. Front. Eng. Manag. 2016, 3, 107–114. [Google Scholar] [CrossRef]
- Liu, D.; Shi, Y.; Lin, X.; Xian, C.; Gu, Z. Polishing surface integrity of TC17 aeroengine blades. J. Mech. Sci. Technol. 2020, 34, 689–699. [Google Scholar] [CrossRef]
- Du, S.; Chen, M.; Xie, L.; Zhu, Z.; Wang, X. Optimization of process parameters in the high-speed milling of titanium alloy TB17 for surface integrity by the Taguchi-Grey relational analysis method. Adv. Mech. Eng. 2016, 8, 1687814016671442. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, Z.; Shen, X. Surface Feature Prediction Modeling and Parameter Optimization for Turning TC17 Titanium Alloy. Int. Trans. Electr. Energy Syst. 2022, 2022, 2979858. [Google Scholar] [CrossRef]
- Hourmand, M.; Sarhan, A.A.D.; Sayuti, M.; Hamdi, M. A Comprehensive Review on Machining of Titanium Alloys. Arab. J. Sci. Eng. 2021, 46, 7087–7123. [Google Scholar] [CrossRef]
- Moussaoui, K.; Mousseigne, M.; Senatore, J.; Chieragatti, R. The effect of roughness and residual stresses on fatigue life time of an alloy of titanium. Int. J. Adv. Manuf. Technol. 2015, 78, 557–563. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, P.; Zhang, C.; Liang, H.; Hua, J. Study on Surface Integrity and Fatigue Properties of TC4 Titanium Alloy by Surface Ultrasonic Rolling. Materials 2023, 16, 485. [Google Scholar] [CrossRef]
- Arif, M.; Rahman, M.; San, W.Y.; Kumar, S. An empirical study on the characterization of machined surface integrity by chip morphology in dry end-milling of titanium alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 471–476. [Google Scholar] [CrossRef]
- Ramesh, S.; Karunamoorthy, L.; Palanikumar, K. Surface Roughness Analysis in Machining of Titanium Alloy. Mater. Manuf. Process. 2008, 23, 174–181. [Google Scholar] [CrossRef]
- Ulutan, D.; Ozel, T. Machining induced surface integrity in titanium and nickel alloys: A review. Int. J. Mach. Tools Manuf. 2011, 51, 250–280. [Google Scholar] [CrossRef]
- Xia, H.; Zhao, G.; Yan, J.; Li, L.; He, N.; Hao, X. Study on laser-induced oxidation assisted micro milling of Ti6Al4V alloy. Int. J. Adv. Manuf. Technol. 2019, 103, 1579–1591. [Google Scholar] [CrossRef]
- Thirumalai, R.; Techato, K.; Chandrasekaran, M.; Venkatapathy, K.; Seenivasan, M. Experimental investigation during turning process of titanium material for surface roughness. Mater. Today Proc. 2020, 45, 1423–1426. [Google Scholar] [CrossRef]
- Gao, T.; Sun, Z.; Xue, H.; Bayraktar, E.; Qin, Z.; Li, B.; Zhang, H. Effect of Turning on the Surface Integrity and Fatigue Life of a TC11 Alloy in Very High Cycle Fatigue Regime. Metals 2020, 10, 1507. [Google Scholar] [CrossRef]
- Zhao, G.; Xin, L.; Li, L.; Zhang, Y.; He, N.; Hansen, H.N. Cutting force model and damage formation mechanism in milling of 70wt% Si/Al composite. Chin. J. Aeronaut. 2023, 36, 114–128. [Google Scholar] [CrossRef]
- Matras, A.; Zębala, W.; Machno, M. Research and Method of Roughness Prediction of a Curvilinear Surface after Titanium Alloy Turning. Materials 2019, 12, 502. [Google Scholar] [CrossRef]
- Mia, M.; Gupta, M.K.; Lozano, J.A.; Carou, D.; Pimenov, D.Y.; Królczyk, G.; Khan, A.M.; Dhar, N.R. Multi-objective optimization and life cycle assessment of eco-friendly cryogenic N2 assisted turning of Ti-6Al-4V. J. Clean. Prod. 2019, 210, 121–133. [Google Scholar] [CrossRef]
- Aslantas, K.; Danish, M.; Hasçelik, A.; Mia, M.; Gupta, M.; Ginta, T.; Ijaz, H. Investigations on Surface Roughness and Tool Wear Characteristics in Micro-Turning of Ti-6Al-4V Alloy. Materials 2020, 13, 2998. [Google Scholar] [CrossRef] [PubMed]
- Yao, C.F.; Tan, L.; Ren, J.X.; Lin, Q.; Liang, Y.S. Surface Integrity and Fatigue Behavior for High-Speed Milling Ti–10V–2Fe–3Al Titanium Alloy. J. Fail. Anal. Prev. 2014, 14, 102–112. [Google Scholar] [CrossRef]
- He, Y.; Xiao, G.; Li, W.; Huang, Y. Residual Stress of a TC17 Titanium Alloy after Belt Grinding and Its Impact on the Fatigue Life. Materials 2018, 11, 2218. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.K. Influence of shot peening on fatigue property of Ti-60 high temperature titanium alloy. Surf. Eng. 2007, 23, 431–433. [Google Scholar] [CrossRef]
- Sahu, N.K.; Andhare, A.B. Multiobjective optimization for improving machinability of Ti-6Al-4V using RSM and advanced algorithms. J. Comput. Des. Eng. 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Xin, H.; Shi, Y.; Ning, L.; Zhao, T. Residual Stress and Affected Layer in Disc Milling of Titanium Alloy. Mater. Manuf. Process. 2016, 31, 1645–1653. [Google Scholar] [CrossRef]
- Cellier, A.; Chalon, F.; Grimal-Perrigouas, V.; Bonhoure, D.; Leroy, R. Effects of Cutting Angles in Ti-6al-4v Milling Process on Surface Integrity: Influence of Roughness and Residual Stresses on Fatigue Limit. Mach. Sci. Technol. 2014, 18, 565–584. [Google Scholar] [CrossRef]
- Yang, D.; Xiao, X.; Liu, Y.; Sun, J. Peripheral milling-induced residual stress and its effect on tensile–tensile fatigue life of aeronautic titanium alloy Ti–6Al–4V. Aeronaut. J. 2019, 123, 212–229. [Google Scholar] [CrossRef]
- Childerhouse, T.; M’Saoubi, R.; Franca, L.; Weston, N.; Crawforth, P.; Jackson, M. The influence of machining induced surface integrity and residual stress on the fatigue performance of Ti-6Al-4V following polycrystalline diamond and coated cemented carbide milling. Int. J. Fatigue 2022, 163, 107054. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, D.; Yao, C.; Tan, L.; Yao, H. Formation mechanism of surface metamorphic layer and influence rule on milling TC17 titanium alloy. Int. J. Adv. Manuf. Technol. 2021, 112, 2259–2276. [Google Scholar] [CrossRef]
- GB/T 10610-2009; Geometrical product specifications (GPS)—Surface texture: Profile method—Rules and procedures for the assessment of surface texture. National Standards of China: Beijing, China, 2009.
- Mia, M.; Bashir, M.A.; Khan, M.A.; Dhar, N.R. Optimization of MQL flow rate for minimum cutting force and surface roughness in end milling of hardened steel (HRC 40). Int. J. Adv. Manuf. Technol. 2017, 89, 675–690. [Google Scholar] [CrossRef]
- AP, Y.; AK, P. Optimization of precipitate hardening parameters of 7075 aluminum alloy using response surface methodology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 7999–8011. [Google Scholar]
- Dai, D.; Zhao, Y.; Cao, C.; Dong, R.; Zhang, H.; Liu, Q.; Song, Z.; Zhang, X.; Zheng, Z.; Zhao, C. Experimental Investigation on Process Parameters during Laser-Assisted Turning of SiC Ceramics Based on Orthogonal Method and Response Surface Methodology. Materials 2022, 15, 4889. [Google Scholar] [CrossRef] [PubMed]
- Sai, G.; Wei, D.; Qinghong, J.; Zhigang, D.; Bi, Z. Surface Integrity of Ultrasonically-Assisted Milled Ti6Al4V Alloy Manufactured by Selective Laser Melting. Chin. J. Mech. Eng. 2021, 34, 67. [Google Scholar]
- Ding, M.C.; Zhang, Y.L.; Lu, H.T. Fatigue life prediction of TC17 titanium alloy based on micro scratch. Int. J. Fatigue 2020, 139, 105793. [Google Scholar] [CrossRef]
- Zhan, Z.; Hu, W.; Meng, Q. Data-driven fatigue life prediction in additive manufactured titanium alloy: A damage mechanics based machine learning framework. Eng. Fract. Mech. 2021, 252, 107850. [Google Scholar] [CrossRef]








| Ti | Al | Sn | Zr | Mo | Cr | N | Fe | C | O | Others |
|---|---|---|---|---|---|---|---|---|---|---|
| Bal. | 4.9 | 2 | 1.9 | 4.2 | 4.2 | 0.02 | 0.1 | 0.02 | 0.1 | Each < 0.10 |
| Total < 0.30 |
) | ) | Density ) | Shrinkage (%) | Elongation (%) | Conductivity °C) | Expansion Coeff °C) |
|---|---|---|---|---|---|---|
| 1180 | 1110 | 4770 | 17.5 | 10 | 6.21 | 11.8 |
| (m/min) | (mm/rev) | (mm) | |
|---|---|---|---|
| Group I | 25, 30, 35, 42 | 0.15 | 0.1 |
| Group II | 35 | 0.15, 0.2, 0.25, 0.35 | 0.1 |
| Group III | 35 | 0.2 | 0.1, 0.2, 0.3, 0.4, 0.5 |
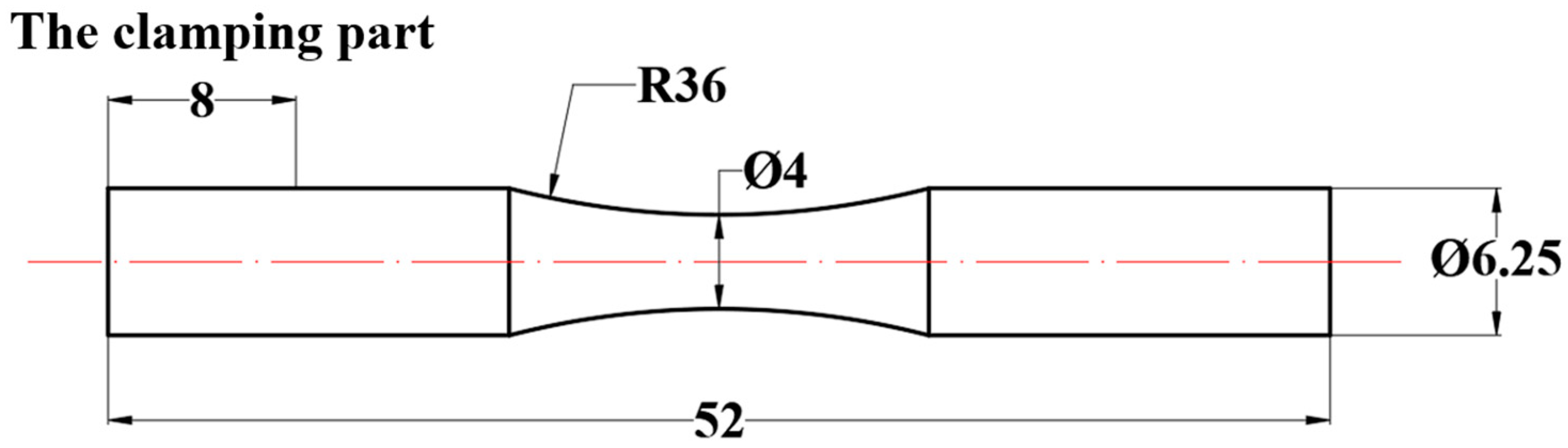
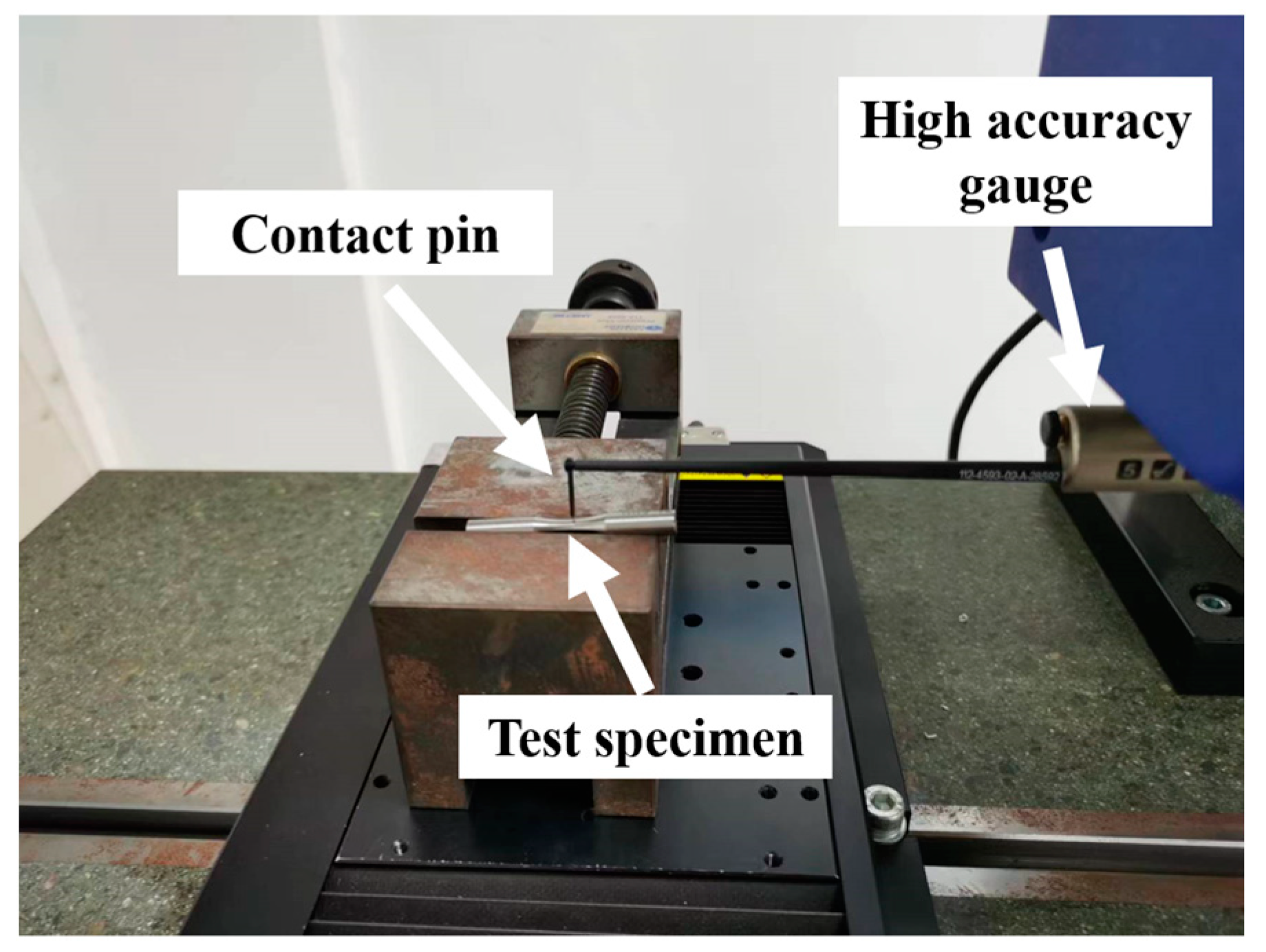
| Experimental Parameter | (Mpa) | r | f (Hz) | (°C) | Waveform | The Form of Failure |
|---|---|---|---|---|---|---|
| Set value | 720 | −1 | 83.3 | 20 | Sine wave | Working section fracture |
| Code | (m/min) | mm/rev) | (mm) |
|---|---|---|---|
| A | 30 | 0.05 | 0.1 |
| B | 40 | 0.15 | 0.2 |
| C | 50 | 0.25 | 0.3 |
| No. | (m/min) | (mm/rev) | (mm) | (μm) | (MPa) |
|---|---|---|---|---|---|
| 1 | 50 | 0.25 | 0.2 | 4.7 | −148 |
| 2 | 40 | 0.25 | 0.3 | 4.82 | −166 |
| 3 | 40 | 0.05 | 0.3 | 0.42 | −375 |
| 4 | 40 | 0.15 | 0.2 | 2.96 | −198 |
| 5 | 30 | 0.05 | 0.2 | 1.06 | −384 |
| 6 | 30 | 0.15 | 0.3 | 2.93 | −231 |
| 7 | 40 | 0.15 | 0.2 | 3.05 | −193 |
| 8 | 40 | 0.25 | 0.1 | 4.9 | −144 |
| 9 | 50 | 0.05 | 0.2 | 0.47 | −336 |
| 10 | 50 | 0.15 | 0.3 | 2.5 | −203 |
| 11 | 40 | 0.15 | 0.2 | 3.06 | −195 |
| 12 | 40 | 0.15 | 0.2 | 2.93 | −207 |
| 13 | 30 | 0.25 | 0.2 | 5.3 | −169 |
| 14 | 30 | 0.15 | 0.1 | 3.22 | −201 |
| 15 | 40 | 0.15 | 0.2 | 3.01 | −203 |
| 16 | 40 | 0.05 | 0.1 | 0.45 | −326 |
| 17 | 50 | 0.15 | 0.1 | 2.76 | −176 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Significant |
|---|---|---|---|---|---|---|
| Model | 9 | 96,107.76 | 10,678.64 | 360.591 | <0.0001 | YES |
| A | 1 | 1860.50 | 1860.50 | 62.824 | <0.0001 | |
| B | 1 | 78,804.50 | 78,804.50 | 2661.030 | <0.0001 | |
| C | 1 | 2048.00 | 2048.00 | 69.156 | <0.0001 | |
| AB | 1 | 182.25 | 182.25 | 6.154 | 0.0229 | |
| BC | 1 | 182.25 | 182.25 | 6.154 | 0.0229 | |
| A2 | 1 | 106.32 | 106.32 | 3.590 | 0.01 | |
| B2 | 1 | 12,748.42 | 12,748.42 | 430.482 | <0.0001 | |
| Residual | 7 | 207.30 | 29.61 | |||
| Lack of Fit | 3 | 74.50 | 24.83 | 0.748 | 0.7565 | |
| Pure Error | 4 | 132.80 | 33.20 | |||
| Cor Total | 16 | 96,315.06 | NO | |||
| R-squared | 0.9997 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Significant |
|---|---|---|---|---|---|---|
| Model | 9 | 38.40 | 4.27 | 438.624 | <0.0001 | YES |
| A | 1 | 0.54 | 0.54 | 55.456 | <0.0001 | |
| B | 1 | 37.53 | 37.53 | 3857.336 | <0.0001 | |
| C | 1 | 0.06 | 0.06 | 5.751 | 0.0305 | |
| AC | 1 | 0.00 | 0.00 | 0.014 | 0.0091 | |
| BC | 1 | 0.00 | 0.00 | 0.064 | 0.0087 | |
| B2 | 1 | 0.11 | 0.11 | 11.196 | 0.0123 | |
| C2 | 1 | 0.16 | 0.16 | 16.032 | 0.0052 | |
| Residual | 7 | 0.07 | 0.01 | |||
| Lack of Fit | 3 | 0.06 | 0.02 | 5.803 | 0.0612 | |
| Pure Error | 4 | 0.01 | 0.00 | |||
| Cor Total | 16 | 38.47 | NO | |||
| R-Squared | 0.9980 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, X.; Wang, Y.; Wang, D.; Zhao, G.; Yang, Y. Research on Surface Integrity and Fatigue Properties in the Turning of TC17 Titanium Alloy Based on the Response Surface Method. Materials 2023, 16, 7180. https://doi.org/10.3390/ma16227180
Lai X, Wang Y, Wang D, Zhao G, Yang Y. Research on Surface Integrity and Fatigue Properties in the Turning of TC17 Titanium Alloy Based on the Response Surface Method. Materials. 2023; 16(22):7180. https://doi.org/10.3390/ma16227180
Chicago/Turabian StyleLai, Xunqing, Yuannan Wang, Dan Wang, Guolong Zhao, and Yinfei Yang. 2023. "Research on Surface Integrity and Fatigue Properties in the Turning of TC17 Titanium Alloy Based on the Response Surface Method" Materials 16, no. 22: 7180. https://doi.org/10.3390/ma16227180
APA StyleLai, X., Wang, Y., Wang, D., Zhao, G., & Yang, Y. (2023). Research on Surface Integrity and Fatigue Properties in the Turning of TC17 Titanium Alloy Based on the Response Surface Method. Materials, 16(22), 7180. https://doi.org/10.3390/ma16227180








