Investigation of Rutting Performance in Geogrid-Reinforced Asphalt by Penetration Test
Abstract
:1. Introduction
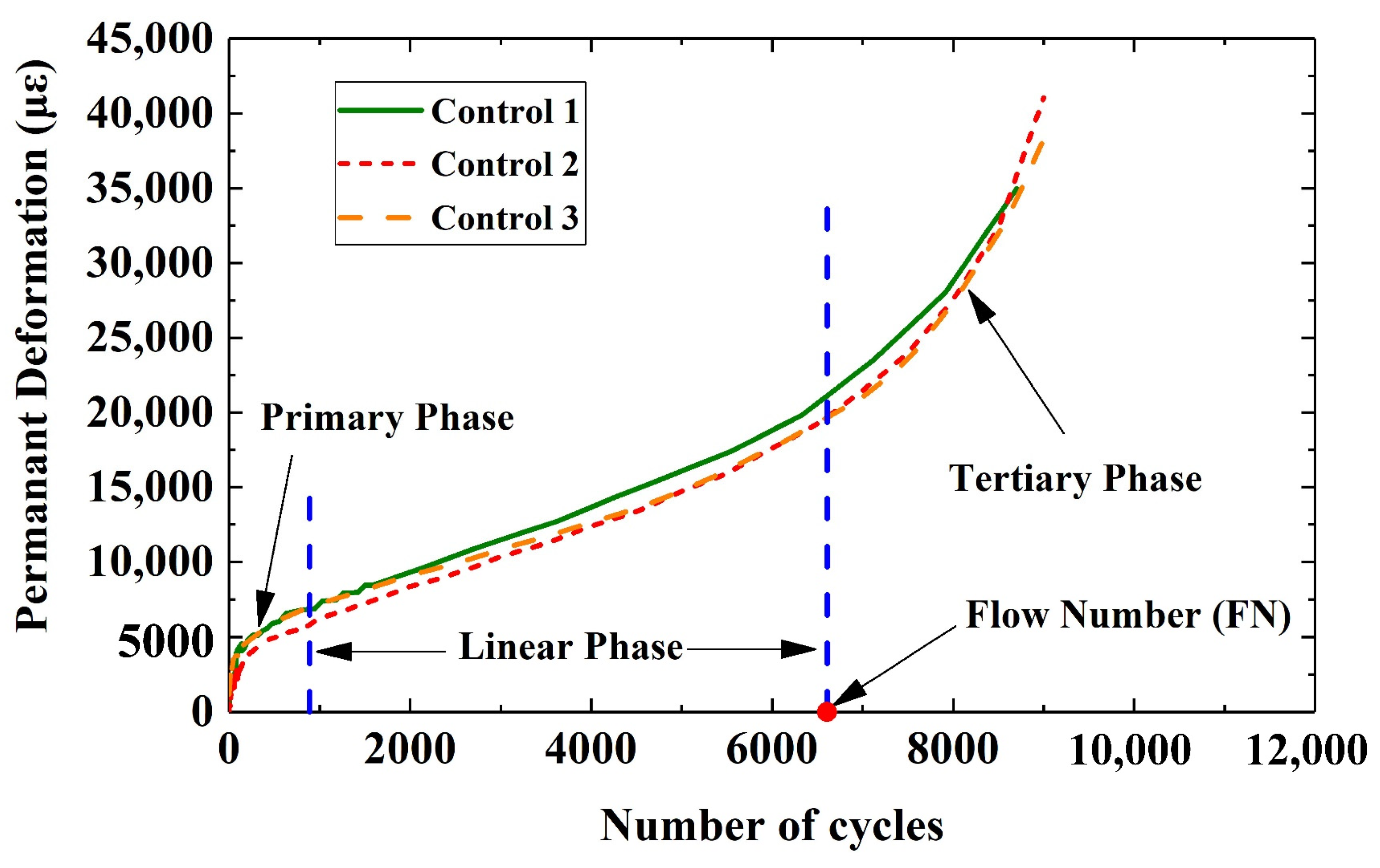
2. Background
- where, εp = accumulated permanent strain, total strain, με;
- εI, εII = accumulated permanent strain corresponding to the end of Stage I and Stage II, με;
- N = number of total load repetitions;
- NI, NII = number of load repetitions corresponding to the end of Stage I and Stage II, onset of next stage.
3. Materials and Methodology
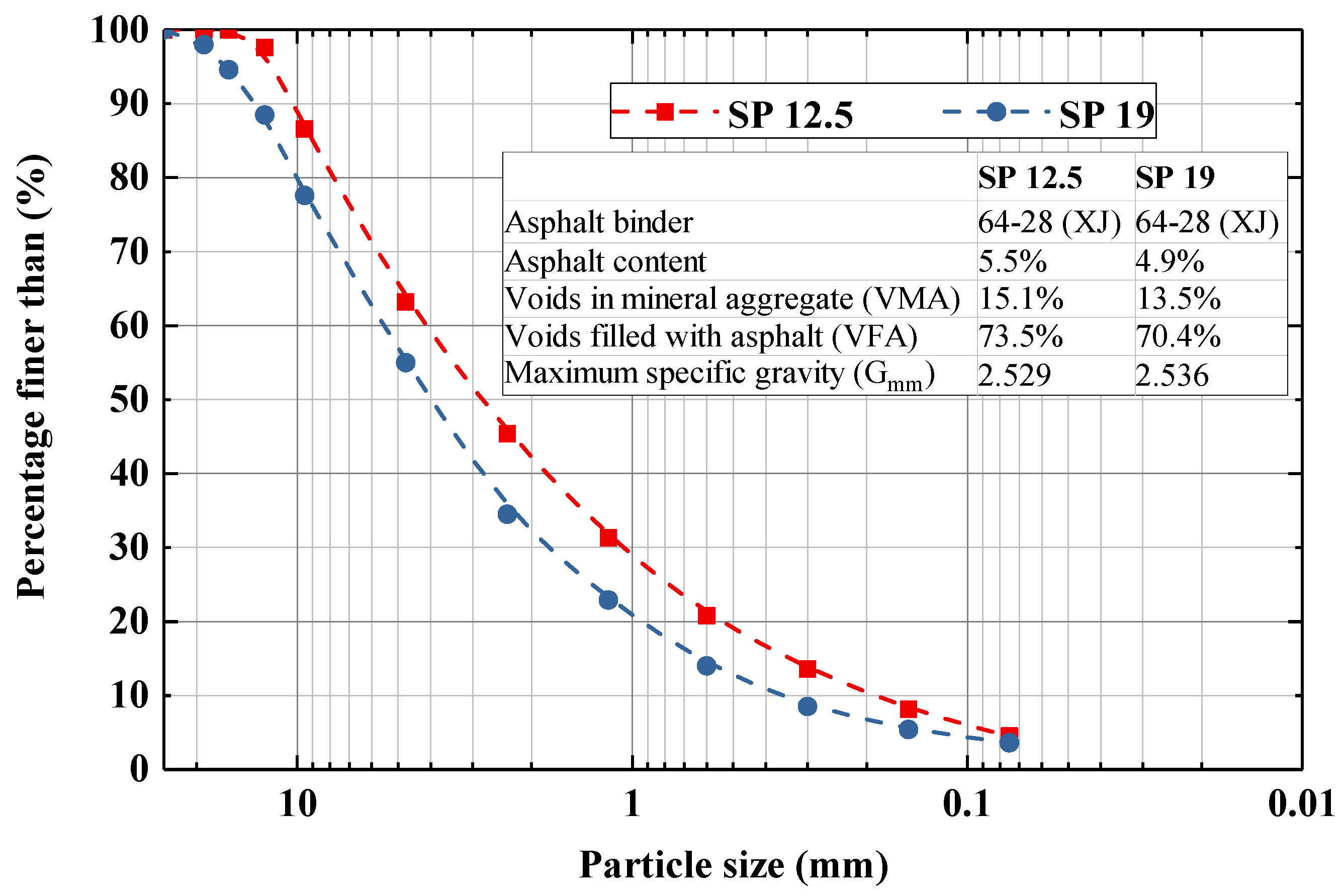
3.1. Asphalt Mixture
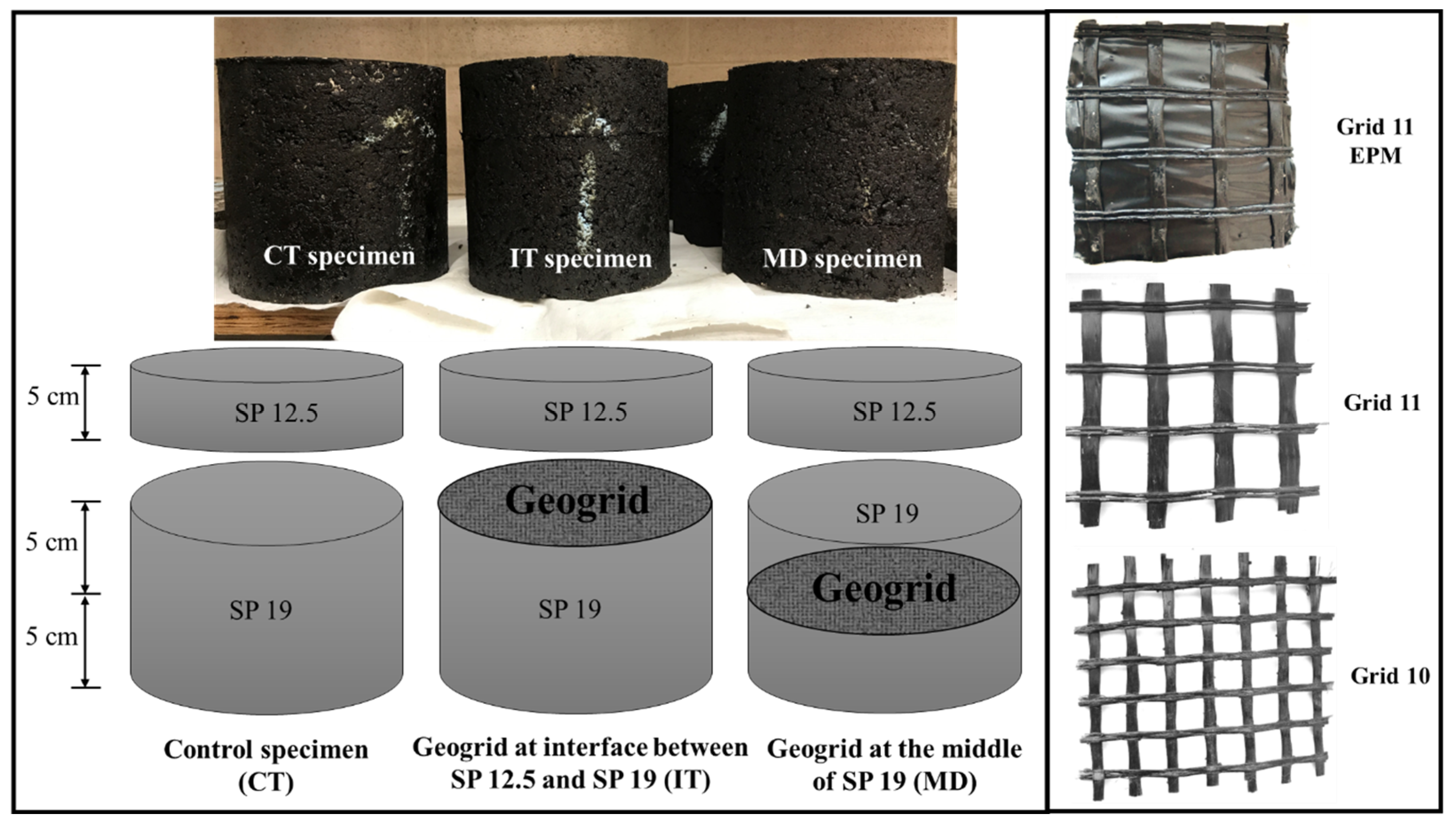
3.2. Fibreglass Geogrids
3.3. Tack Coat
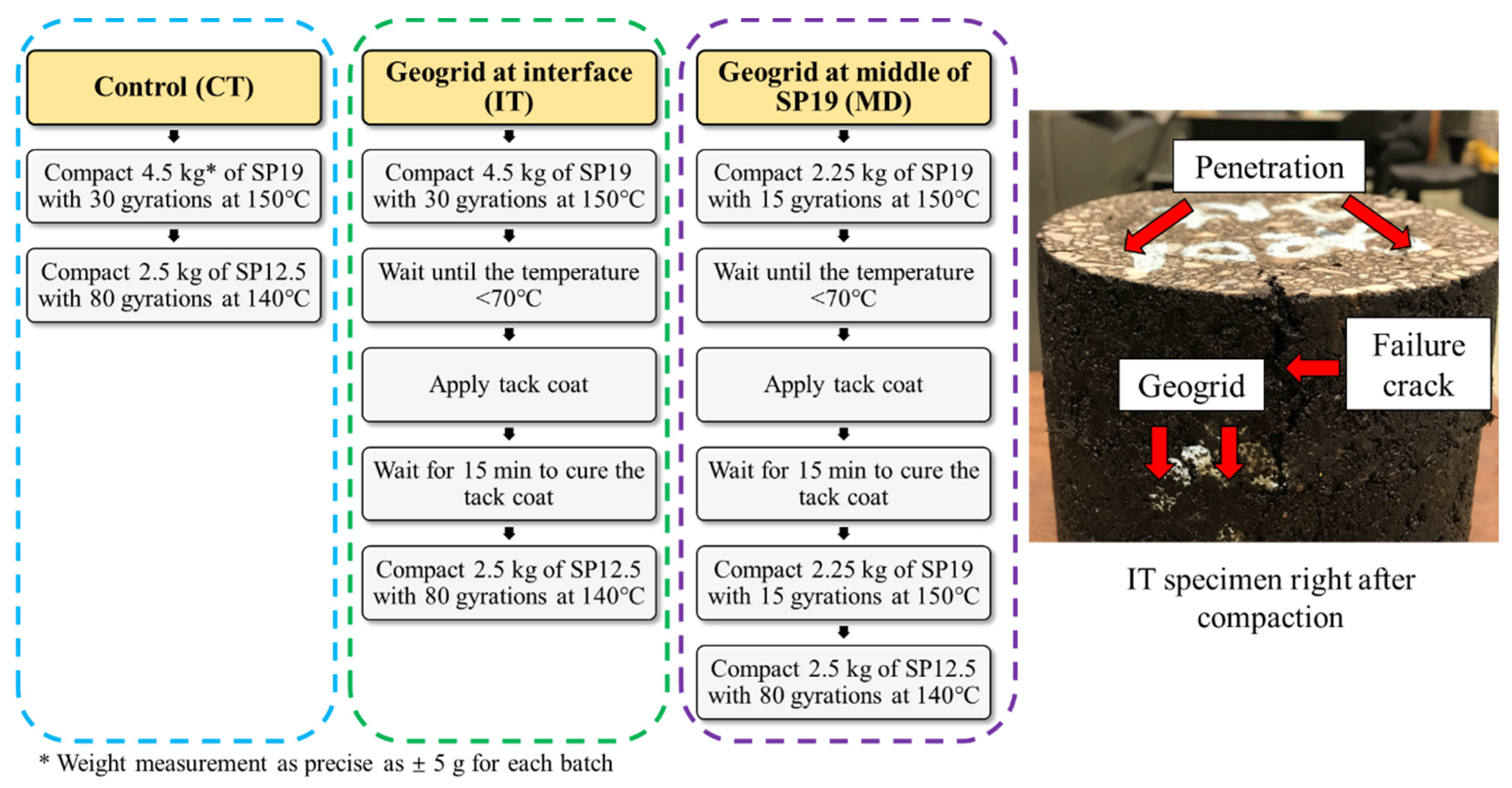
3.4. Sample Preparation
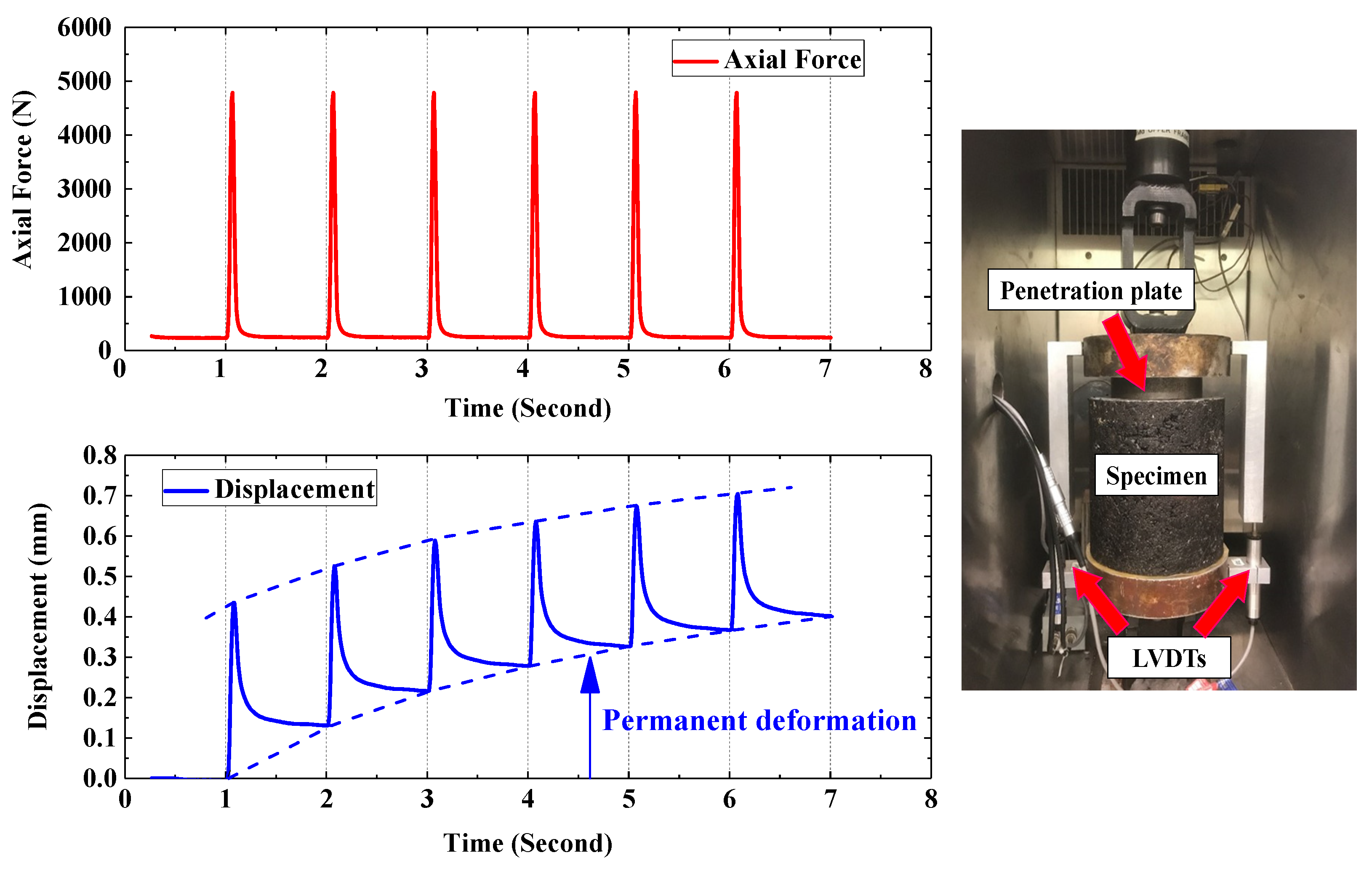
3.5. Test Set-Up
4. Results and Discussion
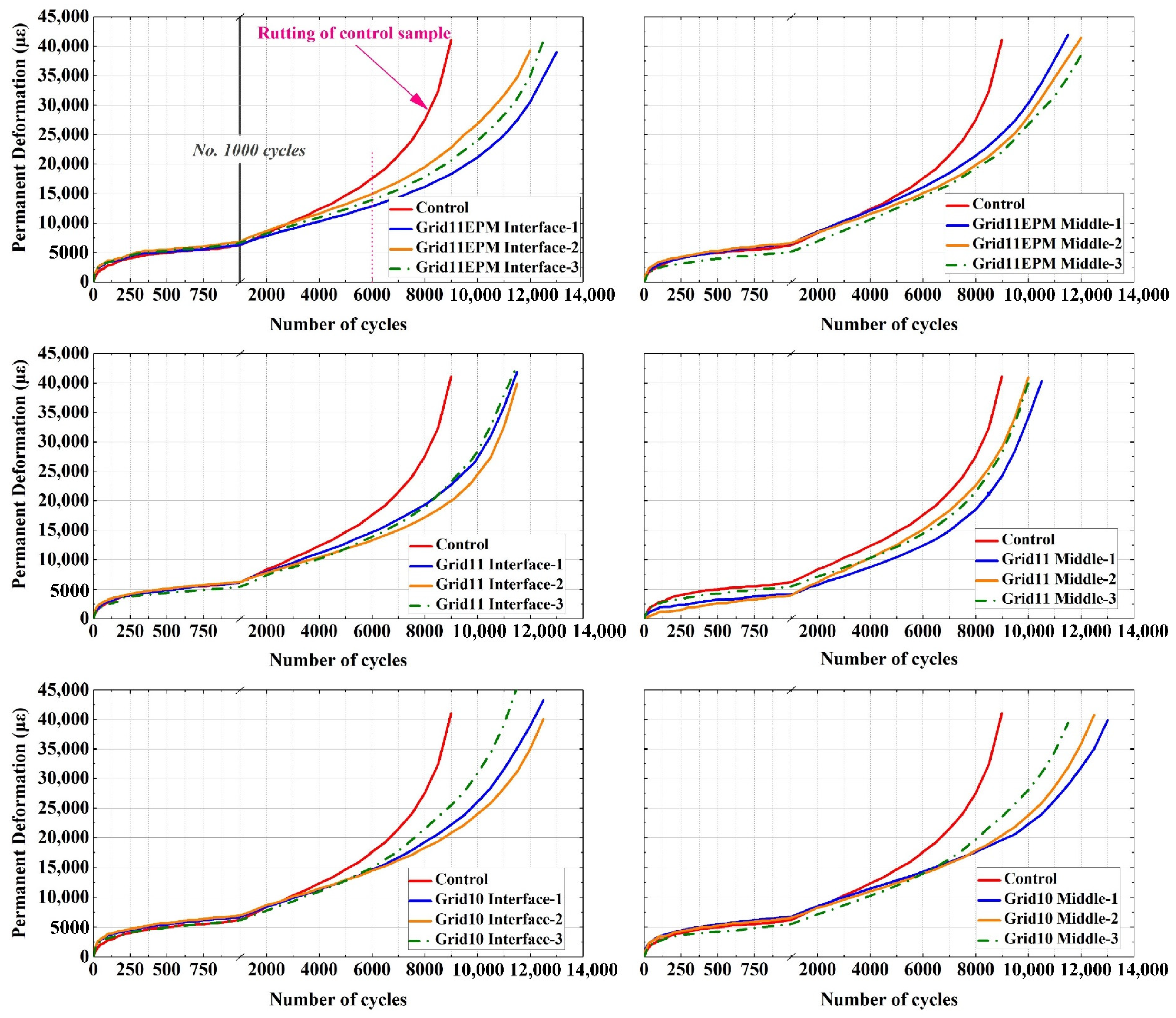
4.1. Development of Permanent Deformation
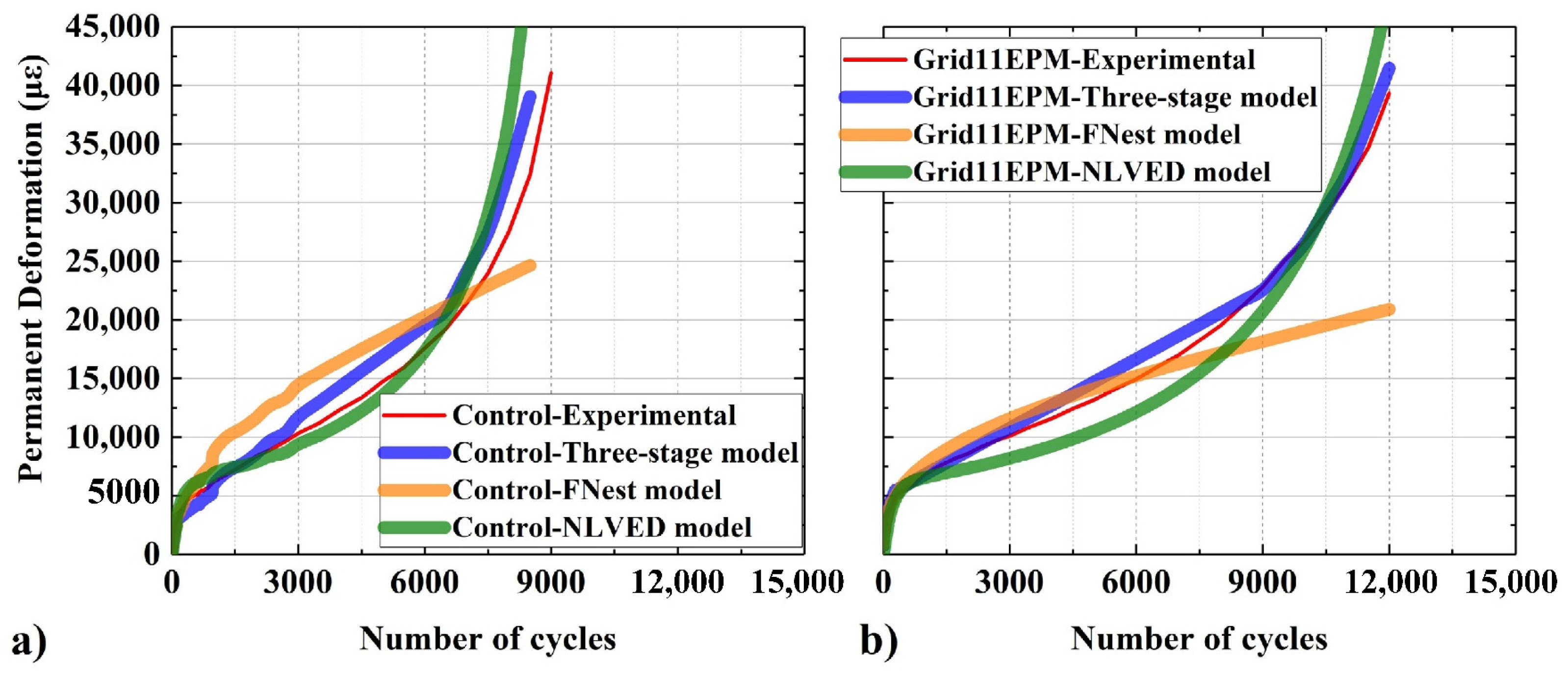
4.2. Fitting of Permanent Deformation
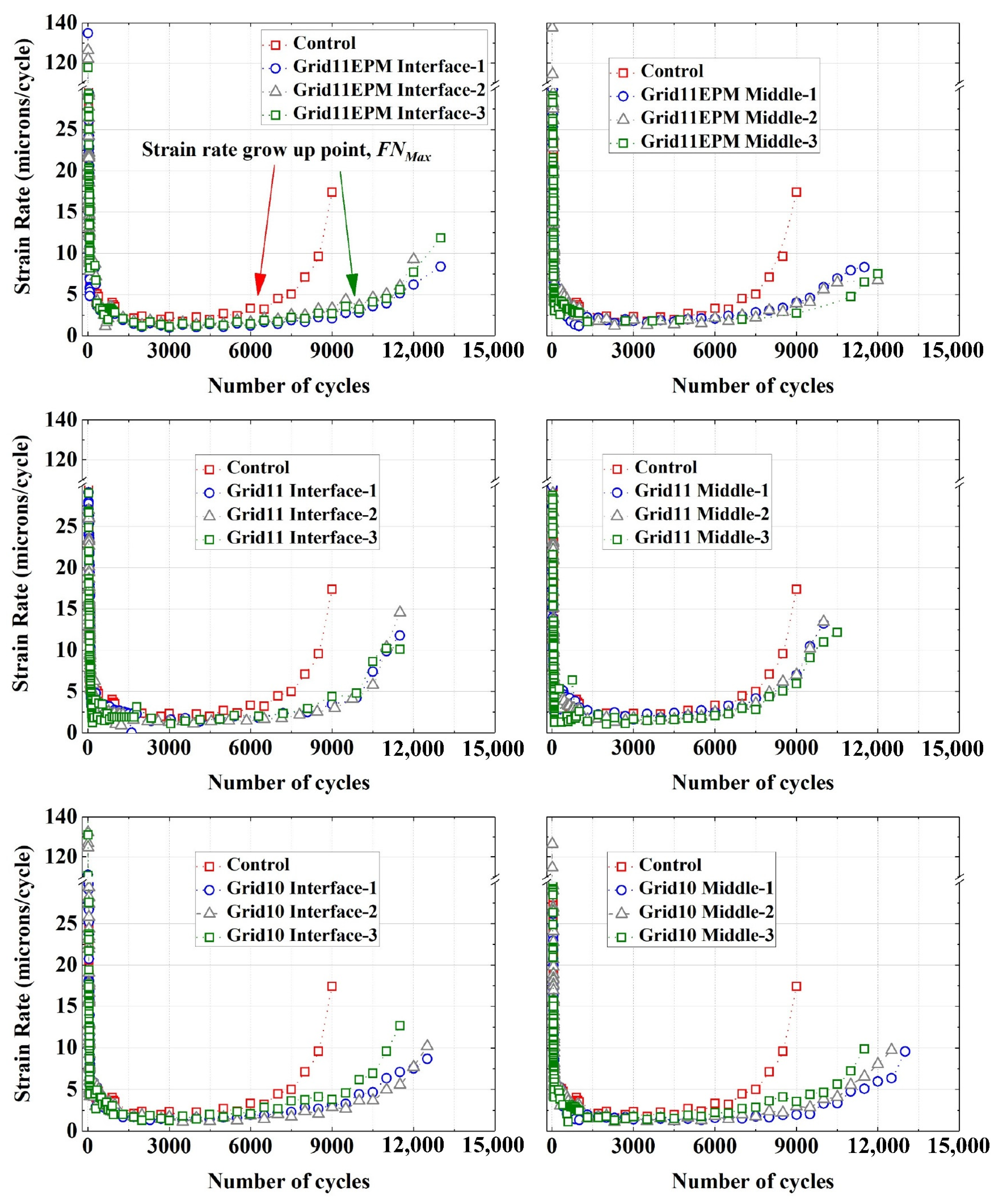
4.3. Strain Rate
- where, = smoothened strain rate at load cycle (microns/cycle), i;
- ∆N = data sampling interval.
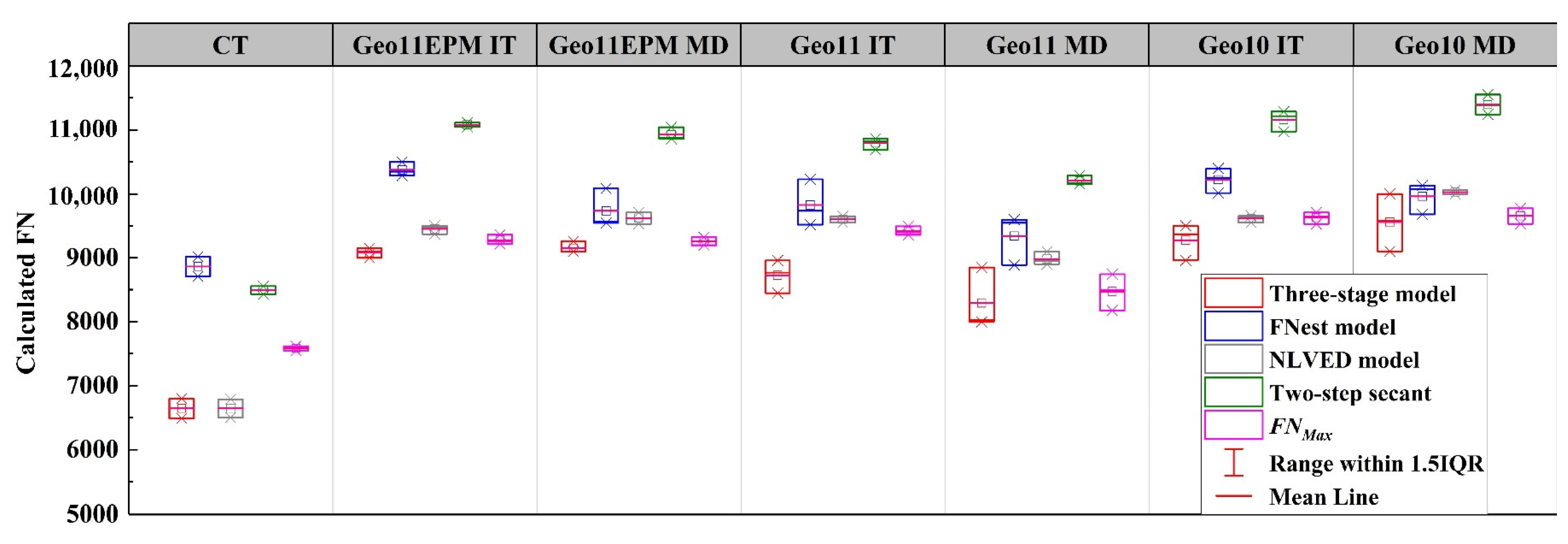
4.4. Flow Number
4.5. Reinforcement Location and Types of Geogrids
5. Conclusions
- (1)
- The proposed penetration test is a convenient experimental method to measure the rutting performance of geogrid-reinforced asphalt mixtures. Under penetration, the performance deformation followed the three-stage phases. In comparison, the geogrid-reinforced asphalt samples entered the tertiary phase later than those of control samples.
- (2)
- The top-down cracks (TDCs) generated by repeated loading were prevented from propagating deeper due to the presence of the geogrid reinforcement. Such phenomenon is more distinct when the geogrid was put at the interface between wearing and binder course.
- (3)
- Among the current fitting models for permanent deformation, the three-stage and NLVED models showed better fitting results compared to the experimental data with higher R2 values. The regression operation for three-stage model was more convenient since the regression was divided into steps and fewer regression coefficients were required to calculate.
- (4)
- The strain rate dropped sharply in the first 500 cycles for both control and geogrid reinforced samples. After 500 cycles, the strain rate remained relatively constant and at very low level, ranging between 0 and 5 microns/cycle. Nevertheless, the constant rate was extended for a greater number of cycles in reinforced specimens than control specimen indicating that the geogrid could delay entering the tertiary phase.
- (5)
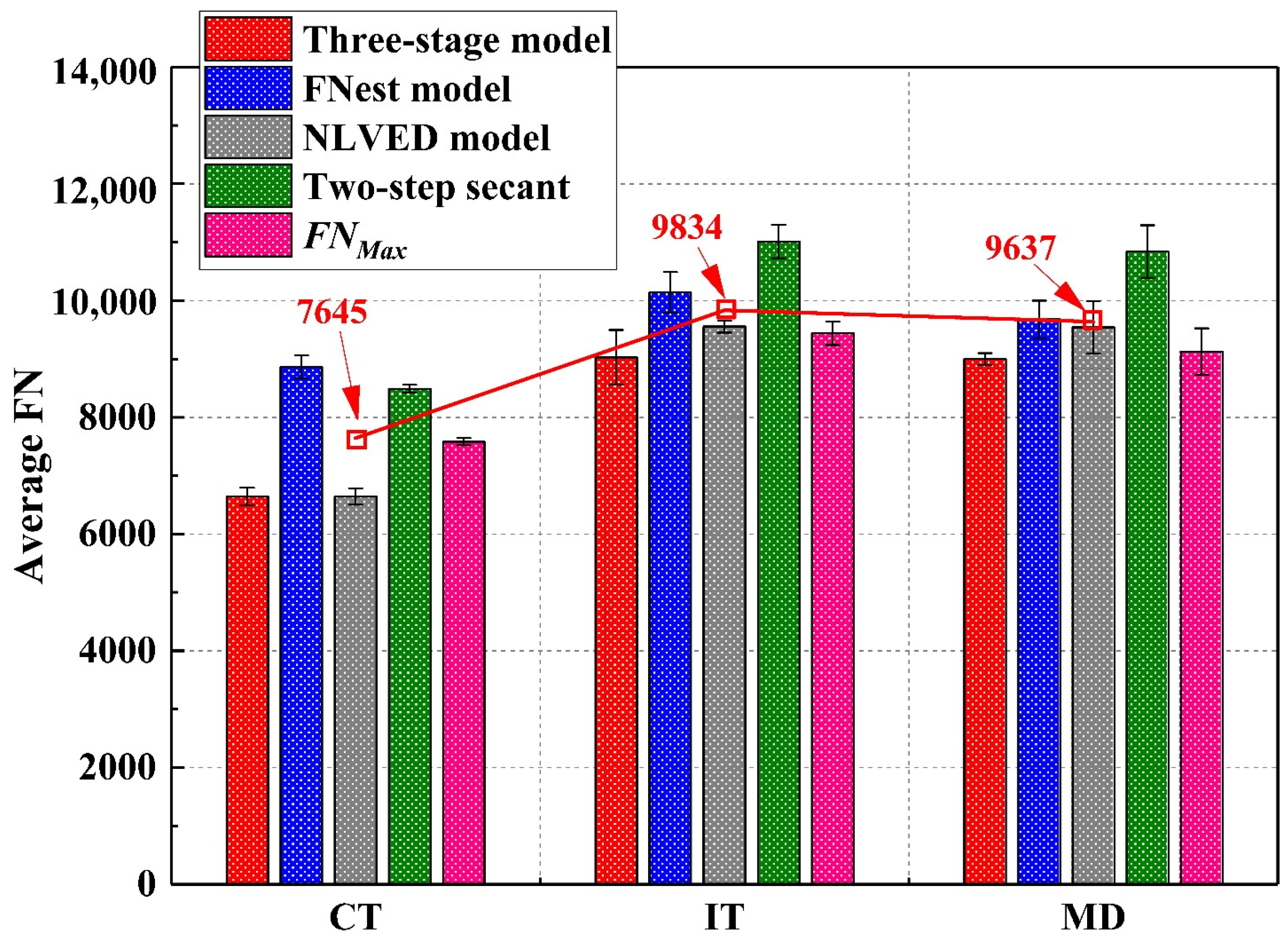
- Based on the strain rate, a new FN calculation was proposed, which is called FNMax. FNMax denoted the maximum number of cycles, which still remains at a low strain rate (<3). FN valued predicted by the NLVED and FNMax methods were similar to each other and were more consistent. In particular, the FNMax method could be more practical given its calculation principle and its simplicity.
- (6)
- An average FN increase between 26% and 29% was observed for geogrid-reinforced asphalt compared to control samples. In addition, there is a small increase in FN in IT samples from MD specimens. On the other hand, Grid10 with smaller aperture size had slightly better rutting resistance compared to the other two geogrid types, followed by Grid11EPM and Grid11.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mounes, S.M.; Karim, M.R.; Khodaii, A.; Almasi, M.H. Evaluation of permanent deformation of geogrid reinforced asphalt concrete using dynamic creep test. Geotext. Geomembr. 2016, 44, 109–116. [Google Scholar] [CrossRef]
- Abdelfattah, H.F.H.; Baaj, H.; Kadhim, H.J. Calibration of MEPDG permanent deformation models using Hamburg Wheel Rut Tester and field data. Int. J. Pavement Eng. 2021, 23, 4174–4189. [Google Scholar] [CrossRef]
- Fang, H.; Liu, Q.; Mo, L.; Javilla, B.; Shu, B.; Wu, S. Characterization of three-stage rutting development of asphalt mixtures. Constr. Build. Mater. 2017, 154, 340–348. [Google Scholar] [CrossRef]
- Javilla, B.; Mo, L.; Hao, F.; Shu, B.; Wu, S. Multi-stress loading effect on rutting performance of asphalt mixtures based on wheel tracking testing. Constr. Build. Mater. 2017, 148, 1–9. [Google Scholar] [CrossRef]
- El-Hakim, M.; Tighe, S.L. Impact of Freeze–Thaw Cycles on Mechanical Properties of Asphalt Mixes. Transp. Res. Rec. J. Transp. Res. Board 2014, 2444, 20–27. [Google Scholar] [CrossRef]
- Nguyen, M.-L.; Blanc, J.; Kerzrého, J.-P.; Hornych, P. Review of glass fibre grid use for pavement reinforcement and APT experiments at IFSTTAR. Road Mater. Pavement Des. 2013, 14 (Suppl. S1), 287–308. [Google Scholar] [CrossRef]
- Koerner, R.M. Designing with Geosynthetics, 6th ed.; Xlibris Corporation: Englewood Cliffs, NJ, USA, 2012. [Google Scholar]
- Wang, D.; Wang, S.-L.; Tighe, S.; Bhat, S.; Yin, S. Construction of Geosynthetic–Reinforced Pavements and Evaluation of Their Impacts. Appl. Sci. 2023, 13, 10327. [Google Scholar] [CrossRef]
- Gu, F.; Luo, X.; Luo, R.; Lytton, R.L.; Hajj, E.Y.; Siddharthan, R.V. Numerical modeling of geogrid-reinforced flexible pavement and corresponding validation using large-scale tank test. Constr. Build. Mater. 2016, 122, 214–230. [Google Scholar] [CrossRef]
- Qadir, A.; Gazder, U.; Choudhary, K.-U.-N. Statistical analysis for comparing and predicting rutting resistance of asphalt pavements with rigid and flexible geogrid layers. Constr. Build. Mater. 2021, 302, 124136. [Google Scholar] [CrossRef]
- Perkins, S.W. Mechanisic-Empirical Modeling and Design Model Development of Geosynthetic Reinforced Felxible Pavements; FHWA/MT-01-002/99160-1A; Montana State University: Bozeman, MT, USA, 2001. [Google Scholar]
- Freire, R.A.; Di Benedetto, H.; Sauzéat, C.; Pouget, S.; Lesueur, D. Crack propagation analysis in bituminous mixtures reinforced by different types of geogrids using digital image correlation. Constr. Build. Mater. 2021, 303, 124522. [Google Scholar] [CrossRef]
- Lee, J.-H.; Baek, S.-B.; Lee, K.-H.; Kim, J.-S.; Jeong, J.-H. Long-term performance of fiber-grid-reinforced asphalt overlay pavements: A case study of Korean national highways. J. Traffic Transp. Eng. Engl. Ed. 2019, 6, 366–382. [Google Scholar] [CrossRef]
- Zhang, J.; Alvarez, A.E.; Lee, S.I.; Torres, A.; Walubita, L.F. Comparison of flow number, dynamic modulus, and repeated load tests for evaluation of HMA permanent deformation. Constr. Build. Mater. 2013, 44, 391–398. [Google Scholar] [CrossRef]
- Liu, H.; Luo, R.; Xi, L.; Hu, L. Development of Two-Step Secant Method to Interpret the Flow Number Test Data of Asphalt Mixtures. J. Mater. Civ. Eng. 2020, 32, 4020027. [Google Scholar] [CrossRef]
- Correia, N.S.; Zornberg, J.G. Strain distribution along geogrid-reinforced asphalt overlays under traffic loading. Geotext. Geomembr. 2018, 46, 111–120. [Google Scholar] [CrossRef]
- Solatiyan, E.; Bueche, N.; Carter, A. Laboratory evaluation of interfacial mechanical properties in geogrid-reinforced bituminous layers. Geotext. Geomembr. 2021, 49, 895–909. [Google Scholar] [CrossRef]
- Virgili, A.; Canestrari, F.; Grilli, A.; Santagata, F.A. Repeated load test on bituminous systems reinforced by geosynthetics. Geotext. Geomembr. 2009, 27, 187–195. [Google Scholar] [CrossRef]
- Kumar, V.V.; Saride, S.; Zornberg, J.G. Mechanical response of full-scale geosynthetic-reinforced asphalt overlays subjected to repeated loads. Transp. Geotech. 2021, 30, 100617. [Google Scholar] [CrossRef]
- Witczak, M. Simple Performance Tests: Summary of Recommended Methods and Database; Northwestern University: Washington, DC, USA, 2006. [Google Scholar]
- Zhang, J.; Fan, Z.; Fang, K.; Pei, J.; Xu, L. Development and validation of nonlinear viscoelastic damage (NLVED) model for three-stage permanent deformation of asphalt concrete. Constr. Build. Mater. 2016, 102, 384–392. [Google Scholar] [CrossRef]
- Biligiri, K.P.; Kaloush, K.E.; Mamlouk, M.S.; Witczak, M.W. Rational Modeling of Tertiary Flow for Asphalt Mixtures. Transp. Res. Rec. J. Transp. Res. Board 2007, 2001, 63–72. [Google Scholar] [CrossRef]
- Zhou, F.; Scullion, T.; Sun, L. Verification and Modeling of Three-Stage Permanent Deformation Behavior of Asphalt Mixes. J. Transp. Eng. 2004, 130, 486–494. [Google Scholar] [CrossRef]
- Archilla, A.R.; Diaz, L.G.; Carpenter, S.H. Proposed Method to Determine the Flow Number in Bituminous Mixtures from Repeated Axial Load Tests. J. Transp. Eng. 2007, 133, 610–617. [Google Scholar] [CrossRef]
- Witczak, M.W.; Kaloush, K.; Pellinen, T.; El-Basyouny, M.; Von Quintus, H. Simple Performance Test for Superpave Mix Design; NCHRP Report 465; Transportation Research Board: Washington, DC, USA, 2002. [Google Scholar]
- Ghaly, N.F.; Ibrahim, I.M.; Noamy, E.M. Tack coats for asphalt paving. Egypt. J. Pet. 2014, 23, 61–65. [Google Scholar] [CrossRef]
- AASHTO T 166; Standard Method of Test for Bulk Specific Gravity (Gmb) of Compacted Asphalt Mixtures Using Saturated Surface-Dry Specimens. American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2022.
- AASHTO T 378; Standard Method of Test for Determining the Dynamic Modulus and Flow Number for Asphalt Mixtures Using the Asphalt Mixture Performance Tester (AMPT). American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2017.
- Correia, N.S.; Zornberg, J.G. Mechanical response of flexible pavements enhanced with geogrid-reinforced asphalt overlays. Geosynth. Int. 2016, 23, 183–193. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, H.; Zhang, S.; Jiang, S. Constitutive model of concrete creep damage considering the deterioration of creep parameters. Constr. Build. Mater. 2021, 308, 125047. [Google Scholar] [CrossRef]
- Li, Y.; Qiang, S.; Xu, W.; Hua, X.; Xu, C.; Lai, J.; Yuan, M.; Chen, B. Verification of concrete nonlinear creep mechanism based on meso-damage mechanics. Constr. Build. Mater. 2021, 276, 122205. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Li, Y.; Li, Y.; Wang, R. Evaluation of concrete creep properties based on indentation test and multiscale homogenization method. Cem. Concr. Compos. 2021, 123, 104135. [Google Scholar] [CrossRef]
- Collop, A.C.; Roque, R. Report on the Prediction of Surface-Initiated Longitudinal Wheel Path Cracking in Asphalt Pavements. Road Mater. Pavement Des. 2011, 5, 409–434. [Google Scholar] [CrossRef]
- Canestrari, F.; Ingrassia, L.P. A review of top-down cracking in asphalt pavements: Causes, models, experimental tools and future challenges. J. Traffic Transp. Eng. Engl. Ed. 2020, 7, 541–572. [Google Scholar] [CrossRef]
- Zou, W.-L.; Wang, Z.; Zhang, H.-M. Field Trial for Asphalt Pavements Reinforced with Geosynthetics and Behavior of Glass-Fiber Grids. J. Perform. Constr. Facil. 2007, 21, 361–367. [Google Scholar] [CrossRef]


| Source | Flow Number (FN) Model | Particular Variable | Equation |
|---|---|---|---|
| [3] | material constant, obtained by regression | (1) | |
| [22] | material constant, obtained by regression | (2) | |
| [23] | Stage I: | material constant, obtained by regression | (3) |
| Stage II: | |||
| Stage III: | |||
| [24] | FNest flow number; equals to NII | (4) | |
| [21] | εNLV permanent viscous strain. εNLVED permanent viscous strainincorporating damage variable. σ0 peak value of the haversine load. t0 loading time of a cycle. A,B material constant D Chaboche and Lemaitre damage variable | (5) | |
| Category | Unit | Grid11EPM | Grid11 | Grid10 |
|---|---|---|---|---|
| Ultimate tensile strength | kN/m | 100.0 | 100.0 | 100.0 |
| Strain at ultimate tensile strength | % | <3 | <3 | <3 |
| Tensile strength at 2% strain | kN/m | 75.0 | 80.0 | 80.0 |
| Secant stiffness at 2% strain | kN/m | 3750 | 4000 | 4000 |
| Aperture size | mm | 25.4 | 25.4 | 12.7 |
| Melting point of coating | °C | 400 | 400 | 400 |
| Melting point of glass | °C | 820 | 820 | 820 |
| Melting point of EPM | °C | 124 | -- | -- |
| Mass/Unit area | g/m2 | 432 | 420 | 420 |
| Specimen Label | Gmm | Gmb | VTM (%) |
|---|---|---|---|
| Control (CT) | 2.534 | 2.354~2.410 | 7.02~7.10 |
| Geo11EPM Interface (IT) | 2.534 | 2.330~2.365 | 6.67~8.05 |
| Geo11EPM Middle (MD) | 2.534 | 2.341~2.367 | 6.59~7.62 |
| Geo11 Interface (IT) | 2.534 | 2.367~2.368 | 6.55~6.59 |
| Geo11 Middle (MD) | 2.534 | 2.370~2.373 | 6.35~6.47 |
| Geo10 Interface (IT) | 2.534 | 2.358~2.367 | 6.59~6.95 |
| Geo10 Middle (MD) | 2.534 | 2.348~2.362 | 6.79~7.34 |
| No. of Specimen | Three-Stage Model (Equation (3)) | FNest Model (Equation (4)) | Nonlinear Viscoelastic (NLVED) Model (Equation (5)) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | NI | NII/FN | Ave. SR | R2 | FN | Ave. SR | R2 | FN | Ave. SR | ||
| CT | 1 | 0.98 | 169 | 6799 | ±0.23 | 0.73 | 9019 | ±1.59 | 0.97 | 6500 | ±0.40 |
| 2 | 0.98 | 189 | 6489 | ±0.36 | 0.75 | 8709 | ±1.45 | 0.95 | 6789 | ±0.54 | |
| Geo11EPM IT | 1 | 0.98 | 299 | 9099 | ±0.25 | 0.83 | 10,348 | ±1.24 | 0.95 | 9369 | ±0.49 |
| 2 | 0.99 | 349 | 8999 | ±0.22 | 0.83 | 10,497 | ±1.47 | 0.96 | 9499 | ±0.56 | |
| 3 | 0.97 | 399 | 9147 | ±0.29 | 0.87 | 10,285 | ±1.54 | 0.98 | 9479 | ±0.52 | |
| Geo11EPM MD | 1 | 0.99 | 269 | 9257 | ±0.30 | 0.84 | 9544 | ±1.54 | 0.92 | 9528 | ±0.55 |
| 2 | 0.94 | 229 | 9099 | ±0.26 | 0.83 | 10,083 | ±1.50 | 0.97 | 9619 | ±0.51 | |
| 3 | 0.96 | 255 | 9099 | ±0.21 | 0.80 | 9567 | ±1.20 | 0.94 | 9709 | ±0.49 | |
| Geo11 IT | 1 | 0.97 | 345 | 8958 | ±0.18 | 0.82 | 9732 | ±1.40 | 0.94 | 9649 | ±0.59 |
| 2 | 0.95 | 296 | 8448 | ±0.14 | 0.81 | 10,227 | ±1.50 | 0.98 | 9549 | ±0.62 | |
| 3 | 0.93 | 286 | 8768 | ±0.21 | 0.78 | 9516 | ±1.70 | 0.96 | 9606 | ±0.48 | |
| Geo11 MD | 1 | 0.98 | 256 | 8847 | ±0.28 | 0.78 | 8886 | ±1.61 | 0.97 | 9098 | ±0.44 |
| 2 | 0.96 | 199 | 7999 | ±0.20 | 0.85 | 9544 | ±1.43 | 0.99 | 8950 | ±0.50 | |
| 3 | 0.95 | 399 | 8028 | ±0.22 | 0.80 | 9594 | ±2.02 | 0.93 | 8899 | ±0.40 | |
| Geo10 IT | 1 | 0.96 | 237 | 9369 | ±0.32 | 0.82 | 10,253 | ±1.56 | 0.94 | 9639 | ±0.55 |
| 2 | 0.96 | 269 | 9499 | ±0.30 | 0.74 | 10,394 | ±1.50 | 0.97 | 9549 | ±0.62 | |
| 3 | 0.95 | 369 | 8959 | ±0.22 | 0.72 | 10,012 | ±0.46 | 0.93 | 9655 | ±0.51 | |
| Geo10 MD | 1 | 0.94 | 305 | 9579 | ±0.30 | 0.85 | 10,129 | ±1.24 | 0.92 | 9998 | ±0.41 |
| 2 | 0.96 | 269 | 9999 | ±0.26 | 0.73 | 10,076 | ±1.50 | 0.97 | 10,059 | ±0.59 | |
| 3 | 0.99 | 257 | 9099 | ±0.28 | 0.83 | 9681 | ±1.38 | 0.97 | 10,028 | ±0.44 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-L.; Wang, D.; Tighe, S.; Bhat, S.; Yin, S. Investigation of Rutting Performance in Geogrid-Reinforced Asphalt by Penetration Test. Materials 2023, 16, 7221. https://doi.org/10.3390/ma16227221
Wang S-L, Wang D, Tighe S, Bhat S, Yin S. Investigation of Rutting Performance in Geogrid-Reinforced Asphalt by Penetration Test. Materials. 2023; 16(22):7221. https://doi.org/10.3390/ma16227221
Chicago/Turabian StyleWang, Sheng-Lin, Danrong Wang, Susan Tighe, Sam Bhat, and Shunde Yin. 2023. "Investigation of Rutting Performance in Geogrid-Reinforced Asphalt by Penetration Test" Materials 16, no. 22: 7221. https://doi.org/10.3390/ma16227221
APA StyleWang, S.-L., Wang, D., Tighe, S., Bhat, S., & Yin, S. (2023). Investigation of Rutting Performance in Geogrid-Reinforced Asphalt by Penetration Test. Materials, 16(22), 7221. https://doi.org/10.3390/ma16227221







