Simulation Study on the Influence of Different Molten Steel Temperatures on Inclusion Distribution under Dual-Channel Induction-Heating Conditions
Abstract
:1. Introduction
2. Mathematical Model Description
2.1. Geometry and Meshing
2.1.1. Geometry
2.1.2. Meshing
2.2. Assumptions
- Molten steel is an incompressible Newtonian fluid.
- The effect of slag on molten steel is not considered.
- The molten steel flow is steady.
- The collision growth of inclusion particles is not taken into account.
- The inclusion particles are eliminated when they reach the top layer of the molten steel.
2.3. Governing Equations
2.4. Model-Solving Process and Boundary Conditions
3. Results and Discussion
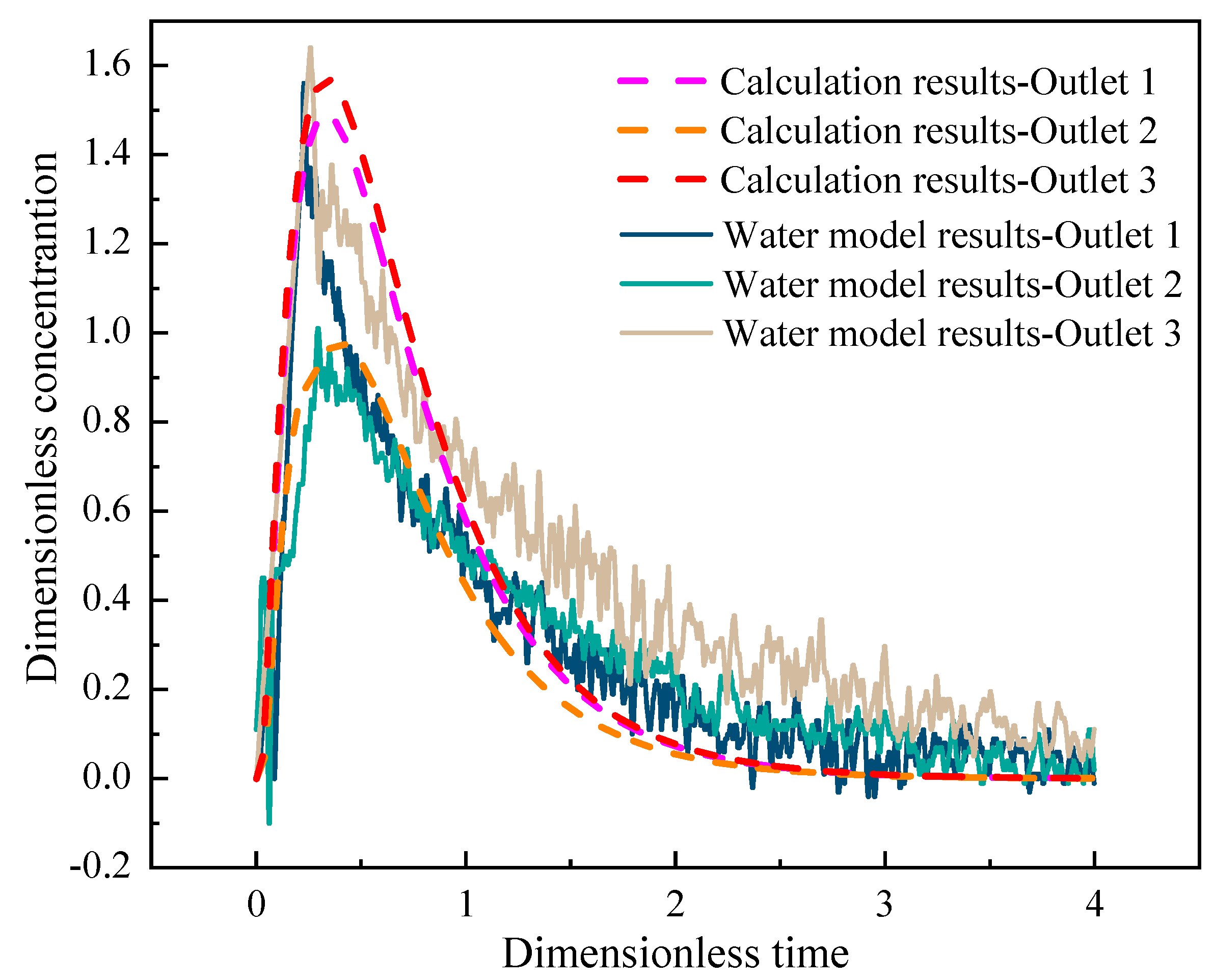
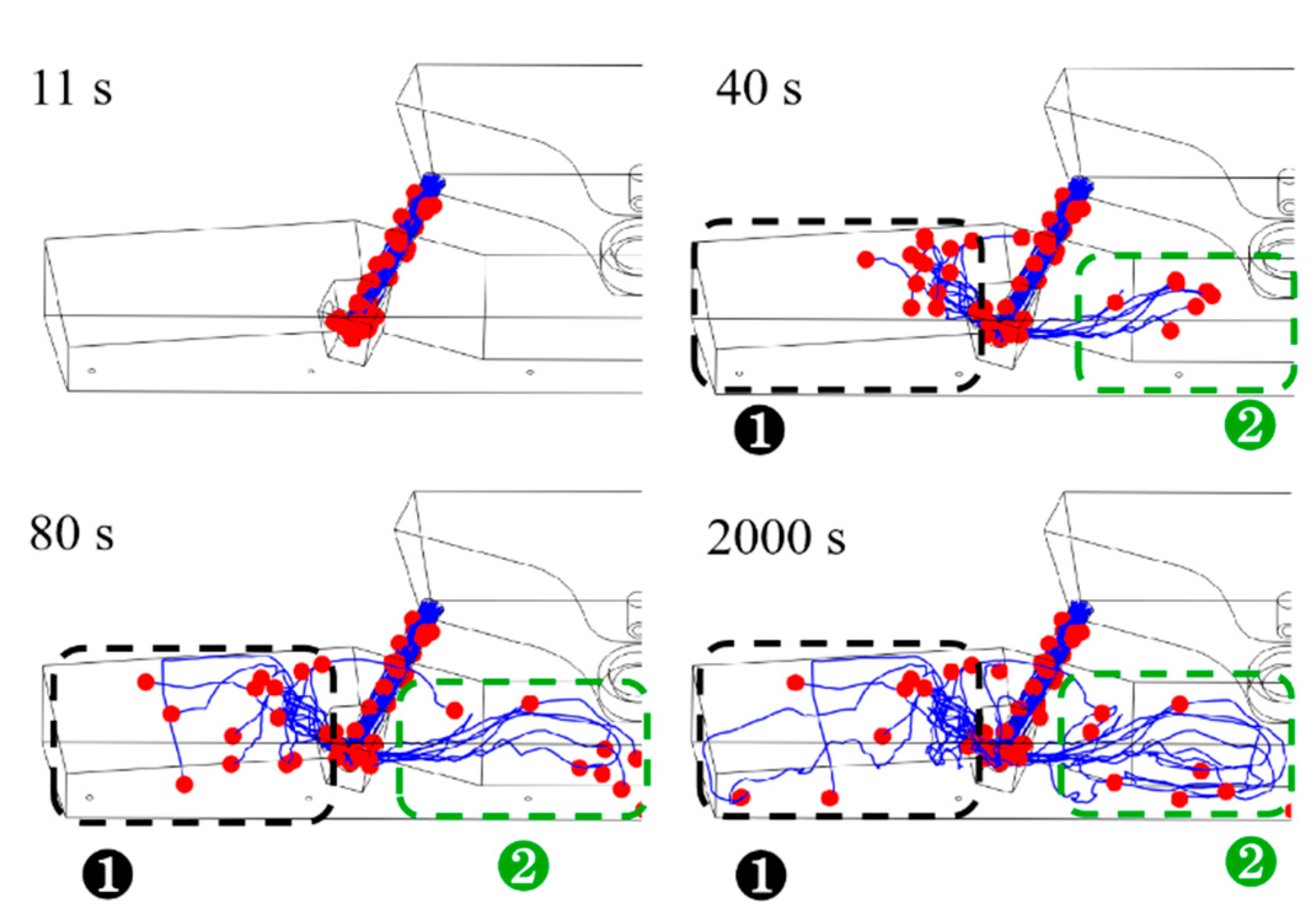
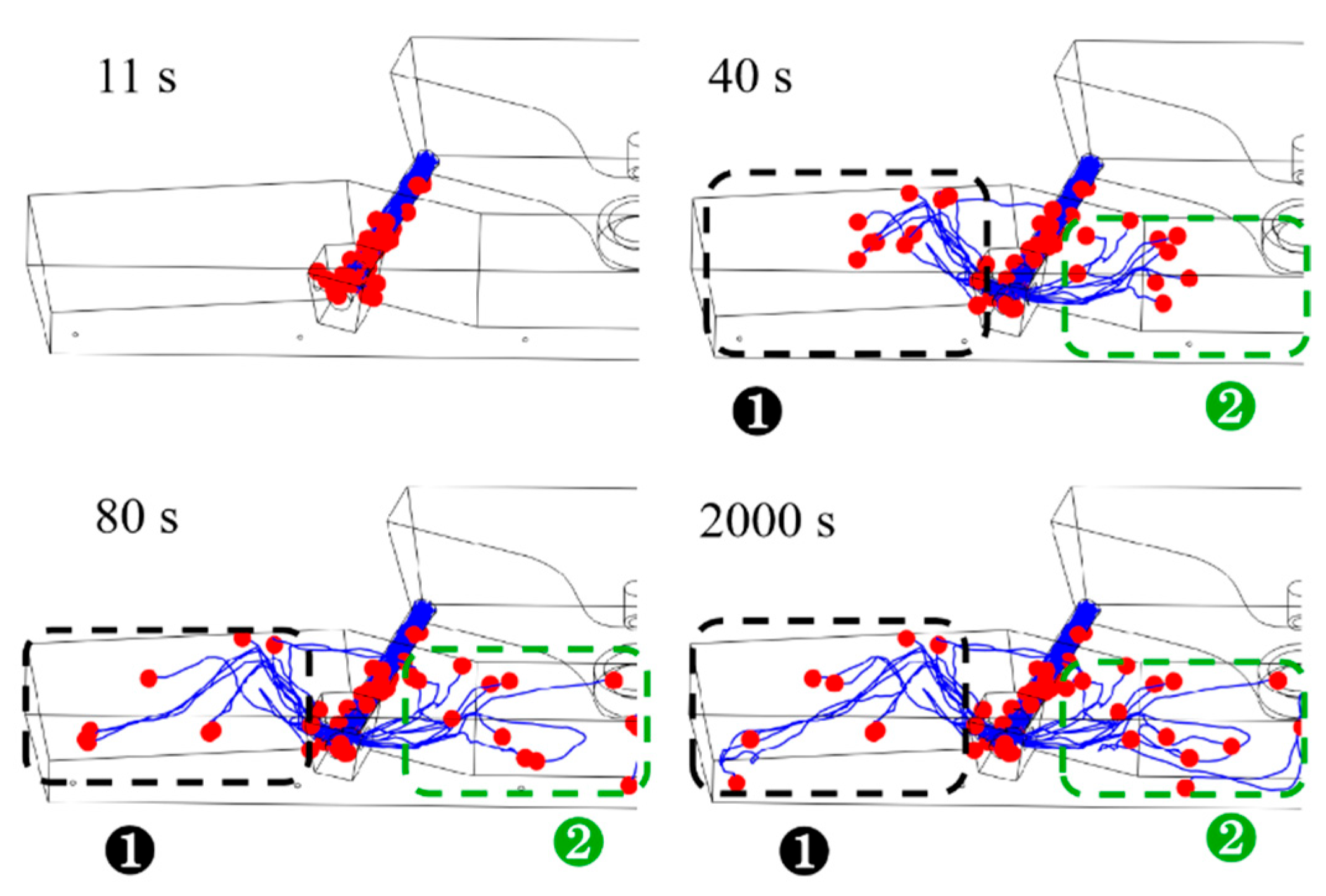
3.1. Model Validation
3.1.1. Physical Model Verification
3.1.2. Mathematical Model Verification
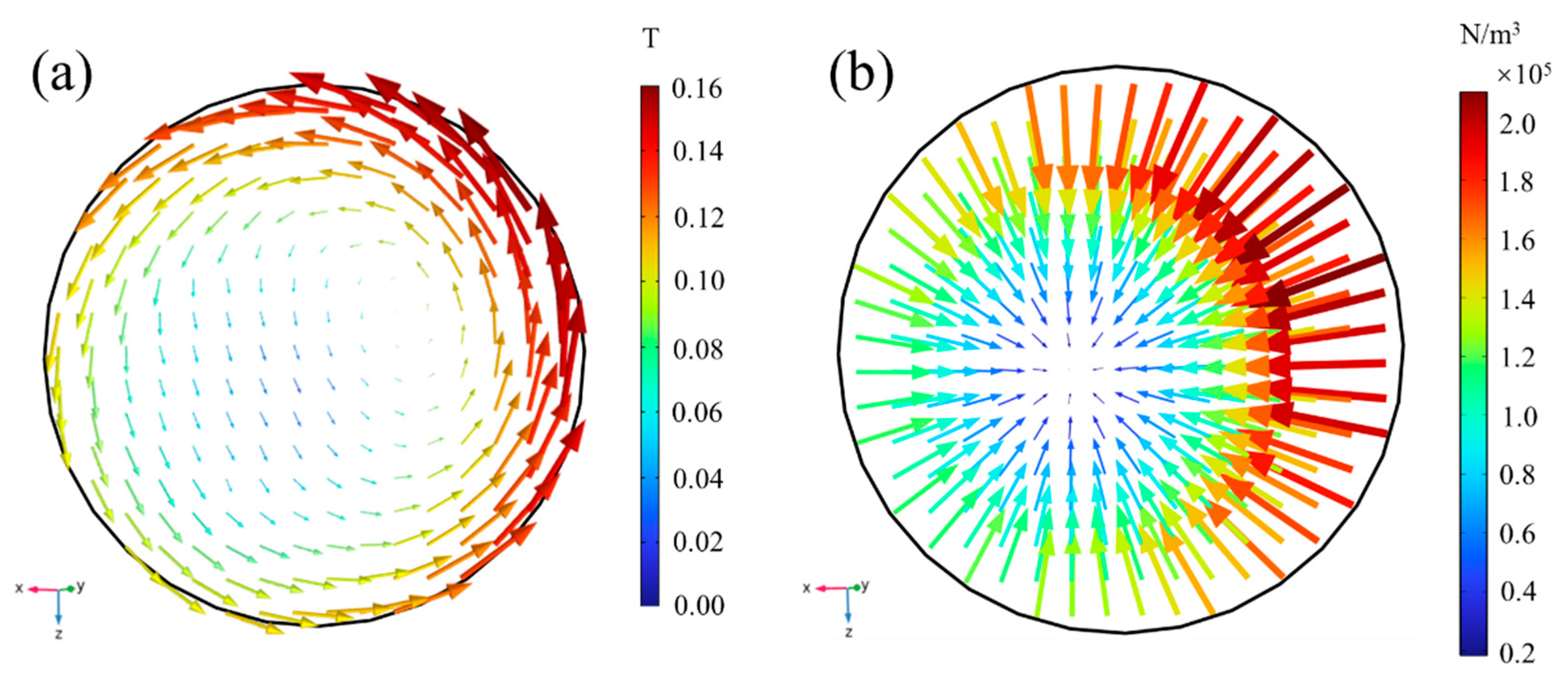
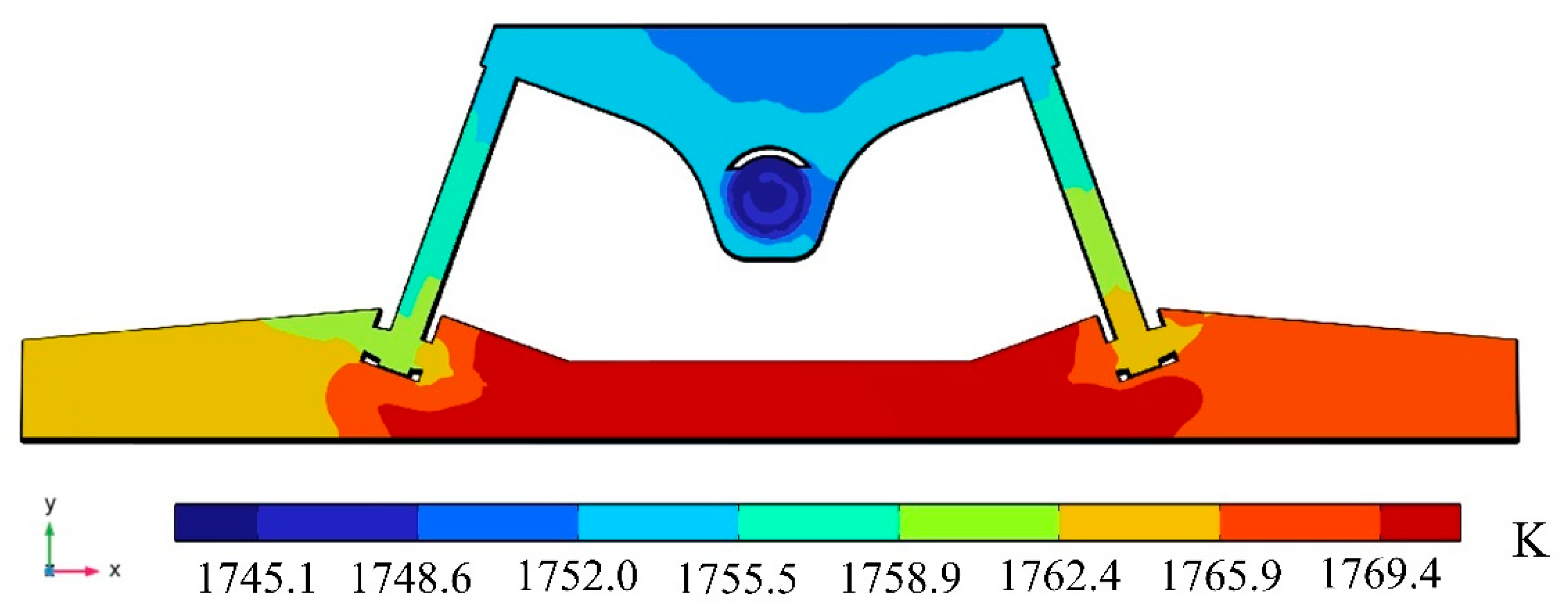
3.2. Magnetic Field, Flow, and Heat Distribution of Molten Steel
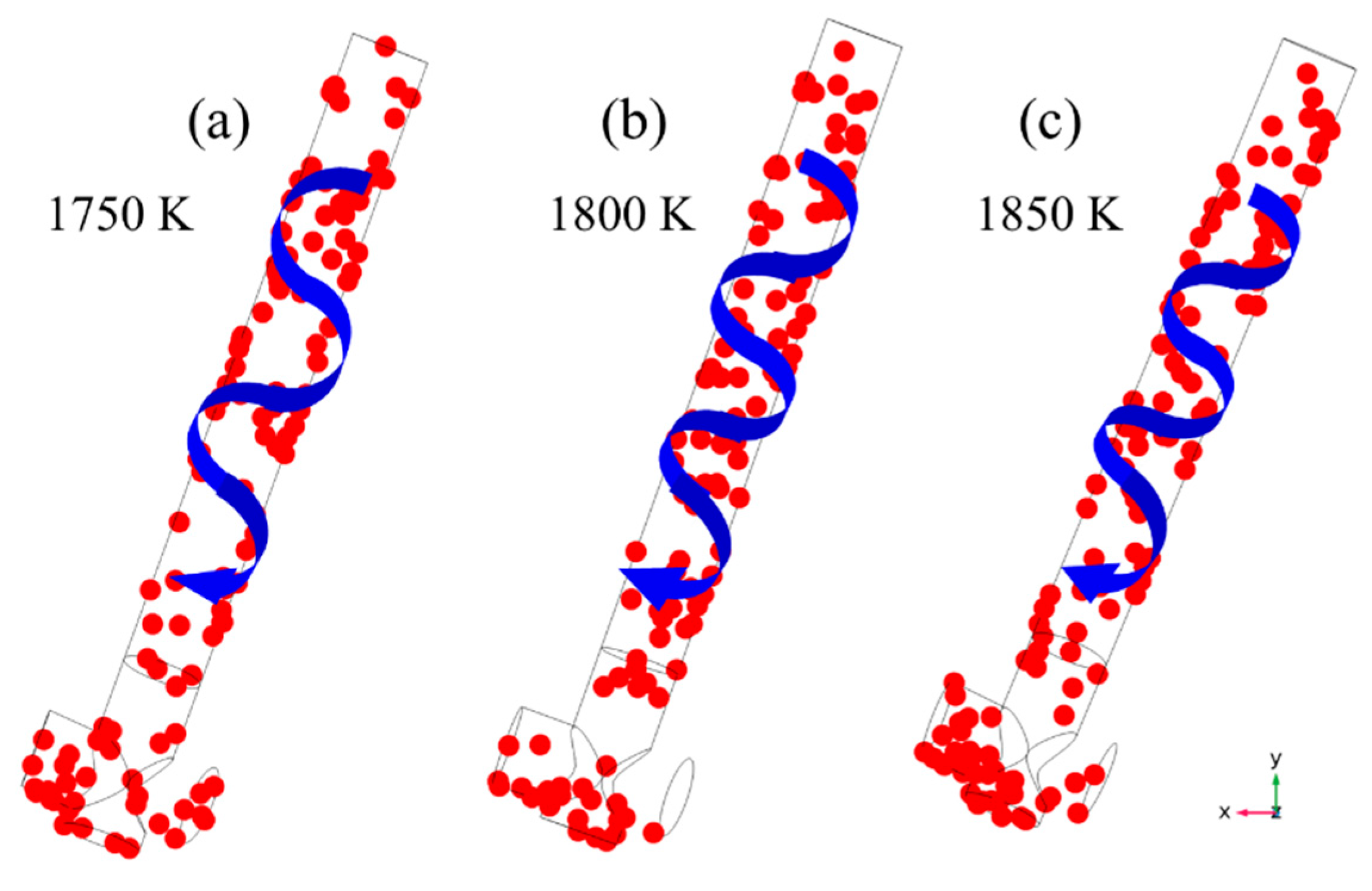
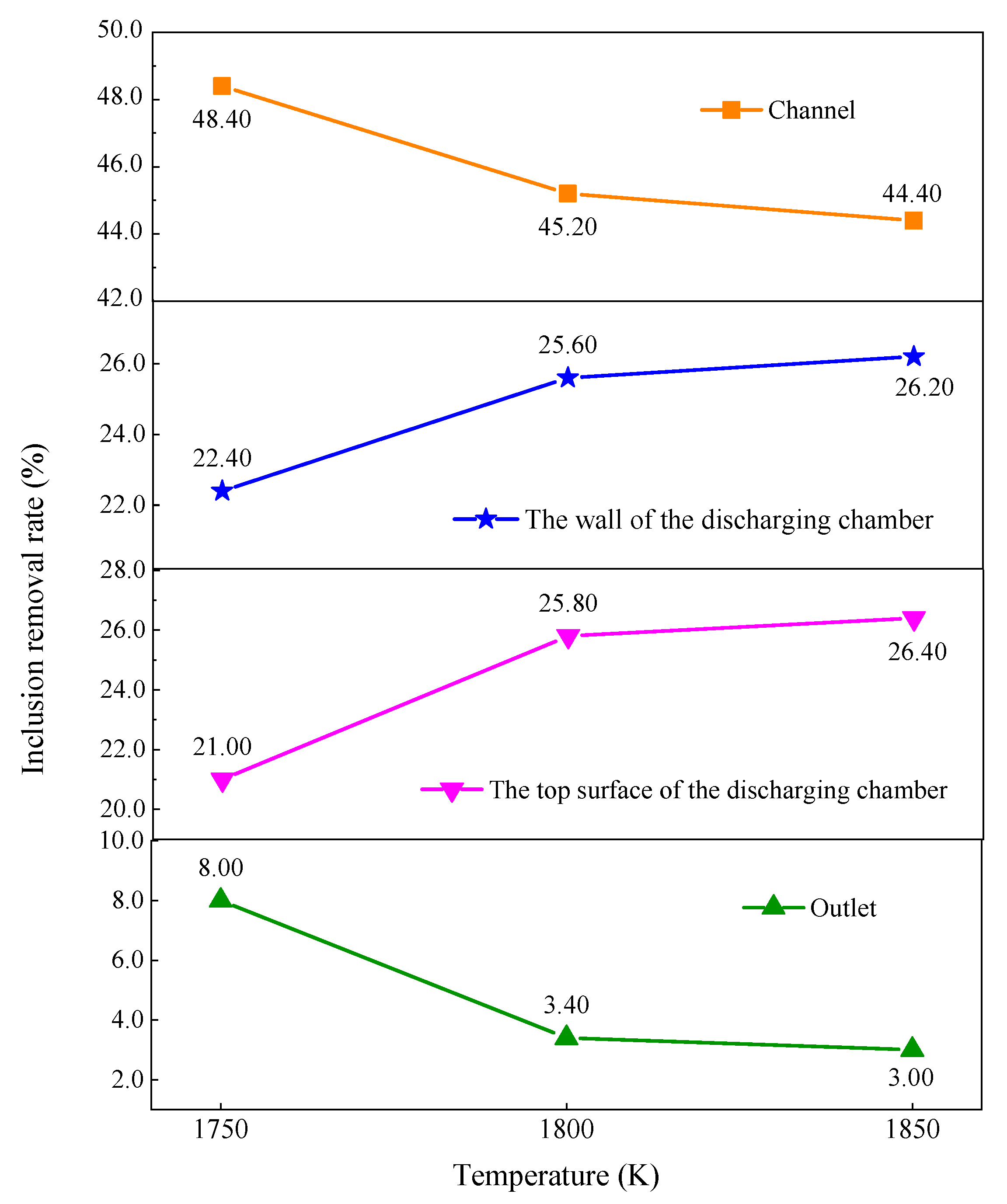
3.3. Effect of Molten Steel Temperature on Inclusion Distribution
4. Conclusions
- Under electromagnetic-induction-heating conditions, the molten steel in the tundish produced a pinch effect. The magnetic field in the channel rotates with a maximum magnetic flux density of 0.158 T; meanwhile, the Lorentz force is directed toward the center of the axis, with a maximum value of 2.11 × 105 N/m3.
- The increase in the temperature of the molten steel prompted the inclusion particles to move faster. When the temperature of the molten steel increased from 1750 K to 1850 K, the average flow velocity of the molten steel in the channel and discharging chamber accelerated from 0.0156 m/s to 0.0177 m/s. Moreover, the distribution of inclusion particles in the channel was similar to the trend of the rotational flow of the molten steel in the channel.
- When the molten steel temperature increased from 1750 K to 1850 K, the removal percentage of inclusion particles on the discharging chamber wall and top layer increased by 9.20%, the removal percentage of inclusion particles on the outlet decreased from 8.00% to 3.00%, and the removal percentage on the channel surface decreased from 48.40% to 44.40%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mazumdar, D. Review, Analysis, and Modeling of Continuous Casting Tundish Systems. Steel Res. Int. 2019, 90, 1800279. [Google Scholar] [CrossRef]
- Emi, T.; Sahai, Y. Tundish Technology for Clean Steel Production; World Scientific: Hackensack, NJ, USA, 2008; p. 316. [Google Scholar]
- Miki, Y.; Thomas, B.G. Modeling of inclusion removal in a tundish. Metall. Mater. Trans. B 1999, 30, 639–654. [Google Scholar] [CrossRef]
- Raghavendra, K.; Sarkar, S.; Ajmani, S.K.; Denys, M.B.; Singh, M.K. Mathematical modelling of single and multi-strand tundish for inclusion analysis. Appl. Math. Model. 2013, 37, 6284–6300. [Google Scholar] [CrossRef]
- Rückert, A.; Warzecha, M.; Koitzsch, R.; Pawlik, M.; Pfeifer, H. Particle Distribution and Separation in Continuous Casting Tundish. Steel Res. Int. 2009, 80, 568–574. [Google Scholar]
- Solorio-Diaz, G.; Morales, R.D.; Palafox-Ramos, J.; Ramos-Banderas, A. Modeling the Effects of a Swirling Flow on Temperature Stratification of Liquid Steel and Flotation of Inclusions in a Tundish. ISIJ Int. 2005, 45, 1129–1137. [Google Scholar] [CrossRef]
- Zhang, L. Fluid Flow, Heat Transfer and Inclusion Motion in a Four-Strand Billet Continuous Casting Tundish. Steel Res. Int. 2005, 76, 784–796. [Google Scholar] [CrossRef]
- Zhang, L.; Taniguchi, S.; Cai, K. Fluid flow and inclusion removal in continuous casting tundish. Metall. Mater. Trans. B 2000, 31, 253–266. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Huang, A.; Yan, W.; Gu, H.; Li, G. CFD Investigation of Effect of Multi-hole Ceramic Filter on Inclusion Removal in a Two-Strand Tundish. Metall. Mater. Trans. B 2020, 51, 276–292. [Google Scholar] [CrossRef]
- Xing, F.; Zheng, S.; Liu, Z.; Zhu, M. Flow Field, Temperature Field, and Inclusion Removal in a New Induction Heating Tundish with Bent Channels. Metals 2019, 9, 561. [Google Scholar] [CrossRef]
- Xing, F.; Zheng, S.; Zhu, M. Motion and Removal of Inclusions in New Induction Heating Tundish. Steel Res. Int. 2018, 89, 1700542. [Google Scholar] [CrossRef]
- Ding, C.; Lei, H.; Zhang, H.; Xu, M.; Zhao, Y.; Li, Q. New insight into relationship between casting speed and inclusion removal in the tundish. J. Mater. Res. Technol. 2023, 23, 5400–5412. [Google Scholar] [CrossRef]
- Wang, P.; Xiao, H.; Chen, X.; Tang, H.; Zhang, J. Effect of channel diameter on magneto-thermal conversion ratio and consistency of each strand in a multi-strand induction heating tundish. J. Iron. Steel Res. Int. 2023, 30, 1199–1210. [Google Scholar] [CrossRef]
- Chen, X.Q.; Xiao, H.; Wang, P.; Lan, P.; Tang, H.Y.; Zhang, J.Q. Effect of Channel Heights on the Flow Field, Temperature Field, and Inclusion Removal in a Channel-type Induction Heating Tundish. In 12th International Symposium on High-Temperature Metallurgical Processing; Springer International Publishing: Cham, Switzerland, 2022; pp. 501–522. [Google Scholar]
- Dadic, Z.; Zivkovic, D.; Catipovic, N.; Marinic-Kragic, I. Influence of steel preheat temperature and molten casting alloy AlSi9Cu3(Fe) impact speed on wear of X38CrMoV5-1 steel in high pressure die casting conditions. Wear 2019, 424, 15–22. [Google Scholar] [CrossRef]
- Tomochika, N.; Nakaoka, T.; Tsukuda, T.; Nagase, Y.; Katsura, H.; Sumida, K. Development of Prediction Technique for Temperature Distribution of Molten Steel in Steelmaking. Kobeco Technol. Rev. 2019, 37, 57–62. [Google Scholar]
- Yi, B.; Zhang, G.; Jiang, Q.; Zhang, P.; Feng, Z.; Tian, N. The Removal of Inclusions with Different Diameters in Tundish by Channel Induction Heating: A Numerical Simulation Study. Materials 2023, 16, 5254. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Li, B.; Tsukihashi, F. Modeling of a Thermo-Electromagneto-Hydrodynamic Problem in Continuous Casting Tundish with Channel Type Induction Heating. ISIJ Int. 2014, 54, 311–320. [Google Scholar] [CrossRef]
- Gutierrez, E.; Garcia-Hernandez, S.; De Jesus Barreto, J. Mathematical Analysis of the Touching Inclusions Parameters at the Tundish Free Surface to Predict More Realistic Inclusion Removal Rates. Steel Res. Int. 2019, 90, 1900328. [Google Scholar] [CrossRef]
- Taniguchi, S.; Brimacombe, J.K. Application of pinch force to the separation of inclusion particles from liquid steel. ISIJ Int. 1994, 34, 722–731. [Google Scholar] [CrossRef]
- Takahashi, K.; Taniguchi, S. Electromagnetic Separation of Nonmetallic Inclusion from Liquid Metal by Imposition of High Frequency Magnetic Field. ISIJ Int. 2003, 43, 820–827. [Google Scholar] [CrossRef]
- Gupta, V.K.; Jha, P.K.; Jain, P.K. Numerical Investigation on Gas Bubbling Assisted Inclusion Transport and Removal in Multistrand Tundish. Met. Mater. Int. 2022, 28, 2146–2165. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, R.; He, Z.; Li, G.; Li, B.; Li, H. Numerical analysis of inclusion motion behavior in electroslag remelting process. Int. J. Heat Mass Tran. 2018, 125, 1333–1344. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, F.; Li, B.; Tsukihashi, F. Behavior of Non-metallic Inclusions in a Continuous Casting Tundish with Channel Type Induction Heating. ISIJ Int. 2014, 54, 2796–2805. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Wang, X.; Li, X.; Yue, Q.; Xiao, H. Channel-Type Induction Heating Tundish Technology for Continuous Casting: A Review. Materials 2023, 16, 493. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xiao, H.; Chen, X.Q.; Li, X.S.; He, H.; Tang, H.Y.; Zhang, J.Q. Influence of Dual-Channel Induction Heating Coil Parameters on the Magnetic Field and Macroscopic Transport Behavior in T-Type Tundish. Metall. Mater. Trans. B 2021, 52, 3447–3467. [Google Scholar] [CrossRef]
- Feng, G.X.; Jiao, K.X.; Zhang, J.L.; Gao, S.C. High-temperature viscosity of iron-carbon melts based on liquid structure: The effect of carbon content and temperature. J. Mol. Liq. 2021, 330, 115603. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, H.; Ding, C.; Chen, S.; Niu, H.; Yang, B. Deep Insight into the Pinch Effect in a Tundish with Channel-Type Induction Heater. Steel Res. Int. 2022, 93, 2200181. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Radius of inlet (mm) | 45 |
| Working level (mm) | 900 |
| Length of bottom of receiving chamber (mm) | 2863 |
| Length of top of discharging chamber (mm) | 8141 |
| Length of main channel (mm) | 1630 |
| Radii of main channel and sub-channel (mm) | 80 |
| The primary channel’s increase angle (°) | 3 |
| The sub-channel’s increase angle (°) | 15 |
| The height of the main channel (mm) | 145 |
| Radius of outlet (mm) | 20 |
| The distance between each outlet (mm) | 1500 |
| Number of outlets | 6 |
| Average Calculation Results | Water Model Results | |||||
|---|---|---|---|---|---|---|
| Outlet 1 | Outlet 2 | Outlet 3 | Outlet 1 | Outlet 2 | Outlet 3 | |
| Theoretical residence time (s) | 841 | 864 | 845 | 834 | 901 | 854 |
| Minimum residence time (s) | 20 | 24 | 18 | 18 | 19 | 12 |
| Peak time (s) | 284 | 340 | 286 | 192 | 248 | 218 |
| Dead space volume fraction (%) | 1.06 | −1.65 | 0.59 | 3.36 | −4.40 | 1.04 |
| Piston area volume fraction (%) | 17.88 | 21.41 | 17.88 | 12.17 | 15.47 | 13.33 |
| Mixing zone volume fraction (%) | 81.06 | 80.24 | 81.53 | 84.47 | 88.93 | 85.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, B.; Zhang, G.; Jiang, Q.; Yan, P.; Feng, Z.; Tian, N. Simulation Study on the Influence of Different Molten Steel Temperatures on Inclusion Distribution under Dual-Channel Induction-Heating Conditions. Materials 2023, 16, 7556. https://doi.org/10.3390/ma16247556
Yi B, Zhang G, Jiang Q, Yan P, Feng Z, Tian N. Simulation Study on the Influence of Different Molten Steel Temperatures on Inclusion Distribution under Dual-Channel Induction-Heating Conditions. Materials. 2023; 16(24):7556. https://doi.org/10.3390/ma16247556
Chicago/Turabian StyleYi, Bing, Guifang Zhang, Qi Jiang, Peng Yan, Zhenhua Feng, and Nan Tian. 2023. "Simulation Study on the Influence of Different Molten Steel Temperatures on Inclusion Distribution under Dual-Channel Induction-Heating Conditions" Materials 16, no. 24: 7556. https://doi.org/10.3390/ma16247556
APA StyleYi, B., Zhang, G., Jiang, Q., Yan, P., Feng, Z., & Tian, N. (2023). Simulation Study on the Influence of Different Molten Steel Temperatures on Inclusion Distribution under Dual-Channel Induction-Heating Conditions. Materials, 16(24), 7556. https://doi.org/10.3390/ma16247556







