Point-Contact Spectroscopy in Bulk Samples of Electron-Doped Cuprate Superconductors
Abstract
:1. Introduction
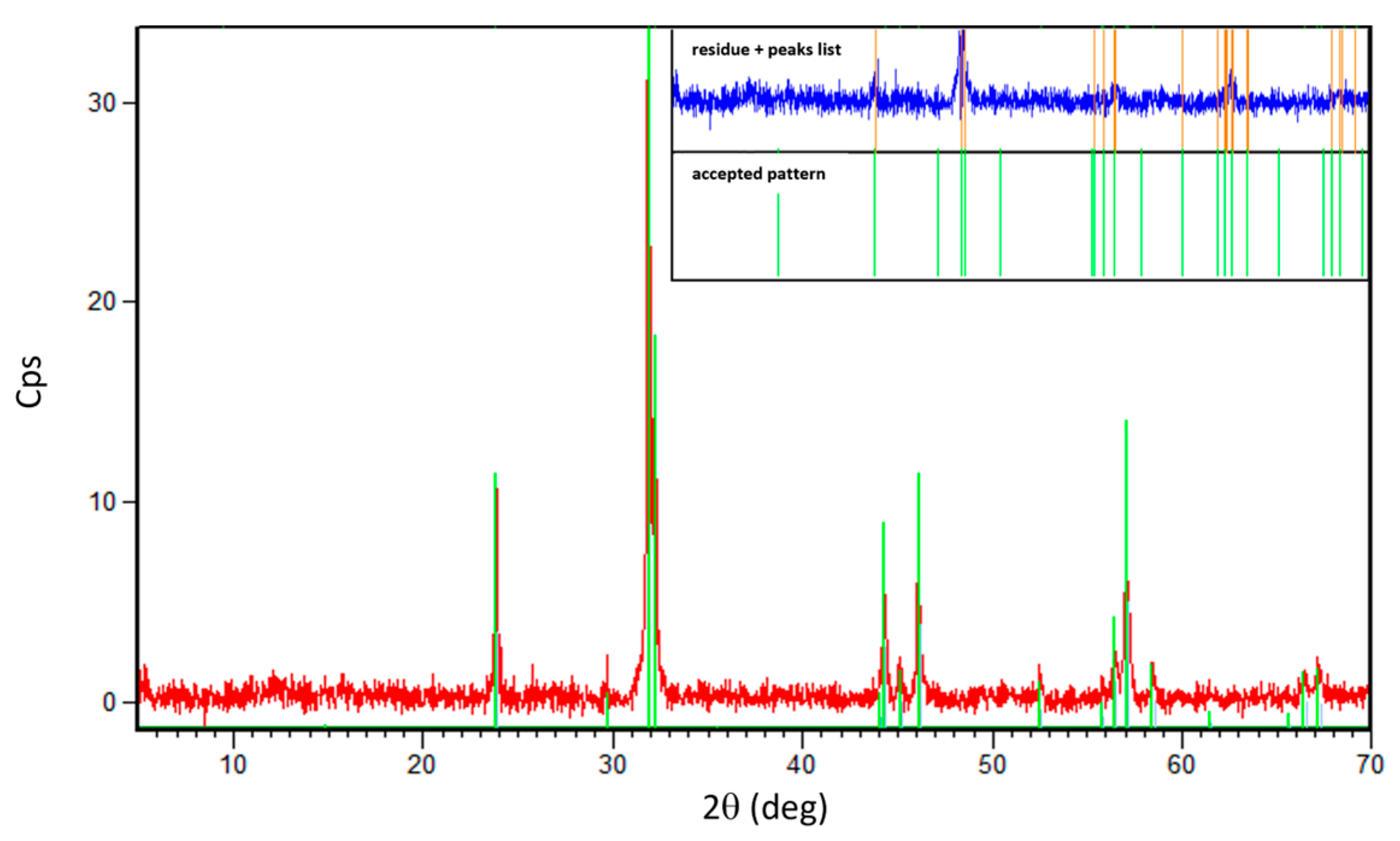
2. Sample Characterization
3. Theory of NS Contacts
4. Experimental Results and Discussion
4.1. Low-Bias Conductance
4.2. High-Bias Conductance
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Q.; Zasadzinski, J.F.; Gray, K.E. Phonon spectroscopy of superconducting Nb using point-contact tunneling. Phys. Rev. B 1990, 42, 7953. [Google Scholar] [CrossRef]
- DeWilde, Y.; Miyakawa, N.; Guptasarma, P.; Iavarone, M.; Ozyuzer, L.; Zasadzinski, J.F.; Romano, P.; Hinks, D.G.; Kendziora, C.; Crabtree, G.W.; et al. Unusual Strong-Coupling Effects in the Tunneling Spectroscopy of Optimally Doped and Overdoped Bi2Sr2CaCu2O8+δ. Phys. Rev. Lett. 1998, 80, 153–156. [Google Scholar] [CrossRef]
- Shan, L.; Wang, Y.; Zhu, X.; Mu, G.; Fang, L.; Ren, C.; Wen, H.-H. Point-contact spectroscopy of iron-based layered superconductor LaO0.9F0.1−δFeAs. Europhys. Lett. 2008, 83, 57004. [Google Scholar] [CrossRef]
- Szabó, P.; Samuely, P.; Kačmarčík, J.; Klein, T.; Marcus, J.; Fruchart, D.; Miraglia, S.; Marcenat, C.; Jansen, A.G.M. Evidence for Two Superconducting Energy Gaps in MgB2 by Point-Contact Spectroscopy. Phys. Rev. Lett. 2001, 87, 137005. [Google Scholar] [CrossRef]
- Giubileo, F.; Romeo, F.; Citro, R.; Di Bartolomeo, A.; Attanasio, C.; Cirillo, C.; Polcari, A.; Romano, P. Point contact Andreev reflection spectroscopy on ferromagnet/superconductor bilayers. Phys. C Supercond. Appl. 2014, 503, 158–161. [Google Scholar] [CrossRef]
- Giubileo, F.; Romeo, F.; Di Bartolomeo, A.; Mizuguchi, Y.; Romano, P. Probing unconventional pairing in LaO0.5F0.5BiS2 layered superconductor by point contact spectroscopy. J. Phys. Chem. Solids 2018, 118, 192–199. [Google Scholar] [CrossRef]
- Wolf, E.L. Principles of Electron Tunneling Spectroscopy, 2nd ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Fournier, P. T’ and infinite-layer electron-doped cuprates. Phys. C 2015, 514, 314–338. [Google Scholar] [CrossRef]
- Armitage, N.P.; Fournier, P.; Greene, R.L. Progress and perspectives on electron-doped cuprates. Rev. Mod. Phys. 2010, 82, 2421–2487. [Google Scholar] [CrossRef]
- Song, D.; Han, G.; Kyung, W.; Seo, J.; Cho, C.; Kim, B.S.; Arita, M.; Shimada, K.; Namatame, H.; Taniguchi, M.; et al. Electron Number-Based Phase Diagram of Pr1−xLaCexCuO4−δ and Possible Absence of Disparity between Electron- and Hole-Doped Cuprate Phase Diagrams. Phys. Rev. Lett. 2017, 118, 137001. [Google Scholar] [CrossRef]
- Helm, T.; Kartsovnik, M.V.; Proust, C.; Vignolle, B.; Putzke, C.; Kampert, E.; Sheikin, I.; Choi, E.-S.; Brooks, J.S.; Bittner, N.; et al. Correlation between Fermi surface transformations and superconductivity in the electron-doped high-Tc superconductor Nd2−xCexCuO4. Phys. Rev. B 2015, 92, 094501. [Google Scholar] [CrossRef]
- Armitage, N.P.; Lu, D.H.; Feng, D.L.; Kim, C.; Damascelli, A.; Shen, K.M.; Ronning, F.; Shen, Z.-X.; Onose, Y.; Taguchi, Y.; et al. Superconducting gap anisotropy in Nd1.85Ce0.15CuO4: Results from photoemission. Phys. Rev. Lett. 2001, 86, 1126–1129. [Google Scholar] [CrossRef]
- Sato, T.; Kamiyama, T.; Takahashi, T.; Kurahashi, K.; Yamada, K. Observation of dx2-y2-like superconducting gap in an electron-doped high-temperature superconductor. Science 2001, 291, 1517–1519. [Google Scholar] [CrossRef]
- Matsui, H.; Terashima, K.; Sato, T.; Takahashi, T.; Fujita, M.; Yamada, K. Direct observation of a nonmonotonic dx2-y2-wave superconducting gap in the electron-doped high-Tc superconductor Pr0:89LaCe0:11CuO4. Phys. Rev. Lett. 2005, 95, 017003. [Google Scholar] [CrossRef] [PubMed]
- Shan, L.; Huang, Y.; Wang, Y.L.; Li, S.; Zhao, J.; Dai, P.; Zhang, Y.Z.; Ren, C.; Wen, H.H. Weak-coupling Bardeen-Cooper-Schrieffer superconductivity in the electron doped cuprate superconductors. Phys. Rev. B 2008, 77, 014526. [Google Scholar] [CrossRef]
- Kokales, J.D.; Fournier, P.; Mercaldo, L.V.; Talanov, V.V.; Greene, R.L.; Anlage, S.M. Microwave electrodynamics of electron-doped cuprate superconductors. Phys. Rev. Lett. 2000, 85, 3696. [Google Scholar] [CrossRef] [PubMed]
- Prozorov, R.; Giannetta, R.; Fournier, P.; Greene, R.L. Evidence for nodal quasiparticles in electron-doped cuprates from penetration depth measurements. Phys. Rev. Lett. 2000, 85, 3700. [Google Scholar] [CrossRef] [PubMed]
- Snezhko, A.; Prozorov, R.; Lawrie, D.D.; Giannetta, R.; Gauthier, J.; Renaud, J.; Fournier, P. Nodal order parameter in electron-doped Pr2-xCexCuO4-d superconducting films. Phys. Rev. Lett. 2004, 92, 157005. [Google Scholar] [CrossRef]
- Blumberg, G.; Koitzsch, A.; Gozar, A.; Dennis, B.S.; Kendziora, C.A.; Fournier, P.; Greene, R.L. Nonmonotonic dx2_y2 superconducting order parameter in Nd2-xCexCuO4. Phys. Rev. Lett. 2002, 88, 107002. [Google Scholar] [CrossRef]
- Tsuei, C.C.; Kirtley, J.R. Phase-sensitive evidence for d-wave pairing symmetry in electron-doped cuprate superconductors. Phys. Rev. Lett. 2000, 85, 182–185. [Google Scholar] [CrossRef]
- Chesca, B.; Ehrhardt, K.; Mossle, M.; Straub, R.; Koelle, D.; Kleiner, R.; Tsukada, A. Magnetic-field dependence of the maximum supercurrent of La2-xCexCuO4-y interferometers: Evidence for a predominant dx2-y2 superconducting order parameter. Phys. Rev. Lett. 2003, 90, 057004. [Google Scholar] [CrossRef]
- Ariando, D.; Darminto, H.J.H.; Smilde, V.; Leca, D.H.A.; Blank, H.; Rogalla, H.; Hilgenkamp, H. Phase-sensitive order parameter symmetry test experiments utilizing Nd2-xCexCuO4-y/Nb zigzag junctions. Phys. Rev. Lett. 2005, 94, 167001. [Google Scholar] [CrossRef]
- Armitage, N.P.; Ronning, F.; Lu, D.H.; Kim, C.; Damascelli, A.; Shen, K.M.; Feng, D.L.; Eisaki, H.; Shen, Z.-X.; Mang, P.K.; et al. Doping dependence of an n-type cuprate superconductor investigated by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2002, 88, 257001. [Google Scholar] [CrossRef] [PubMed]
- Dagan, Y.; Greene, R.L. Hole superconductivity in the electron-doped superconductor Pr2−xCexCuO4. Phys. Rev. B 2007, 76, 024506. [Google Scholar] [CrossRef]
- Yuan, Q.; Chen, Y.; Lee, T.K.; Ting, C.S. Fermi surface evolution in the antiferromagnetic state for the electron-doped t−t′−t′′−J model. Phys. Rev. B 2004, 69, 214523. [Google Scholar] [CrossRef]
- Luo, H.G.; Xiang, T. Superfluid Response in Electron-Doped Cuprate Superconductors. Phys. Rev. Lett. 2005, 94, 027001. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.S.; Luo, H.G.; Wu, W.C.; Xiang, T. Two-band model of Raman scattering on electron-doped high-Tc superconductors. Phys. Rev. B 2006, 73, 174517. [Google Scholar] [CrossRef]
- Shan, L.; Huang, Y.; Gao, H.; Wang, Y.; Li, S.L.; Dai, P.C.; Zhou, F.; Xiong, J.W.; Ti, W.X.; Wen, H.H. Distinct pairing symmetries in Nd1.85Ce0.15CuO4−y and La1.89Sr0.11CuO4 single crystals: Evidence from comparative tunneling measurements. Phys. Rev. B 2005, 72, 144506. [Google Scholar] [CrossRef]
- Li, Y.; Tabis, W.; Tang, Y.; Yu, G.; Jaroszynski, J.; Barišić, N.; Greven, M. Hole pocket-driven superconductivity and its universal features in the electron-doped cuprates. Sci. Adv. 2019, 5, eaap7349. [Google Scholar] [CrossRef]
- Hirsch, J.; Marsiglio, F. Understanding electron-doped cuprate superconductors as hole superconductors. Physica C 2019, 564, 29. [Google Scholar] [CrossRef]
- Qazilbash, M.M.; Koitzsch, A.; Dennis, B.S.; Gozar, A.; Balci, H.; Kendziora, C.A.; Greene, R.L.; Blumberg, G. Evolution of superconductivity in electron-doped cuprates: Magneto-Raman spectroscopy. Phy. Rev. B 2005, 72, 214510. [Google Scholar] [CrossRef]
- Armitage, N.P.; Lu, D.H.; Kim, C.; Damascelli, A.; Shen, K.M.; Ronning, F.; Feng, D.L.; Bogdanov, P.; Shen, Z.X.; Onose, Y.; et al. Anomalous Electronic Structure and Pseudogap Effects in Nd1.85Ce0.15CuO4. Phys. Rev. Lett. 2001, 87, 147003. [Google Scholar] [CrossRef] [PubMed]
- Yamashiro, M.; Tanaka, Y.; Tanuma, Y.; Kashiwaya, S. Theory of tunneling conductance for normal metal/insulator/triplet superconductor junction. J. Phys. Soc. Jpn. 1998, 67, 3224. [Google Scholar] [CrossRef]
- Mourachkine, A. Andreev reflections and tunneling spectroscopy on underdoped Nd1.85Ce0.15CuO4–δ. Europhys. Lett. 2000, 50, 663. [Google Scholar] [CrossRef]
- Biswas, A.; Fournier, P.; Qazilbash, M.M.; Smolyaninova, V.N.; Balci, H.; Greene, R.L. Evidence of a d- to s-Wave Pairing Symmetry Transition in the Electron-Doped Cuprate Superconductor Pr2−xCexCuO4. Phys. Rev. Lett. 2002, 88, 207004. [Google Scholar] [CrossRef]
- Liu, C.S.; Wu, W.C. Theory of point-contact spectroscopy in electron-doped cuprate superconductors. Phys. Rev. B 2007, 76, 220504. [Google Scholar] [CrossRef]
- Kim, M.-S.; Skinta, J.A.; Lemberger, T.R.; Tsukada, A.; Naito, M. Evidence for a Transition in the Pairing Symmetry of the Electron-Doped Cuprates La2−xCexCuO4−y and Pr2−xCexCuO4−y. Phys. Rev. Lett. 2003, 91, 087001. [Google Scholar] [CrossRef] [PubMed]
- Skinta, J.A.; Kim, M.-S.; Lemberger, T.R.; Greibe, T.; Naito, M. Evidence for a Transition in the Pairing Symmetry of the Electron-Doped Cuprates. Phys. Rev. Lett. 2002, 88, 207005. [Google Scholar] [CrossRef]
- Zimmers, A.; Lobo, R.P.S.M.; Bontemps, N.; Homes, C.C.; Barr, M.C.; Dagan, Y.; Greene, R.L. Infrared signature of the superconducting state in Pr2−xCexCuO4. Phys. Rev. B 2004, 70, 132502. [Google Scholar] [CrossRef]
- Cucolo, A.M.; Di Leo, R.; Nigro, A.; Romano, P.; Bobba, F. Linear normal conductance in copper oxide tunnel junctions. Phys. Rev. B 1996, 54, R9686–R9688. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, H.; Chen, Q.; Yang, R.; He, G.; Lin, Z.; Li, Q.; Yuan, J.; Zhu, B.; Li, L.; et al. Quantum criticality tuned by magnetic field in optimally electron-doped cuprate thin films. Phys. Rev. B 2021, 103, 014517. [Google Scholar] [CrossRef]
- Greene, R.L.; Mandal, P.R.; Poniatowski, N.R.; Sarkar, T. The strange metal state of the electron-doped cuprates. Annu. Rev. Condens. Matter Phys. 2020, 11, 213. [Google Scholar] [CrossRef]
- Xu, K.-J.; Guo, Q.; Hashimoto, M.; Li, Z.-X.; Chen, S.-D.; He, J.; He, Y.; Li, C.; Berntsen, M.H.; Rotundu, C.R.; et al. Bogoliubov quasiparticle on the gossamer Fermi surface in electron-doped cuprates. Nat. Phys. 2023, 19, 1834–1840. [Google Scholar] [CrossRef]
- Lin, C.; Adachi, T.; Horio, M.; Ohgi, T.; Baqiya, M.A.; Kawamata, T.; Sato, H.; Sumura, T.; Koshiishi, K.; Nakata, S.; et al. Extended superconducting dome re-vealed by angle-resolved photoemission spectroscopy of electron-doped cuprates prepared by the protect annealing method. Phys. Rev. Res. 2021, 3, 013180. [Google Scholar] [CrossRef]
- Tagay, Z.; Mahmood, F.; Legros, A.; Sarkar, T.; Greene, R.L.; Armitage, N.P. BCS d-wave behavior in the terahertz electrodynamic response of electron-doped cuprate superconductors. Phys. Rev. B 2021, 104, 064501. [Google Scholar] [CrossRef]
- Naito, M.; Krockenberger, Y.; Ikeda, A.; Yamamoto, H. Reassessment of the electronic state, magnetism, and superconductivity in high-Tc cuprates with the Nd2CuO4 structure. Phys. C 2016, 523, 28. [Google Scholar] [CrossRef]
- Radaelli, P.G.; Jorgensen, J.D.; Schultz, A.J.; Peng, J.L.; Greene, R.L. Evidence of apical oxygen in Nd2CuOy determined by single-crystal neutron diffraction. Phys. Rev. B 1994, 49, 15322. [Google Scholar] [CrossRef]
- Mang, P.K.; Larochelle, S.; Mehta, A.; Vajk, O.P.; Erickson, A.S.; Lu, L.; Buyers, W.J.L.; Marshall, A.F.; Prokes, K.; Greven, M. Phase decomposition and chemical inhomogeneity in Nd2−xCexCuO4±δ. Phys. Rev. B 2004, 70, 094507. [Google Scholar] [CrossRef]
- Xu, X.Q.; Mao, S.N.; Jiang, W.; Peng, J.L.; Greene, R.L. Oxygen dependence of the transport properties of Nd1.78Ce0.22CuO4±δ. Phys. Rev. B 1996, 53, 871. [Google Scholar] [CrossRef]
- Higgins, J.S.; Dagan, Y.; Barr, M.C.; Weaver, B.D.; Greene, R.L. Role of oxygen in the electron-doped superconducting cuprates. Phys. Rev. B 2006, 73, 104510. [Google Scholar] [CrossRef]
- Riou, G.; Richard, P.; Jandl, S.; Poirier, M.; Fournier, P.; Nekvasil, V.; Barilo, S.N.; Kurnevich, L.A. Pr3+ crystal-field excitation study of apical oxygen and reduction processes in Pr2−xCexCuO4±δ. Phys. Rev. B 2004, 69, 024511. [Google Scholar] [CrossRef]
- Richard, P.; Riou, G.; Hetel, I.; Jandl, S.; Poirier, M.; Fournier, P. Role of oxygen nonstoichiometry and the reduction process on the local structure of Nd2−xCexCuO4±δ. Phys. Rev. B 2004, 70, 064513. [Google Scholar] [CrossRef]
- Kang, H.J.; Dai, P.; Campbell, B.J.; Chupas, P.J.; Rosenkranz, S.; Lee, P.L.; Huang, Q.; Li, S.; Komiya, S.; Ando, Y. Microscopic annealing process and its impact on superconductivity in T’-structure electron-doped copper oxides. Nat. Mater. 2007, 6, 224. [Google Scholar] [CrossRef]
- Guarino, A.; Autieri, C.; Marra, P.; Leo, A.; Grimaldi, G.; Avella, A.; Nigro, A. Superconductivity induced by structural reorganization in the electron-doped cuprate Nd2−xCexCuO4. Phys. Rev. B 2022, 105, 014512. [Google Scholar] [CrossRef]
- Guarino, A.; Fittipaldi, R.; Romano, A.; Vecchione, A.; Nigro, A. Correlation between structural and transport properties in epitaxial films of Nd2−xCexCuO4±δ. Thin Solid Films 2012, 524, 282. [Google Scholar] [CrossRef]
- Guarino, A.; Leo, A.; Avella, A.; Avitabile, F.; Martucciello, N.; Grimaldi, G.; Romano, A.; Pace, S.; Romano, P.; Nigro, A. Electrical transport properties of sputtered Nd2−xCexCuO4±δ thin films. Phys. B 2018, 536, 742–746. [Google Scholar] [CrossRef]
- Guarino, A.; Romano, P.; Avitabile, F.; Leo, A.; Martucciello, N.; Grimaldi, G.; Ubaldini, A.; D’Agostino, D.; Bobba, F.; Vecchione, A.; et al. Characterization of Nd2−xCexCuO4±δ (x = 0 and 0.15) Ultrathin Films Grown by DC Sputtering Technique. IEEE Trans. Appl. Supercond. 2017, 27, 1–4. [Google Scholar] [CrossRef]
- Romano, P.; Riccio, M.; Guarino, A.; Martucciello, N.; Grimaldi, G.; Leo, A.; Nigro, A. Electron doped superconducting cuprates for photon detectors. Measurement 2018, 122, 502–506. [Google Scholar] [CrossRef]
- Uthayakumar, S.; Fittipaldi, R.; Guarino, A.; Vecchione, A.; Romano, A.; Nigro, A.; Habermeier, H.-U.; Pace, S. Thermal treatments and evolution of bulk Nd1.85Ce0.15CuO4 morphology. Phys. C 2008, 468, 2271–2274. [Google Scholar] [CrossRef]
- Andreev, A.F. The Thermal Conductivity of the Intermediate State in Superconductors. J. Exp. Theor. Phys. 1964, 19, 1228. [Google Scholar]
- Deutscher, G. Andreev–Saint-James reflections: A probe of cuprate superconductors. Rev. Mod. Phys. 2005, 77, 109–135. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Blonder, G.E.; Tinkham, M.; Klapwijk, T.M. Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion. Phys. Rev. B 1982, 25, 4515–4532. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Huang, Q.; Zasadzinski, J.F.; Tralshawala, N.; Gray, K.E.; Hinks, D.G.; Peng, J.L.; Greene, R.L. Tunnelling evidence for predominantly electron–phonon coupling in superconducting Ba1−xKxBiO3 and Nd2−xCexCuO4−y. Nature 1990, 347, 369–372. [Google Scholar] [CrossRef]
- Kashiwaya, S.; Matsubara, N.; Prijamboedi, B.; Shibata, H.; Takita, K.; Kashiwaya, H.; Asano, Y.; Tanaka, Y. Doping Dependence of Superconducting Energy Gap of NCCO Observed by Tunnelling Spectroscopy. J. Low Temp. Phys. 2003, 131, 327–330. [Google Scholar] [CrossRef]
- Wang, Y.; Perdew, J.P. Spin scaling of the electron-gas correlation energy in the high-density limit. Phys. Rev. B 1991, 43, 8911–8916. [Google Scholar] [CrossRef]
- Onose, Y.; Taguchi, Y.; Ishizaka, K.; Tokura, Y. Charge dynamics in underdoped Nd2−xCexCuO4: Pseudogap and related phenomena. Phys. Rev. B 2004, 69, 024504. [Google Scholar] [CrossRef]
- Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287–337. [Google Scholar] [CrossRef]
- Klepikova, A.S.; Charikova, T.B.; Popov, M.R.; Stepanova, E.A.; Ivanov, A.A. Magnetic and transport anisotropy of electron doped Nd2-xCexCuO4+δ with oxygen nonstoichiometric disorder. Phys. E 2023, 146, 115532–115537. [Google Scholar] [CrossRef]
- Duif, A.M.; Jansen, A.G.M.; Wyder, P. Point-contact spectroscopy. J. Phys. Condens. Matter 1989, 1, 3157–3189. [Google Scholar] [CrossRef]
- Dynes, R.C.; Narayanamurti, V.; Garno, J.P. Direct Measurement of Quasiparticle-Lifetime Broadening in a Strong-Coupled Superconductor. Phys. Rev. Lett. 1978, 41, 1509–1512. [Google Scholar] [CrossRef]
- Pleceník, A.; Grajcar, M.; Beňačka, Š.; Seidel, P.; Pfuch, A. Finite-quasiparticle-lifetime effects in the differential conductance of Bi2Sr2CaCu2Oy/Au junctions. Phys. Rev. B 1994, 49, 10016–10019. [Google Scholar] [CrossRef]
- Shan, L.; Huang, Y.; Ren, C.; Wen, H.H. Vortex overlapping in a BCS type-II superconductor revealed by Andreev reflection spectroscopy. Phys. Rev. B 2006, 73, 134508. [Google Scholar] [CrossRef]
- Dagan, Y.; Qazilbash, M.M.; Greene, R.L. Tunneling into the Normal State of Pr2−xCexCuO4. Phys. Rev. Lett. 2005, 94, 187003. [Google Scholar] [CrossRef]
- Dagan, Y.; Beck, R.; Greene, R.L. Dirty Superconductivity in the Electron-Doped Cuprate Pr2−xCexCuO4−δ: Tunneling Study. Phys. Rev. Lett. 2007, 99, 147004. [Google Scholar] [CrossRef]
- Das, T.; Markiewicz, R.S.; Bansil, A. Nodeless d-wave superconducting pairing due to residual antiferromagnetism in underdoped Pr2−xCexCuO4−δ. Phys. Rev. Lett. 2007, 98, 197004. [Google Scholar] [CrossRef]
- Chiu, P.-M.; Liu, C.S.; Wu, W.C. Interplay between antiferromagnetic order and spin polarization in ferromagnetic metal/electron-doped cuprate superconductor junctions. Phys. Rev. B 2009, 79, 064509. [Google Scholar] [CrossRef]
- Simmons, J.G. Electric Tunnel Effect between Dissimilar Electrodes Separated by a Thin Insulating Film. J. Appl. Phys. 1963, 34, 2581–2590. [Google Scholar] [CrossRef]
- Brinkman, W.F.; Dynes, R.C.; Rowell, J.M. Tunneling Conductance of Asymmetrical Barriers. J. Appl. Phys. 1970, 41, 1915–1921. [Google Scholar] [CrossRef]
- Guarino, A.; Romano, P.; Fujii, J.; Ruosi, A.; Avitabile, F.; Vobornik, I.; Panaccione, G.; Vecchione, A.; Nigro, A. Study of the surface properties of NCCO electron-doped cuprate. Eur. Phys. J. Spec. Top. 2019, 228, 733–739. [Google Scholar] [CrossRef]
- Mandrus, D.; Forro, L.; Koller, D.; Mihaly, L. Giant tunnelling anisotropy in the high- Tc superconductor Bi2Sr2CaCu2O8. Nature 1991, 351, 460–462. [Google Scholar] [CrossRef]
- Kirtley, J.R.; Washburn, S.; Scalapino, D.J. Origin of the linear tunneling conductance background. Phys. Rev. B 1992, 45, 336–346. [Google Scholar] [CrossRef] [PubMed]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nigro, A.; Guarino, A.; Leo, A.; Grimaldi, G.; Avitabile, F.; Romano, P. Point-Contact Spectroscopy in Bulk Samples of Electron-Doped Cuprate Superconductors. Materials 2023, 16, 7644. https://doi.org/10.3390/ma16247644
Nigro A, Guarino A, Leo A, Grimaldi G, Avitabile F, Romano P. Point-Contact Spectroscopy in Bulk Samples of Electron-Doped Cuprate Superconductors. Materials. 2023; 16(24):7644. https://doi.org/10.3390/ma16247644
Chicago/Turabian StyleNigro, Angela, Anita Guarino, Antonio Leo, Gaia Grimaldi, Francesco Avitabile, and Paola Romano. 2023. "Point-Contact Spectroscopy in Bulk Samples of Electron-Doped Cuprate Superconductors" Materials 16, no. 24: 7644. https://doi.org/10.3390/ma16247644
APA StyleNigro, A., Guarino, A., Leo, A., Grimaldi, G., Avitabile, F., & Romano, P. (2023). Point-Contact Spectroscopy in Bulk Samples of Electron-Doped Cuprate Superconductors. Materials, 16(24), 7644. https://doi.org/10.3390/ma16247644







