Study on the Effect of Metal Mesh on Pulsed Eddy-Current Testing of Corrosion under Insulation Using an Early-Phase Signal Feature
Abstract
:1. Introduction
2. Numerical Simulations
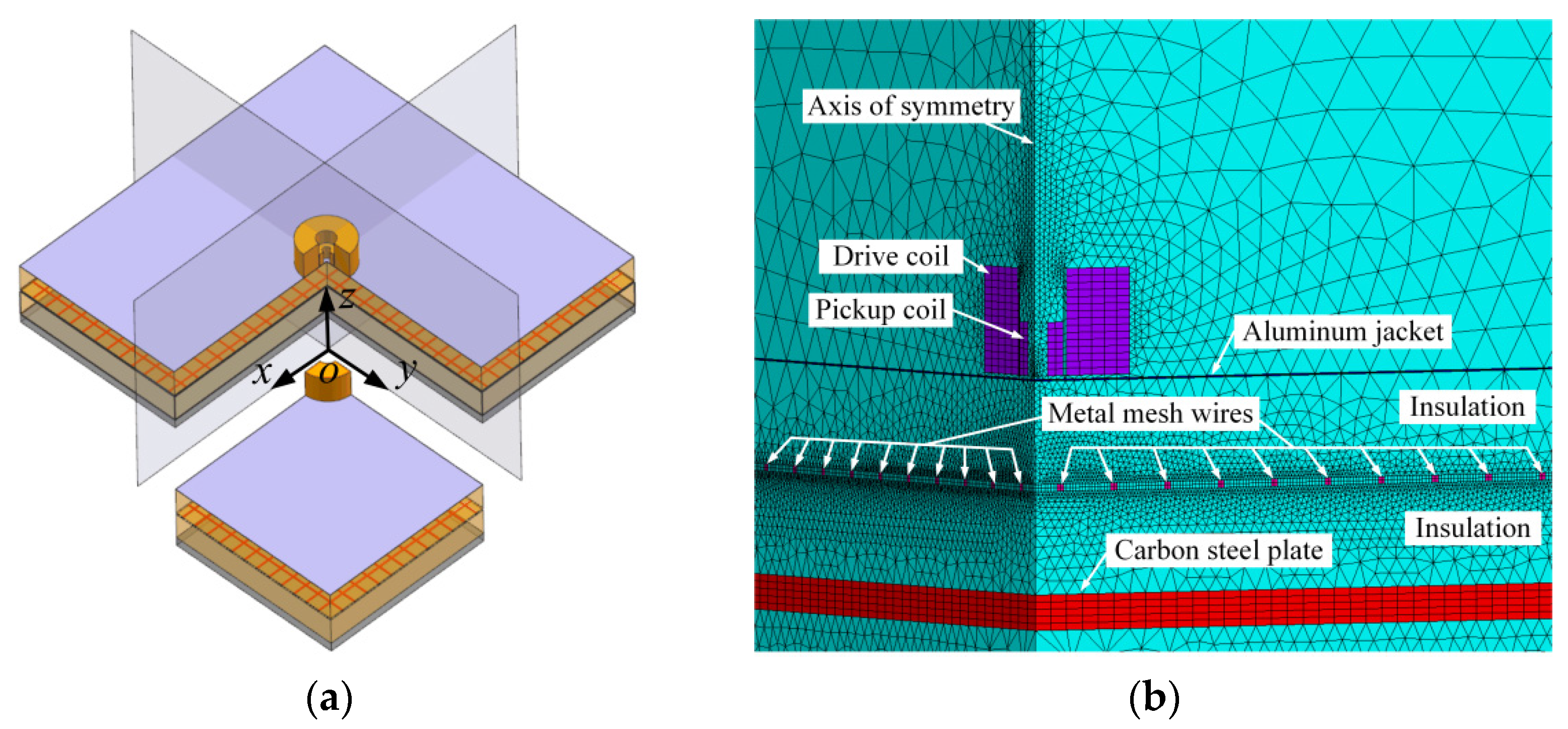
2.1. Simulation Model
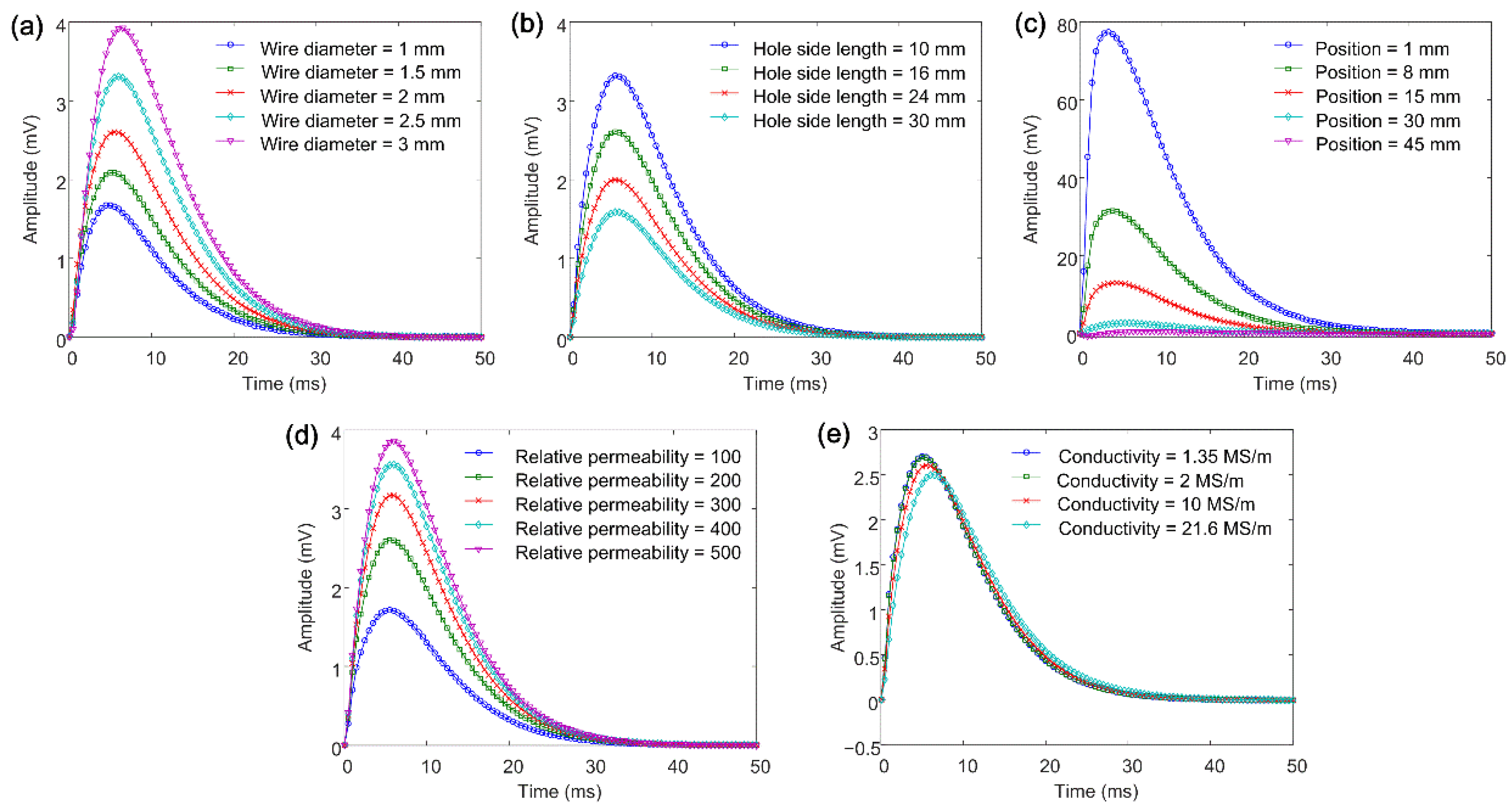
2.2. Simulation Results
3. Experiment Validation
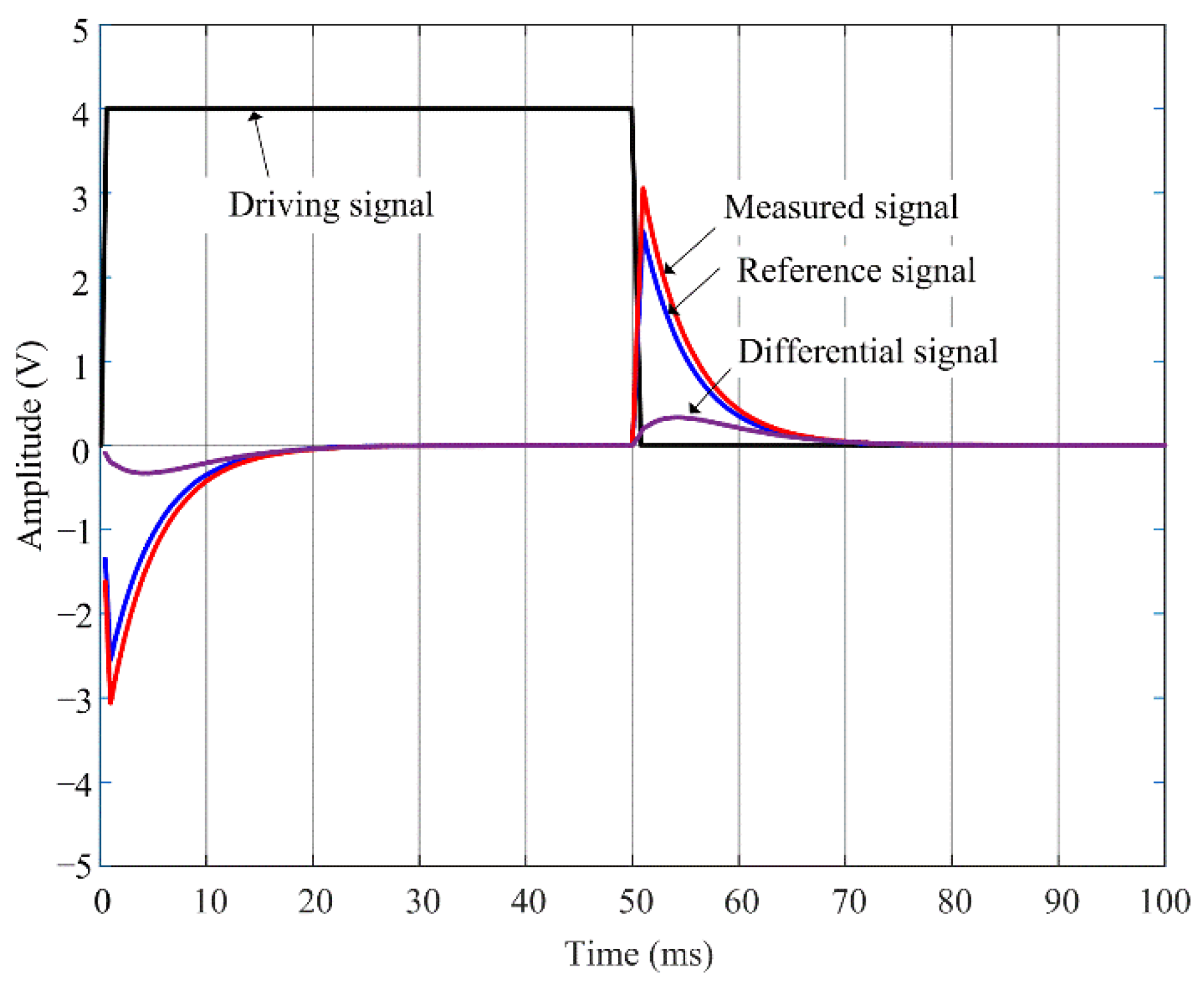
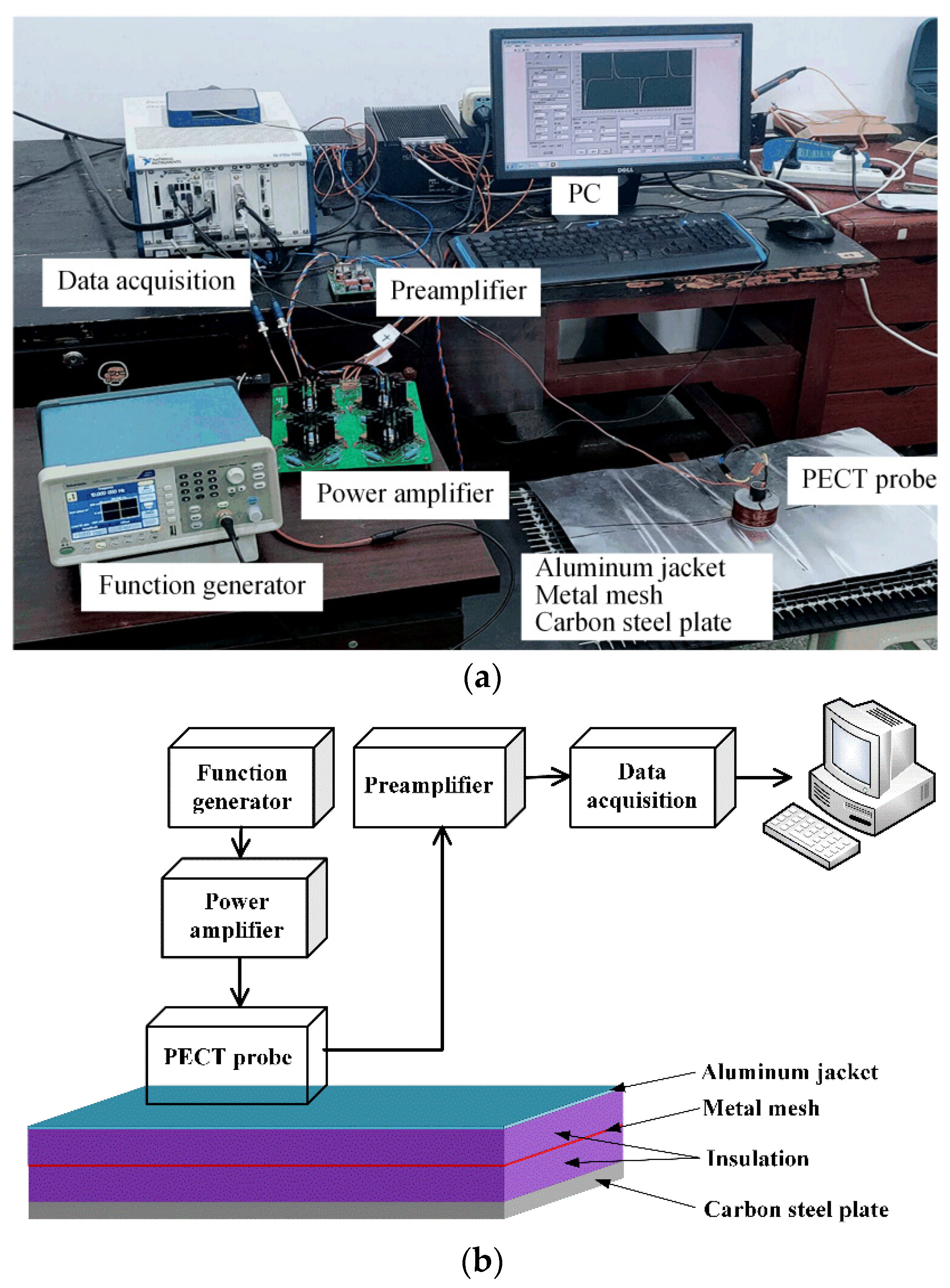
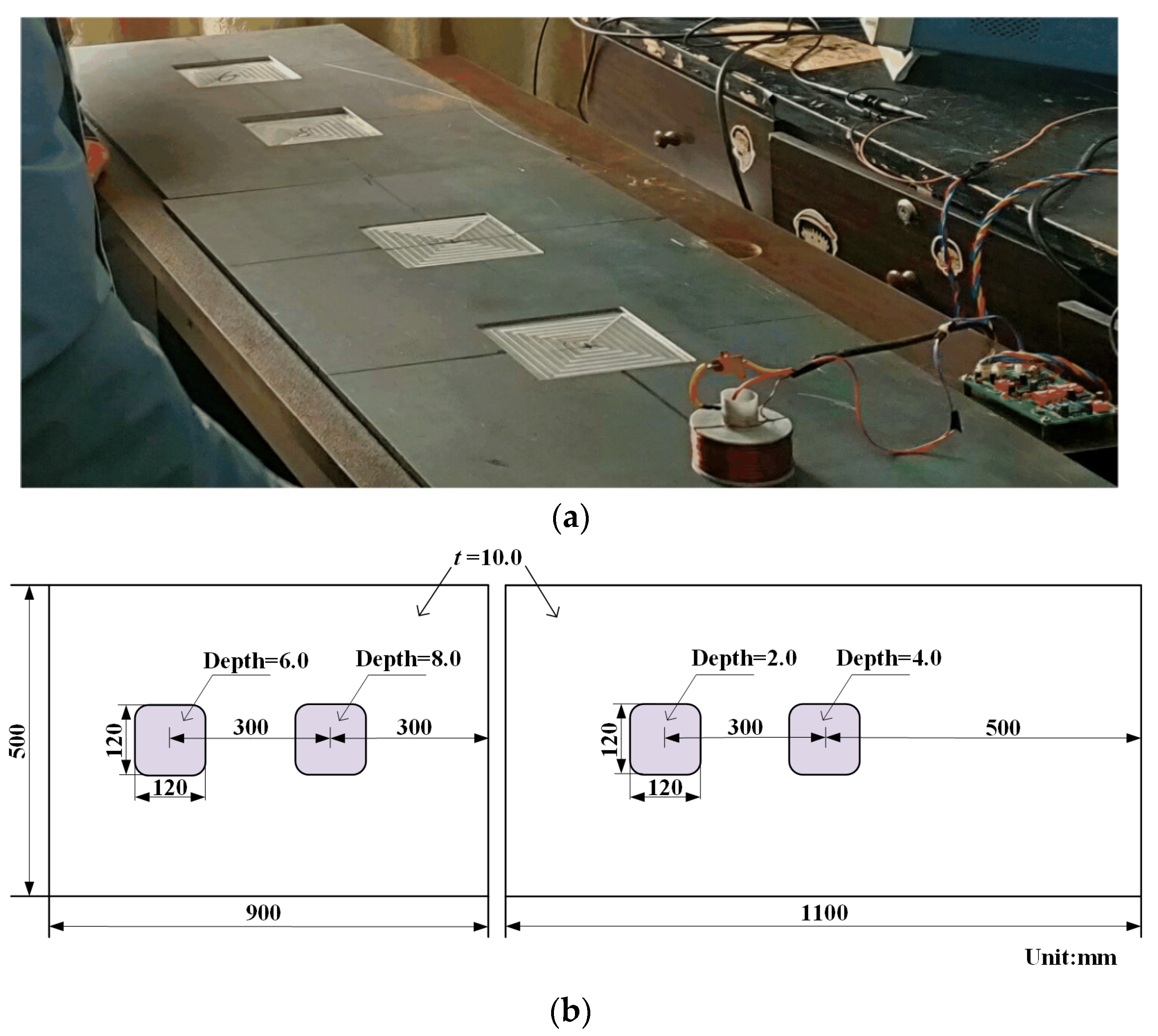
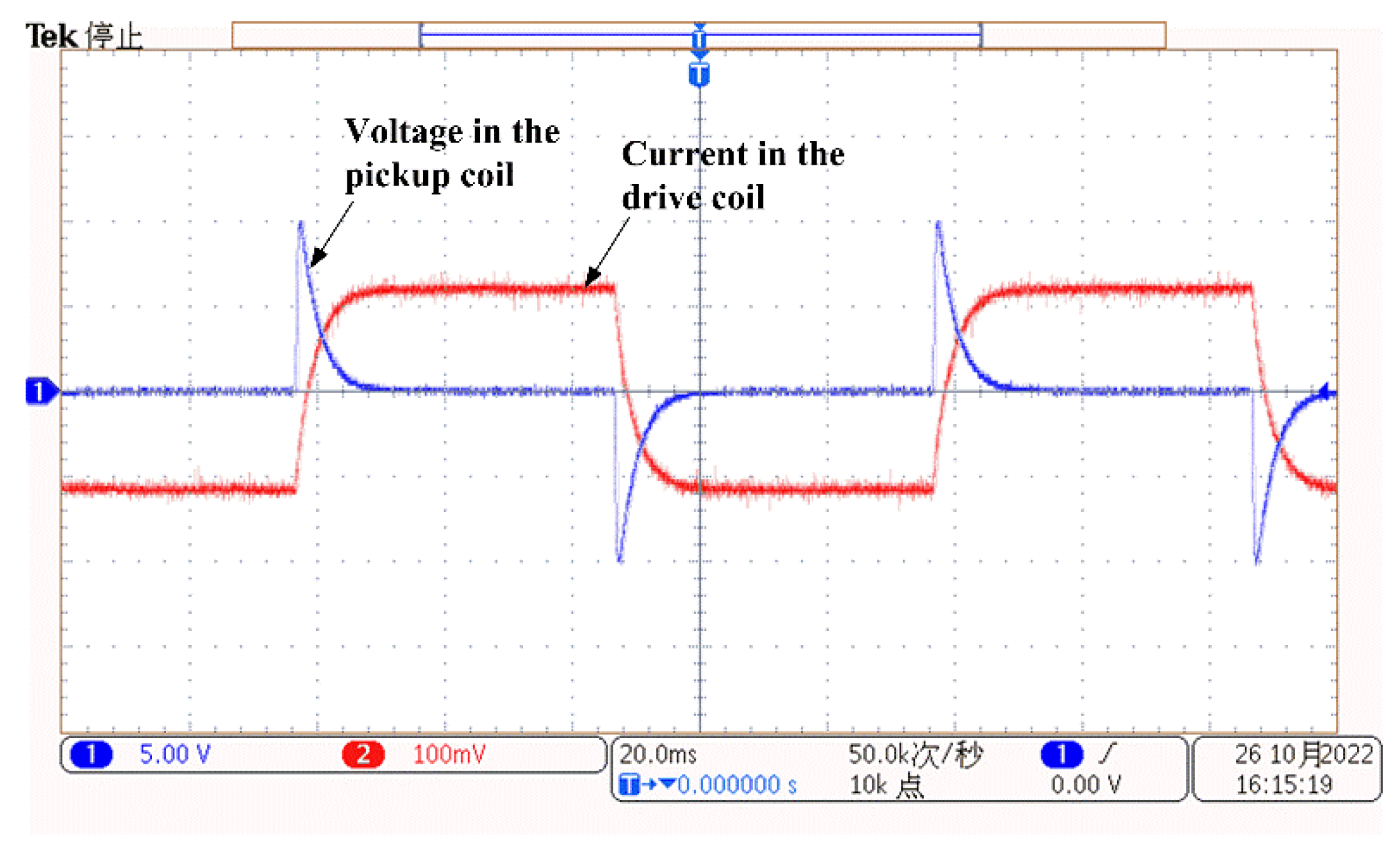
3.1. PECT System
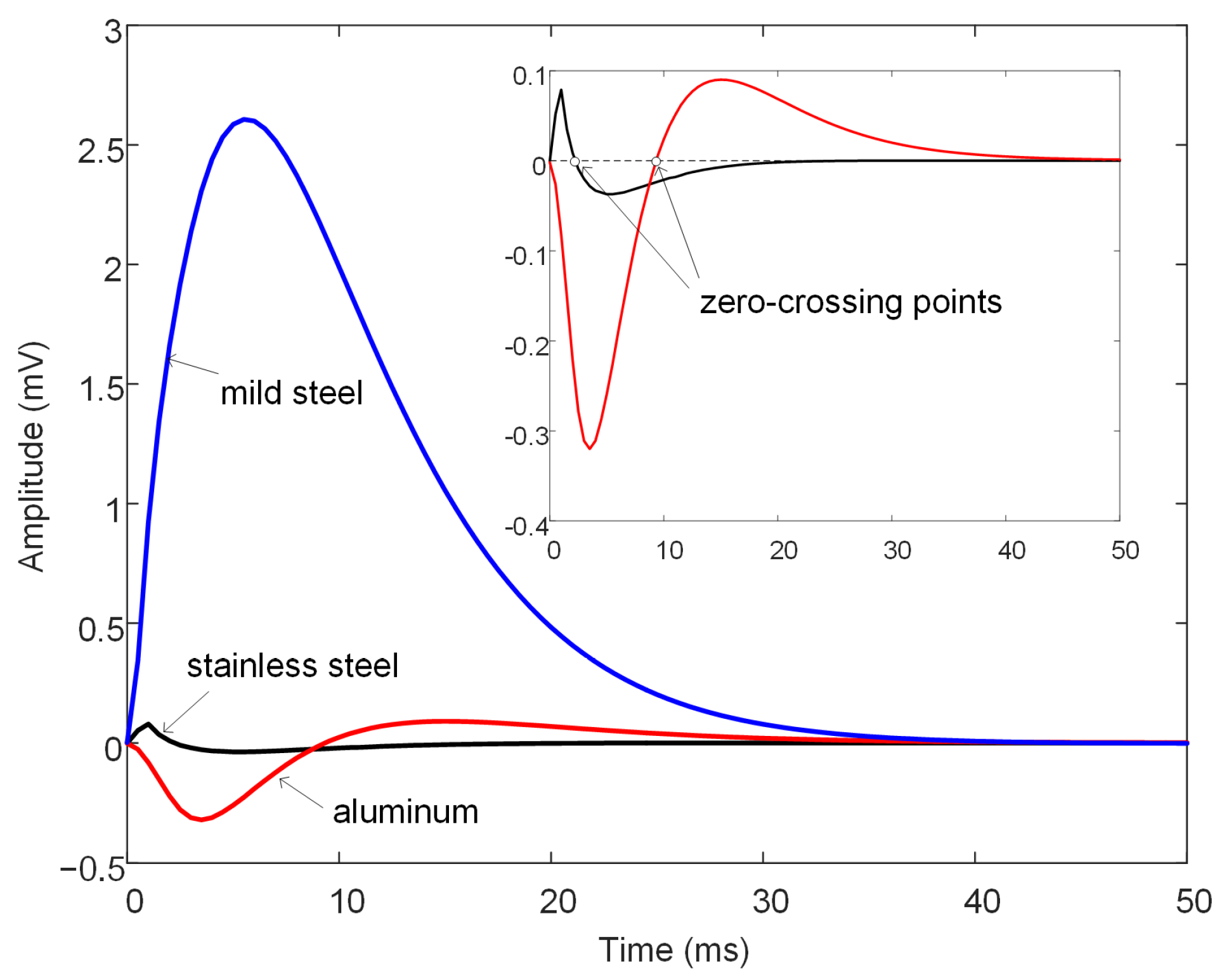
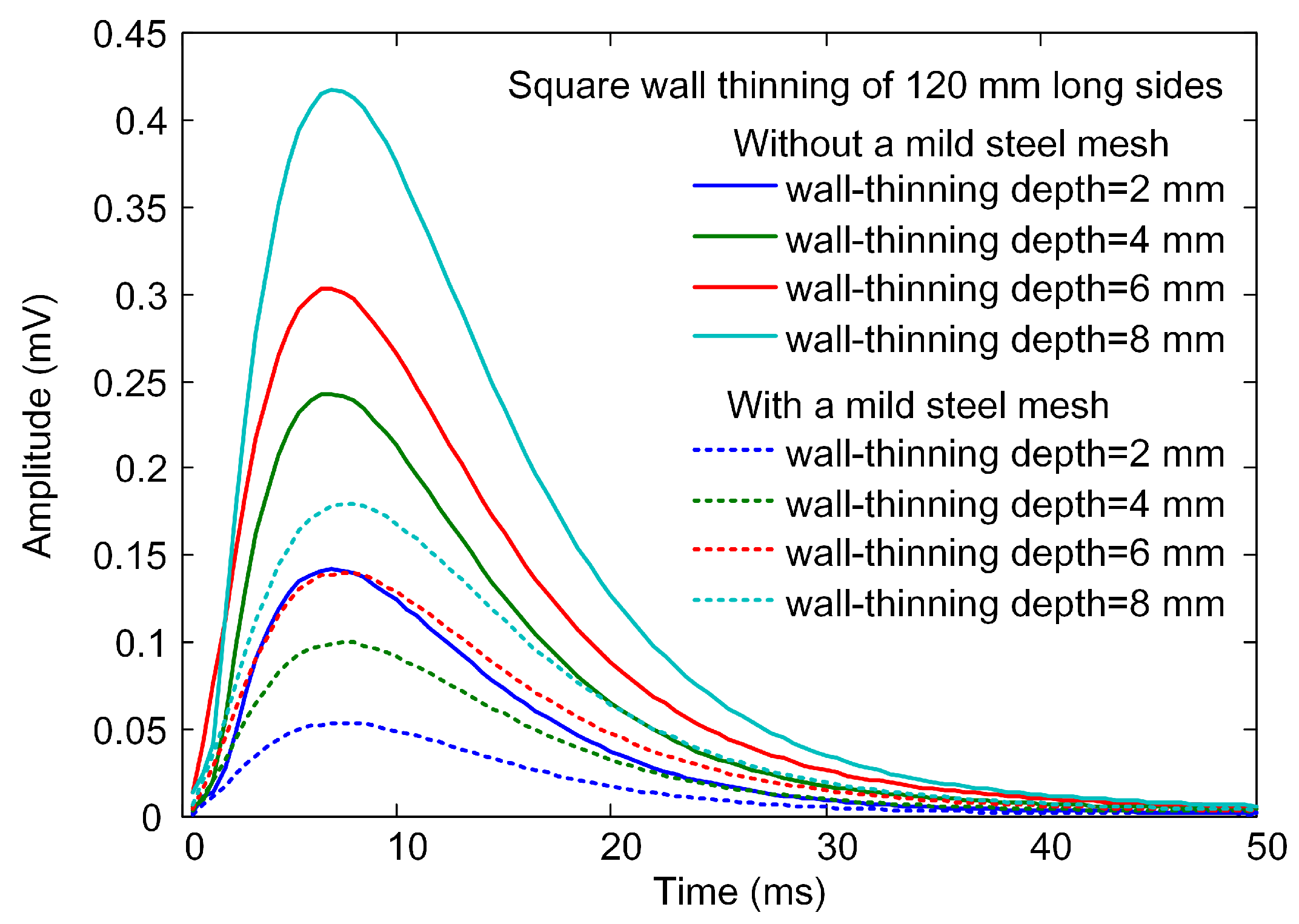
3.2. Experimental Results
4. Discussions and Conclusions
4.1. Discussions
4.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, Q.; Pojtanabuntoeng, T.; Esmaily, M.; Thomas, S.; Brameld, M.; Amer, A.; Birbilis, N. A Review of Corrosion under Insulation: A Critical Issue in the Oil and Gas Industry. Metals 2022, 12, 561. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, Z.; Chen, H.; Qu, Z.; Liu, J. Effects of the wire mesh on pulsed eddy current detection of corrosion under insulation. Nondestruct. Test. Eval. 2022, 1–21. [Google Scholar] [CrossRef]
- Cadelano, G.; Bortolin, A.; Ferrarini, G.; Molinas, B.; Giantin, D.; Zonta, P.; Bison, P. Corrosion Detection in Pipelines Using Infrared Thermography: Experiments and Data Processing Methods. J. Nondestruct. Eval. 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Jarvis, R.; Cawley, P.; Nagy, P.B. Current deflection NDE for the inspection and monitoring of pipes. NDTE Int. 2016, 81, 46–59. [Google Scholar] [CrossRef]
- Pechacek, R.W. Advanced NDE methods of inspecting insulated vessels and piping for ID corrosion and corrosion under insulation (CUI). In Proceedings of the Corrosion 2003, San Diego, CA, USA, 16–20 March 2003. [Google Scholar]
- Licata, M.; Aspinall, M.D.; Bandala, M.; Cave, F.D.; Conway, S.; Gerta, D.; Parker, H.M.O.; Roberts, N.J.; Taylor, G.C.; Joyce, M.J. Depicting corrosion-born defects in pipelines with combined neutron/γ ray backscatter: A biomimetic approach. Sci. Rep. 2020, 10, 1486. [Google Scholar] [CrossRef] [PubMed]
- Alwis, L.; Sun, T.; Grattan, K.T.V. Optical fibre-based sensor technology for humidity and moisture measurement: Review of recent progress. Measurement 2013, 46, 4052–4074. [Google Scholar] [CrossRef]
- Yin, X.; Hutchins, D.; Chen, G.; Li, W. Detecting surface features on conducting specimens through an insulation layer using a capacitive imaging technique. NDTE Int. 2012, 52, 157–166. [Google Scholar] [CrossRef]
- Robers, M.A.; Scottini, R. Pulsed eddy currents in corrosion detection. In Proceedings of the 8th European Conference on Nondestructive Testing (ECNDT), Barcelona, Spain, 17–21 June 2002. [Google Scholar]
- Grenier, M.; Demers-Carpentier, V.; Rochette, M.; Hardy, F. Pulsed eddy current: New developments for corrosion under insulation examinations. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016; pp. 13–17. [Google Scholar]
- Xu, Z.; Wu, X.; Li, J.; Kang, Y. Assessment of wall thinning in insulated ferromagnetic pipes using the time-to-peak of differential pulsed eddy-current testing signals. NDT E Int. 2012, 51, 24–29. [Google Scholar] [CrossRef]
- Wassink, C.; Crouzen, P. Pulsed eddy current testing. Mater. Eval. 2018, 76, 700–705. [Google Scholar]
- Hedengren, K.H.; Ritscher, D.E.; Groshong, B.R. Probe footprint estimation in eddy- current imaging. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Plenum Press: New York, NY, USA, 1990; Volume 9, pp. 845–852. [Google Scholar]
- Morozov, M.; Dobie, G.; Gachagan, A. Assessment of corrosion under insulation and engineered temporary wraps using pulsed eddy-current techniques. In Proceedings of the 56th Annual Conference of the British Institute of Non-Destructive Testing, Telford, UK, 5–7 September 2017. [Google Scholar]
- Tremblay, C.; Sisto, M.M.; Potvin, A. Breakthrough in pulsed eddy current detection and sizing. In Proceedings of the 26th International Conference & Expo on Corrosion, Mumbai, India, 23–26 September 2019. [Google Scholar]
- Cheng, W.; Komura, I. Pulsed eddy current testing of a carbon steel pipe’s wall-thinning. In Proceedings of the 9th International Conference on NDE in Relation to Structural Integrity for Nuclear and Pressurized Components, Seattle, WA, USA, 22–24 May 2012. [Google Scholar]
- Chen, X.; Xu, R. Analytical Method of Probe Footprint Based on Equivalent Model of Pulsed Eddy Current Field. IEEE Trans. Magn. 2022, 58, 6200609. [Google Scholar] [CrossRef]
- Shin, Y.K.; Choi, D.M.; Kim, Y.J.; Lee, S.S. Signal characteristics of differential-pulsed eddy current sensors in the evaluation of plate thickness. NDT E Int. 2009, 42, 215–221. [Google Scholar] [CrossRef]
- Yu, Y.; Yan, Y.; Wang, F.; Tian, G.; Zhang, D. An approach to reduce lift-off noise in pulsed eddy current nondestructive technology. NDT E Int. 2014, 63, 1–6. [Google Scholar] [CrossRef]
- Chen, D.; Shao, K.R.; Lavers, J.D. Very fast numerical analysis of benchmark models of eddy current testing for steam generator tube. IEEE Trans. Magn. 2002, 38, 2355–2357. [Google Scholar] [CrossRef]
- Sophian, A.; Tian, G.; Fan, M. Pulsed eddy current non-destructive testing and evaluation: A review. Chin. J. Mech. Eng. 2017, 30, 500–514. [Google Scholar] [CrossRef]
- Xiao, Q.; Feng, J.; Xu, Z.; Zhang, H. Receiver Signal Analysis on Geometry and Excitation Parameters of Remote Field Eddy Current Probe. IEEE Trans. Ind. Electron. 2022, 69, 3088–3098. [Google Scholar] [CrossRef]
- Tajima, N.; Yusa, N.; Hashizume, H. Application of low frequency eddy current testing to the inspection of a double-walled tank in a reprocessing plant. Nondestruct. Test. Eval. 2018, 33, 189–197. [Google Scholar] [CrossRef]



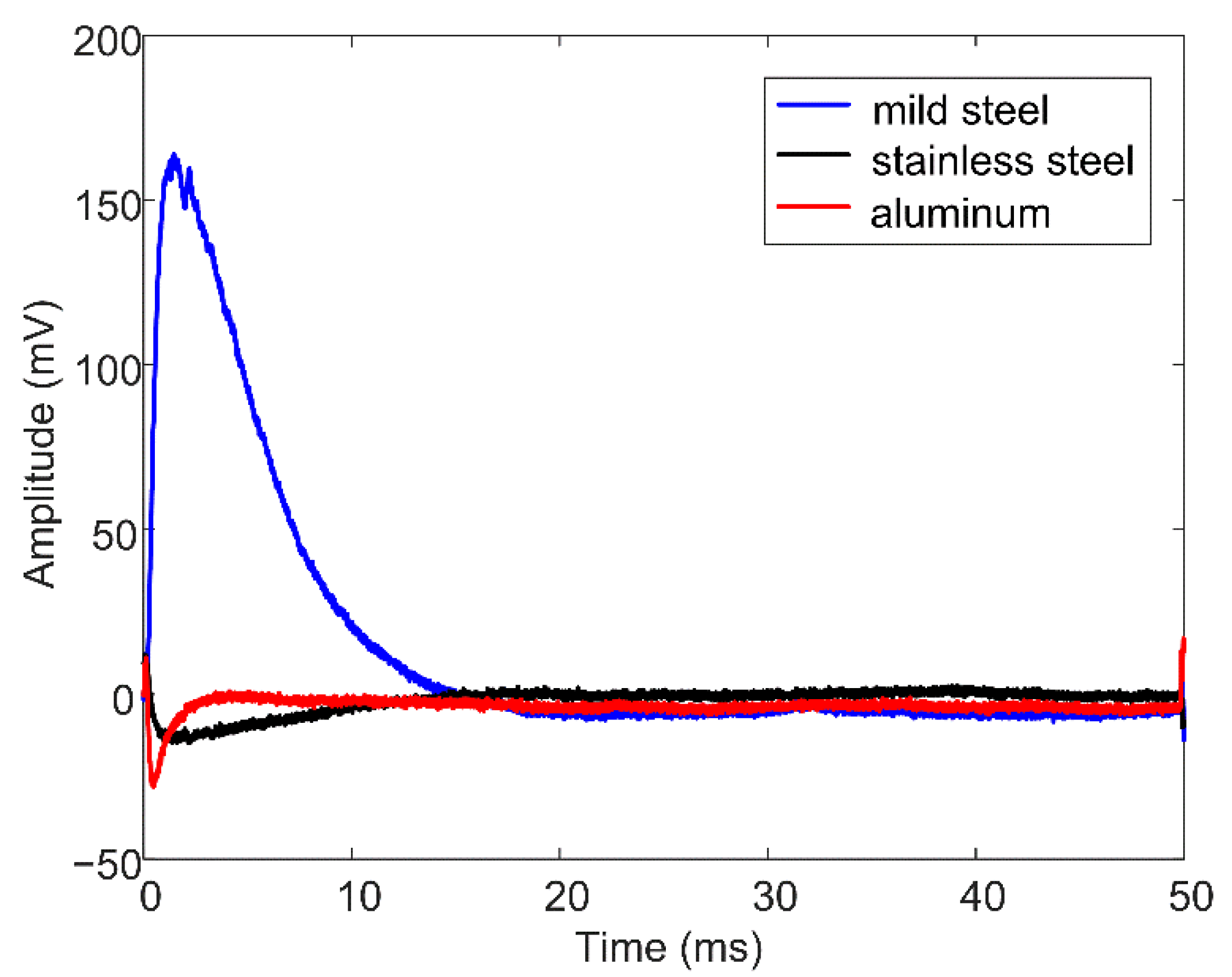
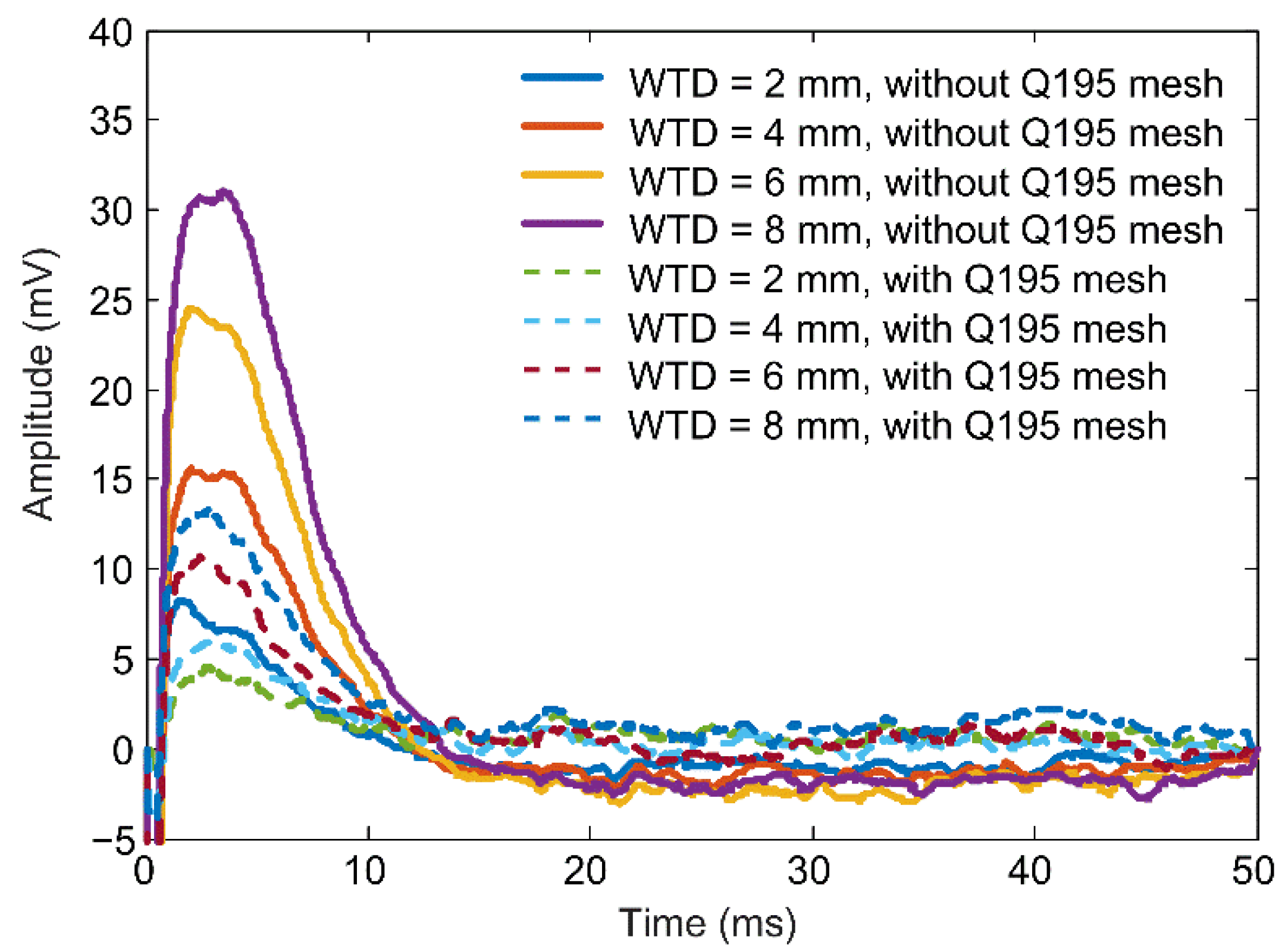
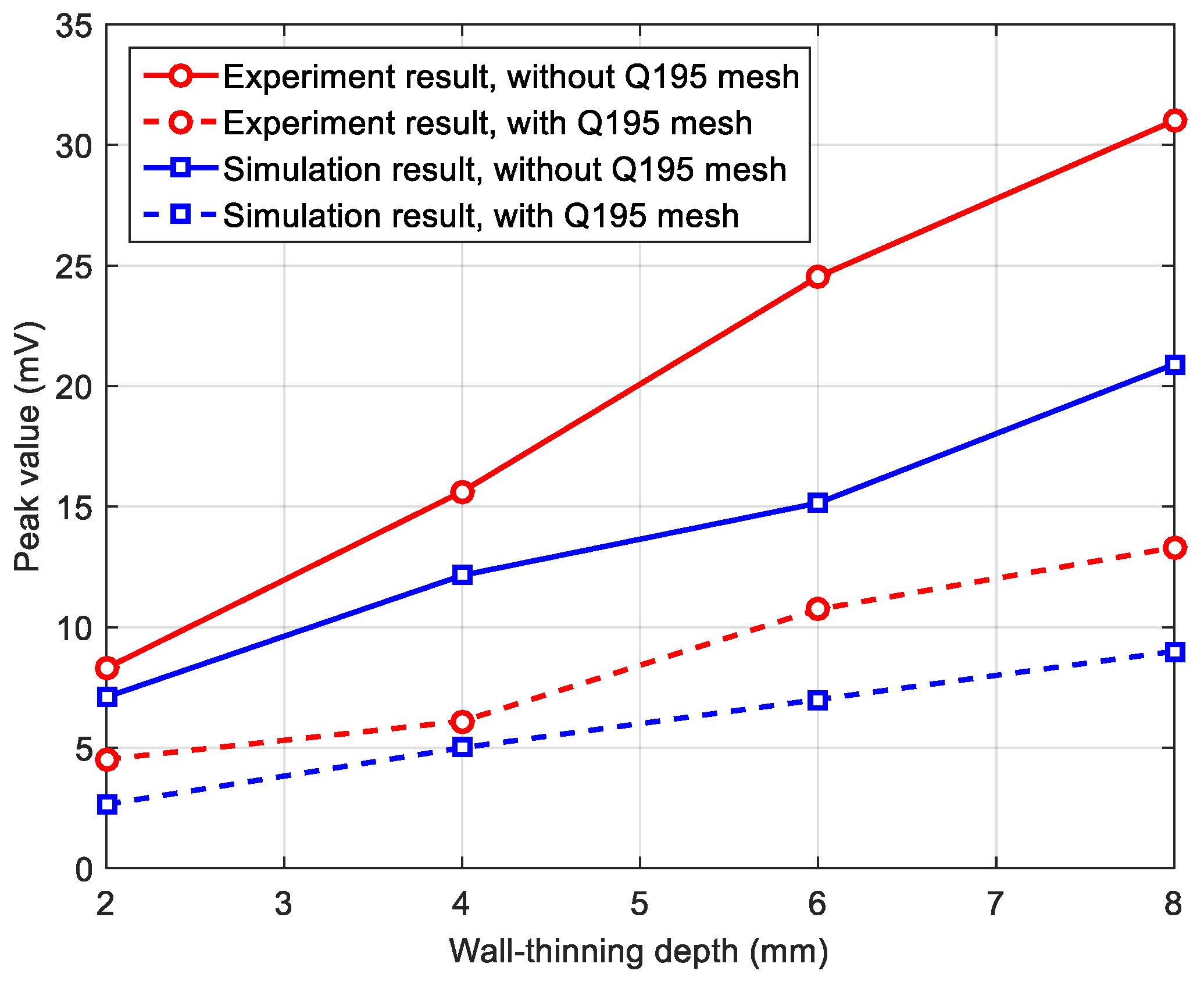
| Parameter | Value |
|---|---|
| Conductivity (MS/m) | 1.35, 2, 10, 21.6 |
| Relative magnetic permeability | 1, 100, 200, 300, 400, 500 |
| Wire diameter (mm) | 1, 1.5, 2, 2.5, 3 |
| Hole side length (mm) | 10, 16, 24, 30 |
| Position (mm) | 10, 20, 30, 40, 50 |
| Parameter | Drive Coil | Pickup Coil |
|---|---|---|
| Inner diameter (mm) | 20 | 8 |
| Outer diameter (mm) | 60 | 18 |
| Height (mm) | 30 | 15 |
| No. of turns | 500 | 350 |
| Wire diameter (mm) | 1 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Xu, Z.; Zhou, Z.; Jin, J.; Hu, Z. Study on the Effect of Metal Mesh on Pulsed Eddy-Current Testing of Corrosion under Insulation Using an Early-Phase Signal Feature. Materials 2023, 16, 1451. https://doi.org/10.3390/ma16041451
Chen H, Xu Z, Zhou Z, Jin J, Hu Z. Study on the Effect of Metal Mesh on Pulsed Eddy-Current Testing of Corrosion under Insulation Using an Early-Phase Signal Feature. Materials. 2023; 16(4):1451. https://doi.org/10.3390/ma16041451
Chicago/Turabian StyleChen, Hanqing, Zhiyuan Xu, Zhen Zhou, Junqi Jin, and Zihua Hu. 2023. "Study on the Effect of Metal Mesh on Pulsed Eddy-Current Testing of Corrosion under Insulation Using an Early-Phase Signal Feature" Materials 16, no. 4: 1451. https://doi.org/10.3390/ma16041451
APA StyleChen, H., Xu, Z., Zhou, Z., Jin, J., & Hu, Z. (2023). Study on the Effect of Metal Mesh on Pulsed Eddy-Current Testing of Corrosion under Insulation Using an Early-Phase Signal Feature. Materials, 16(4), 1451. https://doi.org/10.3390/ma16041451






