Electronic, Optical, Mechanical, and Electronic Transport Properties of SrCu2O2: A First-Principles Study
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
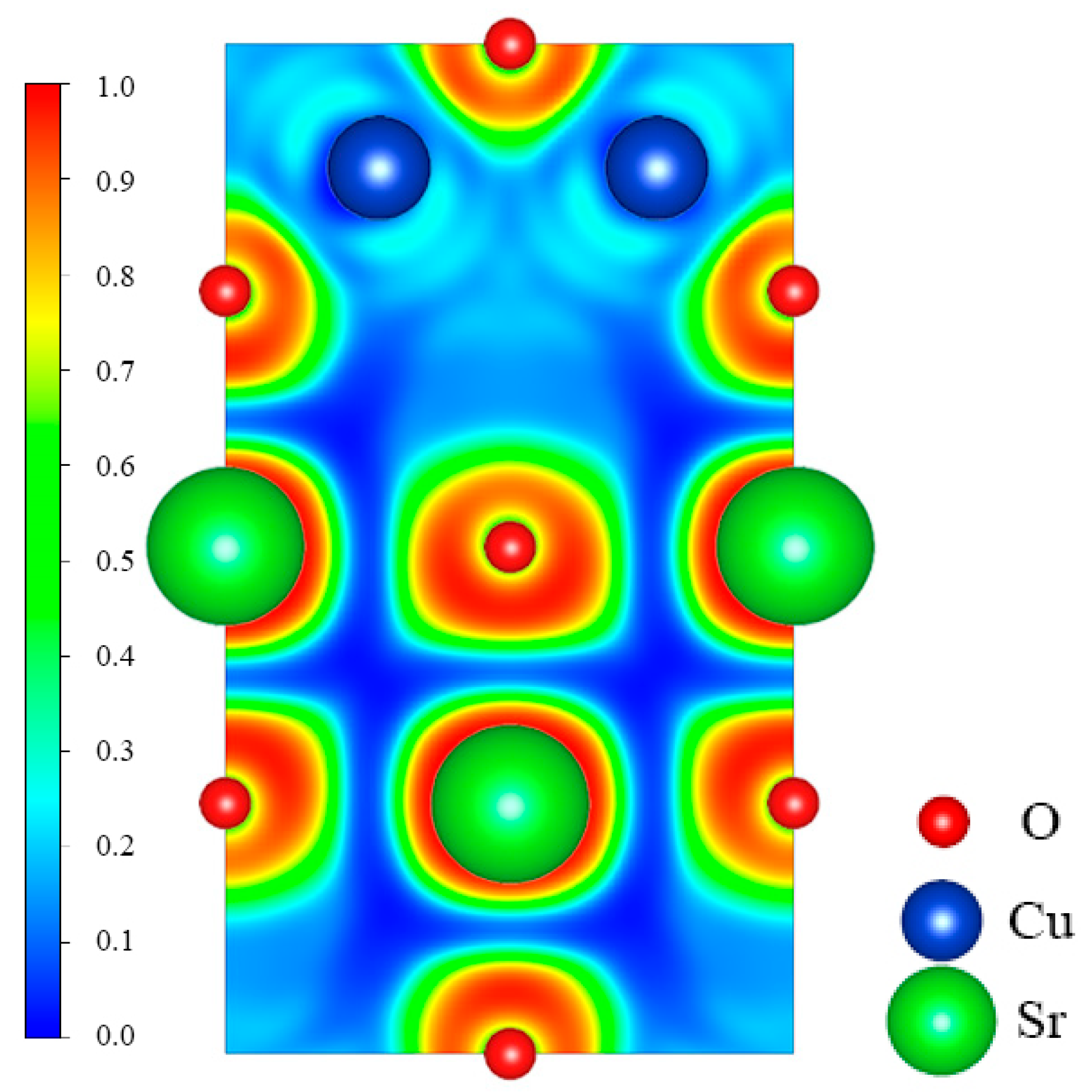
3.1. Crystal Structure of SrCu2O2
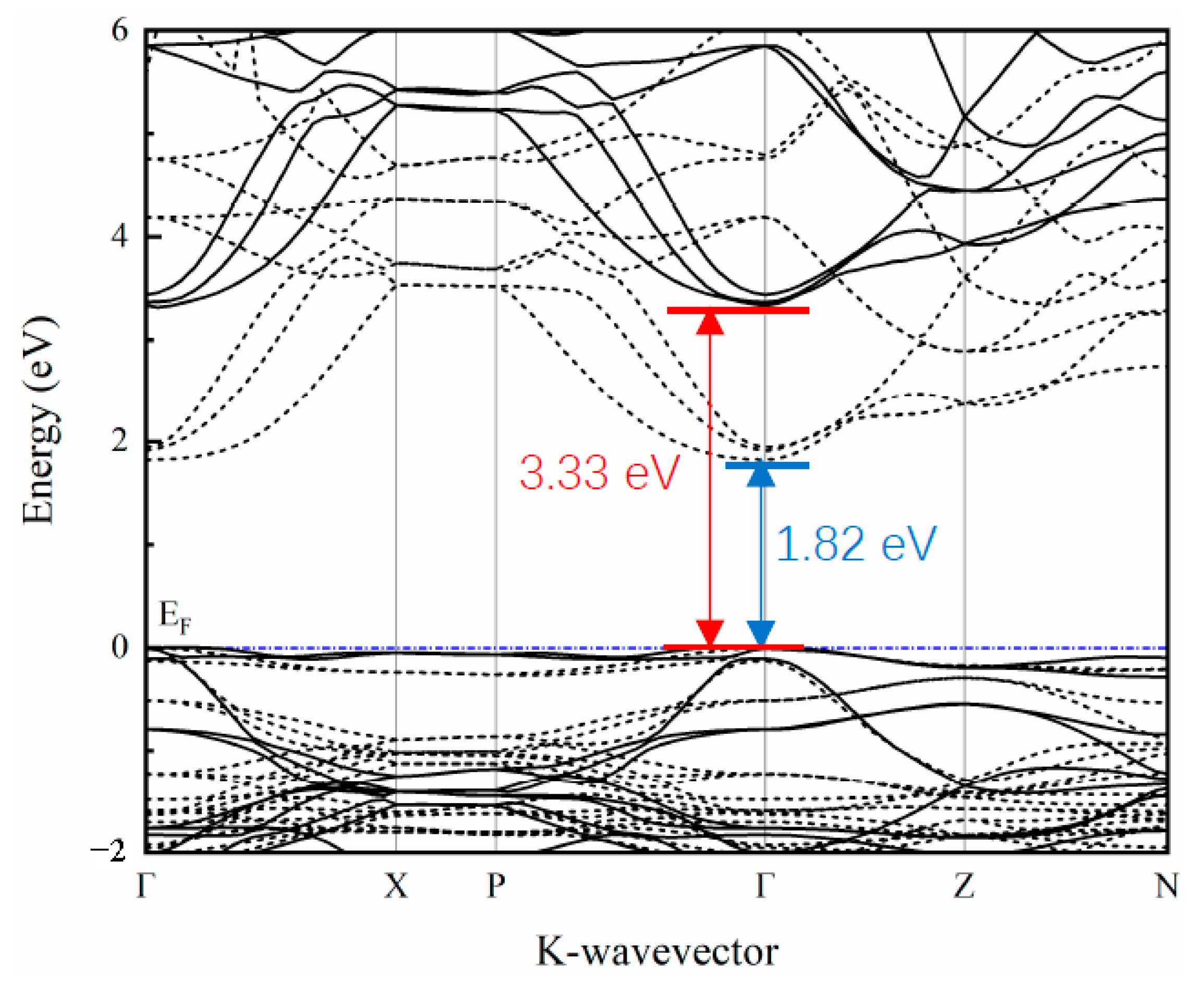
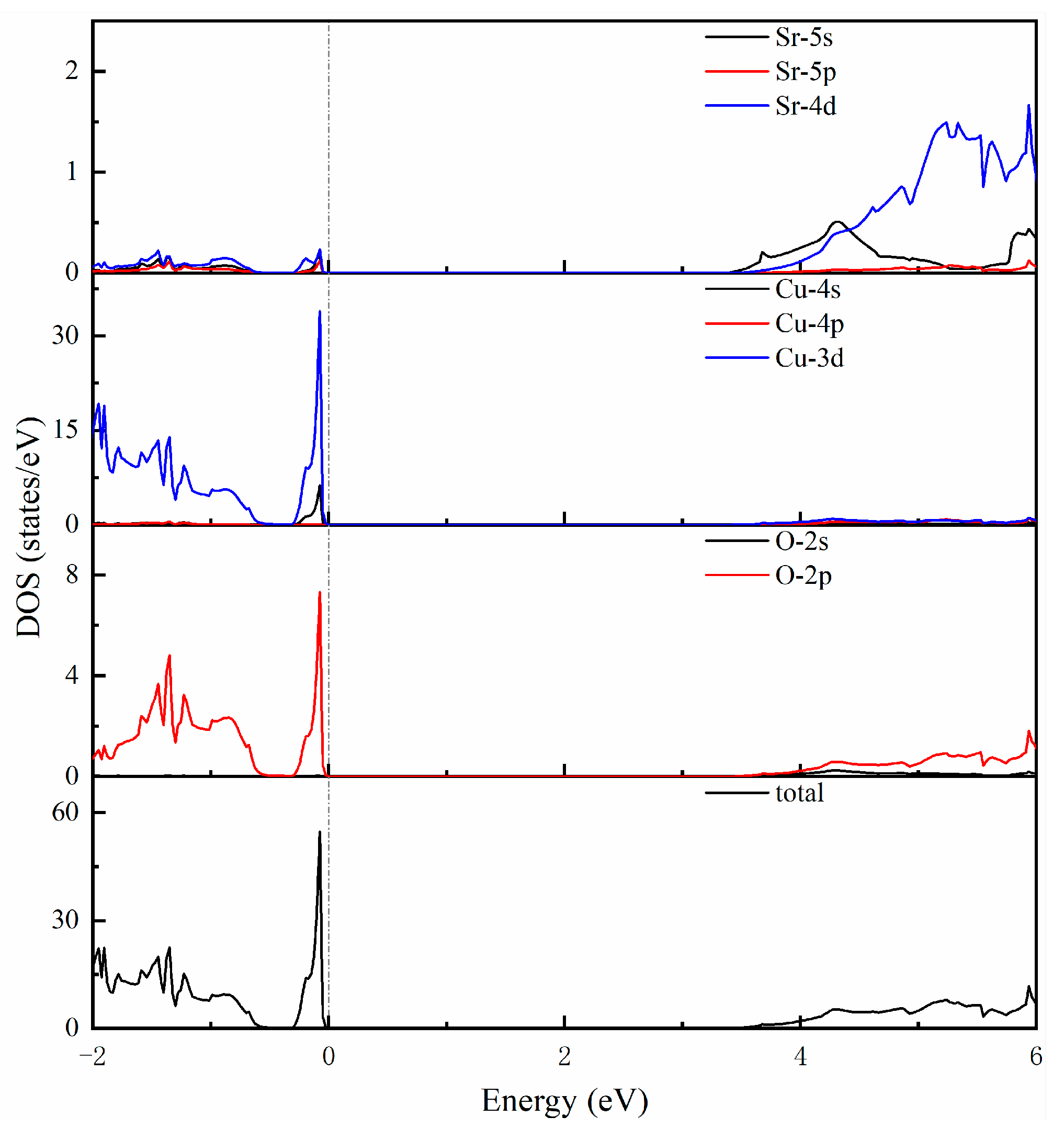
3.2. Electronic Properties of SrCu2O2
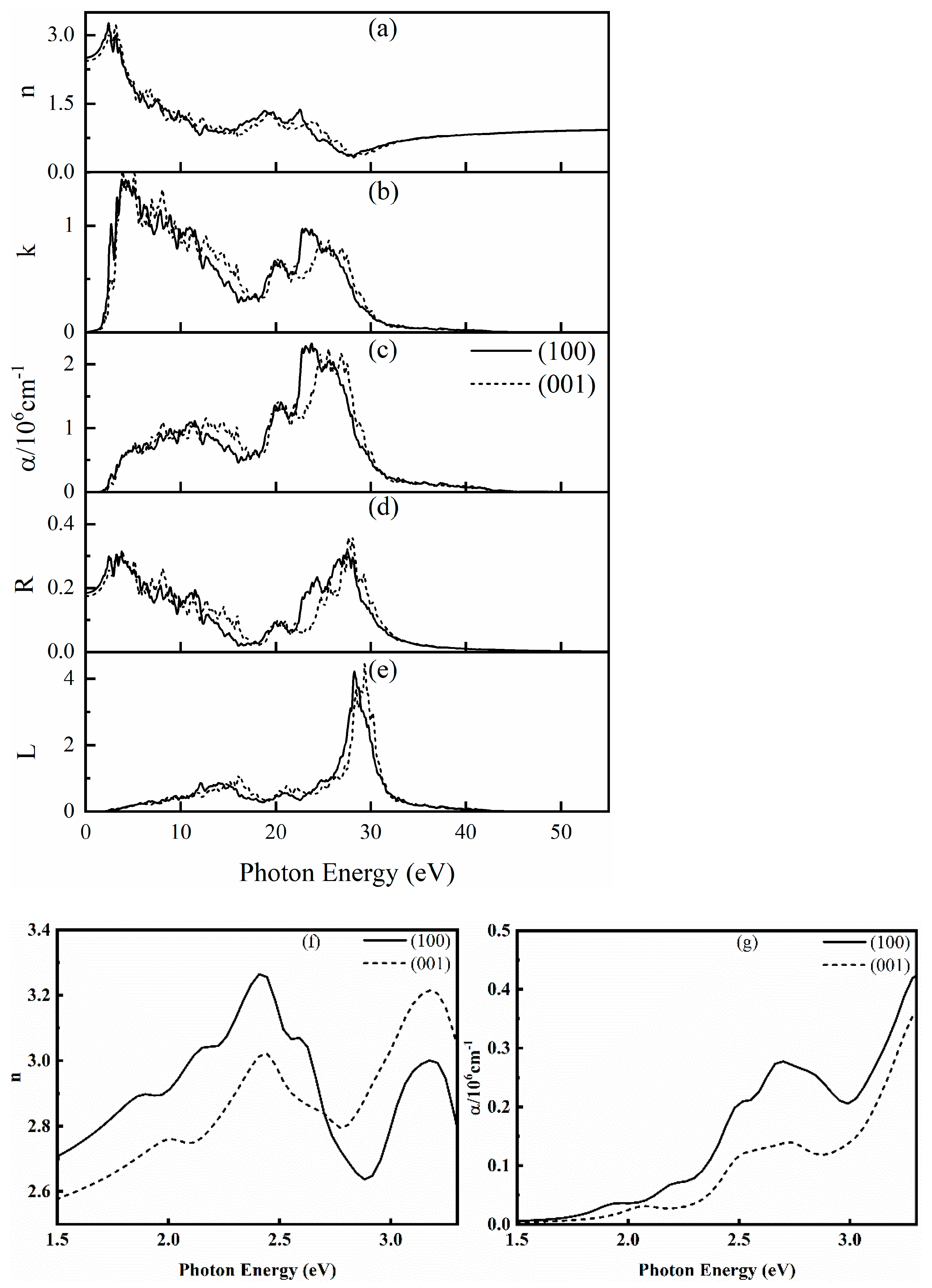
3.3. Optical Properties of SrCu2O2
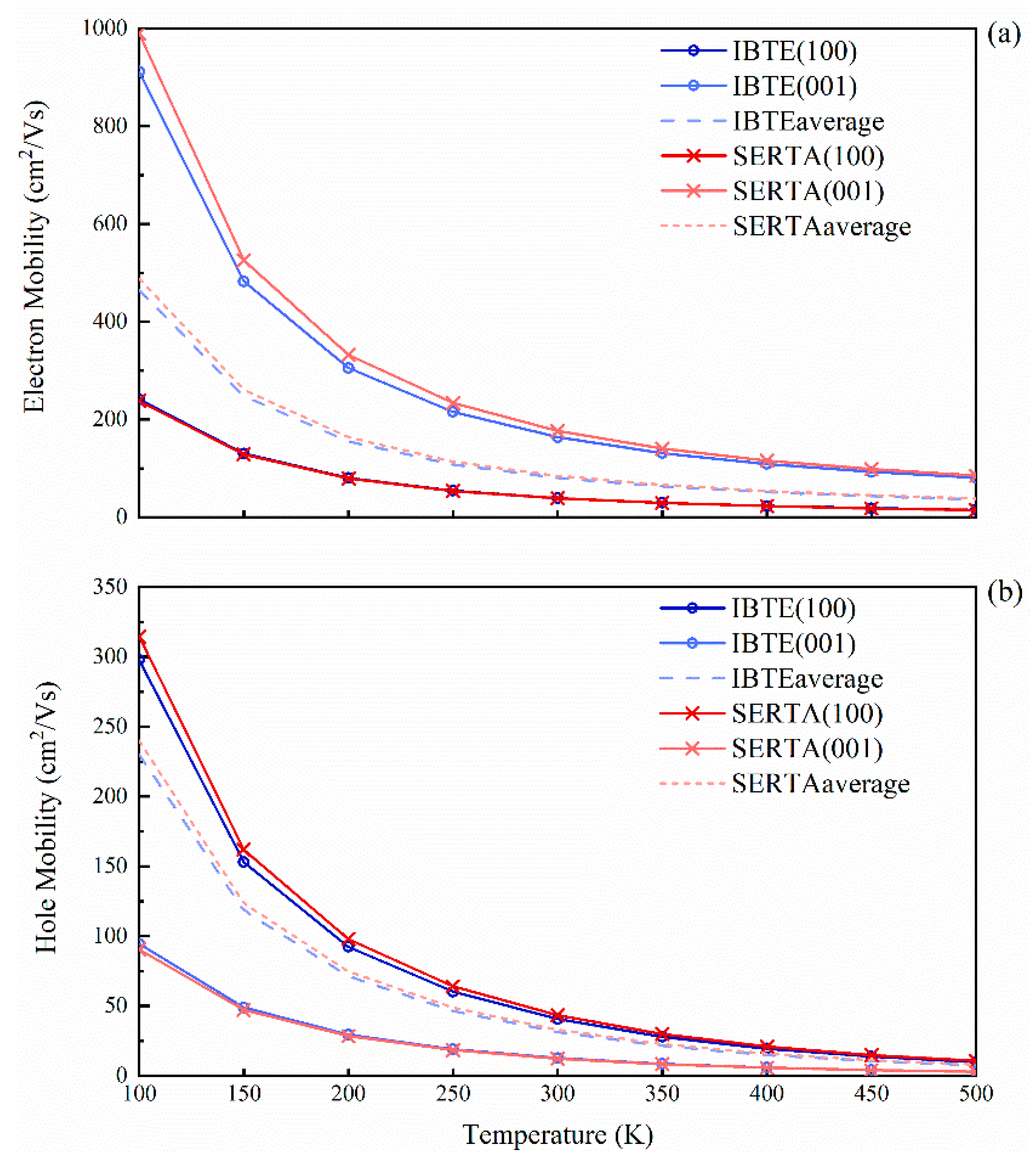
3.4. Electronic Transport Properties of SrCu2O2
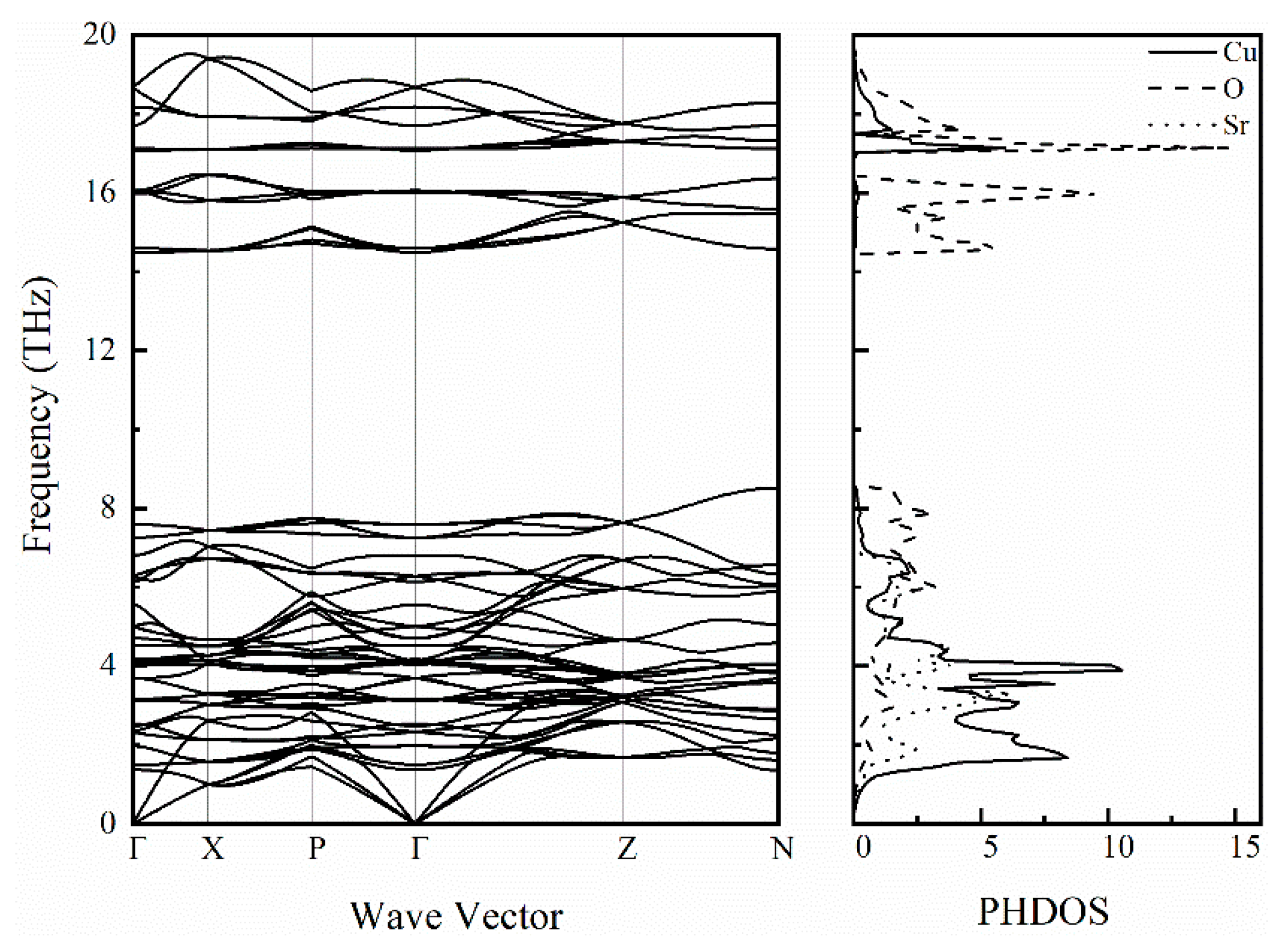
3.5. Lattice Dynamics Properties of SrCu2O2
3.6. Mechanical Properties of SrCu2O2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Kahn, M.E.; Liu, Y.; Wang, Z. The consequences of spatially differentiated water pollution regulation in China. J. Environ. Econ. Manag. 2018, 88, 468–485. [Google Scholar] [CrossRef]
- Fujishima, A.; Honda, K. Electrochemical photolysis of water at a semiconductor electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Ben Azaza, N.; Elleuch, S.; Rasheed, M.; Gindre, D.; Abid, S.; Barille, R.; Abid, Y.; Ammar, H. 3-(p-nitrophenyl)Coumarin derivatives: Synthesis, linear and nonlinear optical properties. Opt. Mater. 2019, 96, 109328. [Google Scholar] [CrossRef]
- Abbas, M.M.; Rasheed, M. Solid state reaction synthesis and characterization of Cu doped TiO2 nanomaterials. J. Phys. Conf. Ser. 2021, 1795, 012059. [Google Scholar] [CrossRef]
- Grundmann, M. Karl Badeker (1877–1914) and the discovery of transparent conductive materials. Phys. Status Solidi A Appl. Mat. 2015, 212, 1409–1426. [Google Scholar] [CrossRef]
- Siripala, W.; Ivanovskaya, A.; Jaramillo, T.F.; Baeck, S.H.; McFarland, E.W. A Cu2O/TiO2 heterojunction thin film cathode for photoelectrocatalysis. Sol. Energy Mater. Sol. Cells 2003, 77, 229–237. [Google Scholar] [CrossRef]
- Hara, M.; Kondo, T.; Komoda, M.; Ikeda, S.; Shinohara, K.; Tanaka, A.; Kondo, J.N.; Domen, K. Cu2O as a photocatalyst for overall water splitting under visible light irradiation. Chem. Commun. 1998, 3, 357–358. [Google Scholar] [CrossRef]
- Fernando, C.A.N.; Wetthasinghe, S.K. Investigation of photoelectrochemical characteristics of n-type Cu2O films. Sol. Energy Mater. Sol. Cells 2000, 63, 299–308. [Google Scholar] [CrossRef]
- Senevirathna, M.K.I.; Pitigala, P.; Tennakone, K. Water photoreduction with Cu2O quantum dots on TiO2 nano-particles. J. Photochem. Photobiol. A Chem. 2005, 171, 257–259. [Google Scholar] [CrossRef]
- Sun, S.D.; Zhang, X.J.; Yang, Q.; Liang, S.H.; Zhang, X.Z.; Yang, Z.M. Cuprous oxide (Cu2O) crystals with tailored architectures: A comprehensive review on synthesis, fundamental properties, functional modifications and applications. Prog. Mater. Sci. 2018, 96, 111–173. [Google Scholar]
- Miao, M.S.; Yarbro, S.; Barton, P.T.; Seshadri, R. Electron affinities and ionization energies of Cu and Ag delafossite compounds: A hybrid functional study. Phys. Rev. B 2014, 89, 045306. [Google Scholar] [CrossRef] [Green Version]
- Nie, X.L.; Wei, S.H.; Zhang, S.B. First-principles study of transparent p-type conductive SrCu2O2 and related compounds. Phys. Rev. B 2002, 65, 075111. [Google Scholar] [CrossRef]
- Kawazoe, H.; Yanagi, H.; Ueda, K.; Hosono, H. Transparent p-type conducting oxides: Design and fabrication of p-n heterojunctions. MRS Bull. 2000, 25, 28–36. [Google Scholar] [CrossRef] [Green Version]
- Even, J.; Pedesseau, L.; Durand, O.; Modreanu, M.; Huyberechts, G.; Servet, B.; Chaix-Pluchery, O. Vibrational properties of SrCu2O2 studied via density functional theory calculations and compared to Raman and infrared spectroscopy measurements. Thin Solid Films 2013, 541, 113–116. [Google Scholar] [CrossRef] [Green Version]
- Curtarolo, S.; Hart, G.L.W.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Shin, Y.; Persson, K.A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 2016, 1, 15004. [Google Scholar] [CrossRef] [Green Version]
- Lejaeghere, K.; Bihlmayer, G.; Bjorkman, T.; Blaha, P.; Blugel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Dal Corso, A.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.D.; Wang, Z.; Setyawan, W.; Mingo, N.; Curtarolo, S. Assessing the thermoelectric properties of sintered compounds via high-throughput ab-initio calculations. Phys. Rev. X 2011, 1, 021012. [Google Scholar]
- Chen, X.; Parker, D.; Singh, D.J. Importance of non-parabolic band effects in the thermoelectric properties of semiconductors. Sci. Rep. 2013, 3, 3168. [Google Scholar] [CrossRef] [Green Version]
- Krishnaswamy, K.; Himmetoglu, B.; Kang, Y.; Janotti, A.; Van de Walle, C.G. First-principles analysis of electron transport in BaSnO3. Phys. Rev. B 2017, 95, 205202. [Google Scholar] [CrossRef] [Green Version]
- Ohta, H.; Orita, M.; Hirano, M.; Yagi, I.; Ueda, K.; Hosono, H. Electronic structure and optical properties of SrCu2O2. J. Appl. Phys. 2002, 91, 3074–3078. [Google Scholar] [CrossRef]
- Boudin, S.; Felser, C.; Studer, F. Cu-Cu interactions in the transparent p-type conductors: CuAlO2 and SrCu2O2. Solid State Sci. 2003, 5, 741–744. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
- Paier, J.; Hirschl, R.; Marsman, M.; Kresse, G. The Perdew-Burke-Ernzerhof exchange-correlation functional applied to the G2-1 test set using a plane-wave basis set. J. Chem. Phys. 2005, 122, 234102. [Google Scholar] [CrossRef] [PubMed]
- Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, I.C.; Angyan, J.G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124, 154709. [Google Scholar] [CrossRef] [Green Version]
- Gonze, X.; Lee, C. Dynamical matrices, born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef] [Green Version]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Giustino, F.; Cohen, M.L.; Louie, S.G. Electron-phonon interaction using Wannier functions. Phys. Rev. B 2007, 76, 165108. [Google Scholar] [CrossRef]
- Ponce, S.; Margine, E.R.; Verdi, C.; Giustino, F. EPW: Electron-phonon coupling, transport and superconducting properties using maximally localized Wannier functions. Comput. Phys. Commun. 2016, 209, 116–133. [Google Scholar] [CrossRef] [Green Version]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys.-Condes. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys.-Condes. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419–1475. [Google Scholar] [CrossRef] [Green Version]
- Pizzi, G.; Vitale, V.; Arita, R.; Blugel, S.; Freimuth, F.; Geranton, G.; Gibertini, M.; Gresch, D.; Johnson, C.; Koretsune, T.; et al. Wannier90 as a community code: New features and applications. J. Phys.-Condes. Matter 2020, 32, 165902. [Google Scholar] [CrossRef]
- Teske, C.L.; Müller-Buschbaum, H.J. Über Erdalkalimetall-Oxocuprate. IV. Zur Kenntnis von SrCu2O2. Z. Für Anorg. Und Allg. Chem. 1970, 379, 113–121. [Google Scholar] [CrossRef]
- Kudo, A.; Yanagi, H.; Hosono, H.; Kawazoe, H. SrCu2O2: A p-type conductive oxide with wide band gap. Appl. Phys. Lett. 1998, 73, 220–222. [Google Scholar] [CrossRef]
- Modreanu, M.; Nolan, M.; Elliott, S.D.; Durand, O.; Servet, B.; Garry, G.; Gehan, H.; Huyberechts, G.; Papadopoulou, E.L.; Androulidaki, M.; et al. Optical and microstructural properties of p-type SrCu2O2: First principles modeling and experimental studies. Thin Solid Films 2007, 515, 8624–8631. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, L.; Zhou, Z. Towards better photocatalysts: First-principles studies of the alloying effects on the photocatalytic activities of bismuth oxyhalides under visible light. Phys. Chem. Chem. Phys. 2012, 14, 1286–1292. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, D.; Sanyal, S.P. Structural phase transition, electronic and lattice dynamical properties of half-Heusler compound CaAuBi. J. Alloys Compd. 2018, 745, 240–246. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annalen. Der Physik. 1889, 274, 573–587. [Google Scholar] [CrossRef] [Green Version]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behavior of crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]


| Lattice Constants | Atomic Coordinates (Fractional) | ||||
|---|---|---|---|---|---|
| (Å) | Atom | Site | x | y | z |
| a = 5.5292 (5.48) | Cu | 8d | 0.375 | 0.125 | 0.75 |
| c = 9.8272 (9.82) | O | 8e | 0.7504 (0.75) | 0.7504 (0.75) | 0 |
| Sr | 4a | 0 | 0 | 0 | |
| Conduction Band | Valence Band | |
|---|---|---|
| Γ |
| μe | μh | |
|---|---|---|
| SERTA | ||
| IBTE |
| Elastic Constants (GPa) | Elastic Moduli (GPa) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 94.9 | 35.6 | 68.3 | 192.6 | 23.6 | 19.5 | 72.9 | 26.2 | 70.1 | 0.34 | 2.79 | 6.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Hu, C.; Wang, D.; Zhong, Y.; Tang, C. Electronic, Optical, Mechanical, and Electronic Transport Properties of SrCu2O2: A First-Principles Study. Materials 2023, 16, 1829. https://doi.org/10.3390/ma16051829
Jiang S, Hu C, Wang D, Zhong Y, Tang C. Electronic, Optical, Mechanical, and Electronic Transport Properties of SrCu2O2: A First-Principles Study. Materials. 2023; 16(5):1829. https://doi.org/10.3390/ma16051829
Chicago/Turabian StyleJiang, Sheng, Chaohao Hu, Dianhui Wang, Yan Zhong, and Chengying Tang. 2023. "Electronic, Optical, Mechanical, and Electronic Transport Properties of SrCu2O2: A First-Principles Study" Materials 16, no. 5: 1829. https://doi.org/10.3390/ma16051829
APA StyleJiang, S., Hu, C., Wang, D., Zhong, Y., & Tang, C. (2023). Electronic, Optical, Mechanical, and Electronic Transport Properties of SrCu2O2: A First-Principles Study. Materials, 16(5), 1829. https://doi.org/10.3390/ma16051829






