Nonlinear Optical Properties in an Epitaxial YbFe2O4 Film Probed by Second Harmonic and Terahertz Generation
Abstract
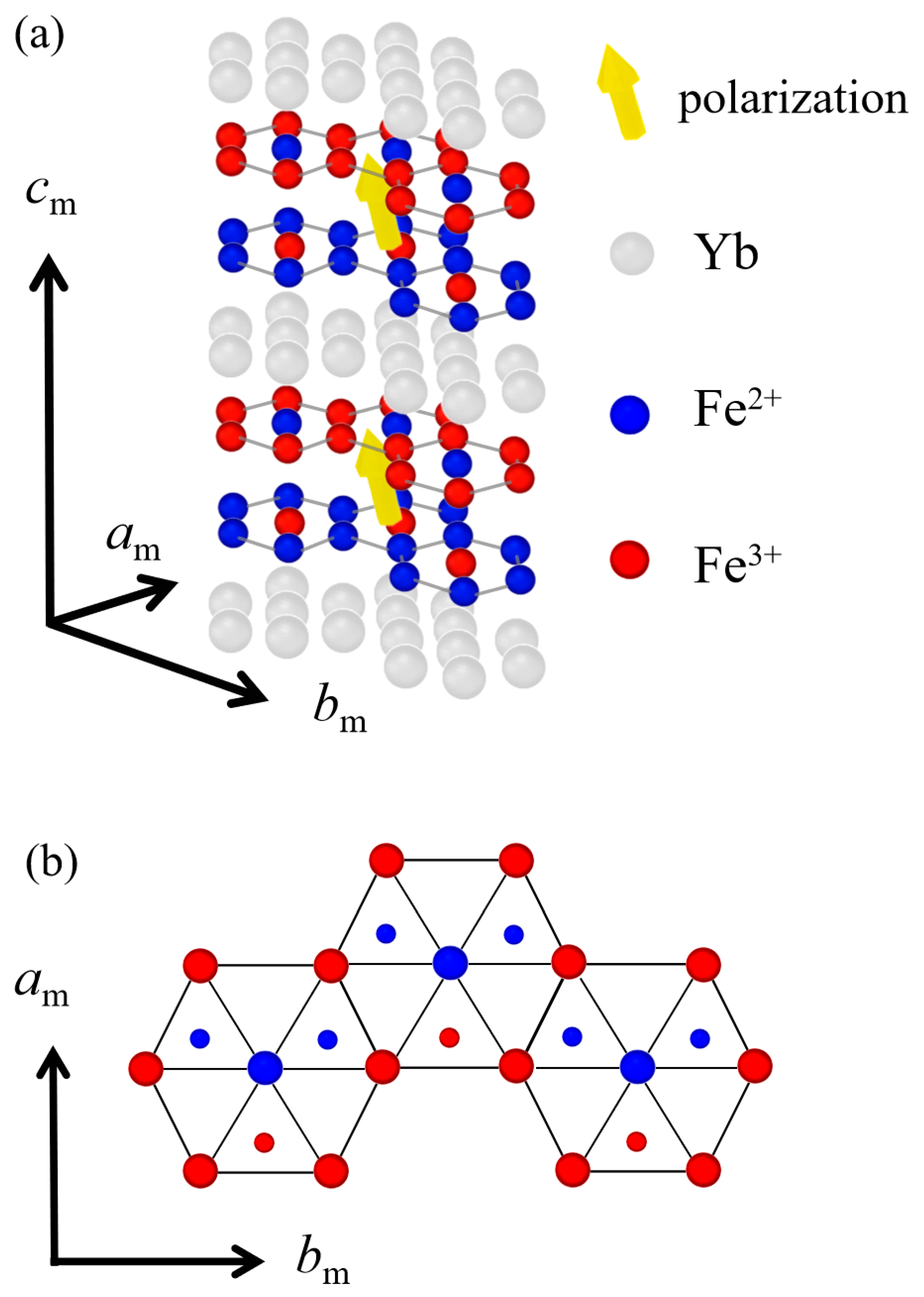
:1. Introduction
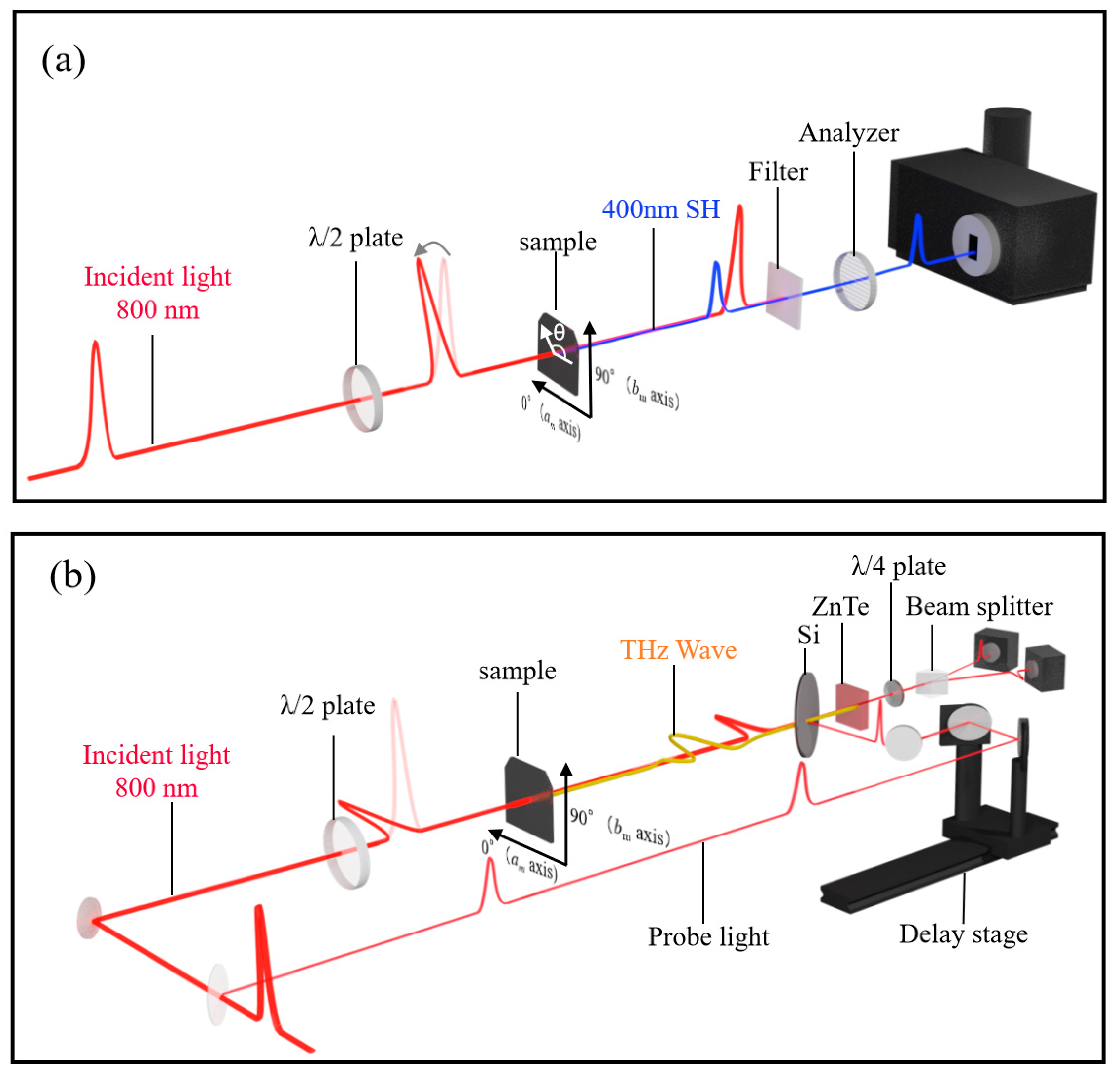
2. Experiment
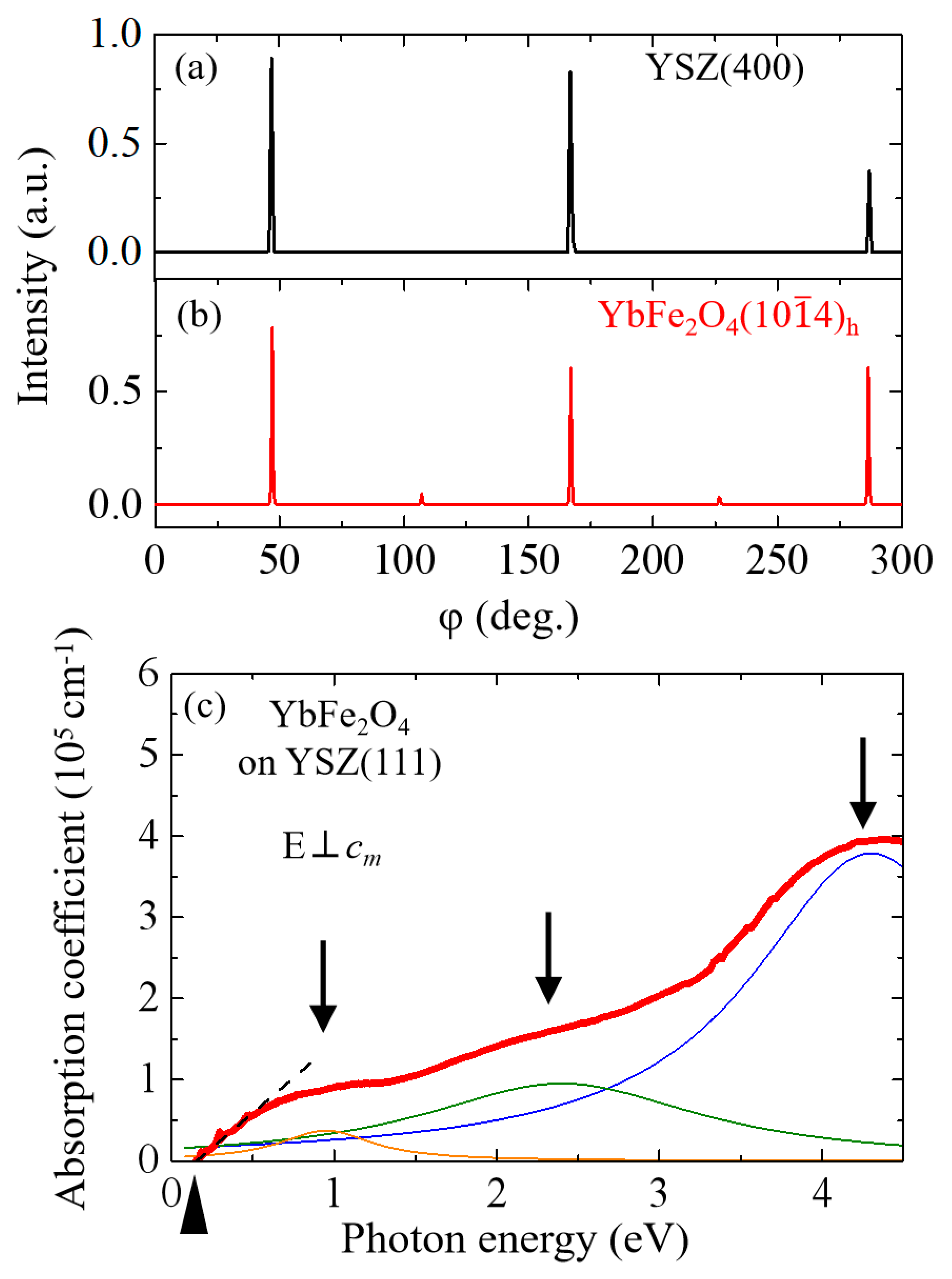
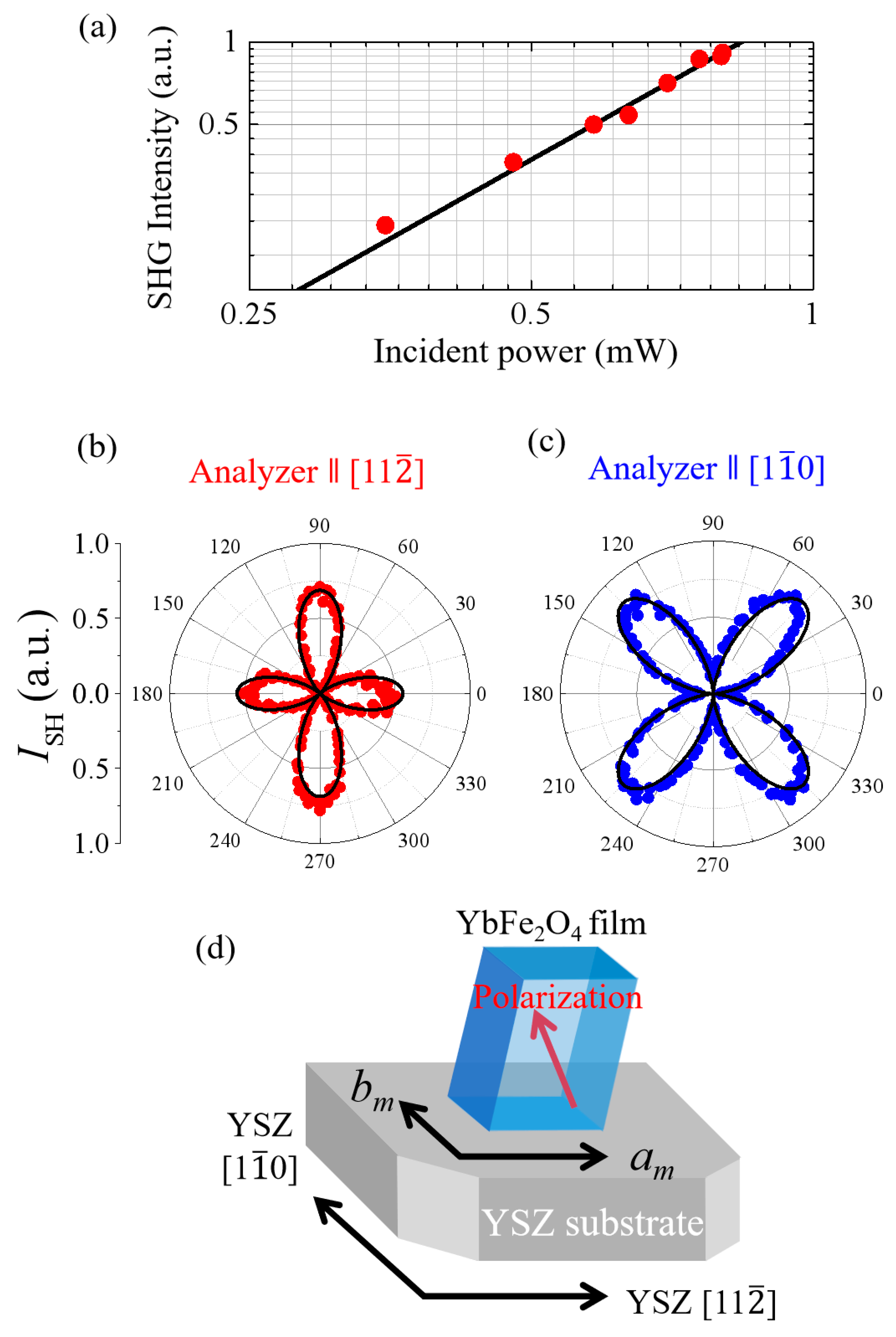
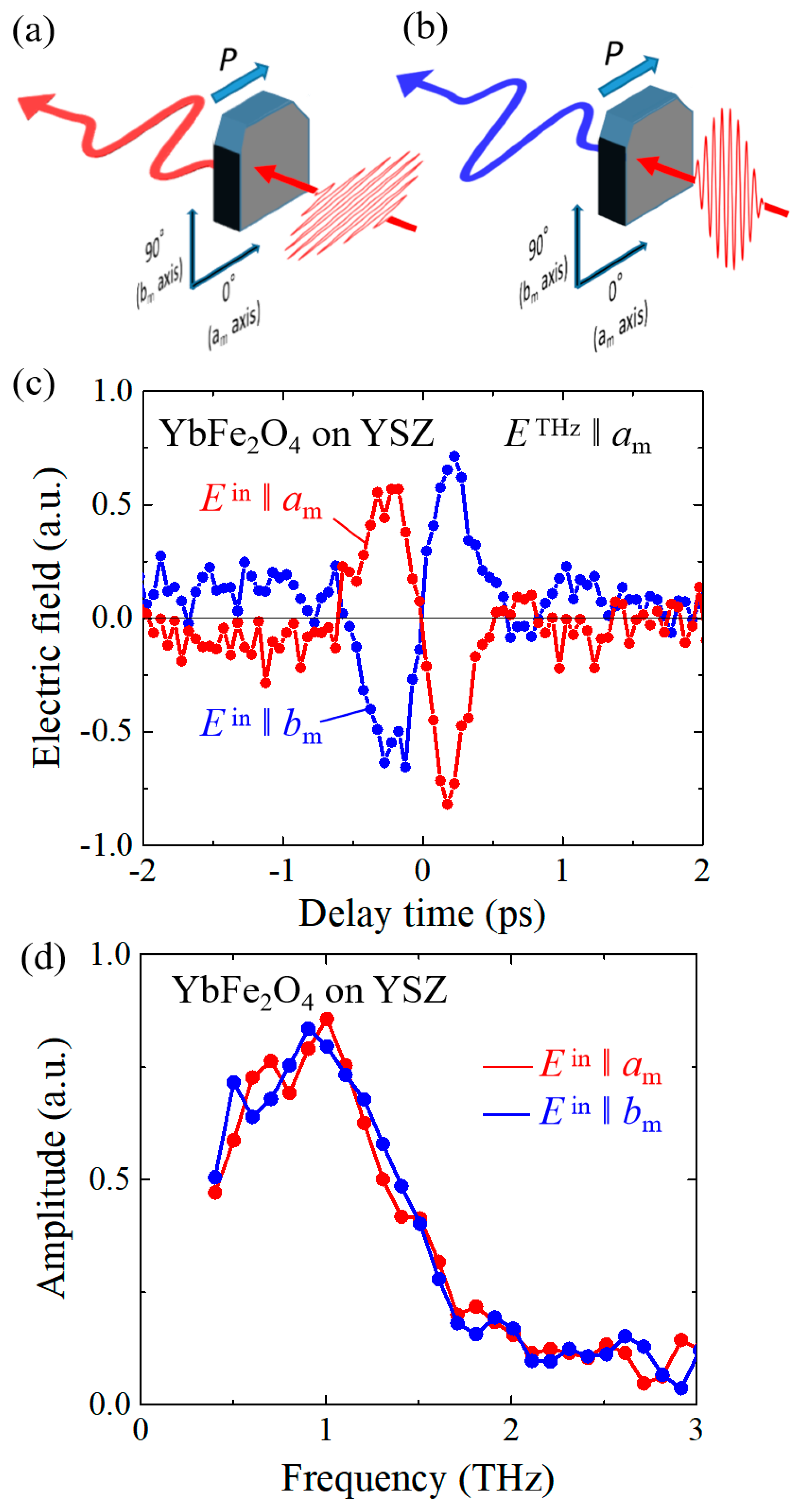
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Notes
- Miyamoto, T.; Yada, H.; Yamakawa, H.; Okamoto, H. Ultrafast modulation of polarization amplitude by terahertz fields in electronic-type organic ferroelectrics. Nat. Commun. 2013, 4, 2586–2594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoegen, A.V.; Mankowsky, R.; Fechner, M.; Först, M.; Cavalleri, A. Probing the interatomic potential of solids with strong-field nonlinear phononics. Nature 2018, 555, 79–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Okimoto, Y.; Xia, P.; Itatani, J.; Matsushima, H.; Ishikawa, T.; Koshihara, S.; Horiuchi, S. Ultrafast opto-protonics in a hydrogen-bonded π-molecular ferroelectric crystal. APL Mater. 2022, 10, 090702. [Google Scholar] [CrossRef]
- Ikeda, N.; Ohsumi, H.; Ohwada, K.; Ishii, K.; Inami, T.; Kakurai, K.; Murakami, Y.; Yoshii, K.; Mori, S.; Horibe, Y.; et al. Ferroelectricity from iron valence ordering in the charge-frustrated system LuFe2O4. Nature 2005, 436, 1136–1138. [Google Scholar] [CrossRef]
- Monceau, P.; Nad, F.Y.; Brazovskii, S. Ferroelectric Mott-Hubbard Phase of Organic (TMTTF)2X Conductors. Phys. Rev. Lett. 2001, 86, 4080–4083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamamoto, K.; Iwai, S.; Boyko, S.; Kashiwazaki, A.; Hiramatsu, F.; Okabe, C.; Nishi, N.; Yakushi, K. Strong Optical Nonlinearity and its Ultrafast Response Associated with Electron Ferroelectricity in an Organic Conductor. J. Phys. Soc. Jpn. 2008, 77, 074709. [Google Scholar] [CrossRef] [Green Version]
- Portengen, T.; Östreich, T.; Sham, L.J. Theory of electronic ferroelectricity. Phys. Rev. B 1996, 54, 17452–17463. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, S. Electronic Ferroelectricity and Frustration. J. Phys. Soc. Jpn. 2010, 79, 011010. [Google Scholar] [CrossRef] [Green Version]
- Fujiwara, K.; Fukada, Y.; Okuda, Y.; Seimiya, R.; Ikeda, N.; Yokoyama, K.; Yu, H.; Koshihara, S.; Okimoto, Y. Direct evidence of electronic ferroelectricity in YbFe2O4 using neutron difraction and nonlinear spectroscopy. Sci. Rep. 2021, 11, 4277–4283. [Google Scholar] [CrossRef]
- Yamada, Y.; Nohdo, S.; Ikeda, N. Incommesurate charge ordering in charge-frustrated LuFe2O4 system. J. Phys. Soc. Jpn. 1997, 66, 3733–3736. [Google Scholar] [CrossRef]
- Angst, M.; Hermann, R.P.; Christianson, A.D.; Lumsden, M.D.; Lee, C.; Whangbo, M.H.; Kim, J.W.; Ryan, P.J.; Nagler, S.E.; Tian, W.; et al. Charge Order in LuFe2O4: Antiferroelectric Ground State and Coupling to Magnetism. Phys. Rev. Lett. 2008, 101, 227601. [Google Scholar] [CrossRef] [Green Version]
- Angst, M. Ferroelectricity from iron valence ordering in rare earth ferrites? Phys. Stat. Solidi. 2013, 7, 383–400. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.J.; Konishi, S.; Hayasaka, Y.; Ota, R.; Kakeya, I.; Tanaka, K. Magnetic properties of epitaxial TmFe2O4 thin films with an anomalous interfacial structure. Cryst. Eng. Comm. 2020, 22, 1096–1105. [Google Scholar] [CrossRef]
- Sakagami, T.; Ota, R.; Kano, J.; Ikedab, N.; Fujii, T. Single domain growth and charge ordering of epitaxial YbFe2O4 films. Cryst. Eng. Comm. 2021, 23, 6163–6170. [Google Scholar] [CrossRef]
- Shimamoto, K.; Tanaka, J.; Miura, K.; Kiriya, D.; Yoshimura, T.; Fujimura, N. Change in the defect structure of composition controlled single-phase YbFe2O4 epitaxial thin films. Jpn. J. Appl. Phys. 2020, 59, SPPB07. [Google Scholar] [CrossRef]
- Wang, W.; Gai, Z.; Chi, M.; Foelkes, J.D.; Yi, J.; Cheng, X.; Keavney, D.J.; Snijders, P.C.; Ward, T.Z.; Shen, J.; et al. Growth diagram and magnetic properties of hexagonal LuFe2O4 thin films. Phys. Rev. B 2012, 85, 155411. [Google Scholar] [CrossRef] [Green Version]
- Fujii, T.; Numata, T.; Nakahata, H.; Nakanishi, M.; Kano, J.; Ikeda, N. Growth and charge ordering of epitaxial YbFe2O4 films on sapphire using Fe3O4 buffer layer. Jpn. J. Appl. Phys. 2018, 57, 010305. [Google Scholar] [CrossRef]
- Rai, R.C.; Hinz, J.; Pascolini, M.; Sun, F.; Zeng, H. Electronic excitations and optical properties of YbFe2O4 thin films. Thin Solid Film. 2019, 673, 57–61. [Google Scholar] [CrossRef]
- Fujiwara, K.; Karasudani, T.; Fukunaga, M.; Kobayashi, H.; Kano, J.; Janolin, P.-E.; Kiat, J.-M.; Nogami, Y.; Kondo, R.; Ikeda, N. Possible charge order structure of stoichiometric YbFe2O4. Ferroelectrics 2017, 512, 85–91. [Google Scholar] [CrossRef] [Green Version]
- Xiang, H.J.; Whangbo, M.-H. Charge order and origin of giant Megnetoncapacitance in LuFe2O4. Phys. Rev. Lett. 2007, 98, 246403. [Google Scholar] [CrossRef] [Green Version]
- Rai, R.C.; Delmont, A.; Sprow, A.; Cai, B.; Nakarmi, M.L. Spin-charge-orbital coupling in multiferroic LuFe2O4 thin films. Appl. Phys. Lett. 2012, 100, 212904. [Google Scholar] [CrossRef]
- Xu, X.S.; Angst, M.; Brinzari, T.V.; Hermann, R.P.; Musfeldt, J.L.; Christianson, A.D.; Mandrus, D.; Sales, B.C.; McGill, S.; Kim, J.-W.; et al. Charge Order, Dynamics, and Magnetostructural Transition in Multiferroic LuFe2O4. Phys. Rev. Lett. 2008, 101, 227602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, H.; (Tokyo Institute of Technology, Tokyo, Japan); Okimoto, Y.; (Tokyo Institute of Technology, Tokyo, Japan); Ikeda, N.; (Okayama university, Okayama, Japan). Unpublished work, 2023.
- Authier, A. International Tables for Crystallography D: Physical Properties of Crystals; International Union of Crystallography: Chester, UK, 2013. [Google Scholar]
- Kida, N.; Miyamoto, T.; Okamoto, H. Emission of Terahertz Electromagnetic Waves: A New Spectroscopic Method to Investigate Physical Properties of Solids. J. Phys. Soc. Jpn. 2022, 91, 112001. [Google Scholar] [CrossRef]
- and are χ(2) tensor components at THz frequency region and proportional to χ(2)aaa(0, −ω, ω) and χ(2)abb(0, −ω, ω), respectively. While and χ(2)aaa(−2ω, ω, ω) and χ(2)abb(−2ω, ω, ω), respectively.
- The fluence and the spot area of the irradiated 800 nm pulses to generate the terahertz pulse were 7.7 μJ/cm2 and 0.79 mm2 in ZnTe (Supplementary Figure S1), while 150 μJ/cm2 and 13 mm2 in YbFe2O4 (Figure 3b), respectively.
| O2 Partial Pressure (10−6 Pa) | Retention Time (min) | c-axis Lattice Constant (Å) | Film Thickness (nm) |
|---|---|---|---|
| 1.36 | 8 | 25.125(2) | ~50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Okimoto, Y.; Morita, A.; Shimanuki, S.; Takubo, K.; Ishikawa, T.; Koshihara, S.-y.; Minakami, R.; Itoh, H.; Iwai, S.; et al. Nonlinear Optical Properties in an Epitaxial YbFe2O4 Film Probed by Second Harmonic and Terahertz Generation. Materials 2023, 16, 1989. https://doi.org/10.3390/ma16051989
Yu H, Okimoto Y, Morita A, Shimanuki S, Takubo K, Ishikawa T, Koshihara S-y, Minakami R, Itoh H, Iwai S, et al. Nonlinear Optical Properties in an Epitaxial YbFe2O4 Film Probed by Second Harmonic and Terahertz Generation. Materials. 2023; 16(5):1989. https://doi.org/10.3390/ma16051989
Chicago/Turabian StyleYu, Hongwu, Yoichi Okimoto, Atsuya Morita, Shuhei Shimanuki, Kou Takubo, Tadahiko Ishikawa, Shin-ya Koshihara, Ryusei Minakami, Hirotake Itoh, Shinichiro Iwai, and et al. 2023. "Nonlinear Optical Properties in an Epitaxial YbFe2O4 Film Probed by Second Harmonic and Terahertz Generation" Materials 16, no. 5: 1989. https://doi.org/10.3390/ma16051989
APA StyleYu, H., Okimoto, Y., Morita, A., Shimanuki, S., Takubo, K., Ishikawa, T., Koshihara, S.-y., Minakami, R., Itoh, H., Iwai, S., Ikeda, N., Sakagami, T., Nozaki, M., & Fujii, T. (2023). Nonlinear Optical Properties in an Epitaxial YbFe2O4 Film Probed by Second Harmonic and Terahertz Generation. Materials, 16(5), 1989. https://doi.org/10.3390/ma16051989






