Crystal Structure, Raman, FTIR, UV-Vis Absorption, Photoluminescence Spectroscopy, TG–DSC and Dielectric Properties of New Semiorganic Crystals of 2-Methylbenzimidazolium Perchlorate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Crystal Synthesis
2.2. Crystal Structure Measurements
2.2.1. Experimental Details of Single Crystal XRD
2.2.2. Experimental Details of Powder XRD
2.3. Mass Density
2.4. Raman Scattering, FTIR, UV-Vis Absorption, and Photoluminescence
2.5. TG–DSC
2.6. Dielectric Measurements
3. Results
3.1. Single Crystal XRD Analysis
3.2. Powder XRD Analysis
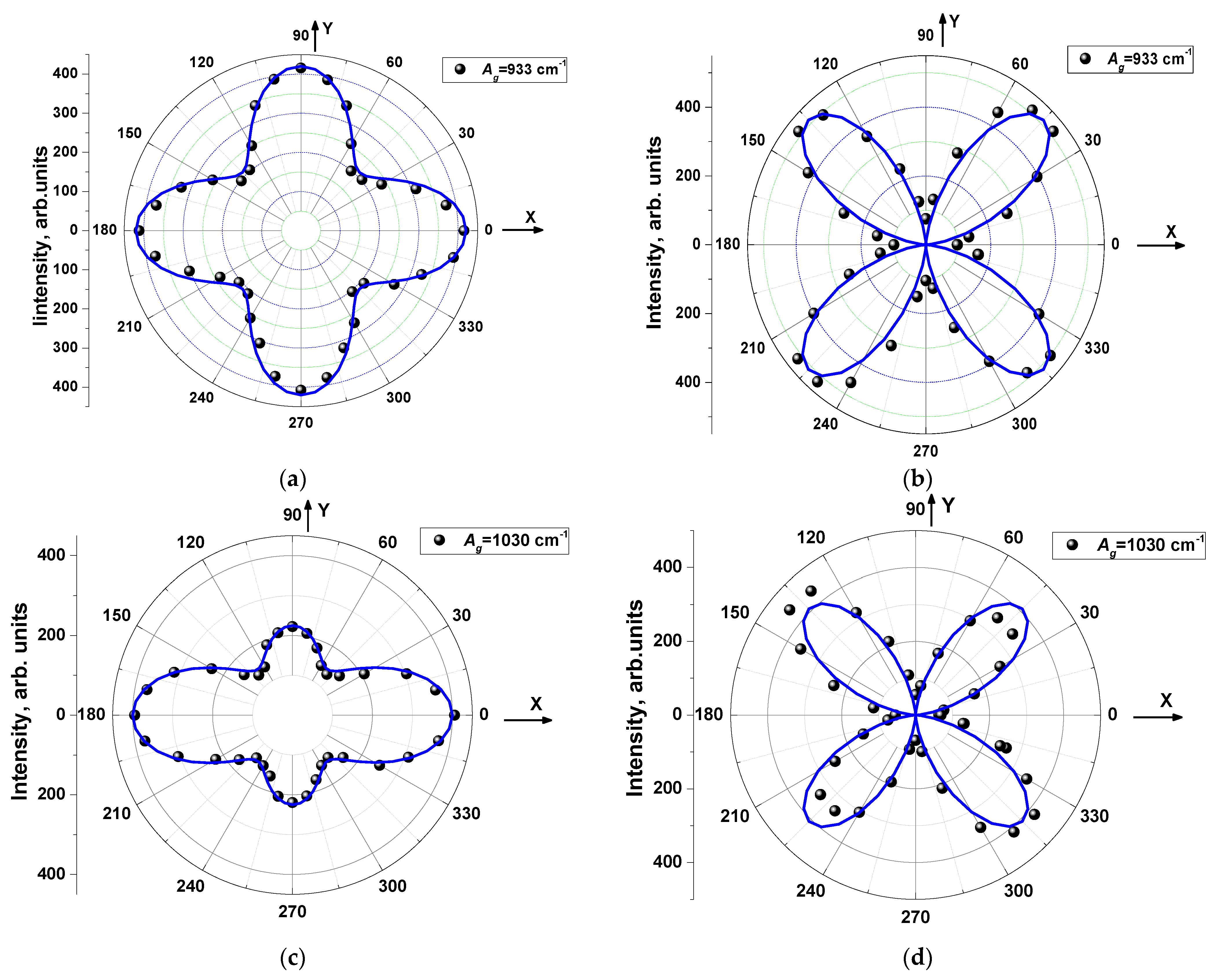
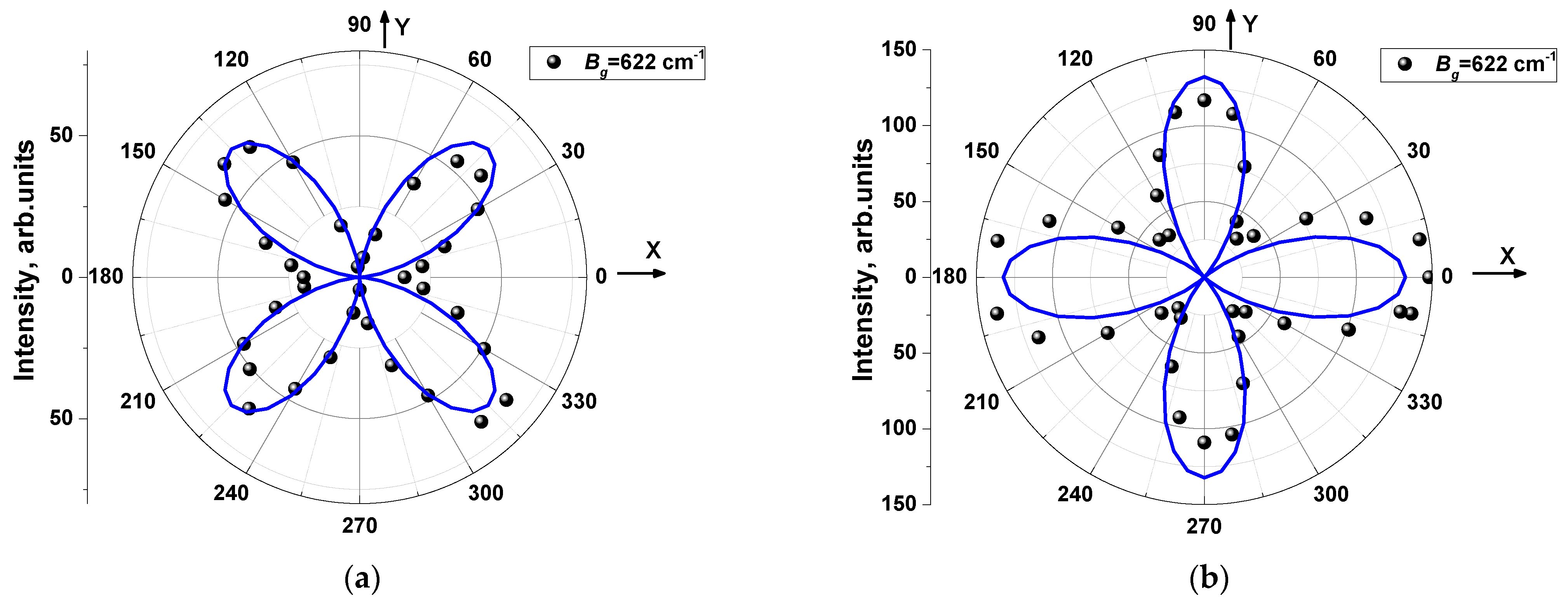
3.3. Raman Scattering and FTIR Absorption Spectroscopy
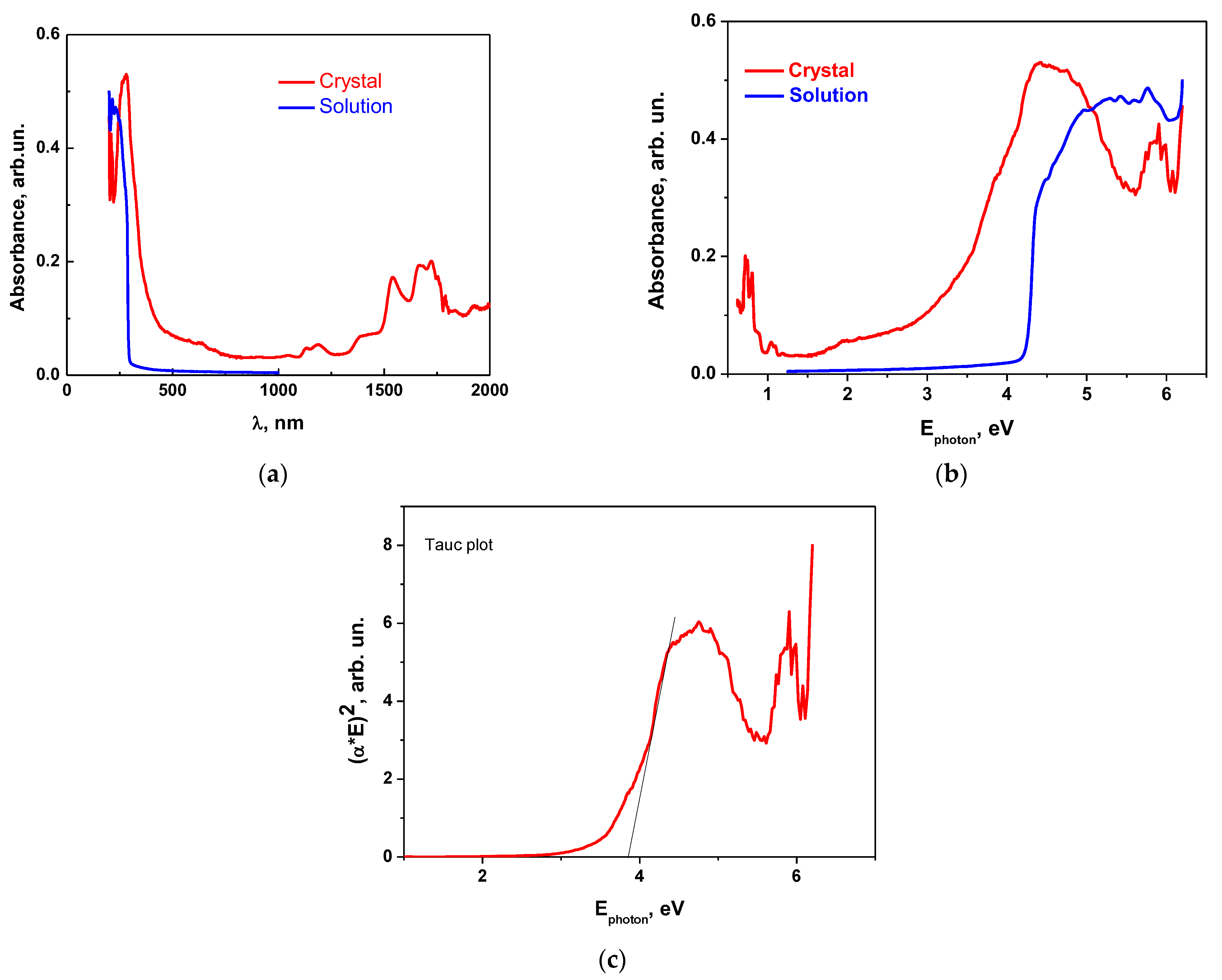
3.4. UV-Vis Absorption
3.5. Photoluminescence
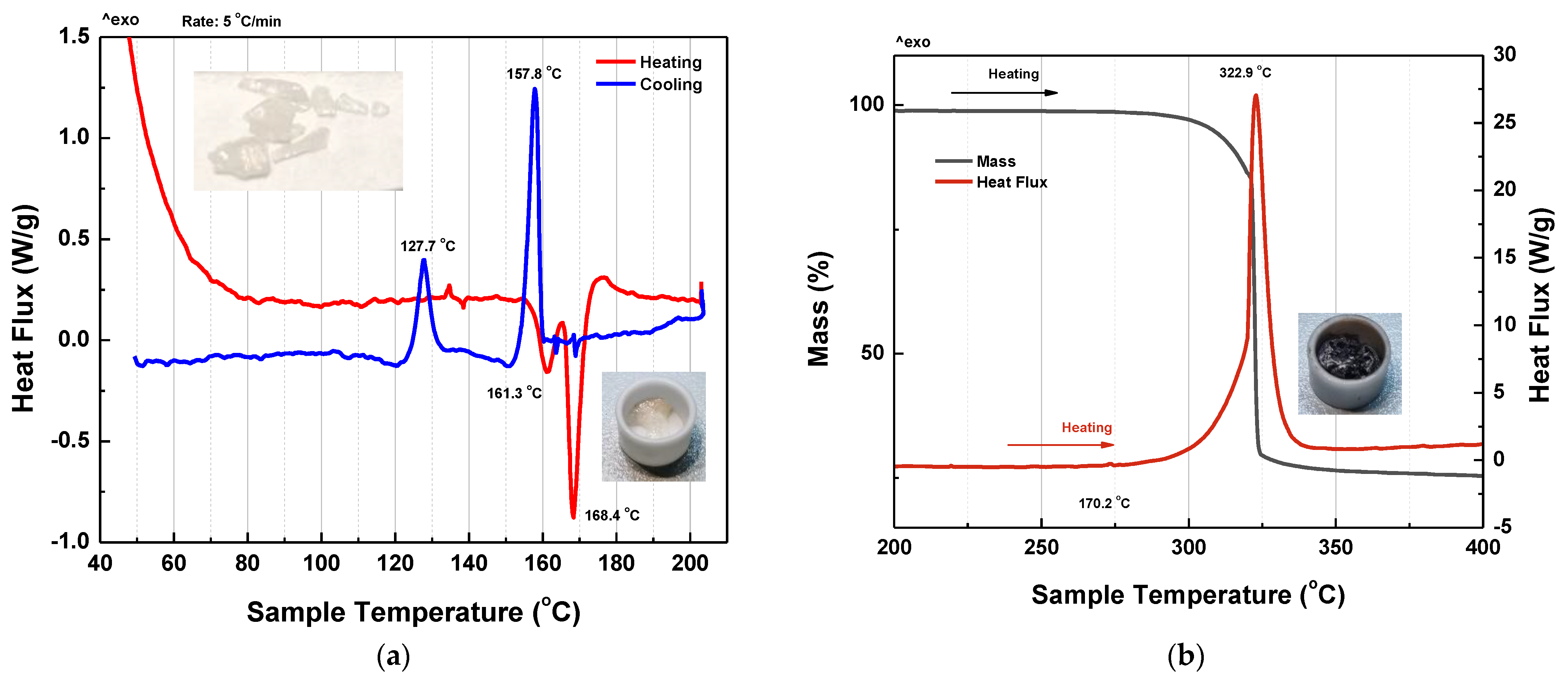
3.6. Thermogravimetry-Differential Scanning Calorimetry (TG–DSC)
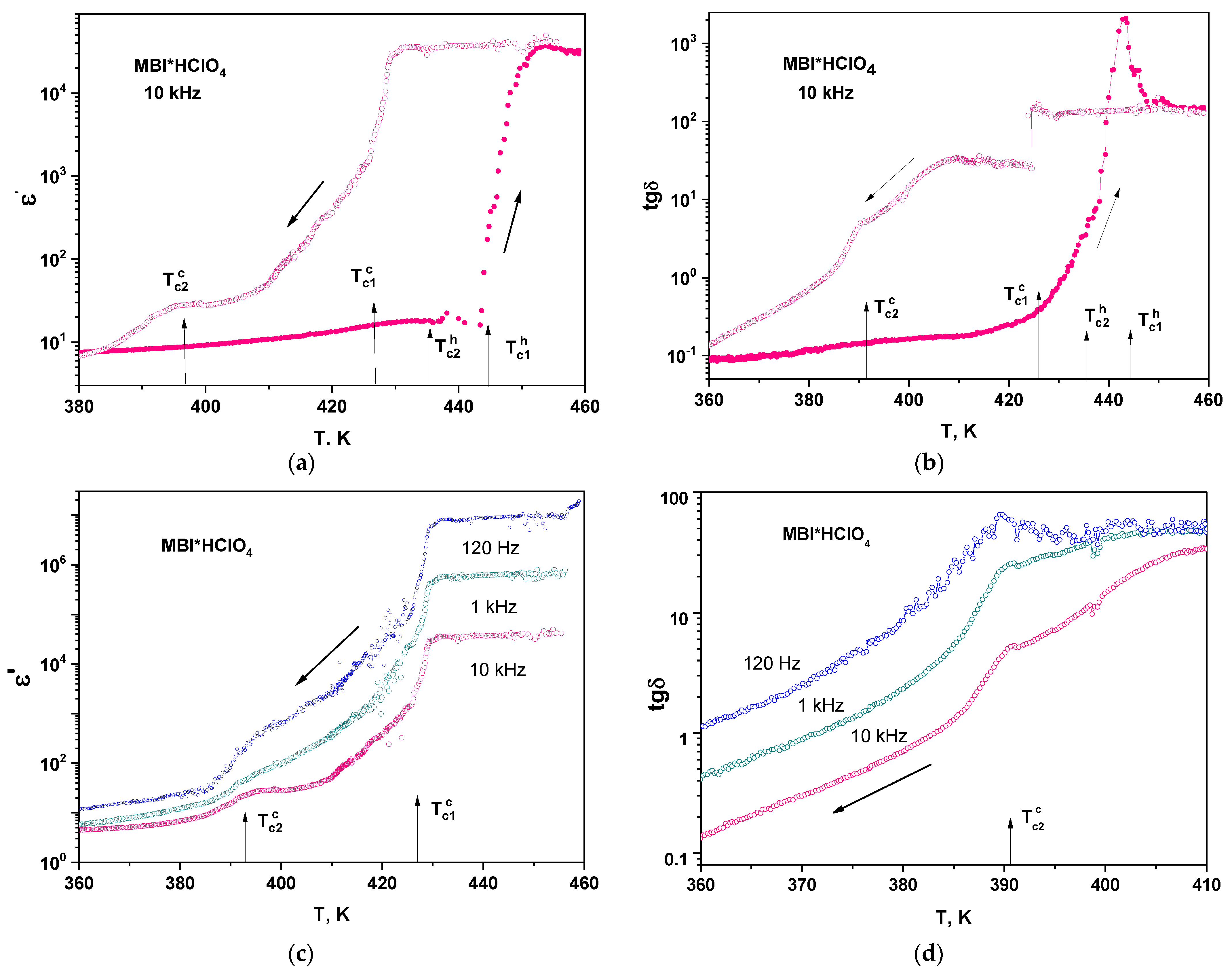
3.7. Dielectric Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vijayakanth, T.; Liptrot, D.J.; Gazit, E.; Boomishankar, R.; Bowen, C.R. Recent Advances in Organic and Organic–Inorganic Hybrid Materials for Piezoelectric Mechanical Energy Harvesting. Adv. Funct. Mater. 2022, 32, 2109492. [Google Scholar] [CrossRef]
- Naber, R.C.G.; Asadi, K.; Blom, P.W.M.; de Leeuw, D.M.; de Boer, B. Organic nonvolatile memory devices based on ferroelectricity. Adv. Mater. 2010, 22, 933–945. [Google Scholar] [CrossRef] [Green Version]
- Park, C.; Lee, K.; Koo, M.; Park, C. Soft Ferroelectrics Enabling High Performance Intelligent Photo Electronics. Adv. Mater. 2020, 33, 2004999. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.H.; Kweon, O.Y.; Kim, H.; Yoo, J.H.; Hana, S.G.; Oh, J.H. Recent advances in organic sensors for health self-monitoring systems. J. Mater. Chem. C 2018, 6, 8569–8612. [Google Scholar] [CrossRef]
- Sun, Z.; Luo, J.; Zhang, S.H.; Ji, C.H.; Zhou, L.; Li, S.H.; Deng, F.; Hong, M. Solid-State Reversible Quadratic Nonlinear Optical Molecular Switch with an Exceptionally Large Contrast. Adv. Mater. 2013, 25, 4159–4163. [Google Scholar] [CrossRef] [PubMed]
- Ghazaryan, V.V.; Zakharov, B.A.; Petrosyan, A.M.; Boldyreva, E.V.L. Argininium phosphite—A new candidate for NLO materials. Acta Crystallogr. 2015, C71, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Haile, S.M.; Boysen, D.A.; Chisholm, C.R.I.; Merle, R.B. Solid acids as fuel cell electrolytes. Nature 2001, 410, 910–913. [Google Scholar] [CrossRef] [Green Version]
- Blazcues-Kastro, A.; Garcia-Kabanes, A.; Carracosa, M. Biological applications of ferroelectric materials. Appl. Phys. Rev. 2018, 5, 041101. [Google Scholar] [CrossRef] [Green Version]
- Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Above-room-temperature ferroelectricity in a single-component molecular crystal. Nature 2010, 463, 789–792. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kobayashi, K.; Kumai, R.; Ishibashi, S. Proton tautomerism for strong polarization switching. Nat. Commun. 2017, 8, 14426. [Google Scholar] [CrossRef] [Green Version]
- Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Above-room-temperature ferroelectricity and antiferroelectricity in benzimidazoles. Nat. Commun. 2012, 3, 1308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saripalli, R.K.; Swain, D.; Prasad, S.; Nhalil, H.; Bhat, H.L.; Guru Row, T.N.; Elizabeth, S. Observation of ferroelectric phase and large spontaneous electric polarization in organic salt of diisopropylammonium iodide. J. Appl. Phys. 2017, 121, 114101. [Google Scholar] [CrossRef]
- Baran, J.; Bator, G.; Jakubas, R.; Sledz, M. Dielectric dispersion and vibrational studies of a new ferroelectric, glycinium phosphite crystal. J. Phys. Condens. Mater. 1996, 8, 10647–10658. [Google Scholar] [CrossRef]
- Matthias, B.T.; Miller, C.E.; Remeika, J.P. Ferroelectricity of glycine sulfate. Phys. Rev. 1956, 104, 849–850. [Google Scholar] [CrossRef]
- Albers, J.; Klopperpieper, A.; Rother, H.J.; Haussühl, S. Ferroelectricity in betaine phosphite. Ferroelectrics 1988, 81, 27–30. [Google Scholar] [CrossRef]
- Banys, J.; Macutkevic, J.; Klimm, C.; Völkel, G.; Kajokas, A.; Brilingas, A.; Grigas, J. Dielectric properties in the vicinity of the ferroelectric phase transition in a mixed crystal of deuterated betaine phosphate 0.03 betaine phosphite 0.97. Phys. Stat. Sol. 2004, 201, 602–612. [Google Scholar] [CrossRef]
- Albers, J.; Klpperpieper, A.; Müser, H.E.; Rother, H.J. Ferroelectric and antiferroelectric properties of deuterated betaine arsenate and betaine phosphate. Ferroelectrics 1984, 54, 45–48. [Google Scholar] [CrossRef]
- Balashova, E.V.; Krichevtsov, B.B.; Yurko, E.I.; Svinarev, F.B.; Pankova, G.A. Dielectric properties of ferroelectric betaine phosphite crystals with a high degree of deuteration. Phys. Solid State 2015, 57, 2382–2388. [Google Scholar] [CrossRef]
- Averbuch-Pouchot, M.T. Crystal structure of L-histidinium phosphite and a structure reinvestigation of the monoclinic form of L-histidine. Z. Kristallogr. 1993, 207, 111–120. [Google Scholar] [CrossRef]
- Balashova, E.V.; Krichevtsov, B.B.; Popov, S.N.; Brunkov, P.N.; Pankova, G.A.; Zolotarev, A.A. Elastic and Piezoelectric Parameters of the Crystals of Histidine Phosphite L-Hist H3PO3 Measured by the Method of Electromechanical Resonance. Tech. Phys. Lett. 2018, 44, 118–122. [Google Scholar] [CrossRef]
- Balashova, E.V.; Svinarev, F.B.; Zolotarev, A.A.; Levin, A.A.; Brunkov, P.N.; Davydov, V.Y.; Smirnov, A.N.; Redkov, A.V.; Pankova, G.A.; Krichevtsov, B.B. Crystal structure, Raman spectroscopy and dielectric properties of new semi-organic crystals based on 2-methylbenzimidazole. Crystals 2019, 9, 573. [Google Scholar] [CrossRef] [Green Version]
- Wayne, W.C. Perchlorate salts, their uses and alternatives. J. Chem. Educ. 1973, 50, A335. [Google Scholar] [CrossRef]
- Matthews, L. (Ed.) Perchlorates: Production, Uses and Health Effects; Nova: New York, NY, USA, 2011; pp. 1–345. [Google Scholar]
- Gault, S.; Jaworek, M.W.; Winter, R.; Cockel, C.S. Perchlorate salts confer psychrophilic characteristics in α-chymotrypsin. Sci. Rep. 2021, 11, 16523. [Google Scholar] [CrossRef] [PubMed]
- Bishop, L.J.; Quinn, R.; Dyar, M.D. Spectral and thermal properties of perchlorate salts and implications for Mars. Am. Mineral. 2014, 99, 1580–1592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pająk, Z.; Czarnecki, P.; Szafrańska, B.; Małuszyńska, H.; Fojud, Z. Ferroelectric ordering in imidazolium perchlorate. J. Chem. Phys. 2006, 124, 144502. [Google Scholar] [CrossRef]
- Szafrański, M. Simple Guanidinium Salts Revisited: Room-Temperature Ferroelectricity in Hydrogen-Bonded Supramolecular Structures. J. Phys. Chem. B 2011, 115, 8755–8762. [Google Scholar] [CrossRef]
- Gao, W.; Chang, L.; Ma, H.; You, L.; Yin, J.; Liu, J.; Liu, Z.; Wang, J.; Yuan, G. Flexible organic ferroelectric films with a large piezoelectric response. NPG Asia Mater. 2015, 7, e189. [Google Scholar] [CrossRef] [Green Version]
- Wojtas, M.; Czupiński, O.; Tylczyński, Z.; Isakov, D.; Belsley, M.; Jakubas, R. Optical nonlinearity and piezoelectricity in 2,4,6-trimethylpyridinium perchlorate. Chem. Phys. 2014, 441, 59–65. [Google Scholar] [CrossRef]
- Kajamuhideen, M.S.; Sethuraman, K.; Ramasamy, P. Crystal growth, physical properties and computational insights of semi-organic non-linear optical crystal diphenylguanidinium perchlorate grown by conventional solvent evaporation method. J. Cryst. Growth 2018, 483, 16–25. [Google Scholar] [CrossRef]
- Craven, B.M.; McMullan, R.K.; Bell, J.D.; Freeman, H.C. The Crystal Structure of Imidazole by Neutron Diffraction at 20 °C and −150 °C. Acta Crystallogr. 1977, B33, 2585–2589. [Google Scholar] [CrossRef]
- Balashova, E.; Levin, A.A.; Fokin, A.; Redkov, A.; Krichevtsov, B. Structural Properties and Dielectric Hysteresis of Molecular Organic Ferroelectric Grown from Different Solvents. Crystals 2021, 11, 1278. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallocr. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Balashova, E.V.; Levin, A.A.; Davydov, V.Y.; Smirnov, A.N.; Starukhin, A.N.; Pavlov, S.I.; Krichevtsov, B.B.; Zolotarev, A.A.; Zhang, H.; Li, F.; et al. Croconic acid doped triglycine sulfate single crystals: Crystal structure, UV VIS, FTIR, Raman, photoluminescence spectroscopy, and dielectric properties. Crystals 2022, 12, 679. [Google Scholar] [CrossRef]
- Balashova, E.; Levin, A.A.; Davydov, V.; Smirnov, A.; Starukhin, A.; Pavlov, S.; Krichevtsov, B.; Zolotarev, A.; Zhang, H.; Li, F.; et al. Croconic Acid Doped Glycine Single Crystals: Growth, Crystal Structure, UV-Vis, FTIR, Raman and Photoluminescence Spectroscopy. Crystals 2022, 12, 1342. [Google Scholar] [CrossRef]
- Diffrac. Suite Eva, Version 5.1.0.5; Brucker AXS: Karlsruhe, Germany, 2019.
- Maunders, C.; Etheridge, J.; Wright, N.; Whitfield, H.J. Structure and microstructure of hexagonal Ba3Ti2RuO9 by electron diffraction and microscopy. Acta Crystallogr. B 2005, 61, 154–159. [Google Scholar] [CrossRef] [Green Version]
- Terlan, B.; Levin, A.A.; Börrnert, F.; Simon, F.; Oschatz, M.; Schmidt, M.; Cardoso-Gil, R.; Lorenz, T.; Baburin, I.A.; Joswig, J.-O.; et al. Effect of Surface Properties on the Microstructure, Thermal, and Colloidal Stability of VB2 Nanoparticles. Chem. Mater. 2015, 27, 5106–5115. [Google Scholar] [CrossRef]
- Terlan, B.; Levin, A.A.; Börrnert, F.; Zeisner, J.; Kataev, V.; Schmidt, M.; Eychmüller, A. A Size-Dependent Analysis of the Structural, Surface, Colloidal, and Thermal Properties of Ti1–xB2 (x = 0.03–0.08) Nanoparticles. Eur. J. Inorg. Chem. 2016, 6, 3460–3468. [Google Scholar] [CrossRef]
- Levin, A.A. Program SizeCr for Calculation of the Microstructure Parameters from X-ray Diffraction Data. Preprint. 2022. Available online: https://www.researchgate.net/profile/Alexander-Levin-6/research (accessed on 5 June 2022).
- Langford, J.I.; Cernik, R.J.; Louer, D. The Breadth and Shape of Instrumental Line Profiles in High-Resolution Powder Diffraction. J. Appl. Phys. 1991, 24, 913–919. [Google Scholar] [CrossRef]
- Gharbi, S.; Dhahri, R.; Rasheed, M.; Dhahri, E.; Barille, R.; Rguiti, M.; Tozri, A.; Berber, M.R. Effect of Bi substitution on nanostructural, morphologic, and electrical behavior of nanocrystalline La1-xBixNi0.5Ti0.5O3 (x = 0 and x = 0.2) for the electrical devices. Mater. Sci. Eng. B 2021, 270, 115191. [Google Scholar] [CrossRef]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mat. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- Rietveld, H.M. Line profiles of neutron powder-diffraction peaks for structure Refinement. Acta Crystallogr. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- TOPAS, Version 5. Technical Reference. Brucker AXS: Karlsruhe, Germany, 2014.
- Cheary, R.W.; Coelho, A.A. A fundamental parameters approach to X-ray line-profile fitting. J. Appl. Crystallogr. 1992, 25, 109–121. [Google Scholar] [CrossRef]
- Balzar, D. Voigt-function model in diffraction line-broadening analysis. In Defect and Microstructure Analysis by Diffraction; Snyder, R.L., Fiala, J., Bunge, H.J., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 94–126. [Google Scholar] [CrossRef]
- Dollase, W.A. Correction of Intensities for Preferred Orientation in Powder Diffractometry: Application of the March Model. J. Appl. Crystallogr. 1986, 19, 267–272. [Google Scholar] [CrossRef]
- Järvinen, M. Application of symmetrized harmonics expansion to correction of the preferred orientation effect. J. Appl. Crystallogr. 1993, 26, 525–531. [Google Scholar] [CrossRef]
- Berger, H. Study of the K alpha emission spectrum of copper. X-ray Spectrom. 1986, 15, 241–243. [Google Scholar] [CrossRef]
- Bérar, J.-F.; Lelann, P.J. ESD’s and Estimated Probable Error Obtained in Rietveld Refinements with Local Correlations. J. Appl. Crystallogr. 1991, 24, 1–5. [Google Scholar] [CrossRef]
- Levin, A.A. Program RietESD for Correction of Estimated Standard Deviations Obtained in Rietveld-Refinement Program. Preprint. 2022. Available online: https://www.researchgate.net/publication/359342753_Program_RietESD_for_correction_of_estimated_standard_deviations_obtained_in_Rietveld-refinement_programs (accessed on 5 June 2022).
- Hill, R.J.; Fischer, R.X. Profile agreement indices in Rietveld and pattern-fitting analysis. J. Appl. Crystallogr. 1990, 23, 462–468. [Google Scholar] [CrossRef]
- Farrugia, L.J. ORTEP-3 for Windows—A version of ORTEP-III with a Graphical User Interface (GUI). J. Appl. Crystallogr. 1997, 30, 565. [Google Scholar] [CrossRef]
- Obodovskaya, A.E.; Starikova, Z.A.; Belous, S.N.; Pokrovskaya, I.E. Crystal and molecular structure of 2-methylbenzimidazole. J. Struct. Chem. 1991, 32, 421–422. [Google Scholar] [CrossRef]
- Freeman, H.C.; Huq, F.; Rosalky, J.M.; Taylor, I.F., Jr. The Crystal and Molecular Structure of Imidazolium Sulphate Dihydrate. Acta Cryst. 1975, B31, 2833. [Google Scholar] [CrossRef]
- Blessing, H.R.; McGandy, E.L. Base stacking and hydrogen bonding in crystals of imidazolium dihydrogen orthophosphate. J. Amer. Chem. Soc. 1972, 94, 4034–4035. [Google Scholar] [CrossRef]
- Güllüoglu, M.T.; Özduran, M.; Kurt, M.; Kalaichelvan, S.; Sundaraganesan, N. Molecular structure and vibrational spectra of 2- and 5-methylbenzimidazole molecules by density functional theory. Spectrochim. Acta Part A 2010, 76, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Antić-Jovanović, A.; Jeremic, M.; Lalic, M.; Long, D.A. Raman Spectral Study of the Mg(C104)2-NaNCS-H20 System at Ambient and Elevated Temperatures. J. Raman Spectrosc. 1989, 20, 523–528. [Google Scholar] [CrossRef]
- Sugai, S.; Shirotani, I. Raman and infrared reflection spectroscopy in black phosphorus. Solid State Commun. 1985, 53, 753–755. [Google Scholar] [CrossRef]
- Ribeiro-Soares, J.; Almeida, R.M.; Cançado, L.G.; Dresselhaus, M.S.; Jorio, A. Group theory for structural analysis and lattice vibrations in phosphorene systems. Phys. Rev. B 2015, 91, 205421. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, H.B.; Pimenta, M.A.; de Matos, C.J.S.; Moreira, R.L.; Rodin, A.S.; Zapata, J.D.; de Souza, E.A.T.; Castro Neto, A.H. Unusual Angular Dependence of the Raman Response in Black Phosphorus. ACS Nano 2015, 9, 4270–4276. [Google Scholar] [CrossRef]
- Strach, T.; Brunen, J.; Lederle, B.; Zegenhagen, J.; Cardona, M. Determination of the phase difference between the Raman tensor elements of the A1g-like phonons in SmBa2Cu3O7−δ. Phys. Rev. B 1998, 57, 1292–1297. [Google Scholar] [CrossRef]
- Kranert, C.; Sturm, C.; Schmidt-Grund, R.; Grundmann, M. Raman Tensor Formalism for Optically Anisotropic Crystals. Phys. Rev. Lett. 2016, 116, 127401. [Google Scholar] [CrossRef]
- Lei, Z.; Chen, B.; Koo, Y.-M.; MacFarlane, D.R. Introduction: Ionic Liquids. Chem. Rev. 2017, 117, 6633–6635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferdeghini, C.; Mezzetta, A.; D’Andrea, F.; Pomelli, C.S.; Guazzelli, L.; Guglielmero, L. The Structure–Property Relationship of Pyrrolidinium and Piperidinium-Based Bromide Organic Materials. Materials 2022, 15, 8483. [Google Scholar] [CrossRef] [PubMed]
- Leys, J.; Wübbenhorst, M.; Menon, C.P.; Rajesh, R.; Thoen, J.; Glorieux, C. Temperature dependence of the electrical conductivity of imidazolium ionic liquids. J. Chem. Phys. 2008, 128, 064509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macutkevic, J.; Banys, J.; Kania, A. Electrical Conductivity and Dielectric Relaxation in Ag1−xLixNbO3. Crystals 2022, 12, 158. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric Relaxation in Solids. J. Phys. D Appl. Phys. 1999, 32, R57. [Google Scholar] [CrossRef]
- Enneffatia, M.; Rasheed, M.; Louatia, B.; Guidaraa, K.; Shihab, S.; Barillé, R. Investigation of structural, morphology, optical properties and electrical transport conduction of Li0.25Na0.75CdVO4 compound. J. Phys. Conf. Ser. 2021, 1795, 012050. [Google Scholar] [CrossRef]
- Totz, J.; Michel, D.; Bany, J.; Klopperpieper, A. Conductivity processes in deuterated betaine phosphate1−xbetaine phosphitex mixed crystals. J. Phys. Condens. Matter 1998, 10, 9281–9292. [Google Scholar] [CrossRef]
- Balashova, E.V.; Svinarev, F.B.; Ankudinov, A.V.; Pankova, G.A.; Lityagin, G.A.; Kunkel, T.S.; Krichevtsov, B.B. Polarization switching, dielectric, structural and elastic properties of 2-Methylbenzimidazole crystals and films. Ferroelectrics 2019, 538, 74–82. [Google Scholar] [CrossRef]

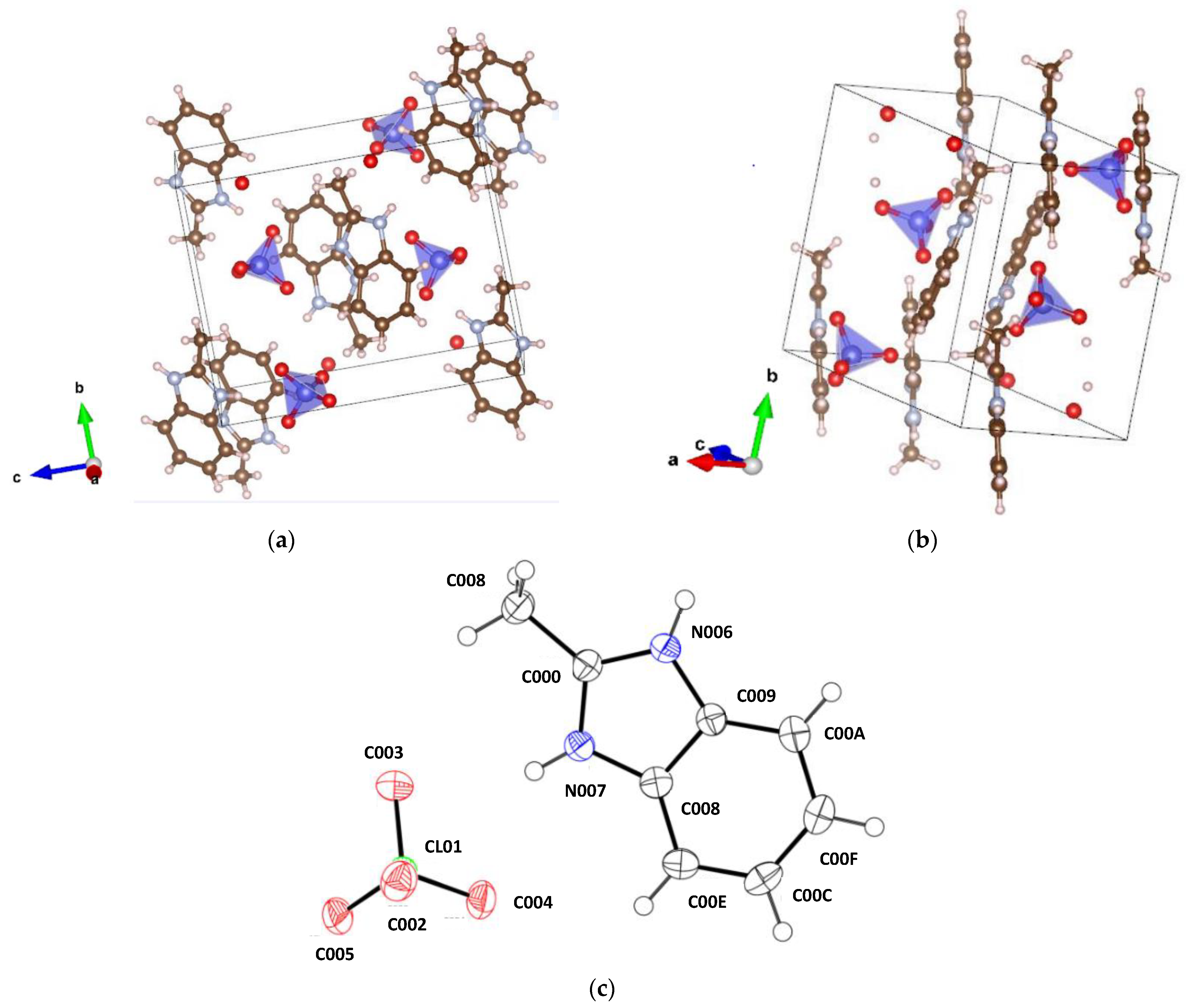






| MBI-Perchlorate | |
|---|---|
| Chemical formula | C8H9ClN2O4 |
| Formula weight, Da | 232.62 |
| Space group | P21/n (14) |
| a, Å | 7.6940(2) |
| b, Å | 9.9774(2) |
| c, Å | 12.4450(4) |
| β, ° | 94.674(3) |
| Vcell, Å3 | 952.17(4) |
| Z | 4 |
| ρcalc, g/cm3 | 1.6236(1) |
| F(000) | 480.0 |
| μ, mm−1 | 3.582 |
| Radiation (λ, Å) | Cu-Kα (1.54184) |
| Θ max, ° | 70.391 |
| h, k, l max | 9, 10, 15 |
| Reflections collected | 5321 |
| Independent reflections | 1812 |
| Data/restraints/parameters | 1812/0/137 |
| GoF | 1.105 |
| Final R indexes [Reflections I >= 2σ(I)] | R1 = 0.0499, wR2 = 0.1399 |
| Final R indexes [Reflections all] | R1 = 0.0553, wR2 = 0.1477 |
| Largest diff. peak/hole, e∙Å−3 | 0.64/−0.60 |
| Temperature of measurements, Tmeas, K | 100 ± 2 |
| Crystal | Bond, Å C00D-N007 | Bond, Å C00D-N006 | Angle, ° N007-C00D-N006 | Angle, ° C00D-N007-C008 | Angle, ° C00D-N006-C009 |
|---|---|---|---|---|---|
| MBI [57] | 1.339 | 1.335 | 112.7 | 106.1 | 106.3 |
| Imidazole (Im) [31] | 1.337(3) | 1.316(2) | 112.0(1) | 107.3 | 105.3 |
| (ImHz)SO4·2H20 [58] | 1.323(4) | 1.333(4) | 108.4(2) | 108.7(2) | 108.2(2) |
| MBI-phosphate-2 [21] | 1.3299(13) | 1.3347(13) | 109.38(9) | 109.19(8) | 108.96(8) |
| (ImH2)H2PO4 [59] | 1.320(4) | 1.320(4) | 108.7(3) | 108.6(6) | 108.6(6) |
| MBI⋅HClO4 (Sample 1) | 1.330(3) | 1.330(3) | 108.6(2) | 109.6(2) | 109.8(2) |
| a, Å b, Å | c, Å β, ° | Vcell, Å3 D, nm | ρcalc, g/cm3 | Rwp, % Rp, % | cRwp, % a cRp, % a | RB, % me.s.d. a |
|---|---|---|---|---|---|---|
| 7.9123(1) 9.9617(5) | 12.6787(3) 95.404(1) | 994.89(6) 93(1) | 1.5539(1) | 12.67 9.29 | 18.57 16.59 | 0.98 4.127 |
| Raman Z(YY) | Raman Z(XX) | Raman Z(XY) | Symmetry Raman Modes | FTIR | Assignment |
|---|---|---|---|---|---|
| 3358–3206b | -‘- | -‘- | Ag (3318) | 3136–3373b | MBI: νNH, νCH, MνCH |
| 3083s 3074s | 3083s 3047w | 3083m 3074m | Ag (AI) Ag (AI) | 3080m | MBI: νCH |
| 3049vw | 3049w | 3022w | MBI: MνCH | ||
| 2971w | 2972vw | 2992w | MBI: MνCH | ||
| 2937s | 2938w | 2935w | Ag | 2938m | MBI: MνCH |
| 2880m | |||||
| 2826w | |||||
| 2729–2792b | |||||
| 2656m | |||||
| 2590m | |||||
| 2479m | |||||
| 2436m | |||||
| 2371m | |||||
| 2235m | |||||
| 2153w | |||||
| 2118w | |||||
| 2087m | |||||
| 2056s | |||||
| 2008s | |||||
| 1946s | |||||
| 1908w | |||||
| 1890w | |||||
| 1863 m | |||||
| 1853m | |||||
| 1815m | |||||
| 1748sh | MBI: δNH | ||||
| 1724m | MBI: δNH | ||||
| 1662m | MBI: δNH | ||||
| 1625vw | 1626m | 1626w | Ag (AI) | 1624vs | MBI: νCC + νCN |
| 1573vs | 1573m | 1576s | Ag (AI) | 1570vs | MBI: νCC |
| 1549vw | 1531m | MBI: δHCC + νCC | |||
| 1505vw 1495vw | 1503vw 1497vw | 1501vw 1497vw | 1485sh | MBI: MδCH2 MBI: MδCH2 + ΓCCCN + δCCH | |
| 1463s | 1462w | 1463m | Ag (AI) | 1462s 1458vs | MBI: δCCH + νCC |
| 1443vw 1439vw | 1444vw 1435vw | 1439m | MBI: δCNH + νCN + νCC + δCCH | ||
| 1420vw | Ag (AI) | 1420vs | MBI: MδCH2 + δCCH | ||
| 1401m | 1400w | 1401w | Ag (AI.) | 1396m | MBI: MδCH2 + δCCH |
1356w | 1357m | 1356m | Ag (AI) | 1369m 1358m | MBI: νCC + νCN + MδCH2 |
| 1327vw | 1326vw | 1327vw | 1327m | MBI: δCCH + νCN | |
| 1290vs | 1290m | 1290s | Ag (AI) | 1292s | MBI: νCN + νCC + δCCH |
| 1255vw | 1255w | 1254m | 1256s | MBI: δCCH + νCN + νCC | |
| 1222m | 1220w | 1223w | Ag (AI) | 1223s 1219s | MBI: δCNH +νCN + νCC |
| 1155w | 1157w | 1153vw | Ag (AI) | 1184s | MBI: δCCH |
| 1128w | Bg (I) | νas(ClO4) v3(F2) | |||
| 1120w | 1120m | 1118w | Ag (AI) | 1153–1020b | MBI: δCCH + νCC |
| 1030s | 1030s | 1030m | Ag (AI) | MBI: νCC + νCN | |
| 1002m 997m | 1002m 999m | 1002w 997w | Ag (AI) Ag (AI) | 1001s 997s | MBI: νCC+ δCCH |
| 958w | 968vw | 953s | MBI: ΓHCCH + ΓCCCH | ||
| 933s | 933s | 933m | Ag (I) | 932s | νs(ClO4) v1(A1) |
| 924s | 924s | 925w | Ag (I) | 921m | νas(ClO4) v3(F2) |
| 907w | 907m | 906vw | Ag (I) | νas(ClO4) v3(F2) | |
| 893w | 891vw | 891vw | 891s | MBI: δCCC + δCCH | |
| 866w | 870vw | 865vw | 868m | MBI: ΓCCCH + ΓHCCN+ ΓHCCH + ΓCCCH | |
| 833m | 833s | 834m | Ag (AI) | 831s | MBI: νCC |
754s | 773s 754m | MBI: ΓCCCH + ΓCCCC MBI: ΓHCCH +ΓCCCH | |||
| 667s | 667m | 667m | Ag(AI) | 665s | MBI: νCC + δCCC + δCCN |
| 658vwsh | 658vw | Ag (AI) | MBI: ΓCNCN + ΓHCCN + ΓCCCN + ΓHNCN | ||
| 647w | 647vw | 647w | Ag (AI) | δas(ClO4) V4(F1) | |
| 630m | 627s | Ag(AI) | MBI: δCCN + δCCC + νCC | ||
| 626m | 624m | 622s | Bg (I) | δas(ClO4) V4(F1) | |
| 618m | 615m | 618sh | Ag(AI) | δas(ClO4) V4(F1) | |
| 495vs | 494m | 496s | Ag | MBI: δCCC + νCC + νCN | |
| 464w 454m | 463m 454m | 464m 455m | Bg Ag | δs(ClO4) V2(E) δs(ClO4) V2(E) | |
| 434m | 434w | Ag | MBI: ΓCCCC + ΓCCCH + ΓCCNH + ΓCCNC | ||
| 327m | 325vw | 324w | MBI: ΓCCCN + ΓCCNH | ||
| 279vw | MBI: δCCN | ||||
| 161w | 157vw | MBI: ΓCCCN + ΓHCCN? | |||
| 112s | 113s | 110sh | Ag | Lattice mode | |
| 103s | 101s | 102s | Bg | Lattice mode | |
| 83w | Bg | Lattice mode | |||
| 73w | 74w | 74w | |||
| 69 | 69 | Ag | Lattice mode | ||
| 61 | Lattice mode | ||||
| 47.7 | 47.8 | 41.6 | Ag | Lattice mode | |
| 32.3s | 30.5w | Lattice mode |
| Ag | Bg | |
|---|---|---|
| Parallel polarizations (PP) | I ~{|a|cos2θ + |c| sin2θ · cos(φc − φa)}2 + |c|2 sin4θ · sin2(φc − φa) | |e|sin22θ |
| Crossed polarizations (CP) | I ~1/4·[{|a|– |c| cos(φc − φa)}2 + |c|2 sin2(φc − φa)] sin22θ | |e|cos22θ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balashova, E.; Zolotarev, A.; Levin, A.A.; Davydov, V.; Pavlov, S.; Smirnov, A.; Starukhin, A.; Krichevtsov, B.; Zhang, H.; Li, F.; et al. Crystal Structure, Raman, FTIR, UV-Vis Absorption, Photoluminescence Spectroscopy, TG–DSC and Dielectric Properties of New Semiorganic Crystals of 2-Methylbenzimidazolium Perchlorate. Materials 2023, 16, 1994. https://doi.org/10.3390/ma16051994
Balashova E, Zolotarev A, Levin AA, Davydov V, Pavlov S, Smirnov A, Starukhin A, Krichevtsov B, Zhang H, Li F, et al. Crystal Structure, Raman, FTIR, UV-Vis Absorption, Photoluminescence Spectroscopy, TG–DSC and Dielectric Properties of New Semiorganic Crystals of 2-Methylbenzimidazolium Perchlorate. Materials. 2023; 16(5):1994. https://doi.org/10.3390/ma16051994
Chicago/Turabian StyleBalashova, Elena, Andrey Zolotarev, Aleksandr A. Levin, Valery Davydov, Sergey Pavlov, Alexander Smirnov, Anatoly Starukhin, Boris Krichevtsov, Hongjun Zhang, Fangzhe Li, and et al. 2023. "Crystal Structure, Raman, FTIR, UV-Vis Absorption, Photoluminescence Spectroscopy, TG–DSC and Dielectric Properties of New Semiorganic Crystals of 2-Methylbenzimidazolium Perchlorate" Materials 16, no. 5: 1994. https://doi.org/10.3390/ma16051994
APA StyleBalashova, E., Zolotarev, A., Levin, A. A., Davydov, V., Pavlov, S., Smirnov, A., Starukhin, A., Krichevtsov, B., Zhang, H., Li, F., Luo, H., & Ke, H. (2023). Crystal Structure, Raman, FTIR, UV-Vis Absorption, Photoluminescence Spectroscopy, TG–DSC and Dielectric Properties of New Semiorganic Crystals of 2-Methylbenzimidazolium Perchlorate. Materials, 16(5), 1994. https://doi.org/10.3390/ma16051994







