The Influence of Magnetic Fields on the Electrical Conductivity of Membranes based on Cotton Fabric, Honey, and Microparticles of Carbonyl Iron and Silver
Abstract
1. Introduction
2. Materials and Methods
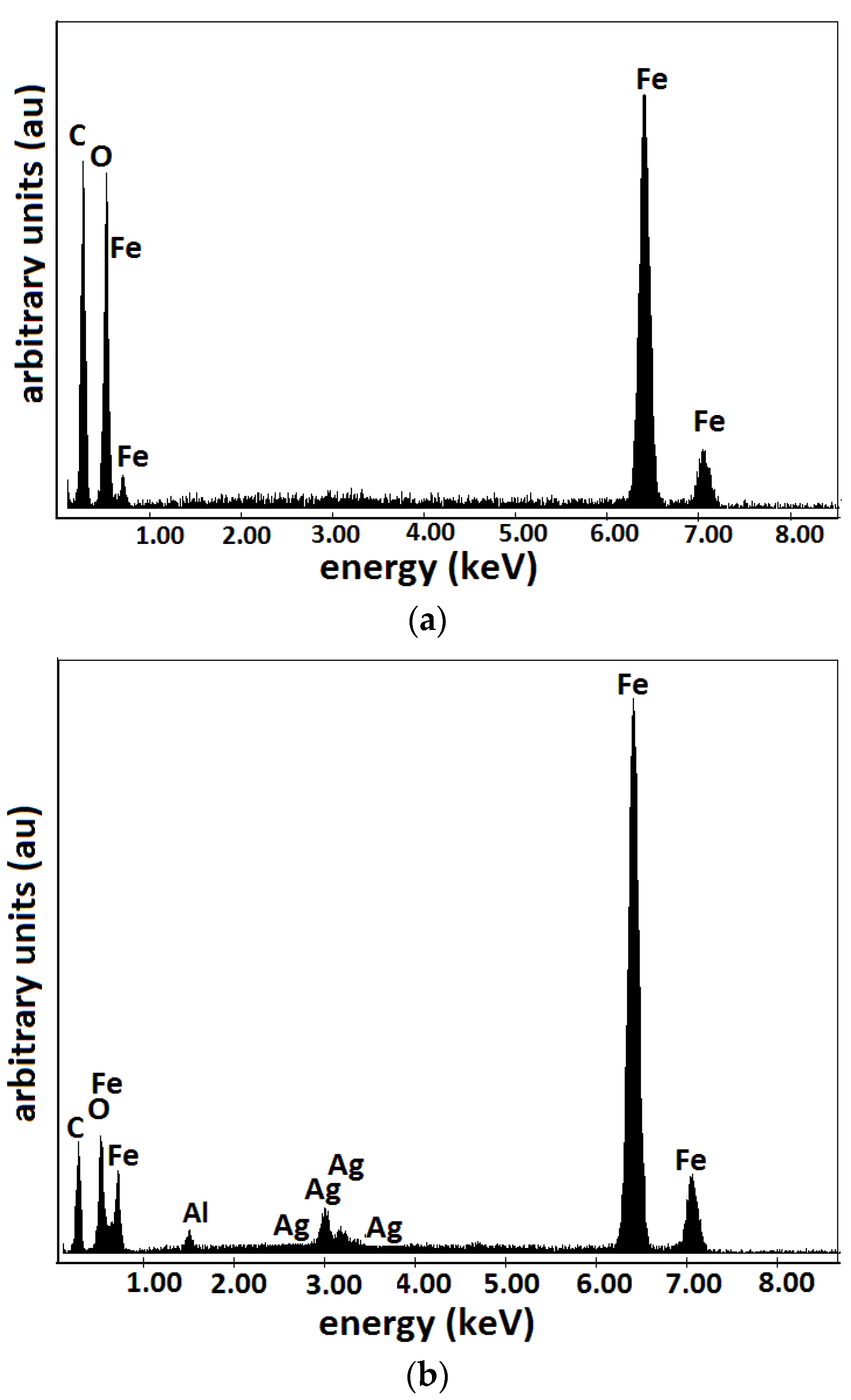
2.1. Materials for Ms Manufacture
- (a)
- Sterile compresses (GBs) were produced by Shaoxing Gangfeng Hospital Products Co Ltd. (Gaobu Town, Shaoxing, Zhejiang, China) and purchased through Labomed Pharma SA (Bucuresti, Romania). The GBs were made using cotton microfibers (CmF) with 100% purity and mass density of at a temperature of 22 °C and a relative air humidity of 60%.
- (b)
- Bee honey (HB) was purchased through Biosimttera Cluj (Cluj-Napoca, Romania) with mass density at a temperature of 22 °C.
- (c)
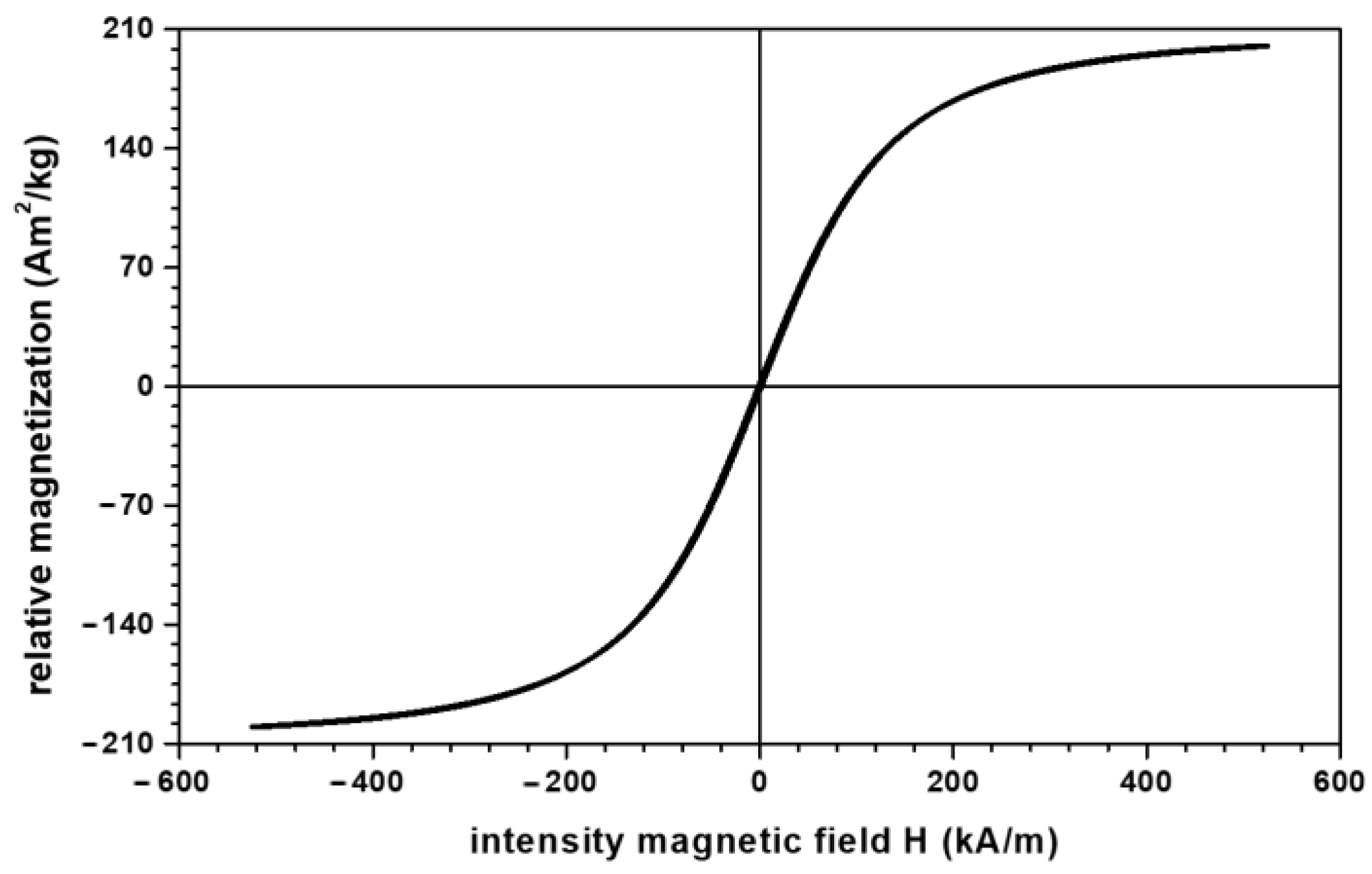
- Microparticles of carbonyl iron (CI) from Sigma-Aldrich Chemie GmbH (Taufkirchen, Germany), product code C-3518, with a minimum purity of 99.7% and an average diameter at a temperature of 24 °C. The electrical resistivity of CI microparticles is at a temperature of 20 °C, and the bulk density of CI microparticles is at a temperature of 22 °C. From the magnetization slope of CI microparticles, recorded using the experimental set-up described in [23], we measured the relative saturation magnetization as at (Figure 1).
- (d)
- Silver microparticles (SmP), from Sigma-Aldrich (Saint Louis, MO, USA), product code 327085, with a minimum purity of 99.9%, average diameter electrical resistivity of and bulk density at a temperature of 20 °C.
2.2. Ms Manufacturing
2.3. ED Manufacturing
- A textolite plate coated with copper foil (PCu) with dimensions of 100 × 75 × 0.8 mm3, from Electronic Light Tech (Romania). The plate (PCu) was based on epoxy resin, FR40type, reinforced with fiberglass, and copper foil of 35 μm thickness.
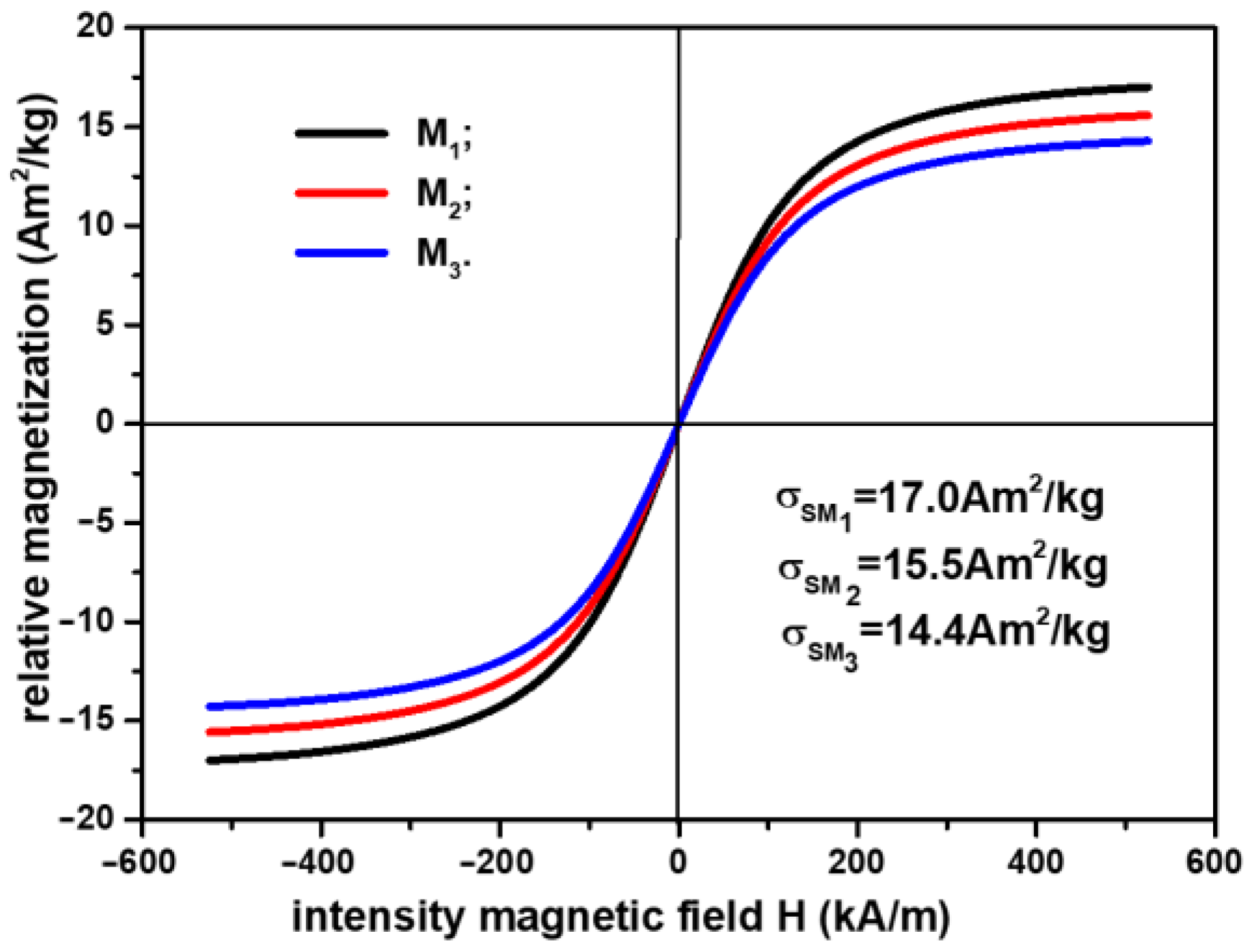
- membranes (Table 3) with dimensions of 30 × 30 × 0.4 mm3.
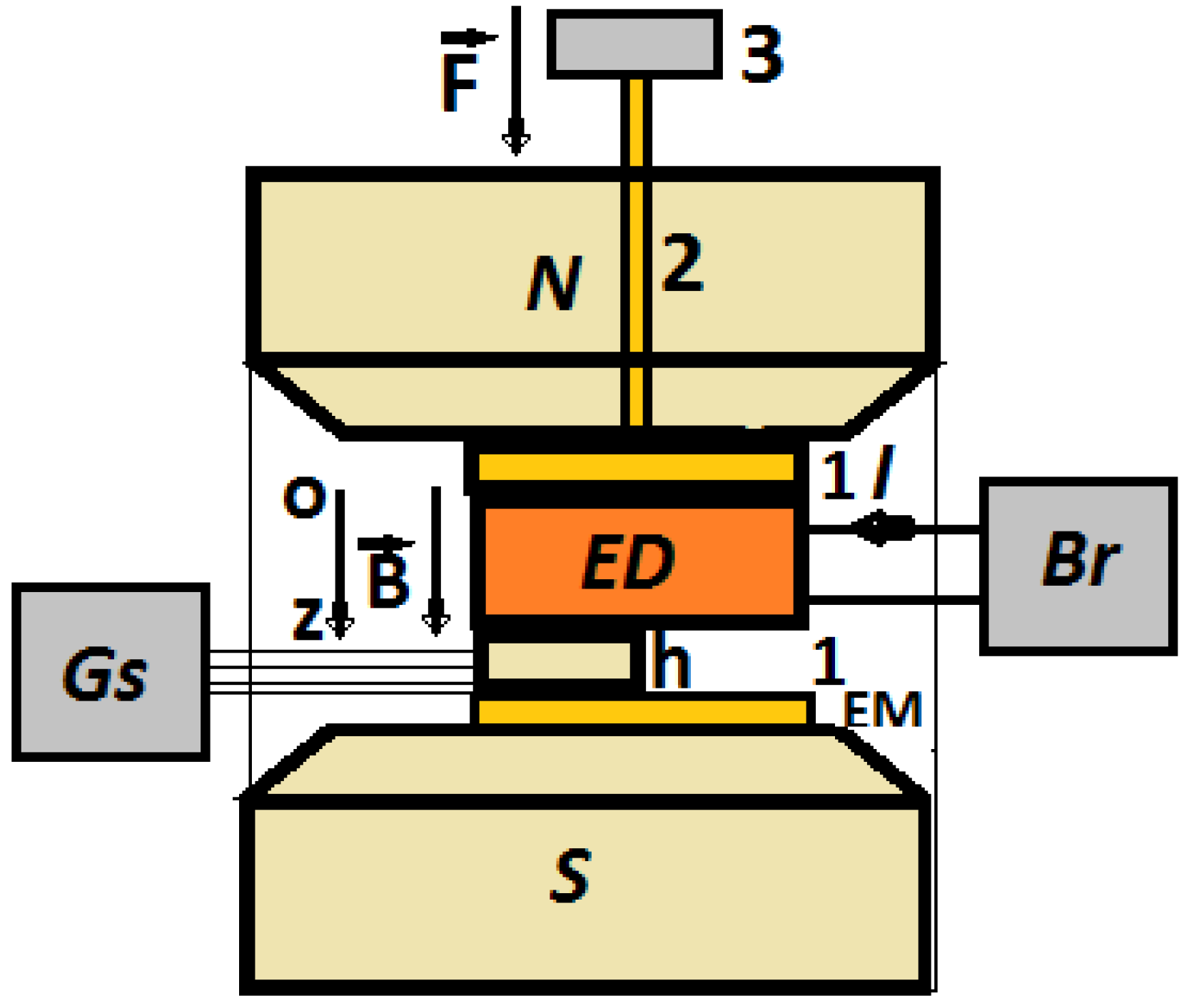
2.4. Experimental Set-Up and Measurements
3. Results and Discussion
3.1. The Study of the Electrical Conductivity of Ms in the Absence of the Magnetic Field
- 2.19 ⁄ 0.64 ≈ 3.42 times for ;
- 4.93 ⁄ 0.64 ≈ 7.70 times for ;
- 8.03 ⁄ 0.64 ≈ 12.55 times for .
- 4.93 ⁄ 2.19 ≈ 2.25 times for ;
- 8.03 ⁄ 2.19 ≈ 3.67 times for .
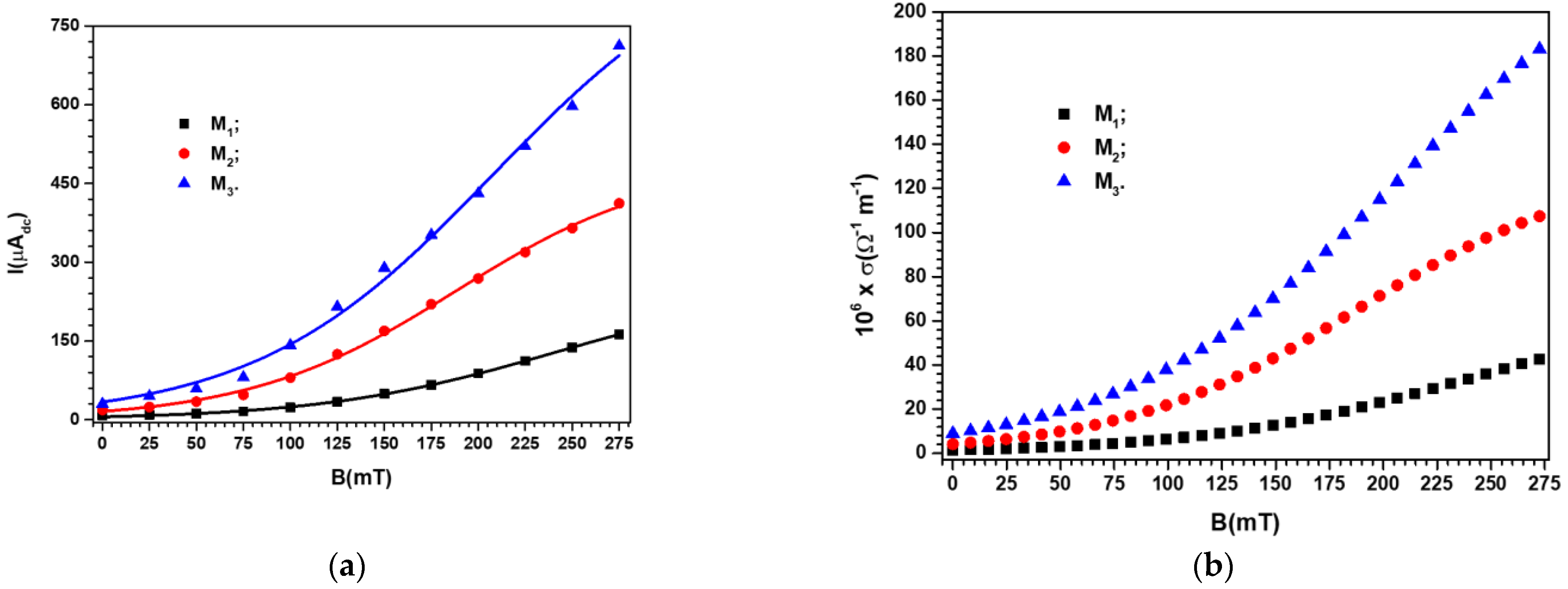
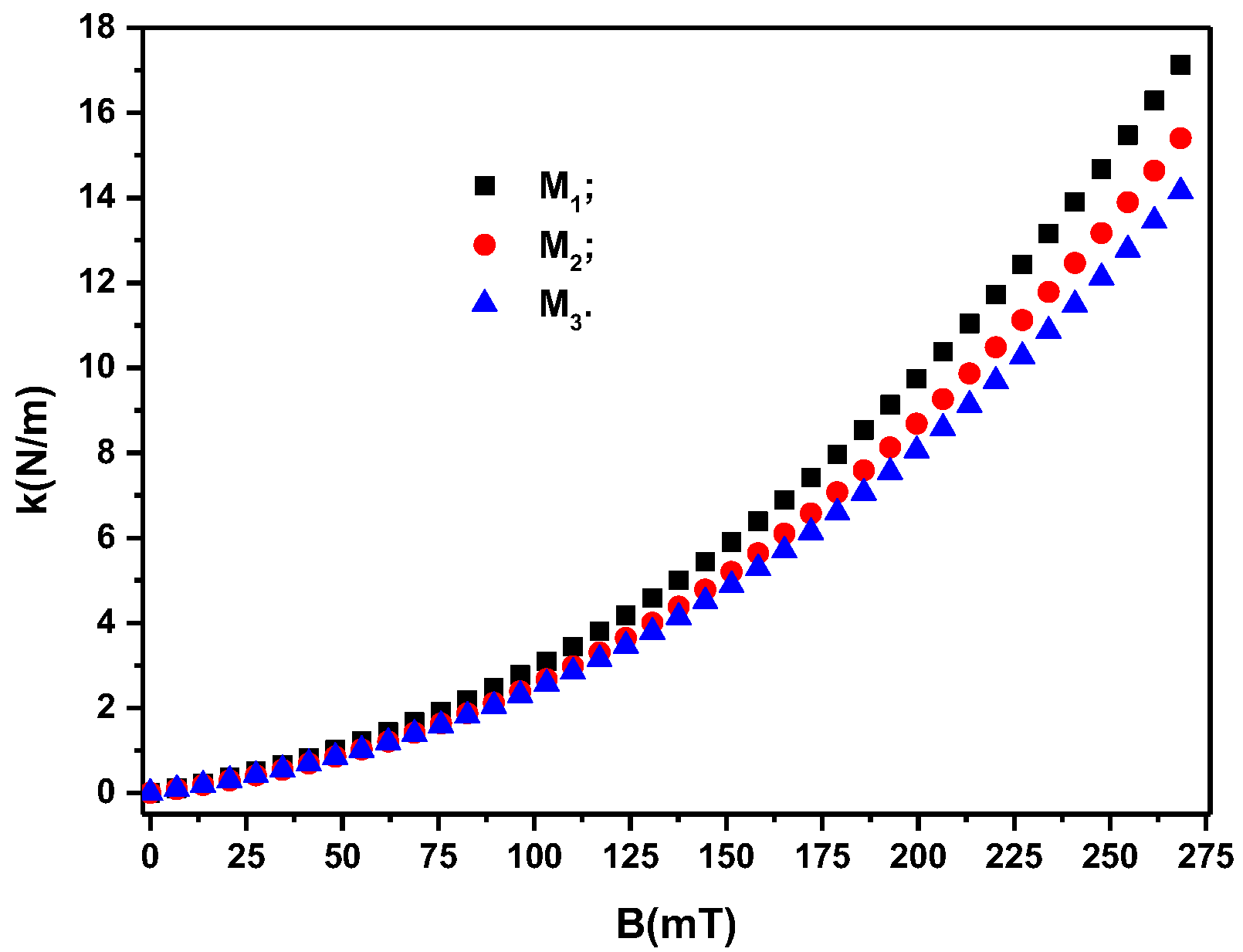
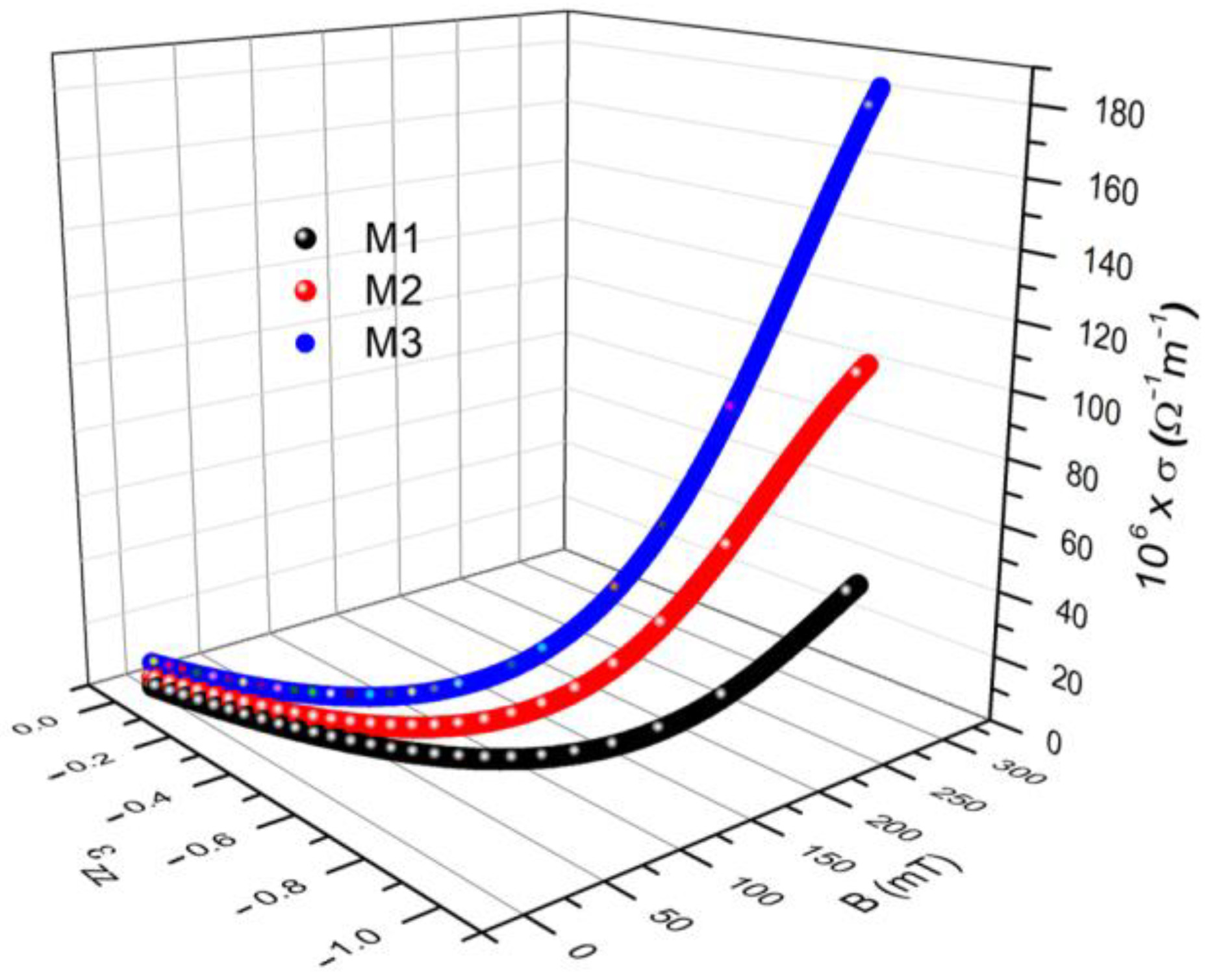
3.2. Studying the Electrical Conductivity of Ms in the Presence of a Magnetic Field
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ms | Membranes |
| GB | Sterile compresse |
| CmF | Cotton microfibers |
| HB | Bee honey |
| CI | Carbonyl iron |
| SmP | Silver microparticles |
| ED | Electrical device |
References
- Jose, K.; Gedeon, F.L.; Cheng, C.-H. Organic-Inorganic Hybrid Membranes for Agricultural Wastewater Treatment. In Advances in Membrane Technologies; Abdelrasoul, A., Ed.; IntechOpen: London, UK, 2020; p. 15. [Google Scholar] [CrossRef]
- Nain, A.; Sangili, A.; Hu, S.-R.; Chen, C.-H.; Chen, Y.-L.; Chang, H.-T. Recent progress in nanomaterial-functionalized membranes for removal of pollutants. iScience 2022, 25, 104616. [Google Scholar] [CrossRef]
- Mansourpanah, Y.; Emamian, F. Membrane and Bioseparation. In Advances in Membrane Technologies; Abdelrasoul, A., Ed.; IntechOpen: London, UK, 2020; p. 32. [Google Scholar] [CrossRef]
- Zhou, J.; Zuo, C.; Tian, H.; Wang, W.; Yang, J.; Crommen, J.; Jiang, Z.; Wang, Q. Magnetic composite membrane roll column for rapid and high efficiency separation of antibodies. Sep. Purif. Technol. 2023, 309, 123107. [Google Scholar] [CrossRef]
- Mollahosseini, A.; Amira Abdelrasoul, A.; Shoker, A. Challenges and Advances in Hemodialysis Membranes. In Advances in Membrane Technologies; Abdelrasoul, A., Ed.; IntechOpen: London, UK, 2020; p. 150. [Google Scholar] [CrossRef]
- Zaman, S.U.; Rafiq, S.; Ali, A.; Mehdi, M.S.; Arshad, A.; Saif-ur, R.; Muhammad, N.; Irfan, M.; Khurram, M.S.; Zaman, M.K.U.; et al. Recent advancement challenges with synthesis of biocompatible hemodialysis membranes. Chemosphere 2022, 307, 135626. [Google Scholar] [CrossRef]
- Shirazi, M.M.A.; Bazgir, S.; Meshkani, F. Electrospun Nanofibrous Membranes for Water Treatment. In Advances in Membrane Technologies; Abdelrasoul, A., Ed.; IntechOpen: London, UK, 2020; p. 113. [Google Scholar] [CrossRef]
- Imsong, R.; Dhar Purkayastha, D. Dual-functional superhydrophilic/underwater superoleophobic 2D Ti3C2TX MXene-PAN membrane for efficient oil-water separation and adsorption of organic dyes in wastewater. Sep. Purif. Technol. 2023, 306, 122636. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M. Magnetodielectric effects in membranes based on magnetorheological bio-suspensions. Mater. Design 2018, 155, 317–324. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M. Light transmission, magnetodielectric and magnetoresistive effects in membranes based on hybrid magnetorheological suspensions in a static magnetic field superimposed on a low/medium frequency electric field. J. Magn. Magn. Mater. 2020, 511, 166975. [Google Scholar] [CrossRef]
- Lal, A.; Chohan, K.; Chohan, A.; Chakravarti, A. Role of honey after tonsillectomy: A systematic review and meta-analysis of randomised controlled trials. Clin. Otolaryngol. 2017, 42, 651–660. [Google Scholar] [CrossRef]
- Jicman Stan, D.; Sârbu, M.I.; Fotea, S.; Nechifor, A.; Bălan, G.; Anghele, M.; Vasile, C.I.; Elena Niculet, E.; Sârbu, N.; Rebegea, L.-F.; et al. Oral Mucositis Induced by Chemoradiotherapy in Head. Medicina 2022, 58, 751. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.S.; Macedo, C.; Silva, A.M.; Delerue-Matos, C.; Costa, P.; Rodrigues, F. Natural Products for the Prevention and Treatment of Oral Mucositis—A Review. Int. J. Mol. Sci. 2022, 23, 4385. [Google Scholar] [CrossRef] [PubMed]
- Khanjani Pour-Fard-Pachekenari, A.; Rahmani, A.; Ghahramanian, A.; Asghari Jafarabadi, M.; Onyeka, T.C.; Davoodi, A. The effect of an oral care protocol and honey mouthwash on mucositis in acute myeloid leukemia patients undergoing chemotherapy: A single-blind clinical trial. Clin. Oral Investig. 2019, 23, 1811–1821. [Google Scholar] [CrossRef]
- Zhang, X.; Kevin, Y.K.; Xu, A. Biological Effects of Static Magnetic Fields; Springer Nature: Singapore, 2017. [Google Scholar]
- Tofani, S. Magnetic fields and apoptosis: A possible mechanism. Electromagn. Biol. Med. 2022, 41, 293–303. [Google Scholar] [CrossRef] [PubMed]
- Burdușel, A.-C.; Gherasim, O.; Grumezescu, A.M.; Mogoantă, L.; Ficai, A.; Andronescu, E. Biomedical Applications of Silver Nanoparticles: An Up-To-Date Overview. Nanomaterials 2018, 8, 681. [Google Scholar] [CrossRef] [PubMed]
- Yin, I.X.; Zhang, J.; Zhao, I.S.; Mei, M.L.; Li, Q.; Chu, C.H. The Antibacterial Mechanism of Silver Nanoparticles and Its Application in Dentistry. Int. J. Nanomed. 2020, 15, 2555–2562. [Google Scholar] [CrossRef] [PubMed]
- Wen, L.; Li, M.; Lin, X.; Li, Y.; Huidong, S.H.; Chen, H. AgNPs Aggravated Hepatic Steatosis, Inflammation, Oxidative Stress, and Epigenetic Changes in Mice With NAFLD Induced by HFD. Front. Bioeng. Biotechnol. 2022, 10, 912178. [Google Scholar] [CrossRef] [PubMed]
- Nayek, S.; Lund, A.K.; Verbeck, G.F. Inhalation Exposure to Silver Nanoparticles Induces Hepatic Inflammation and Oxidative Stress, Associated with Altered Renin-angiotensin System Signaling, in Wistar Rats. Environ. Toxicol. 2022, 37, 457–467. [Google Scholar] [CrossRef]
- Ahmed, T.N.; Iram Shahriar, I.; Iqbal, J.U.M.; Rowshan, M.M.; Yusuf, R. Comparison of Efficacy and Tolerability of Ferrous Sulfate and Carbonyl Iron in Iron Deficiency Anemia in Pregnant Woman. Sir Salimullah Med. Coll. J. 2022, 30, 83–88. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Sfirloaga, P. Magnetizable Membranes Based on Cotton Microfibers, Honey, Carbonyl Iron, and Silver Nanoparticles: Effects of Static Magnetic Fields and Medium-Frequency Electric Fields on Electrical Properties. Magnetochemistry 2023, 9, 19. [Google Scholar] [CrossRef]
- Ercuta, A. Sensitive AC Hysteresigraph of Extended Driving Field Capability. IEEE Trans. Instrum. Meas. 2020, 69, 1643–1651. [Google Scholar] [CrossRef]
- Genç, S. Synthesis and Properties of Magnethoreological (MR) Fluids. Ph.D. Thesis, University of Pitsburgh, Pitsburgh, PA, USA, 2003. [Google Scholar]
- Stepanov, G.V.; Borin, D.Y.; Raikher, Y.L.; Melenev, P.V.; Perov, N.S. Motion of ferroparticles inside the polymeric matrix in magnetoactive elastomers. J. Phys. Condens. Matter 2008, 20, 204121. [Google Scholar] [CrossRef] [PubMed]
- Bica, I. The influence of hydrostatic pressure and transverse magnetic field on the electric conductivity of the magnetorheological elastomers. J. Ind. Eng. Chem. 2012, 18, 483–486. [Google Scholar] [CrossRef]
- Bica, I.; Balasoiu, M.; Sfirloaga, P. Effects of electric and magnetic fields on dielectric and elastic properties of membranes composed of cotton fabric and carbonyl iron microparticles. Results Phys. 2022, 35, 105332. [Google Scholar] [CrossRef]
- Behera, S.K.; Ranjan, R.A.; Sarangi, S. Field dependent magneto-viscoelasticity in particle reinforced elastomer. Eur. J. Mech. A Solids 2023, 99, 104929. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Ter-Yesayants, T.; Moreno-Mateos, M.A.; Lopez-Donaire, M.L. Hard-magnetic phenomena enable autonomous self-healing elastomers. Compos. Part B Eng. 2023, 248, 110357. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Jiang, L.; Cheng, L. Magneto-mechanical properties of anisotropic magnetorheological elastomers with tilt angle of magnetic chain under compression mode. J. Magn. Magn. Mater. 2023, 570, 170441. [Google Scholar] [CrossRef]
- Liu, Q.; Ye, X.; Chui, E.C.-S.; Pu, Z. Impact of interface stress on responsive deformation of magnetic hydrogel. Int. J. Mech. Sci. 2023, 247, 108151. [Google Scholar] [CrossRef]
- Kchit, N.; Bossis, G. Piezoresistivity of magnetorheological elastomers. J. Phys. Condens. Matter 2008, 20, 204136. [Google Scholar] [CrossRef]




| 1.20 | 0.00 | 0.00 | 100.00 | 0.00 | 0.00 | |
| 1.20 | 0.40 | 0.00 | 75.00 | 25.00 | 0.00 | |
| 1.20 | 0.40 | 0.20 | 66.67 | 22.22 | 11.11 | |
| 1.20 | 0.40 | 0.40 | 60.00 | 20.00 | 20.00 |
| 0.200 | 0.776 | 0.000 | 0.000 | |
| 0.200 | 0.776 | 0.258 | 0.000 | |
| 0.200 | 0.776 | 0.258 | 0.129 | |
| 0.200 | 0.776 | 0.258 | 0.258 |
| 0.2720 | 0.5187 | 0.0000 | 0.0000 | 34.39989 | 65.60011 | 0.00000 | 0.000000 | |
| 0.2720 | 0.5187 | 0.0735 | 0.0000 | 31.47430 | 60.02080 | 8.50490 | 0.000000 | |
| 0.2720 | 0.5187 | 0.0735 | 0.0966 | 28.30970 | 53.98630 | 7.64499 | 10.05410 | |
| 0.2720 | 0.5187 | 0.0735 | 0.1932 | 25.72350 | 49.05420 | 6.95100 | 18.27130 |
| 2.40 | 0.64 | ||
| 8.20 | 2.19 | ||
| 18.50 | 4.93 | ||
| 30.10 | 8.03 |
| B (mT) | |||
|---|---|---|---|
| 25 | −0.32236 | 2.11025 | |
| −0.35263 | 6.50703 | ||
| −0.31506 | 13.12206 | ||
| 275 | −0.96701 | 43.34193 | |
| −0.96109 | 108.25721 | ||
| −0.95140 | 184.99065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bica, I.; Iacobescu, G.-E. The Influence of Magnetic Fields on the Electrical Conductivity of Membranes based on Cotton Fabric, Honey, and Microparticles of Carbonyl Iron and Silver. Materials 2023, 16, 1995. https://doi.org/10.3390/ma16051995
Bica I, Iacobescu G-E. The Influence of Magnetic Fields on the Electrical Conductivity of Membranes based on Cotton Fabric, Honey, and Microparticles of Carbonyl Iron and Silver. Materials. 2023; 16(5):1995. https://doi.org/10.3390/ma16051995
Chicago/Turabian StyleBica, Ioan, and Gabriela-Eugenia Iacobescu. 2023. "The Influence of Magnetic Fields on the Electrical Conductivity of Membranes based on Cotton Fabric, Honey, and Microparticles of Carbonyl Iron and Silver" Materials 16, no. 5: 1995. https://doi.org/10.3390/ma16051995
APA StyleBica, I., & Iacobescu, G.-E. (2023). The Influence of Magnetic Fields on the Electrical Conductivity of Membranes based on Cotton Fabric, Honey, and Microparticles of Carbonyl Iron and Silver. Materials, 16(5), 1995. https://doi.org/10.3390/ma16051995







