Analytical Method for the Optimization of the Open-Hole and Filled-Hole Laminates at the Preliminary Design Stage
Abstract
:Highlights
- A simplified analytical procedure was presented for the preliminary design of composite structures with open and filled holes.
- Filling material stiffness plays a crucial role in enhancing the bearing performance of filled-hole laminates.
- The CLT-Lekhnitskii coupled theory can generate carpet plots, which is useful for the stacking sequence optimization of open-hole and filled-hole composite structures during the preliminary design stage.
1. Introduction
2. Material Used and Laminate Sequence
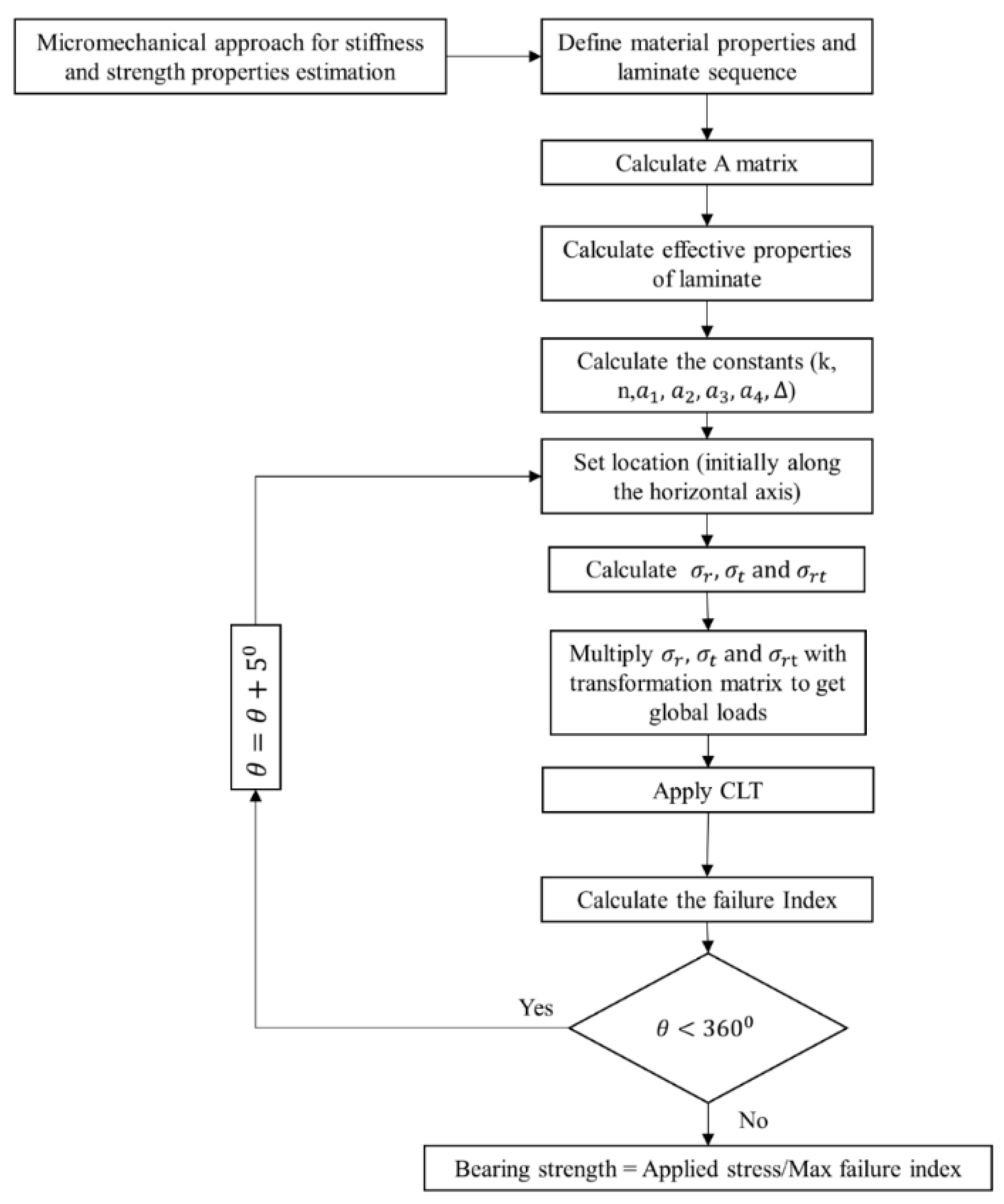
3. Analytical Modeling
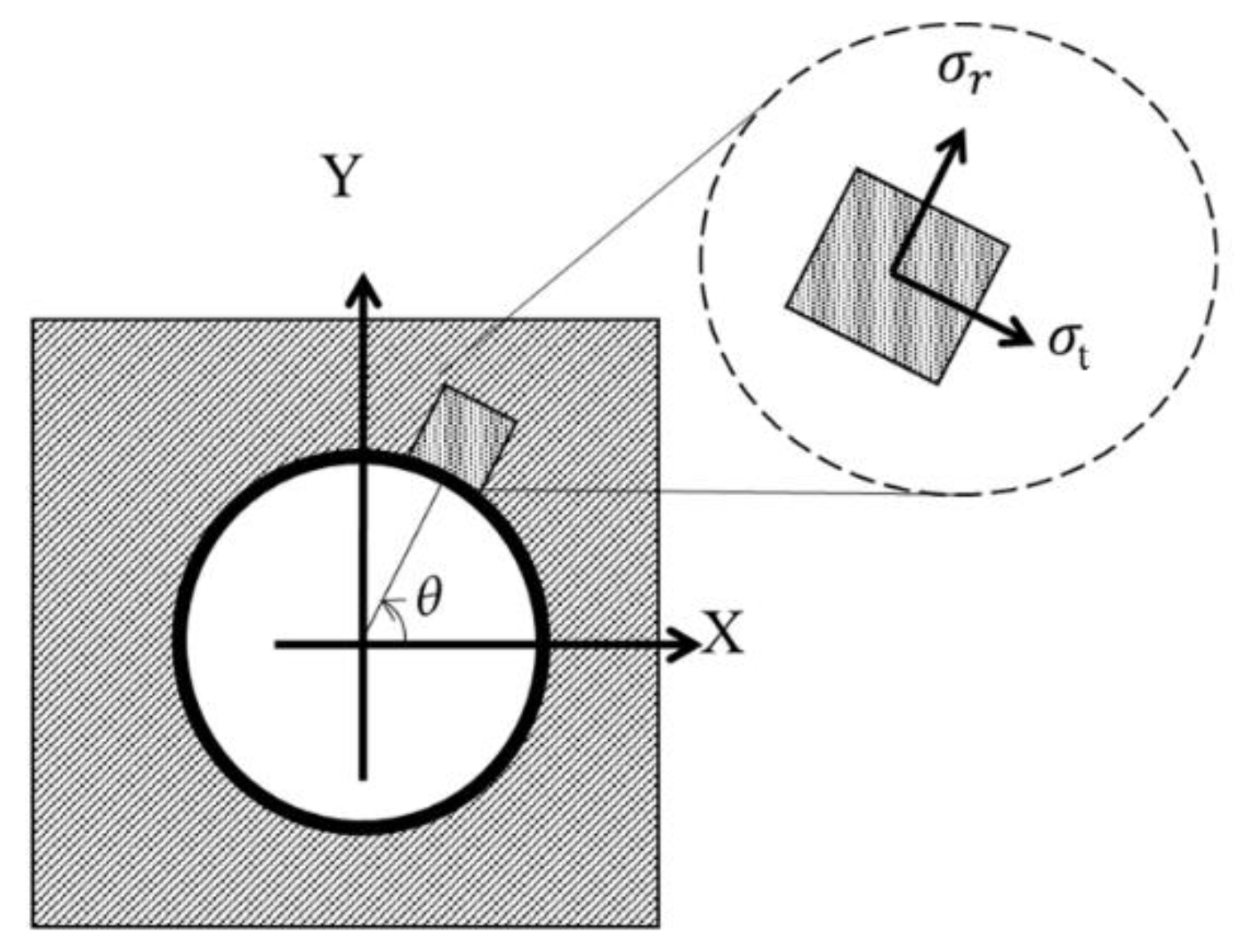
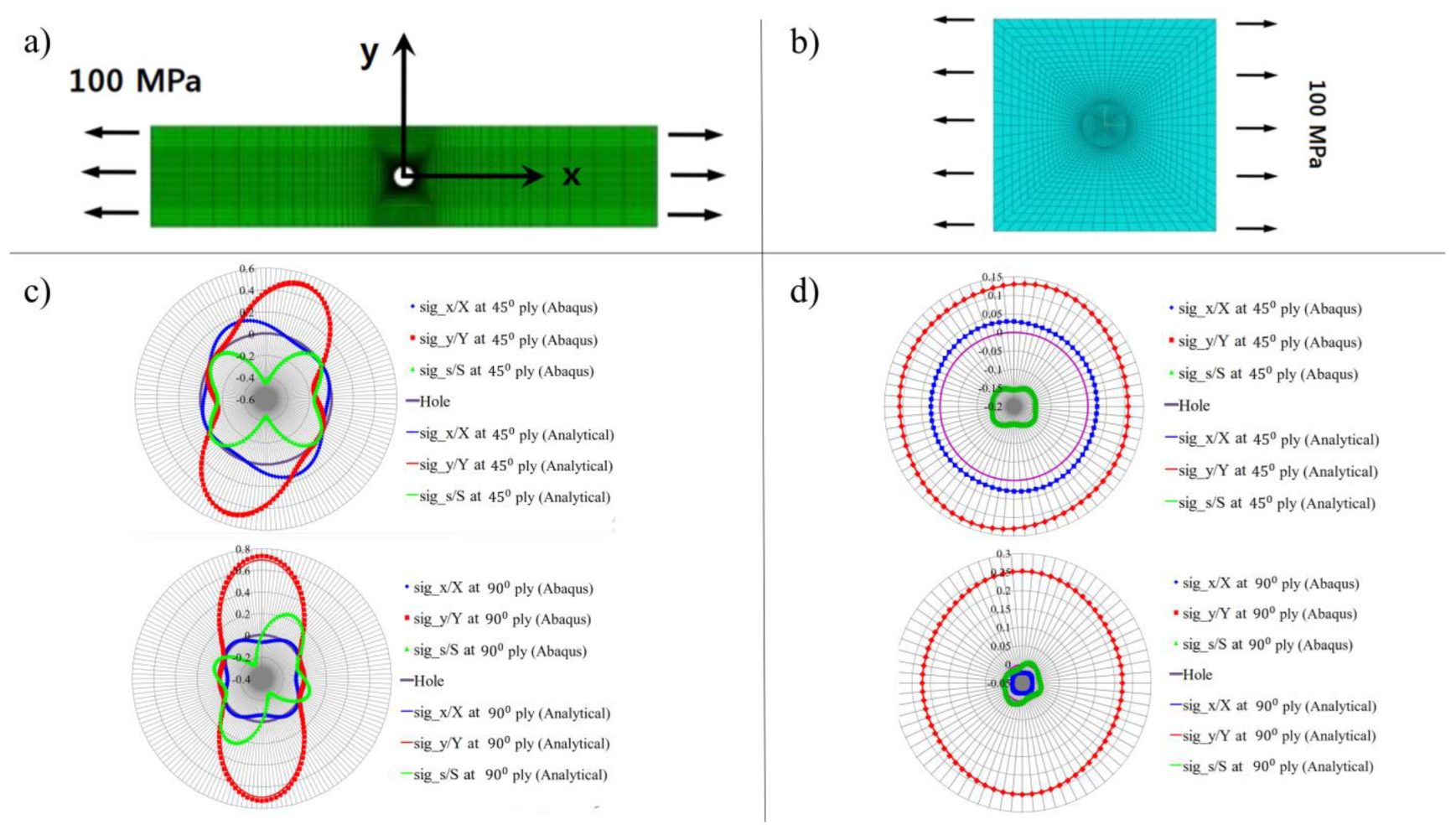
4. Results and Discussion
4.1. Strain-Based Failure Envelops
4.2. Effect of Filling Material on Load Bearing Capacity
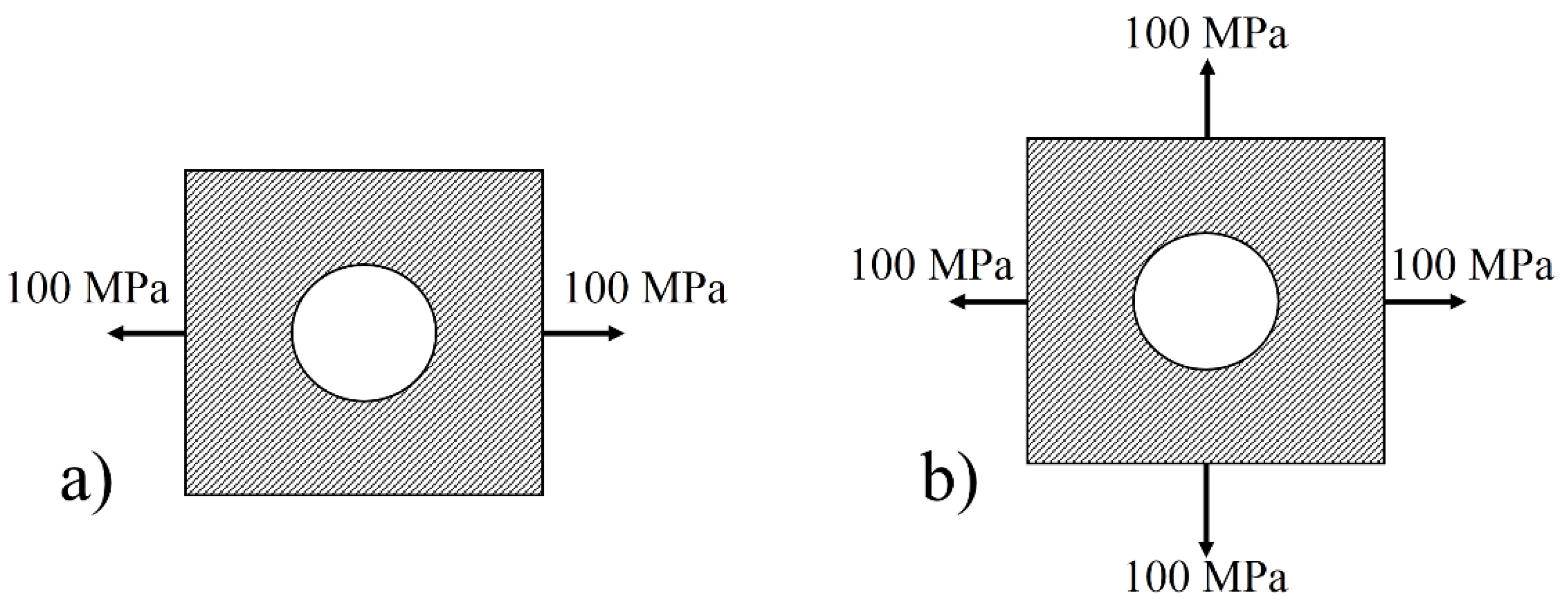
4.3. Effect of Laminate Sequence on Load Bearing Capacity
5. Conclusions
- The CLT-Lekhnikstii coupled approach can generate failure envelops for open-hole and filled-hole composite structures, which is a very beneficial finding for the preliminary design stage of these structures.
- To achieve maximum bearing strength, the stiffness of the filler material for joining two composite laminates should be equal to or close to the stiffness of the joining composite laminates. For uniaxial loading conditions, the stiffness of the filler material should be close to the longitudinal equivalent stiffness of the base laminate. Meanwhile, for multiaxial loading conditions, it should be close to the transverse-equivalent stiffness of the base laminate.
- Carpet plots produced by CLT-Lekhnikstii coupled method can be very effective for deciding the stacking sequence of open-hole and filled-hole composite structures at the preliminary design stage.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, R.; Li, C.; Xian, G. Water absorption and long-term thermal and mechanical properties of carbon/glass hybrid rod for bridge cable. Eng. Struct. 2023, 274, 115176. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Iwashita, K.; Sasaki, T.; Hamaguchi, Y. Tensile fatigue behaviour of FRP and hybrid FRP sheets. Compos. Part B Eng. 2010, 41, 396–402. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C.; Wang, Y. Mechanical performance evolution and life prediction of prestressed CFRP plate exposed to hygrothermal and freeze-thaw environments. Compos. Struct. 2022, 293, 115719. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Ahmadi-Pari, A.R. Circumferential vibration analysis of nano-porous-sandwich assembled spherical-cylindrical-conical shells under elastic boundary conditions. Eng. Struct. 2022, 273, 115094. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Arabi, E.; Masoodi, A.R. Nonlinear analysis of FG-sandwich plates and shells. Aerosp. Sci. Technol. 2019, 87, 178–189. [Google Scholar] [CrossRef]
- Khechai, A.; Tati, A.; Guerira, B.; Guettala, A.; Mohite, P. Strength degradation and stress analysis of composite plates with circular, square and rectangular notches using digital image correlation. Compos. Struct. 2018, 185, 699–715. [Google Scholar] [CrossRef]
- Jin, B.C.; Li, X.; Mier, R.; Pun, A.; Joshi, S.; Nutt, S. Parametric modeling, higher order FEA and experimental investigation of hat-stiffened composite panels. Compos. Struct. 2015, 128, 207–220. [Google Scholar] [CrossRef]
- Shah, S.; Megat-Yusoff, P.; Karuppanan, S.; Choudhry, R.; Sajid, Z. Multiscale damage modelling of 3D woven composites under static and impact loads. Compos. Part A Appl. Sci. Manuf. 2021, 151, 106659. [Google Scholar] [CrossRef]
- Shah, S.; Megat-Yusoff, P.; Karuppanan, S.; Choudhry, R.; Ahmad, F.; Sajid, Z.; Gerard, P.; Sharp, K. Performance comparison of resin-infused thermoplastic and thermoset 3D fabric composites under impact loading. Int. J. Mech. Sci. 2021, 189, 105984. [Google Scholar] [CrossRef]
- Shah, S.Z.H.; Megat-Yusoff, P.S.M.; Karuppanan, S.; Choudhry, R.S.; Ahmad, F.; Sajid, Z. Mechanical Properties and Failure Mechanisms of Novel Resin-infused Thermoplastic and Conventional Thermoset 3D Fabric Composites. Appl. Compos. Mater. 2021, 29, 515–545. [Google Scholar] [CrossRef]
- Shah, S.; Megat-Yusoff, P.; Choudhry, R.; Sajid, Z.; Din, I.U. Experimental investigation on the quasi-static crush performance of resin-infused thermoplastic 3D fibre-reinforced composites. Compos. Commun. 2021, 28, 100916. [Google Scholar] [CrossRef]
- Shah, S.Z.H.; Yusoff, P.S.M.; Karuppanan, S.; Sajid, Z. Elastic Constants Prediction of 3D Fiber-Reinforced Composites Using Multiscale Homogenization. Processes 2020, 8, 722. [Google Scholar] [CrossRef]
- Shah, S.; Karuppanan, S.; Megat-Yusoff, P.; Sajid, Z. Impact resistance and damage tolerance of fiber reinforced composites: A review. Compos. Struct. 2019, 217, 100–121. [Google Scholar] [CrossRef]
- Rana, K.; Sajid, Z.; Tao, J.; Khan, L. Effect of vacuum manipulation on inter laminar shear strength and flexural strength in double bag vacuum infusion moulding. Polym. Polym. Compos. 2021, 29, S432–S440. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T.; Aoki, K.; Uchiyama, S.; Ogasawara, T. Effects of ply thickness and 0°-layer ratio on failure mechanism of open-hole and filled-hole tensile tests of thin-ply composite laminates. Compos. Struct. 2022, 280, 114926. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, X.; Wu, T. Damage characteristics of open-hole laminated composites subjected to longitudinal loads. Compos. Struct. 2019, 230, 111474. [Google Scholar] [CrossRef]
- Higuchi, R.; Warabi, S.; Yoshimura, A.; Nagashima, T.; Yokozeki, T.; Okabe, T. Experimental and numerical study on progressive damage and failure in composite laminates during open-hole compression tests. Compos. Part A: Appl. Sci. Manuf. 2021, 145, 106300. [Google Scholar] [CrossRef]
- Su, Z.; Tay, T.; Ridha, M.; Chen, B. Progressive damage modeling of open-hole composite laminates under compression. Compos. Struct. 2015, 122, 507–517. [Google Scholar] [CrossRef]
- Bao, H.; Liu, G. Progressive failure analysis on scaled open-hole tensile composite laminates. Compos. Struct. 2016, 150, 173–180. [Google Scholar] [CrossRef]
- Djabali, A.; Toubal, L.; Zitoune, R.; Rechak, S. An experimental investigation of the mechanical behavior and damage of thick laminated carbon/epoxy composite. Compos. Struct. 2018, 184, 178–190. [Google Scholar] [CrossRef]
- Kotelnikova-Weiler, N.; Baverel, O.; Ducoulombier, N.; Caron, J.-F. Progressive damage of a unidirectional composite with a viscoelastic matrix, observations and modelling. Compos. Struct. 2018, 188, 297–312. [Google Scholar] [CrossRef] [Green Version]
- Kaddour, A.; Hinton, M.; Smith, P.; Li, S. A comparison between the predictive capability of matrix cracking, damage and failure criteria for fibre reinforced composite laminates: Part A of the third world-wide failure exercise. J. Compos. Mater. 2013, 47, 2749–2779. [Google Scholar] [CrossRef]
- Zubair, S.; Saravanan, K.; Mohd, A. Effect of hybridization on the buckling behavior of perforated CFRP/BFRP laminates. Emerg. Mater. Res. 2021, 10, 66–74. [Google Scholar]
- Sajid, Z.; Karuppanan, S.; Shah, S. Effect of Washer Size and Tightening Torque on Bearing Performance of Basalt Fiber Composite Bolted Joints. J. Nat. Fibers 2021, 19, 5910–5927. [Google Scholar] [CrossRef]
- Sajid, Z.; Karuppanan, S.; Shah, S. Open-Hole and Filled-Hole Failure Envelopes of BFRP and GFRP: A Comparative Study. In Advances in Manufacturing Engineering; Lecture Notes in Mechanical Engineering; Emamian, S., Awang, M., Yusof, F., Eds.; Springer: Singapore, 2020. [Google Scholar]
- Sajid, Z.; Karuppanan, S.; Sallih, N.; Kee, K.; Shah, S. Role of washer size in mitigating adverse effects of bolt-hole clearance in a single-lap, single-bolt basalt composite joint. Compos. Struct. 2021, 266, 113802. [Google Scholar] [CrossRef]
- Sajid, Z.; Karuppanan, S.; Kee, K.; Sallih, N.; Shah, S. Bearing performance improvement of single-lap, single-bolt basalt composite joints by locally strengthening the joint location using carbon fibre. Thin Walled Struct. 2022, 180, 109873. [Google Scholar] [CrossRef]
- Sajid, Z.; Karuppanan, S.; Kee, K.; Sallih, N.; Shah, S. Carbon/basalt hybrid composite bolted joint for improved bearing performance and cost efficiency. Compos. Struct. 2021, 275, 114427. [Google Scholar] [CrossRef]
- Yan, Y.; Wen, W.-D.; Chang, F.-K.; Shyprykevich, P. Experimental study on clamping effects on the tensile strength of composite plates with a bolt-filled hole. Compos. Part A Appl. Sci. Manuf. 1999, 30, 1215–1229. [Google Scholar] [CrossRef]
- Muskhelishvili, N. Some Basic Problems of the Mathematical Theory of Elasticity; Noordhoff Groningen: Groningen, The Netherlands, 1953. [Google Scholar]
- Savin, G.N. Stress Concentration Around Holes; Pergamon Press: Oxford, UK, 1961. [Google Scholar]
- Lekhnitskii, S.; Tsai, S.; Cheron, T. Anisotropic Plates; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1968. [Google Scholar]
- Theocaris, P.; Philippidis, T. Stress distribution in orthotropic plates with coupled elastic properties. Acta Mech. 1989, 80, 95–111. [Google Scholar] [CrossRef]
- Nuismer, R.; Whitney, J. Uniaxial Failure of Composite Laminates Containing Stress Concentrations; ASTM International: West Conshohocken, PA, USA, 1975. [Google Scholar]
- Tan, S. Laminated composites containing an elliptical opening. I. Approximate stress analyses and fracture models. J. Compos. Mater. 1987, 21, 925–948. [Google Scholar] [CrossRef]
- Tan, S. Laminated composites containing an elliptical opening. II. Experiment and model modification. J. Compos. Mater. 1987, 21, 949–968. [Google Scholar] [CrossRef]
- Xiao, X.; Al-Hmouz, I. Effect of Load Frequency on the Tensile Fatigue Behaviour of Angle-Ply AS4/PEEK. In Proceedings of the 11th International Conference on Composite Materials, Gold Coast, Queensland, Australia, 14–18 July 1997; pp. 124–134. [Google Scholar]
- Yum, Y.; Hong, C. Stress intensity factors in finite orthotropic plates with a crack under mixed mode deformation. Int. J. Fract. 1991, 47, 53–67. [Google Scholar] [CrossRef]
- Whitworth, H.; Mahase, H. Failure of orthotropic plates containing a circular opening. Compos. Struct. 1999, 46, 53–57. [Google Scholar] [CrossRef]
- Chang, F.-K.; Scott, R.; Springer, G. Failure strength of nonlinearly elastic composite laminates containing a pin loaded hole. J. Compos. Mater. 1984, 18, 464–477. [Google Scholar] [CrossRef] [Green Version]
- Yamada, S.; Sun, C. Analysis of laminate strength and its distribution. J. Compos. Mater. 1978, 12, 275–284. [Google Scholar] [CrossRef]
- Zheng, X.; Xu, X. Stress analysis of finite composite laminates with elliptical inclusion. Comput. Struct. 1999, 70, 357–361. [Google Scholar] [CrossRef]
- Hufenbach, W.; Zhou, B. Solutions for an anisotropic, finite plate with an elastic inclusion and a loaded boundary. Compos. Struct. 2001, 52, 161–166. [Google Scholar] [CrossRef]
- Grüber, B.; Hufenbach, W.; Kroll, L.; Lepper, M.; Zhou, B. Stress concentration analysis of fibre-reinforced multilayered composites with pin-loaded holes. Compos. Sci. Technol. 2007, 67, 1439–1450. [Google Scholar] [CrossRef]
- Bradshaw, R.; Pang, S. Failure analysis of composite laminated plates with circular holes under bending. Compos. Mater. Technol. 1991, 1991, 125–135. [Google Scholar]
- Ko, C.-C.; Lin, C.-C. Interlaminar stresses around a hole in symmetric cross-ply laminatesunder bending/torsion. AIAA J. 1993, 31, 1118–1124. [Google Scholar] [CrossRef]
- Sakai, S.-i.; Noma, Y.; Kida, A. End-of-life vehicle recycling and automobile shredder residue management in Japan. J. Mater. Cycles Waste Manag. 2007, 9, 151–158. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R. A green material from rock: Basalt fiber—A review. J. Text. Inst. 2015, 107, 923–937. [Google Scholar] [CrossRef]
- Pickering, K.; Efendy, M.; Le, T. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef] [Green Version]
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Allison, J.; Schott, R.; Longridge, R.; Adams, D. Vehicle Component Including Basalt and Method for Making Same. US Patent 2013/0071574 A1, 21 March 2013. [Google Scholar]
- Huang, Z.-M.; Xin, L.-M. In situ strengths of matrix in a composite. Acta Mech. Sin. 2017, 33, 120–131. [Google Scholar] [CrossRef]
- Liu, G. A step-by-step method of rule-of-mixture of fiber-and particle-reinforced composite materials. Compos. Struct. 1997, 40, 313–322. [Google Scholar] [CrossRef]
- Hashin, Z.; Rosen, B. The elastic moduli of fiber-reinforced materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Nerilli, F.; Marino, M.; Vairo, G. A Numerical Failure Analysis of Multi-bolted Joints in FRP Laminates Based on Basalt Fibers. Procedia Eng. 2015, 109, 492–506. [Google Scholar] [CrossRef]
- Hart-Smith, L. The ten-percent rule for preliminary sizing of fibrous composite structures. Weight. Eng. 1992, 52, 29–45. [Google Scholar]
- Godines, C.; DorMohammadi, S.; Abdi, F.; Montero, M.V.; Huang, D.; Minnetyan, L. Damage tolerant composite design principles for aircraft components under static service loading using multi-scale progressive failure analysis. J. Compos. Mater. 2017, 51, 1393–1419. [Google Scholar] [CrossRef]
- Dalgarno, R.; Action, J.; Robbins, D.; Engelstad, S. Failure simulations of open-hole and unnotched IM7/977-3 coupons subjected to quasi-static loading using Autodesk Helius PFA. J. Compos. Mater. 2017, 51, 1421–1432. [Google Scholar] [CrossRef]
- Bert, C. Classical Lamination Theory, Manual on Experimental Methods for Mechanical Testing of Composites; Springer: Berlin/Heidelberg, Germany, 1989; pp. 11–16. [Google Scholar]
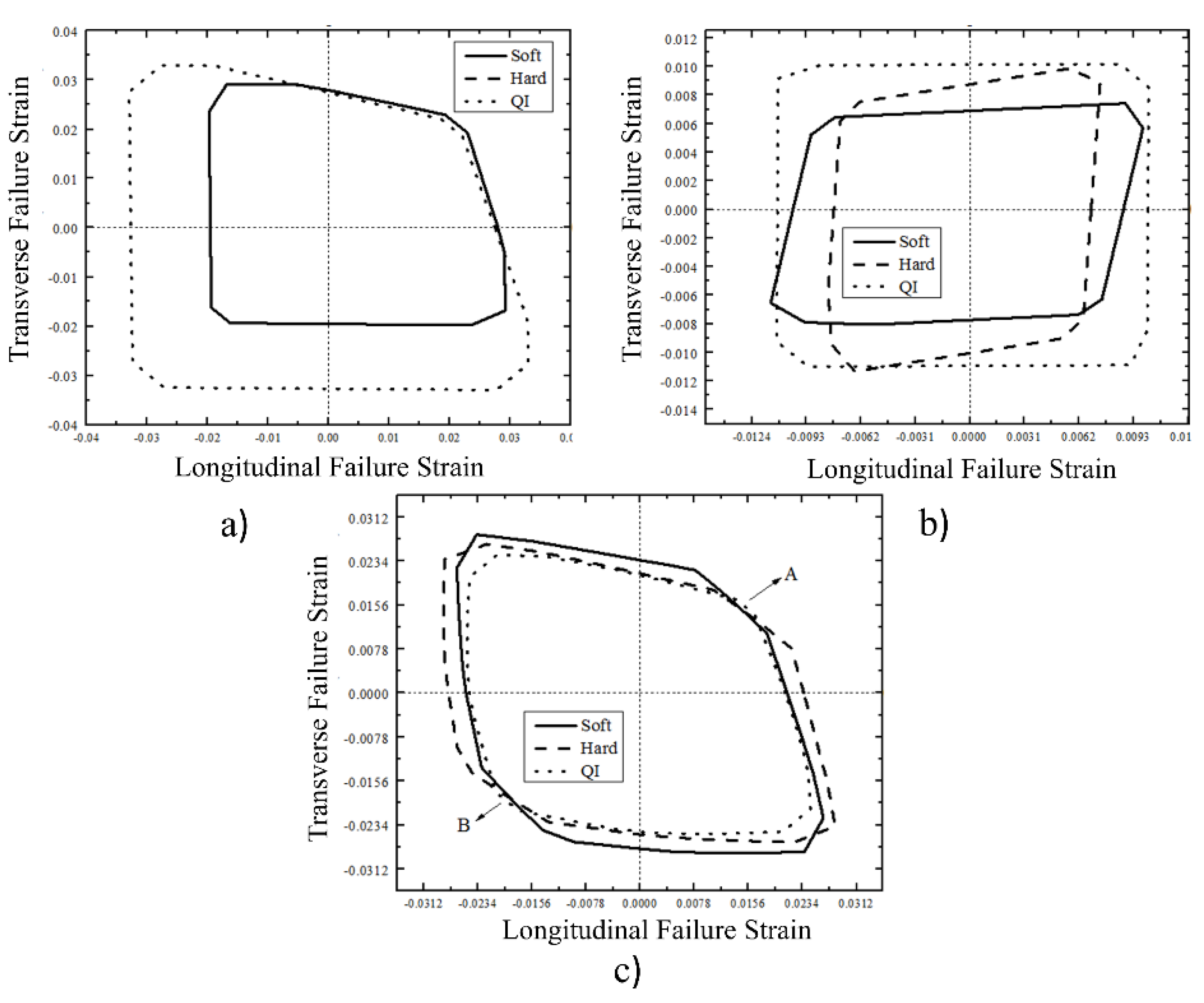
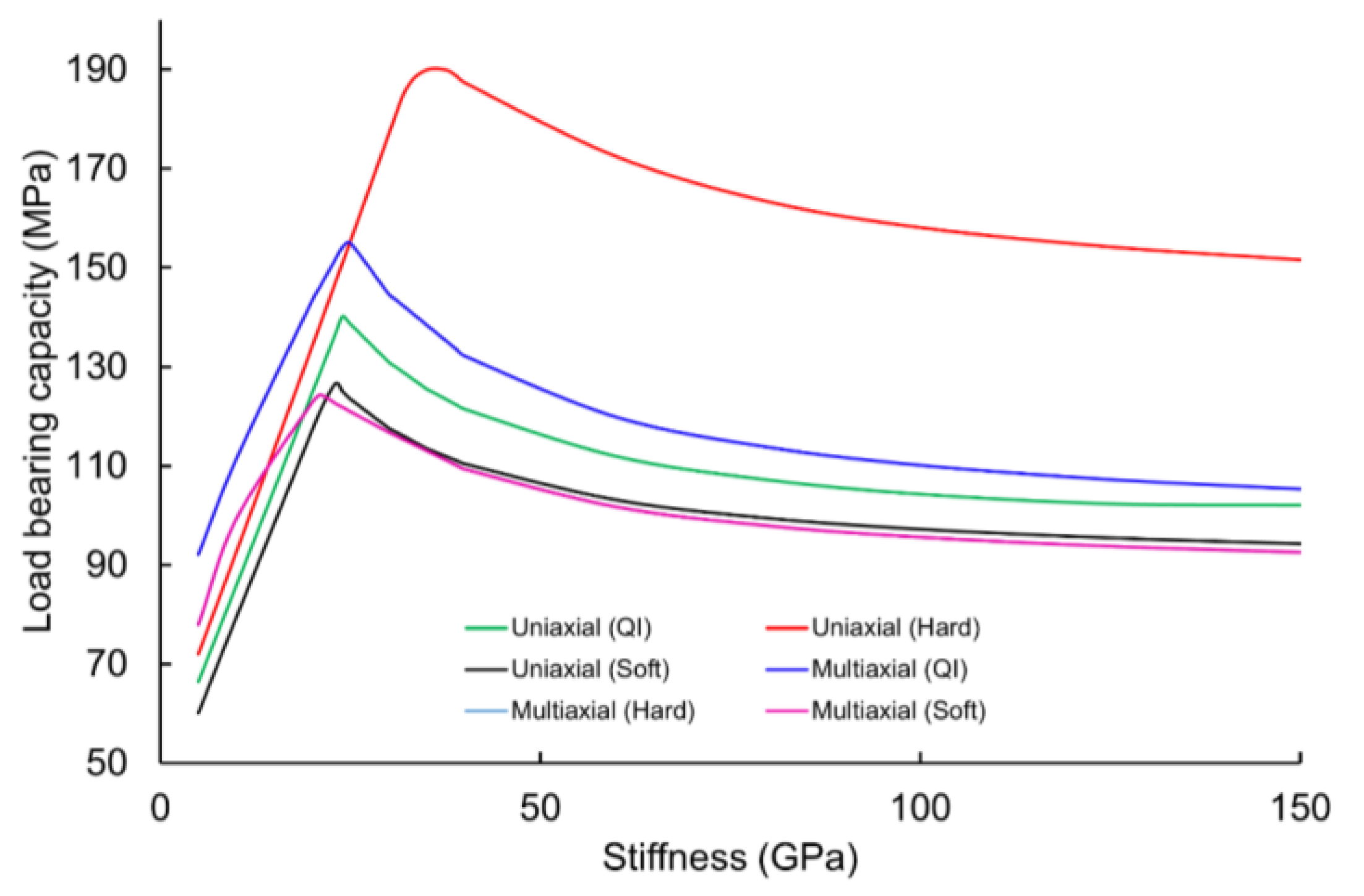
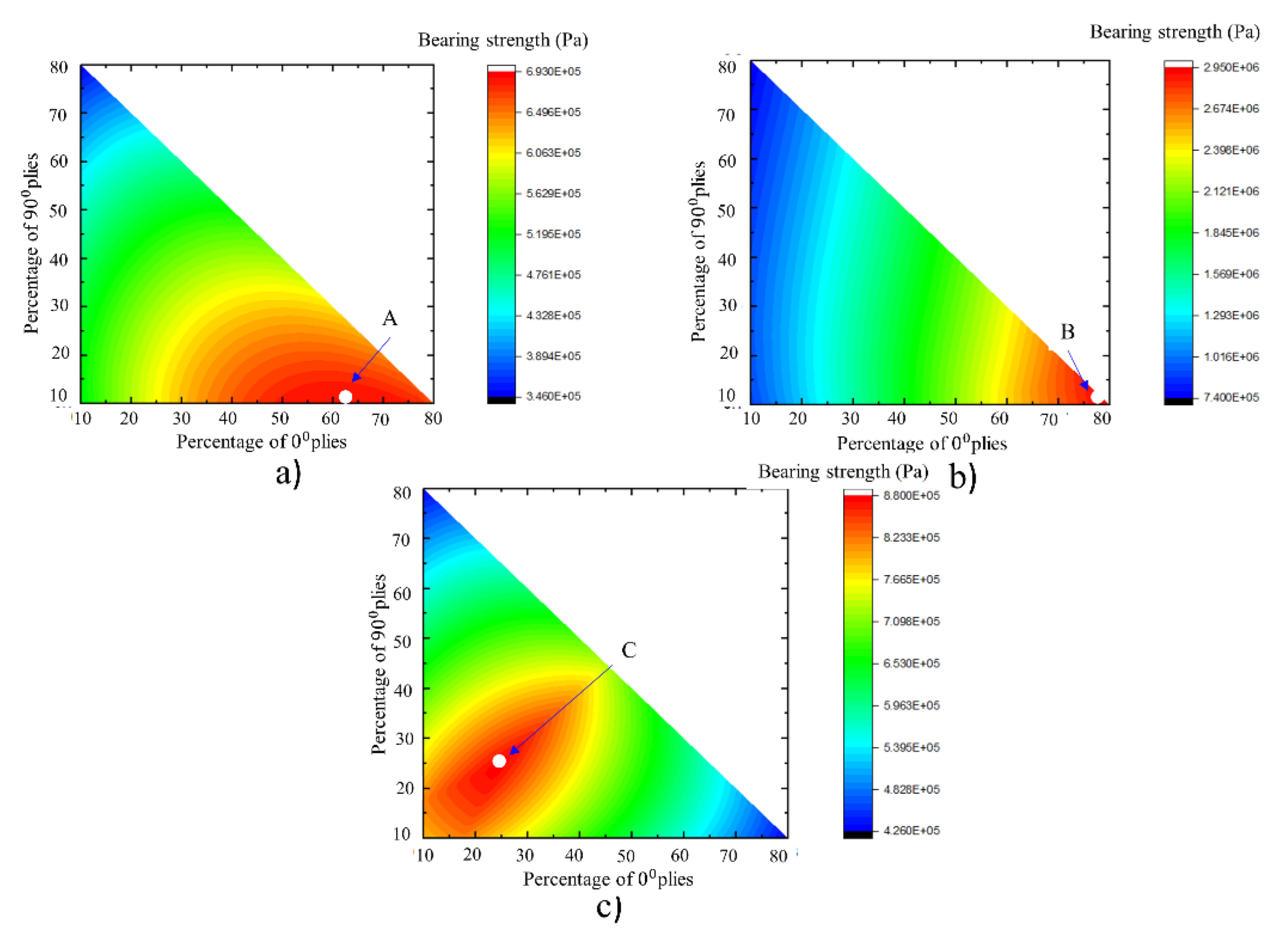
| Fiber | Failure Strain (%) | Tensile Strength (MPa) | Stiffness (GPa) | |
|---|---|---|---|---|
| Basalt | 2.63–2.8 | 3.1–6 | 3000–4840 | 93–110 |
| E-glass | 2.54–2.57 | 4.7 | 3100–3800 | 72.5–75.5 |
| Carbon | 1.78 | 1.5–2.0 | 3500–6000 | 230–600 |
| Material Properties | Values |
|---|---|
| Stiffness properties (fiber) | E11 = E22 = 90 GPa, G12 = 35.70 GPa, v12 = v23 = 0.26 |
| Strength properties (fiber) | XT = XC = 2950 MPa |
| Stiffness properties (Matrix) | E11 = 3.20 GPa, G12 = 1.18 GPa, v12 = 0.35 |
| Strength properties (Matrix) | XT = 73 MPa, XC = 120 MPa, S = 52 MPa |
| Stiffness properties (Laminate) | E11 = 55.28 GPa, E22 = 8.95 GPa, G12 = 3.32 GPa, G23 = 2.70 GPa, v12 = 0.29, v23 = 0.40 |
| Strength properties (Laminate) | XT = XC = 1811.95 MPa, YT = 49.29 MPa, YC = 127.97 MPa, S = 87.42 MPa |
| Laminate Seq. | Uniaxial Loadings (Gpa) | Multiaxial Loading (Gpa) | (Gpa) | (Gpa) |
|---|---|---|---|---|
| QI | 24 | 24 | 24.1 | 24.1 |
| Hard | 36 | 21 | 34.2 | 22.9 |
| Soft | 23 | 21 | 22.9 | 34.2 |
| Laminate | Loading | 0° | 90° | 45° |
|---|---|---|---|---|
| Open hole (A) | Uniaxial | 63 | 10 | 27 |
| Al. filled hole | 80 | 10 | 10 | |
| St. filled hole (B) | 80 | 10 | 10 | |
| Rigid filled hole | 80 | 10 | 10 | |
| Open hole (C) | Multiaxial loading | 25 | 25 | 50 |
| Al. filled hole | 25 | 25 | 50 | |
| St. filled hole | 25 | 25 | 50 | |
| Rigid filled hole | 25 | 25 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajid, Z.; Karuppanan, S.; Eng, K.K.; Shah, S.Z.H. Analytical Method for the Optimization of the Open-Hole and Filled-Hole Laminates at the Preliminary Design Stage. Materials 2023, 16, 2213. https://doi.org/10.3390/ma16062213
Sajid Z, Karuppanan S, Eng KK, Shah SZH. Analytical Method for the Optimization of the Open-Hole and Filled-Hole Laminates at the Preliminary Design Stage. Materials. 2023; 16(6):2213. https://doi.org/10.3390/ma16062213
Chicago/Turabian StyleSajid, Zubair, Saravanan Karuppanan, Kee Kok Eng, and Syed Zulfiqar Hussain Shah. 2023. "Analytical Method for the Optimization of the Open-Hole and Filled-Hole Laminates at the Preliminary Design Stage" Materials 16, no. 6: 2213. https://doi.org/10.3390/ma16062213
APA StyleSajid, Z., Karuppanan, S., Eng, K. K., & Shah, S. Z. H. (2023). Analytical Method for the Optimization of the Open-Hole and Filled-Hole Laminates at the Preliminary Design Stage. Materials, 16(6), 2213. https://doi.org/10.3390/ma16062213





