Design of Two-Dimensional Transient Circular Thermal Cloaks with Imperfect Interfaces
Abstract
:1. Introduction
2. Results
2.1. Ideal Interface
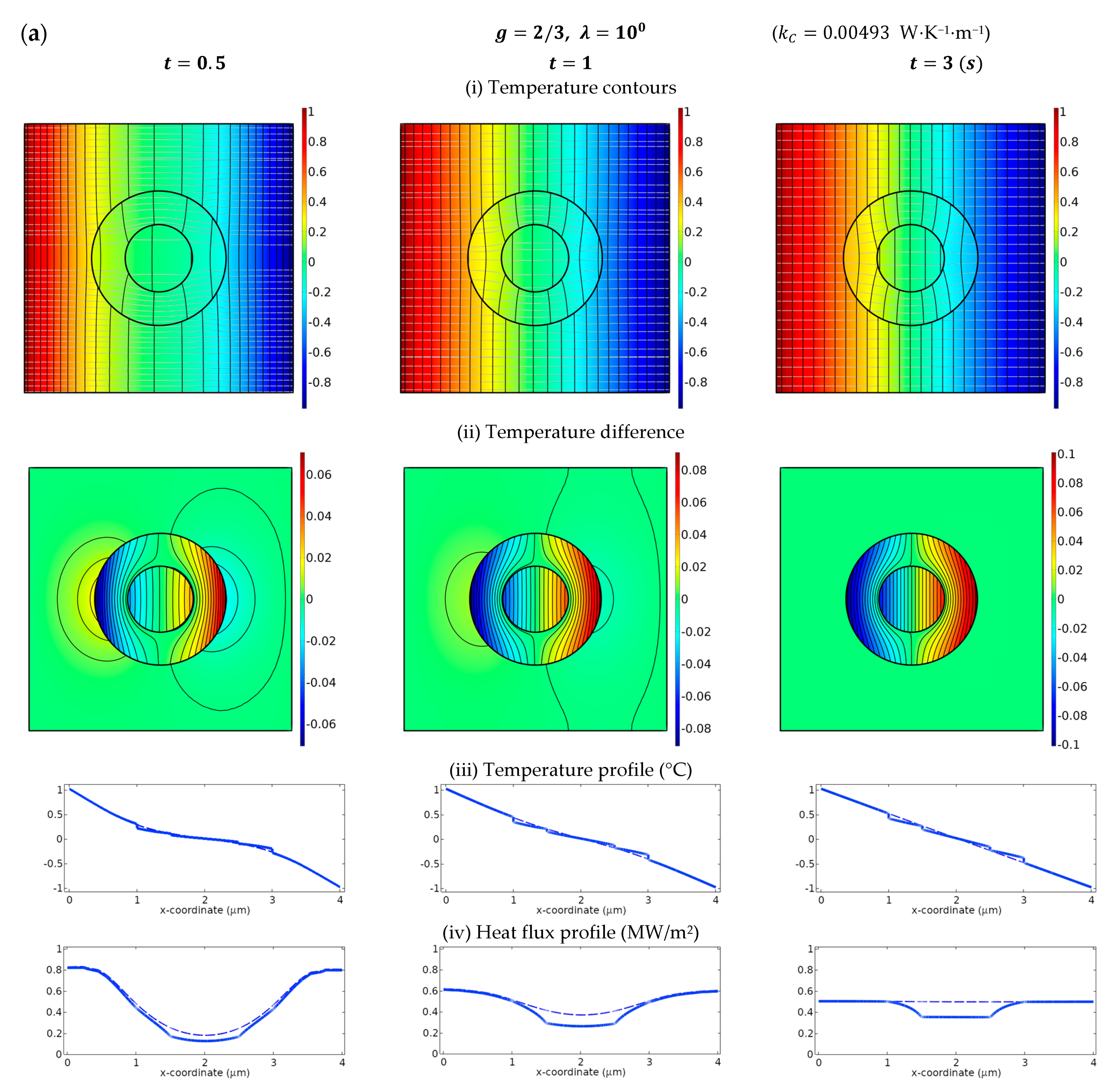
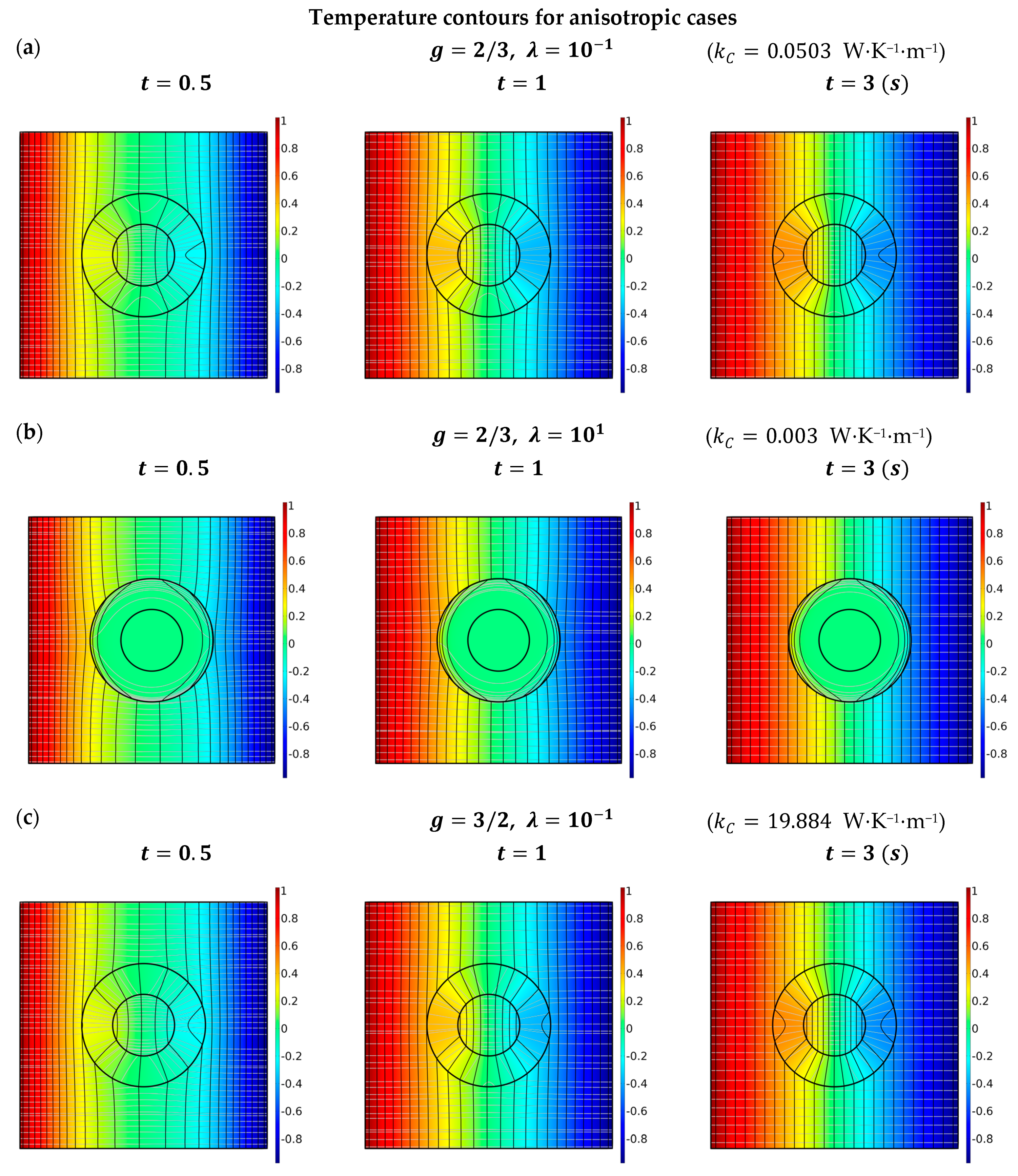
2.2. Low Conductivity-Type Interface
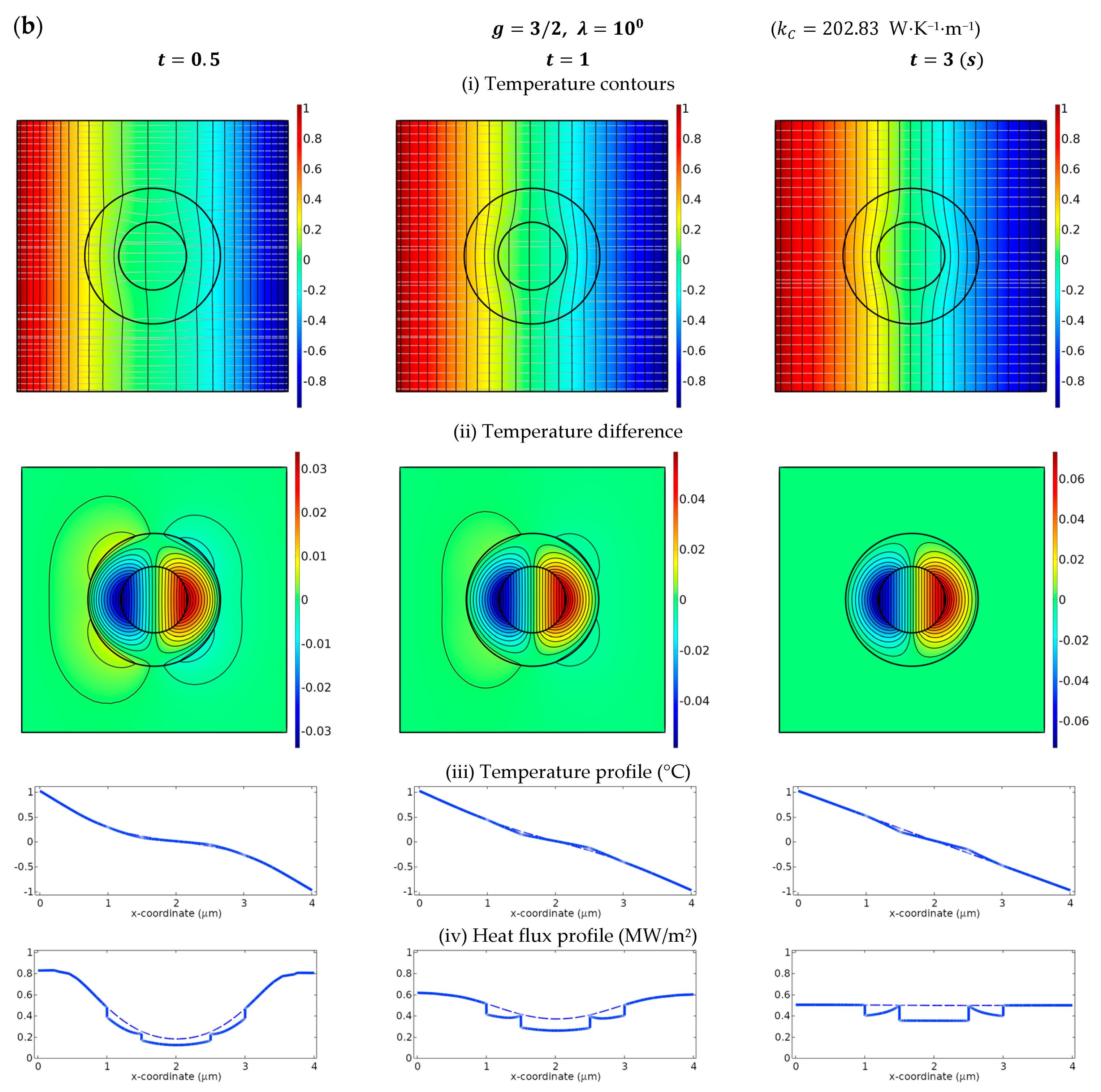
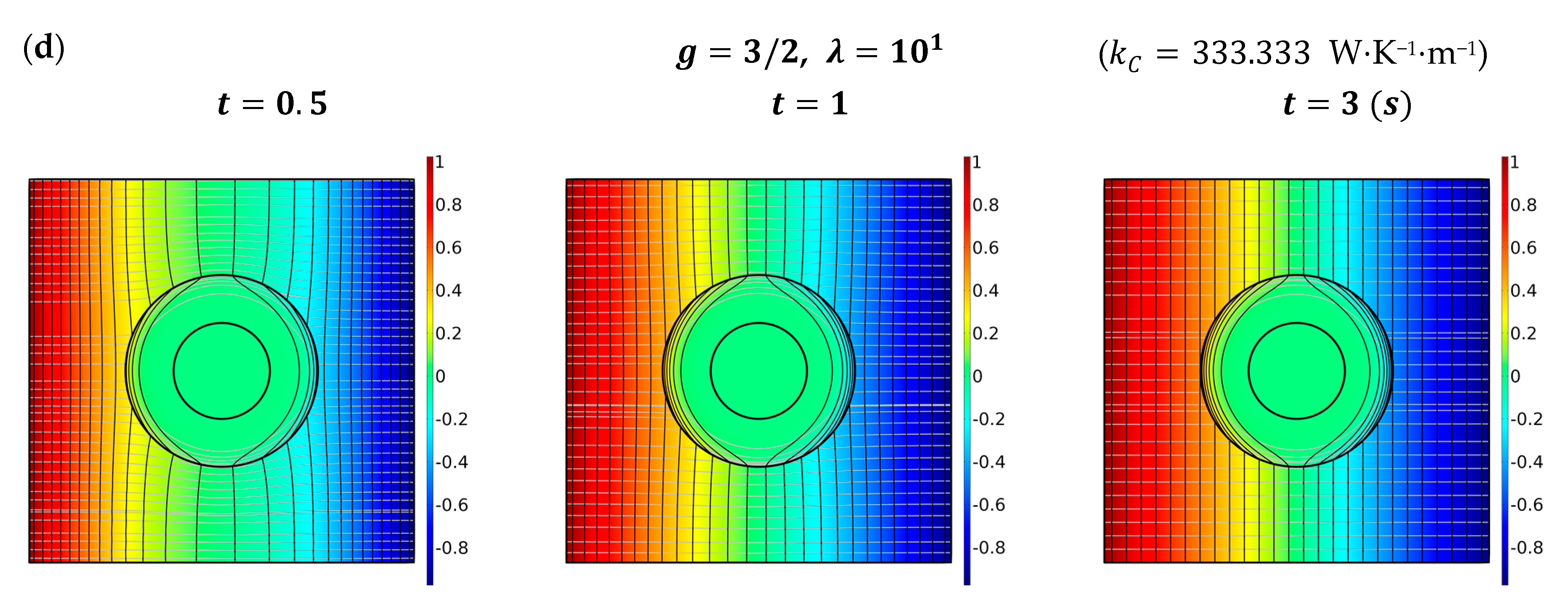
2.3. High Conductivity-Type Interface
3. Theoretical Analysis
4. Methods
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Scattering Width for a Two-Dimensional System
Appendix B. Derivation of Weak Thermal Invisibility Conditions
Appendix B.1. LC-Type Interfaces
Appendix B.2. HC-Type Interfaces
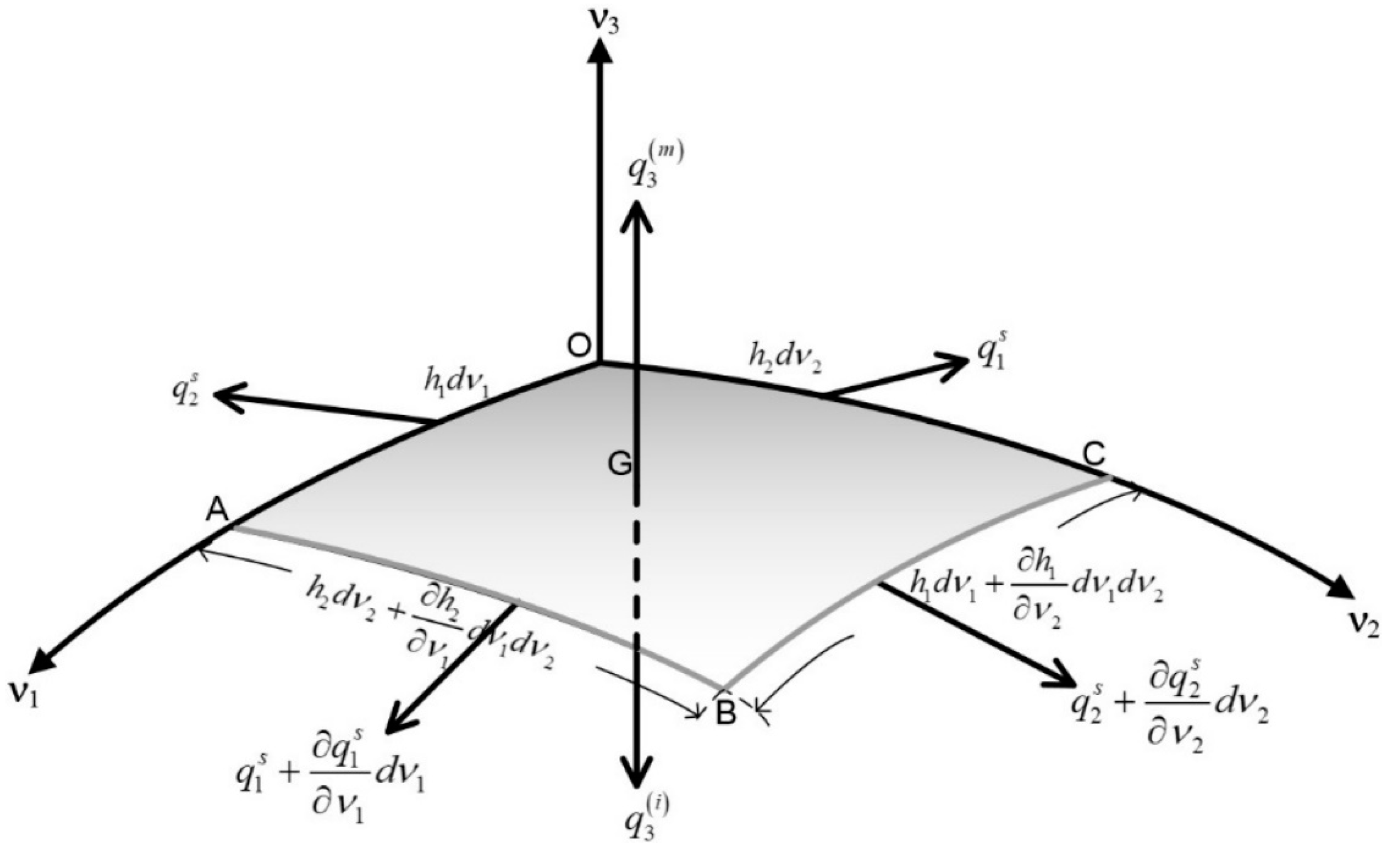
Appendix C. Derivation of the Interface Condition for Heat Flux with Surface Effect under Transient Regime
Appendix D. Numerical Simulations of a Homogeneous Background Medium

References
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, C.Z.; Gao, Y.; Huang, J.P. Shaped graded materials with an apparent negative thermal conductivity. Appl. Phys. Lett. 2008, 92, 251907. [Google Scholar] [CrossRef]
- Chen, T.; Weng, C.-N.; Chen, J.-S. Cloak for curvilinearly anisotropic media in conduction. Appl. Phys. Lett. 2008, 93, 114103. [Google Scholar] [CrossRef]
- Leonhardt, U. Applied physics: Cloaking of heat. Nature 2013, 498, 440–441. [Google Scholar] [CrossRef]
- Alù, A. Thermal cloaks get hot. Physics 2014, 7, 12. [Google Scholar] [CrossRef] [Green Version]
- Sklan, S.R.; Li, B. Thermal metamaterials: Functions and prospects. Natl. Sci. Rev. 2018, 5, 138–141. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, Y.; Li, T.; Wang, W.; Li, L.; Qiu, C.-W. Doublet Thermal Metadevice. Phys. Rev. Appl. 2019, 11, 044021. [Google Scholar] [CrossRef]
- Huang, J.-P. Theoretical Thermotics: Transformation Thermotics and Extended Theories for Thermal Metamaterials; Springer Nature: Singapore, 2020. [Google Scholar]
- Li, Y.; Li, W.; Han, T.; Zheng, X.; Li, J.; Li, B.; Fan, S.; Qiu, C.-W. Transforming heat transfer with thermal metamaterials and devices. Nat. Rev. Mater. 2021, 6, 488–507. [Google Scholar] [CrossRef]
- Hu, R.; Xi, W.; Liu, Y.; Tang, K.; Song, J.; Luo, X.; Wu, J.; Qiu, C.-W. Thermal camouflaging metamaterials. Mater. Today 2021, 45, 120–141. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, Z.; Liu, T.; Hu, R. Inverse design of thermal metamaterials with holey engineering strategy. J. Appl. Phys. 2022, 132, 145102. [Google Scholar] [CrossRef]
- Sha, W.; Hu, R.; Xiao, M.; Chu, S.; Zhu, Z.; Qiu, C.-W.; Gao, L. Topology-optimized thermal metamaterials traversing full-parameter anisotropic space. Npj Comput. Mater. 2022, 8, 179. [Google Scholar] [CrossRef]
- Guo, J.; Xu, G.; Tian, D.; Qu, Z.; Qiu, C.W. Passive Ultra-Conductive Thermal Metamaterials. Adv. Mater. 2022, 34, 2200329. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Li, B. Effect of interfacial thermal resistance in a thermal cloak. Phys. Rev. Appl. 2020, 13, 024071. [Google Scholar] [CrossRef] [Green Version]
- Kapitza, P.L. The study of heat transfer in helium II. J. Phys.-USSR 1941, 4, 181–210. [Google Scholar] [CrossRef]
- Giri, A.; Hopkins, P.E. A review of experimental and computational advances in thermal boundary conductance and nanoscale thermal transport across solid interfaces. Adv. Funct. Mater. 2019, 30, 1903857. [Google Scholar] [CrossRef]
- Narayana, S.; Sato, Y. Heat flux manipulation with engineered thermal materials. Phys. Rev. Lett. 2012, 108, 214303. [Google Scholar] [CrossRef] [Green Version]
- Han, T.; Zhao, J.; Yuan, T.; Lei, D.Y.; Li, B.; Qiu, C.-W. Theoretical realization of an ultra-efficient thermal-energy harvesting cell made of natural materials. Energy Environ. Sci. 2013, 6, 3537–3541. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Weng, C.-N.; Tsai, Y.-L. Materials with constant anisotropic conductivity as a thermal cloak or concentrator. J. Appl. Phys. 2015, 117, 054904. [Google Scholar] [CrossRef]
- Tsai, Y.-L.; Li, J.; Chen, T. Simultaneous focusing and rotation of a bifunctional thermal metamaterial with constant anisotropic conductivity. J. Appl. Phys. 2019, 126, 095103. [Google Scholar] [CrossRef]
- Guenneau, S.; Amra, C.; Veynante, D. Transformation thermodynamics: Cloaking and concentrating heat flux. Opt. Express 2012, 20, 8207–8218. [Google Scholar] [CrossRef]
- Han, T.; Bai, X.; Thong, J.T.L.; Li, B.; Qiu, C.W. Full control and manipulation of heat signatures: Cloaking, camouflage and thermal metamaterials. Adv. Mater. 2014, 26, 1731–1734. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Shi, X.; Gao, F.; Sun, H.; Zhang, B. Ultrathin three-dimensional thermal cloak. Phys. Rev. Lett. 2014, 112, 054301. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.Y.; Bagci, H.; Amra, C.; Guenneau, S.; Alù, A. Thermal invisibility based on scattering cancellation and mantle cloaking. Sci. Rep. 2015, 5, 9876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sklan, S.R.; Bai, X.; Li, B.; Zhang, X. Detecting thermal cloaks via transient effects. Sci. Rep. 2016, 6, 32915. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ji, Q.; Chen, X.; Fang, G.; Liang, J.; Yan, X.; Laude, V.; Kadic, M. Thermal cloaking of complex objects with the neutral inclusion and the coordinate transformation methods. AIP Adv. 2019, 9, 045029. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Lin, J.-H. Novel connections and physical implications of thermal metamaterials with imperfect interfaces. Sci. Rep. 2022, 12, 2734. [Google Scholar] [CrossRef]
- Chen, T.; Lin, J.-H. Exact thermal invisibility for spherical cloaks with imperfect interfaces. AIP Adv. 2022, 12, 075214. [Google Scholar] [CrossRef]
- Pham Huy, H.; Sanchez-Palencia, E. Phénomènes de transmission à travers des couches minces de conductivitéélevée. J. Math. Anal. Appl. 1974, 47, 284–309. [Google Scholar] [CrossRef] [Green Version]
- Benveniste, Y.; Miloh, T. Neutral inhomogeneities in conduction phenomena. J. Mech. Phys. Solids 1999, 47, 1873–1892. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 2005, 72, 016623. [Google Scholar] [CrossRef] [Green Version]
- Norris, A.N.; Parnell, W.J. Static elastic cloaking, low-frequency elastic wave transparency and neutral inclusions. Proc. R. Soc. Lond. A 2020, 476, 20190725. [Google Scholar] [CrossRef]
- Zhang, X.; He, X.; Wu, L. Experimental investigation of thermal architected metamaterials for regulating transient heat transfer. Int. J. Heat Mass Transf. 2022, 193, 122960. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Knott, E.F.; Shaeffer, J.F.; Tuley, M.T. Radar Cross Section; Artech House: Boston, MA, USA, 1992. [Google Scholar]
- Christensen, R.M.; Lo, K.H. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Han, T.; Yuan, T.; Li, B.; Qiu, C.W. Homogeneous thermal cloak with constant conductivity and tunable heat localization. Sci. Rep. 2013, 3, 1593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hashin, Z. Thin interphase/imperfect interface in conduction. J. Appl. Phys. 2001, 89, 2261–2267. [Google Scholar] [CrossRef]
- Benveniste, Y.; Miloh, T. The effective conductivity of composites with imperfect thermal contact at constituent interfaces. Int. J. Eng. Sci. 1986, 24, 1537–1552. [Google Scholar] [CrossRef]
- Chen, T. Thermal conduction of a circular inclusion with variable interface parameter. Int. J. Solids Struct. 2001, 38, 3081–3097. [Google Scholar] [CrossRef]
- Sanchez-Palencia, E. Comportement limite d’un probleme de transmissiona travers une plaque faiblement conductrice. CR Acad. Sci. Paris Ser. A 1970, 270, 1026–1028. [Google Scholar]
- Cheng, H.; Torquato, S. Effective conductivity of dispersions of spheres with a superconducting interface. Proc. R. Soc. Lond. A 1997, 453, 1331–1344. [Google Scholar] [CrossRef]
- Milton, G.W. The Theory of Composites; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Hashin, Z.; Rosen, B.W. The elastic moduli of fiber-reinforced materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Sten, J.C.-E. DC fields and analytical image solutions for a radially anisotropic spherical conductor. IEEE Trans. Diel. Elec. Insul. 1995, 2, 360–367. [Google Scholar] [CrossRef]
- Hahn, D.W.; Özışık, M.N. Heat Conduction, 3rd ed.; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Chen, T.Y.; Chiu, M.S.; Weng, C.N. Derivation of the generalized Young-Laplace equation of curved interfaces in nanoscaled solids. J. Appl. Phys. 2006, 100, 074308. [Google Scholar] [CrossRef] [Green Version]

| 2D Steady State (Strong Invisibility Condition) | 2D Transient State (Weak Invisibility Conditions) | |
|---|---|---|
| Thermal invisibility conditions for perfect interfaces | . [37] | , for . for |
| Thermal invisibility conditions for LC-type interfaces | . [27] | , for . for |
| Thermal invisibility conditions for HC-type interfaces | . [27] | , for . for , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.-H.; Chen, T. Design of Two-Dimensional Transient Circular Thermal Cloaks with Imperfect Interfaces. Materials 2023, 16, 2297. https://doi.org/10.3390/ma16062297
Lin J-H, Chen T. Design of Two-Dimensional Transient Circular Thermal Cloaks with Imperfect Interfaces. Materials. 2023; 16(6):2297. https://doi.org/10.3390/ma16062297
Chicago/Turabian StyleLin, Jun-Hong, and Tungyang Chen. 2023. "Design of Two-Dimensional Transient Circular Thermal Cloaks with Imperfect Interfaces" Materials 16, no. 6: 2297. https://doi.org/10.3390/ma16062297




