The Calibration Methods of Geometric Parameters of Crystal for Mid-Infrared Acousto-Optic Tunable Filter-Based Imaging Systems Design
Abstract
1. Introduction
2. Background
3. Simulation and Method
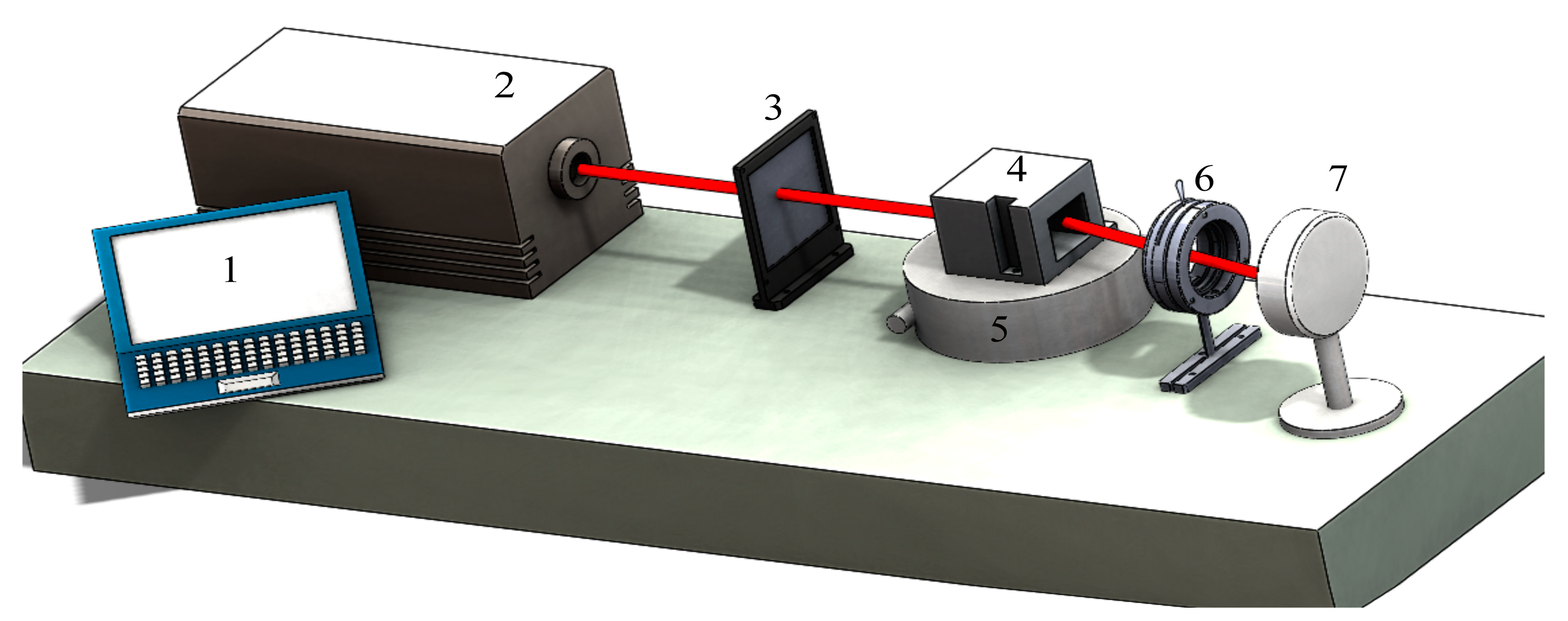
- Ensure that the incident laser is perpendicular to the front surface of the AOTF;
- Adjust the rotation angle of the AOTF using the precision turntable;
- The spectral response at different angles can be obtained by adjusting the output wavelength of the laser (the minimum-central wavelength method);
- The frequency response at different angles can be obtained by adjusting the frequency of the transducer (the minimum-frequency method).
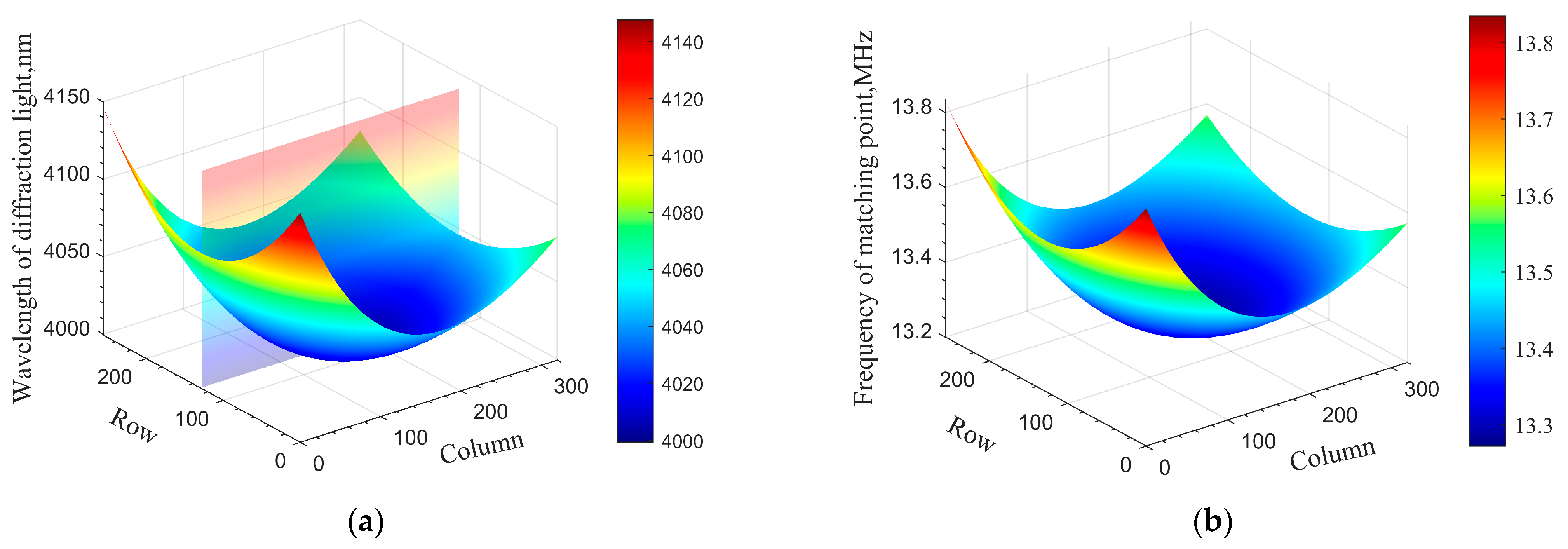
4. Experiment and Results
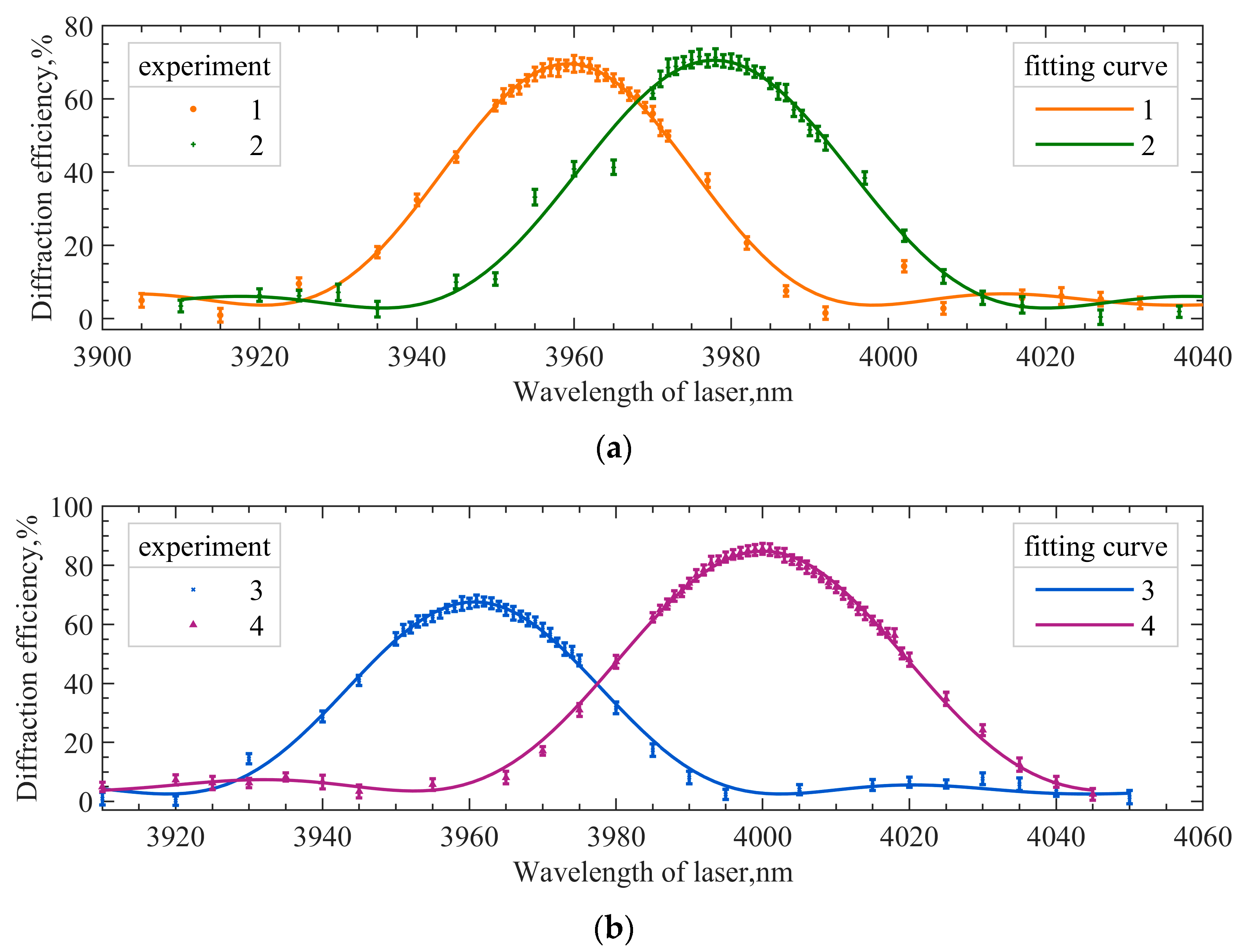
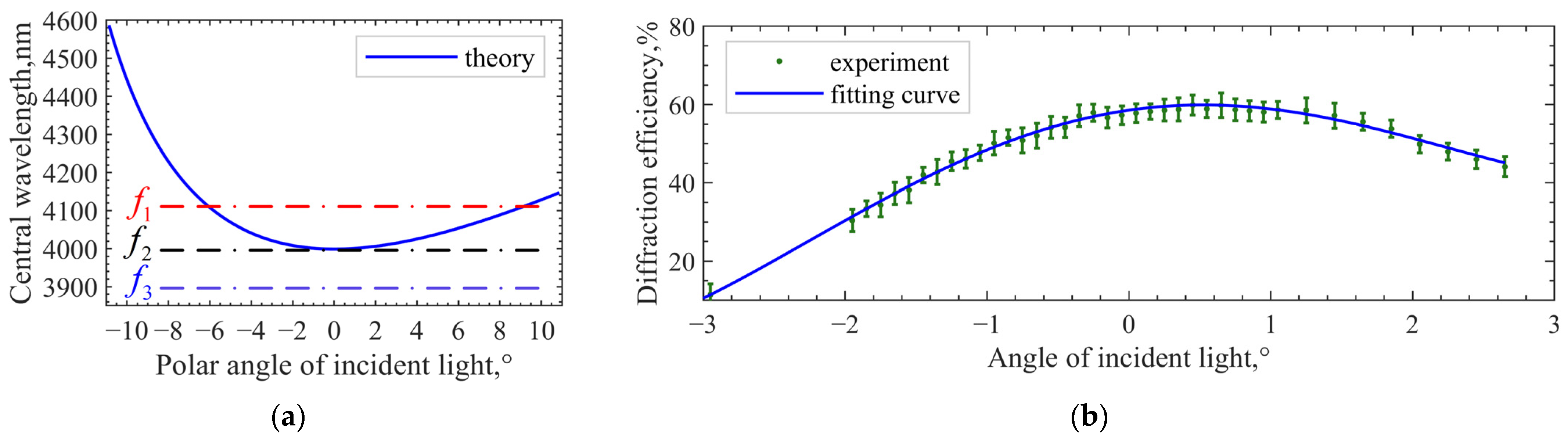
4.1. The Minimum-Central Wavelength Method
4.2. The Minimum-Frequency Method
5. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, H.; Wang, Z.; Jia, G.; Zhang, Y.; Xu, Z. Chromatic aberrations correction for imaging spectrometer based on acousto-optic tunable filter with two transducers. Opt. Express. 2017, 25, 23809–23825. [Google Scholar] [CrossRef] [PubMed]
- Glenar, D.A.; Hillman, J.J.; Saif, B.; Bergstralh, J. Acousto-optic imaging spectropolarimetry for remote sensing. Appl. Opt. 1994, 33, 7412–7424. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, H.; Huang, J.; Gao, Q. The visible to the near infrared narrow band acousto-optic tunable filter and the hyperspectral microscopic imaging on biomedicine study. J. Opt. 2014, 16, 125303. [Google Scholar] [CrossRef]
- Wachman, E.S.; Niu, W.H.; Farkas, D.L. Imaging acousto-optic tunable filter with 0.35-micrometer spatial resolution. Appl. Opt. 1996, 35, 5220–5226. [Google Scholar] [CrossRef]
- Machikhin, A.; Batshev, V.; Pozhar, V.; Naumov, A.; Gorevoy, A. Acousto-optic tunable spectral filtration of stereoscopic images. Opt. Lett. 2018, 43, 1087–1090. [Google Scholar] [CrossRef] [PubMed]
- Kastelik, J.C.; Champagne, J.; Dupont, S.; Yushkov, K.B. Wavelength characterization of an acousto-optic notch filter for unpolarized near-infrared light. Appl. Opt. 2018, 57, C36–C41. [Google Scholar] [CrossRef] [PubMed]
- Gupta, N.; Suhre, D.R. Notch filtering using a multiple passband AOTF in the SWIR region. Appl. Opt. 2016, 55, 7855–7860. [Google Scholar] [CrossRef]
- Yushkov, K.B.; Molchanov, V.Y.; Belousov, P.V.; Abrosimov, A.Y. Contrast enhancement in microscopy of human thyroid tumors by means of acousto-optic adaptive spatial filtering. J. Biomed. Opt. 2016, 21, 016003. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, H.; Zhang, Z.; Yuan, J.; Shi, L.; Sheng, Z.; Zhang, X. Narrowband double-filtering hyperspectral imaging based on a single AOTF. Opt. Lett. 2018, 43, 2126–2129. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, W.; Tong, H.; Liu, Y.; Wang, X.; Zhang, C.; Wang, Y.; Wang, H.; Sheng, Z.; Tan, Z.; et al. High-Resolution Hyperspectral Microscopic Imaging With Single Acousto-Optic Tunable Filter Based on Double Filtering. IEEE Access. 2020, 8, 11570–11576. [Google Scholar] [CrossRef]
- Dyakonov, E.; Porokhovnichenko, D.; Ryu, J.; Balakshy, V. Implementation of the wide-angle acousto-optical interaction geometry in a mercury bromide single crystal. Appl. Opt. 2021, 60, 2348–2353. [Google Scholar] [CrossRef]
- Hurtado-Aviles, E.A.; Torres, J.A.; Trejo-Valdez, M.; Urriolagoitia-Sosa, G.; Villalpando, I.; Torres-Torres, C. Acousto-plasmonic sensing assisted by nonlinear optical interactions in bimetallic Au-Pt nanoparticles. Micromachines 2017, 8, 321. [Google Scholar] [CrossRef]
- Chang, I.C. Noncollinear acousto-optic filter with large angular aperture. Appl. Phys. Lett. 1974, 25, 370–372. [Google Scholar] [CrossRef]
- Chang, I.C. Acousto-optic devices and applications. IEEE Trans. Ultrason. 1976, 23, 2–21. [Google Scholar] [CrossRef]
- Yushkov, K.B.; Chizhikov, A.I.; Makarov, O.Y.; Molchanov, V.Y. Optimization of noncollinear AOTF design for laser beam shaping. Appl. Opt. 2020, 59, 8575–8581. [Google Scholar] [CrossRef] [PubMed]
- Obydennov, D.V.; Yushkov, K.B.; Molchanov, V.Y. Ring-shaped optical trap based on an acousto-optic tunable spatial filter. Opt. Lett. 2021, 46, 4494–4497. [Google Scholar] [CrossRef] [PubMed]
- Batshev, V.; Machikhin, A.; Gorevoy, A.; Martynov, G.; Khokhlov, D.; Boritko, S.; Pozhar, V.; Lomonov, V. Spectral Imaging Experiments with Various Optical Schemes Based on the Same AOTF. Materials 2021, 14, 2984. [Google Scholar] [CrossRef] [PubMed]
- Batshev, V.I.; Gorevoy, A.V.; Pozhar, V.E.; Machikhin, A.S. Aberration analysis of AOTF-based stereoscopic spectral imager using optical design software. J. Phys. Conf. Ser. 2021, 2127, 012035. [Google Scholar] [CrossRef]
- Gorevoy, A.; Machikhin, A.; Martynov, G.; Pozhar, V. Computational technique for field-of-view expansion in AOTF-based imagers. Opt. Lett. 2022, 47, 585–588. [Google Scholar] [CrossRef]
- Bürmen, M.; Pernuš, F.; Likar, B. Spectral characterization of near-infrared acousto-optic tunable filter (AOTF) hyperspectral imaging systems using standard calibration materials. Appl. Spectrosc. 2011, 65, 393–401. [Google Scholar] [CrossRef]
- Li, C.; Zhao, H.; Zhang, Y.; Zhou, P. Crystal geometry measurement of an acousto-optic tunable filter using the tested tuning curves. In Proceedings of the 2012 8th IEEE International Symposium on Instrumentation and Control Technology (ISICT) Proceedings, London, UK, 11–13 July 2012. [Google Scholar]
- Vila-Francés, J.; Calpe-Maravilla, J.; Gómez-Chova, L.; Amorós-López, J. Improving the performance of acousto-optic tunable filters in imaging applications. J. Electron. Imaging 2010, 19, 043022. [Google Scholar] [CrossRef]
- Machikhin, A.S.; Pozhar, V.E. Image aberrations in an acousto-optical tunable filter. Opt. Quant. Electron. 2010, 55, 1490–1496. [Google Scholar] [CrossRef]
- Machikhin, A.; Batshev, V.; Pozhar, V. Aberration analysis of AOTF-based spectral imaging systems. J. Opt. Soc. Am. A 2017, 34, 1109–1113. [Google Scholar] [CrossRef]
- Martynov, G.N.; Gorevoy, A.V.; Machikhin, A.S.; Pozhar, V.E.; Lehmann, P.; Osten, W.; Albertazzi Gonçalves, A. On inherent spatio-spectral image distortion in AOTF-based imagers. In Proceedings of the Optical Measurement Systems for Industrial Inspection XII, SPIE, Online, 21–26 June 2021; Volume 11782, pp. 268–277. [Google Scholar]
- Liu, H.; Hou, X.; Hu, B.; Yu, T.; Zhang, Z.; Liu, X.; Liu, J.; Wang, X.; Zhong, J.; Tan, Z. Image blurring and spectral drift in imaging spectrometer system with an acousto-optic tunable filter and its application in UAV remote sensing. Int. J. Remote Sens. 2022, 43, 6957–6978. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, S.; Jiang, H.; Zhang, Y.; Xu, Z. Calibration of AOTF-based 3D measurement system using multiplane model based on phase fringe and BP neural network. Opt. Express 2017, 25, 10413–10433. [Google Scholar] [CrossRef]
- Katrašnik, J.; Bürmen, M.; Pernuš, F. Spectral characterization and calibration of AOTF spectrometers and hyper-spectral imaging systems. Chemometr. Intell. Lab. 2010, 101, 23–29. [Google Scholar] [CrossRef]
- Špiclin, Ž.; Katrašnik, J.; Bürmen, M.; Pernuš, F.; Likar, B. Geometrical calibration of an AOTF hyper-spectral imaging system. In Proceedings of the Design and Quality for Biomedical Technologies III, San Francisco, CA, USA, 23 February 2010. [Google Scholar]
- Katrašnik, J.; Pernuš, F.; Likar, B. Radiometric calibration and noise estimation of acousto-optic tunable filter hyperspectral imaging systems. Appl. Opt. 2013, 52, 3526–3537. [Google Scholar] [CrossRef]
- Healey, G.E.; Kondepudy, R. Radiometric CCD camera calibration and noise estimation. IEEE. Trans. Pattern. Anal. 1994, 16, 267–276. [Google Scholar] [CrossRef]
- Tian, H.; Fowler, B.; Gamal, A.E. Analysis of temporal noise in CMOS photodiode active pixel sensor. IEEE J. Solid-St. Circ. 2001, 36, 92–101. [Google Scholar] [CrossRef]
- Trutna, W.R.; Dolfi, D.W.; Flory, C.A. Anomalous sidelobes and birefringence apodization in acousto-optic tunable filters. Opt. Lett. 1993, 18, 28–30. [Google Scholar] [CrossRef]
- Yano, T.; Watanabe, A. Acoustooptic TeO 2 tunable filter using far-off-axis anisotropic Bragg diffraction. Appl. Opt. 1976, 15, 2250–2258. [Google Scholar] [CrossRef] [PubMed]
- Yushkov, K.B.; Dupont, S.; Kastelik, J.C.; Voloshinov, V.B. Polarization-independent imaging with an acousto-optic tandem system. Opt. Lett. 2010, 35, 1416–1418. [Google Scholar] [CrossRef] [PubMed]
- Gorevoy, A.V.; Machikhin, A.S.; Martynov, G.N.; Pozhar, V.E. Spatiospectral transformation of noncollimated light beams diffracted by ultrasound in birefringent crystals. Photonics Res. 2021, 9, 687–693. [Google Scholar] [CrossRef]
- Berny, J.G.; Bourgoin, J.P.; Ayrault, B. Dispersion des indices de refraction du Molybdate de Plomb (PbMoO4) et de la paratellurite (TeO2). Opt. Commun. 1972, 6, 383–387. [Google Scholar] [CrossRef]
- Georgiev, G.; Glenar, D.A.; Hillman, J.J. Spectral characterization of acousto-optic filters used in imaging spectroscopy. Appl. Opt. 2002, 41, 209–217. [Google Scholar] [CrossRef]
- Yu, K.; Zhao, H. Analysis on the Influence of Incident Light Angle on the Spatial Aberrations of Acousto-Optical Tunable Filter Imaging. Materials 2022, 15, 4464. [Google Scholar] [CrossRef] [PubMed]








| AOTF-Related Work | Recent Research |
|---|---|
| Calibration | Bürmen, Li, Vila-Francés, spectral calibration [21,22]; Pozhar, Machikhin [23,24,25] and Liu [26], geometric calibration; Katrašnik, Healey, Tian, radiometric calibration [30,31,32]; Trutna, Yano, thermal calibration [33,34]; Shi [27], 3D calibration; Katrašnik [28,29], automatic geometrical calibration methods. |
| Optical design and optimization | Batshev and Machikhin [17], typical optical schemes; Batshev and Gorevoy [18], Zemax integration. |
| Operating mode | Zhang [13], noncollinear AOTF operating mode, the principle of parallel tangent, tuning curve. |
| Ray tracing | Yushkov [15], tuning frequency at oblique incidence; Pozhar and Machikhin [23], 2D to 3D ray tracing. |
| Method | Calibration Time/Min | Calibration Results/° | Frequency Error |
|---|---|---|---|
| A: The minimum-central wavelength method | ~270 | ≤1% | |
| B: The minimum-frequency method | ~30 | ≤1.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Guo, Q.; Zhao, H.; Cheng, C. The Calibration Methods of Geometric Parameters of Crystal for Mid-Infrared Acousto-Optic Tunable Filter-Based Imaging Systems Design. Materials 2023, 16, 2341. https://doi.org/10.3390/ma16062341
Yu K, Guo Q, Zhao H, Cheng C. The Calibration Methods of Geometric Parameters of Crystal for Mid-Infrared Acousto-Optic Tunable Filter-Based Imaging Systems Design. Materials. 2023; 16(6):2341. https://doi.org/10.3390/ma16062341
Chicago/Turabian StyleYu, Kai, Qi Guo, Huijie Zhao, and Chi Cheng. 2023. "The Calibration Methods of Geometric Parameters of Crystal for Mid-Infrared Acousto-Optic Tunable Filter-Based Imaging Systems Design" Materials 16, no. 6: 2341. https://doi.org/10.3390/ma16062341
APA StyleYu, K., Guo, Q., Zhao, H., & Cheng, C. (2023). The Calibration Methods of Geometric Parameters of Crystal for Mid-Infrared Acousto-Optic Tunable Filter-Based Imaging Systems Design. Materials, 16(6), 2341. https://doi.org/10.3390/ma16062341






