A Size-Dependent Finite Element Method for the 3D Free Vibration Analysis of Functionally Graded Graphene Platelets-Reinforced Composite Cylindrical Microshells Based on the Consistent Couple Stress Theory
Abstract
:1. Introduction
2. Effective Material Properties
3. The 3D CCST for an Elastic Solid
4. The CCST-Based Semi-Analytical Finite Element Formulation
4.1. Kinematics Assumptions
4.2. Hamilton’s Principle
4.3. Hermitian C2 Finite Element Equations
5. Numerical Examples
5.1. Homogeneous Isotropic SWCNTs
5.2. FG Cylindrical Macroshells
5.3. Laminated GPLRC Cylindrical Microshells
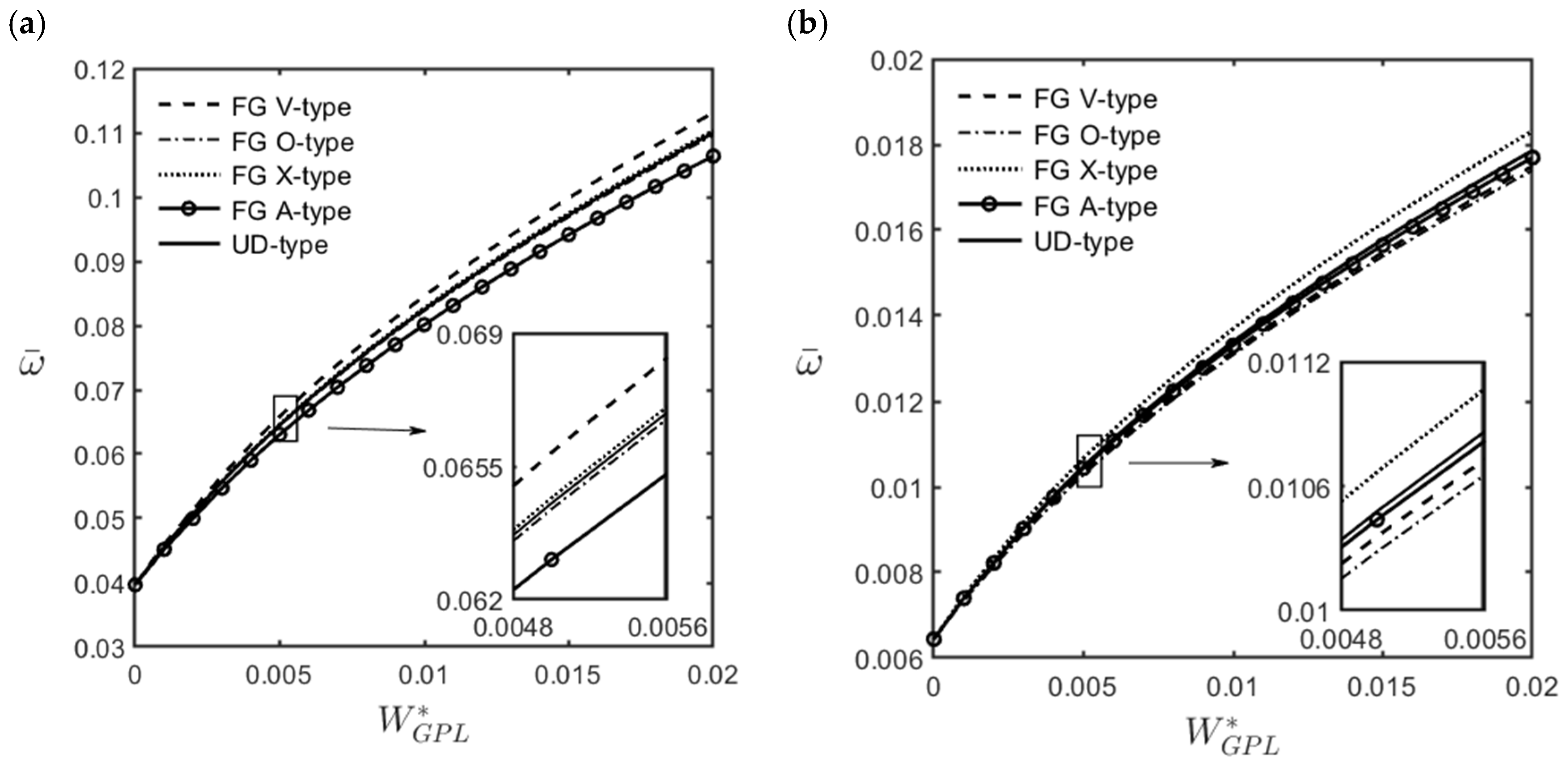
5.4. FG-GPLRC Cylindrical Microshells
6. Concluding Remarks
- The CCST-based Hermitian C2 FEM was validated to be accurate and to converge rapidly by comparing the solutions it produced with the 3D exact and the quasi-3D solutions for FG cylindrical macroshell reported in the literature by assigning the length scale parameter to a value of zero.
- In numerical examples, the results showed that:
- (a)
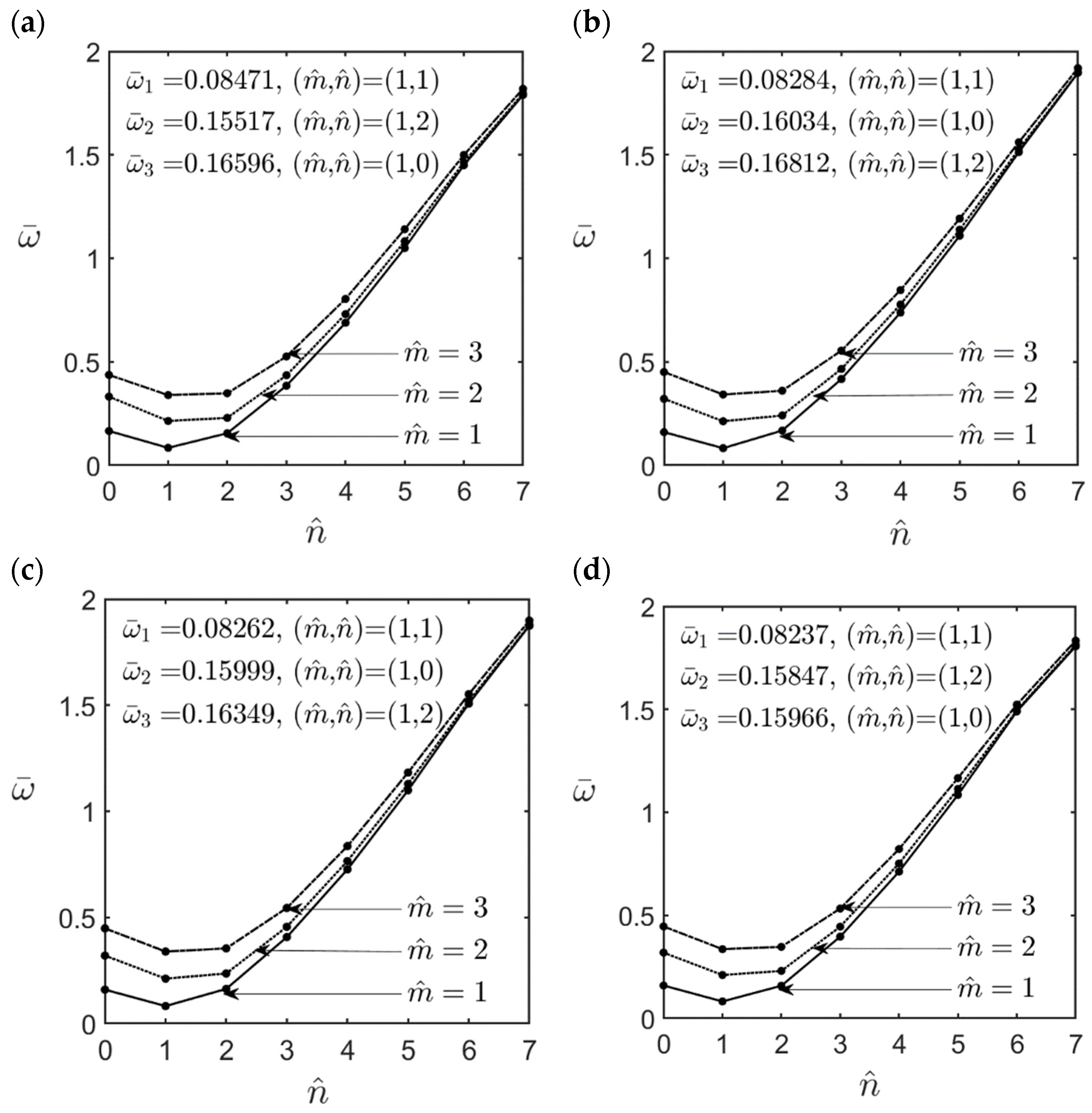
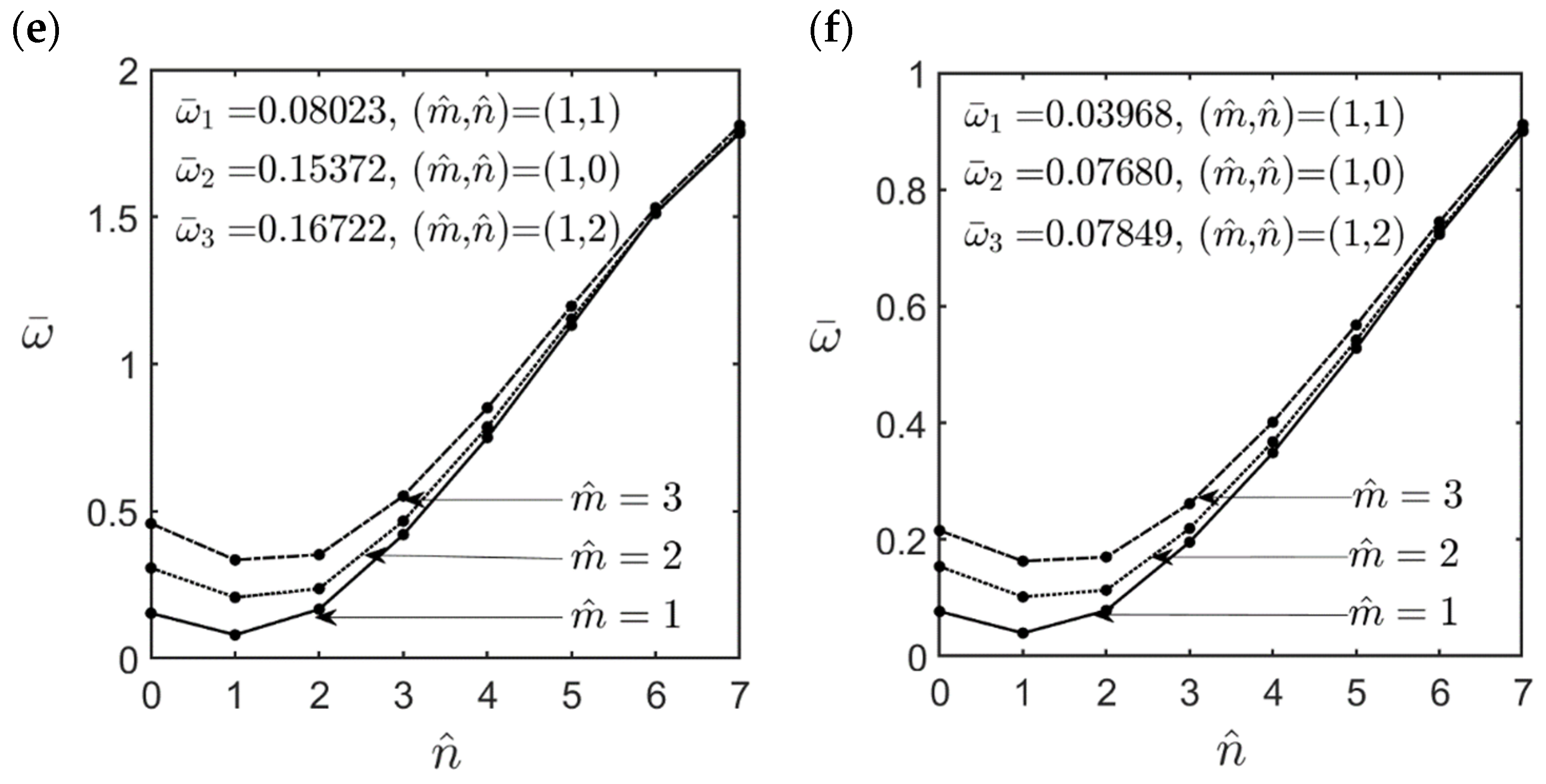
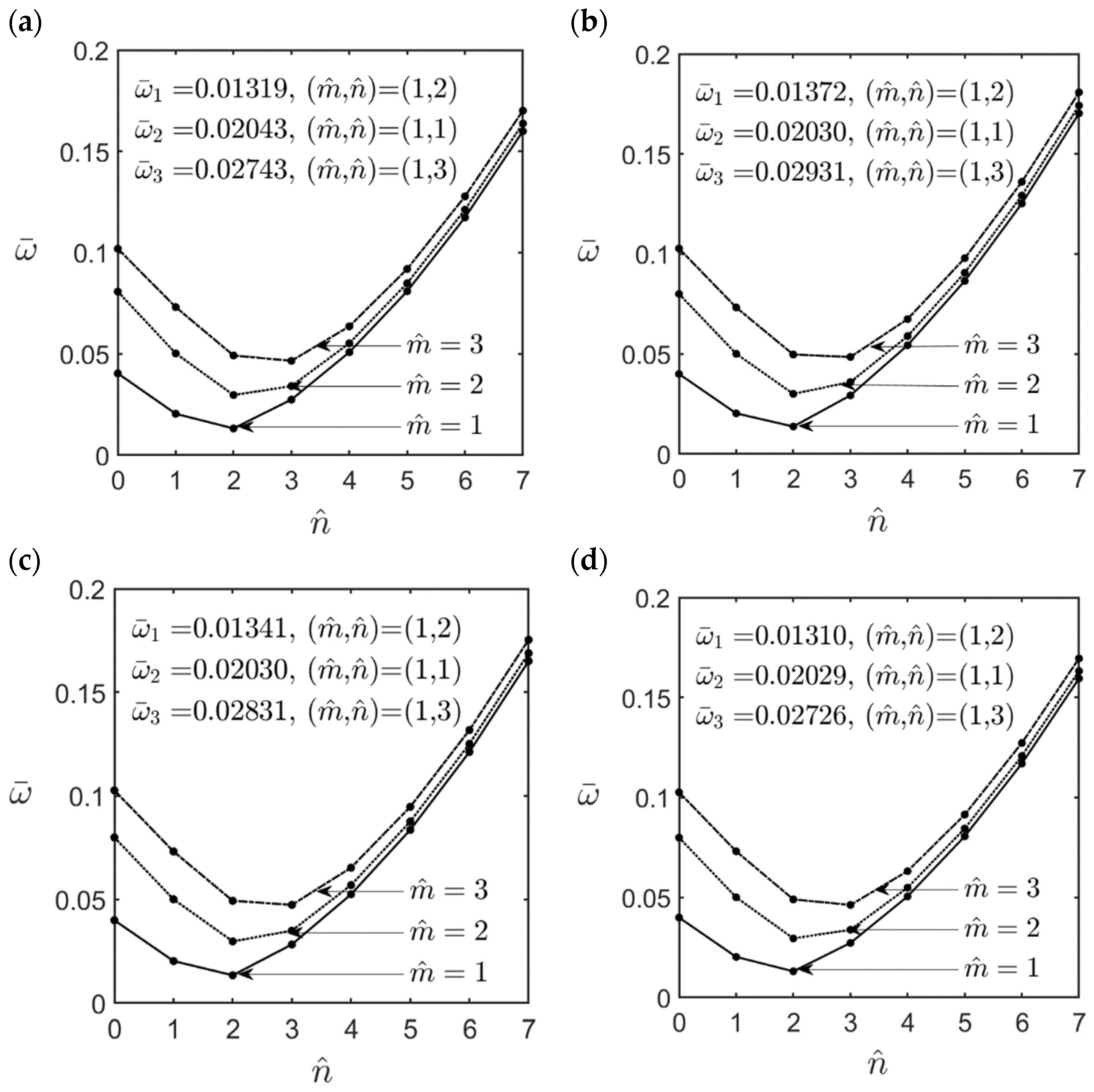
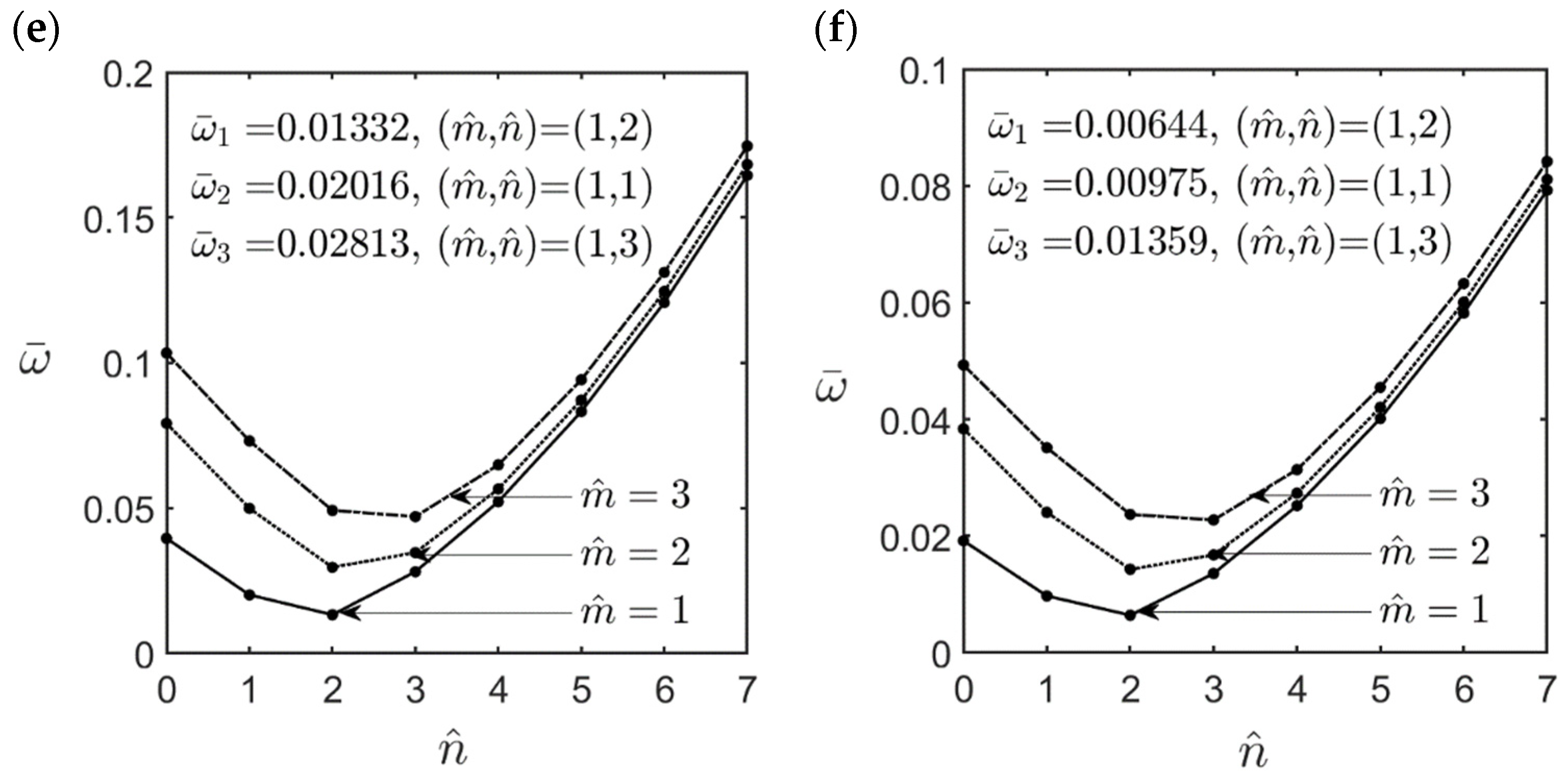
- An increase in the material length scale parameter caused the FG cylindrical microshell to become stiffer, increasing the lowest natural frequency of the microshell. The effect of the material length scale parameter on the lowest natural frequency for the high-frequency vibration modes was more significant than that for the fundamental vibration mode.
- (b)
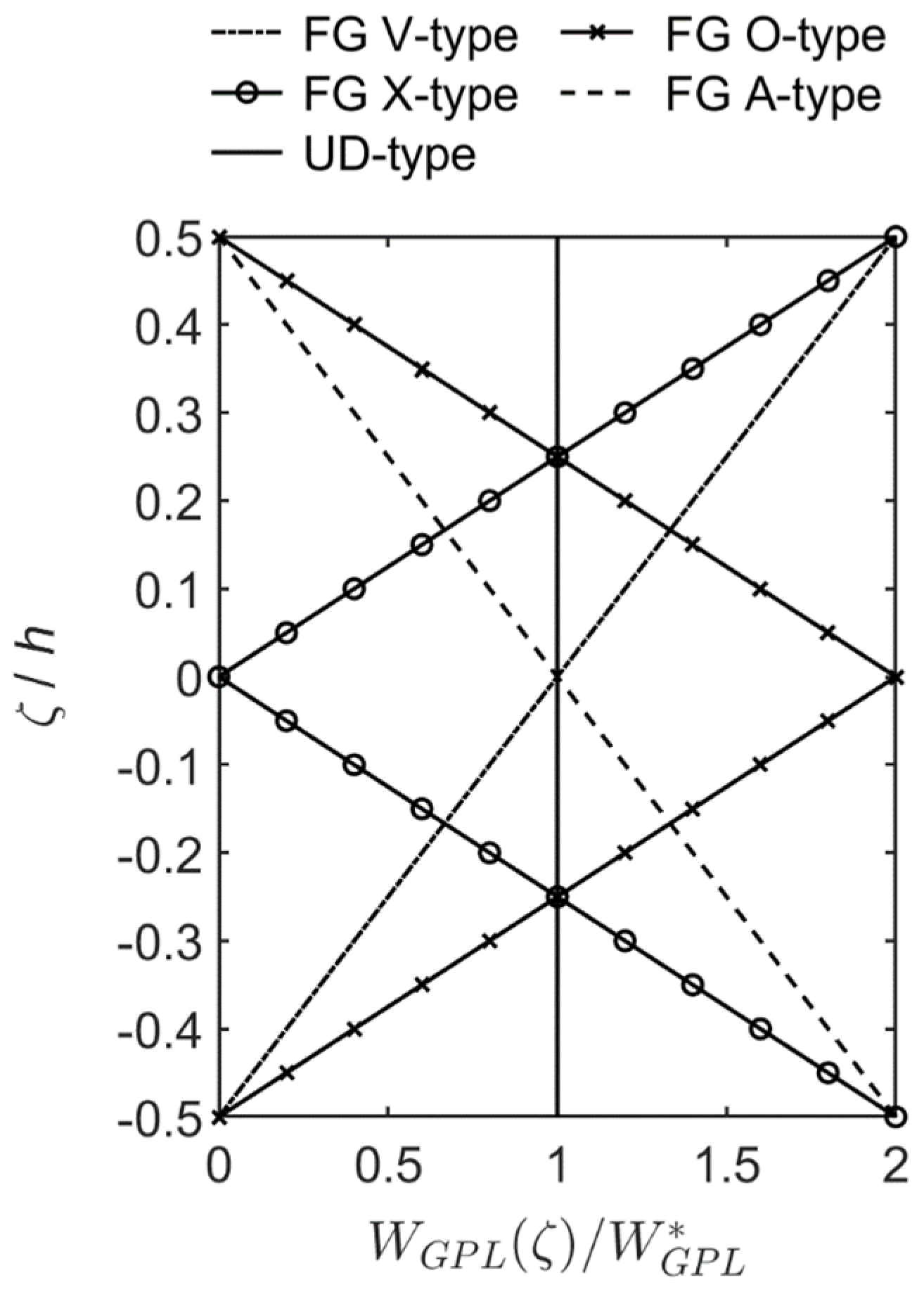
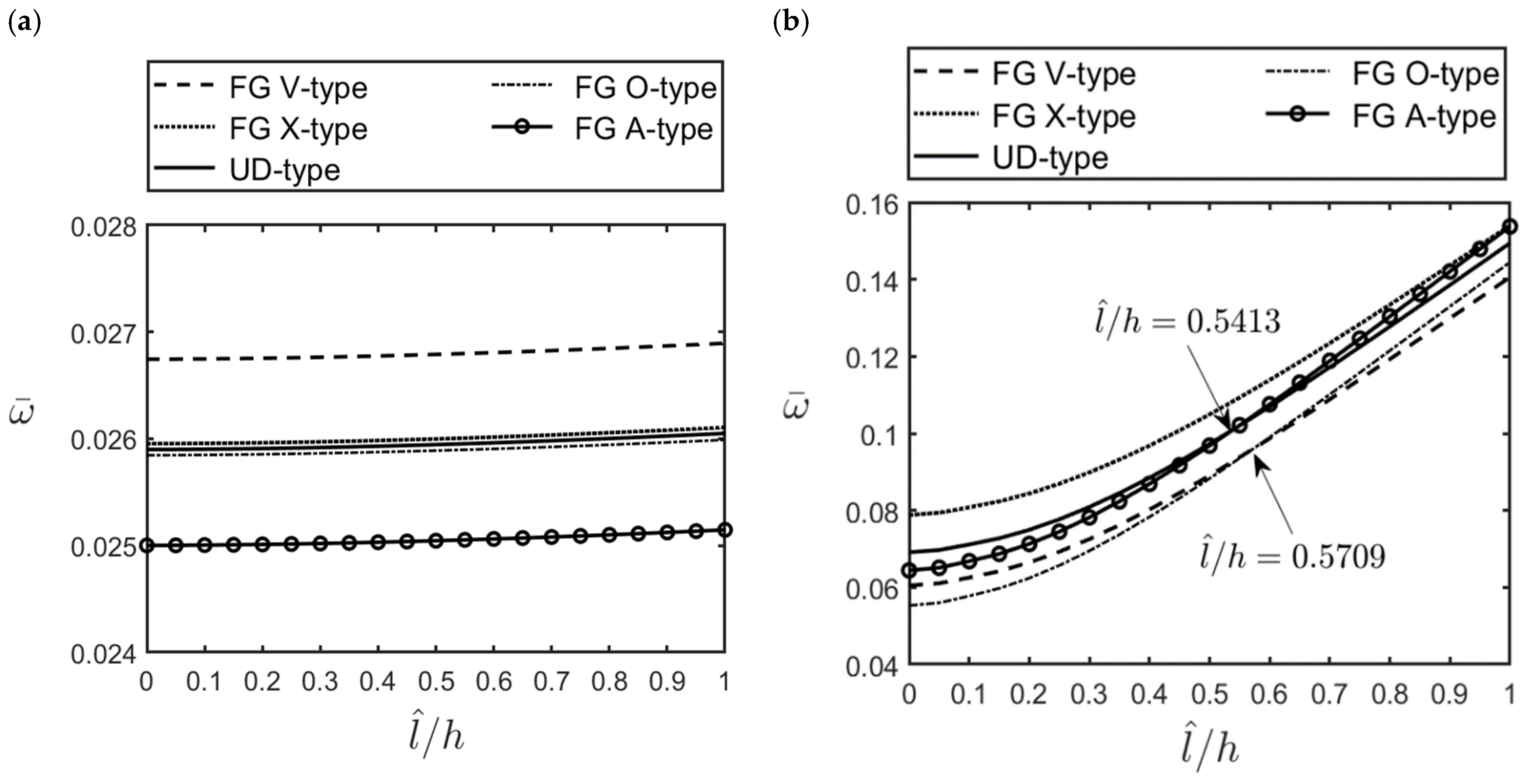
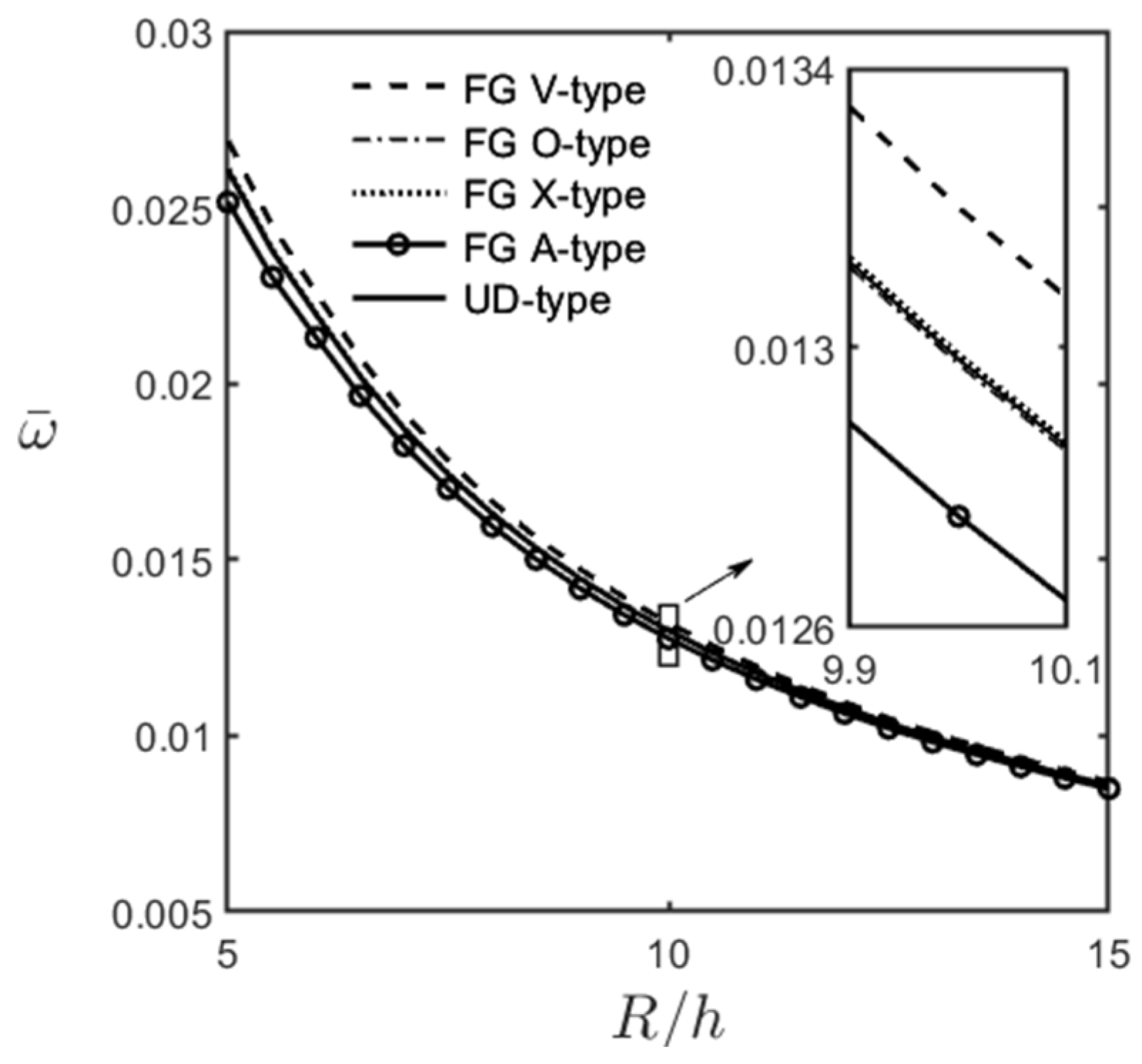
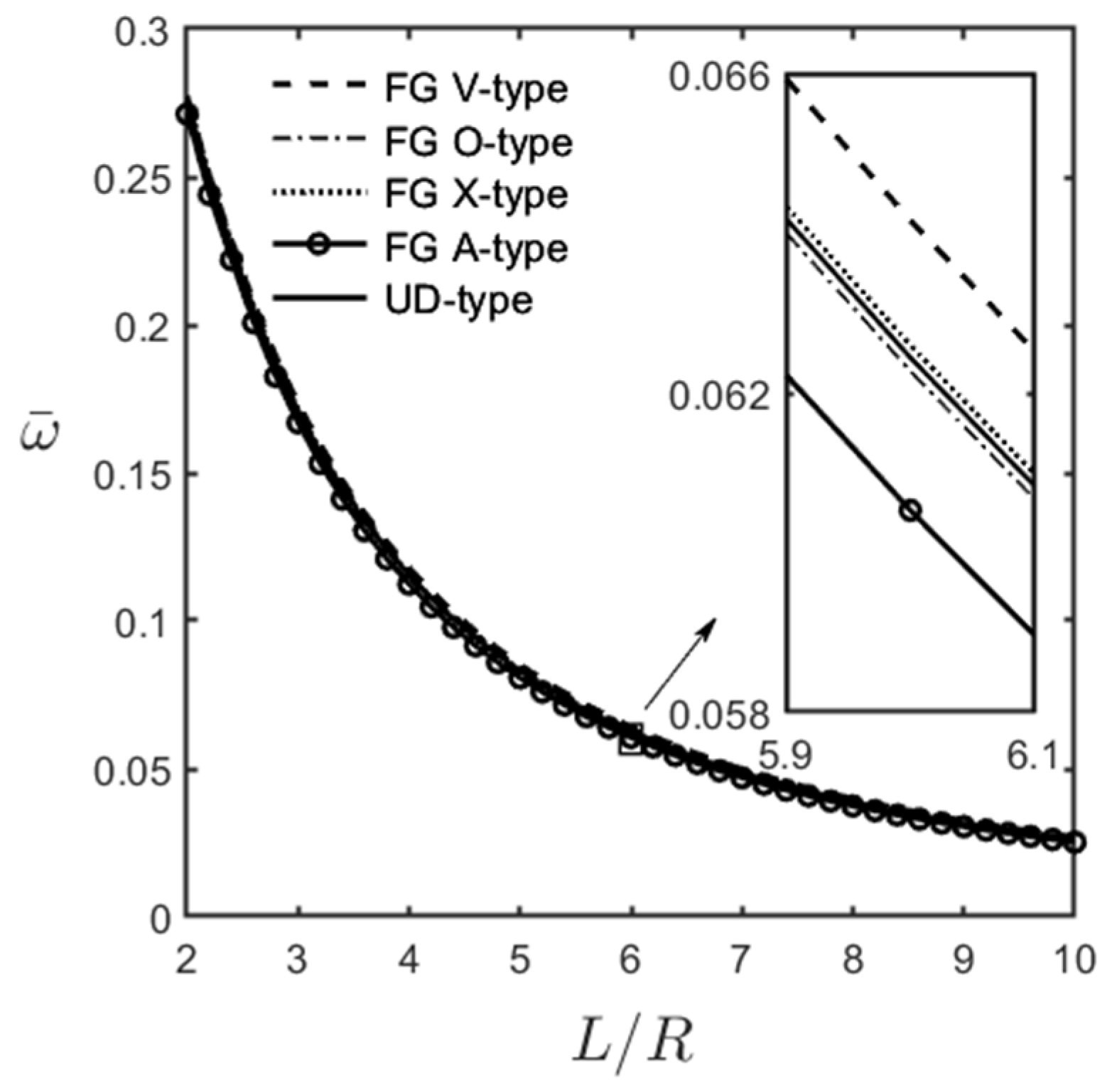
- For moderately thick (R/h = 10) and thick (R/h = 5) cylindrical microshells, the fundamental mode of vibration always occurred when the wave number pair was = (1, 1). In that case, the values of the dimensionless natural frequencies for different GPL distribution patterns can be arranged in descending order as follows: FG V-type > FG X-type > UD > FG O-type > FG A-type distributions.
- (c)
- For thin (R/h = 20) microshells, the fundamental mode of vibration always occurred when the wave number pair was = (1, 2). In that case, the values of the dimensionless natural frequencies for different GPL distribution patterns can be arranged in descending order as follows: FG X-type > (FG A-type, UD) > (FG O-type, FG V-type) distributions.
- (d)
- By increasing the weight fraction of GPLs by 1%, the natural frequency of FG-GPLRC cylindrical microshells can be increased to more than twice that of the homogeneous cylindrical microshells.
- (e)
- The dimensionless fundamental frequency decreased when the microshells became thinner and longer.
- (f)
- The dimensionless fundamental frequency increased when the weight fraction of the GPL increased and when the length–to–thickness ratio of the GPL increased.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iijima, S. Helical microtubults of graphitic carbon. Nature 1991, 354, 56058. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Esashi, M. Micro/nano electro mechanical systems for practical applications. J. Phys. 2009, 187, 012001. [Google Scholar] [CrossRef]
- Young, R.J.; Kinloch, I.A.; Gong, I.; Novoselov, K.S. The mechanics of graphene nanocomposites: A review. Compos. Sci. Technol. 2012, 72, 1459–1476. [Google Scholar] [CrossRef]
- Raflee, M.A.; Raflee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube-polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Esaw, A.M.K.; Farag, M.M. Carbon nanotube reinforced composites: Potential and current challenges. Mater. Des. 2007, 28, 2394–2401. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Ma, Q.; Clarke, D.R. Size dependent hardness of silver single crystals. J. Mater. Res. 1995, 10, 853–863. [Google Scholar] [CrossRef]
- Chong, A.C.M.; Lam, D.C.C. Strain gradient plasticity effect in indentation hardness of polymers. J. Mater. Res. 1999, 14, 4103–4110. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2013, 51, 1477–1508. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Wu, C.P.; Yu, J.J. A review of mechanical analyses of rectangular nanobeams and single-, double-, and multi-walled carbon nanotubes using Eringen’s nonlocal elasticity theory. Arch. Appl. Mech. 2019, 89, 1761–1792. [Google Scholar] [CrossRef]
- Wu, C.P.; Hu, H.X. A review of dynamic analyses of single- and multi-layered graphene sheets/nanoplates using various nonlocal continuum mechanics-based plate theories. Acta Mech. 2021, 232, 4497–4531. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar elasticity. In Microcontinuum Field Theories; Springer: New York, NY, USA, 1999; pp. 101–248. [Google Scholar]
- Granik, V.T.; Ferrari, M. Microstructural mechanics of granular medium. Mech. Mater. 1993, 15, 301–322. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Rational Mech. Anal. 1962, 11, 415–488. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar elasticity. In Fracture; Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress-based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef] [Green Version]
- Hadjesfandiari, A.R.; Dargush, G.F. Fundamental solutions for isotropic size-dependent couple stress elasticity. Int. J. Solids Struct. 2013, 50, 1253–1265. [Google Scholar] [CrossRef] [Green Version]
- Tang, F.; He, S.; Shi, S.; Xue, S.; Dong, F.; Liu, S. Analysis of size-dependent linear static bending, buckling, and free vibration based on a modified couple stress theory. Materials 2022, 15, 7583. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T. Thermo-electro-mechanical buckling analysis of cylindrical nanoshell on the basis of modified couple stress theory. J. Mech. Sci. Technol. 2017, 31, 1773–1787. [Google Scholar] [CrossRef]
- Zeighampour, H.; Beni, Y.T. Analysis of conical shells in the framework of coupled stresses theory. Int. J. Eng. Sci. 2014, 81, 107–122. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y. Size-dependent free vibration and buckling of three-dimensional graphene form microshells based on modified couple stress theory. Materials 2019, 12, 729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soleimani, I.; Beni, Y.T.; Dehkordi, M.B. Size-dependent two-node axisymmetric shell element for buckling analysis with couple stress theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4729–4741. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R.; Darvizeh, A.; Sahmani, S. Axial buckling and dynamic stability of functionally graded microshells based on the modified couple stress theory. Int. J. Struct. Stab. Dyn. 2014, 15, 1450070. [Google Scholar] [CrossRef]
- Salehipour, H.; Shahsavar, A.; Civalek, Ö. Free vibration and static deflection analysis of functionally graded and porous micro/nanoshells with clamped and simply supported edges. Compos. Struct. 2019, 221, 110842. [Google Scholar] [CrossRef]
- Zeighampour, H.; Beni, Y.T. A shear deformable cylindrical shell model based on couple stress theory. Arch. Appl. Mech. 2015, 85, 539–553. [Google Scholar] [CrossRef]
- Esfahani, M.N.; Hashemian, M.; Aghadavoudi, F. The vibration study of a sandwich conical shell with a saturated FGP core. Sci. Rep. 2022, 12, 4950. [Google Scholar] [CrossRef]
- Shameli, R.; Aghadavoudi, F.; Hashemian, M. Free torsional vibration analysis of nanorods with non-circular cross-sections based on the second-order strain gradient theory. J. Vibr. Eng. Technol. 2022. [Google Scholar] [CrossRef]
- Lyu, Z.; Liu, W.; Liu, C.; Zhang, Y.; Fang, M. Thermo-electro-mechanical vibration and buckling analysis of a functionally graded piezoelectric porous cylindrical microshell. J. Mech. Sci. Technol. 2021, 35, 4655–4672. [Google Scholar] [CrossRef]
- Thai, S.; Thai, H.T.; Vo, T.P.; Reddy, J.N. Post-buckling of functionally graded microplates under mechanical and thermal loads using isogeometric analysis. Eng. Struct. 2017, 150, 905–917. [Google Scholar] [CrossRef]
- Thai, S.; Thai, H.; Vo, T.P.; Nguyen-Xuan, H. Nonlinear static and transient isogeometric analysis of functionally graded microplates based on the modified strain gradient theory. Eng. Struct. 2017, 153, 598–612. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Atroshchenko, E.; Ngo, T.; Nguyen-Xuan, H.; Vo, T.P. Vibration of cracked functionally graded microplates by the strain gradient theory and extended isogeometric analysis. Eng. Struct. 2019, 187, 251–266. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.Q.; Liu, Y.F.; Zu, J.W. Size-dependent vibration of circular cylindrical polymetric microshells reinforced with graphene platelets. Int. J. Appl. Mech. 2019, 11, 1950036. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Baghbadorani, A.A.; Kiani, Y. Free vibration analysis of functionally graded cylindrical shells reinforced with graphene platelets. Compos. Struct. 2021, 276, 114546. [Google Scholar] [CrossRef]
- Safarpour, H.; Hajilak, Z.E.; Habibi, M. A size-dependent exact theory for thermal buckling, free and forced vibration analysis of temperature dependent FG multilayer GPLRC composite nanostructures resting on elastic foundation. Int. J. Mech. Mater. Des. 2019, 15, 569–583. [Google Scholar] [CrossRef]
- Salehi, M.; Gholami, R.; Ansari, R. Analytical solution approach for nonlinear vibration of shear deformable imperfect FG-GPLR porous nanocomposite cylindrical shells. Mech. Based Des. Struct. Mach. 2021, 51, 2177–2199. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, T.; Zhang, W. An accurate size-dependent sinusoidal shear deformable framework for GNP-reinforced cylindrical panels: Applications to dynamic stability analysis. Thin-Walled Struct. 2021, 160, 107400. [Google Scholar] [CrossRef]
- Moayedi, H.; Aliakbarlou, H.; Jebeli, M.; Noormohammadi-Arani, O.; Habibi, M.; Safapour, H.; Foong, I.K. Thermal buckling responses of a graphene reinforced composite micropanel structure. Int. J. Appl. Mech. 2020, 12, 2050010. [Google Scholar] [CrossRef]
- Wu, C.P.; Hsu, C.H. A three-dimensional weak formulation for stress, deformation, and free vibration analyses of functionally graded microplates based on the consistent couple stress theory. Compos. Struct. 2022, 296, 115829. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.A. A Hermite-family C1 finite layer method for the three-dimensional free vibration of exponentially graded piezoelectric microplates based on the consistent couple stress theory. Int. J. Struct. Stab. Dyn. 2023, 23, 2350044. [Google Scholar] [CrossRef]
- Yang, J.; Wu, H.; Kitipornchai, S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos. Struct. 2017, 161, 111–118. [Google Scholar] [CrossRef] [Green Version]
- Zeighampour, H.; Beni, Y.T. Cylindrical thin-shell model based on modified strain gradient theory. Int. J. Eng. Sci. 2014, 78, 27–47. [Google Scholar] [CrossRef]
- Loy, C.T.; Lam, K.Y.; Reddy, J.N. Vibration of functionally graded cylindrical shells. Int. J. Mech. Sci. 1999, 41, 309–324. [Google Scholar] [CrossRef]
- Liu, D.; Kitipornchai, S.; Chen, W.; Yang, J. Three-dimensional buckling and free vibration analyses of initially stressed functionally graded reinforced composite cylindrical shell. Compos. Struct. 2018, 189, 560–569. [Google Scholar] [CrossRef] [Green Version]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef] [Green Version]


| Zeighampour and Beni [46] | Two-Node CCST-Based FLMs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lagrangian C0 FLMs | Hermitian C1 FLMs | Hermitian C2 FLMs | ||||||||
| nl = 1 | nl = 2 | nl = 4 | nl = 1 | nl = 2 | nl = 1 | nl = 2 | Relative Errors | |||
| (1, 1) | 0 | 0.19588 | 0.195441 | 0.195435 | 0.195434 | 0.195434 | 0.195434 | 0.195434 | 0.195434 | 0.2% |
| 1 | 0.21109 | 0.196435 | 0.196430 | 0.196428 | 0.196066 | 0.196065 | 0.196065 | 0.196065 | 7.7% | |
| (2, 2) | 0 | 0.26245 | 0.260008 | 0.258832 | 0.258534 | 0.258434 | 0.258434 | 0.258434 | 0.258434 | 1.6% |
| 1 | 0.39538 | 0.360147 | 0.359365 | 0.359167 | 0.357885 | 0.357883 | 0.357883 | 0.357883 | 10.5% | |
| (3, 3) | 0 | 0.32242 | 0.322392 | 0.315408 | 0.313598 | 0.312990 | 0.312990 | 0.312990 | 0.312990 | 3.0% |
| 1 | 0.76443 | 0.732952 | 0.730358 | 0.729696 | 0.727972 | 0.727969 | 0.727969 | 0.727969 | 5.0% | |
| (4, 4) | 0 | 0.43010 | 0.436538 | 0.418090 | 0.413173 | 0.411505 | 0.411505 | 0.411505 | 0.411505 | 3.0% |
| 1 | 1.34110 | 1.296770 | 1.292101 | 1.290895 | 1.288570 | 1.288566 | 1.288566 | 1.288566 | 4.1% | |
| (5, 5) | 0 | 0.60367 | 0.610821 | 0.577106 | 0.567870 | 0.564713 | 0.564712 | 0.564712 | 0.564712 | 6.9% |
| 1 | 2.20417 | 2.016211 | 2.009530 | 2.007785 | 2.003963 | 2.003955 | 2.003954 | 2.003954 | 10.0% | |
| Theories | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1, 0) | (1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) | (1, 7) | (1, 8) | (1, 9) | (1, 10) | ||
| 0.5 | Two-node Hermitian C2 () | 76.4537 | 13.3336 | 4.5196 | 4.1850 | 7.0831 | 11.3125 | 16.5600 | 22.7794 | 29.9612 | 38.1026 | 47.2026 |
| Two-node Hermitian C2 () | 76.4536 | 13.3336 | 4.5198 | 4.1846 | 7.0831 | 11.3125 | 16.5599 | 22.7795 | 29.9611 | 38.1026 | 47.2025 | |
| Three-node Hermitian C2 () | 76.4537 | 13.3337 | 4.5197 | 4.1847 | 7.0832 | 11.3126 | 16.5600 | 22.7794 | 29.9612 | 38.1026 | 47.2026 | |
| Three-node Hermitian C2 () | 76.4536 | 13.3337 | 4.5197 | 4.1844 | 7.0830 | 11.3130 | 16.5602 | 22.7793 | 29.9613 | 38.1026 | 47.2026 | |
| Liu et al. [49] | NA | 13.341 | 4.5295 | 4.1830 | 7.0913 | 11.328 | 16.583 | 22.811 | 30.002 | 38.155 | 47.267 | |
| Loy et al. [48] | NA | 13.321 | 4.5168 | 4.1911 | 7.0972 | 11.336 | 16.594 | 22.826 | 30.023 | 38.181 | 47.301 | |
| 1 | Two-node Hermitian C2 () | 75.8588 | 13.2236 | 4.4827 | 4.1508 | 7.0243 | 11.2182 | 16.4216 | 22.5888 | 29.7104 | 37.7835 | 46.8073 |
| Two-node Hermitian C2 () | 75.8588 | 13.2236 | 4.4829 | 4.1507 | 7.0244 | 11.2182 | 16.4215 | 22.5888 | 29.7104 | 37.7836 | 46.8073 | |
| Three-node Hermitian C2 () | 75.8588 | 13.2236 | 4.4826 | 4.1508 | 7.0242 | 11.2182 | 16.4215 | 22.5888 | 29.7104 | 37.7836 | 46.8073 | |
| Three-node Hermitian C2 () | 75.8588 | 13.2236 | 4.4829 | 4.1512 | 7.0246 | 11.2184 | 16.4215 | 22.5888 | 29.7105 | 37.7836 | 46.8072 | |
| Liu et al. [49] | NA | 13.242 | 4.480 | 4.1459 | 7.0325 | 11.229 | 16.438 | 22.612 | 29.741 | 37.822 | 46.855 | |
| Loy et al. [48] | NA | 13.211 | 4.480 | 4.1569 | 7.0384 | 11.241 | 16.455 | 22.635 | 29.771 | 37.862 | 46.905 | |
| 30 | Two-node Hermitian C2 () | 74.2516 | 12.9261 | 4.3793 | 4.0517 | 6.8590 | 10.9559 | 16.0387 | 22.0628 | 29.0189 | 36.9045 | 45.7185 |
| Two-node Hermitian C2 () | 74.2516 | 12.9261 | 4.3790 | 4.0518 | 6.8589 | 10.9560 | 16.0387 | 22.0628 | 29.0189 | 36.9045 | 45.7185 | |
| Three-node Hermitian C2 () | 74.2516 | 12.9262 | 4.3793 | 4.0515 | 6.8590 | 10.9559 | 16.0386 | 22.0628 | 29.0189 | 36.9045 | 45.7185 | |
| Three-node Hermitian C2 () | 74.2516 | 12.9259 | 4.3791 | 4.0526 | 6.8590 | 10.9561 | 16.0388 | 22.0629 | 29.0190 | 36.9045 | 45.7185 | |
| Liu et al. [49] | NA | 12.945 | 4.3810 | 4.0469 | 6.8561 | 10.949 | 16.029 | 22.049 | 29.001 | 36.882 | 45.691 | |
| Loy et al. [48] | NA | 12.914 | 4.3765 | 4.0576 | 6.8726 | 10.978 | 16.071 | 22.108 | 29.078 | 36.981 | 45.813 | |
| GPL Distribution Patterns | () | () | () | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Liu et al. [49] | Liu et al. [49] | Liu et al. [49] | ||||||||||||||
| 2 | Epoxy | 0.9659 | 0.9659 (1) | 1.0320 (1) | 1.1644 (1) | 1.3349 (1) | 0.9996 | 0.9996 (0) | 1.0707 (0) | 1.2431 (0) | 1.3442 (0) | 1.0161 | 1.0161 (2) | 1.0999 (2) | 1.2576 (2) | 1.4874 (2) |
| UD | 2.3674 | 2.3674 (1) | 2.5300 (1) | 2.8555 (1) | 3.2745 (0) | 2.4499 | 2.4499 (0) | 2.6247 (0) | 3.0482 (0) | 3.2972 (1) | 2.4904 | 2.4904 (2) | 2.6964 (2) | 3.0842 (2) | 3.6485 (2) | |
| FG V-type | 2.2362 | 2.2359 (1) | 2.4412 (1) | 2.8687 (1) | 3.4376 (1) | 2.2518 | 2.2516 (0) | 2.4518 (0) | 2.9132 (0) | 3.4590 (0) | 2.3753 | 2.3750 (2) | 2.6221 (2) | 3.0965 (2) | 3.7089 (2) | |
| FG A-type | 2.2517 | 2.2515 (1) | 2.3613 (1) | 2.5086 (1) | 2.5664 (0) | 2.3636 | 2.3633 (2) | 2.5189 (0) | 2.5403 (0) | 2.6216 (1) | 2.4659 | 2.4653 (0) | 2.5321 (2) | 2.7482 (2) | 2.9088 (2) | |
| FG X-type | 2.3030 | 2.3028 (1) | 2.5173 (1) | 2.8614 (1) | 3.4279 (0) | 2.3663 | 2.3663 (2) | 2.6274 (0) | 3.0562 (0) | 3.4285 (1) | 2.4109 | 2.4107 (0) | 2.6586 (2) | 3.0813 (2) | 3.7938 (2) | |
| FG O-type | 2.2171 | 2.2170 (1) | 2.4044 (1) | 2.7498 (1) | 2.9874 (0) | 2.2915 | 2.2913 (0) | 2.4900 (0) | 2.9528 (0) | 3.0260 (1) | 2.3348 | 2.3347 (2) | 2.5687 (2) | 2.9735 (2) | 3.3336 (2) | |
| 5 | Epoxy | 2.6997 | 2.6997 (0) | 3.2633 (1) | 3.6532 (0) | 3.9184 (0) | 2.7156 | 2.7156 (1) | 3.2779 (0) | 3.6761 (1) | 3.9446 (1) | 2.7680 | 2.7680 (2) | 3.3038 (2) | 3.7496 (2) | 4.0230 (2) |
| UD | 6.6185 | 6.6185 (0) | 8.0037 (1) | 8.9610 (0) | 9.6115 (0) | 6.6576 | 6.6576 (1) | 8.0390 (0) | 9.0173 (1) | 9.6760 (1) | 6.7861 | 6.7861 (2) | 8.1031 (2) | 9.1975 (2) | 9.8682 (2) | |
| FG V-type | 6.2760 | 6.2172 (0) | 6.8898 (0) | 7.1421 (0) | 7.3011 (0) | 6.2435 | 6.2437 (1) | 6.9063 (1) | 7.1761 (1) | 7.3372 (1) | 6.3383 | 6.3387 (2) | 6.9986 (2) | 7.2997 (2) | 7.4661 (2) | |
| FG A-type | 5.4878 | 5.4895 (0) | 5.7000 (0) | 5.8302 (0) | 5.9099 (0) | 5.5120 | 5.5137 (1) | 5.7298 (1) | 5.8620 (1) | 5.9422 (1) | 5.5865 | 5.5882 (2) | 5.8192 (2) | 5.9563 (2) | 6.0376 (2) | |
| FG X-type | 6.1009 | 6.1012 (0) | 7.6554 (1) | 9.1384 (0) | 11.2431 (0) | 6.1354 | 6.1357 (1) | 7.7157 (0) | 9.1948 (1) | 11.3290 (1) | 6.2496 | 6.2499 (2) | 7.7429 (2) | 9.3989 (2) | 11.5879 (2) | |
| FG O-type | NA | 6.5361 (0) | 6.9735 (0) | 7.1062 (0) | 7.1863 (0) | NA | 6.5658 (1) | 7.0069 (1) | 7.1451 (1) | 7.2257 (1) | NA | 6.6742 (2) | 7.1128 (2) | 7.2609 (2) | 7.3422 (2) | |
| 10 | Epoxy | 5.6503 | 5.6503 (0) | 7.5607 (0) | 8.0905 (0) | 8.2791 (0) | 5.6603 | 5.6603 (1) | 7.5733 (1) | 8.1027 (1) | 8.2911 (1) | 5.6897 | 5.6897 (2) | 7.6109 (2) | 8.1393 (2) | 8.3270 (2) |
| UD | 13.8540 | 13.8540 (0) | 18.5459 (0) | 19.8455 (0) | 20.3082 (0) | 13.8785 | 13.8785 (1) | 18.5767 (1) | 19.8755 (1) | 20.3376 (1) | 13.9504 | 13.9504 (2) | 18.6690 (2) | 19.9652 (2) | 20.4257 (2) | |
| FG V-type | 10.3491 | 10.3531 (0) | 11.7683 (0) | 12.1279 (0) | 12.2624 (0) | 10.3520 | 10.3560 (1) | 11.8016 (1) | 12.1623 (1) | 12.2969 (1) | 10.3782 | 10.3822 (2) | 11.9024 (2) | 12.2663 (2) | 12.4010 (2) | |
| FG A-type | 9.6421 | 9.6458 (0) | 10.6379 (0) | 10.8929 (0) | 10.9890 (0) | 9.6527 | 9.6563 (1) | 10.6519 (1) | 10.9071 (1) | 11.0031 (1) | 9.6843 | 9.6880 (2) | 10.6937 (2) | 10.9494 (2) | 11.0454 (2) | |
| FG X-type | 12.0604 | 12.0645 (0) | 16.9969 (0) | 23.9794 (0) | 24.0569 (0) | 12.0798 | 12.0839 (1) | 17.0399 (1) | 24.0224 (1) | 24.0996 (1) | 12.1380 | 12.1422 (2) | 17.1694 (2) | 24.1506 (2) | 24.2267 (2) | |
| FG O-type | 11.7123 | 11.7164 (0) | 12.6699 (0) | 12.8855 (0) | 12.9659 (0) | 11.7251 | 11.7291 (1) | 12.6857 (1) | 12.9014 (1) | 12.9818 (1) | 11.7632 | 11.7673 (2) | 12.7328 (2) | 12.9490 (2) | 13.0293 (2) | |
| R/h | Types | (l/h) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 (0) | 0.2 (0.1) | 0.4 (0.2) | 0.6 (0.3) | 0.8 (0.4) | 1.0 (0.5) | |||
| (1, 1) | 5 | FG V-type | 0.03156 | 0.03157 | 0.03160 | 0.03163 | 0.03168 | 0.03174 |
| FG X-type | 0.03056 | 0.03057 | 0.03059 | 0.03063 | 0.03068 | 0.03074 | ||
| UD | 0.03049 | 0.03050 | 0.03052 | 0.03056 | 0.03061 | 0.03067 | ||
| FG O-type | 0.03042 | 0.03043 | 0.03045 | 0.03049 | 0.03053 | 0.03059 | ||
| FG A-type | 0.02934 | 0.02935 | 0.02937 | 0.02941 | 0.02945 | 0.02951 | ||
| (1, 1) | 10 | FG V-type | 0.01546 | 0.01546 | 0.01546 | 0.01547 | 0.01547 | 0.01548 |
| FG X-type | 0.01519 | 0.01519 | 0.01520 | 0.01520 | 0.01521 | 0.01521 | ||
| UD | 0.01518 | 0.01518 | 0.01519 | 0.01519 | 0.01520 | 0.01521 | ||
| FG O-type | 0.01517 | 0.01518 | 0.01518 | 0.01518 | 0.01519 | 0.01520 | ||
| FG A-type | 0.01490 | 0.01490 | 0.01490 | 0.01491 | 0.01491 | 0.01492 | ||
| (1, 1) | 20 | FG V-type | 0.00765 | 0.00765 | 0.00765 | 0.00765 | 0.00765 | 0.00766 |
| FG X-type | 0.00758 | 0.00759 | 0.00759 | 0.00759 | 0.00759 | 0.00759 | ||
| UD | 0.00758 | 0.00758 | 0.00758 | 0.00758 | 0.00759 | 0.00759 | ||
| FG O-type | 0.00758 | 0.00758 | 0.00758 | 0.00758 | 0.00758 | 0.00759 | ||
| FG A-type | 0.00751 | 0.00751 | 0.00751 | 0.00751 | 0.00752 | 0.00752 | ||
| (1, 2) | 10 | FG V-type | 0.01845 | 0.02011 | 0.02441 | 0.03021 | 0.03678 | 0.04372 |
| FG X-type | 0.02468 | 0.02606 | 0.02970 | 0.03487 | 0.04096 | 0.04758 | ||
| UD | 0.02115 | 0.02269 | 0.02677 | 0.03241 | 0.03890 | 0.04584 | ||
| FG O-type | 0.01661 | 0.01854 | 0.02337 | 0.02969 | 0.03670 | 0.04402 | ||
| FG A-type | 0.01906 | 0.02086 | 0.02548 | 0.03167 | 0.03865 | 0.04601 | ||
| (2, 2) | 10 | FG V-type | 0.02732 | 0.02867 | 0.03237 | 0.03771 | 0.04404 | 0.05095 |
| FG X-type | 0.03234 | 0.03359 | 0.03697 | 0.04192 | 0.04792 | 0.05459 | ||
| UD | 0.02935 | 0.03067 | 0.03431 | 0.03960 | 0.04593 | 0.05288 | ||
| FG O-type | 0.02578 | 0.02728 | 0.03134 | 0.03708 | 0.04382 | 0.05109 | ||
| FG A-type | 0.02752 | 0.02900 | 0.03302 | 0.03877 | 0.04554 | 0.05289 | ||
| (1, 3) | 10 | FG V-type | 0.04901 | 0.05376 | 0.06591 | 0.08210 | 0.10023 | 0.11922 |
| FG X-type | 0.06623 | 0.07034 | 0.08066 | 0.09502 | 0.11177 | 0.12980 | ||
| UD | 0.05686 | 0.06124 | 0.07271 | 0.08842 | 0.10633 | 0.12529 | ||
| FG O-type | 0.04392 | 0.04949 | 0.06325 | 0.08099 | 0.10042 | 0.12051 | ||
| FG A-type | 0.05113 | 0.05627 | 0.06937 | 0.08673 | 0.10607 | 0.12625 | ||
| (2, 3) | 10 | FG V-type | 0.05140 | 0.05624 | 0.06868 | 0.08531 | 0.10394 | 0.12345 |
| FG X-type | 0.06883 | 0.07306 | 0.08365 | 0.09840 | 0.11561 | 0.13412 | ||
| UD | 0.05933 | 0.06380 | 0.07555 | 0.09167 | 0.11007 | 0.12953 | ||
| FG O-type | 0.04622 | 0.05188 | 0.06592 | 0.08409 | 0.10404 | 0.12466 | ||
| FG A-type | 0.05347 | 0.05870 | 0.07208 | 0.08986 | 0.10970 | 0.13040 | ||
| (3, 3) | 10 | FG V-type | 0.05705 | 0.06194 | 0.07464 | 0.09178 | 0.11111 | 0.13142 |
| FG X-type | 0.07450 | 0.07885 | 0.08979 | 0.10507 | 0.12295 | 0.14220 | ||
| UD | 0.06492 | 0.06947 | 0.08152 | 0.09817 | 0.11725 | 0.13749 | ||
| FG O-type | 0.05185 | 0.05749 | 0.07173 | 0.09040 | 0.11105 | 0.13248 | ||
| FG A-type | 0.05896 | 0.06424 | 0.07786 | 0.09616 | 0.11670 | 0.13819 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-P.; Tan, T.-F.; Hsu, H.-T. A Size-Dependent Finite Element Method for the 3D Free Vibration Analysis of Functionally Graded Graphene Platelets-Reinforced Composite Cylindrical Microshells Based on the Consistent Couple Stress Theory. Materials 2023, 16, 2363. https://doi.org/10.3390/ma16062363
Wu C-P, Tan T-F, Hsu H-T. A Size-Dependent Finite Element Method for the 3D Free Vibration Analysis of Functionally Graded Graphene Platelets-Reinforced Composite Cylindrical Microshells Based on the Consistent Couple Stress Theory. Materials. 2023; 16(6):2363. https://doi.org/10.3390/ma16062363
Chicago/Turabian StyleWu, Chih-Ping, Tech-Fatt Tan, and Hao-Ting Hsu. 2023. "A Size-Dependent Finite Element Method for the 3D Free Vibration Analysis of Functionally Graded Graphene Platelets-Reinforced Composite Cylindrical Microshells Based on the Consistent Couple Stress Theory" Materials 16, no. 6: 2363. https://doi.org/10.3390/ma16062363






