Research on an Optimized Evaluation Method of the Bearing Capacity of Reinforced Concrete Beam Based on the Bayesian Theory
Abstract
1. Introduction
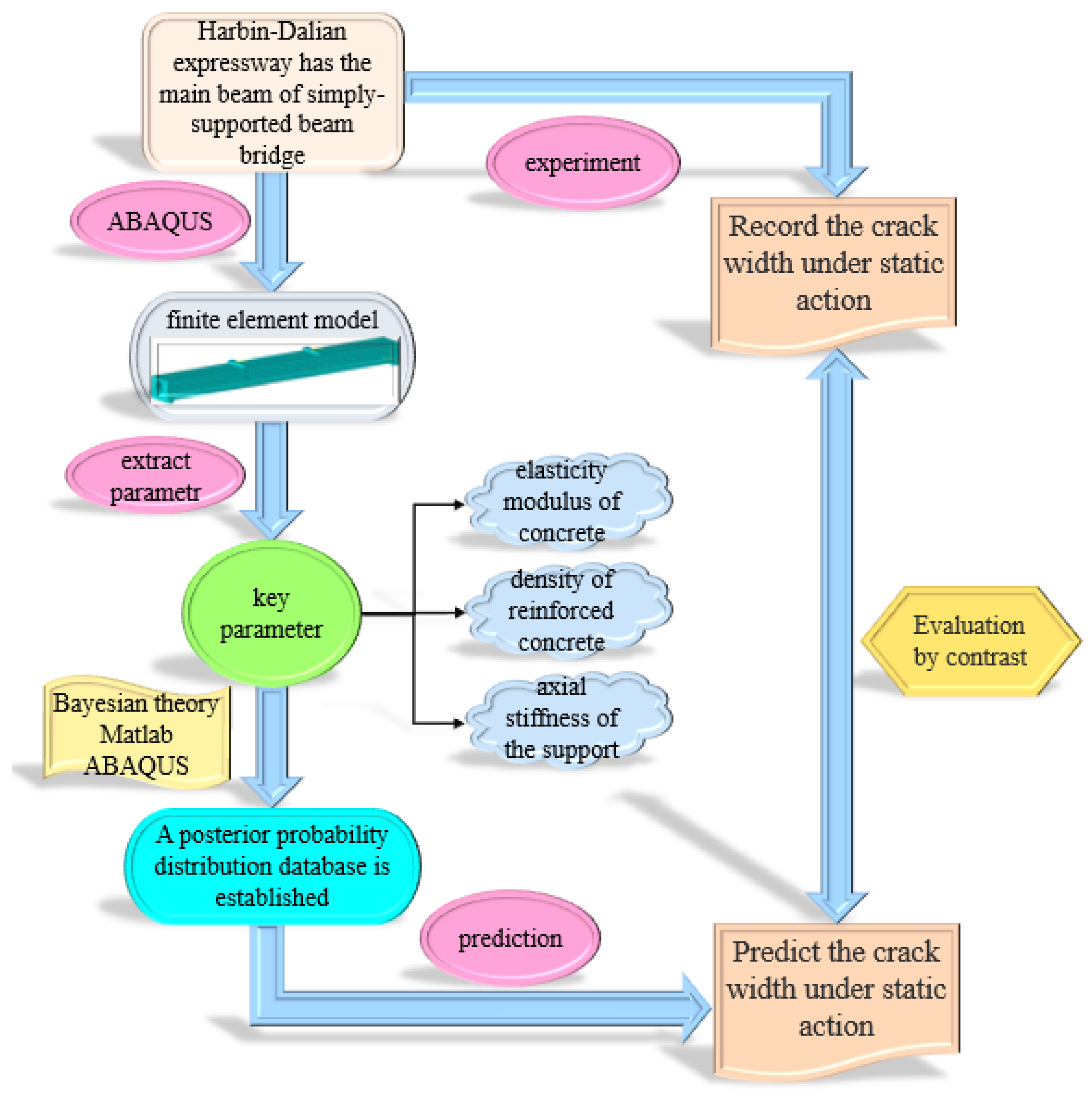
2. Identification of the Bridge Bearing Capacity Based on the Bayesian Theory
2.1. Basic Framework of Bearing Capacity Identification
- (1)
- To observe the structure and obtain prior information. The distribution of uncertain parameters can be determined by analyzing the structure type, determining the material and load transfer path, and understanding the historical test data and other information.
- (2)
- To establish models and select key parameters. Based on the known information, the finite element parent model was established. Sensitivity analysis was carried out using relevant response indicators. Additionally, key parameters that had a great impact on bearing capacity were selected.
- (3)
- Structural testing. To carry out the test with corresponding test instruments to complete the collection of static data.
- (4)
- Data analysis. By analyzing the static test data of the structure, the static test information of the structure was extracted.
- (5)
- A posteriori probability distribution database and model identification were established by sampling. Based on the obtained analysis data and Bayesian theory, a representative posteriori probability distribution database was selected by the efficient sampling method to complete the identification of key parameters.
- (6)
- Prediction and evaluation of bearing capacity. After establishing a posteriori probability distribution database, the bearing capacity prediction and performance evaluation were completed, by using multiple posteriori probability distributions in the database to meet the requirements of structural characteristics.
2.2. The Bayesian Formula and Derivation
2.3. MCMC Sampling Method
- (1)
- Select the starting sample of the Markov chain with physical significance, so that its initial probability distribution .
- (2)
- The next sample in the Markov chain only depends on the current sample, and has nothing to do with other historical samples. Therefore, the proposed distribution is used to generate candidate sample based on the previous sample .
- (3)
- Based on candidate sample and candidate system model , the acceptance probability function is calculated according to Formula (7):where is the sample acceptance probability, is the posterior probability of candidate sample corresponding to , and is the probability of generating candidate sample based on the previous sample .
- (4)
- Generate random number μ in (0,1) uniform distribution. When , accept candidate point , and then iterate again from step (2). On the contrary, reject candidate point and take .
- (5)
- Repeat steps (2)–(4) to finally produce a convergent Markov chain: , which represents the candidate sample model.
2.4. Improved MH Sampling Method
2.5. Sampling Method of TMCMC
- (1)
- Select a priori distribution, , , and sample it to obtain , .
- (2)
- Calculate the variance of probability density weight , to make close to the preset threshold value to determine .
- (3)
- The initial value is obtained by resampling and the Markov chain is constructed. The proposed distribution is a normal distribution with as the mean and as the variance. Conduct MCMC sampling, and use the Metropolis criteria [35] to judge whether to accept it, obtaining , in the next stage, at this time .
- (4)
- Repeat step (2) until . After m stages, , sample formed an approximate posterior distribution function.
2.6. Response Prediction of Bearing Capacity
3. Verification Example: Evaluation of the Bearing Capacity of the Test Beam
3.1. Destructive Test of the Bearing Capacity of the Test Beam
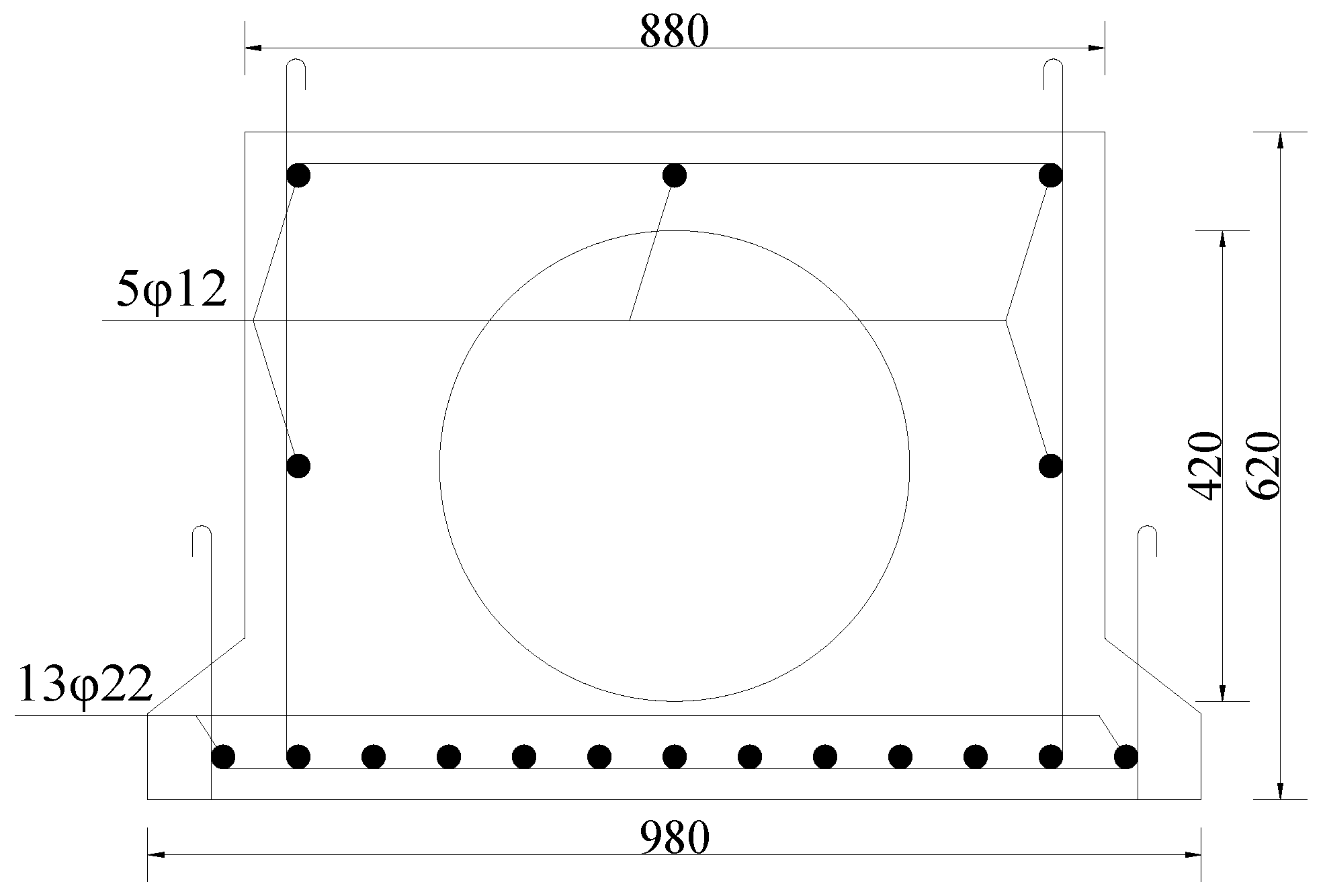
3.1.1. Project Overview
3.1.2. Support Device of Plate Beam
3.1.3. Loading Position of the Plate Beam
3.1.4. Plate Beam Experimental Loading Device
3.1.5. Experimental Loading Scheme Design
3.1.6. Experimental Loading Steps
- (1)
- Before the formal test, the test beam shall be preloaded first. The calculated bearing capacity (Fu) with a preload grade of 0.05 times was applied twice to check whether the test instrument and sensor work normally, to ensure that the test beam and support and jack were in close contact, and whether the load was eccentric, so as to reduce the test error. After the check was correct, we zeroed the instrument equipment and entered the formal test stage. Note that the preload should control the force within the elastic range and should not produce cracks and other forms of loading residual value.
- (2)
- When the load reached 90% of the technical value of the load for the bearing capacity test. The load shall be 0.05 Fr per level until the structure reaches the limit bearing capacity mark specified in 7.3.3 of “The Standard for Test Methods of Concrete Structures (GB/T 50152-2012) [37]”. That means that the concrete in the bending and compression area of the flexural member is subject to compression cracking and damage.
- (3)
- We continued to load (the loading amount was controlled by deformation) until the structure was completely destroyed; during the loading process at this stage, the structure will be completely damaged when loaded at 0.5 kN/s.
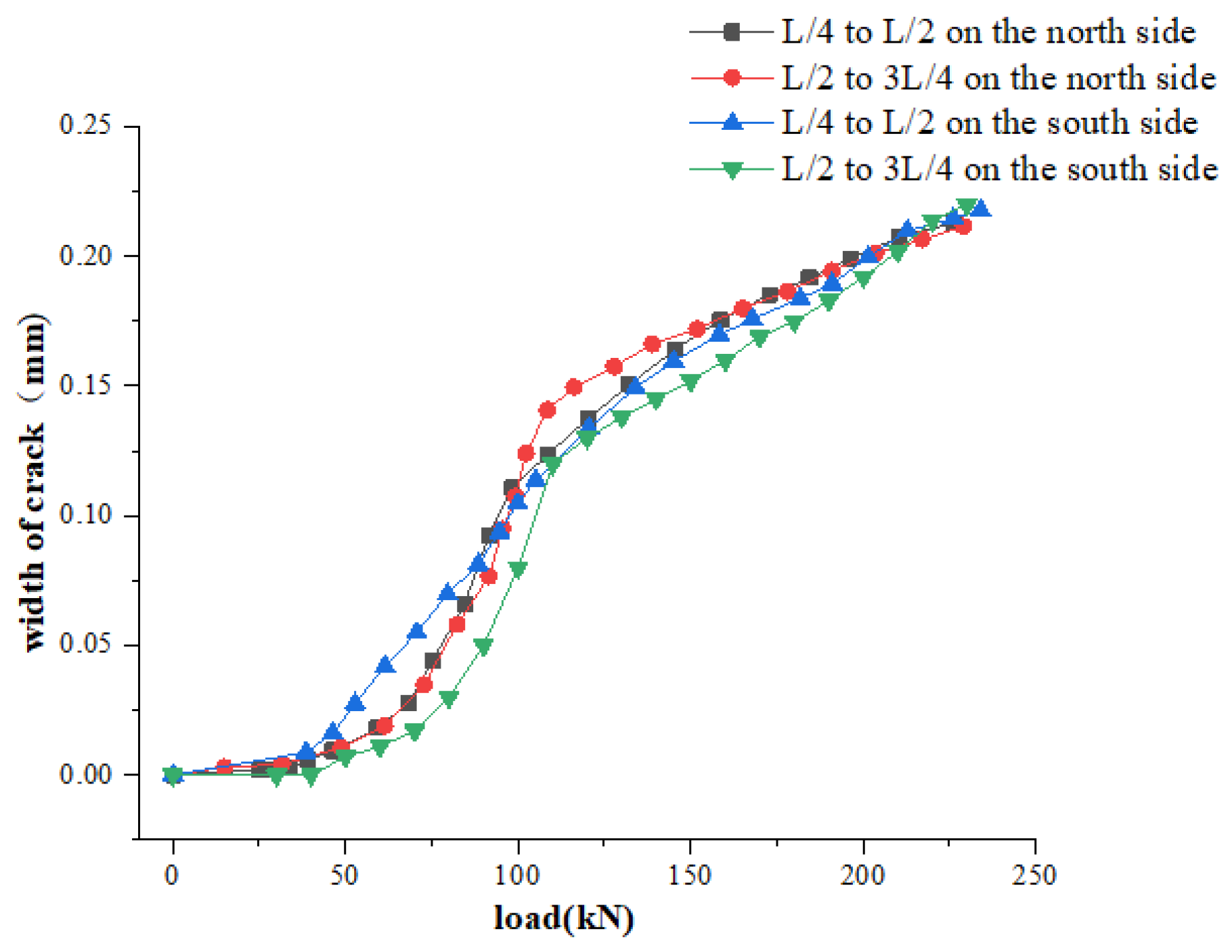
3.1.7. Crack Development of Main Beam
- (1)
- The crack develops slowly at the initial stage;
- (2)
- Inclined cracks appear;
- (3)
- The crack flourished until it was destroyed.
3.2. Establishment of Finite Element Parent Model
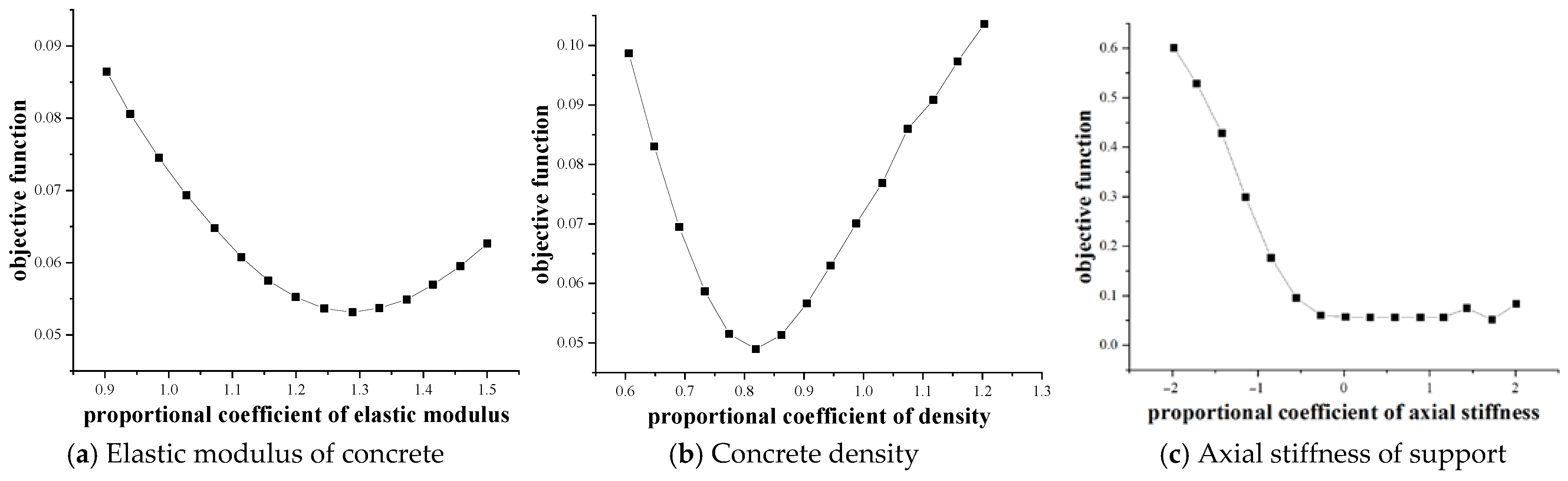
3.2.1. Sensitivity Analysis of Key Parameters
3.2.2. Concrete Parameter Setting in ABAQUS
3.2.3. Rebar Parameter Setting in ABAQUS
3.2.4. Model Establishment and Grid Division
3.2.5. Unit Type
3.2.6. Action Mode
3.2.7. Boundary Conditions and Loading Mode
3.2.8. Verification of the Finite Element Model
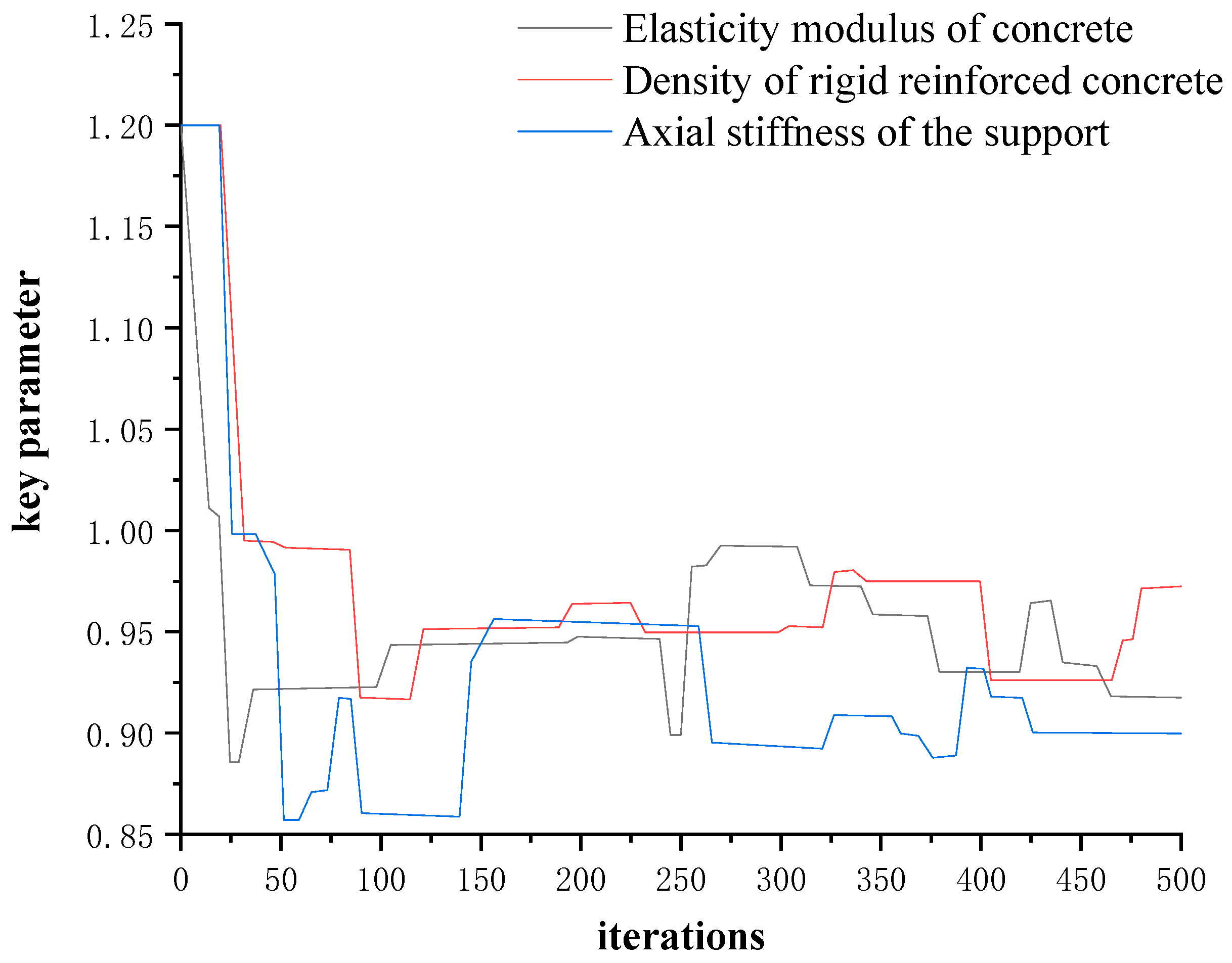
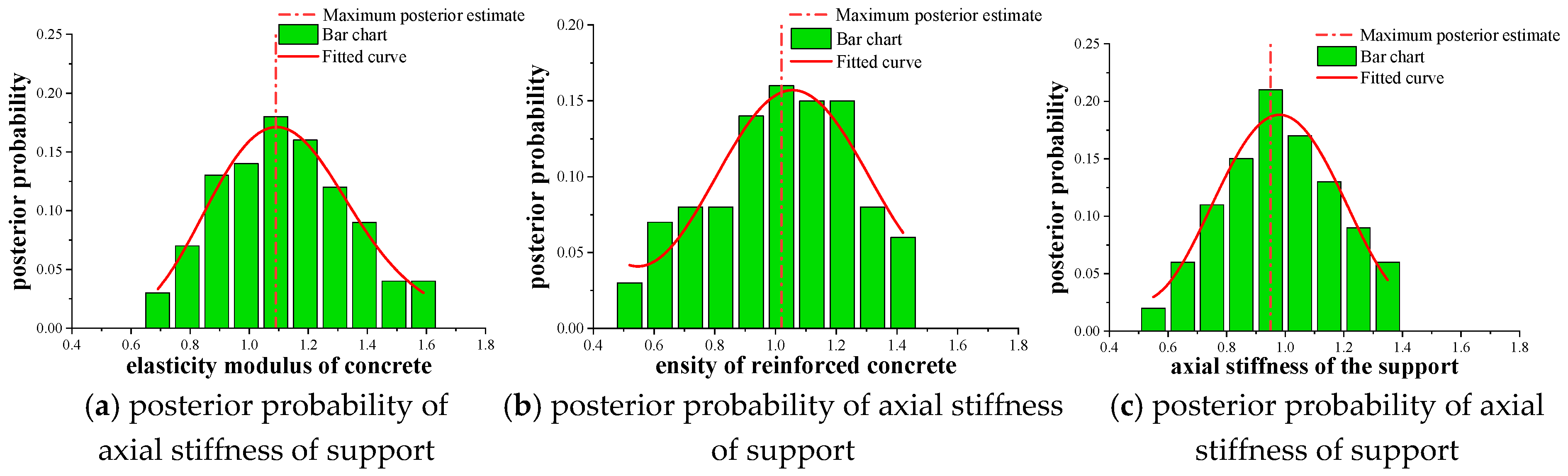
3.3. Improved MH Sampling
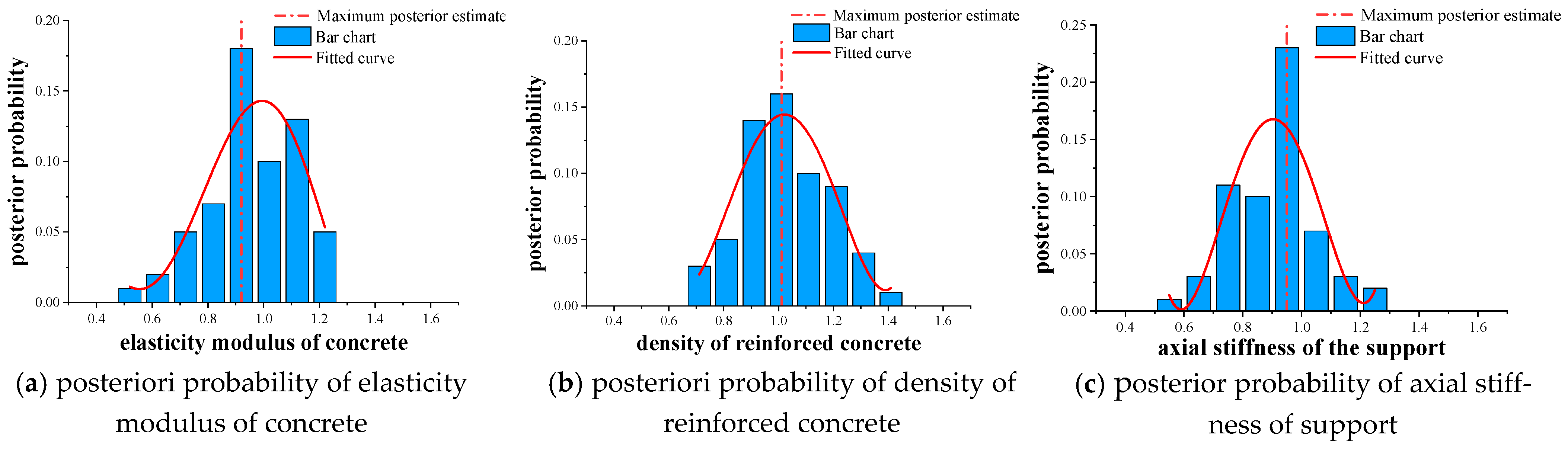
3.4. TMCMC Sampling
3.5. Prediction and Evaluation of the Bearing Capacity
4. Conclusions
- (1)
- Based on the Bayesian theory, the new method for evaluation of the bearing capacity of test beam bridges was to comprehensively analyze the cognitive error and random error of the structure, combine each “model components” into a model sample, and select the model library most suitable for the structural performance characteristics from the complex model samples by comparing the test results and the prediction results of the finite element model. Then, the probability distribution of the structural response prediction was obtained by using the model base and the performance evaluation was completed. The results are of statistical significance and more scientific and accurate.
- (2)
- This paper introduced the traditional Markov Chain-Monte Carlo Simulation (MCMC) sampling method, and then proposes two optimized MCMC sampling methods: an improved MH sampling method and a TMCMC sampling method. It can overcome the problems of traditional MCMC method, such as difficult convergence and low computational efficiency, when the model is complex and the parameter dimension is high. The derived MCMC sampling method improved by the above optimization can better achieve the evaluation of the bearing capacity of the structure.
- (3)
- Based on the static test results of reinforced concrete beams, the finite element model of the reinforced concrete beam was established by selecting three model components. The elastic modulus of concrete, the density of reinforced concrete and the axial stiffness of the support, and the sensitivity analysis of the model components was carried out. Based on the Bayesian theory, a posteriori probability distribution library was established using ABAQUS finite element software and Matlab. The improved MH sampling method and TMCMC sampling method were used to obtain the load-crack width curve of the reinforced concrete beam. The comparison shows that the prediction curve and the experimental test curve fit well. Among them, under the same crack width, the relative error of the bearing capacity obtained from the TMCMC sampling was less than 2.8%, and the relative error of the bearing capacity obtained from the improved MH sampling was less than 3.3%. Moreover, the measured value of the bearing capacity was within the confidence interval, which reflected the feasibility and effectiveness of the new method for the evaluation of the bearing capacity of the test beam bridge based on the Bayesian theory.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| φ | diameter of reinforcement |
| HRB | hot rolled ribbed steel bar |
| HPB | hot rolled plain round steel bar |
| C40 | concrete with compressive strength of 40 MPa |
| Fu | calculated bearing capacity |
| Fr | flexural tensile strength of concrete |
| E | elastic modulus of concrete |
| ρ | reinforced concrete density |
| K | axial stiffness of support |
| Ψ | expansion angle |
| e | eccentricity |
| fb0/fc0 | ultimate strength ratio of biaxial bearing and uniaxial bearing |
| μ | coefficient of viscosity |
| v | Poisson ratio |
| f′c | axial compressive strength of concrete |
| ft | tensile strength of concrete |
References
- Pan, Y.; Cai, D.; Feng, Z. Analysis and consideration of the current situation of bridge structure health monitoring technical standards. Railw. Constr. 2022, 62, 8–16. [Google Scholar]
- Jin, C.; Jang, S.; Sun, X.; Li, J.; Christenson, R. Damage detection of a highway bridge under severe temperature changes using extended Kalman filter trained neural network. J. Civ. Struct. Health Monit. 2016, 6, 545–560. [Google Scholar] [CrossRef]
- Jin, C.; Li, J.; Jang, S.; Sun, X.; Christenson, R. Structural damage detection for in-service highway bridge under operational and environmental variability. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9435, pp. 943–952. [Google Scholar]
- Farreras-Alcover, I.; Chryssanthopoulos, M.K.; Andersen, J.E. Data-based models for fatigue reliability of orthotropic steel bridge decks based on temperature, traffic and strain monitoring. Int. J. Fatigue 2017, 95, 104–119. [Google Scholar] [CrossRef]
- Sousa, H.; Bento, J.; Figueiras, J. Assessment and management of concrete bridges supported by monitoring data-based finite-element modeling. J. Bridge Eng. 2014, 19, 05014002. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, Z.; Yang, C. Refined finite element modeling of a damaged bridge with virtual distortion method coupling solid superelement. Mech. Syst. Signal Process. 2017, 93, 559–577. [Google Scholar] [CrossRef]
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of bridge structural health monitoring aided by big data and artificial intelligence: From condition assessment to damage detection. J. Struct. Eng. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Elbeltagi, E.; Hu, J.W. Estimating the dynamic behavior of highway steel plate girder bridges using real-time strain measurements. Appl. Sci. 2020, 10, 4215. [Google Scholar] [CrossRef]
- Fradelos, Y.; Thalla, O.; Biliani, I.; Stiros, S. Study of lateral displacements and the natural frequency of a pedestrian bridge using low-cost cameras. Sensors 2020, 20, 3217. [Google Scholar] [CrossRef]
- Tan, C.; Zhao, H.; O’Brien, E.J.; Uddin, N.; Fitzgerald, P.C.; McGetrick, P.J.; Kim, C.W. Extracting mode shapes from drive-by measurements to detect global and local damage in bridges. Struct. Infrastruct. Eng. 2021, 17, 1582–1596. [Google Scholar] [CrossRef]
- Wu, G.M.; Yang, D.H.; Yi, T.H.; Li, H.N.; Liu, H. Sliding life prediction of sliding bearings using dynamic monitoring data of bridges. Struct. Control Health Monit. 2020, 27, e2515. [Google Scholar] [CrossRef]
- Bao, L.; Cao, Y.; Zhao, N.; Meng, X.; Zhang, X. Application of BP neural network and curvature mode theory in bridge damage identification. J. Shenyang Archit. Univ. (Nat. Sci. Ed.) 2021, 37, 296–302. [Google Scholar]
- He, H.X.; Zheng, J.C.; Liao, L.C.; Chen, Y.J. Damage identification based on convolutional neural network and recurrence graph for beam bridge. Struct. Health Monit. 2021, 20, 1392–1408. [Google Scholar] [CrossRef]
- Tang, Y.; Yue, J.; Hua, X. Local stiffness correction of bridge finite element model based on artificial bee colony algorithm. J. Railw. Sci. Eng. 2021, 18, 2333–2343. [Google Scholar]
- Shabbir, F.; Omenzetter, P. Model updating using genetic algorithms with sequential niche technique. Eng. Struct. 2016, 120, 166–182. [Google Scholar] [CrossRef]
- He, S.; Li, Y.; Ren, W. Long-term deflection measurement analysis and prediction of long-span continuous rigid frame bridge. J. Wuhan Univ. Technol. 2014, 36, 113–115. [Google Scholar]
- Li, Y.; He, S.; Hou, W.; Ren, W. Long-term deflection calculation of bridges based on structural degradation analysis. J. Chang. Univ. (Nat. Sci. Ed.) 2014, 34, 54–59. [Google Scholar]
- Hou, N.; Sun, L.; Chen, L. Cable reliability assessments for cable-stayed bridges using identified tension forces and monitored loads. J. Bridge Eng. 2020, 25, 05020003. [Google Scholar] [CrossRef]
- Mao, L.; Lin, X.; Dai, L. Research on safety state assessment of small and medium-sized span bridges. Highw. Eng. 2020, 45, 214–219. [Google Scholar]
- Xiao, X. Reliability assessment of structural bearing capacity of steel truss bridge based on health monitoring. Railw. Stand. Des. 2020, 64, 89–95. [Google Scholar]
- Chen, Z. Fatigue reliability assessment of long-span multi-load bridges based on health monitoring system. Eng. Mech. 2014, 31, 99–105. [Google Scholar]
- Chen, C.; Wang, Z.; Gao, Q. A reliability evaluation method for concrete box girder bridges. J. Harbin Inst. Technol. 2017, 49, 113–119. [Google Scholar]
- Yue, Q.; Zhu, L. Evaluation method of bridge health status of Donghai Bridge Health Monitoring System. Bridge Constr. 2006, S2, 166–170. [Google Scholar]
- Xie, M.; Yang, Y.; Zhuang, Z.; Huang, S. Influence of structural uncertainty on probabilistic seismic demand of high-speed railway low-tower cable-stayed bridges. J. Railw. Sci. Eng. 2022, 19, 1475–1484. [Google Scholar]
- Zhang, L.; Li, M.; Liu, J.; Zhu, B. Seismic vulnerability analysis of frame-shear wall structures considering structural uncertainty. J. Nat. Disasters 2018, 27, 112–118. [Google Scholar]
- Goulet, J.A.; Kripakaran, P.; Smith, I.F. Multimodel structural performance monitoring. J. Struct. Eng. 2010, 136, 1309–1318. [Google Scholar] [CrossRef]
- Li, Q.; Lu, Q. A revised time domain force identification method based on Bayesian formulation. Int. J. Numer. Methods Eng. 2019, 118, 411–431. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Z.; Xin, Y.; Ding, Y. Modification of stochastic nonlinear model based on modular Bayesian reasoning. Vib. Shock 2023, 42, 79–88. [Google Scholar]
- Beck, J.L. Bayesian system identification based on probability logic. Struct. Control Health Monit. 2010, 17, 825–847. [Google Scholar] [CrossRef]
- Miao, N.; Zhou, H.; Mou, L.; Yan, R.; Li, L. Cgmh: Constrained sentence generation by metropolis-hastings sampling. Proc. AAAI Conf. Artif. Intell. 2019, 33, 6834–6842. [Google Scholar] [CrossRef]
- Wang, Z.; Ling, C. On the geometric ergodicity of Metropolis-Hastings algorithms for lattice Gaussian sampling. IEEE Trans. Inf. Theory 2017, 64, 738–751. [Google Scholar] [CrossRef]
- Yi, W.; Zhou, Y.; Li, H. Research on damage diagnosis of frame structure based on Bayesian statistical inference. Eng. Mech. 2009, 26, 121129. [Google Scholar]
- Sun, H.; Mordret, A.; Prieto, G.A.; Toksöz, M.N.; Büyüköztürk, O. Bayesian characterization of buildings using seismic interferometry on ambient vibrations. Mech. Syst. Signal Process. 2017, 85, 468–486. [Google Scholar] [CrossRef]
- Dey, K.K.; Bhattacharya, S. A brief review of optimal scaling of the main MCMC approaches and optimal scaling of additive TMCMC under non-regular cases. arXiv 2019, arXiv:1405.0913. [Google Scholar] [CrossRef]
- Yang, Q.; Deng, M.; Peng, Y. Urban UAV path planning based on improved beetle search algorithm. J. Syst. Simul. 2022, 1–11. [Google Scholar] [CrossRef]
- Zhang, J.; Wan, C.; Sato, T. Advanced Markov chain Monte Carlo approach for finite element calibration under uncertainty. Comput. Aided Civ. Infrastruct. Eng. 2013, 28, 522–530. [Google Scholar] [CrossRef]
- GB/T 50152-2012; The Standard for Test Methods of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
- Zhang, S.; Liu, J.; Sun, W.; Tian, Q. Effect of cracks on medium transmission in concrete. Concrete 2009, 12, 1–4. [Google Scholar]
- Xie, L. Theoretical and Experimental Research on Damage Identification of Reinforced Concrete Structures Based on Modal Flexibility. Master’s Thesis, Hunan University, Changsha, China, 2014. [Google Scholar]
- Zhou, Y.; Jia, F.; Xi, S. Experimental study on multi-model structure recognition based on Bayesian theory. J. Hunan Univ. (Nat. Sci. Ed.) 2018, 45, 36–45. [Google Scholar]
- Nie, J.; Wang, Y. Comparative study of concrete constitutive model in ABAQUS for simulating static behavior of structures. Eng. Mech. 2013, 30, 59–67, 82. [Google Scholar]
- Mansour, W. Numerical analysis of the shear behavior of FRP-strengthened continuous RC beams having web openings. Eng. Struct. 2021, 227, 111451. [Google Scholar] [CrossRef]
- Liu, L.; Wang, L.; Xiao, Z. Comparison of flexural capacity of different hollow slab beams with/without pavement layer reinforced by steel plates. Multidiscip. Model. Mater. Struct. 2022, 18, 95–110. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- Shafieifar, M.; Farzad, M.; Azizinamini, A. A comparison of existing analytical methods to predict the flexural capacity of Ultra High Performance Concrete (UHPC) beams. Constr. Build. Mater. 2018, 172, 10–18. [Google Scholar] [CrossRef]
- Duan, S.; Niu, R.; Wang, W. Research on crack propagation mechanism and crack width of double-sided composite continuous beam. J. Railw. 2012, 34, 96–101. [Google Scholar]
- Amiri, A.M.; Olfati, A.; Najjar, S.; Beiranvand, P.; Naseri Fard, M.H. The effect of fly ash on flexural capacity concrete beams. Adv. Sci. Technol. Res. J. 2016, 10, 89–95. [Google Scholar] [CrossRef]






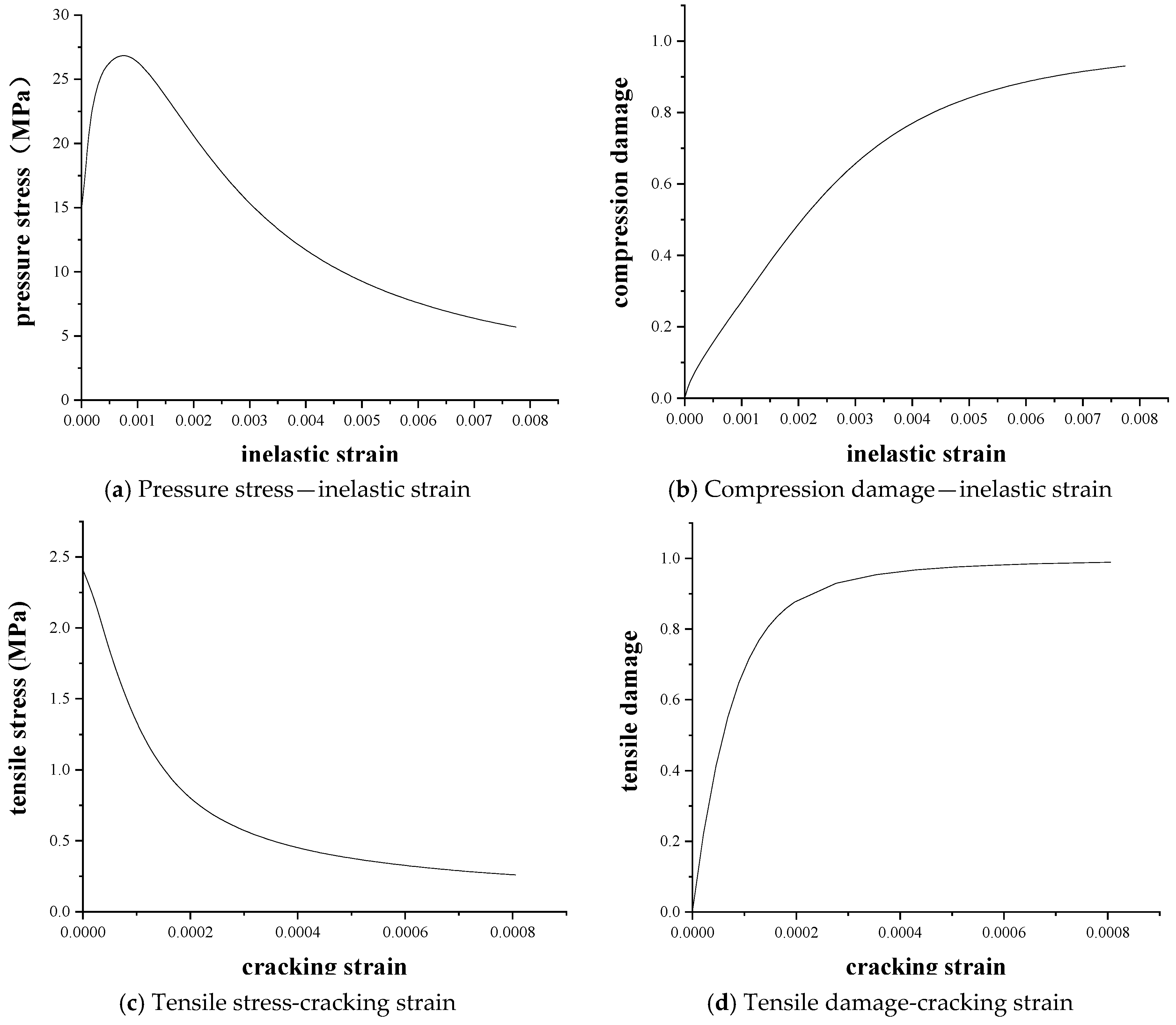

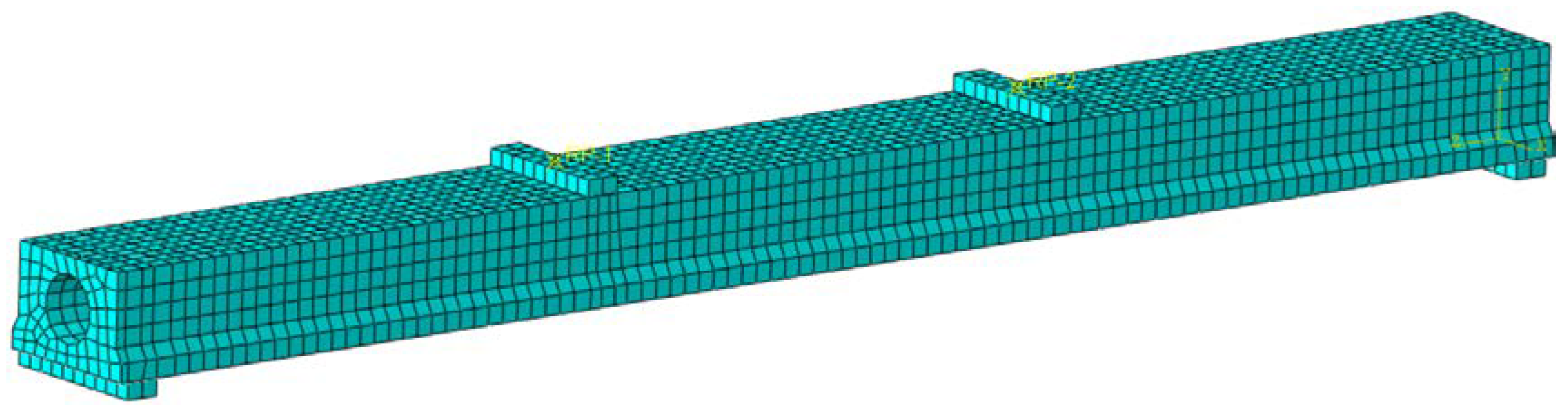




| Classification | Loading Value (kN) | Classification | Loading Value (kN) | Classification | Loading Value (kN) |
|---|---|---|---|---|---|
| preload level 1 | 5 | level 11 | 95 | level 25 | 235 |
| preload level 2 | 10 | level 12 | 105 | level 26 | 245 |
| preload level 3 | 15 | level 13 | 115 | level 27 | 255 |
| uninstall | 0 | level 14 | 125 | level 28 | 265 |
| level 1 | 5 | level 15 | 135 | level 29 | 275 |
| level 2 | 10 | level 16 | 145 | level 30 | 285 |
| level 3 | 15 | level 17 | 155 | level 31 | 295 |
| level 4 | 25 | level 18 | 165 | level 32 | 305 |
| level 5 | 35 | level 19 | 175 | level 33 | 315 |
| level 6 | 45 | level 20 | 185 | level 34 | 350 |
| level 7 | 55 | level 21 | 195 | level 35 | 365 |
| level 8 | 65 | level 22 | 205 | level 36 | 380 |
| level 9 | 75 | level 23 | 215 | level 37 | 395 |
| level 10 | 85 | level 24 | 225 | level 38 | 410 |
| Model Components | Parameter Lower Limit | Parameter Upper Limit | Number of Samples | Proportional Spacing |
|---|---|---|---|---|
| elastic modulus E | 0.9 E0 | 1.5 E0 | 15 | linear average |
| Density ρ | 0.6 ρ0 | 1.2 ρ0 | 15 | linear average |
| support stiffness K | 0.01 K0 | 100 K0 | 15 | logarithmic average |
| Parameter | Reference Value |
|---|---|
| ψ | 36° |
| e | 0.1 |
| fb0/fc0 | 1.16 |
| K | 0.667 |
| μ | 0.0005 |
| Parameter | E0 (MPa) | v | f′c (MPa) | ft (MPa) |
|---|---|---|---|---|
| Reference Value | 32,500 | 0.2 | 26.8 | 2.4 |
| Parameter | E (MPa) | Yield Stress (MPa) | Yield Strain | Ultimate Strength (MPa) | Ultimate Strain | |
|---|---|---|---|---|---|---|
| HRB335 | 210,000 | 0.3 | 335 | 0.00160 | 510 | 0.01884 |
| HPB235 | 210,000 | 0.3 | 235 | 0.00120 | 310 | 0.04200 |
| Standardized Key Parameters | Improved MH Algorithm (500 Sample Models) | TMCMC Algorithm (500 Sample Models) | TMCMC Algorithm (300 Sample Models) |
|---|---|---|---|
| E | 0.97 | 1.06 | 1.09 |
| ρ | 1.03 | 0.98 | 1.02 |
| K | 0.91 | 1.02 | 0.93 |
| Crack Width (mm) | Test Measured Value (kN) | Predicted Value of Improved MH Algorithm (kN) | Relative Error | Predicted Value of TMCMC Algorithm (kN) | Relative Error |
|---|---|---|---|---|---|
| 0.13 | 100.1 | 96.9 | 3.2% | 97.8 | 2.3% |
| 0.14 | 108.6 | 105.4 | 3.0% | 106.1 | 2.3% |
| 0.15 | 120.0 | 116.1 | 3.3% | 118.4 | 1.4% |
| 0.16 | 127.4 | 125.3 | 1.7% | 124.6 | 2.2% |
| 0.17 | 138.2 | 135.7 | 1.8% | 134.4 | 2.8% |
| 0.18 | 151.2 | 146.9 | 2.9% | 147.7 | 2.4% |
| 0.19 | 169.8 | 167.7 | 1.3% | 166.3 | 2.1% |
| 0.20 | 192.3 | 188.8 | 1.9% | 190.3 | 1.1% |
| 0.21 | 211.7 | 206.5 | 2.5% | 208.2 | 1.7% |
| 0.22 | 232.0 | 228.2 | 1.7% | 229.1 | 1.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Xiao, Z.; Yu, F.; Li, W.; Fu, N. Research on an Optimized Evaluation Method of the Bearing Capacity of Reinforced Concrete Beam Based on the Bayesian Theory. Materials 2023, 16, 2489. https://doi.org/10.3390/ma16062489
Wang L, Xiao Z, Yu F, Li W, Fu N. Research on an Optimized Evaluation Method of the Bearing Capacity of Reinforced Concrete Beam Based on the Bayesian Theory. Materials. 2023; 16(6):2489. https://doi.org/10.3390/ma16062489
Chicago/Turabian StyleWang, Lifeng, Ziwang Xiao, Fei Yu, Wei Li, and Ning Fu. 2023. "Research on an Optimized Evaluation Method of the Bearing Capacity of Reinforced Concrete Beam Based on the Bayesian Theory" Materials 16, no. 6: 2489. https://doi.org/10.3390/ma16062489
APA StyleWang, L., Xiao, Z., Yu, F., Li, W., & Fu, N. (2023). Research on an Optimized Evaluation Method of the Bearing Capacity of Reinforced Concrete Beam Based on the Bayesian Theory. Materials, 16(6), 2489. https://doi.org/10.3390/ma16062489






