Experimental Investigation on Shear Capacity of Steel-Fiber-Reinforced High-Strength Concrete Corbels
Abstract
:1. Introduction
2. Test Overview
2.1. Specimen Design
2.2. Test Setup and Instrumentation
2.3. Material Properties
3. Test Discussion and Results
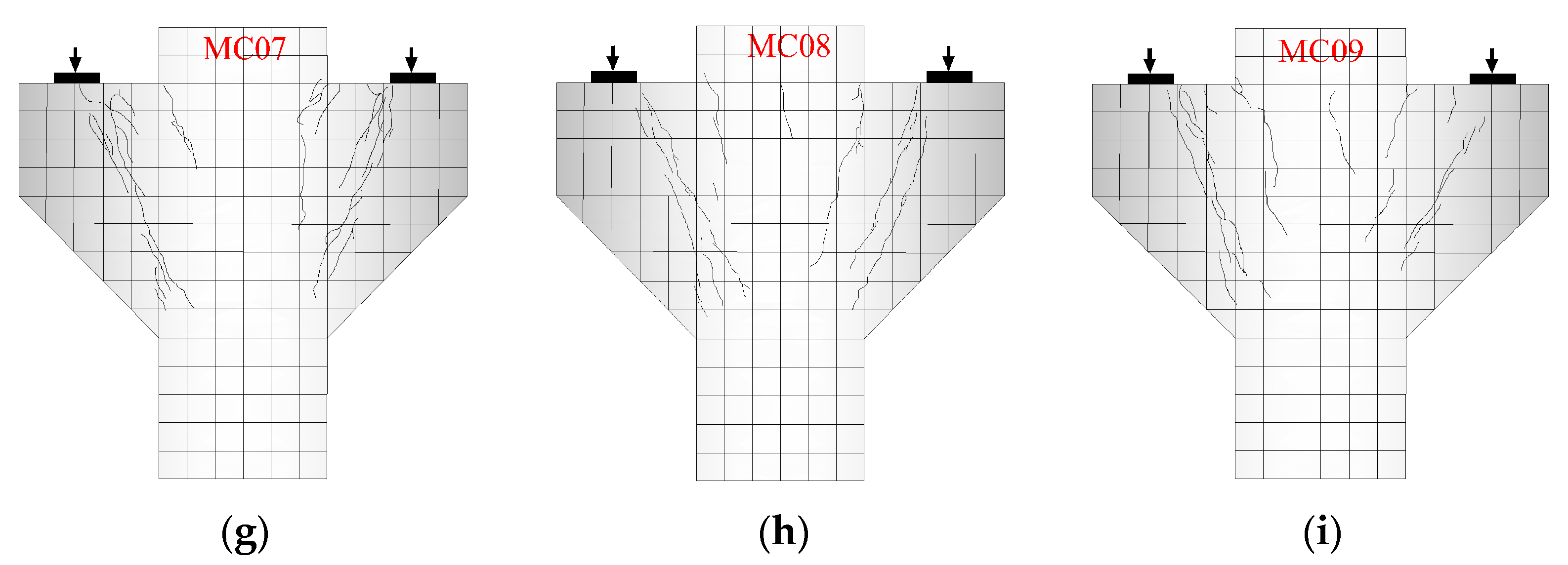
3.1. Failure Mode of Corbel with Small Shear Span/Depth Ratio
3.2. Failure Process of Corbel with Small Shear Span/Depth Ratio
3.3. Concrete Strain of Corbels Normal Section and Diagonal Section
3.4. Strain of Longitudinal Bars in Corbel
4. Influencing Factors of Shear Capacity of Corbels
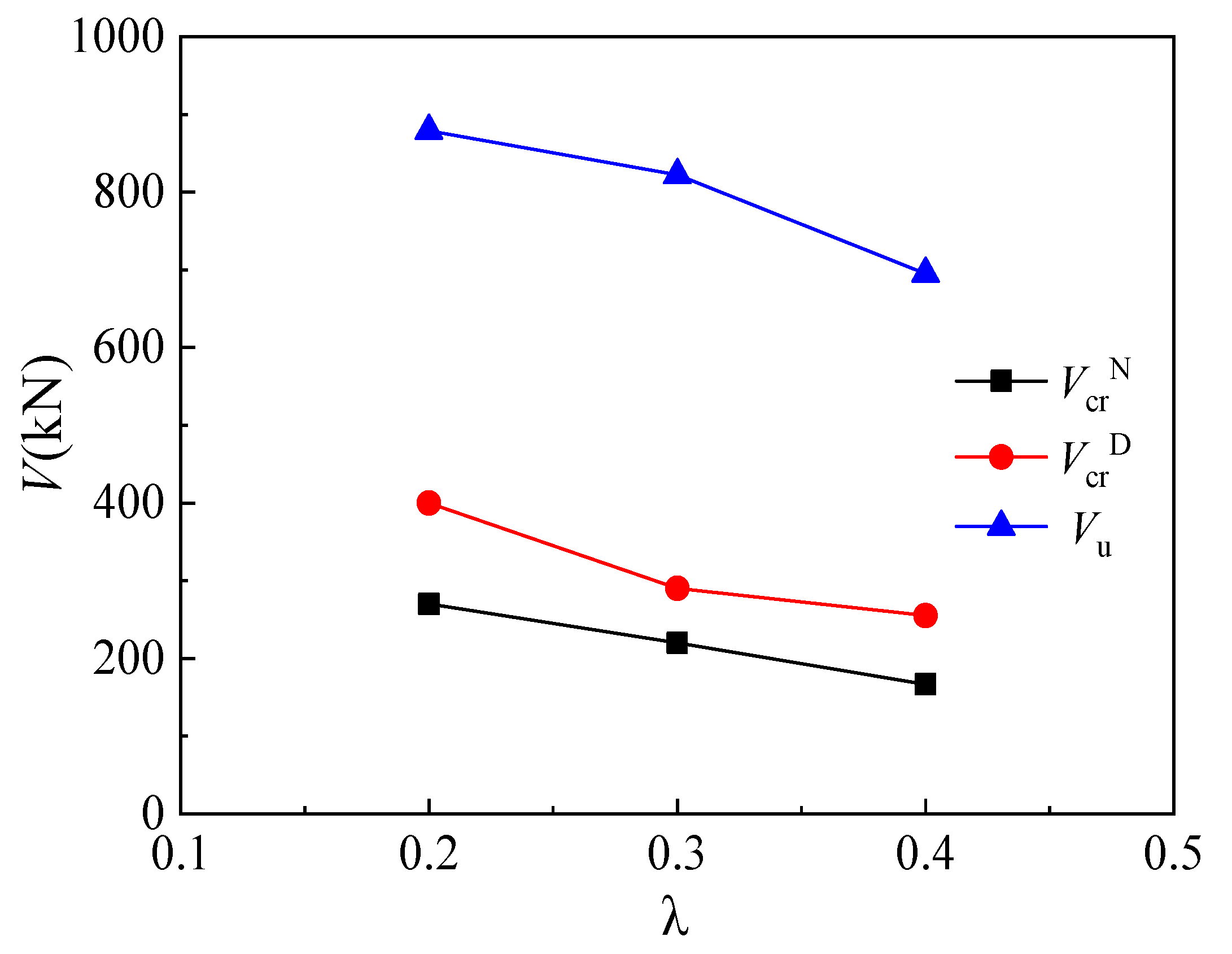
4.1. Shear Span/Depth Ratio
4.2. Longitudinal Reinforcement Ratio
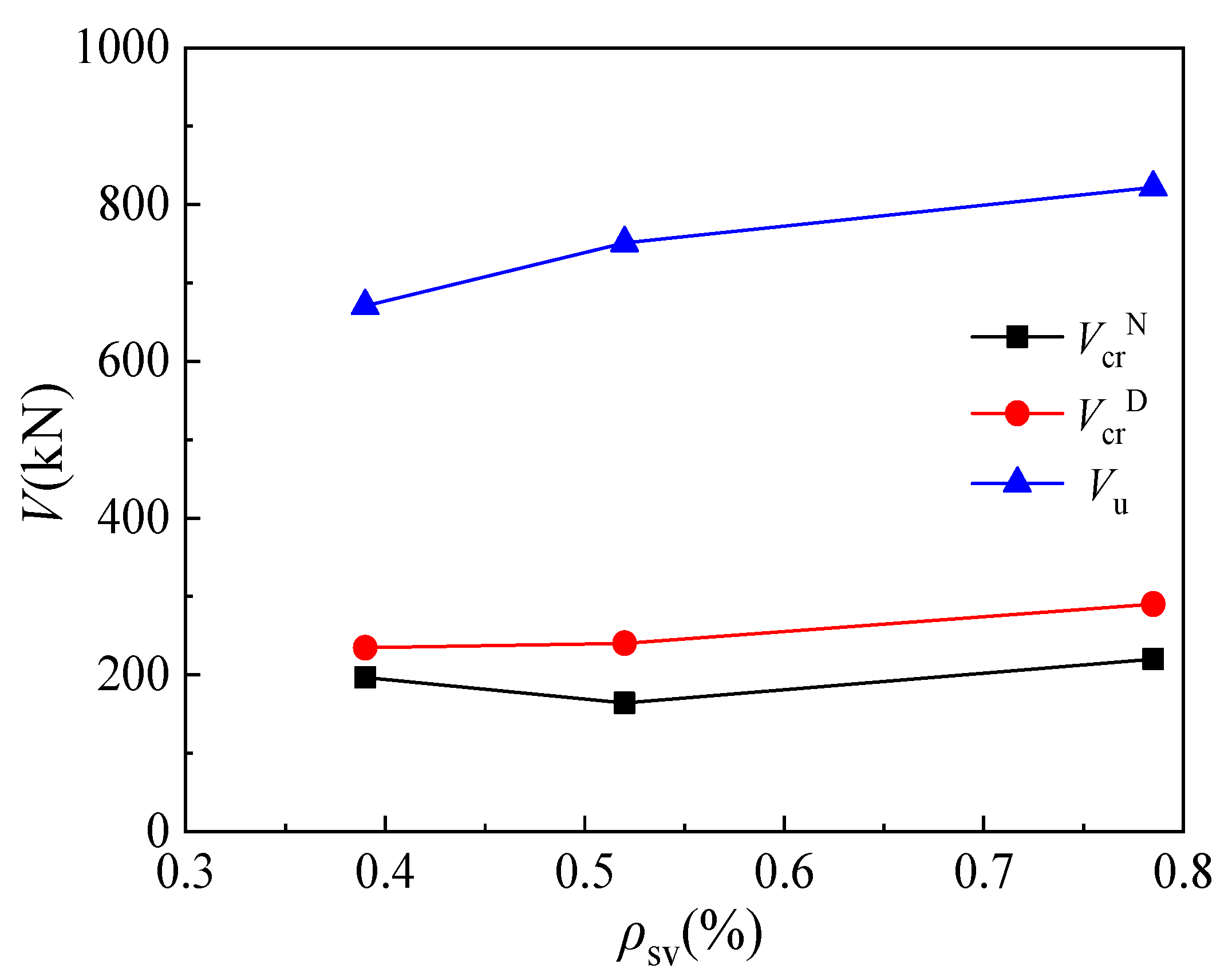
4.3. Stirrup Ratio
4.4. Steel Fiber Content
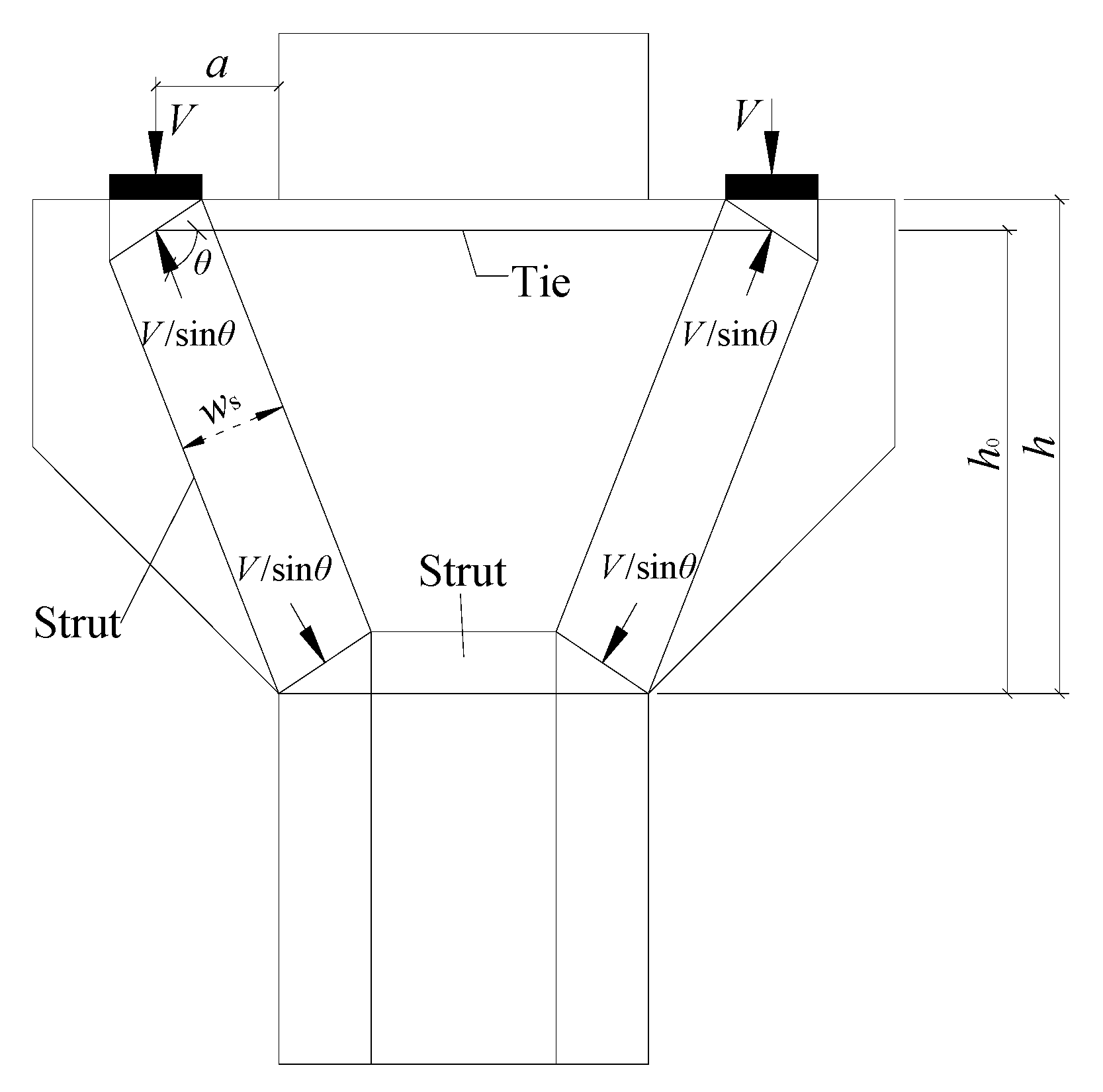
5. Calculation Method of Shear Capacity of Corbel
5.1. GB 50010-2010 Code
5.2. ACI 318-19 Code
5.3. EN 1992-1-1:2004 Code
5.4. CSA A23.3-19 Code
5.5. Comparative Analysis of Test Results
6. Conclusions
- (1)
- Steel-fiber-reinforced high-strength concrete corbel specimens with a shear span/depth ratio ranging from 0.2 to 0.4 exhibit two typical failure modes: inclined compression failure and inclined shear failure. With the decrease in shear span/depth ratio, the shear effect along the cylinder surface is increasingly apparent, and the failure mode transforms from diagonal compression failure to diagonal shear failure. At the same time, the effects of longitudinal reinforcement and stirrup gradually decrease.
- (2)
- The shear span/depth ratio exerts a significant influence on the shear performance of steel-fiber-reinforced high-strength concrete corbels, and the bearing capacity decreases obviously with an increase in the shear span/depth ratio. For a given shear span/depth ratio, the shear capacity of a corbel specimen under concentrated loads is greatly affected by the longitudinal reinforcement ratio, followed by the stirrup reinforcement ratio and the steel fiber content.
- (3)
- Under the same shear span/depth ratio, the cracking load increases with the increase in steel fiber content. Moreover, the second influence results from the stirrup reinforcement ratio, followed by the longitudinal reinforcement ratio.
- (4)
- The calculation values of the shear capacity of steel fiber high-strength concrete corbel specimens with GB 50010-2010 are close to the test values. It is important to note that the empirical formula used in GB 50010-2010 is based on ordinary concrete corbel specimens. While the prediction results of the ACI 318-19 code, EN 1992-1-1:2004 code, and CSA A23.3-19 code using the strut-and-tie model are more conservative, it is generally considered as an alternative design scheme.
- (5)
- It is worth noting that these conclusions are based on the test results of multivariate finite specimens. Further research is needed to thoroughly study corbels with different steel fiber content.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| λ | shear span-to-depth ratio, dimensionless |
| ρs | longitudinal reinforcement ratio, dimensionless |
| ρsh | stirrup reinforcement ratio, dimensionless |
| fcu | concrete compressive strength, MPa |
| ρf | steel fiber content, MPa |
| h0 | the effective height of section, mm |
| a | shear span length, mm |
| b | width of the specimen section, mm |
| fy | yield strength for reinforcement, MPa |
| fc’ | ultimate strength for reinforcement, MPa |
| ϕc | resistance coefficient of concrete, dimensionless |
| ε1 | principal tensile strain |
| ws | width of the diagonal strut, mm |
| As | cross-sectional area of the compression bar, mm2 |
| V | shear bearing force of the corbel, kN |
| θs | minimum angle between the concrete diagonal strut and the steel tie connected to it, and the American code stipulates it should not be less than 25° |
| fc | prism compressive strength of concrete, MPa |
| εs | tensile strain of the longitudinal reinforcement, dimensionless |
| θ | minimum value of the angle between the compression strut and the node |
| diagonal cracking load, kN | |
| cracking load of the normal section, kN | |
| γc | the sub-coefficient of concrete γc is 1.5 in persistent state and 1.2 in accidental state, dimensionless |
| αcc | coefficient considering the adverse effect of long-term effect and load type on compressive strength, the recommended value in code is 0.85, dimensionless |
| σRd,max | effective compressive strength of concrete in compression bar, MPa |
| fcd | compressive strength value of concrete, MPa |
| ν | reduction coefficient, dimensionless |
| fce | yield strength of the longitudinal reinforcement |
| βs | strength reduction coefficient after cracking of the strut, dimensionless |
| Fns | normal shear force of the concrete strut |
| fce | nominal compressive strength of the concrete strut, MPa |
| βc | strength coefficient by the influence of concrete confinement on the effective compressive strength of a strut or node, dimensionless |
| Vn | ultimate load, kN |
| Ec | elastic modulus of steel fiber, GPa |
| ft | steel fiber concrete tensile strength, MPa |
References
- Abdul-Razzaq, K.S.; Dawood, A.A.; Mohammed, A.H. A Review of Previous Studies on the Reinforced Concrete Corbels. IOP Conf. Ser. Mater. Sci. Eng. 2019, 518, 022057. [Google Scholar] [CrossRef]
- Khosravikia, F.; Kim, H.S.; Yi, Y.; Wilson, H.; Yousefpour, H.; Hrynyk, T.; Bayrak, O. Experimental and Numerical Assessment of Corbels Designed Based on Strut-and-Tie Provisions. J. Struct. Eng. ASCE 2018, 144, 134. [Google Scholar] [CrossRef]
- Kassem, W. Strength Prediction of Corbels Using Strut-and-Tie Model Analysis. Int. J. Concr. Struct. Mater. 2015, 9, 255–266. [Google Scholar] [CrossRef] [Green Version]
- Hafez, A.; Ahmed, M.M. Shear behaviour of high strength fiber reinforced concrete corbels. J. Struct. Eng. ASCE 2012, 40, 969–987. [Google Scholar] [CrossRef]
- Wadekar, A.P.; Kakade, D.N. The Behavior of Reinforced Concrete Corbels with Steel Fibers and Shear Strength Prediction. IJIRSET. ASCE 2016, 5, 14979–14987. [Google Scholar] [CrossRef]
- Thomas, H.K.; Kim, S.; Shin, J.H.; LaFave, J.M. Seismic Behavior of Exterior Beam-Column Connections with High-Strength Materials and Steel Fibers. ACI Struct. J. 2019, 116, 31–43. [Google Scholar] [CrossRef]
- Ghassan, A.; Shih-Ho, C. A New Reinforcing Configuration for Achieving High-Ductility and High-Strength Rectangular Squat Structural Walls. ACI Struct. J. 2023, 120, 253–268. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Z.; Wen, C.; Cheng, S.; Wei, Y. Prediction model for the flexural strength of steel fiber reinforced concrete beams with fiber–reinforced polymer bars under repeated loading. Compos. Struct. 2020, 250, 112609. [Google Scholar] [CrossRef]
- GB50010–2010; Code for Design of Concrete Structures. China Construction Industry Press: Beijing, China, 2010.
- ACI 318 Committee. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- BS EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures: Part 1: General Rules and Rules for Buildings. British Standards Institution: Brussels, Belgium, 2004.
- CSA A23.3:19; Design of Concrete Structures. Canadian Standards Association: Mississauga, ON, Canada, 2004.
- Ring, J.D.; Tanne, J.E. Evaluation of Masonry Beams with Openings and Validation Using a Strut-and-Tie Model. J. Struct. Eng. ASCE 2021, 147, 33. [Google Scholar] [CrossRef]
- Faleh, A.B. Shear strength of reinforced concrete beam–column joints. Asian J. Civ. Eng. 2022, 24, 33. [Google Scholar] [CrossRef]
- Liu, L.Q.; Wang, J.J. Research on strut-and-tie model based on tests of simply supported reinforced concrete deep beams. Build. Struct. 2013, 34, 137–143. [Google Scholar]
- Panatchai, C.; Jaruek, T.; Sukit, D. Modified interactive strut-and-tie modeling of reinforced concrete deep beams and corbels. J. Struct. 2022, 45, 284–298. [Google Scholar] [CrossRef]
- Xing, G.H.; Liu, B.Q.; Niu, D.T. Shear strength of reinforced concrete frame joints using modified softened strut-and-tie model. J. Eng. Mech. 2013, 30, 60–66. [Google Scholar]
- Wael, K. Strut-and-tie modelling for the analysis and design of RC beam-column joints. J. Mater. Struct. 2016, 49, 18. [Google Scholar] [CrossRef]
- Fattuhi, N.I. Strength of SFRC corbels subjected to vertical load. J. Struct. Eng. ASCE 1990, 116, 701–718. [Google Scholar] [CrossRef]
- Fattuhi, N.I. Strength of FRC corbels in flexure. J. Struct. Eng. ASCE 1994, 120, 360–377. [Google Scholar] [CrossRef]
- Yong, Y.; Baraguru, P. Behavior of reinforced high-strength concrete corbels. J. Struct. Eng. ASCE 1994, 120, 1182–1201. [Google Scholar] [CrossRef]
- Foster, S.J.; Powell, R.E.; Selim, H.S. Performance of high strength concrete corbels. ACI Struct. J. 1996, 93, 555–563. [Google Scholar]
- Hwang, S.J.; Lu, W.Y.; Lee, H.J.; Yong, Y.; Baraguru, P. Shear strength prediction for reinforced concrete corbels. ACI Struct. J. 2000, 97, 543–552. [Google Scholar] [CrossRef]
- Russo, G.; Venir, R.; Pauletta, M.; Somma, G.S. Reinforced concrete corbels-Shear strength model and design formula. ACI Struct. J. 2006, 103, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Campione, G.; La, M.L.; Mangiavillano, M.L. Steel fibers reinforced concrete corbels: Experimental behavior and shear strength prediction. ACI Struct. J. 2007, 104, 570–579. [Google Scholar] [CrossRef]
- Gao, J.F.; Qiu, H.X.; Jiang, Y.S. Investigation on design method of the steel-fiber high-strength concrete bracket. J. Southeast Univ. 1993, 23, 41–46. [Google Scholar]
- Gao, D.Y.; Zhao, J.; Zhu, H.T. Experimental study on shear capacity of reinforced concrete corbel with steel fiber. J. Build. Struct. 2006, 27, 100–106. [Google Scholar]
- Gao, D.Y.; Zhu, H.T.; Xu, L. Experimental study on flexural capacity of steel fiber reinforced concrete corbel with reinforcement. J. Hydro. Struct. 2005, 24, 68–72. [Google Scholar]
- Chen, L.H.; Yuan, M.L.; Zhan, Y.X. Experimental study on carrying capability of corbels of small shear span-depth ratio. J. Hohai Univ. 2008, 36, 550–553. [Google Scholar]
- Gulsan, M.E.; Cevik, A.; Mohmmad, S.H. Crack pattern and failure mode prediction of SFRC corbels: Experimental and numerical study. J. Comp. Concr. 2021, 28, 507–519. [Google Scholar] [CrossRef]
- Faleh, S.K.; Chkheiwer, A.H.; Saleh, I.S. Structural behavior of high-strength concrete corbels involving steel fibers or closed stirrups. J. Period. Eng. Nat. Sci. 2022, 10, 239–252. [Google Scholar] [CrossRef]
- Ferdous, W.; Bai, Y.; Almutairi, A.D.; Satasivam, S.; Jeske, J. Modular assembly of water-retaining walls using GFRP ho-llow profiles: Components and connection performance. Compos. Struct. 2018, 194, 1–11. [Google Scholar] [CrossRef]
- Huang, Y.; Yin, W.; Yi, W. Study on Design Modification Factor for Shear Capacity of Reinforced Concrete Corbels. J. Hunan Univ. Nat. Sci. 2021, 48, 61–70. [Google Scholar]
- CECS 38:2004; Technical Specification for Fiber Reinfored Concrete Structures. China Planning Press: Beijing, China, 2004.
- Khalifa, E.S. Macro-mechanical strut and tie model for analysis of fibrous high-strength concrete corbels. Ain Shames Eng. J. 2012, 3, 359–365. [Google Scholar] [CrossRef] [Green Version]
- Abdul-Razzaq, K.S.; Dawood, A.A. Reinforcing struts and ties in concrete corbels. ACI Struct. J. 2021, 118, 153–162. [Google Scholar] [CrossRef]
- Yang, J.M.; Lee, J.H.; Yoon, Y.S. Influence of Steel Fibers and Headed Bars on the Serviceability of High-Strength Concrete Corbels. J. Struct. Eng. ASCE 2012, 138, 123–129. [Google Scholar] [CrossRef]
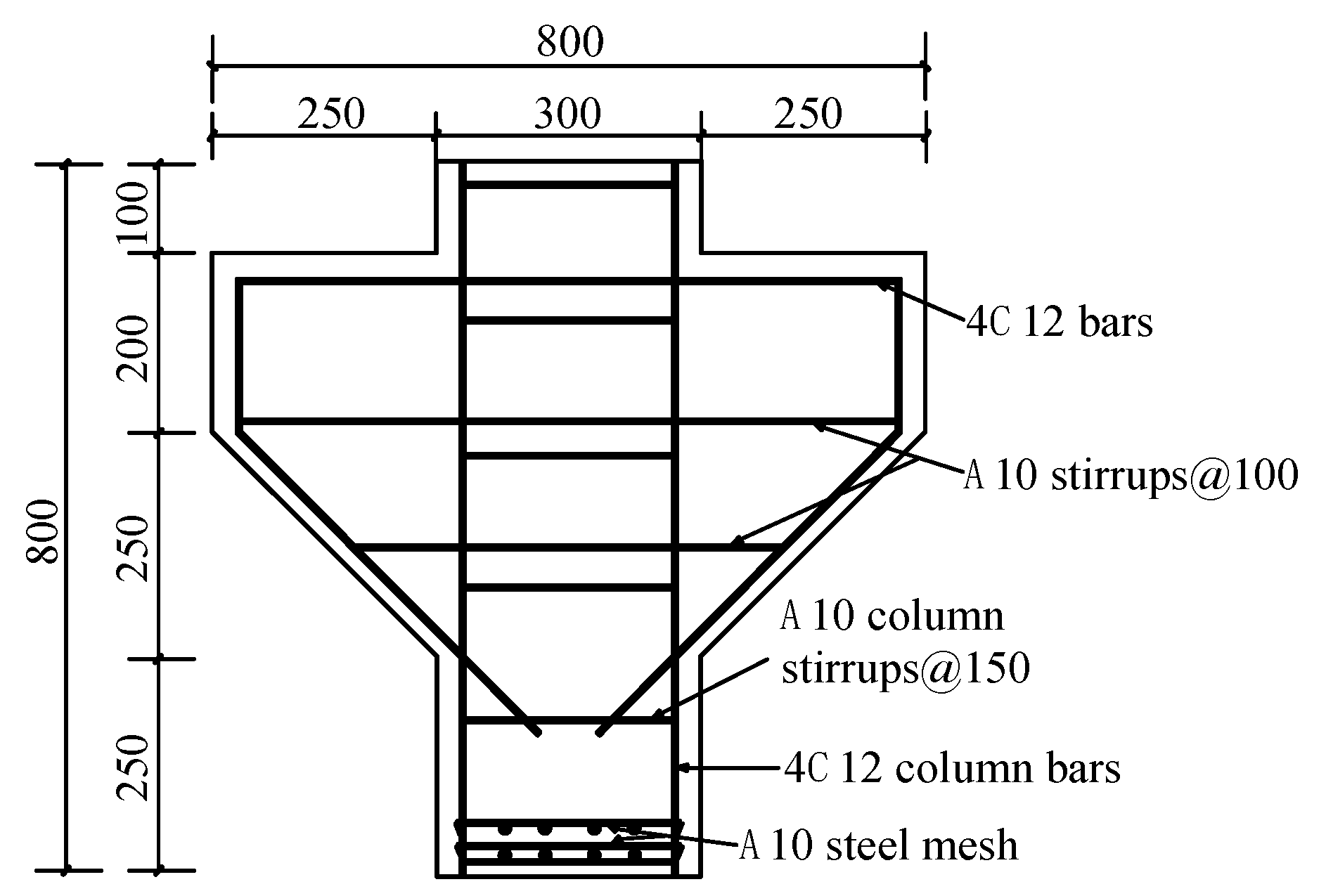










| Specimen Number | Shear Span/Depth Ratio λ | Longitudinal Reinforcement Ratio ρs (%) | Stirrup Reinforcement Ratio ρsh (%) | Steel Fiber Content ρf (%) | fy /MPa | fys /MPa | fcu /MPa | ft /MPa |
|---|---|---|---|---|---|---|---|---|
| MC01 | 0.2 | 0.55 | 0.785 | 1.5 | 425.2 | 333.7 | 72.6 | 3.6 |
| MC02 | 0.3 | 0.55 | 0.785 | 1.5 | 425.2 | 333.7 | 72.6 | 3.6 |
| MC03 | 0.4 | 0.55 | 0.785 | 1.5 | 425.2 | 333.7 | 72.6 | 3.6 |
| MC04 | 0.3 | 0.75 | 0.785 | 1.5 | 425.2 | 333.7 | 72.6 | 3.6 |
| MC05 | 0.3 | 0.98 | 0.785 | 1.5 | 425.2 | 333.7 | 72.6 | 3.6 |
| MC06 | 0.3 | 0.55 | 0.39 | 1.5 | 425.2 | 333.7 | 72.6 | 3.6 |
| MC07 | 0.3 | 0.55 | 0.52 | 1.5 | 425.2 | 333.7 | 72.6 | 3.6 |
| MC08 | 0.3 | 0.55 | 0.785 | 0 | 425.2 | 333.7 | 73.2 | 4 |
| MC09 | 0.3 | 0.55 | 0.785 | 0.75 | 425.2 | 333.7 | 69.8 | 3.3 |
| Number | Water (kg) | Cement (kg) | Sand (kg) | Stone (kg) | Superplasticizer (kg) | Steel Fiber (kg) |
|---|---|---|---|---|---|---|
| MC01 | C60 | 573.3 | 681.9 | 1022.8 | 8.6 | 117 |
| MC02 | C60 | 573.3 | 681.9 | 1022.8 | 8.6 | 117 |
| MC03 | C60 | 573.3 | 681.9 | 1022.8 | 8.6 | 117 |
| MC04 | C60 | 573.3 | 681.9 | 1022.8 | 8.6 | 117 |
| MC05 | C60 | 573.3 | 681.9 | 1022.8 | 8.6 | 117 |
| MC06 | C60 | 573.3 | 681.9 | 1022.8 | 8.6 | 117 |
| MC07 | C60 | 573.3 | 681.9 | 1022.8 | 8.6 | 117 |
| MC08 | C60 | 500 | 612 | 1188 | 7.5 | 0 |
| MC09 | C60 | 533.35 | 702.35 | 1054 | 8 | 58.5 |
| Steel Fiber Content ρf/% | Concrete Strength (MPa) | fcu (MPa) | fc (MPa) | Ec (GPa) |
|---|---|---|---|---|
| 0 | C60 | 73.2 | 55.9 | 38.7 |
| 0.75 | C60 | 69.8 | 51.7 | 37.6 |
| 1.5 | C60 | 72.6 | 49.8 | 37.2 |
| Specimen Number (λ) | Test Values Vtest (kN) | Calculated Values Vc(kN) | Vtest/Vc | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GB 50010-2010 | ACI318- 19 | EN 1992-1- 1:2004 | CSA A23.3 -19 | GB 50010-2010 | ACI318- 19 | EN 1992-1- 1:2004 | CSA A23.3 -19 | ||
| MC01 (0.2) | 879.0 | 716.40 | 456.38 | 479.19 | 473.67 | 1.227 | 1.926 | 1.834 | 1.856 |
| MC02 (0.3) | 822.0 | 477.60 | 423.22 | 444.37 | 417.22 | 1.721 | 1.942 | 1.850 | 1.970 |
| MC03 (0.4) | 695.0 | 358.20 | 390.33 | 409.83 | 363.60 | 1.940 | 1.781 | 1.696 | 1.911 |
| MC04 (0.3) | 874.0 | 648.53 | 423.22 | 444.37 | 417.22 | 1.348 | 2.065 | 1.967 | 2.095 |
| MC05 (0.3) | 981.5 | 844.89 | 423.22 | 444.37 | 417.22 | 1.162 | 2.319 | 2.209 | 2.352 |
| MC06 (0.3) | 670.5 | 477.60 | 423.22 | 444.37 | 417.22 | 1.404 | 1.584 | 1.509 | 1.607 |
| MC07 (0.3) | 751.0 | 477.60 | 423.22 | 424.54 | 417.22 | 1.572 | 1.774 | 1.690 | 1.800 |
| MC08 (0.3) | 775.0 | 477.60 | 404.82 | 424.54 | 399.08 | 1.623 | 1.914 | 1.826 | 1.942 |
| MC09 (0.3) | 767.0 | 477.60 | 427.22 | 448.62 | 421.16 | 1.606 | 1.795 | 1.710 | 1.821 |
| Mean | 1.511 | 1.900 | 1.810 | 1.928 | |||||
| Square | 0.055 | 0.038 | 0.035 | 0.038 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.-S.; Zheng, J.-Y.; Zhang, J.-H.; Li, H.-M.; Guo, G.-Q.; Chen, A.-J.; Xie, W. Experimental Investigation on Shear Capacity of Steel-Fiber-Reinforced High-Strength Concrete Corbels. Materials 2023, 16, 3055. https://doi.org/10.3390/ma16083055
Li S-S, Zheng J-Y, Zhang J-H, Li H-M, Guo G-Q, Chen A-J, Xie W. Experimental Investigation on Shear Capacity of Steel-Fiber-Reinforced High-Strength Concrete Corbels. Materials. 2023; 16(8):3055. https://doi.org/10.3390/ma16083055
Chicago/Turabian StyleLi, Shu-Shan, Jin-Yan Zheng, Jun-Hong Zhang, Hong-Mei Li, Gui-Qiang Guo, Ai-Jiu Chen, and Wei Xie. 2023. "Experimental Investigation on Shear Capacity of Steel-Fiber-Reinforced High-Strength Concrete Corbels" Materials 16, no. 8: 3055. https://doi.org/10.3390/ma16083055







