An Approach to the Automated Characterization of Out-of-Plane and In-Plane Local Defect Resonances
Abstract
1. Introduction
- Possibility of investigating structures with multiple defects;
- Detection of multiple frequencies (and their mode shapes) for the same defect, which is needed for in-plane LDRs extraction associated with higher-order modes;
- Possibility of examining structures without a priori knowledge of defects’ locations or limits regarding their size.
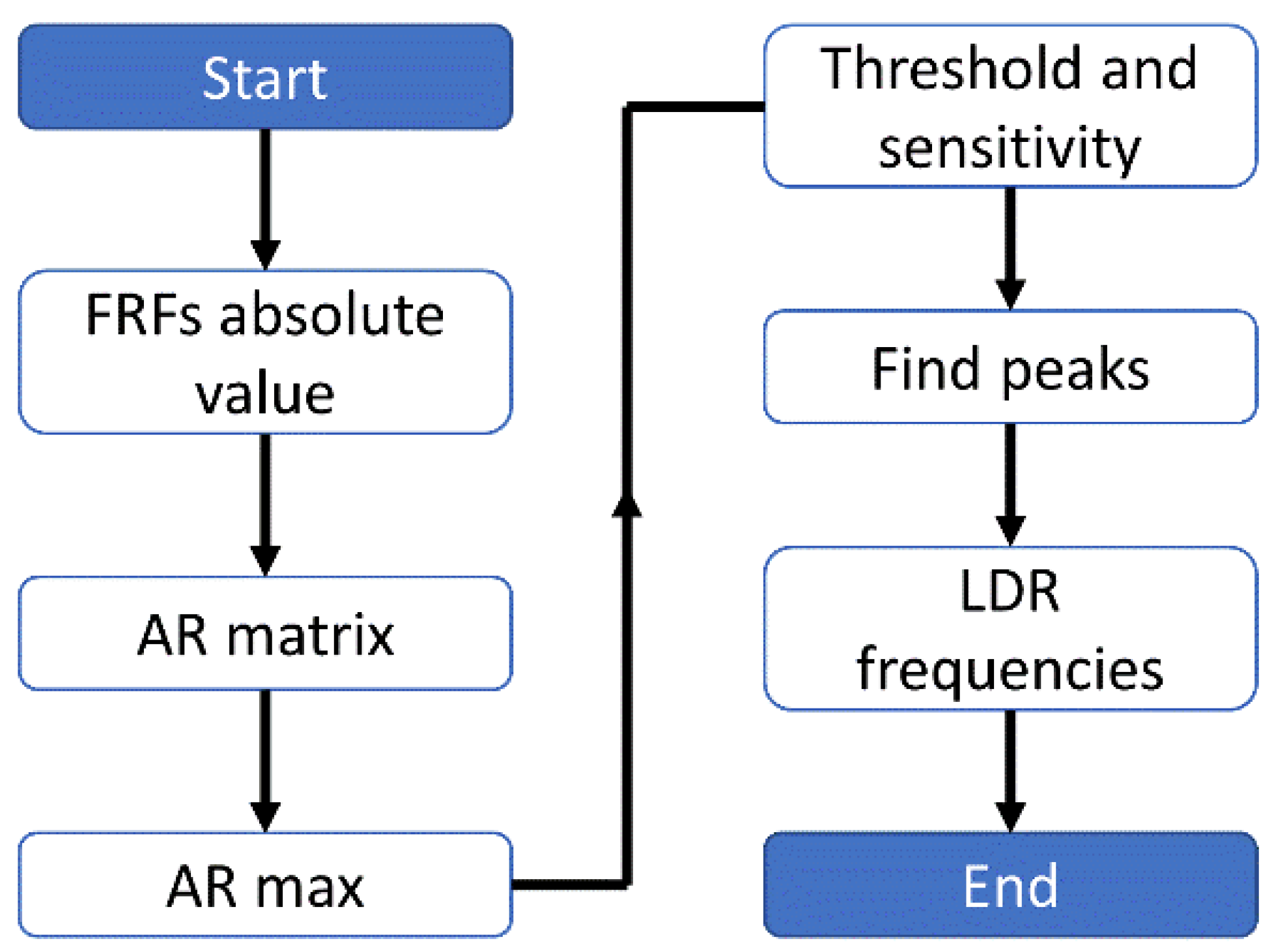
2. Materials and Methods
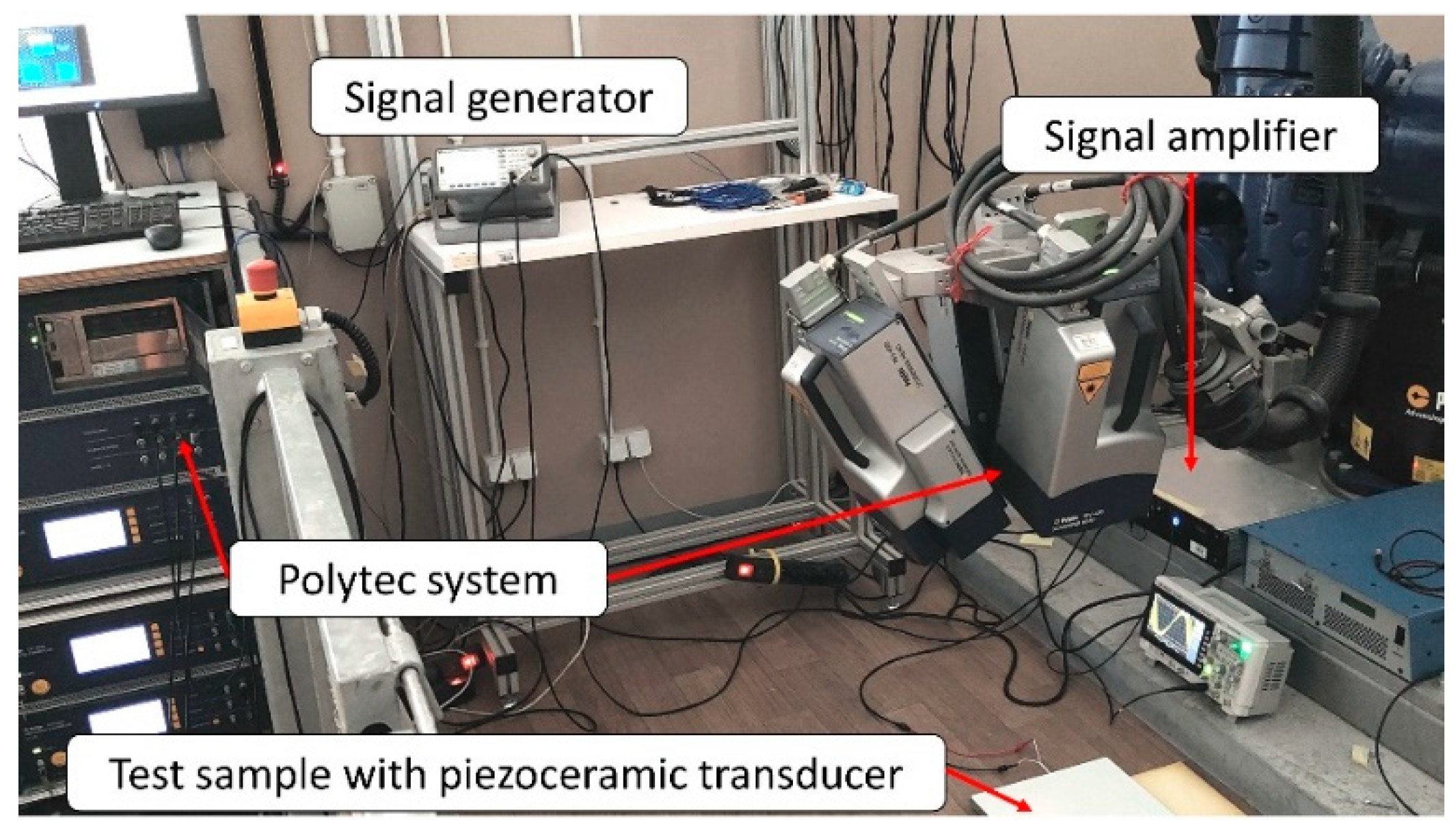
3. Examination Setup
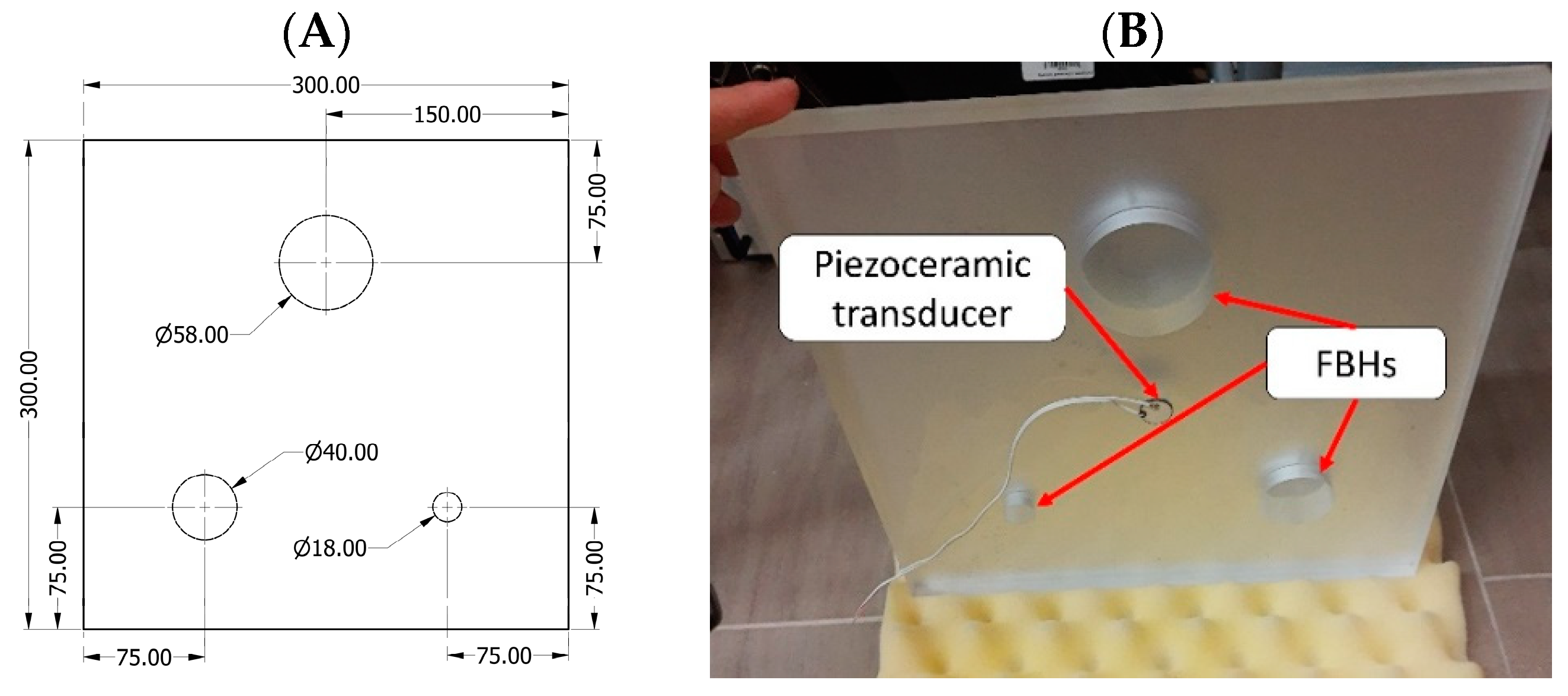
3.1. Test Sample with FBHs
3.2. Experimental Modal Analysis
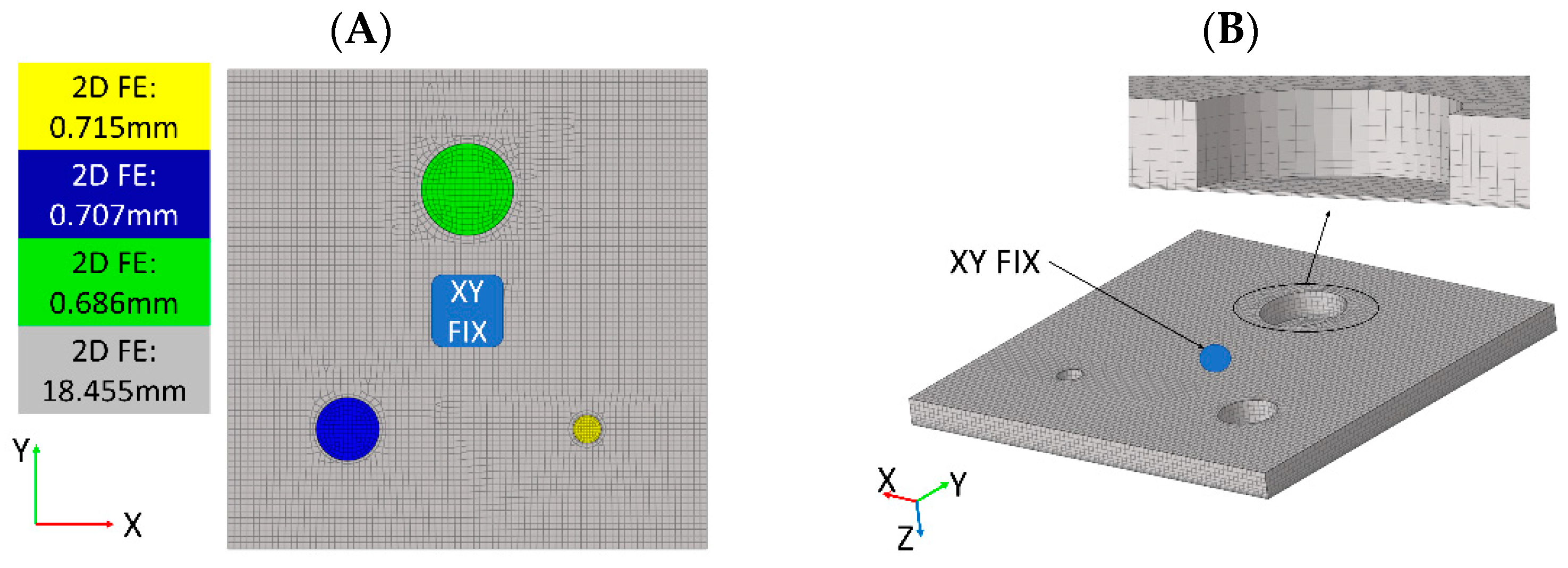
3.3. Numerical Models
4. Results and Discussion
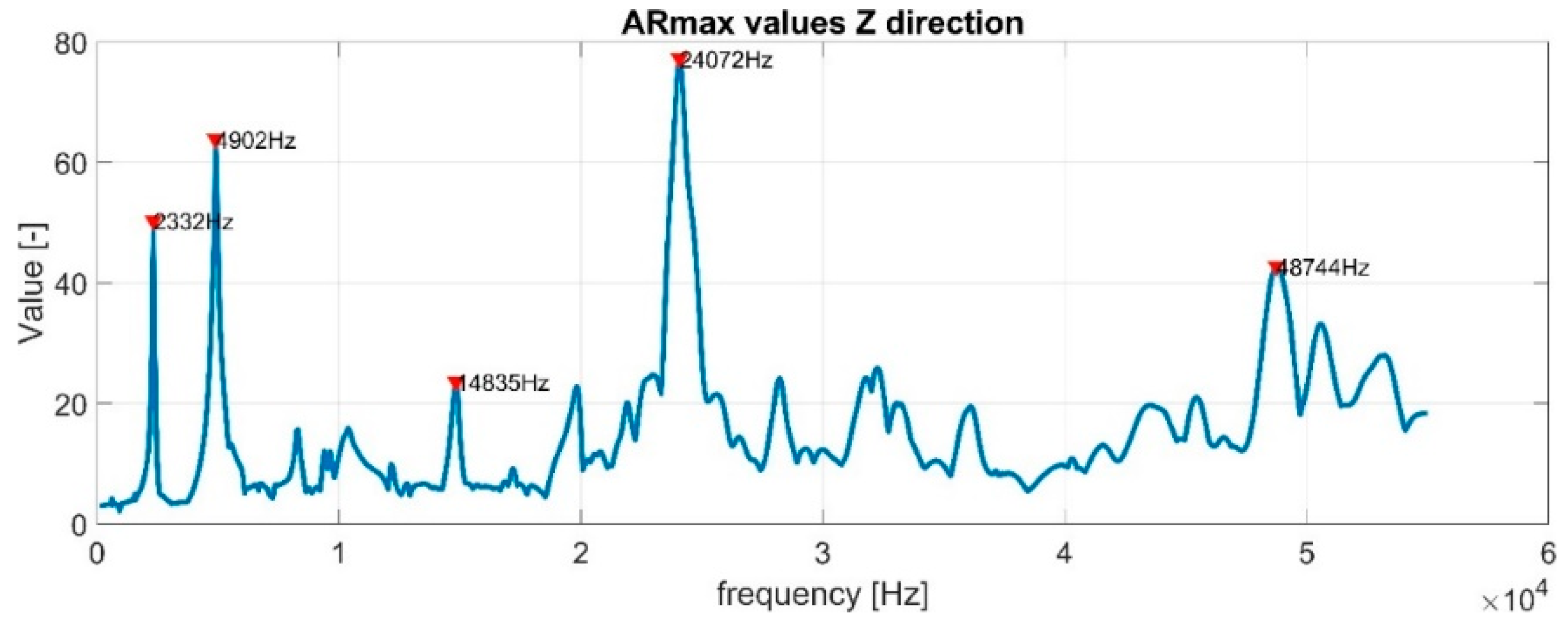
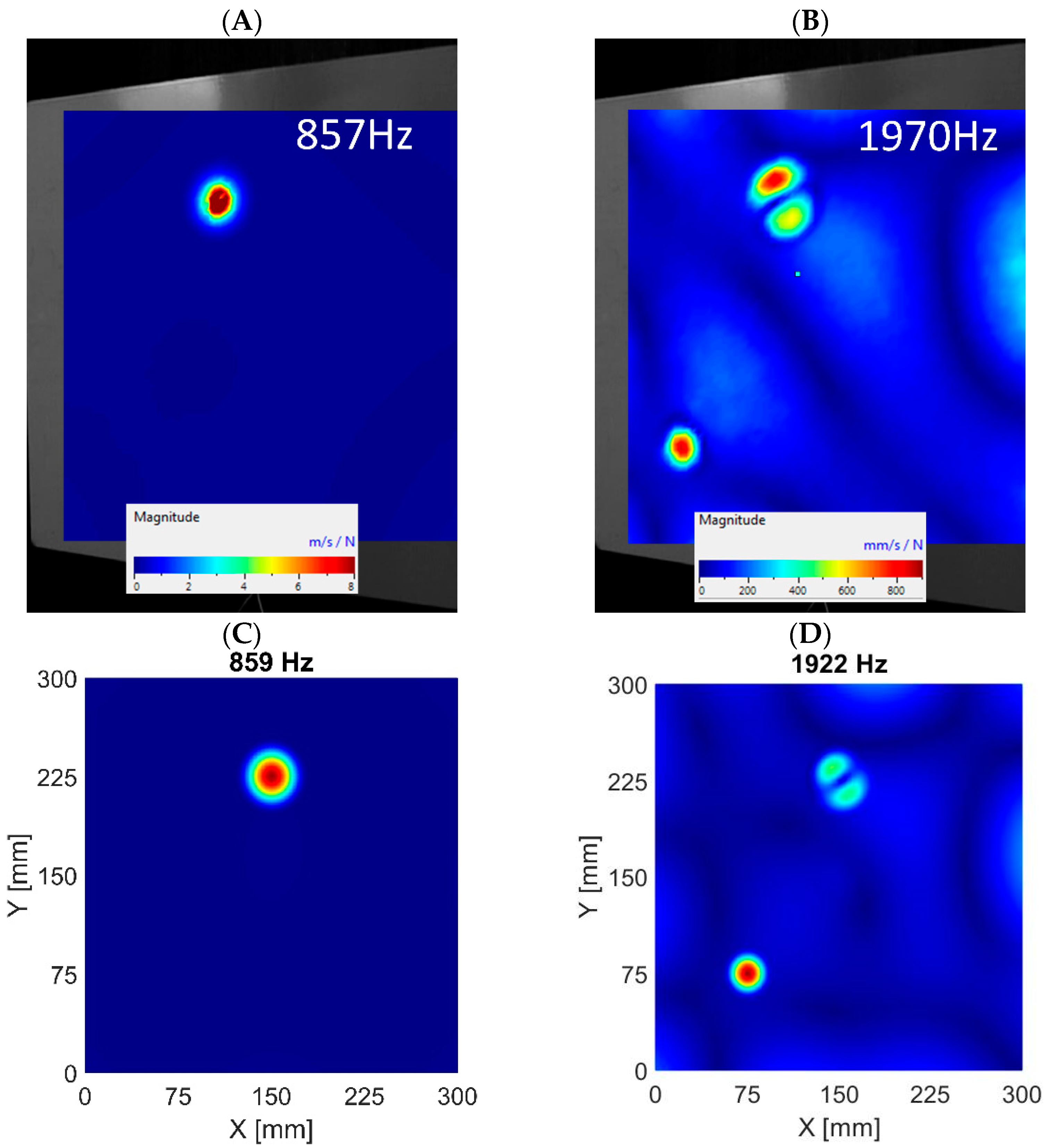
4.1. Out-of-Plane LDRs
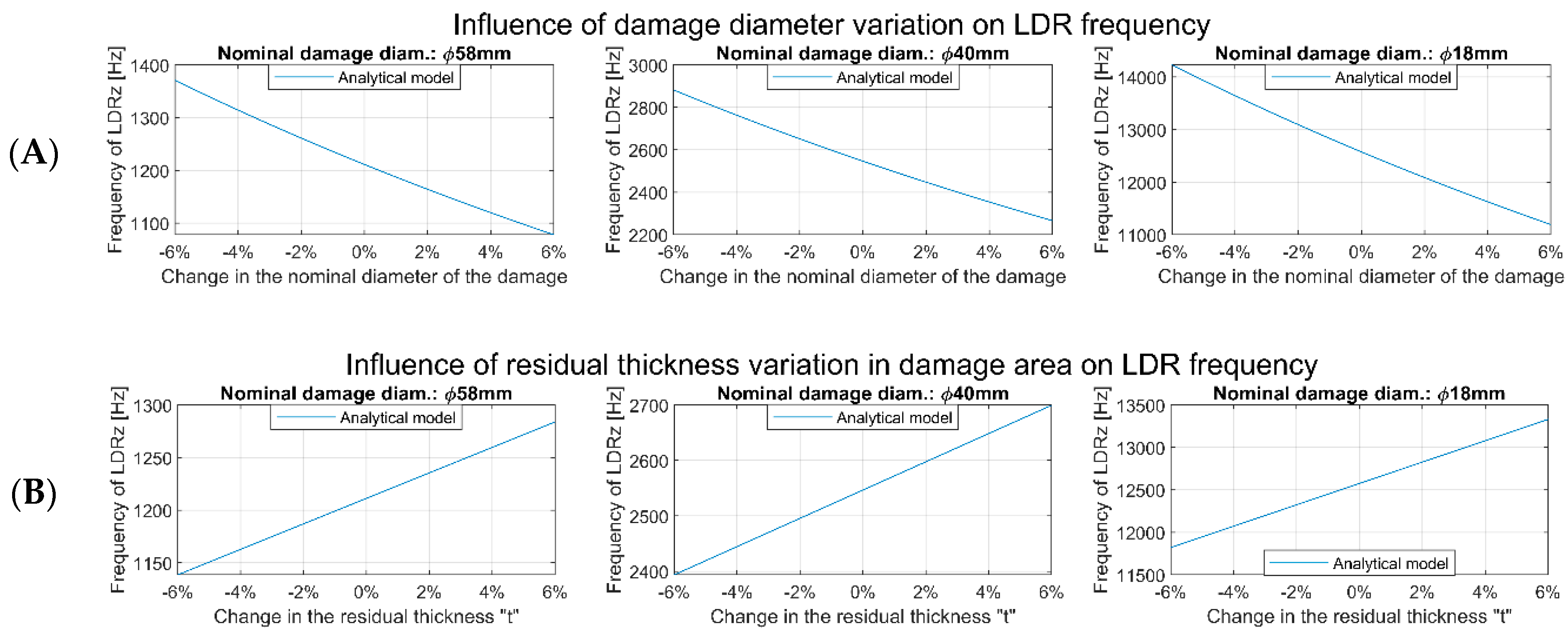
4.2. Damage Size Assessment
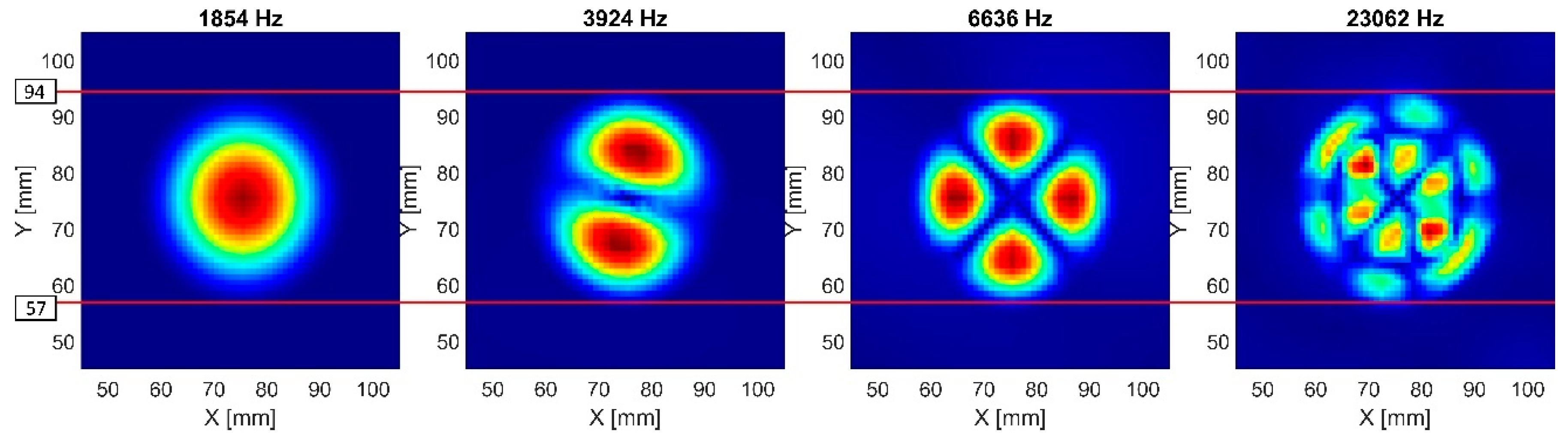
4.3. In-Plane LDRs
5. Conclusions
- A novel algorithm for the automatic extraction of LDRs was developed. The algorithm was successfully implemented to identify out-of-plane and in-plane modes of LDRs. Various datasets, including experimental and numerical data of a test specimen with FBH of different diameters, were examined;
- The algorithm allowed the determination of higher-order LDR modes, which usually better represented FBH shape and size. Finding higher-order LDRs was also essential to correctly extract in-plane modes. This feature was a significant improvement compared to the current state-of-the-art methods;
- Two numerical models based on the FEM were developed. One employed 3D FEs, and the other was based on 2D FEs. The algorithm worked successfully with the results provided by both models;
- The indicated LDRs proved that, in most cases, the 2D model was sufficient for determining FBH-type out-of-plane LDRs. The recorded error between corresponding LDRs in experiments and results of the 2D FE model was less than 3%. On the other hand, a false negative indication was noted for this dataset. The results provided by the 3D FE model were better fitted with an actual structure, which corresponded with the relative error of less than 2% in out-of-plane modes;
- The 3D FE numerical model allowed the capturing of in-plane modes of FBHs more accurately than the 2D FE model. The errors of in-plane LDRs called into question the applicability of the 2D modeling technique to represent in-plane modes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moore, P.O. Nondestructive Testing Overview; The American Society for Nondestructive Testing: Columbus, OH, USA, 2012; ISBN 978-1-57117-187-0. [Google Scholar]
- Stepinski, T.; Uhl, T.; Staszewski, W. Advanced Structural Damage Detection: From Theory to Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-1-118-53612-4. [Google Scholar]
- Kundu, T. Nonlinear Ultrasonic and Vibro-Acoustical Techniques for Nondestructive Evaluation; Springer International Publishing AG: Cham, Switzerland, 2019; ISBN 978-3-319-94474-6. [Google Scholar]
- Delsanto, P.P. Universality of Nonclassical Nonlinearity: Applications to Non-Destructive Evaluations and Ultrasonics; Springer: New York, NY, USA, 2006; ISBN 978-0-387-33860-6. [Google Scholar]
- Jhang, K. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Pieczonka, L.; Klepka, A.; Martowicz, A.; Staszewski, W.J. Nonlinear vibroacoustic wave modulations for structural damage detection: An overview. Opt. Eng. 2015, 55, 011005. [Google Scholar] [CrossRef]
- Broda, D.; Mendrok, K.; Silberschmidt, V.V.; Pieczonka, L.; Staszewski, W.J. The Study of Localized Crack-Induced Effects of Nonlinear Vibro-Acoustic Modulation. Materials 2023, 16, 1653. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Choi, S.; Jhang, K.Y.; Kim, T. Experimental Verification of Contact Acoustic Nonlinearity at Rough Contact Interfaces. Materials 2021, 14, 2988. [Google Scholar] [CrossRef] [PubMed]
- Solodov, I.; Bai, J.; Bekgulyan, S.; Busse, G. A Local Defect Resonance to Enhance Acoustic Wave-Defect Interaction in Ultrasonic Nondestructive Evaluation. Appl. Phys. Lett. 2011, 99, 211911. [Google Scholar] [CrossRef]
- Solodov, I.; Bai, J.; Busse, G. Resonant Ultrasound Spectroscopy of Defects: Case Study of Flat-Bottomed Holes. J. Appl. Phys. 2013, 113, 223512. [Google Scholar] [CrossRef]
- Solodov, I. Resonant Acoustic Nonlinearity of Defects for Highly-Efficient Nonlinear NDE. J. Nondestruct. Eval. 2014, 33, 252–262. [Google Scholar] [CrossRef]
- Pieczonka, L.; Zietek, L.; Klepka, A.; Staszewski, W.J.; Aymerich, F.; Uhl, T. Damage Imaging in Composites Using Nonlinear Vibro-Acoustic Wave Modulations. Struct. Control Health Monit. 2018, 25, e2063. [Google Scholar] [CrossRef]
- Hedayatrasa, S.; Segers, J.; Poelman, G.; Paepegem, W.V.; Kersemans, M. Vibro-Thermal Wave Radar: Application of Barker Coded Amplitude Modulation for Enhanced Low-Power Vibrothermographic Inspection of Composites. Materials 2021, 14, 2436. [Google Scholar] [CrossRef] [PubMed]
- Solodov, I.; Rahammer, M.; Kreutzbruck, M. Analytical Evaluation of Resonance Frequencies for Planar Defects: Effect of a Defect Shape. NDT E Int. 2019, 102, 274–280. [Google Scholar] [CrossRef]
- Derusova, D.A.; Vavilov, V.P.; Druzhinin, N.V.; Shpil’noi, V.Y.; Pestryakov, A.N. Detecting Defects in Composite Polymers by Using 3D Scanning Laser Doppler Vibrometry. Materials 2022, 15, 7176. [Google Scholar] [CrossRef] [PubMed]
- Hettler, J.; Tabatabaeipour, M.; Delrue, S.; van den Abeele, K. Detection and Characterization of Local Defect Resonances Arising from Delaminations and Flat Bottom Holes. J. Nondestruct. Eval. 2017, 36, 2. [Google Scholar] [CrossRef]
- Segers, J.; Kersemans, M.; Hedayatrasa, S.; Calderon, J.; van Paepegem, W. Towards in-Plane Local Defect Resonance for Non-Destructive Testing of Polymers and Composites. NDT E Int. 2018, 98, 130–133. [Google Scholar] [CrossRef]
- Segers, J.; Hedayatrasa, S.; Verboven, E.; Poelman, G.; van Paepegem, W.; Kersemans, M. In-Plane Local Defect Resonances for Efficient Vibrothermography of Impacted Carbon Fiber-Reinforced Polymers (CFRP). NDT E Int. 2019, 102, 218–225. [Google Scholar] [CrossRef]
- Roy, S.; Bose, T.; Debnath, K. Detection of Local Defect Resonance Frequencies Using Bicoherence Analysis. J. Sound Vib. 2019, 443, 703–716. [Google Scholar] [CrossRef]
- Roy, S.; Bose, T. Efficient Determination of Local Defect Resonance Frequencies from Bicoherence Plots Using Double Excitations. Mech. Syst. Signal Process. 2019, 127, 595–609. [Google Scholar] [CrossRef]




| Dimension Type | Nominal Value | Identified Values |
|---|---|---|
| Thickness of plate | 18 mm | 18.455 mm |
| FBH “Ø58 mm” diameter | 58 mm | 57.646 mm |
| FBH “Ø58 mm” residual thickness | 1 mm | 0.686 mm |
| FBH “Ø40 mm” diameter | 40 mm | 39.64 mm |
| FBH “Ø40 mm” residual thickness | 1 mm | 0.707 mm |
| FBH “Ø18 mm” diameter | 18 mm | 17.566 mm |
| FBH “Ø18 mm” residual thickness | 1 mm | 0.715 mm |
| Parameter | Value |
|---|---|
| Young’s modulus | 4919 MPa |
| Poisson ratio | 0.4 |
| Density | 1.204 g/cm3 |
| Model with 2D FEs | Model with 3D FEs | ||||
|---|---|---|---|---|---|
| Global Mode | Experiment | Simulation | Error | Simulation | Error |
| ‘A’ | 478 Hz | 476 Hz | 0.4% | 480 Hz | 0.4% |
| ‘B’ | 1207 Hz | 1121 Hz | 7.1% | 1151 Hz | 4.6% |
| ‘C’ | 2360 Hz | 2181 Hz | 7.6% | 2296 Hz | 2.7% |
| The Model with 2D FEs | The Model with 3D FEs | |||||
|---|---|---|---|---|---|---|
| Defect Type | Experiment | Simulation | Error | Simulation | Error | |
| First LDR (out-of-plane) | FBH Ø58 mm | 857 Hz | 855 Hz | 0.23% | 859 Hz | 0.23% |
| FBH Ø40 mm | 1867 Hz | 1859 Hz | 0.43% | 1854 Hz | 0.70% | |
| FBH Ø18 mm | 9189 Hz | 9455 Hz | 2.90% | 9250 Hz | 0.67% | |
| Second LDR (out-of-plane) | FBH Ø58 mm | Not found | Not found | --- | Not found | --- |
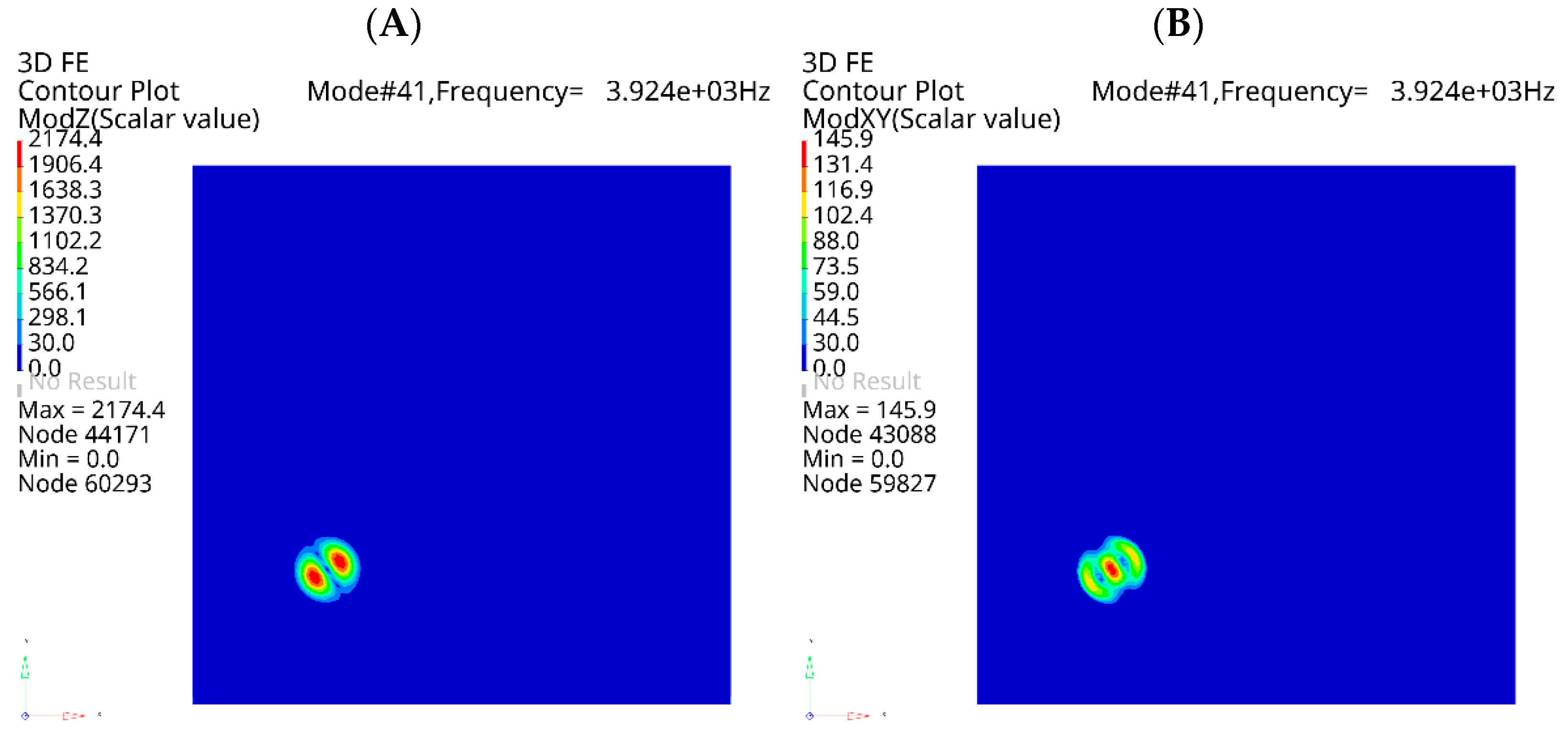
| FBH Ø40 mm | 3997 Hz | Not found | --- | 3924 Hz | 1.83% | |
| FBH Ø18 mm | 19,350 Hz | 19,771 Hz | 2.18% | 19,684 Hz | 1.73% | |
| The Model with 2D FEs | The Model with 3D FEs | ||||
|---|---|---|---|---|---|
| Defect Type | Experiment | Simulation | Error | Simulation | Error |
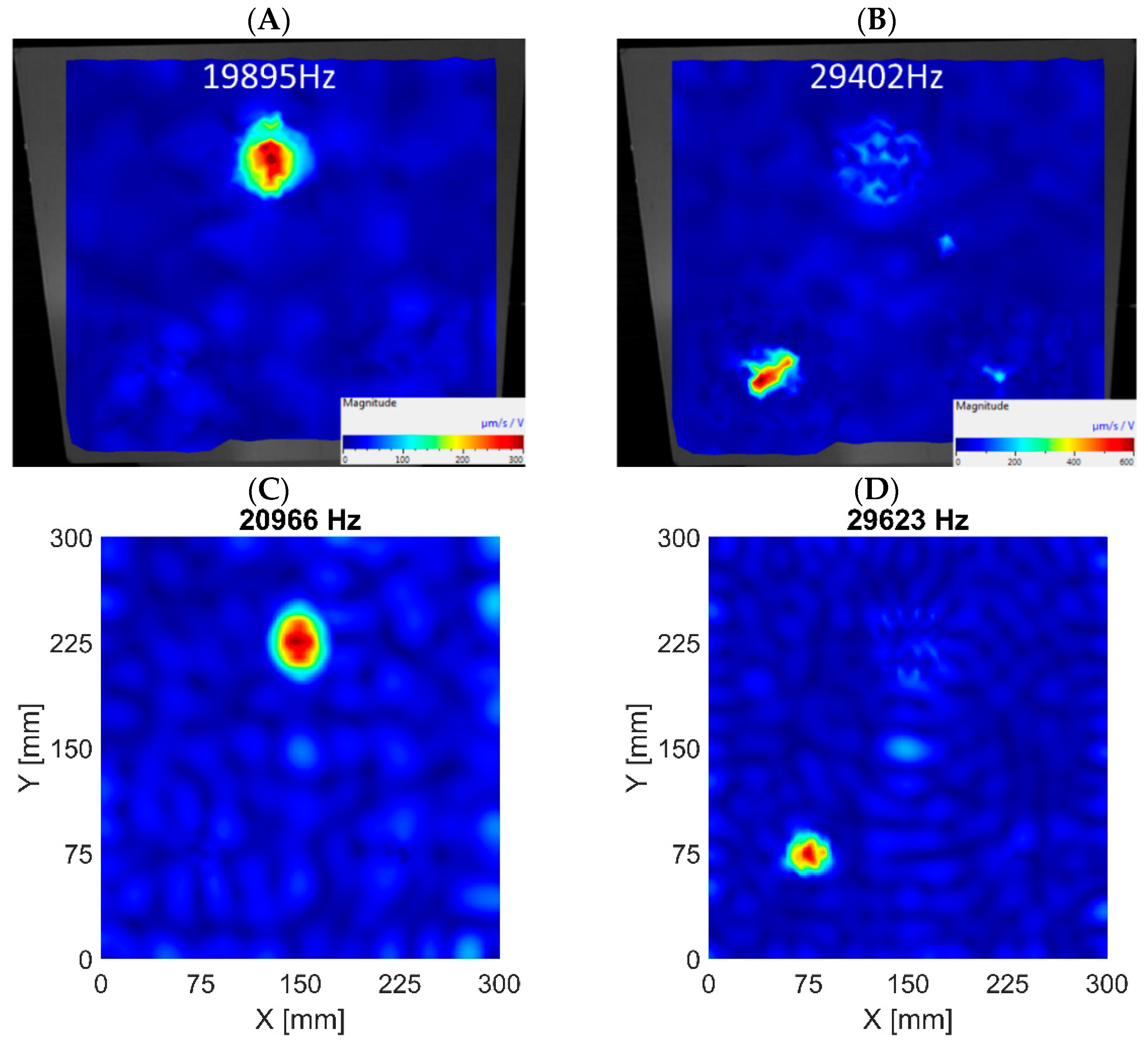
| FBH Ø58 mm | 19,895 Hz | 23,164 Hz | 16.43 % | 20,966 Hz | 5.38% |
| FBH Ø40 mm | 29,402 Hz | 33,443 Hz | 13.74 % | 29,623 Hz | 0.75% |
| FBH Ø18 mm | Not found | Not found | --- | Not found | --- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zdziebko, P.; Krzemiński, M.; Okoń, M.; Loi, G.; Aymerich, F.; Pieczonka, Ł.; Klepka, A. An Approach to the Automated Characterization of Out-of-Plane and In-Plane Local Defect Resonances. Materials 2023, 16, 3084. https://doi.org/10.3390/ma16083084
Zdziebko P, Krzemiński M, Okoń M, Loi G, Aymerich F, Pieczonka Ł, Klepka A. An Approach to the Automated Characterization of Out-of-Plane and In-Plane Local Defect Resonances. Materials. 2023; 16(8):3084. https://doi.org/10.3390/ma16083084
Chicago/Turabian StyleZdziebko, Paweł, Mateusz Krzemiński, Maciej Okoń, Gabriela Loi, Francesco Aymerich, Łukasz Pieczonka, and Andrzej Klepka. 2023. "An Approach to the Automated Characterization of Out-of-Plane and In-Plane Local Defect Resonances" Materials 16, no. 8: 3084. https://doi.org/10.3390/ma16083084
APA StyleZdziebko, P., Krzemiński, M., Okoń, M., Loi, G., Aymerich, F., Pieczonka, Ł., & Klepka, A. (2023). An Approach to the Automated Characterization of Out-of-Plane and In-Plane Local Defect Resonances. Materials, 16(8), 3084. https://doi.org/10.3390/ma16083084








