A Review of Ultrathin Piezoelectric Films
Abstract
:1. Introduction
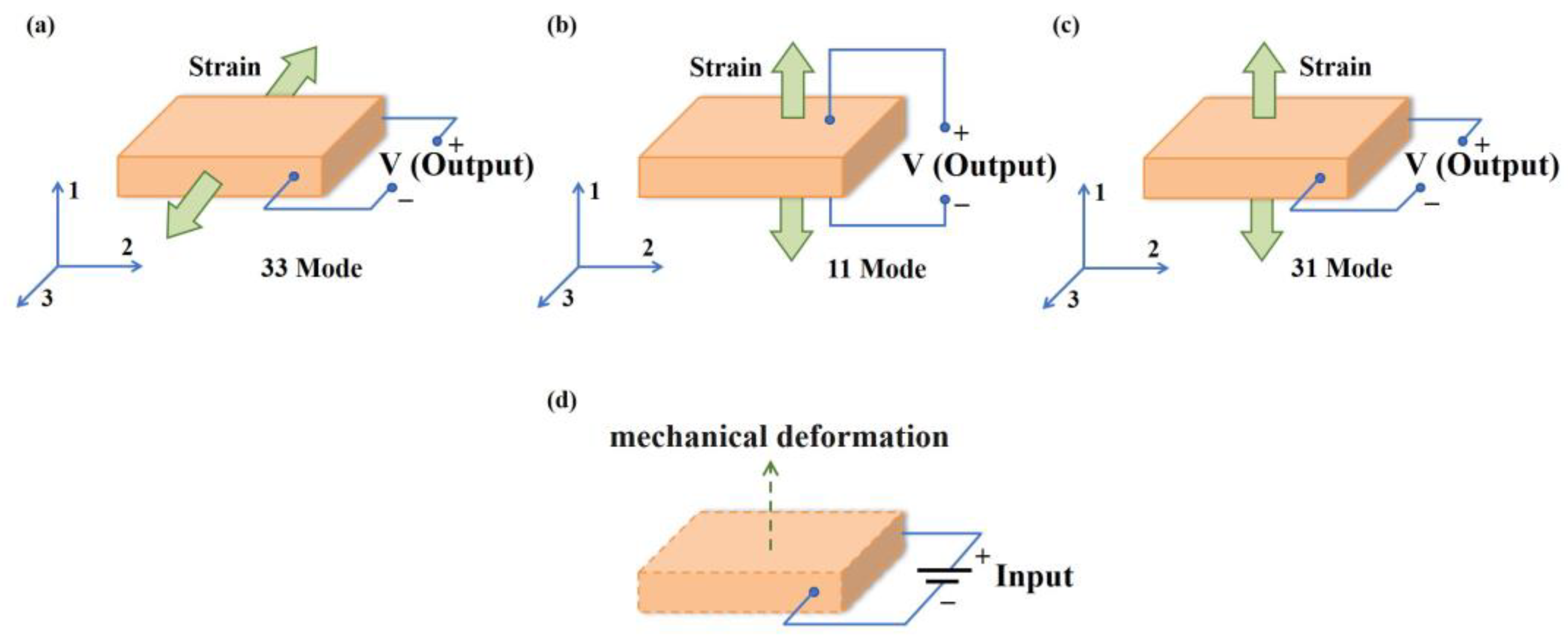
2. Piezoelectric Effect and Polarization Mechanisms
3. Piezoelectric Thin Films
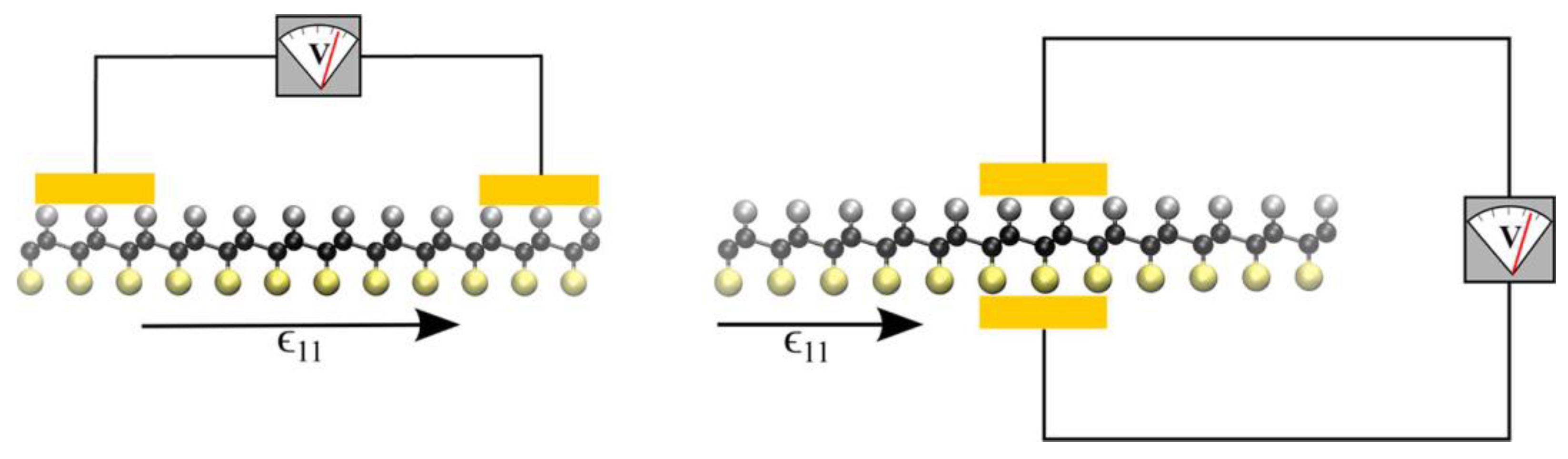
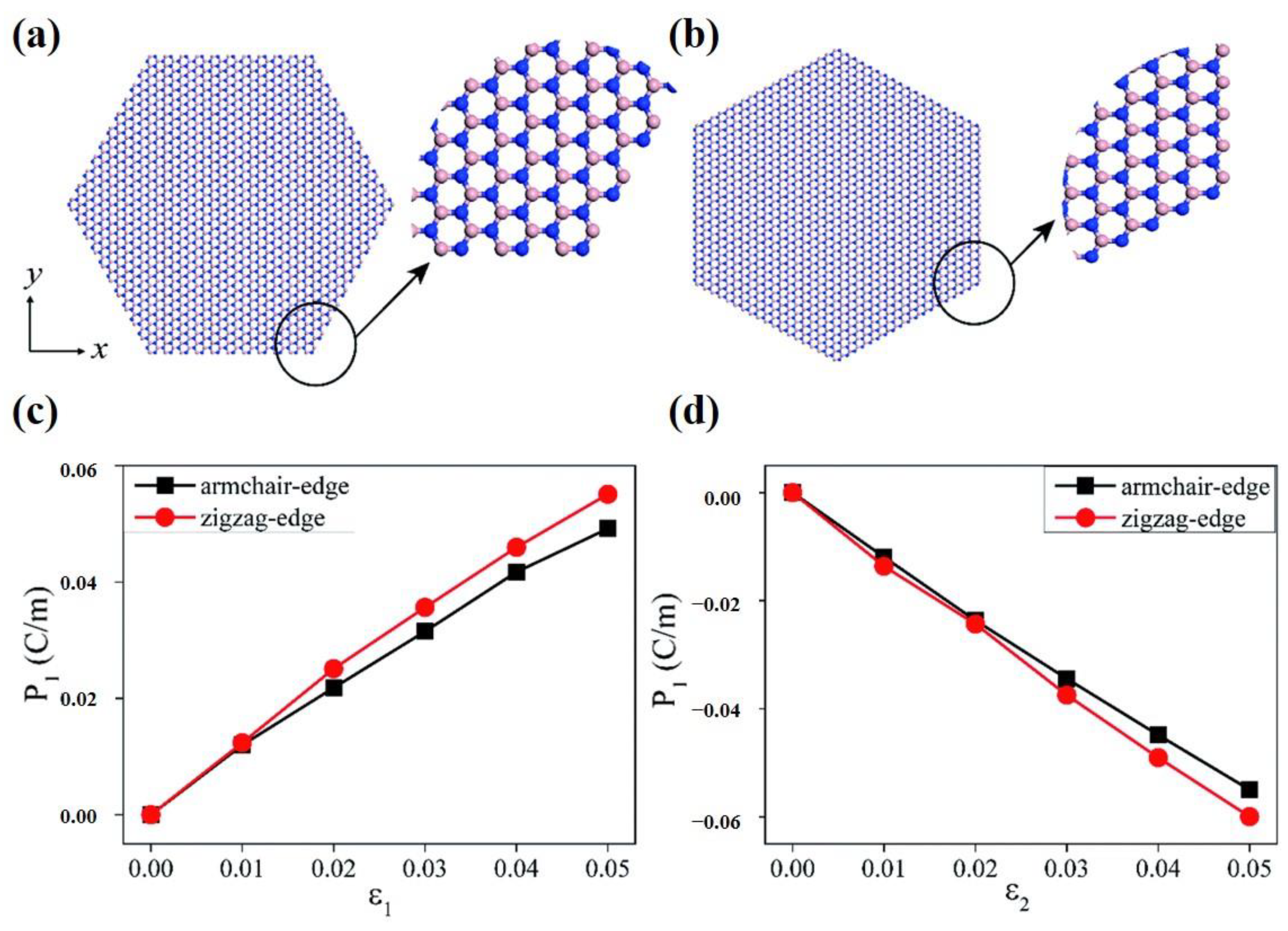
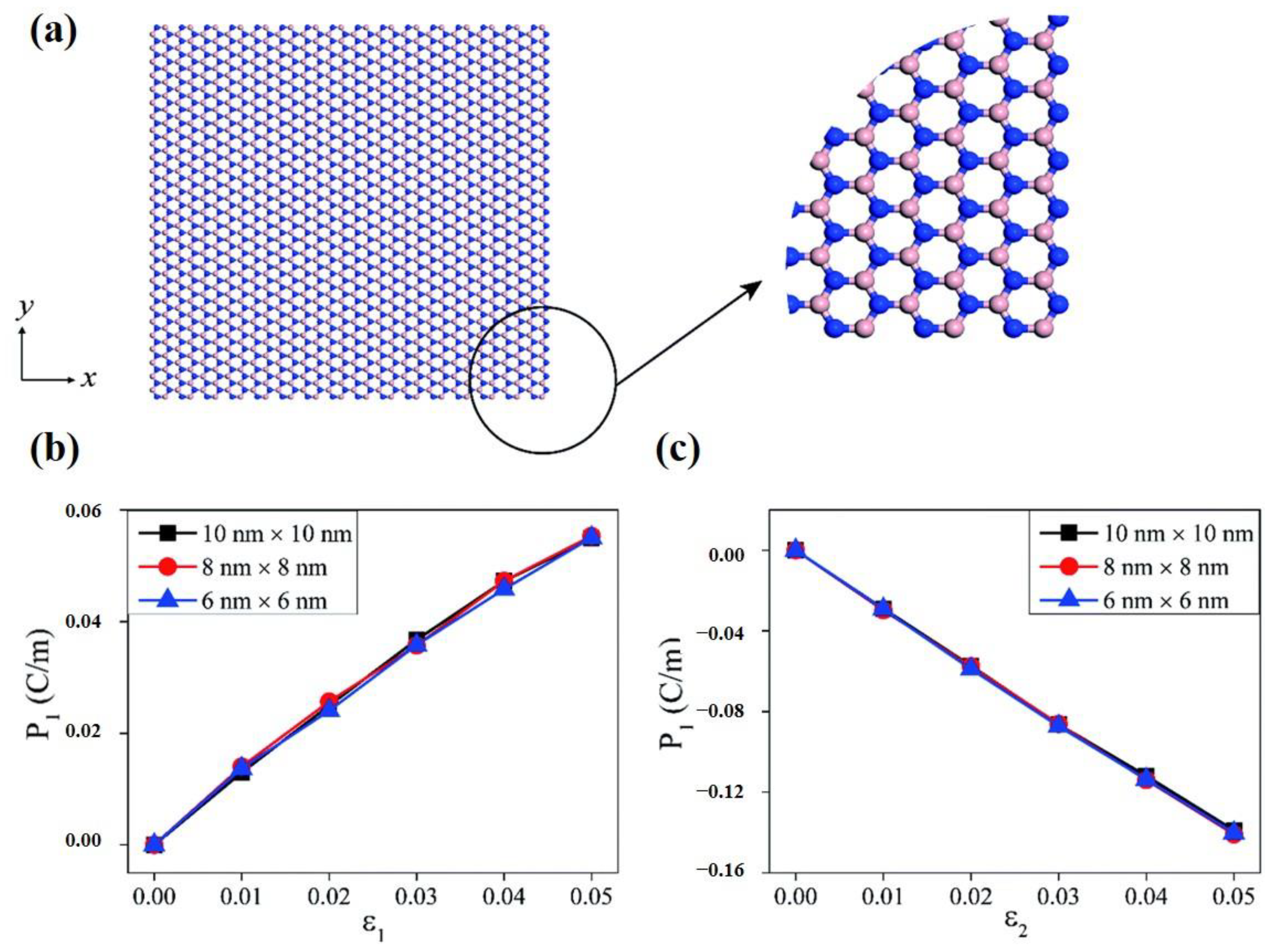
3.1. Ultrathin In-Plane Piezoelectric Films
3.2. Ultrathin Out-of-Plane Piezoelectric Films
3.2.1. Out-of-Plane Piezoelectricity Obtained by Controlling Structures
Deformation
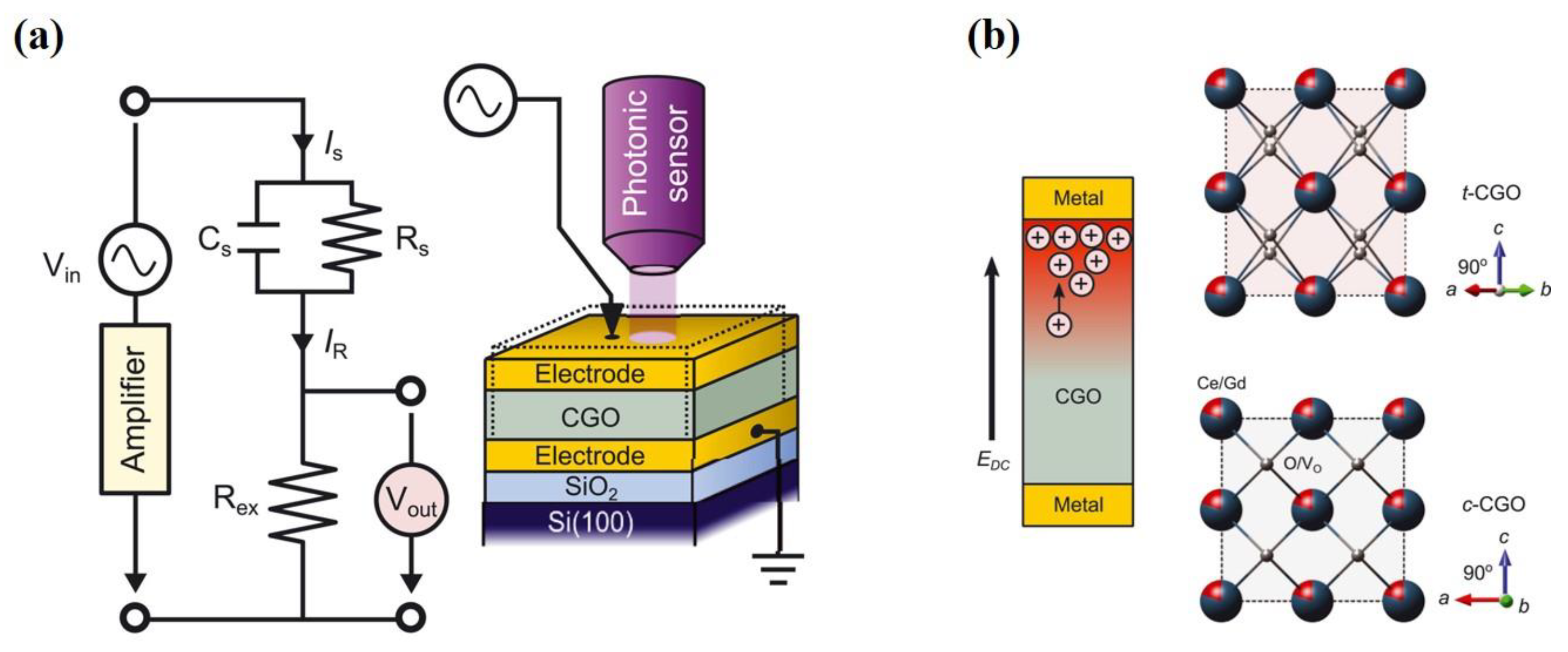
Defect Engineering
Doping
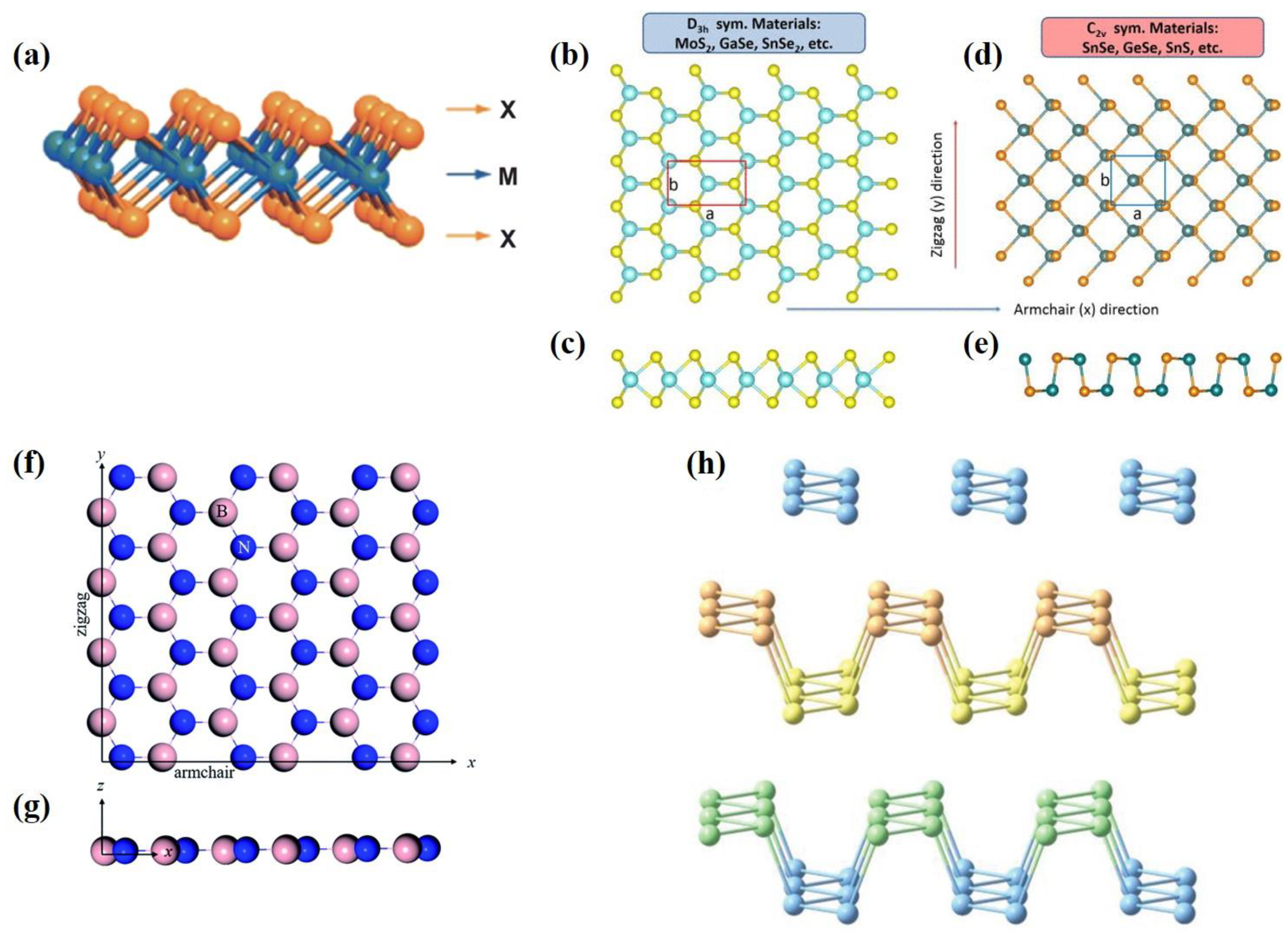
3.2.2. Out-of-Plane Piezoelectricity in Janus Structures
Conventional TMDs Janus Structures
Janus Derivatives
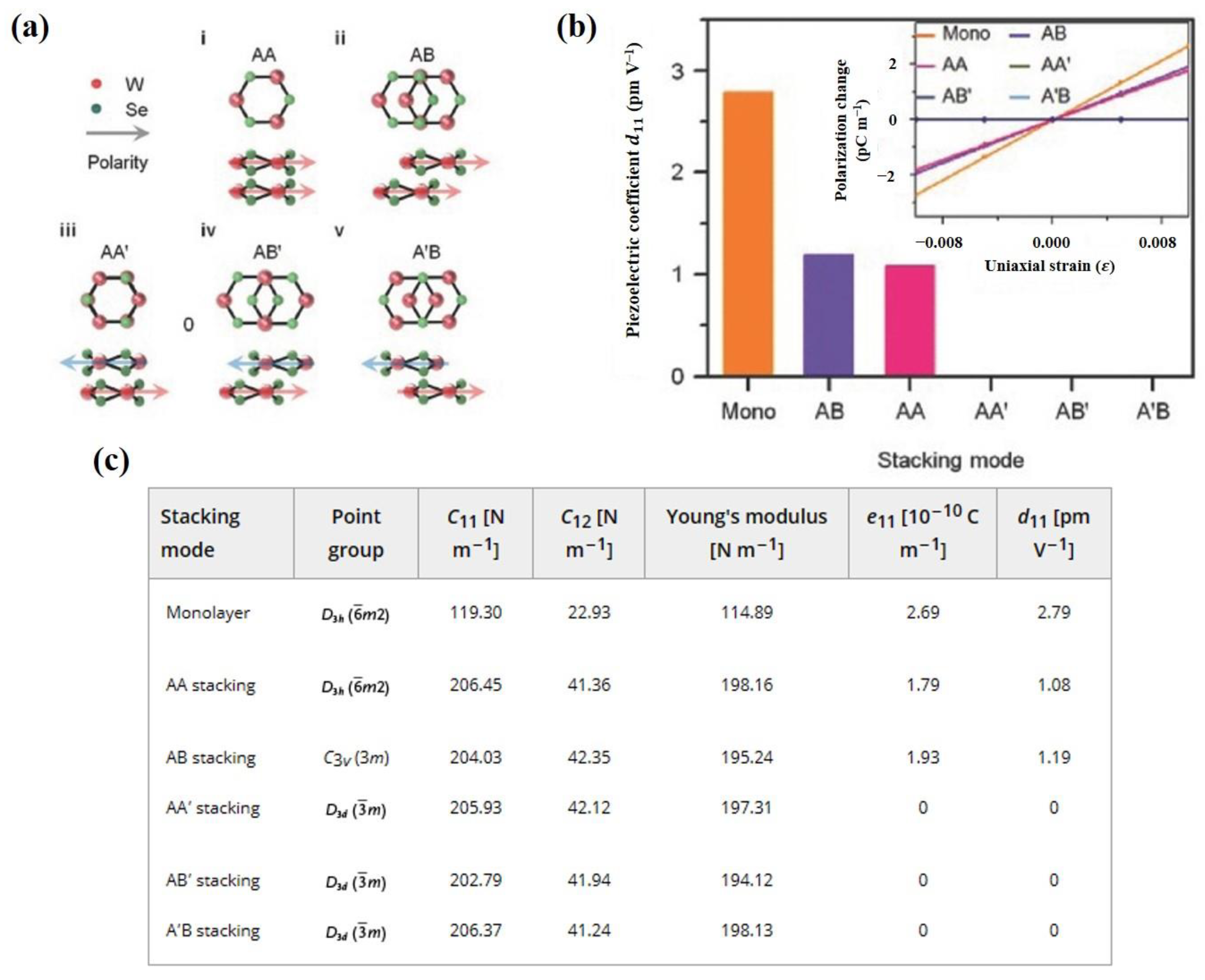
3.2.3. Out-of-Plane Piezoelectricity in Multi-Element Transition Metal Materials
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Surmenev, R.A.; Chernozem, R.V.; Pariy, I.O.; Surmeneva, M.A. A review on piezo- and pyroelectric responses of flexible nano- and micropatterned polymer surfaces for biomedical sensing and energy harvesting applications. Nano Energy 2021, 79, 105442. [Google Scholar] [CrossRef]
- Laurila, M.-M.; Peltokangas, M.; Montero, K.L.; Verho, J.; Haapala, M.; Oksala, N.; Vehkaoja, A.; Mäntysalo, M. Self-powered, high sensitivity printed e-tattoo sensor for unobtrusive arterial pulse wave monitoring. Nano Energy 2022, 102, 107625. [Google Scholar] [CrossRef]
- Wu, C.-W.; Ren, X.; Xie, G.; Zhou, W.-X.; Zhang, G.; Chen, K.-Q. Enhanced High-Temperature Thermoelectric Performance by Strain Engineering in BiOCl. Phys. Rev. Appl. 2022, 18, 014053. [Google Scholar] [CrossRef]
- Mariello, M.; Fachechi, L.; Guido, F.; De Vittorio, M. Conformal, Ultra-thin Skin-Contact-Actuated Hybrid Piezo/Triboelectric Wearable Sensor Based on AlN and Parylene-Encapsulated Elastomeric Blend. Adv. Funct. Mater. 2021, 31, 2101047. [Google Scholar] [CrossRef]
- Li, W.; Yang, T.; Liu, C.; Huang, Y.; Chen, C.; Pan, H.; Xie, G.; Tai, H.; Jiang, Y.; Wu, Y.; et al. Optimizing Piezoelectric Nanocomposites by High-Throughput Phase-Field Simulation and Machine Learning. Adv. Sci. 2022, 9, e2105550. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Ding, W.; Liu, J.; Yang, B. Flexible PVDF based piezoelectric nanogenerators. Nano Energy 2020, 78, 105251. [Google Scholar] [CrossRef]
- Shepelin, N.A.; Glushenkov, A.M.; Lussini, V.C.; Fox, P.J.; Dicinoski, G.W.; Shapter, J.G.; Ellis, A.V. New developments in composites, copolymer technologies and processing techniques for flexible fluoropolymer piezoelectric generators for efficient energy harvesting. Energy Environ. Sci. 2019, 12, 1143–1176. [Google Scholar] [CrossRef]
- Yu, D.; Zheng, Z.; Liu, J.; Xiao, H.; Huangfu, G.; Guo, Y. Superflexible and Lead-Free Piezoelectric Nanogenerator as a Highly Sensitive Self-Powered Sensor for Human Motion Monitoring. Nano-Micro Lett. 2021, 13, 117. [Google Scholar] [CrossRef]
- Zhong, J.; Zhong, Q.; Zang, X.; Wu, N.; Li, W.; Chu, Y.; Lin, L. Flexible PET/EVA-based piezoelectret generator for energy harvesting in harsh environments. Nano Energy 2017, 37, 268–274. [Google Scholar] [CrossRef]
- Takeshita, T.; Nguyen, T.-V.; Zymelka, D.; Takei, Y.; Kobayashi, T. Mechanical characteristics of laminated film vibrator using an ultra-thin MEMS actuator. J. Micromech. Microeng. 2022, 32, 105001. [Google Scholar] [CrossRef]
- Michael, G.; Hu, G.; Zheng, D.; Zhang, Y. Piezo-phototronic solar cell based on 2D monochalcogenides materials. J. Phys. D Appl. Phys. 2019, 52, 204001. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Z.L. Piezotronics and piezo-phototronics for adaptive electronics and optoelectronics. Nat. Rev. Mater. 2016, 1, 16031. [Google Scholar] [CrossRef]
- Casamento, J.; Chang, C.S.; Shao, Y.-T.; Wright, J.; Muller, D.A.; Xing, H.; Jena, D. Structural and piezoelectric properties of ultra-thin ScxAl1−xN films grown on GaN by molecular beam epitaxy. Appl. Phys. Lett. 2020, 117, 112101. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, Y.; Yu, Z.; Zheng, J.; Wang, Y.; Zhou, H. PANI/PVDF-TrFE porous aerogel bulk piezoelectric and triboelectric hybrid nanogenerator based on in-situ doping and liquid nitrogen quenching. Nano Energy 2021, 80, 105519. [Google Scholar] [CrossRef]
- Shi, K.; Chai, B.; Zou, H.; Shen, P.; Sun, B.; Jiang, P.; Shi, Z.; Huang, X. Interface induced performance enhancement in flexible BaTiO3/PVDF-TrFE based piezoelectric nanogenerators. Nano Energy 2021, 80, 105515. [Google Scholar] [CrossRef]
- Zhou, Z.; Bowland, C.C.; Malakooti, M.H.; Tang, H.; Sodano, H.A. Lead-free 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 nanowires for energy harvesting. Nanoscale 2016, 8, 5098–5105. [Google Scholar] [CrossRef]
- Zheng, T.; Wu, J.; Xiao, D.; Zhu, J. Recent development in lead-free perovskite piezoelectric bulk materials. Prog. Mater. Sci. 2018, 98, 552–624. [Google Scholar] [CrossRef]
- Jeong, C.K.; Park, K.-I.; Ryu, J.; Hwang, G.-T.; Lee, K.J. Large-Area and Flexible Lead-Free Nanocomposite Generator Using Alkaline Niobate Particles and Metal Nanorod Filler. Adv. Funct. Mater. 2014, 24, 2620–2629. [Google Scholar] [CrossRef]
- Cheon, G.; Duerloo, K.-A.N.; Sendek, A.D.; Porter, C.; Chen, Y.; Reed, E.J. Data Mining for New Two- and One-Dimensional Weakly Bonded Solids and Lattice-Commensurate Heterostructures. Nano Lett. 2017, 17, 1915–1923. [Google Scholar] [CrossRef]
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2020, 30, 013002. [Google Scholar] [CrossRef]
- Wang, J.; Cao, X.-H.; Zeng, Y.-J.; Luo, N.-N.; Tang, L.-M.; Chen, K.-Q. Excellent thermoelectric properties of monolayer MoS2-MoSe2 aperiodic superlattices. Appl. Surf. Sci. 2023, 612, 155914. [Google Scholar] [CrossRef]
- Jia, P.-Z.; Xie, Z.-X.; Deng, Y.-X.; Zhang, Y.; Tang, L.-M.; Zhou, W.-X.; Chen, K.-Q. High thermoelectric performance induced by strong anharmonic effects in monolayer (PbX)2 (X = S, Se, Te). Appl. Phys. Lett. 2022, 121, 043901. [Google Scholar] [CrossRef]
- He, R.; Wang, D.; Luo, N.; Zeng, J.; Chen, K.-Q.; Tang, L.-M. Nonrelativistic Spin-Momentum Coupling in Antiferromagnetic Twisted Bilayers. Phys. Rev. Lett. 2023, 130, 046401. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.-L.; Sun, Y.; Wang, D.; Chen, K.-Q.; Tang, L.-M. A review of ultra-thin ferroelectric films. J. Phys. Condens. Matter 2021, 33, 403003. [Google Scholar] [CrossRef]
- Li, Q.; Chen, K.-Q.; Tang, L.-M. Large Valley Splitting in van der Waals Heterostructures with Type-III Band Alignment. Phys. Rev. Appl. 2020, 13, 014064. [Google Scholar] [CrossRef]
- Park, D.-S.; Hadad, M.; Riemer, L.M.; Ignatans, R.; Spirito, D.; Esposito, V.; Tileli, V.; Gauquelin, N.; Chezganov, D.; Jannis, D.; et al. Induced giant piezoelectricity in centrosymmetric oxides. Science 2022, 375, 653–657. [Google Scholar] [CrossRef]
- Li, F. Breaking symmetry for piezoelectricity. Science 2022, 375, 618–619. [Google Scholar] [CrossRef]
- Yang, X.; Liu, C.; Fang, L.; Su, T.; Hu, M.; Chen, Y.; Zhou, B.; Su, H.; Kong, X.; Bellaiche, L.; et al. Strain-induced ferroelectricity and piezoelectricity in centrosymmetric binary oxides. Phys. Rev. B 2022, 106, 064106. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, H. Piezoelectricity in Two-Dimensional Materials. Angew. Chem. Int. Ed. 2015, 54, 4432–4434. [Google Scholar] [CrossRef]
- Brennan, C.J.; Ghosh, R.; Koul, K.; Banerjee, S.K.; Lu, N.; Yu, E.T. Out-of-Plane Electromechanical Response of Monolayer Molybdenum Disulfide Measured by Piezoresponse Force Microscopy. Nano Lett. 2017, 17, 5464–5471. [Google Scholar] [CrossRef]
- Cao, X.-H.; Wu, D.; Zeng, J.; Luo, N.-N.; Zhou, W.-X.; Tang, L.-M.; Chen, K.-Q. Controllable anisotropic thermoelectric properties in 2D covalent organic radical frameworks. Appl. Phys. Lett. 2021, 119, 263901. [Google Scholar] [CrossRef]
- Kim, S.K.; Bhatia, R.; Kim, T.-H.; Seol, D.; Kim, J.H.; Kim, H.; Seung, W.; Kim, Y.; Lee, Y.H.; Kim, S.-W. Directional dependent piezoelectric effect in CVD grown monolayer MoS 2 for flexible piezoelectric nanogenerators. Nano Energy 2016, 22, 483–489. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Xiao, J.; Liu, M.; Xiong, S.; Wong, Z.J.; Ye, Z.; Ye, Y.; Yin, X.; Zhang, X. Observation of piezoelectricity in free-standing monolayer MoS2. Nat. Nanotechnol. 2015, 10, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zeng, J.; Jiang, X.; Tang, L.; Chen, K. Exact first-principles calculation reveals universal moiré potential in twisted two-dimensional materials. Phys. Rev. B 2023, 107, L081402. [Google Scholar] [CrossRef]
- Varjovi, M.J.; Yagmurcukardes, M.; Peeters, F.M.; Durgun, E. Janus two-dimensional transition metal dichalcogenide oxides: First-principles investigation of WXO monolayers with X = S, Se, and Te. Phys. Rev. B 2021, 103, 195438. [Google Scholar] [CrossRef]
- Lu, A.-Y.; Zhu, H.; Xiao, J.; Chuu, C.-P.; Han, Y.; Chiu, M.-H.; Cheng, C.-C.; Yang, C.-W.; Wei, K.-H.; Yang, Y.Y.P.; et al. Janus monolayers of transition metal dichalcogenides. Nat. Nanotechnol. 2017, 12, 744–749. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Zhou, S.; Bai, Y.; Zhao, J. Enhanced piezoelectric effect in Janus group-III chalcogenide monolayers. Appl. Phys. Lett. 2017, 110, 163102. [Google Scholar] [CrossRef]
- Mortazavi, B.; Javvaji, B.; Shojaei, F.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Exceptional piezoelectricity, high thermal conductivity and stiffness and promising photocatalysis in two-dimensional MoSi2N4 family confirmed by first-principles. Nano Energy 2020, 82, 105716. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Das Mahapatra, S.; Mohapatra, P.C.; Aria, A.I.; Christie, G.; Mishra, Y.K.; Hofmann, S.; Thakur, V.K. Piezoelectric Materials for Energy Harvesting and Sensing Applications: Roadmap for Future Smart Materials. Adv. Sci. 2021, 8, e2100864. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric Energy Harvesting Solutions: A Review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Shen, T.; Wang, C.; Zhang, Y.; Qi, J.; Zhang, H. Recent Advances in Strain-Induced Piezoelectric and Piezoresistive Effect-Engineered 2D Semiconductors for Adaptive Electronics and Optoelectronics. Nano-Micro Lett. 2020, 12, 106. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.; Yan, X.; Li, F.; Du, J.; Meng, J.; Zhang, Y. Polarity-Dependent Piezotronic Effect and Controllable Transport Modulation of ZnO with Multifield Coupled Interface Engineering. Adv. Mater. Interfaces 2017, 4, 1600842. [Google Scholar] [CrossRef]
- Mishra, S.; Unnikrishnan, L.; Nayak, S.K.; Mohanty, S. Advances in Piezoelectric Polymer Composites for Energy Harvesting Applications: A Systematic Review. Macromol. Mater. Eng. 2019, 304, 1800463. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.-J.; Liu, Y.-Y.; Pan, H.; Ding, Z.-K.; Zhou, W.-X.; Tang, L.-M.; Li, B.; Chen, K.-Q. Thermoelectric Conversion From Interface Thermophoresis and Piezoelectric Effects. Front. Phys. 2022, 10, 823284. [Google Scholar] [CrossRef]
- 176-1978; IEEE Standard on Piezoelectricity. IEEE: Piscatvie, NJ, USA, 1988.
- Li, W.; Li, J. Piezoelectricity in two-dimensional group-III monochalcogenides. Nano Res. 2015, 8, 3796–3802. [Google Scholar] [CrossRef] [Green Version]
- Hu, T.; Dong, J. Two new phases of monolayer group-IV monochalcogenides and their piezoelectric properties. Phys. Chem. Chem. Phys. 2016, 18, 32514–32520. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2020, 80, 105567. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.-W.; Lin, L. A comprehensive review on piezoelectric energy harvesting technology: Materials, mechanisms, and applications. Appl. Phys. Rev. 2018, 5, 041306. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.; Tang, L.-M.; Chen, K.-Q. Quantum mechanical modeling of magnon-phonon scattering heat transport across three-dimensional ferromagnetic/nonmagnetic interfaces. Phys. Rev. B 2022, 105, 064401. [Google Scholar] [CrossRef]
- Zheng, Y.; Jiang, X.; Xue, X.-X.; Yao, X.; Zeng, J.; Chen, K.-Q.; Wang, E.; Feng, Y. Nuclear Quantum Effects on the Charge-Density Wave Transition in NbX2 (X = S, Se). Nano Lett. 2022, 22, 1858–1865. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Rao, Y.; Mak, K.F.; You, Y.; Wang, S.; Dean, C.R.; Heinz, T.F. Probing Symmetry Properties of Few-Layer MoS2 and h-BN by Optical Second-Harmonic Generation. Nano Lett. 2013, 13, 3329–3333. [Google Scholar] [CrossRef] [PubMed]
- Cui, C.; Xue, F.; Hu, W.-J.; Li, L.-J. Two-dimensional materials with piezoelectric and ferroelectric functionalities. Npj 2D Mater. Appl. 2018, 2, 18. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, G.D.C.; Zelenovskiy, P.; Romanyuk, K.; Luchkin, S.; Kopelevich, Y.; Kholkin, A. Strong piezoelectricity in single-layer graphene deposited on SiO2 grating substrates. Nat. Commun. 2015, 6, 7572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, Z.; Yan, W.; Shang, J.; Liu, J.Z. Piezoelectric properties of graphene oxide: A first-principles computational study. Appl. Phys. Lett. 2014, 105, 023103. [Google Scholar] [CrossRef] [Green Version]
- Ong, M.T.; Reed, E.J. Engineered Piezoelectricity in Graphene. ACS Nano 2012, 6, 1387–1394. [Google Scholar] [CrossRef]
- Baturin, A.S.; Bulakh, K.; Zenkevich, A.V.; Minnekaev, M.N.; Chuprik, A.A. Study of the ferroelectric properties of BaTiO3 films grown on an iron sublayer using atomic force microscopy. J. Surf. Investig. X-ray, Synchrotron Neutron Tech. 2012, 6, 733–737. [Google Scholar] [CrossRef]
- Nagarajan, V.; Junquera, J.; He, J.Q.; Jia, C.L.; Waser, R.; Lee, K.; Kim, Y.K.; Baik, S.; Zhao, T.; Ramesh, R.; et al. Scaling of structure and electrical properties in ultrathin epitaxial ferroelectric heterostructures. J. Appl. Phys. 2006, 100, 051609. [Google Scholar] [CrossRef]
- Hussain, N.; Zhang, M.-H.; Zhang, Q.; Zhou, Z.; Xu, X.; Murtaza, M.; Zhang, R.; Wei, H.; Ou, G.; Wang, D.; et al. Large Piezoelectric Strain in Sub-10 Nanometer Two-Dimensional Polyvinylidene Fluoride Nanoflakes. ACS Nano 2019, 13, 4496–4506. [Google Scholar] [CrossRef]
- Zelisko, M.; Hanlumyuang, Y.; Yang, S.; Liu, Y.; Lei, C.; Li, J.; Ajayan, P.M.; Sharma, P. Anomalous piezoelectricity in two-dimensional graphene nitride nanosheets. Nat. Commun. 2014, 5, 4284. [Google Scholar] [CrossRef] [Green Version]
- Syed, N.; Zavabeti, A.; Ou, J.Z.; Mohiuddin, M.; Pillai, N.; Carey, B.J.; Zhang, B.Y.; Datta, R.S.; Jannat, A.; Haque, F.; et al. Printing two-dimensional gallium phosphate out of liquid metal. Nat. Commun. 2018, 9, 3618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
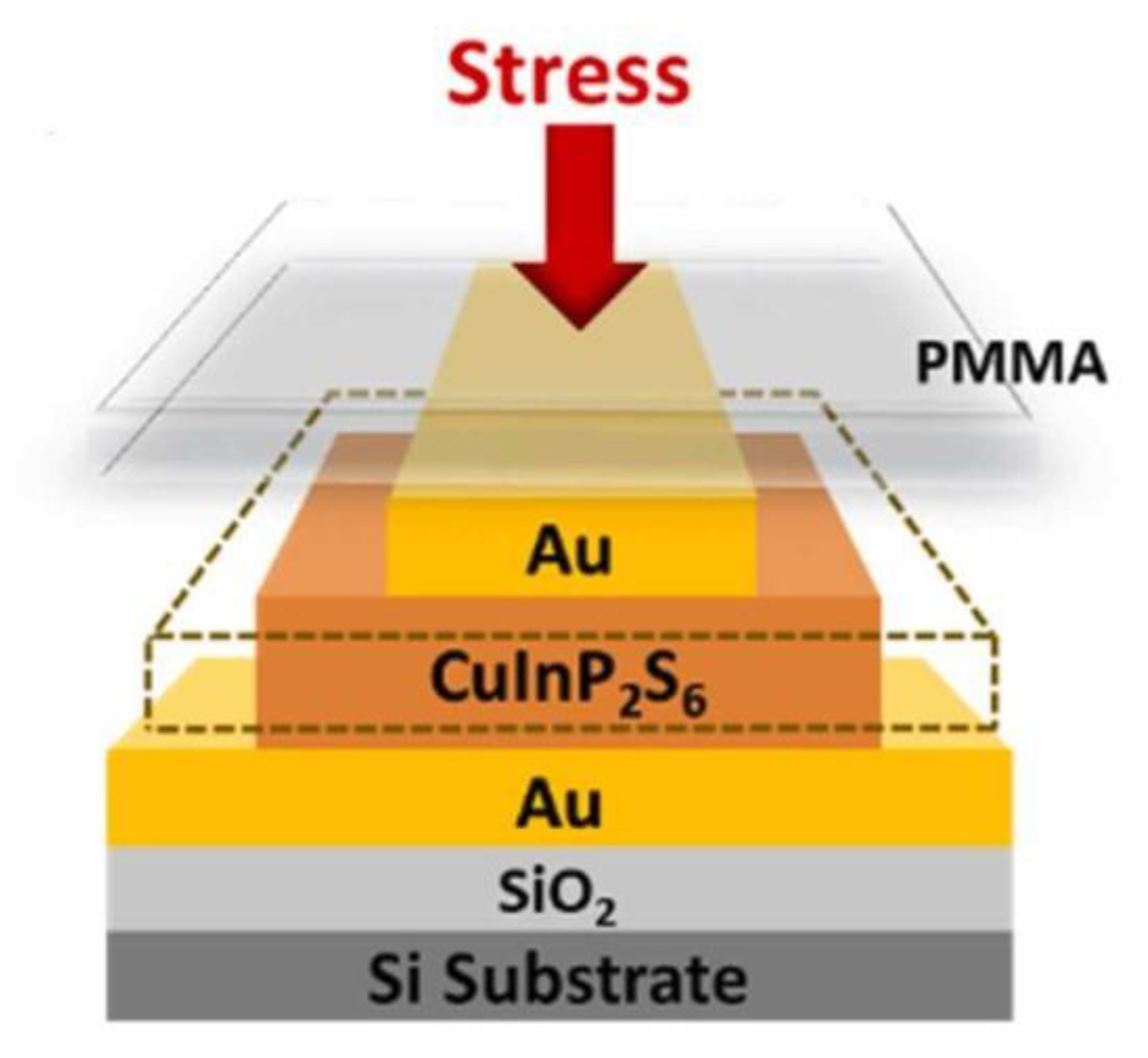
- Io, W.F.; Wong, M.-C.; Pang, S.-Y.; Zhao, Y.; Ding, R.; Guo, F.; Hao, J. Strong piezoelectric response in layered CuInP2S6 nanosheets for piezoelectric nanogenerators. Nano Energy 2022, 99, 107371. [Google Scholar] [CrossRef]
- Blonsky, M.N.; Zhuang, H.L.; Singh, A.K.; Hennig, R.G. Ab Initio Prediction of Piezoelectricity in Two-Dimensional Materials. ACS Nano 2015, 9, 9885. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Lou, J.; Shenoy, V.B. Large In-Plane and Vertical Piezoelectricity in Janus Transition Metal Dichalchogenides. ACS Nano 2017, 11, 8242. [Google Scholar] [CrossRef] [PubMed]
- Duerloo, K.-A.N.; Ong, M.T.; Reed, E.J. Intrinsic Piezoelectricity in Two-Dimensional Materials. J. Phys. Chem. Lett. 2012, 3, 2871–2876. [Google Scholar] [CrossRef]
- Feng, W.; Guo, G.-Y.; Yao, Y. Tunable magneto-optical effects in hole-doped group-IIIA metal-monochalcogenide monolayers. 2D Mater. 2016, 4, 015017. [Google Scholar] [CrossRef]
- Fei, R.; Li, W.; Li, J.; Yang, L. Giant piezoelectricity of monolayer group IV monochalcogenides: SnSe, SnS, GeSe, and GeS. Appl. Phys. Lett. 2015, 107, 173104. [Google Scholar] [CrossRef]
- Yin, H.; Gao, J.; Zheng, G.-P.; Wang, Y.; Ma, Y. Giant Piezoelectric Effects in Monolayer Group-V Binary Compounds with Honeycomb Phases: A First-Principles Prediction. J. Phys. Chem. C 2017, 121, 25576–25584. [Google Scholar] [CrossRef]
- Zhuang, X.; He, B.; Javvaji, B.; Park, H.S. Intrinsic bending flexoelectric constants in two-dimensional materials. Phys. Rev. B 2019, 99, 054105. [Google Scholar] [CrossRef]
- Wu, W.; Wang, L.; Li, Y.; Zhang, F.; Lin, L.; Niu, S.; Chenet, D.; Zhang, X.; Hao, Y.; Heinz, T.F.; et al. Piezoelectricity of single-atomic-layer MoS2 for energy conversion and piezotronics. Nature 2014, 514, 470–474. [Google Scholar] [CrossRef]
- Lee, J.-H.; Park, J.Y.; Cho, E.B.; Kim, T.Y.; Han, S.A.; Liu, Y.; Kim, S.K.; Roh, C.J.; Yoon, H.-J.; Ryu, H.; et al. Reliable Piezoelectricity in Bilayer WSe2 for Piezoelectric Nanogenerators. Adv. Mater. 2017, 29, 1606667. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.-H.; Wang, Z.-L.; Mao, S.X. Piezoelectric Characterization of Individual Zinc Oxide Nanobelt Probed by Piezoresponse Force Microscope. Nano Lett. 2004, 4, 587–590. [Google Scholar] [CrossRef]
- Wang, L.; Liu, S.; Gao, G.; Pang, Y.; Yin, X.; Feng, X.; Zhu, L.; Bai, Y.; Chen, L.; Xiao, T.; et al. Ultrathin Piezotronic Transistors with 2 nm Channel Lengths. ACS Nano 2018, 12, 4903–4908. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Liu, S.; Zhang, Z.; Feng, X.; Zhu, L.; Guo, H.; Ding, W.; Chen, L.; Qin, Y.; Wang, Z.L. 2D piezotronics in atomically thin zinc oxide sheets: Interfacing gating and channel width gating. Nano Energy 2019, 60, 724–733. [Google Scholar] [CrossRef]
- Ghasemian, M.B.; Zavabeti, A.; Abbasi, R.; Kumar, P.V.; Syed, N.; Yao, Y.; Tang, J.; Wang, Y.; Elbourne, A.; Han, J.; et al. Ultra-thin lead oxide piezoelectric layers for reduced environmental contamination using a liquid metal-based process. J. Mater. Chem. A 2020, 8, 19434–19443. [Google Scholar] [CrossRef]
- Li, J.; Zhao, T.; He, C.; Zhang, K.-W. Surface oxidation: An effective way to induce piezoelectricity in 2D black phosphorus. J. Phys. D Appl. Phys. 2018, 51, 12LT01. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Zhu, H.; Sun, L.; Fu, W.; Wang, X.; Hoong, L.C.; Wang, H.; Zeng, Q.; Zhao, W.; et al. Subatomic deformation driven by vertical piezoelectricity from CdS ultrathin films. Sci. Adv. 2016, 2, e1600209. [Google Scholar] [CrossRef] [Green Version]
- Cao, V.A.; Kim, M.; Hu, W.; Lee, S.; Youn, S.; Chang, J.; Chang, H.S.; Nah, J. Enhanced Piezoelectric Output Performance of the SnS2/SnS Heterostructure Thin-Film Piezoelectric Nanogenerator Realized by Atomic Layer Deposition. ACS Nano 2021, 15, 10428–10436. [Google Scholar] [CrossRef]
- Wang, Y.; Vu, L.-M.; Lu, T.; Xu, C.; Liu, Y.; Ou, J.Z.; Li, Y. Piezoelectric Responses of Mechanically Exfoliated Two-Dimensional SnS2 Nanosheets. ACS Appl. Mater. Interfaces 2020, 12, 51662–51668. [Google Scholar] [CrossRef]
- Yang, P.-K.; Chou, S.-A.; Hsu, C.-H.; Mathew, R.J.; Chiang, K.-H.; Yang, J.-Y.; Chen, Y.-T. Tin disulfide piezoelectric nanogenerators for biomechanical energy harvesting and intelligent human-robot interface applications. Nano Energy 2020, 75, 104879. [Google Scholar] [CrossRef]
- Xue, F.; Zhang, J.; Hu, W.; Hsu, W.-T.; Han, A.; Leung, S.-F.; Huang, J.-K.; Wan, Y.; Liu, S.; Zhang, J.; et al. Multidirection Piezoelectricity in Mono- and Multilayered Hexagonal α-In2Se3. ACS Nano 2018, 12, 4976–4983. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Li, D.; Zhou, H.; Zhang, C.; Li, Z.; Li, G.; Zhang, B.; Huang, X.; Gao, B. Intrinsic room-temperature ferromagnetic semiconductor InCrTe3 monolayers with large magnetic anisotropy and large piezoelectricity. Appl. Phys. Lett. 2021, 118, 123102. [Google Scholar] [CrossRef]
- Dimple, D.; Jena, N.; Rawat, A.; Ahammed, R.; Mohanta, M.K.; De Sarkar, A. Emergence of high piezoelectricity along with robust electron mobility in Janus structures in semiconducting Group IVB dichalcogenide monolayers. J. Mater. Chem. A 2018, 6, 24885–24898. [Google Scholar] [CrossRef]
- Xiao, W.-Z.; Luo, H.-J.; Xu, L. Elasticity, piezoelectricity, and mobility in two-dimensional BiTeI from a first-principles study. J. Phys. D Appl. Phys. 2020, 53, 245301. [Google Scholar] [CrossRef]
- Tan, J.; Wang, Y.; Wang, Z.; He, X.; Liu, Y.; Wang, B.; Katsnelson, M.I.; Yuan, S. Large out-of-plane piezoelectricity of oxygen functionalized MXenes for ultrathin piezoelectric cantilevers and diaphragms. Nano Energy 2019, 65, 104058. [Google Scholar] [CrossRef]
- Liu, S.; Chen, W.; Liu, C.; Wang, B.; Yin, H. Coexistence of large out-of-plane and in-plane piezoelectricity in 2D monolayer Li-based ternary chalcogenides LiMX2. Results Phys. 2021, 26, 104398. [Google Scholar] [CrossRef]
- Lv, Q.; Qiu, J.; Wen, Q.; Li, D.; Zhou, Y.; Lu, G. Large in-plane and out-of-plane piezoelectricity in 2D γ-LiMX2 (M=Al, Ga and In; X=S, Se and Te) monolayers. Mater. Sci. Semicond. Process. 2023, 154, 107222. [Google Scholar] [CrossRef]
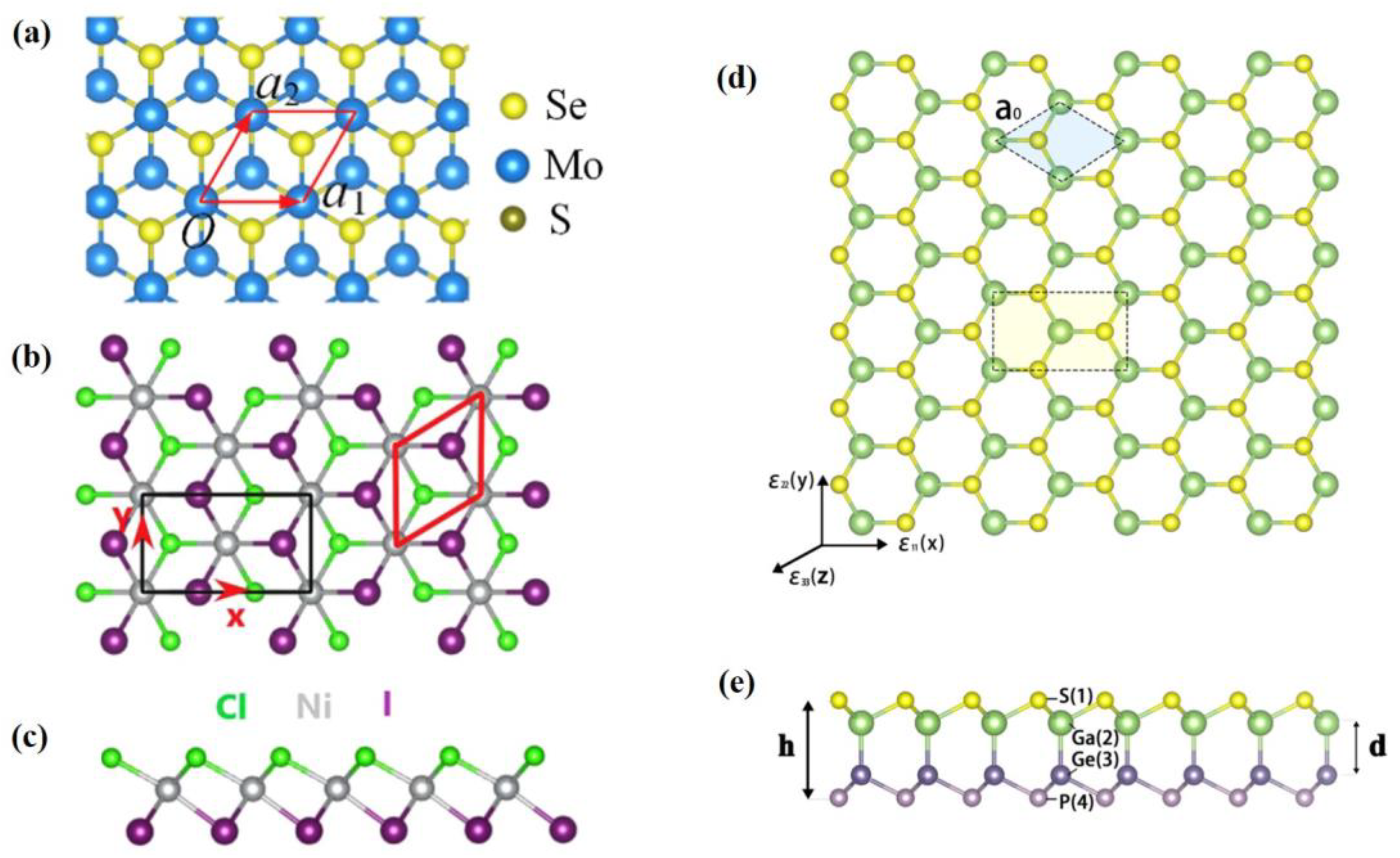
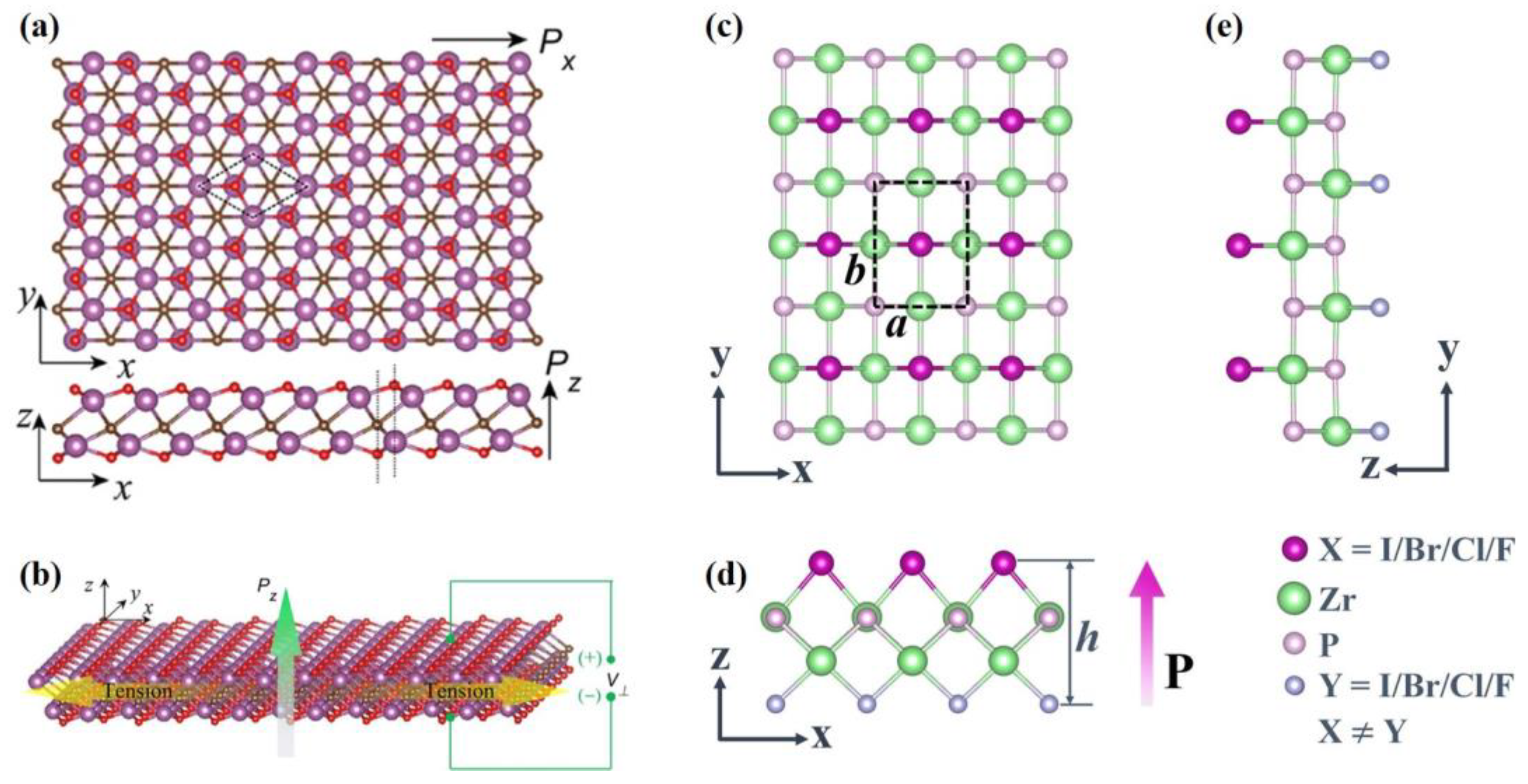
- Li, Y.-Q.; Zhang, H.-N.; Yang, C.; Wang, X.-Y.; Zhu, S.-Y.; Wang, X.-C. Ferroelastic Zr2P2XY (X/Y = I, Br, Cl or F; X ≠ Y) monolayers with tunable in-plane electronic anisotropy and remarkable out-of-plane piezoelectricity. Appl. Surf. Sci. 2023, 608. [Google Scholar] [CrossRef]
- Qi, Y.; McAlpine, M.C. Nanotechnology-enabled flexible and biocompatible energy harvesting. Energy Environ. Sci. 2010, 3, 1275–1285. [Google Scholar] [CrossRef]
- Park, K.-I.; Xu, S.; Liu, Y.; Hwang, G.-T.; Kang, S.-J.L.; Wang, Z.L.; Lee, K.J. Piezoelectric BaTiO3 Thin Film Nanogenerator on Plastic Substrates. Nano Lett. 2010, 10, 4939–4943. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Luo, J.; Nguyen, N.; Walton, A.; Flewitt, A.; Zu, X.; Li, Y.; McHale, G.; Matthews, A.; Iborra, E.; et al. Advances in piezoelectric thin films for acoustic biosensors, acoustofluidics and lab-on-chip applications. Prog. Mater. Sci. 2017, 89, 31–91. [Google Scholar] [CrossRef] [Green Version]
- Wan, C.; Bowen, C.R. Multiscale-structuring of polyvinylidene fluoride for energy harvesting: The impact of molecular-, micro- and macro-structure. J. Mater. Chem. A 2017, 5, 3091–3128. [Google Scholar] [CrossRef] [Green Version]
- Zhu, G.; Wang, A.C.; Liu, Y.; Zhou, Y.; Wang, Z.L. Functional Electrical Stimulation by Nanogenerator with 58 V Output Voltage. Nano Lett. 2012, 12, 3086–3090. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, G.; Yang, B.; Liu, J.-Q.; Xu, B.; Zhu, H.-Y.; Yang, C.-S. Development of high performance piezoelectric d33 mode MEMS vibration energy harvester based on PMN-PT single crystal thick film. Sens. Actuators A Phys. 2014, 205, 150–155. [Google Scholar] [CrossRef]
- Li, F.; Lin, D.; Chen, Z.; Cheng, Z.; Wang, J.; Li, C.; Xu, Z.; Huang, Q.; Liao, X.; Chen, L.-Q.; et al. Ultrahigh piezoelectricity in ferroelectric ceramics by design. Nat. Mater. 2018, 17, 349–354. [Google Scholar] [CrossRef]
- Hwang, G.-T.; Annapureddy, V.; Han, J.H.; Joe, D.J.; Baek, C.; Park, D.Y.; Kim, D.H.; Park, J.H.; Jeong, C.K.; Park, K.-I.; et al. Self-Powered Wireless Sensor Node Enabled by an Aerosol-Deposited PZT Flexible Energy Harvester. Adv. Energy Mater. 2016, 6, 1600237. [Google Scholar] [CrossRef]
- Stoppel, F.; Schröder, C.; Senger, F.; Wagner, B.; Benecke, W. AlN-based piezoelectric micropower generator for low ambient vibration energy harvesting. Procedia Eng. 2011, 25, 721–724. [Google Scholar] [CrossRef]
- Doll, J.C.; Petzold, B.C.; Ninan, B.; Mullapudi, R.; Pruitt, B.L. Aluminum nitride on titanium for CMOS compatible piezoelectric transducers. J. Micromech. Microeng. 2010, 20, 25008. [Google Scholar] [CrossRef] [Green Version]
- Persano, L.; Dagdeviren, C.; Su, Y.; Zhang, Y.; Girardo, S.; Pisignano, D.; Huang, Y.; Rogers, J.A. High performance piezoelectric devices based on aligned arrays of nanofibers of poly(vinylidenefluoride-co-trifluoroethylene). Nat. Commun. 2013, 4, 1633. [Google Scholar] [CrossRef] [Green Version]
- Nan, Y.; Tan, D.; Zhao, J.; Willatzen, M.; Wang, Z.L. Shape- and size dependent piezoelectric properties of monolayer hexagonal boron nitride nanosheets. Nanoscale Adv. 2020, 2, 470–477. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Lu, J.; Wan, B.; Peng, D.; Xu, Q.; Hu, G.; Peng, Y.; Pan, C.; Wang, Z.L. Piezoelectricity in Multilayer Black Phosphorus for Piezotronics and Nanogenerators. Adv. Mater. 2020, 32, e1905795. [Google Scholar] [CrossRef]
- Ding, Z.-K.; Zeng, Y.-J.; Pan, H.; Luo, N.; Zeng, J.; Tang, L.-M.; Chen, K.-Q. Edge states of topological acoustic phonons in graphene zigzag nanoribbons. Phys. Rev. B 2022, 106, L121401. [Google Scholar] [CrossRef]
- Zeng, Y.-J.; Feng, Y.-X.; Tang, L.-M.; Chen, K.-Q. Effect of out-of-plane strain on the phonon structures and anharmonicity of twisted multilayer graphene. Appl. Phys. Lett. 2021, 118, 183103. [Google Scholar] [CrossRef]
- Zeng, B.; Ding, Z.-K.; Pan, H.; Luo, N.; Zeng, J.; Tang, L.-M.; Chen, K.-Q. Strong strain-dependent phonon hydrodynamic window in bilayer graphene. Appl. Phys. Lett. 2022, 121, 252202. [Google Scholar] [CrossRef]
- Chandratre, S.; Sharma, P. Coaxing graphene to be piezoelectric. Appl. Phys. Lett. 2012, 100, 023114. [Google Scholar] [CrossRef] [Green Version]
- Ong, M.T.; Duerloo, K.-A.N.; Reed, E.J. The Effect of Hydrogen and Fluorine Coadsorption on the Piezoelectric Properties of Graphene. J. Phys. Chem. C 2013, 117, 3615–3620. [Google Scholar] [CrossRef] [Green Version]
- Ganatra, R.; Zhang, Q. Few-Layer MoS2: A Promising Layered Semiconductor. ACS Nano 2014, 8, 4074–4099. [Google Scholar] [CrossRef]
- Chhowalla, M.; Shin, H.S.; Eda, G.; Li, L.-J.; Loh, K.P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263–275. [Google Scholar] [CrossRef]
- Tang, D.; Dan, M.; Zhang, Y. High performance piezotronic thermoelectric devices based on zigzag MoS2 nanoribbon. Nano Energy 2022, 104, 107888. [Google Scholar] [CrossRef]
- Michel, K.H.; Verberck, B. Theory of elastic and piezoelectric effects in two-dimensional hexagonal boron nitride. Phys. Rev. B 2009, 80, 224301. [Google Scholar] [CrossRef]
- Wang, D.; Chen, L.; Wang, X.; Cui, G.; Zhang, P. The effect of substrate and external strain on electronic structures of stanene film. Phys. Chem. Chem. Phys. 2015, 17, 26979–26987. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.; Kong, X.; Hu, Z.-X.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 5, 4475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ng, L.-R.; Chen, G.-F.; Lin, S.-H. Generating large out-of-plane piezoelectric properties of atomically thin MoS2via defect engineering. Phys. Chem. Chem. Phys. 2021, 23, 23945–23952. [Google Scholar] [CrossRef] [PubMed]
- Brennan, C.J.; Koul, K.; Lu, N.; Yu, E.T. Out-of-plane electromechanical coupling in transition metal dichalcogenides. Appl. Phys. Lett. 2020, 116, 053101. [Google Scholar] [CrossRef]
- Cui, C.; Hu, W.-J.; Yan, X.; Addiego, C.; Gao, W.; Wang, Y.; Wang, Z.; Li, L.; Cheng, Y.; Li, P.; et al. Intercorrelated In-Plane and Out-of-Plane Ferroelectricity in Ultrathin Two-Dimensional Layered Semiconductor In2Se3. Nano Lett. 2018, 18, 1253–1258. [Google Scholar] [CrossRef] [Green Version]
- Esfahani, E.N.; Li, T.; Huang, B.; Xu, X.; Li, J. Piezoelectricity of atomically thin WSe2 via laterally excited scanning probe microscopy. Nano Energy 2018, 52, 117–122. [Google Scholar] [CrossRef] [Green Version]
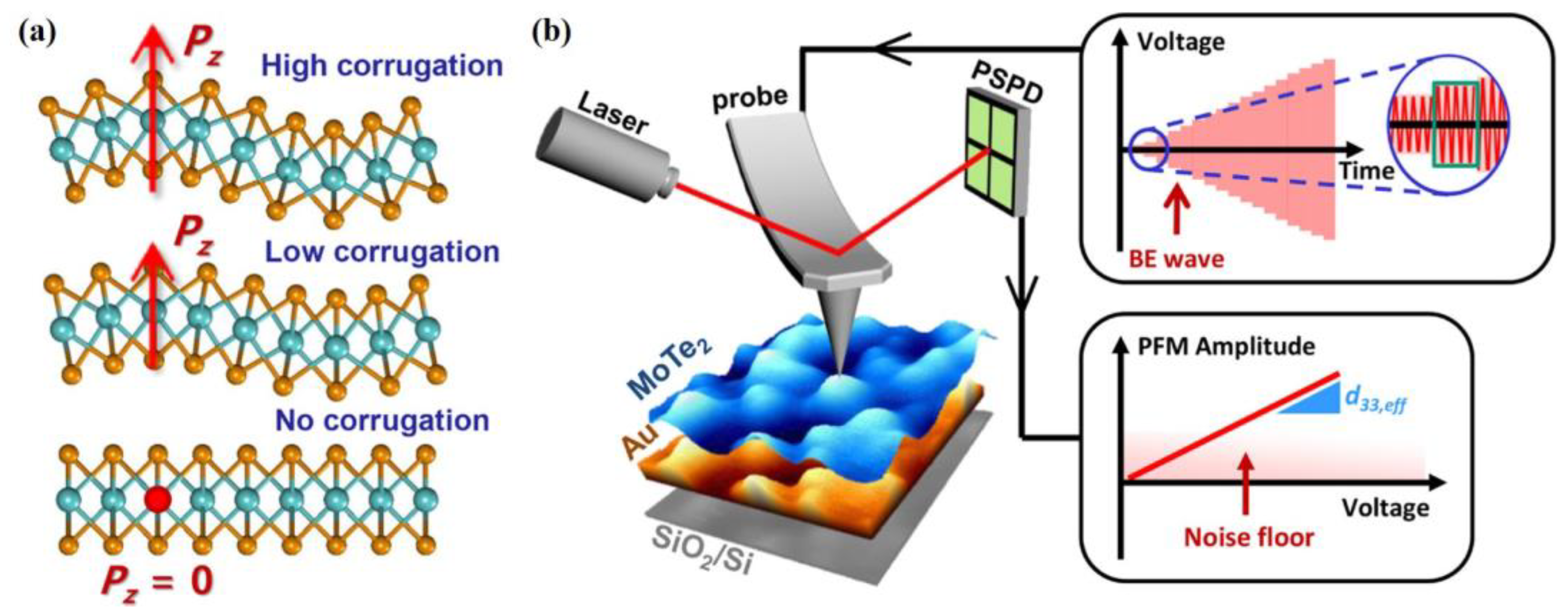
- Kang, S.; Jeon, S.; Kim, S.; Seol, D.; Yang, H.; Lee, J.; Kim, Y. Tunable Out-of-Plane Piezoelectricity in Thin-Layered MoTe2 by Surface Corrugation-Mediated Flexoelectricity. ACS Appl. Mater. Interfaces 2018, 10, 27424. [Google Scholar] [CrossRef]
- Kang, S.; Kim, S.; Jeon, S.; Jang, W.-S.; Seol, D.; Kim, Y.-M.; Lee, J.; Yang, H.; Kim, Y. Atomic-scale symmetry breaking for out-of-plane piezoelectricity in two-dimensional transition metal dichalcogenides. Nano Energy 2019, 58, 57. [Google Scholar] [CrossRef]
- Seol, D.; Kim, S.; Jang, W.-S.; Jin, Y.; Kang, S.; Kim, S.; Won, D.; Lee, C.; Kim, Y.-M.; Lee, J.; et al. Selective patterning of out-of-plane piezoelectricity in MoTe2 via focused ion beam. Nano Energy 2021, 79, 105451. [Google Scholar] [CrossRef]
- Guo, S.-D.; Zhu, Y.-T.; Qin, K.; Ang, Y.-S. Large out-of-plane piezoelectric response in ferromagnetic monolayer NiClI. Appl. Phys. Lett. 2022, 120, 232403. [Google Scholar] [CrossRef]
- Cai, H.; Guo, Y.; Gao, H.; Guo, W. Tribo-piezoelectricity in Janus transition metal dichalcogenide bilayers: A first-principles study. Nano Energy 2019, 56, 33–39. [Google Scholar] [CrossRef]
- Zhao, Y.-Z.; Jia, H.-J.; Zhao, S.-N.; Wang, Y.-B.; Li, H.-Y.; Zhao, Z.-L.; Wu, Y.-X.; Wang, X.-C. Janus structure derivatives SnP–InS, GeP-GaS and SiP–AlS monolayers with in-plane and out-of-plane piezoelectric performance. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 117, 113817. [Google Scholar] [CrossRef]
- Hu, Y.; Li, T.; Liu, L.; Tan, Y.; Hu, L.; Wu, K.; Yang, C. Janus XM-GaS (M=Si, Ge, Sn; X=N, P) monolayers: Multifunctional properties for photocatalysis, piezoelectricity and second harmonic generation. Phys. B Condens. Matter 2020, 594, 412366. [Google Scholar] [CrossRef]
- Qiu, J.; Zhang, F.; Li, H.; Chen, X.; Zhu, B.; Guo, H.; Ding, Z.; Bao, J.; Yu, J. Giant Piezoelectricity of Janus M₂SeX (M = Ge, Sn; X = S, Te) Monolayers. IEEE Electron Device Lett. 2021, 42, 561–564. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, C.-H.; Zhang, H.-N.; Zhu, L.-H.; Wang, X.-Y.; Li, Y.-Q.; Zhu, S.-Y.; Wang, X.-C. The flexible Janus X2PAs (X = Si, Ge and Sn) monolayers with in-plane and out-of-plane piezoelectricity. Appl. Surf. Sci. 2022, 589, 152999. [Google Scholar] [CrossRef]
- Guo, S.-D.; Mu, W.-Q.; Xiao, X.-B.; Liu, B.-G. Intrinsic room-temperature piezoelectric quantum anomalous hall insulator in Janus monolayer Fe2IX (X = Cl and Br). Nanoscale 2021, 13, 12956–12965. [Google Scholar] [CrossRef]
- Song, G.; Zhang, C.; Zhang, Z.; Li, G.; Li, Z.; Du, J.; Zhang, B.; Huang, X.; Gao, B. Coexistence of intrinsic room-temperature ferromagnetism and piezoelectricity in monolayer BiCrX3 (X = S, Se, and Te). Phys. Chem. Chem. Phys. 2022, 24, 1091–1098. [Google Scholar] [CrossRef]



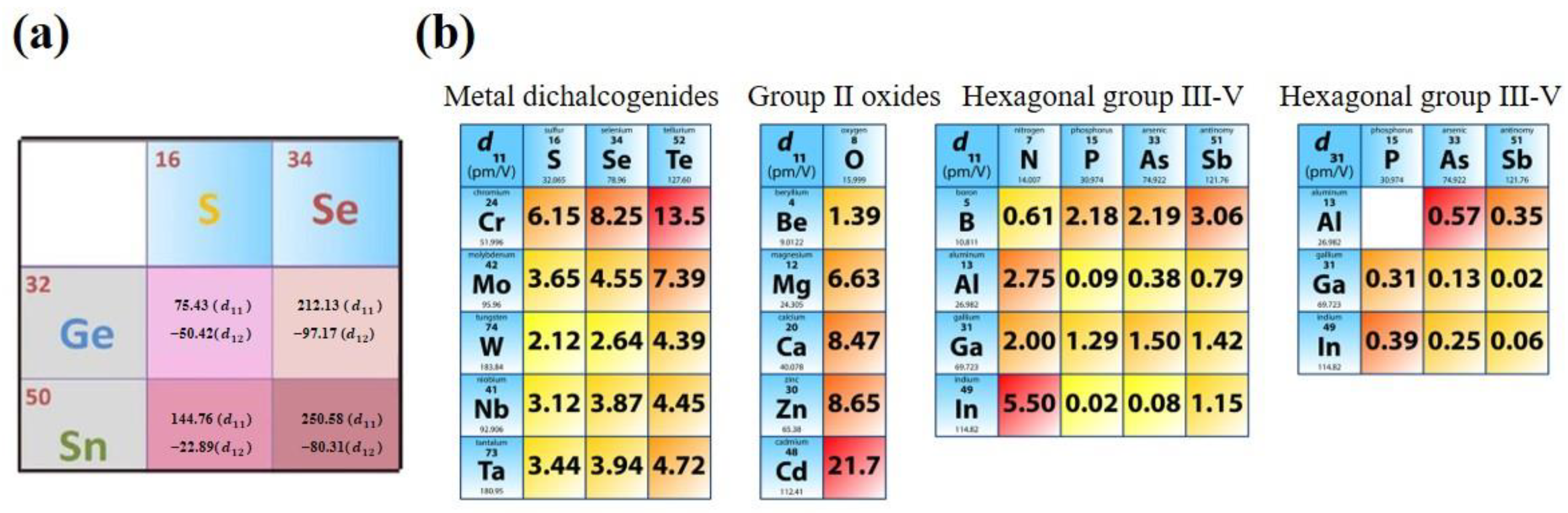

| Materials | (pm V−1) | (pm V−1) | (pm V−1) | (pm V−1) | Ref |
|---|---|---|---|---|---|
| Graphene/SiO2 | 14 | [54,55] | |||
| Graphene oxide | 0.24 | [56] | |||
| Graphene (K doped) | 0.23 | [57] | |||
| Graphene (Li doped) | 0.15 | [57] | |||
| Graphene (H doped) | 0.11 | [57] | |||
| Graphene (F doped) | 0.0018 | [57] | |||
| Graphene (F, Li doped) | 0.30 | [57] | |||
| Graphene (H, F doped) | 0.03 | [57] | |||
| BaTiO3 | 8 | [58] | |||
| PZT | 7–15 | [59] | |||
| PVDF | −36 | [60] | |||
| C3N4 | 1 | [61] | |||
| LiNbO3 | 7.50 | [30] | |||
| GaPO4 | ~8.50 | [62] | |||
| CuInP2S6 (3.5 nm) | 17.40 | [63] | |||
| CuInP2S6 (82 nm) | 83 | [63] | |||
| 2H-CrS2 | 6.15 | [64] | |||
| 2H-CrSe2 | 8.25 | [64] | |||
| 2H-CrTe2 | 13.45 | [64] | |||
| 2H-MoS2 | 3.65 | [64,65] | |||
| 2.5–4 | [54,66] | ||||
| 3.73 | [66,67,68,69] | ||||
| 3.34 | [65] | ||||
| 3.73 | [65] | ||||
| 1.35 | [30] | ||||
| 1.03 | [70] | ||||
| 3 | [66,71] | ||||
| 2H-MoSe2 | 4.55 | [64,65] | |||
| 4.17 | [65] | ||||
| 4.72 | [65,66] | ||||
| 2H-MoTe2 | 7.39 | [64,65] | |||
| 7.00 | [65] | ||||
| 9.13 | [65,66] | ||||
| 2H-WS2 | 2.12 | [64,65] | |||
| 2.02 | [65] | ||||
| 2.19 | [65,66] | ||||
| 2H-WSe2 | 2.64 | [64,65] | |||
| 2.53 | [65] | ||||
| 2.79 | [65,66] | ||||
| ~3.26 | [72] | ||||
| 2H-WTe2 | 4.39 | [64,65] | |||
| 4.29 | [65] | ||||
| 4.60 | [65,66] | ||||
| 2H-NbS2 | 3.12 | [64] | |||
| 2H-NbSe2 | 3.87 | [64] | |||
| 2H-NbTe2 | 4.45 | [64] | |||
| 2H-TaS2 | 3.44 | [64] | |||
| 2H-TaSe2 | 3.94 | [64] | |||
| 2H-TaTe2 | 4.72 | [64] | |||
| BeO | 1.39 | [64] | |||
| MgO | 6.63 | [64] | |||
| CaO | 8.47 | [64] | |||
| ZnO | 8.65 | 14.30–26.70 | [64,73] | ||
| 23.70 | [74] | ||||
| 21.50 | [75] | ||||
| CdO | 21.70 | [64] | |||
| PbO | 73.10 | 29.60 | 3.90 | [64,76] | |
| -SbAs | 243.45 | −63.65 | [69] | ||
| -SbP | 142.44 | −27.64 | [69] | ||
| -SbN | 118.29 | −13.20 | [69] | ||
| -AsP | 18.90 | −4.74 | [69] | ||
| -AsN | 29.14 | −5.75 | [69] | ||
| -PN | 6.94 | −2.44 | [69] | ||
| -SbAs | 1.65 | −0.03 | [69] | ||
| -SbP | 2.26 | −0.03 | [69] | ||
| -SbN | 5.30 | −0.26 | [69] | ||
| -AsP | 0.67 | 0.01 | [69] | ||
| -AsN | 4.83 | −0.09 | [69] | ||
| -PN | 2.77 | −0.09 | [69] | ||
| BP | 2.18 | [64] | |||
| surface-oxidized BP | 88.54 | [77] | |||
| BAs | 2.19 | [64] | |||
| BSb | 3.06 | [64] | |||
| AlN | 2.75 | [64] | |||
| AlP | 0.09 | [64] | |||
| AlAs | 0.38 | 0.57 | [42,64] | ||
| AlSb | 0.79 | 0.35 | [42,64] | ||
| GaN | 2.00 | [64] | |||
| GaP | 1.29 | 0.31 | [42,64] | ||
| GaAs | 1.50 | 0.13 | [42,64] | ||
| GaSb | 1.42 | 0.02 | [42,64] | ||
| InN | 5.50 | [64] | |||
| InP | 0.02 | 0.39 | [42,64] | ||
| InAs | 0.08 | 0.25 | [42,64] | ||
| InSb | 1.15 | 0.06 | [42,64] | ||
| BN | 0.61 | [64] | |||
| h-BN | 0.60 | [47,66,67] | |||
| CdS | 32.80 | [78] | |||
| GaS | 1.72 | [37] | |||
| 2.06 | [47,76] | ||||
| GaSe | 1.77 | [37] | |||
| 2.30 | [47,68,76] | ||||
| GaTe | 1.93 | [37] | |||
| InS | 1.12 | [37] | |||
| InSe | 1.98 | [37] | |||
| 1.46 | [47,76] | ||||
| InTe | 1.18 | [37] | |||
| GeS | 75.43 | −50.42 | [42,68] | ||
| A-GeS | 20.71 | 11.16 | [48] | ||
| H-GeS | −5.65 | 5.65 | [48] | ||
| GeSe | 212.13 | −97.17 | [42,68,69] | ||
| A-GeSe | 40.61 | 14.96 | [48] | ||
| H-GeSe | −4.88 | 4.88 | [48] | ||
| SnS | 144.76 | −22.89 | ~1.85 | [42,68,79] | |
| A-SnS | 91.56 | −4.02 | [48] | ||
| H-SnS | −5.28 | 5.28 | [48] | ||
| SnSe | 250.58 | −80.31 | [42,68,69] | ||
| A-SnSe | 74.73 | 0.85 | [48] | ||
| H-SnSe | −4.63 | 4.63 | [48] | ||
| SnS2 | 2.20 | [80] | |||
| ~5 | [81] | ||||
| -In2Se3 | 0.34 | [82] | |||
| 0.53 | [63] | ||||
| In2Te3 | 10.64 | 0.40 | [83] | ||
| Ga2SSe | 5.23 | 0.07 | [37,76] | ||
| Ga2STe | 2.46 | 0.25 | [37,76] | ||
| Ga2SeTe | 2.32 | 0.21 | [37,76] | ||
| In2SSe | 8.47 | 0.18 | [37,76] | ||
| In2STe | 1.91 | 0.25 | [37,76] | ||
| In2SeTe | 4.73 | 0.13 | [37,76] | ||
| GaInS2 | 8.33 | 0.38 | [37,76] | ||
| GaInSe2 | 3.19 | 0.46 | [37,76] | ||
| GaInTe2 | 2.99 | 0.32 | [37,76] | ||
| InCrTe3 | 6.94 | 0.52 | [83] | ||
| 1H-WSO | 1.8 | [35] | |||
| 1H-WSeO | 1.9 | [35] | |||
| 1H-WTeO | 2.8 | [35] | |||
| MoSSe | 3.76 | 0.10 | 0.02 | [36,54,65,76] | |
| MoSeTe | 5.30 | 0.03 | [65,76] | ||
| MoSTe | 5.04 | 0.03 | [65,76] | ||
| WSSe | 2.26 | 0.01 | [65,76] | ||
| WSeTe | 3.52 | 0.01 | [65,76] | ||
| WSTe | 3.33 | 0.01 | [65,76] | ||
| ZrSSe | 0.01 | [84] | |||
| ZrSeTe | −0.19 | [84] | |||
| ZrSTe | 0.004 | [84] | |||
| HfSSe | 0.05 | [84] | |||
| HfSeTe | 0.41 | [84] | |||
| HfSTe | 0.18 | [84] | |||
| BiTeI | 8.49 | 0.56 | [85] | ||
| Sc2CO2 | 0.78 | [86] | |||
| Y2CO2 | 0.40 | [86] | |||
| La2CO2 | 0.65 | [86] | |||
| LiAlS2 | 2.64 | 0.53 | [87,88] | ||
| -LiAlS2 | 8.04 | 1.17 | [88] | ||
| LiAlSe2 | 3.57 | 0.61 | [87,88] | ||
| -LiAlSe2 | 10.50 | 1.62 | [88] | ||
| LiAlTe2 | 4.58 | 0.83 | [87,88] | ||
| -LiAlTe2 | 11.30 | 0.39 | [88] | ||
| LiGaS2 | 5.03 | 0.47 | [87,88] | ||
| -LiGaS2 | 12.02 | 0.05 | [88] | ||
| LiGaSe2 | 6.60 | 0.49 | [87,88] | ||
| -LiGaSe2 | 14.48 | 0.31 | [88] | ||
| LiGaTe2 | 8.66 | 0.70 | [87,88] | ||
| -LiGaTe2 | 17.44 | 0.84 | [88] | ||
| LiInS2 | 1.48 | 0.38 | [87,88] | ||
| -LiInS2 | 5.90 | 0.12 | [88] | ||
| LiInSe2 | 2.18 | 0.29 | [87,88] | ||
| -LiInSe2 | 7.81 | 0.28 | [88] | ||
| LiInTe2 | 3.13 | 0.24 | [87,88] | ||
| -LiInTe2 | 8.93 | 0.83 | [88] | ||
| Zr2P2IBr | 29.95 | 0.93 | [89] | ||
| Zr2P2ICl | 91.12 | 2.65 | [89] | ||
| Zr2P2IF | 33.87 | 0.43 | [89] | ||
| Zr2P2BrCl | 129.71 | 3.21 | [89] | ||
| Zr2P2BrF | 22.77 | 0.09 | [89] | ||
| Zr2P2ClF | 51.05 | 0.91 | [89] |
| Materials | (pC N−1) | (pC N−1) | (pC N−1) | (pC N−1) | Ref |
|---|---|---|---|---|---|
| BaTiO3 | 191 | 78 | [90] | ||
| ~190 | [90,91] | ||||
| ZnO | 5.90 | [90] | |||
| 12 | [92] | ||||
| 12.40 | [93] | ||||
| ~5–10 | [90,94] | ||||
| Quartz | 2.30 | [90] | |||
| ST-cut Quartz | 2.30 | [92] | |||
| PMN-PT | ~2000–3000 | [90] | |||
| PMN-PZT/PT | ~1500–2000 | [95,96] | |||
| PZT | ~60–130 | [90] | |||
| 225–590 | 110 | [41,44,93] | |||
| 289–380 | [92] | ||||
| 117 | [92] | ||||
| ~250–700 | [97] | ||||
| AlN | 4.50 | [92] | |||
| 6.40 | [92] | ||||
| 5 | [98,99] | ||||
| Sapphire | 6.40 | [92] | |||
| GaN | 4.50 | [92] | |||
| 128° cut LiNbO3 | 12 | [92] | |||
| 36° YX cut LiTaO3 | 12 | [92] | |||
| PVDF Film | −33 | 23 | [44] | ||
| −35 | [92] | ||||
| ~20–30 | [90,100] |
| 2D Materials | Crystal Structure | Piezoelectric Direction | Estimated Piezocoefficient | Notes |
|---|---|---|---|---|
| Monolayer MoS2 | Hexagonal | In-plane Angle dependence | [66] [33,66] | Odd–even effect with the thickness increased |
| Monolayer h-BN | Hexagonal | In-plane Angle dependence | [66] | Odd–even effect with the thickness increased [53] |
| Graphitic carbon nitride | In-plane | [61] | Existence of piezoelectricity regardless of thickness | |
| Doped graphene | Hexagonal | Out-of-plane | [55] | Extrinsic piezoelectricity |
| -In2Se3 | Rhombohedral | Out-of-plane and in-plane | Indirectly confirmed by the ferroelectricity [116] | |
| Janus MoSSe | Hexagonal | Out-of-plane and in-plane | [36] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Xie, Z.; Liu, H.; Tang, L.; Chen, K. A Review of Ultrathin Piezoelectric Films. Materials 2023, 16, 3107. https://doi.org/10.3390/ma16083107
Li B, Xie Z, Liu H, Tang L, Chen K. A Review of Ultrathin Piezoelectric Films. Materials. 2023; 16(8):3107. https://doi.org/10.3390/ma16083107
Chicago/Turabian StyleLi, Bingyue, Zude Xie, Hanzhong Liu, Liming Tang, and Keqiu Chen. 2023. "A Review of Ultrathin Piezoelectric Films" Materials 16, no. 8: 3107. https://doi.org/10.3390/ma16083107





