Vibration Analysis of a Unimorph Nanobeam with a Dielectric Layer of Both Flexoelectricity and Piezoelectricity
Abstract
:1. Introduction
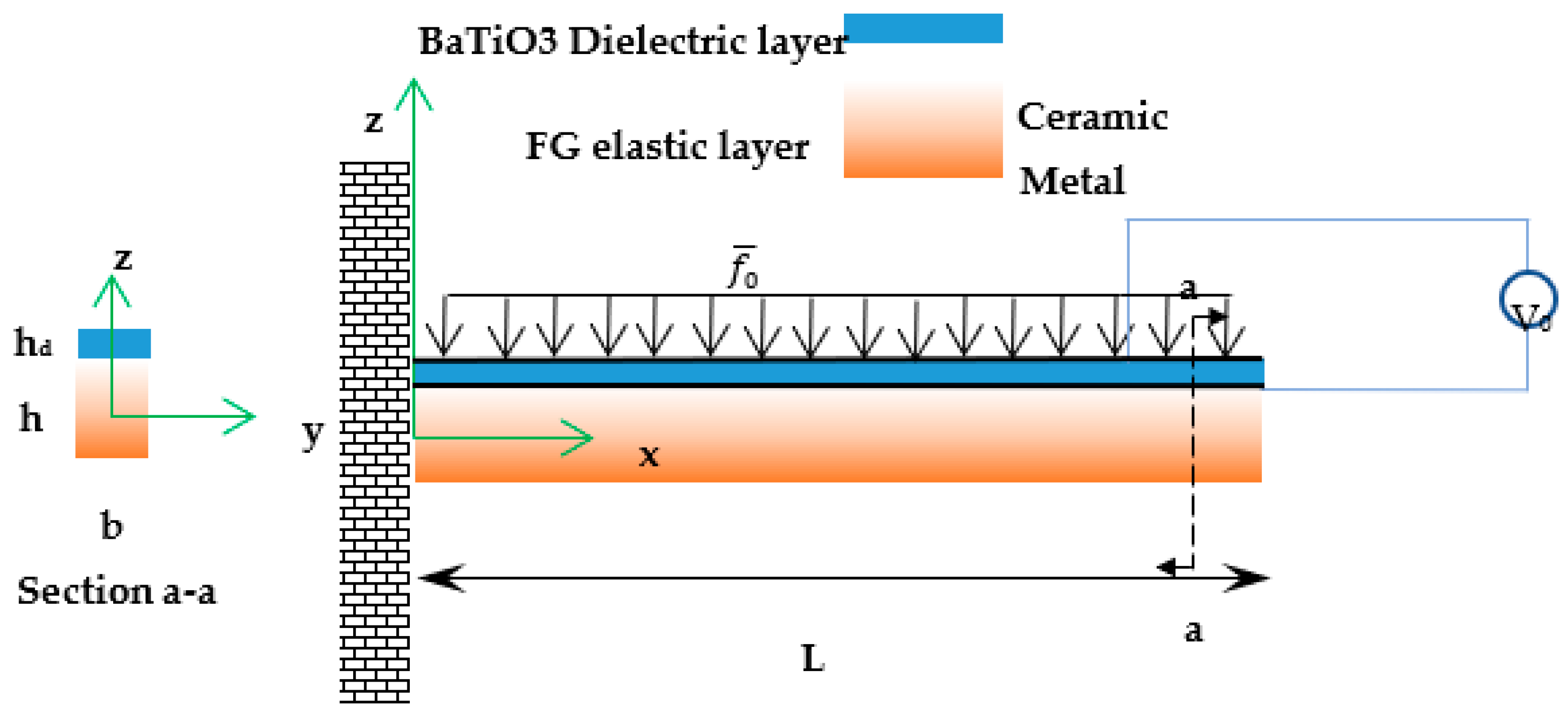
2. Problem Formulation
Two-Phase Local/Nonlocal Theory
3. Solution Procedure
Generalized Differential Quadrature Method
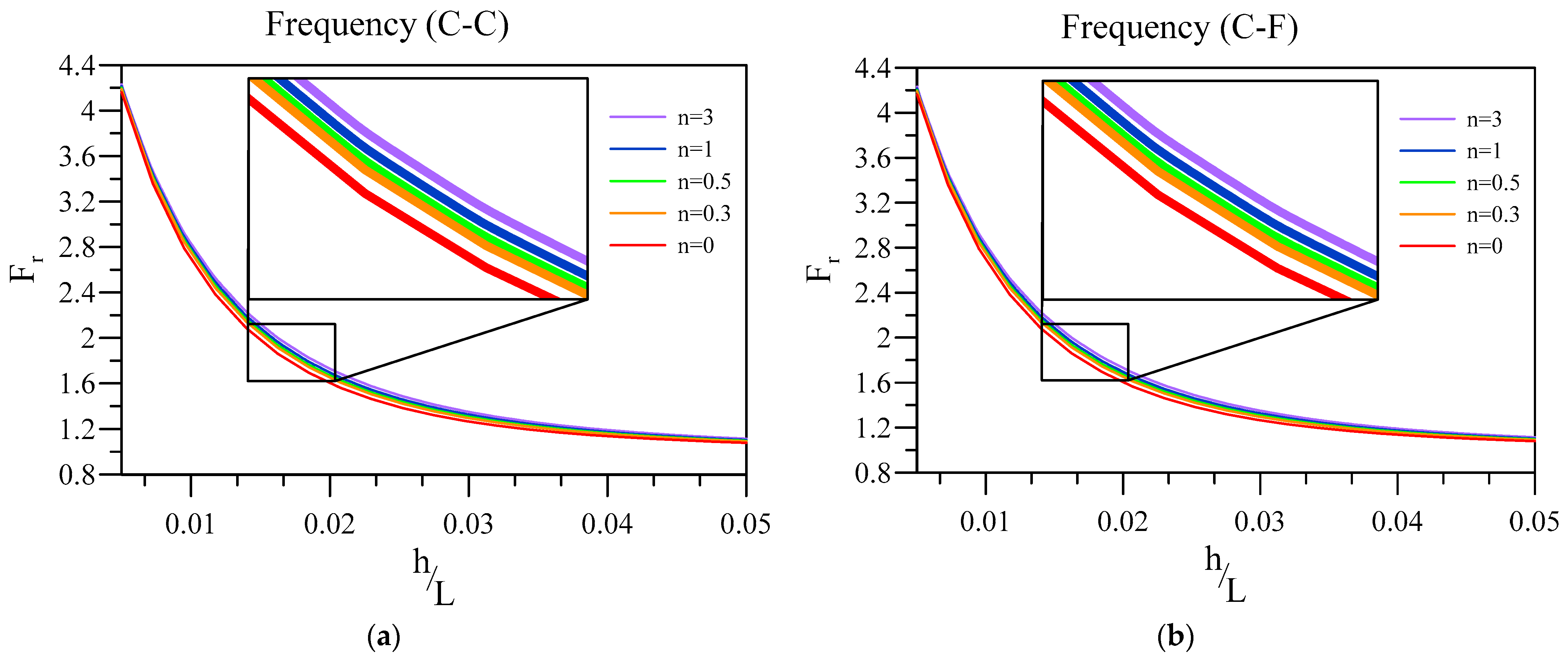
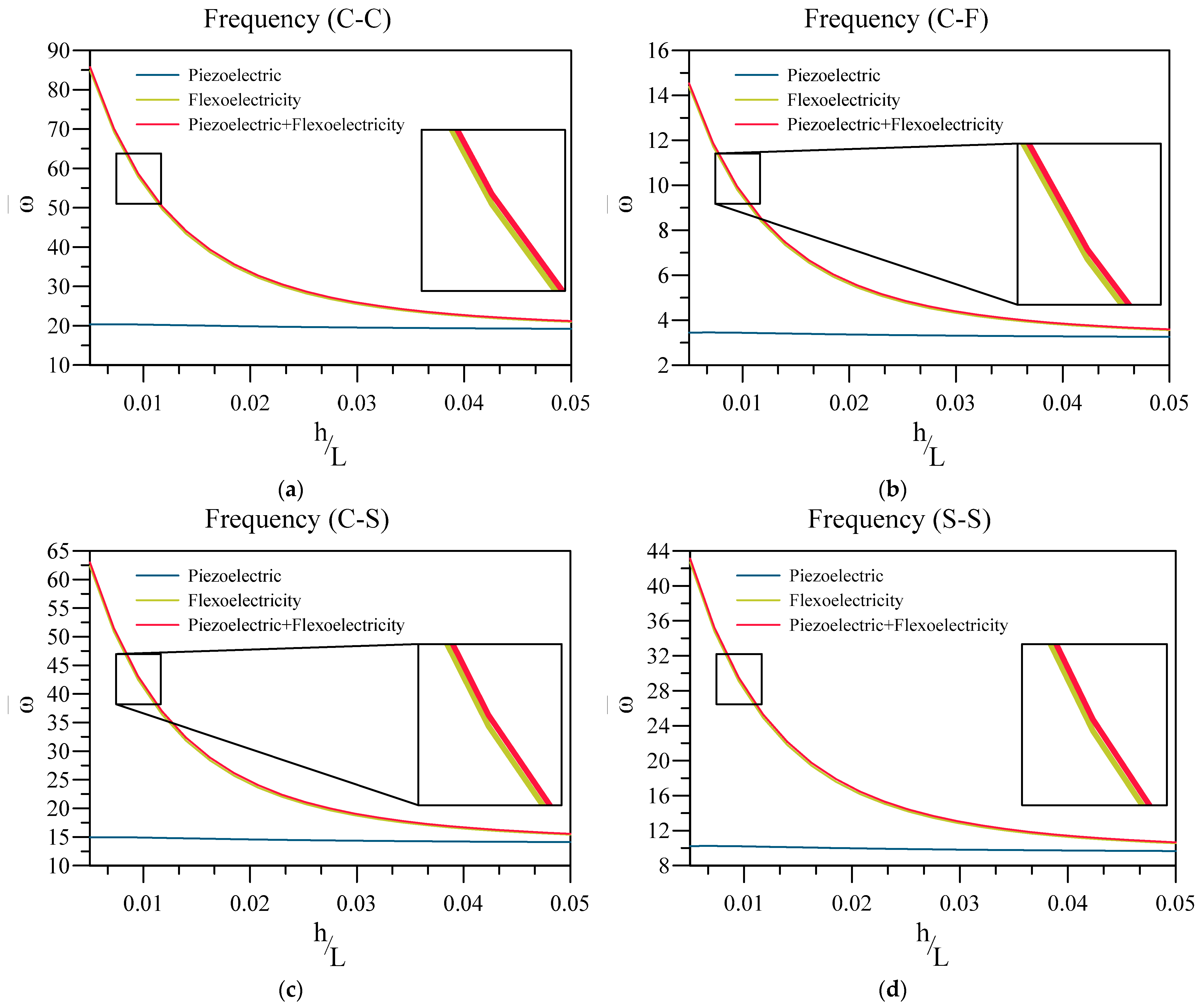
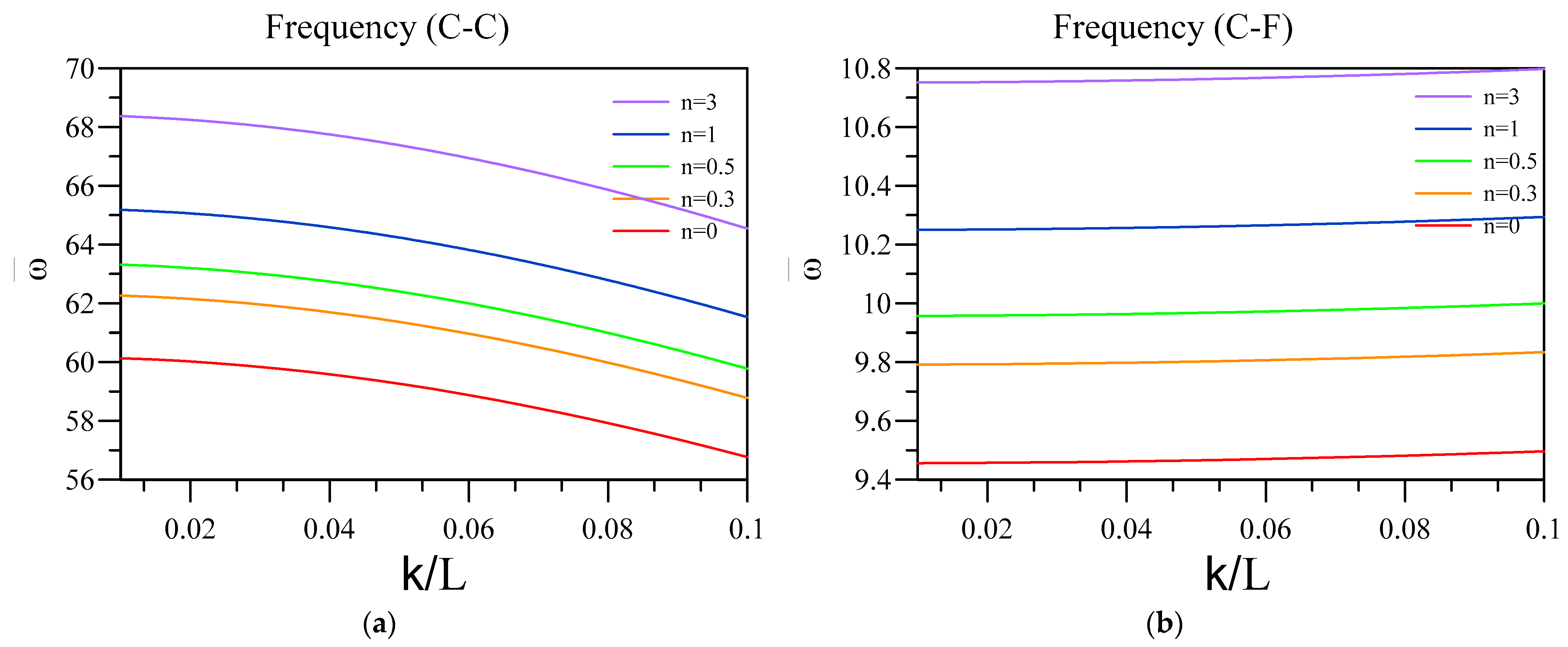
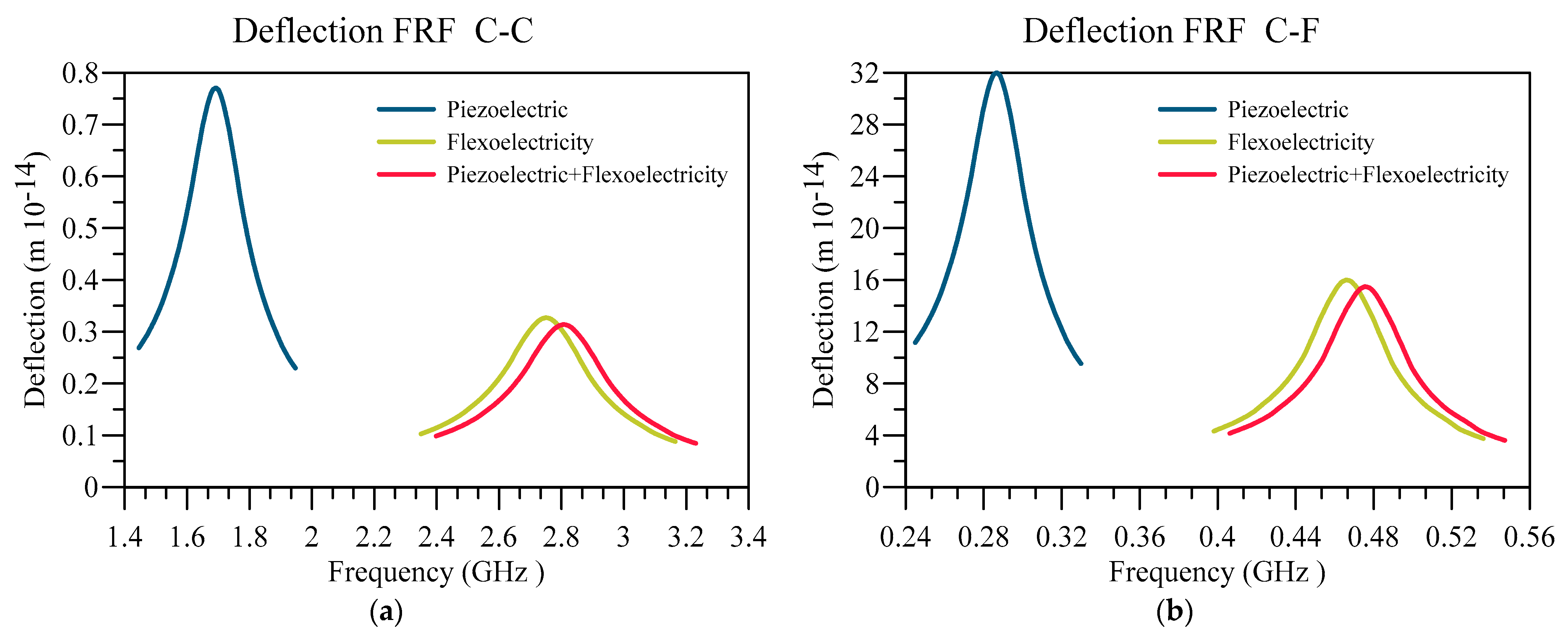
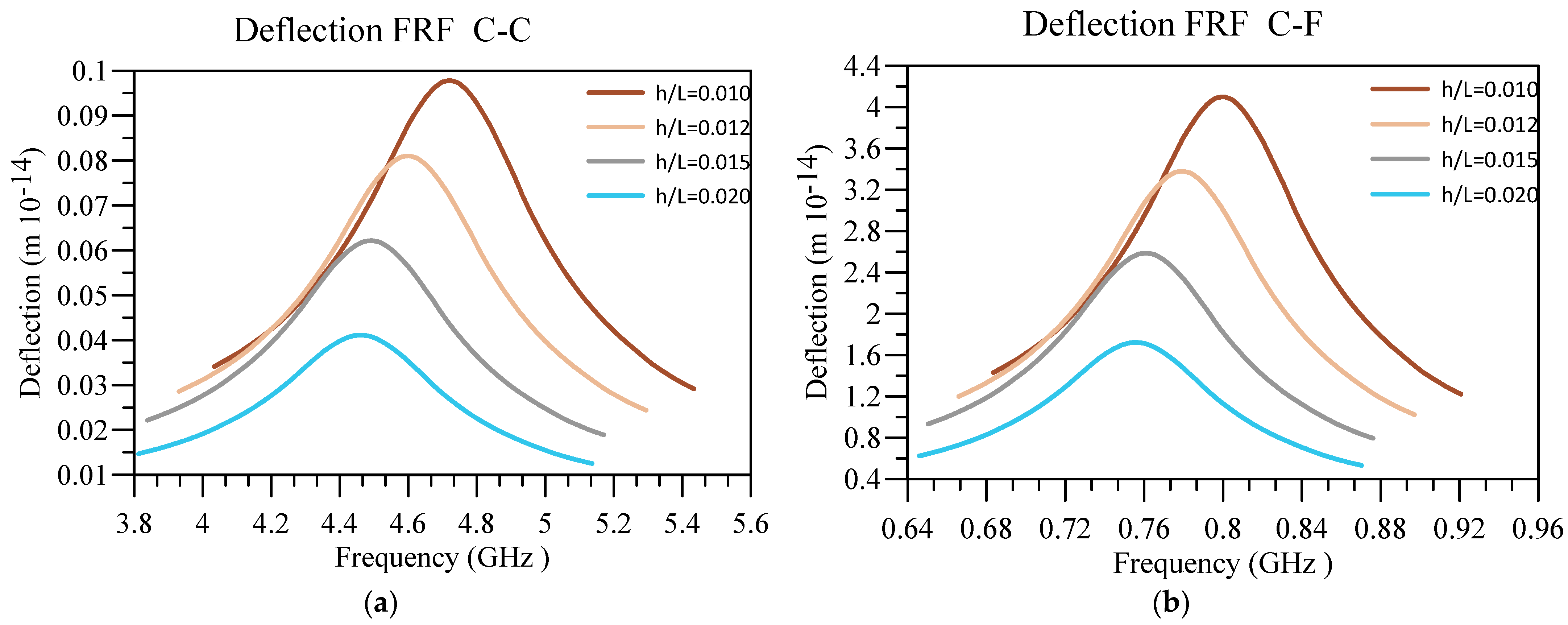
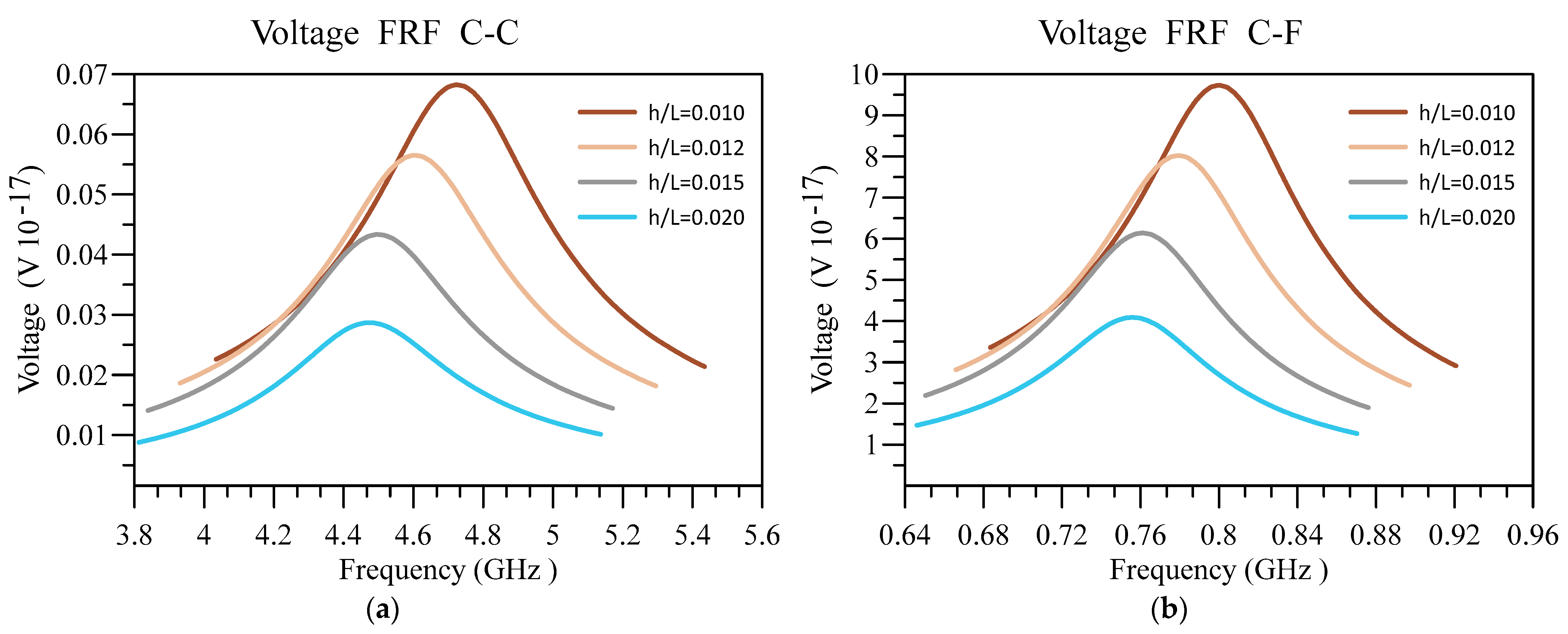
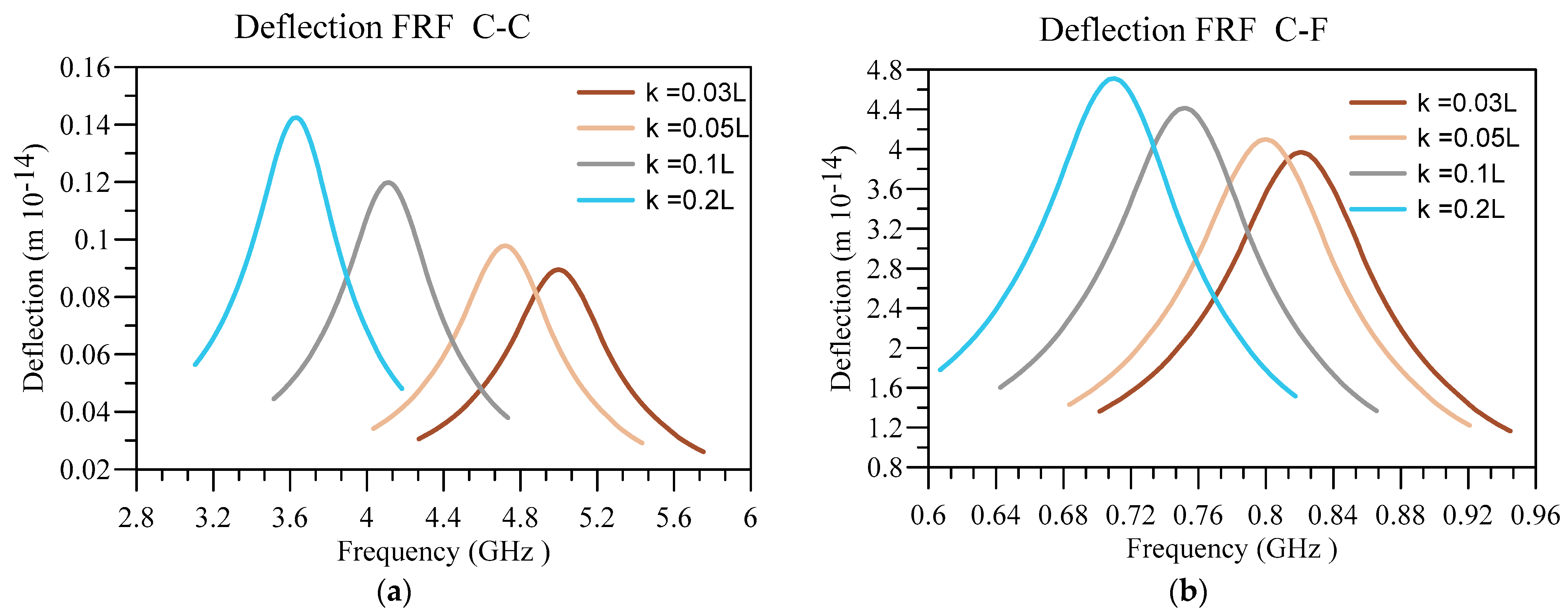
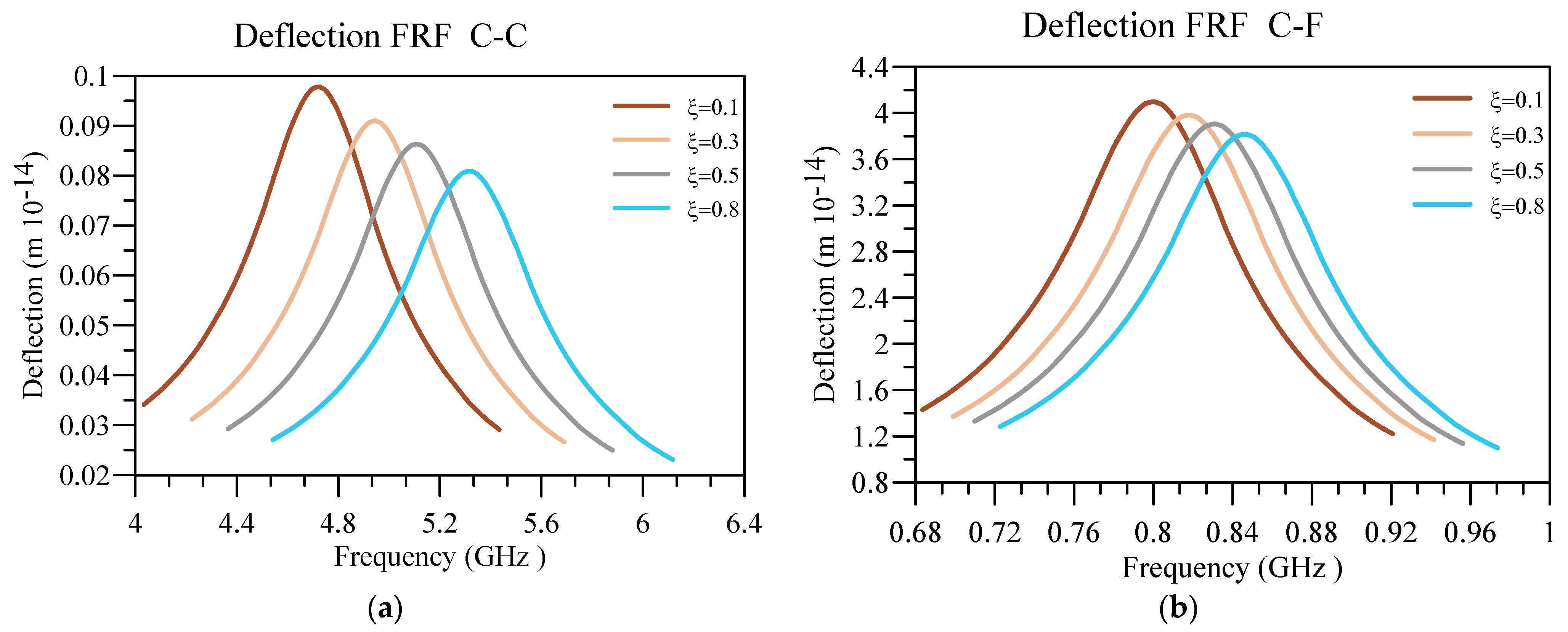
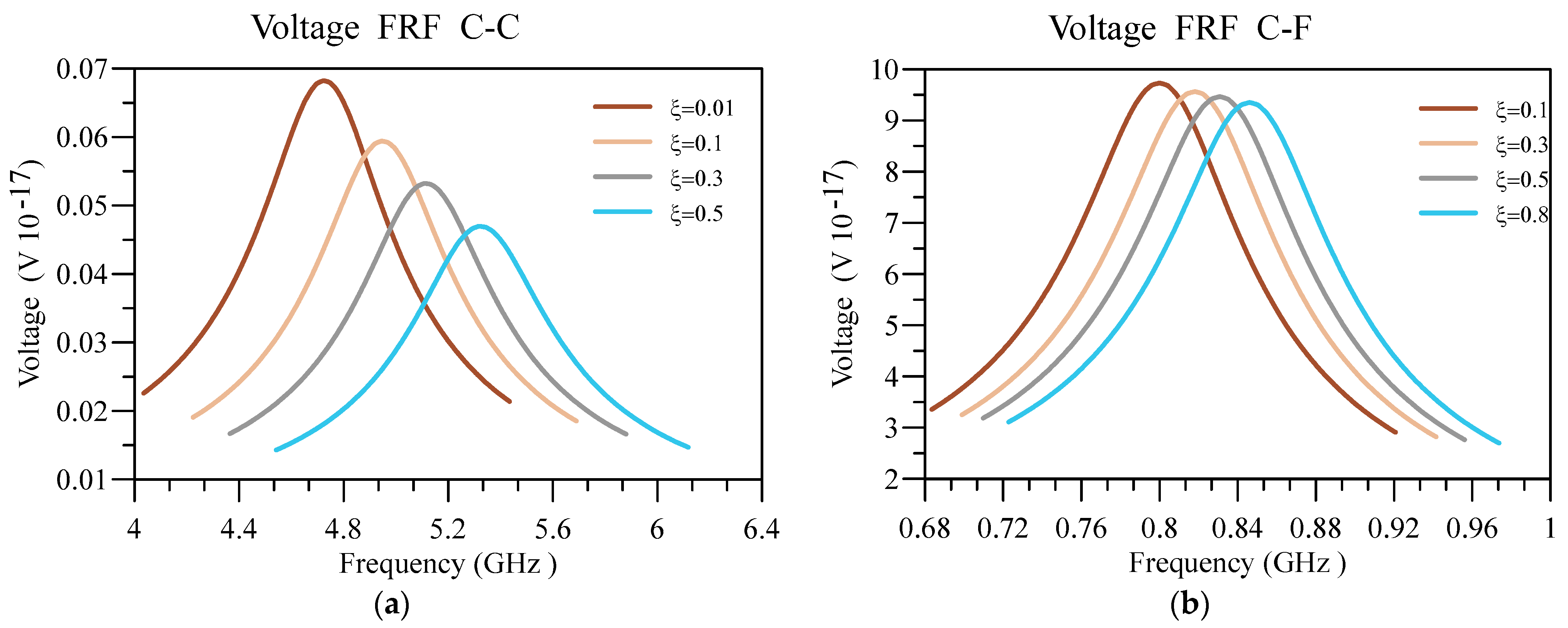
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| L, b, h, and hd | Nanobeam’s length and width, the thickness of FG base beam, and thickness of the dielectric layer |
| Elastic constant | |
| The dielectric constant tensor | |
| , and | Flexoelectric constant, nonlocal electrical coupling, and piezoelectric constant |
| and | Electrical field |
| Strain tensor | |
| and | Displacement in x and z directions. |
| and | Transverse deflection and rotation of the neutral plane of the beam |
| Elastic modulus associated with the FG layer | |
| The stress tensor related to the base layer | |
| Electrical potential | |
| as well as | Normal and second order stress in the dielectric layer |
| and | Electrical displacement and quadrupolar contribution |
| and | Mass density related to metal and ceramic |
| and | The ceramic and metal elastic modulus |
| and | Poisson’s ratio of metal and ceramic |
| N | FG power index |
| and | Strain and kinetic energy of the nanobeam |
| , , , , , , , and | The fourth-order elasticity tensor, Cauchy stress tensor in the two-phase state, the strain tensor, reference point, kernel function, local phase fraction factor, domain volume, as well as nonlocal parameter, respectively |
| Hermit interpolation | |
| The location corresponded to the grid points | |
| , , | Discretized form of bending moment, higher-order bending moment, and lateral displacement |
| Lagrange interpolation | |
| and | The amplitude and the frequency of the force |
| Damping ratio | |
| C-C, C-F, C-S, and S-S | Clamped–Clamped, Clamped-Free, Clamped–Simply, and Simply–Simply boundary conditions |
Appendix A
Appendix A.1. Differential Two-Phase Bending Moment
Appendix A.2. Differential Two-Phase Higher-Order Bending Moment
Appendix A.3. Constants Used for GDQM
Appendix A.4. The Discretized Formulation and Boundary Conditions
Appendix A.5. The Discretized Formulation of the Purely Nonlocal
References
- Naderi, A.; Behdad, S.; Fakher, M.; Hosseini-Hashemi, S. Vibration analysis of mass nanosensors with considering the axial-flexural coupling based on the two-phase local/nonlocal elasticity. Mech. Syst. Signal Process. 2020, 145, 106931. [Google Scholar] [CrossRef]
- Jiang, X.; Kim, K.; Zhang, S.; Johnson, J.; Salazar, G. High-Temperature Piezoelectric Sensing. Sensors 2014, 14, 144–169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rahman, A.; Jing, G.; Datta, S.; Lundstrom, M.S. Theory of ballistic nanotransistors. IEEE Trans. Electron Devices 2003, 50, 1853–1864. [Google Scholar] [CrossRef] [Green Version]
- Naderi, A.; Fakher, M.; Hosseini-Hashemi, S. On the local/nonlocal piezoelectric nanobeams: Vibration, buckling, and energy harvesting. Mech. Syst. Signal Process. 2021, 151, 107432. [Google Scholar] [CrossRef]
- Xu, T.-B.; Siochi, E.J.; Kang, J.H.; Zuo, L.; Zhou, W.; Tang, X.; Jiang, X. Energy harvesting using a PZT ceramic multilayer stack. Smart Mater. Struct. 2013, 22, 065015. [Google Scholar] [CrossRef] [Green Version]
- Hong, J.; Catalan, G.; Scott, J.; Artacho, E. The flexoelectricity of barium and strontium titanates from first principles. J. Phys. Condens. Matter 2010, 22, 112201. [Google Scholar] [CrossRef]
- Huang, W.; Yan, X.; Kwon, S.R.; Zhang, S.; Yuan, F.-G.; Jiang, X. Flexoelectric strain gradient detection using Ba0.64Sr0.36TiO3 for sensing. Appl. Phys. Lett. 2012, 101, 252903. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C.A.; Wegner, J.L.R. Nonlocal Continuum Field Theories. Appl. Mech. Rev. 2003, 56, B20–B22. [Google Scholar] [CrossRef]
- Lei, Y.; Adhikari, S.; Friswell, M. Vibration of nonlocal Kelvin–Voigt viscoelastic damped Timoshenko beams. Int. J. Eng. Sci. 2013, 66, 1–13. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, H. Uncertainty modeling for vibration and buckling behaviors of functionally graded nanobeams in thermal environment. Compos. Struct. 2018, 184, 1165–1176. [Google Scholar] [CrossRef]
- Lei, J.; He, Y.; Li, Z.; Guo, S.; Liu, D. Effect of nonlocal thermoelasticity on buckling of axially functionally graded nanobeams. J. Therm. Stress. 2019, 42, 526–539. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R.; Haghi, P. Wave propagation analysis of size-dependent rotating inhomogeneous nanobeams based on nonlocal elasticity theory. J. Vib. Control. 2018, 24, 3809–3818. [Google Scholar] [CrossRef]
- Assadi, A.; Farshi, B. Size-dependent longitudinal and transverse wave propagation in embedded nanotubes with consideration of surface effects. Acta Mech. 2011, 222, 27–39. [Google Scholar] [CrossRef]
- Pham, Q.-H.; Nhan, H.T.; Tran, V.K.; Zenkour, A.M. Hygro-thermo-mechanical vibration analysis of functionally graded porous curved nanobeams resting on elastic foundations. Waves Random Complex Media 2023, 1–32. [Google Scholar] [CrossRef]
- Pham, Q.-H.; Tran, V.K.; Nguyen, P.-C. Nonlocal strain gradient finite element procedure for hygro-thermal vibration analysis of bidirectional functionally graded porous nanobeams. Waves Random Complex Media 2023, 1–32. [Google Scholar] [CrossRef]
- Challamel, N.; Wang, C. The small length scale effect for a non-local cantilever beam: A paradox solved. Nanotechnology 2008, 19, 345703. [Google Scholar] [CrossRef]
- Challamel, N.; Zhang, Z.; Wang, C.; Reddy, J.; Wang, Q.; Michelitsch, T.; Collet, B. On nonconservativeness of Eringen’s nonlocal elasticity in beam mechanics: Correction from a discrete-based approach. Arch. Appl. Mech. 2014, 84, 1275–1292. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.-J.; Deng, Z.-C.; Zhang, K.; Xu, W. Observations of the softening phenomena in the nonlocal cantilever beams. Compos. Struct. 2016, 145, 43–57. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; de Sciarra, F.M. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Tuna, M.; Kirca, M. Exact solution of Eringen’s nonlocal integral model for bending of Euler–Bernoulli and Timoshenko beams. Int. J. Eng. Sci. 2016, 105, 80–92. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. Part B Eng. 2017, 114, 184–188. [Google Scholar] [CrossRef]
- Zhu, X.; Li, L. Longitudinal and torsional vibrations of size-dependent rods via nonlocal integral elasticity. Int. J. Mech. Sci. 2017, 133, 639–650. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R. Vibrations of Bernoulli-Euler beams using the two-phase nonlocal elasticity theory. Int. J. Eng. Sci. 2017, 119, 232–248. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, Y.; Dai, H.-H. Buckling analysis of Euler–Bernoulli beams using Eringen’s two-phase nonlocal model. Int. J. Eng. Sci. 2017, 116, 130–140. [Google Scholar] [CrossRef]
- Fakher, M.; Behdad, S.; Naderi, A.; Hosseini-Hashemi, S. Thermal vibration and buckling analysis of two-phase nanobeams embedded in size dependent elastic medium. Int. J. Mech. Sci. 2020, 171, 105381. [Google Scholar] [CrossRef]
- Behdad, S.; Fakher, M.; Naderi, A.; Hosseini-Hashemi, S. Vibrations of defected local/nonlocal nanobeams surrounded with two-phase Winkler–Pasternak medium: Non-classic compatibility conditions and exact solution. Waves Random Complex Media 2021, 1–36. [Google Scholar] [CrossRef]
- Behdad, S.; Fakher, M.; Hosseini-Hashemi, S. Dynamic stability and vibration of two-phase local/nonlocal VFGP nanobeams incorporating surface effects and different boundary conditions. Mech. Mater. 2021, 153, 103633. [Google Scholar] [CrossRef]
- Selvamani, R.; Tornabene, F.; Baleanu, D. Two phase local/nonlocal thermo elastic waves in a graphene oxide composite nanobeam subjected to electrical potential. ZAMM J. Appl. Math. Mech. Z. Für Angew. Math. Mech. 2023, 103, e202100390. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Behdad, S.; Fakher, M. Vibration analysis of two-phase local/nonlocal viscoelastic nanobeams with surface effects. Eur. Phys. J. Plus 2020, 135, 190. [Google Scholar] [CrossRef]
- Naderi, A.; Behdad, S.; Fakher, M. Size dependent effects of two phase viscoelastic medium on damping vibrations of smart nanobeams: An efficient implementation of GDQM. Smart Mater. Struct. 2022, 31, 045007. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Nanthakumar, S.S.; Zhuang, X.; Wriggers, P.; Jiang, X.; Rabczuk, T. Dynamic flexoelectric effect on piezoelectric nanostructures. Eur. J. Mech.—A/Solids 2018, 71, 404–409. [Google Scholar] [CrossRef]
- Ghasemi, H.; Park, H.S.; Rabczuk, T. A multi-material level set-based topology optimization of flexoelectric composites. Comput. Methods Appl. Mech. Eng. 2018, 332, 47–62. [Google Scholar] [CrossRef] [Green Version]
- Thai, T.Q.; Zhuang, X.; Park, H.S.; Rabczuk, T. A staggered explicit-implicit isogeometric formulation for large deformation flexoelectricity. Eng. Anal. Bound. Elem. 2021, 122, 1–12. [Google Scholar] [CrossRef]
- Yan, X.; Huang, W.; Ryung Kwon, S.; Yang, S.; Jiang, X.; Yuan, F.-G. A sensor for the direct measurement of curvature based on flexoelectricity. Smart Mater. Struct. 2013, 22, 085016. [Google Scholar] [CrossRef]
- Huang, W.; Yang, S.; Zhang, N.; Yuan, F.-G.; Jiang, X. Direct Measurement of Opening Mode Stress Intensity Factors Using Flexoelectric Strain Gradient Sensors. Exp. Mech. 2015, 55, 313–320. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, W.; Zhang, S. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Majdoub, M.; Sharma, P.; Çağin, T. Dramatic enhancement in energy harvesting for a narrow range of dimensions in piezoelectric nanostructures. Phys. Rev. B 2008, 78, 121407. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.; Jiang, L. Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J. Appl. Phys. 2013, 113, 194102. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L. Size-dependent bending and vibration behaviour of piezoelectric nanobeams due to flexoelectricity. J. Phys. D Appl. Phys. 2013, 46, 355502. [Google Scholar] [CrossRef]
- Sidhardh, S.; Ray, M. Effect of nonlocal elasticity on the performance of a flexoelectric layer as a distributed actuator of nanobeams. Int. J. Mech. Mater. Des. 2018, 14, 297–311. [Google Scholar] [CrossRef]
- Qi, L.; Huang, S.; Fu, G.; Li, A.; Zhou, S.; Jiang, X. Modeling of the flexoelectric annular microplate based on strain gradient elasticity theory. Mech. Adv. Mater. Struct. 2019, 26, 1958–1968. [Google Scholar] [CrossRef]
- Li, X.; Luo, Y. Flexoelectric effect on vibration of piezoelectric microbeams based on a modified couple stress theory. Shock. Vib. 2017, 2017, 4157085. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Zhang, R.; Hu, S.; Shen, S. Flexoelectric energy harvesters based on Timoshenko laminated beam theory. J. Intell. Mater. Syst. Struct. 2017, 28, 2064–2073. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Size-dependent buckling and vibration behaviors of piezoelectric nanostructures due to flexoelectricity. Smart Mater. Struct. 2015, 24, 105012. [Google Scholar] [CrossRef]
- Zhang, D.; Lei, Y.; Adhikari, S. Flexoelectric effect on vibration responses of piezoelectric nanobeams embedded in viscoelastic medium based on nonlocal elasticity theory. Acta Mech. 2018, 229, 2379–2392. [Google Scholar] [CrossRef] [Green Version]
- Amiri, A.; Vesal, R.; Talebitooti, R. Flexoelectric and surface effects on size-dependent flow-induced vibration and instability analysis of fluid-conveying nanotubes based on flexoelectricity beam model. Int. J. Mech. Sci. 2019, 156, 474–485. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Integral Equations; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Nonlocal and surface effects on vibration behavior of axially loaded flexoelectric nanobeams subjected to in-plane magnetic field. Arab. J. Sci. Eng. 2018, 43, 1423–1433. [Google Scholar] [CrossRef]
- Barati, M.R. On non-linear vibrations of flexoelectric nanobeams. Int. J. Eng. Sci. 2017, 121, 143–153. [Google Scholar] [CrossRef]
- Khaniki, H.B. On vibrations of FG nanobeams. Int. J. Eng. Sci. 2019, 135, 23–36. [Google Scholar] [CrossRef]
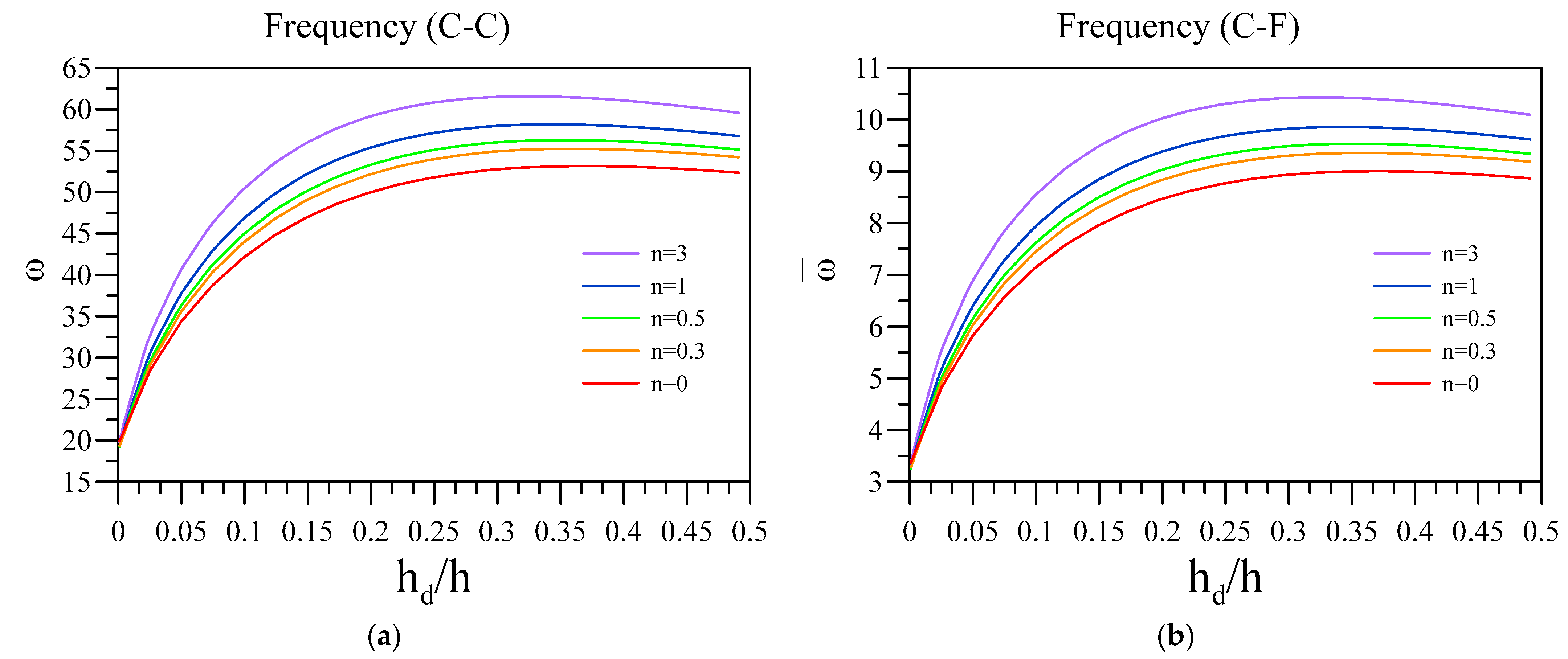
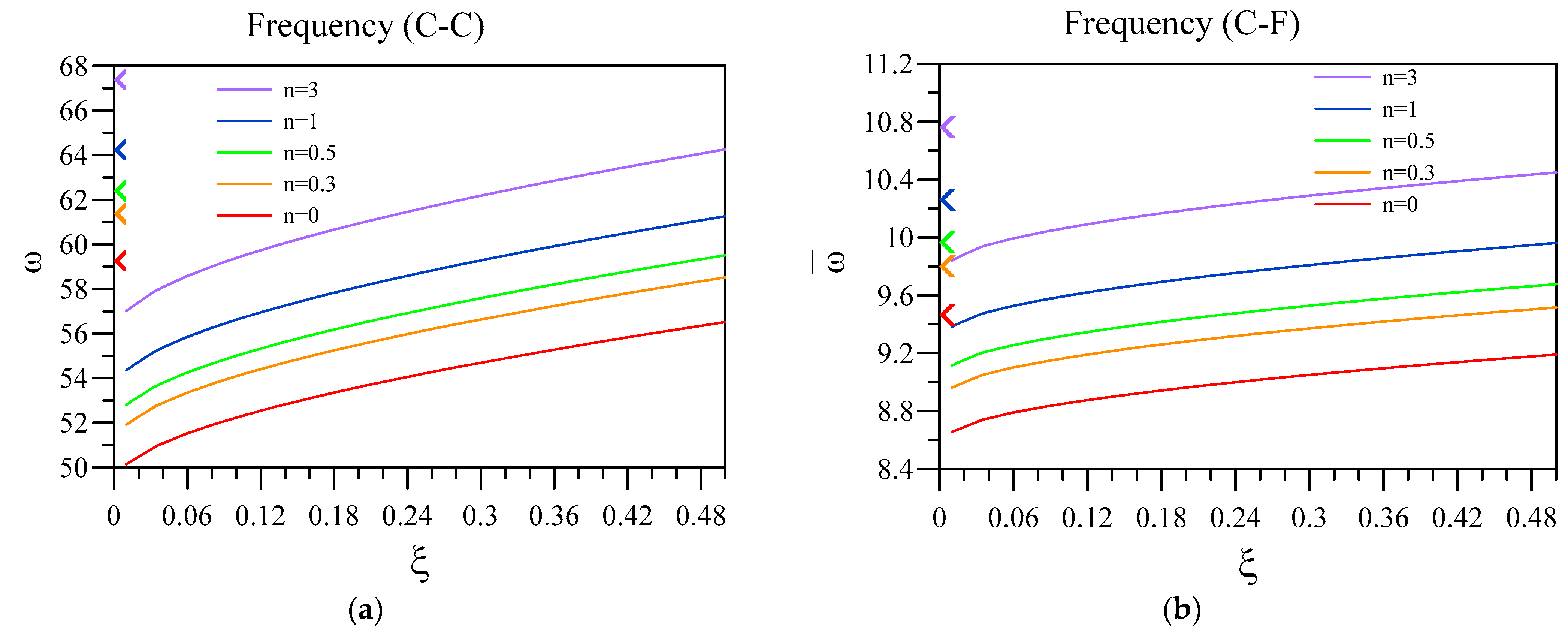
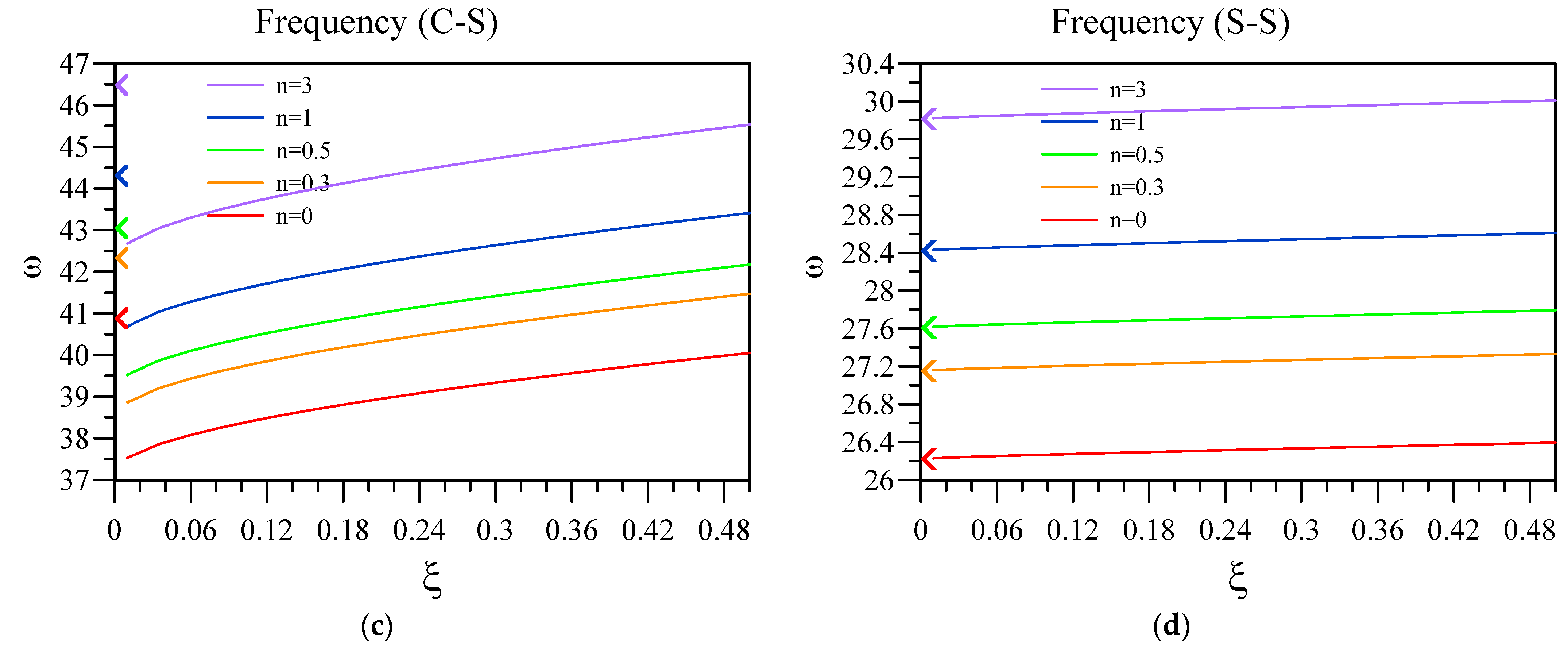
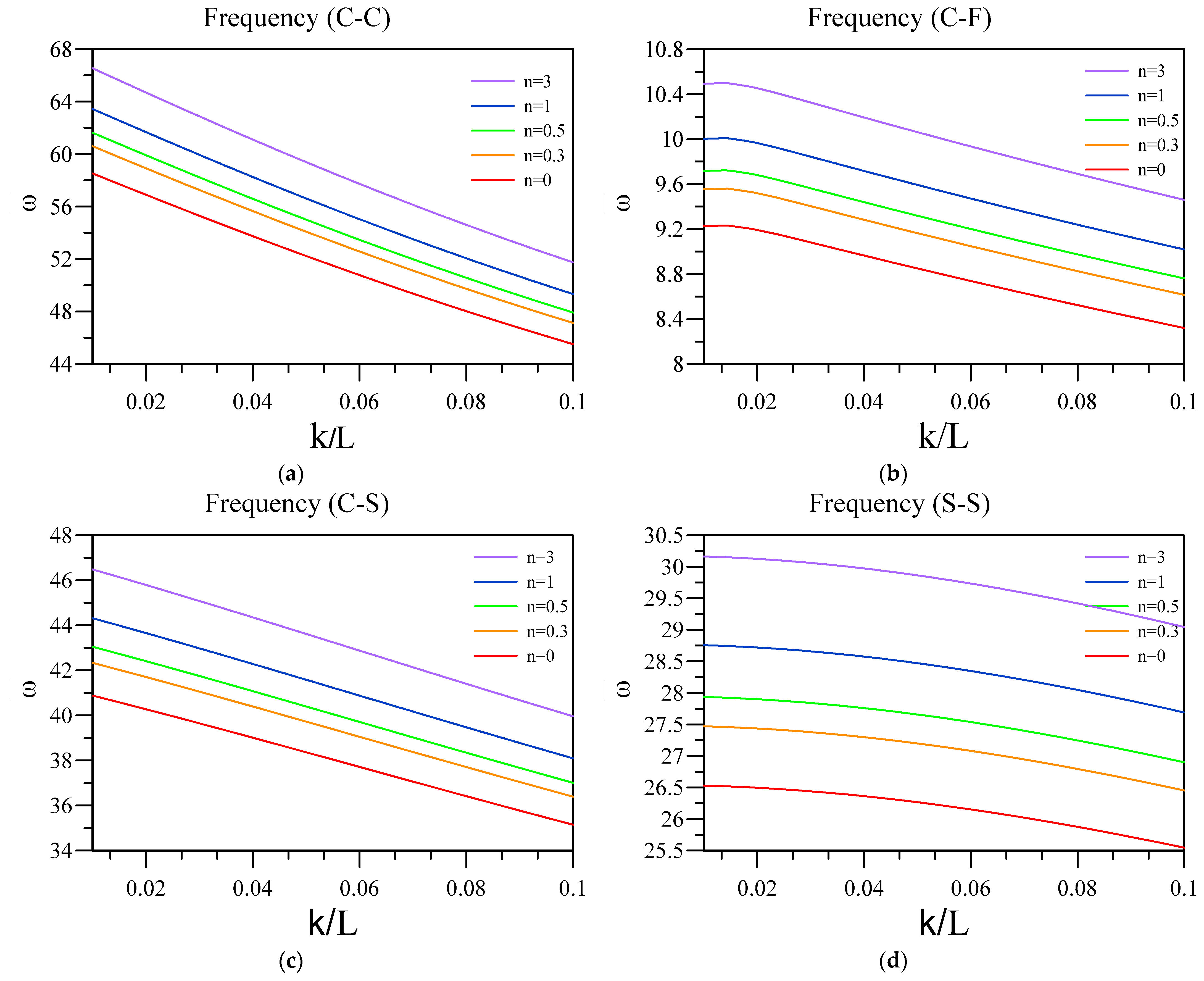



| 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|
| Present results | 0.83504 | 0.96573 | 0.98432 | 0.99109 | 0.99427 |
| Ref. [42] * | 0.83419 | 0.96318 | 0.98386 | 0.99092 | 0.99420 |
| Error % | 0.10 | 0.26 | 0.04 | 0.01 | 0.01 |
| Modes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | ||||||||
| BCs | Ref. [26] * | Exact [26] ** | Present | Error % | Ref. [26] * | Exact [26] ** | Present | Error % | |
| SS | 1.00 | 9.8696 | 9.8696 | 9.8696 | 0.00 | 39.4784 | 39.4784 | 39.4784 | 0.00 |
| 0.50 | 9.8192 | 9.8148 | 9.8145 | 0.01 | 38.6493 | 38.6502 | 38.6502 | 0.00 | |
| 0.10 | 9.7610 | 9.7671 | 9.7671 | 0.00 | 37.8993 | 37.9218 | 37.9218 | 0.00 | |
| 0.05 | - | 9.7601 | 9.7601 | 0.00 | - | 37.8150 | 37.8150 | 0.00 | |
| 0.01 | - | 9.7533 | 9.7533 | 0.00 | - | 37.7125 | 37.7125 | 0.00 | |
| CF | 1.00 | 3.5160 | 3.5160 | 3.5160 | 0.00 | 22.0344 | 22.0345 | 22.0345 | 0.00 |
| 0.50 | 3.4105 | 3.4173 | 3.4173 | 0.00 | 21.2628 | 21.2626 | 21.2626 | 0.00 | |
| 0.10 | 3.2874 | 3.2908 | 3.2908 | 0.00 | 20.2713 | 20.3538 | 20.3538 | 0.00 | |
| 0.05 | - | 3.2617 | 3.2617 | 0.00 | - | 20.1592 | 20.1592 | 0.00 | |
| 0.01 | - | 3.2233 | 3.2233 | 0.00 | - | 19.9118 | 19.9118 | 0.00 | |
| BC | ||||||
|---|---|---|---|---|---|---|
| 20 | 50 | 100 | 200 | 500 | 1000 | |
| S-S | 1.19167 | 1.03937 | 1.01247 | 1.00438 | 1.0013 | 1.00058 |
| C-F | 1.19167 | 1.03937 | 1.01247 | 1.00438 | 1.0013 | 1.00058 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naderi, A.; Quoc-Thai, T.; Zhuang, X.; Jiang, X. Vibration Analysis of a Unimorph Nanobeam with a Dielectric Layer of Both Flexoelectricity and Piezoelectricity. Materials 2023, 16, 3485. https://doi.org/10.3390/ma16093485
Naderi A, Quoc-Thai T, Zhuang X, Jiang X. Vibration Analysis of a Unimorph Nanobeam with a Dielectric Layer of Both Flexoelectricity and Piezoelectricity. Materials. 2023; 16(9):3485. https://doi.org/10.3390/ma16093485
Chicago/Turabian StyleNaderi, Ali, Tran Quoc-Thai, Xiaoying Zhuang, and Xiaoning Jiang. 2023. "Vibration Analysis of a Unimorph Nanobeam with a Dielectric Layer of Both Flexoelectricity and Piezoelectricity" Materials 16, no. 9: 3485. https://doi.org/10.3390/ma16093485






