A Parameterized Leblond–Devaux Equation for Predicting Phase Evolution during Welding E36 and E36Nb Marine Steels
Abstract
:1. Introduction
2. Materials and Methods
3. Leblond–Devaux and Koistinen–Marburger Equations for Phase Transformations during Welding
4. Results and Discussion
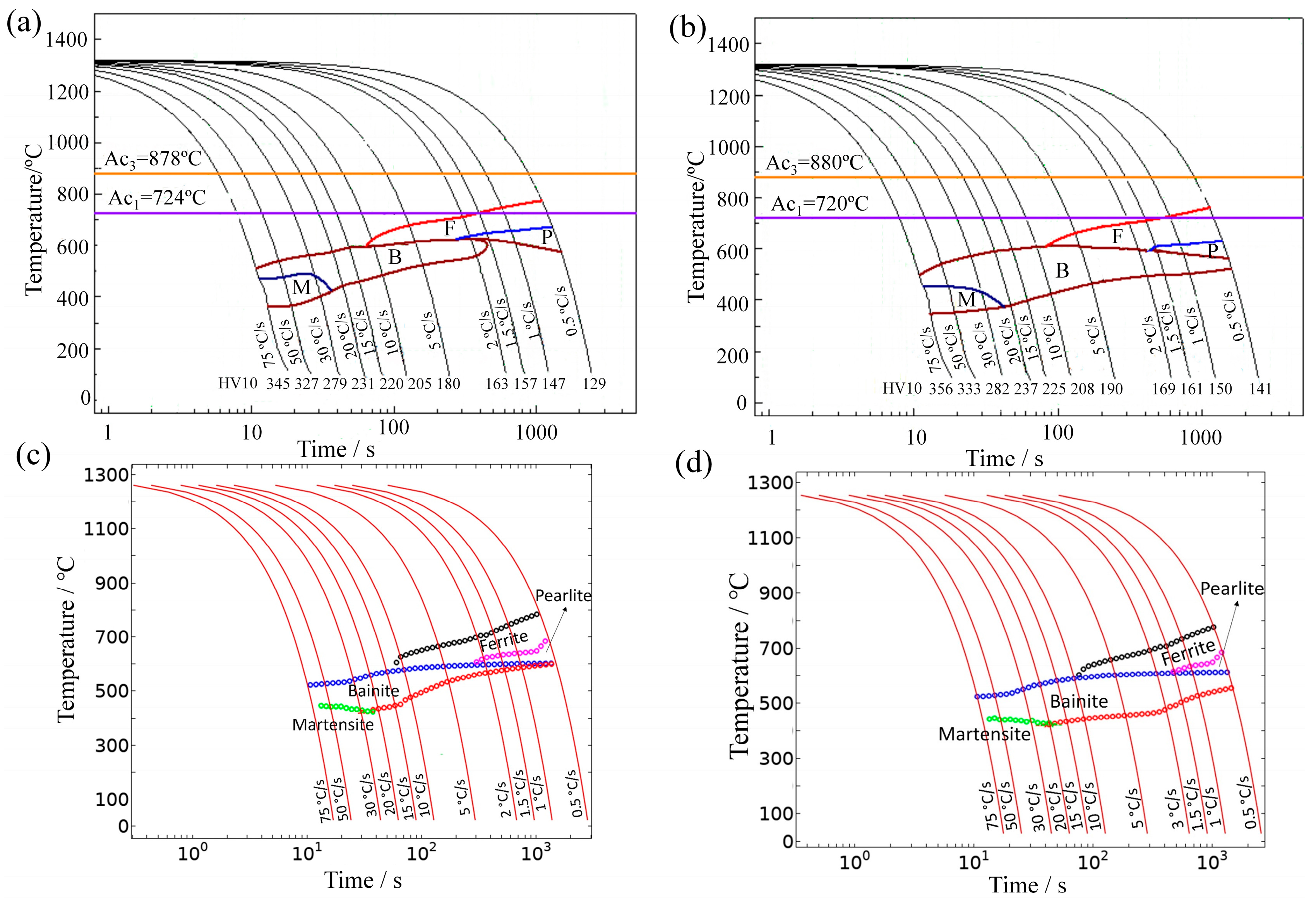
4.1. Phase Evolution of E36 and E36Nb in Experiments at Different Cooling Rates
4.2. SH-CCT Diagrams and Temperature-Dependent Parameters of Leblond–Devaux Equation for E36Nb
5. Application of Parameterized Leblond–Devaux Equation
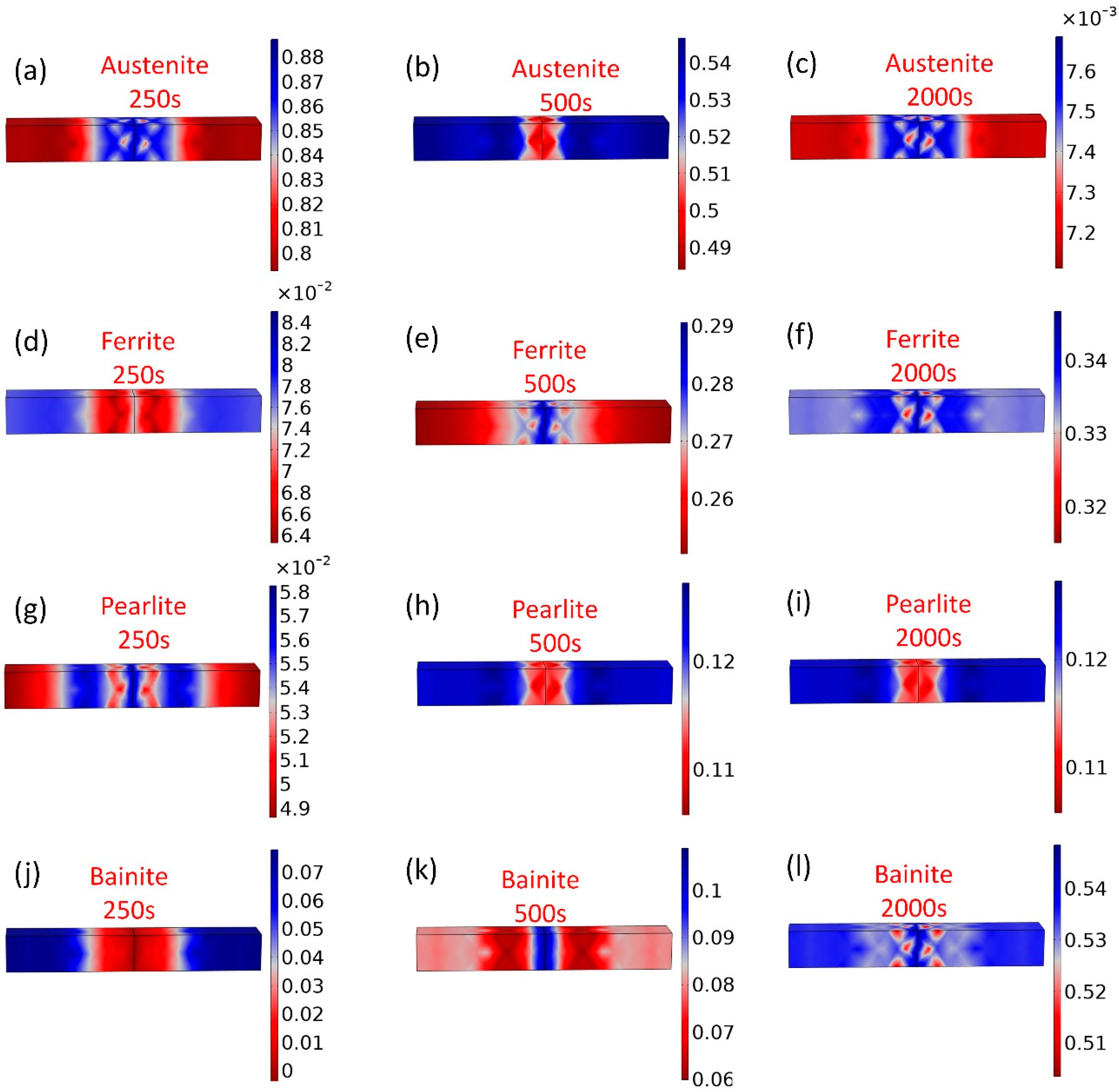
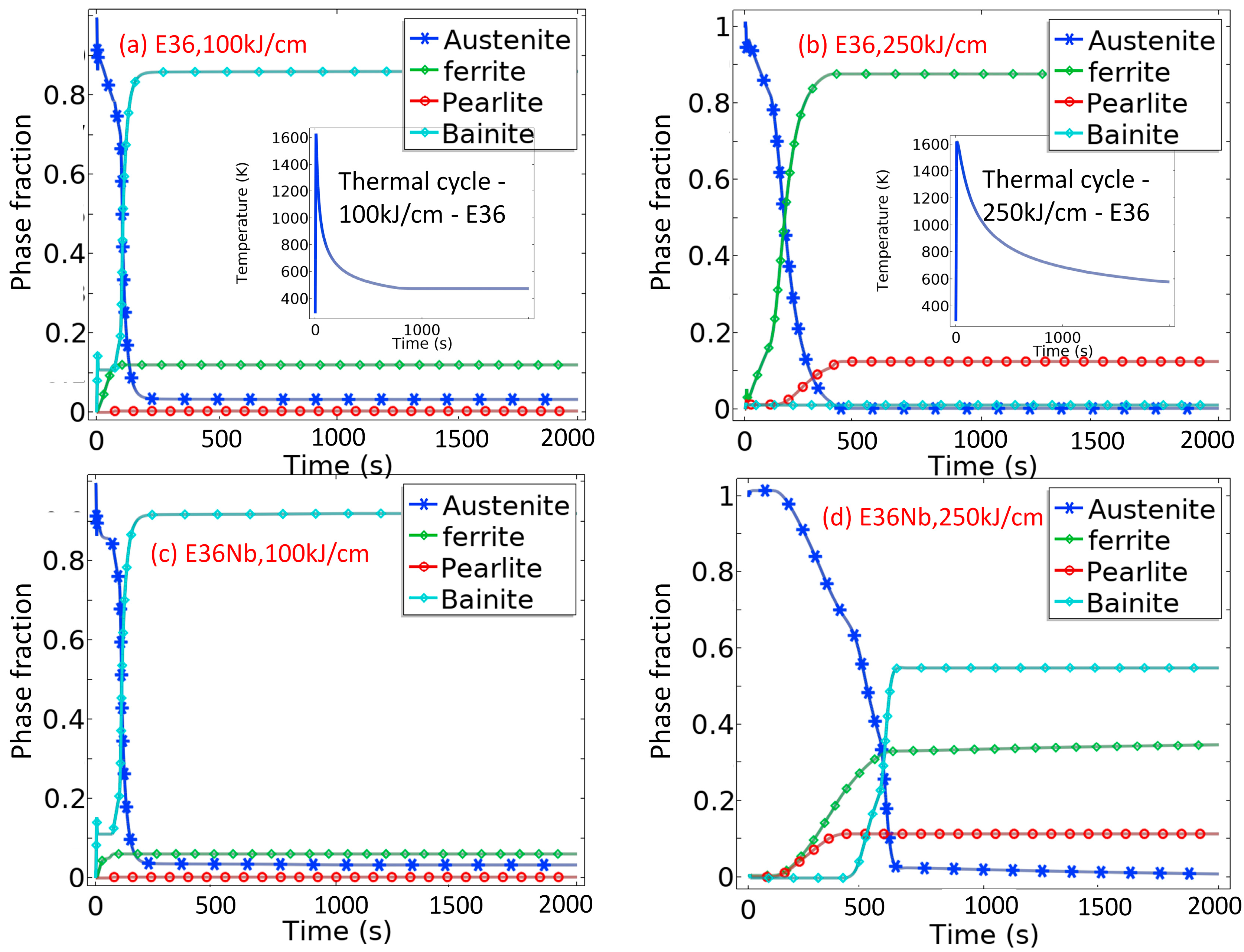
5.1. Predicted Phase Evolution of E36 and E36Nb with High Heat Inputs Using Parameterized Leblond–Devaux Equation
5.2. Phases in HAZ of E36 and E36Nb Welded with Heat Inputs of 100 kJ/cm and 250 kJ/cm
6. Conclusions
- Niobium addition on E36 marine steel reduces the cooling rate range of acicular ferrite transformation. The acicular ferrite formed within broader cooling rates for E36 steel from 2 °C/s to 20 °C/s and a narrower cooling rate for E36Nb steel from 1 °C/s to 2 °C/s;
- Phases in HAZ of E36Nb welded with a high heat input of 100 kJ/cm consist of acicular ferrite, proeutectoid ferrite, and bainite; phases in HAZ of E36 contain granular bainite and pearlite. Phases in HAZ of E36, welded with a high heat input of 250 kJ/cm, are ferrite and pearlite, but phases in HAZ of E36Nb are proeutectoid ferrite and bainite;
- Leblond–Devaux equation parameters of and for both steels have been evaluated and simulated as temperature-dependent functions. A parameterized model based on the Leblond–Devaux and Koistinen–Marburger equations is provided for the thermal welding cycle to predict the phase fraction of marine steels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Corigliano, P.; Crupi, V. Review of Fatigue Assessment Approaches for Welded Marine Joints and Structures. Metals 2022, 12, 1010. [Google Scholar] [CrossRef]
- Hashiba, Y.; Kojima, K.; Kasuya, T.; Kumagai, T. Development of welding consumables and welding process for newly developed steel plates. Nippon. Steel Sumitomo Met. Tech. Rep. 2015, 110, 90. [Google Scholar]
- Fu, J.; Tao, Q.; Yang, X.; Nenchev, B.; Li, M.; Tao, B.; Dong, H. The Effect of Heat Source Path on Thermal Evolution during Electro-Gas Welding of Thick Steel Plates. Materials 2022, 15, 2215. [Google Scholar] [CrossRef] [PubMed]
- Lan, L.; Kong, X.; Qiu, C.; Zhao, D. Influence of microstructural aspects on impact toughness of multi-pass submerged arc welded HSLA steel joints. Mater. Des. 2016, 90, 488–498. [Google Scholar] [CrossRef]
- Shi, M.; Zhang, P.; Zhu, F. Toughness and Microstructure of Coarse Grain Heat Affected Zone with High Heat Input Welding in Zr-bearing Low Carbon Steel. ISIJ Int. 2014, 54, 188–192. [Google Scholar] [CrossRef]
- Yang, Y.; Jia, X.; Ma, Y.; Wang, P.; Zhu, F. Effect of Nb on inclusions and phase transformation in simulated high heat input coarse-grain HAZ of Nb/Ti low carbon microalloyed steel. Mater. Charact. 2022, 189, 111966. [Google Scholar] [CrossRef]
- Moravec, J.; Novakova, I.; Sobotka, J.; Neumann, H. Determination of Grain Growth Kinetics and Assessment of Welding Effect on Properties of S700MC Steel in the HAZ of Welded Joints. Metals 2019, 9, 707. [Google Scholar] [CrossRef]
- Kojima, A.; Kiyose, A.; Uemori, R.; Minagawa, M. Super high HAZ toughness technology with fine microstructure imparted by fine particles. Shinnittetsu Giho 2004, 90, 2–5. [Google Scholar]
- Francis, J.; Bhadeshia, H.K.D.H.; Withers, P. Welding residual stresses in ferritic power plant steels. Mater. Sci. Technol. 2007, 23, 1009–1020. [Google Scholar] [CrossRef]
- Bhadeshia, H. Possible effects of stress on steel weld microstructures. Math. Model. Weld Phenom. 1995, 2, 71–118. [Google Scholar]
- Leblond, J.; Devaux, J. A new kinetic model for anisothermal metallurgical transformations in steels including effect of austenite grain size. Acta Metall. 1984, 32, 137–146. [Google Scholar] [CrossRef]
- Li, M.V.; Niebuhr, D.V.; Meekisho, L.L.; Atteridge, D.G. A computational model for the prediction of steel hardenability. Met. Mater. Trans. B 1998, 29, 661–672. [Google Scholar] [CrossRef]
- Ni, J.; Voorde, J.V.; Antonissen, J.; Wahab, M.A. Dependency of phase transformation on the prior austenite grain size and its influence on welding residual stress of S700 steel. Weld. World 2018, 62, 699–712. [Google Scholar] [CrossRef]
- Åkerström, P.; Oldenburg, M. Austenite decomposition during press hardening of a boron steel—Computer simulation and test. J. Mater. Process. Technol. 2006, 174, 399–406. [Google Scholar] [CrossRef]
- Kirkaldy, J. Prediction of microstructure and hardenability in low alloy steels. In Proceedings of the International Conference on Phase Transformation in Ferrous Alloys, Philadelphia, PA, USA, 4–6 October 1983; AIME: New York, NY, USA, 1983. [Google Scholar]
- Pohjonen, A.; Somani, M.; Porter, D. Modelling of austenite transformation along arbitrary cooling paths. Comput. Mater. Sci. 2018, 150, 244–251. [Google Scholar] [CrossRef]
- Hu, L.; Wang, Y.; Li, S.; Chaohua, Z.; Dean, D. Study on Computational Prediction about Microstructure and Hardness of Q345 Steel Welded Joint Based on SH-CCT Diagram. Acta Metall. Sin. 2021, 57, 1073–1086. [Google Scholar]
- Hutchinson, B.; Komenda, J.; Rohrer, G.S.; Beladi, H. Heat affected zone microstructures and their influence on toughness in two microalloyed HSLA steels. Acta Mater. 2015, 97, 380–391. [Google Scholar] [CrossRef]
- Viesca, J.; González-Cachón, S.; García, A.; González, R.; Battez, A.H. Tribological behaviour of microalloyed and conventional C–Mn rail steels in a pure sliding condition. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 2201–2214. [Google Scholar] [CrossRef]
- Dey, I.; Chandra, S.; Saha, R.; Ghosh, S. Effect of Nb micro-alloying on microstructure and properties of thermo-mechanically processed high carbon pearlitic steel. Mater. Charact. 2018, 140, 45–54. [Google Scholar] [CrossRef]
- Villalobos, J.C.; Del-Pozo, A.; Campillo, B.; Mayen, J.; Serna, S. Microalloyed Steels through History until 2018: Review of Chemical Composition, Processing and Hydrogen Service. Metals 2018, 8, 351. [Google Scholar] [CrossRef]
- Rules for Classification, Ships, Part 2: Materials and Welding; DNV GL: Oslo, Norway, 2017; p. 35.
- Guo, Z.; Saunders, N.; Schillé, J.; Miodownik, A. Material properties for process simulation. Mater. Sci. Eng. A 2009, 499, 7–13. [Google Scholar] [CrossRef]
- Saunders, N.; Guo, U.K.Z.; Li, X.; Miodownik, A.P.; Schillé, J.-P. Using JMatPro to model materials properties and behavior. Jom 2003, 55, 60–65. [Google Scholar] [CrossRef]
- Watt, D.; Coon, L.; Bibby, M.; Goldak, J.; Henwood, C. An algorithm for modelling microstructural development in weld heat-affected zones (part a) reaction kinetics. Acta Metall. 1988, 36, 3029–3035. [Google Scholar] [CrossRef]
- Koistinen, D.P.; Marburger, R.E. A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbon alloys and plain carbon steels. Acta Metall. 1959, 7, 59–60. [Google Scholar] [CrossRef]
- Gyhlesten Back, J. Modelling and Characterisation of the Martensite Formation in Low Alloyed Carbon Steels. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2017. [Google Scholar]
- El-Fallah, G. Structural Evolution during the Plastic Deformation of Nanostructured Steel. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2020. [Google Scholar]
- El Fallah, G.; Bhadeshia, H. Tensile Behaviour of Thermally-Stable Nanocrystalline Bainitic-Steels. Mater. Sci. Eng. A 2019, 746, 145–153. [Google Scholar] [CrossRef]
- Abramoff, M.; Magalhaes, P.; Ram, S. Image processing with imageJ. Biophoton. Int 2004, 11, 36–42. [Google Scholar]
- Babasafari, Z.; Pan, A.V.; Pahlevani, F.; Hossain, R.; Sahajwalla, V.; du Toit, M.; Dippenaar, R. Effects of austenizing temperature, cooling rate and isothermal temperature on overall phase transformation characteristics in high carbon steel. J. Mater. Res. Technol. 2020, 9, 15286–15297. [Google Scholar] [CrossRef]
- Handoko, W.; Pahlevani, F.; Sahajwalla, V. Enhancing Corrosion Resistance and Hardness Properties of Carbon Steel through Modification of Microstructure. Materials 2018, 11, 2404. [Google Scholar] [CrossRef]
- Tao, X.L.; Wu, K.M.; Wan, X.L. Effect of Nb on Microstructure Evolution of Coarse-Grained Heat-Affected Zone with Large Heat Input Welding. Adv. Mater. Res. 2011, 284–286, 1174–1179. [Google Scholar] [CrossRef]
- Bansal, G.; Srivastava, V.; Chowdhury, S.G. Role of solute Nb in altering phase transformations during continuous cooling of a low-carbon steel. Mater. Sci. Eng. A 2019, 767, 138416. [Google Scholar] [CrossRef]
- Sung, H.K.; Shin, S.Y.; Cha, W.; Oh, K.; Lee, S.; Kim, N.J. Effects of acicular ferrite on charpy impact properties in heat affected zones of oxide-containing API X80 linepipe steels. Mater. Sci. Eng. A 2011, 528, 3350–3357. [Google Scholar] [CrossRef]
- Zou, X.; Sun, J.; Matsuura, H.; Wang, C. Unravelling Microstructure Evolution and Grain Boundary Misorientation in Coarse-Grained Heat-Affected Zone of EH420 Shipbuilding Steel Subject to Varied Welding Heat Inputs. Metall. Mater. Trans. A 2020, 51, 1044–1050. [Google Scholar] [CrossRef]
- Zhan, X.; Qi, C.; Gao, Z.; Tian, D.; Wang, Z. The influence of heat input on microstructure and porosity during laser cladding of Invar alloy. Opt. Laser Technol. 2019, 113, 453–461. [Google Scholar] [CrossRef]
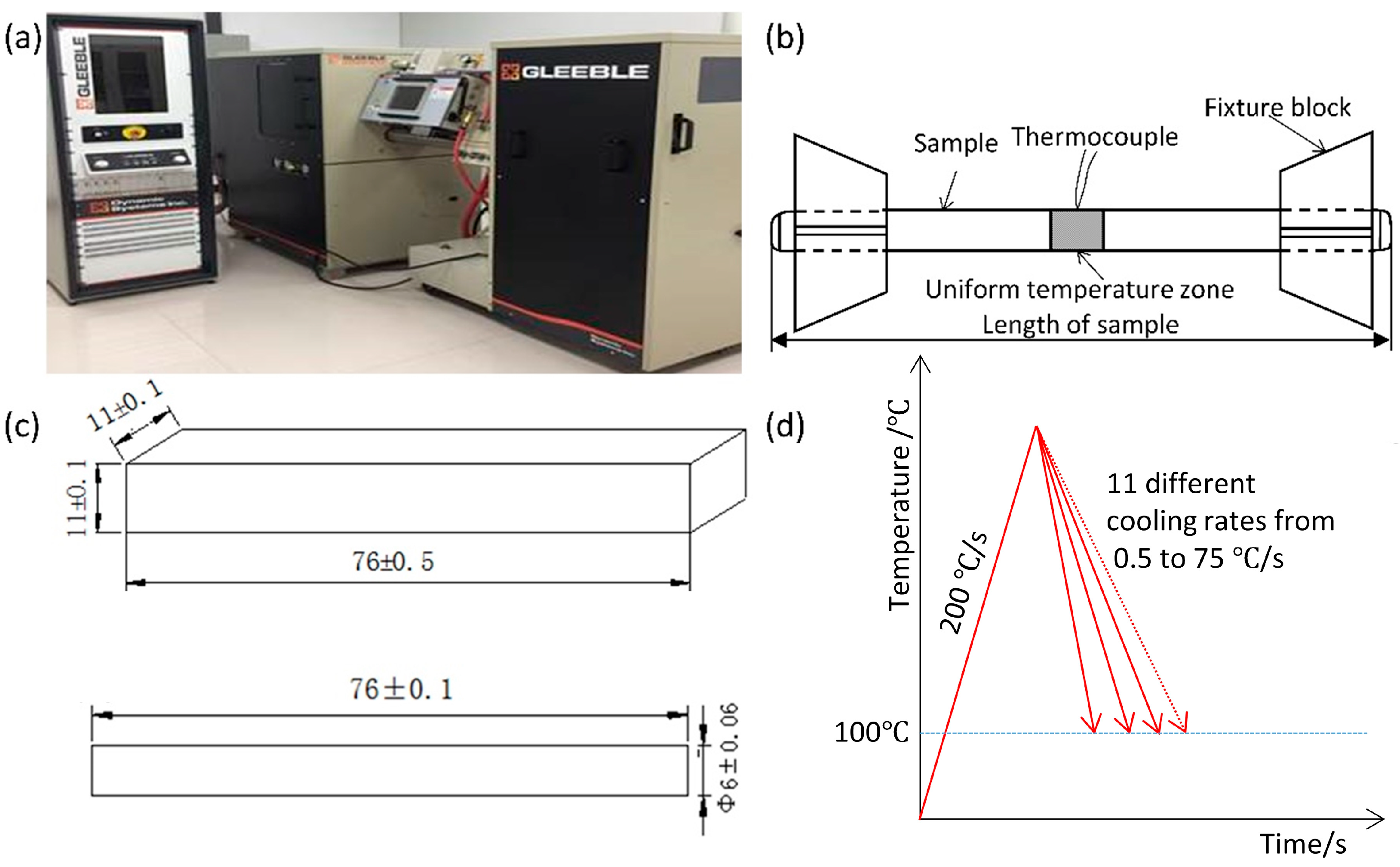



| Steel | C % | Si % | Mn % | S % | P % | Nb % | Ti % | Al % |
|---|---|---|---|---|---|---|---|---|
| E36 | 0.08 | 0.21 | 1.51 | 0.002 | 0.012 | / | 0.016 | 0.03 |
| E36Nb | 0.08 | 0.25 | 1.52 | 0.002 | 0.013 | 0.012 | 0.016 | 0.03 |
| Peak Temperature °C | Heating Rate °C/s | Holding Time s | Δt8/5 s | Heat Input kJ/cm |
|---|---|---|---|---|
| 1350 | 200 | 1.0 | 71.2 | 100 |
| 180 | 2.0 | 444.8 | 250 |
| Cooling Rate °C/s | Steel Grade | F % | P % | PF % | B % | AF % | M % |
|---|---|---|---|---|---|---|---|
| 0.5 | E36 | 84 | 16 | - | - | - | - |
| E36Nb | 86 | 14 | - | - | - | - | |
| 1 | E36 | 86 | 14 | - | - | - | - |
| E36Nb | - | 3 | 55.5 | 40 | 1.5 | - | |
| 1.5 | E36 | 90 | 10 | - | - | - | - |
| E36Nb | - | - | 15 | 80 | 5 | - | |
| 2 | E36 | - | 6 | 60 | 30 | 4 | - |
| E36Nb | - | - | - | 99 | 1 | - | |
| 5 | E36 | - | 10 | 40 | 35 | 15 | - |
| E36Nb | 2 | - | - | 98 | - | - | |
| 10 | E36 | - | - | 15 | 35 | 50 | - |
| E36Nb | 5 | - | - | 95 | - | - | |
| 15 | E36 | - | - | - | 60 | 40 | - |
| E36Nb | - | - | - | 100 | - | - | |
| 20 | E36 | - | - | - | 90 | 10 | |
| E36Nb | - | - | - | 96 | - | 4 | |
| 30 | E36 | - | - | - | 80 | - | 20 |
| E36Nb | - | - | - | 70 | - | 30 | |
| 50 | E36 | - | - | - | 70 | - | 30 |
| E36Nb | - | - | - | 60 | - | 40 | |
| 75 | E36 | - | - | - | 50 | - | 50 |
| E36Nb | - | - | - | 20 | - | 80 |
| Temperature/°C | Austenite to Ferrite | Austenite to Bainite | Austenite to Pearlite | |||
|---|---|---|---|---|---|---|
| K (1/s) | L (1/s) | K (1/s) | K (1/s) | L (1/s) | L (1/s) | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 300 | 0 | 0 | ||||
| 400 | ||||||
| 450 | ||||||
| 470 | ||||||
| 520 | 0 | 0.05 | 0 | |||
| 540 | 0.005 | |||||
| 560 | 0.005 | |||||
| 580 | 0.002 | |||||
| 600 | 0 | 0.005 | 0 | |||
| 620 | 0 | 0.0002 | ||||
| 640 | 0.0012 | 0.0004 | ||||
| 650 | 0.0002 | 0.00004 | 0.0002 | |||
| 710 | 0.00017 | |||||
| 800 | 0.002 | 0.0002 | ||||
| 1000 | 0.002 | 0.002 | 0 | 0.002 | ||
| Temperature/°C | Austenite to Ferrite | Austenite to Bainite | Austenite to Pearlite | |||
|---|---|---|---|---|---|---|
| K (1/s) | L (1/s) | K (1/s) | L (1/s) | K (1/s) | L (1/s) | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 300 | 0 | 0 | ||||
| 400 | ||||||
| 440 | ||||||
| 460 | ||||||
| 470 | ||||||
| 520 | 0 | 0.05 | 0 | |||
| 540 | 0.005 | |||||
| 560 | 0.005 | |||||
| 580 | 0.002 | |||||
| 590 | 0.005 | |||||
| 600 | 0 | 0 | ||||
| 610 | 0 | |||||
| 620 | 0.0002 | |||||
| 640 | 0.002 | 0.0007 | ||||
| 650 | 0.0002 | 0.00004 | 0.0002 | |||
| 710 | 0.0025 | |||||
| 800 | 0.002 | 0.0002 | ||||
| 1000 | 0.002 | 0.002 | 0 | 0.002 | ||
| Steel | Heat Input kJ/cm | Ferrite Fraction % | Pearlite Fraction % | Bainite Fraction % | |||
|---|---|---|---|---|---|---|---|
| Experiment | Simulation | Experiment | Simulation | Experiment | Simulation | ||
| E36 | 100 | 12.1 | 12.1 | / | / | 87.9 | 86.1 |
| 250 | 85.9 | 87.7 | 14.1 | 12.5 | / | 1.1 | |
| E36Nb | 100 | 4.2 | 6.1 | / | / | 95.8 | 91.9 |
| 250 | 38.6 | 34.6 | 9.7 | 11.2 | 51.7 | 54.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; El-Fallah, G.M.A.M.; Tao, Q.; Dong, H. A Parameterized Leblond–Devaux Equation for Predicting Phase Evolution during Welding E36 and E36Nb Marine Steels. Materials 2023, 16, 3150. https://doi.org/10.3390/ma16083150
Fu J, El-Fallah GMAM, Tao Q, Dong H. A Parameterized Leblond–Devaux Equation for Predicting Phase Evolution during Welding E36 and E36Nb Marine Steels. Materials. 2023; 16(8):3150. https://doi.org/10.3390/ma16083150
Chicago/Turabian StyleFu, Jun, G. M. A. M. El-Fallah, Qing Tao, and Hongbiao Dong. 2023. "A Parameterized Leblond–Devaux Equation for Predicting Phase Evolution during Welding E36 and E36Nb Marine Steels" Materials 16, no. 8: 3150. https://doi.org/10.3390/ma16083150




