Multiscale Data Treatment in Additive Manufacturing
Abstract
:1. Introduction
2. Materials and Methods
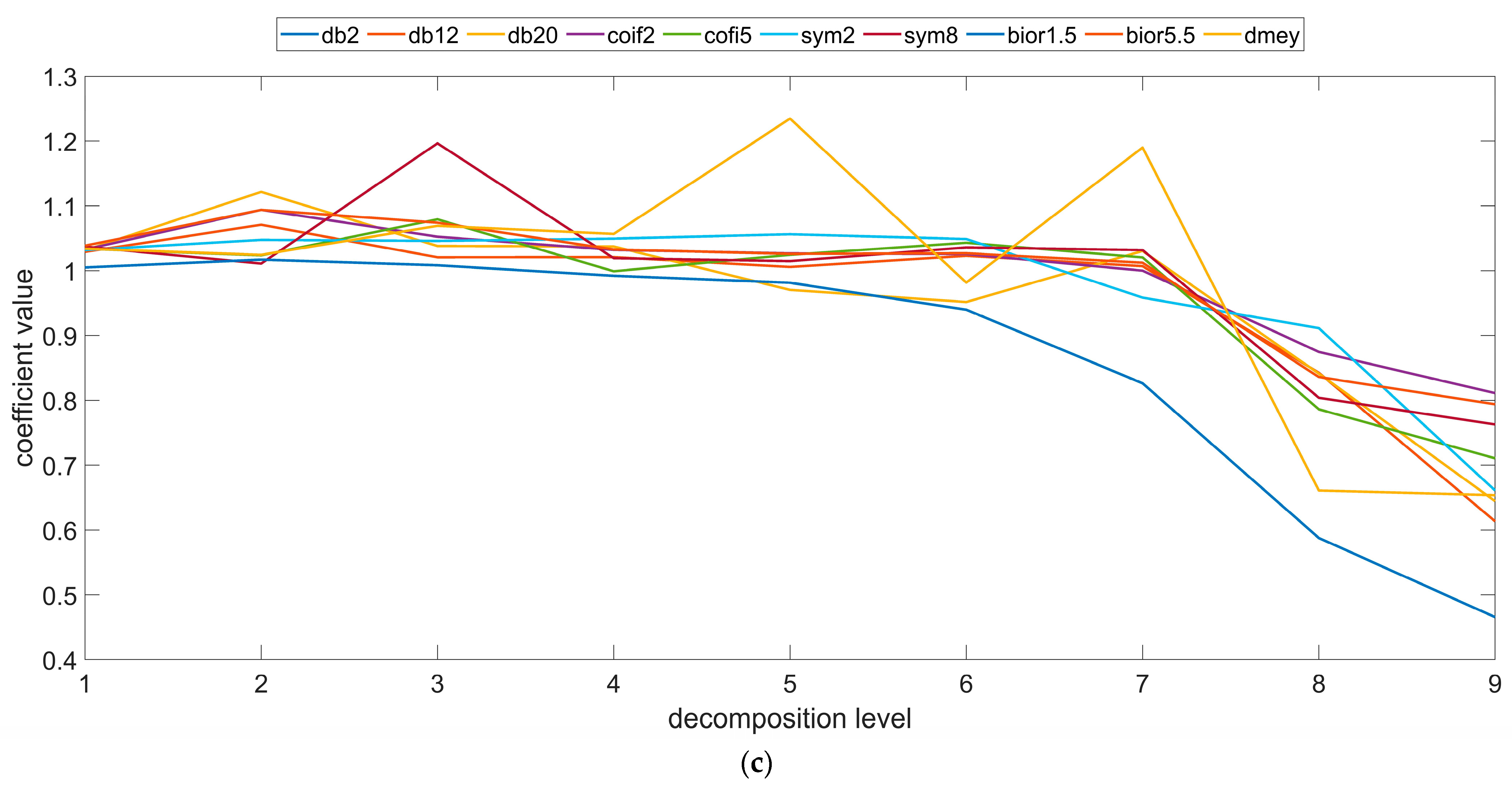
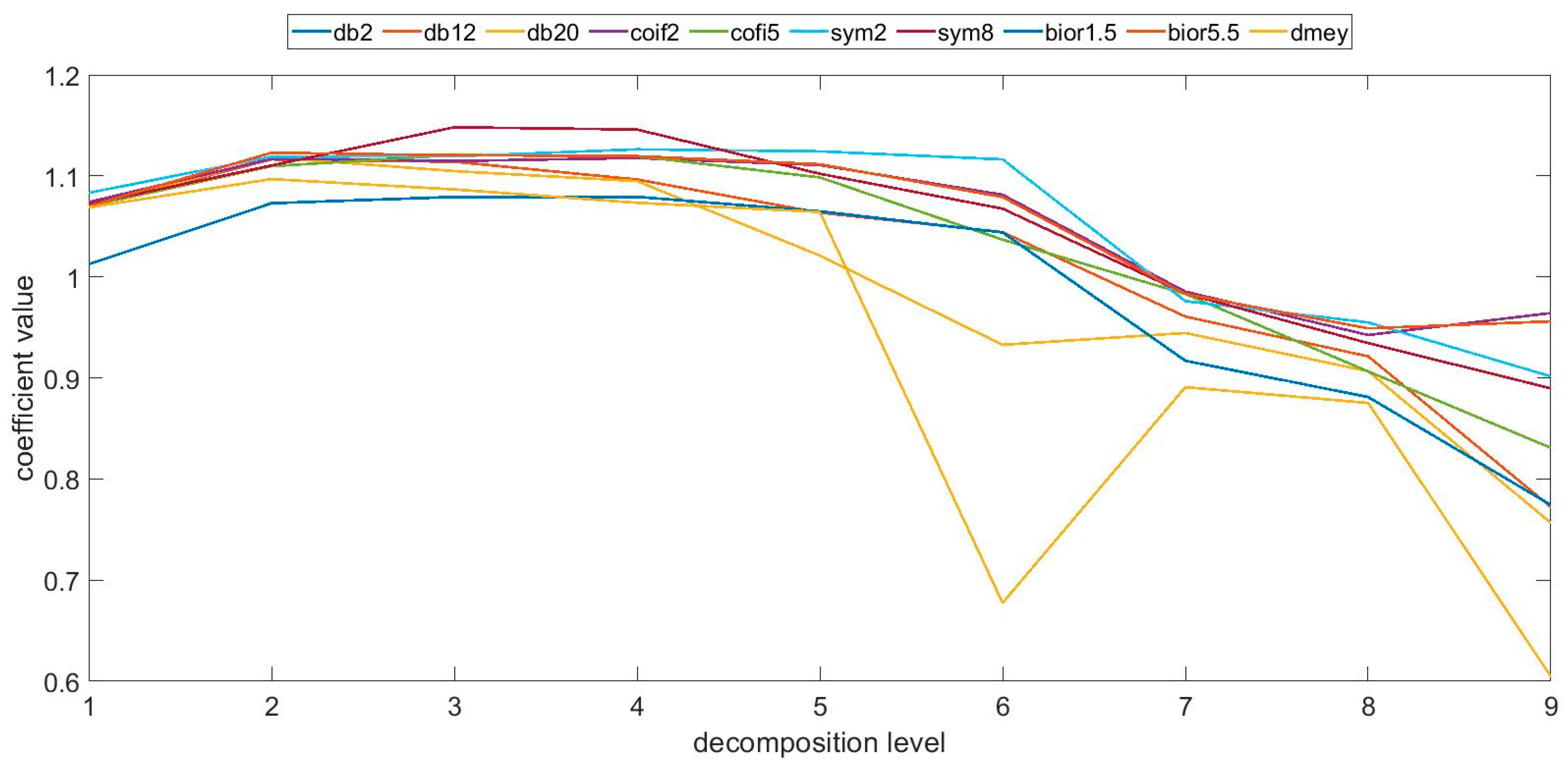
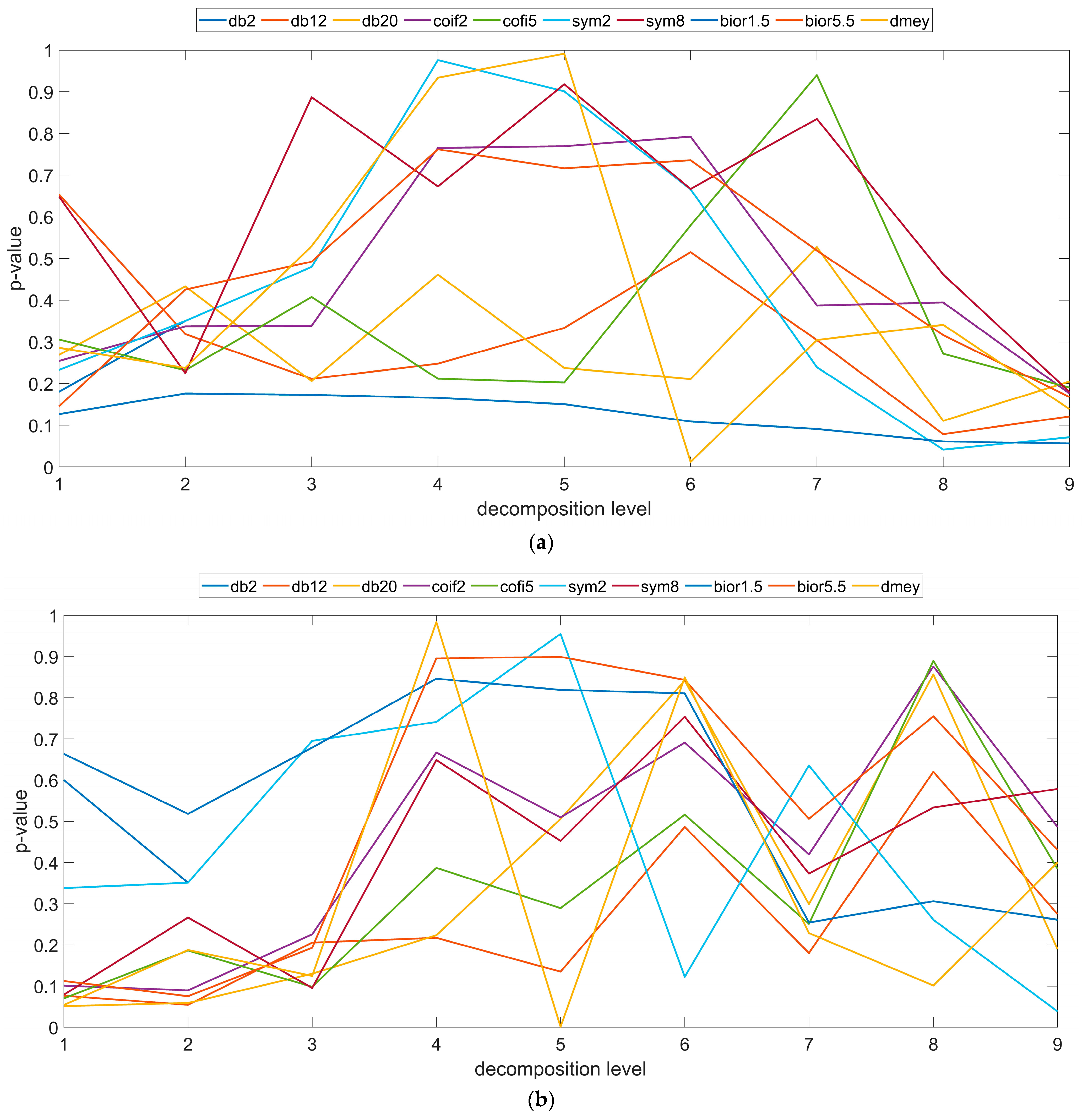
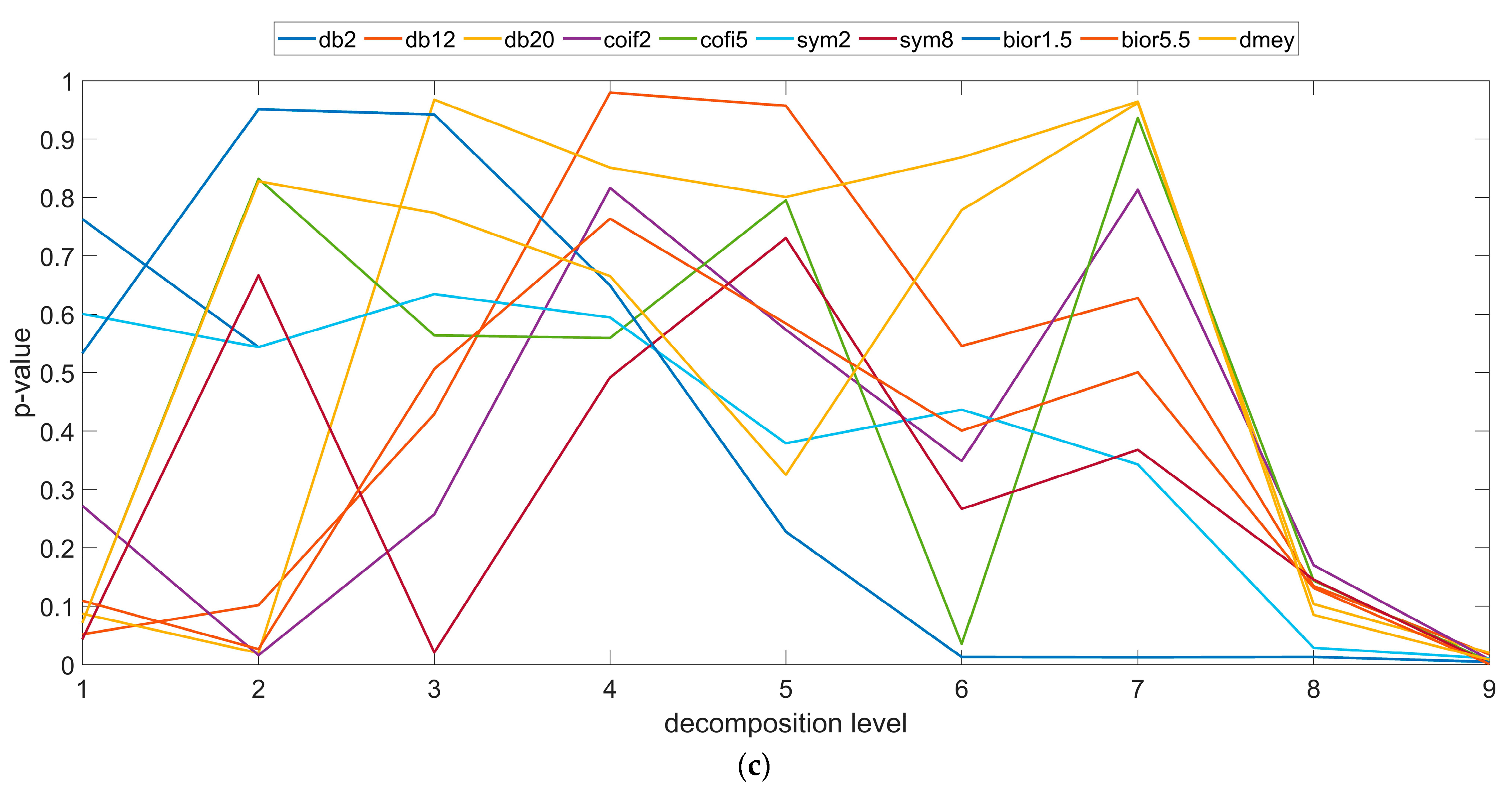
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Xu, C.; Xiao, G.; Yi, M.; Chen, Z.; Zhang, J. Analysis of the relationship between roughness parameters of wear surface and tribology performance of 5CB liquid crystal. J. Mol. Liq. 2022, 352, 118711. [Google Scholar] [CrossRef]
- Niemczewska-Wójcik, M. Wear mechanisms and surface topography of artificial hip joint components at the subsequent stages of tribological tests. Meas. J. Int. Meas. Confed. 2017, 107, 89–98. [Google Scholar] [CrossRef]
- Liu, S.; Jin, S.; Zhang, X.; Chen, K.; Wang, L.; Zhao, H. Optimization of 3D surface roughness induced by milling operation for adhesive-sealing. Procedia CIRP 2018, 71, 279–284. [Google Scholar] [CrossRef]
- Gogolewski, D.; Bartkowiak, T.; Kozior, T.; Zmarzły, P. Multiscale analysis of surface texture quality of models manufactured by laser powder-bed fusion technology and machining from 316l steel. Materials 2021, 14, 2794. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.A.; Hansen, H.N.; Jiang, X.J.; Blateyron, F.; Berglund, J.; Senin, N.; Bartkowiak, T.; Dixon, B.; Le Goïc, G.; Quinsat, Y.; et al. Multiscale analyses and characterizations of surface topographies. CIRP Ann. 2018, 67, 839–862. [Google Scholar] [CrossRef]
- Bartkowiak, T.; Berglund, J.; Brown, C.A. Multiscale characterizations of surface anisotropies. Materials 2020, 13, 3028. [Google Scholar] [CrossRef] [PubMed]
- Maleki, I.; Wolski, M.; Woloszynski, T.; Podsiadlo, P.; Stachowiak, G. A comparison of multiscale surface curvature characterization methods for tribological surfaces. Tribol. Online 2019, 14, 8–17. [Google Scholar] [CrossRef]
- Serafin, D.; Bartkowiak, T.; Nowak, W.J.; Wierzba, B. Influence of microgeometry of iron surface on the oxidation process—A comparison of multiscale geometric methods and their applicability. Appl. Surf. Sci. 2020, 527, 146838. [Google Scholar] [CrossRef]
- Bartkowiak, T.; Grochalski, K.; Gapiński, B.; Wieczorowski, M. Discrimination of surface topographies created by two-stage process by means of multiscale analysis. Materials 2021, 14, 7044. [Google Scholar] [CrossRef]
- Bartkowiak, T.; Brown, C.A. Multiscale 3D curvature analysis of processed surface textures of aluminum alloy 6061 T6. Materials 2019, 12, 257. [Google Scholar] [CrossRef]
- Zare, M.; Solaymani, S.; Shafiekhani, A.; Kulesza, S.; Ţǎlu, Ş.; Bramowicz, M. Evolution of rough-surface geometry and crystalline structures of aligned TiO2 nanotubes for photoelectrochemical water splitting. Sci. Rep. 2018, 8, 10870. [Google Scholar] [CrossRef] [PubMed]
- Blateyron, F. New Sliding Bandpass Filters for Multiscale Exploration of Surface Texture. In Proceedings of the 16th International Conference on Metrology and Properties of Engineering Surfaces, Gothenburg, Sweden, 26–29 June 2017. [Google Scholar]
- Sysyn, M.; Gruen, D.; Gerber, U.; Nabochenko, O.; Kovalchuk, V. Turnout monitoring with vehicle based inertial measurements of operational trains: A machine learning approach. Commun. Sci. Lett. Univ. Zilina 2019, 21, 42–48. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, M.; Zhang, P.; Geng, G.; Liu, X.; Zhang, H. Skull Sex Estimation Based on Wavelet Transform and Fourier Transform. Biomed Res. Int. 2020, 2020, 8608209. [Google Scholar] [CrossRef] [PubMed]
- Elânio Bezerra, F.; Zemuner Garcia, F.A.; Ikuyo Nabeta, S.; Martha de Souza, G.F.; Chabu, I.E.; Santos, J.C.; Junior, S.N.; Pereira, F.H. Wavelet-Like Transform to Optimize the Order of an Autoregressive Neural Network Model to Predict the Dissolved Gas Concentration in Power Transformer Oil from Sensor Data. Sensors 2020, 20, 2730. [Google Scholar] [CrossRef]
- Seid Ahmed, Y.; Arif, A.F.M.; Veldhuis, S.C. Application of the wavelet transform to acoustic emission signals for built-up edge monitoring in stainless steel machining. Meas. J. Int. Meas. Confed. 2020, 154, 107478. [Google Scholar] [CrossRef]
- Pahuja, R.; Ramulu, M. Study of surface topography in Abrasive Water Jet machining of carbon foam and morphological characterization using Discrete Wavelet Transform. J. Mater. Process. Technol. 2019, 273, 116249. [Google Scholar] [CrossRef]
- Jiang, X.; Scott, P.; Whitehouse, D. Wavelets and their applications for surface metrology. CIRP Ann. Manuf. Technol. 2008, 57, 555–558. [Google Scholar] [CrossRef]
- Lucas, K.; Sanz-Lobera, A.; Antón-Acedos, P.; Amatriain, A. A Survey of bidimensional wavelet filtering in surface texture characterization. Procedia Manuf. 2019, 41, 811–818. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Hua, J.; Cheng, Y. High-order spline filter: Design and application to surface metrology. Precis. Eng. 2015, 40, 74–80. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Piao, W. A universal spline filter for surface metrology. Measurement 2010, 43, 1575–1582. [Google Scholar] [CrossRef]
- Wang, X.; Shi, T.; Liao, G.; Zhang, Y.; Hong, Y.; Chen, K. Using wavelet packet transform for surface roughness evaluation and texture extraction. Sensors 2017, 17, 933. [Google Scholar] [CrossRef] [PubMed]
- Zawada-Tomkiewicz, A.; Ściegienka, R.; Zuperl, U.; Stępień, K. Images of the Machined Surface in Evaluation of the Efficiency of a Micro-Smoothing Process. Strojniški Vestn. J. Mech. Eng. 2019, 65, 410–419. [Google Scholar] [CrossRef]
- Gogolewski, D. Fractional spline wavelets within the surface texture analysis. Meas. J. Int. Meas. Confed. 2021, 179, 109435. [Google Scholar] [CrossRef]
- Li, G.; Zhang, K.; Gong, J.; Jin, X. Calculation method for fractal characteristics of machining topography surface based on wavelet transform. Procedia CIRP 2019, 79, 500–504. [Google Scholar] [CrossRef]
- Morala-Argüello, P.; Barreiro, J.; Alegre, E. A evaluation of surface roughness classes by computer vision using wavelet transform in the frequency domain. Int. J. Adv. Manuf. Technol. 2012, 59, 213–220. [Google Scholar] [CrossRef]
- Josso, B.; Burton, D.R.; Lalor, M.J. Frequency normalised wavelet transform for surface roughness analysis and characterisation. Wear 2002, 252, 491–500. [Google Scholar] [CrossRef]
- Yesilli, M.C.; Chen, J.; Khasawneh, F.A.; Guo, Y. Automated surface texture analysis via Discrete Cosine Transform and Discrete Wavelet Transform. Precis. Eng. 2022, 77, 141–152. [Google Scholar] [CrossRef]
- Gogolewski, D. Influence of the edge effect on the wavelet analysis process. Meas. J. Int. Meas. Confed. 2020, 152, 107314. [Google Scholar] [CrossRef]
- Gogolewski, D. Multiscale assessment of additively manufactured free-form surfaces. Metrol. Meas. Syst. 2023, 30. [Google Scholar] [CrossRef]
- Gogolewski, D.; Zmarzły, P.; Kozior, T.; Mathia, T.G. Possibilities of a Hybrid Method for a Time-Scale-Frequency Analysis in the Aspect of Identifying Surface Topography Irregularities. Materials 2023, 16, 1228. [Google Scholar] [CrossRef]
- Sun, J.; Song, Z.; He, G.; Sang, Y. An improved signal determination method on machined surface topography. Precis. Eng. 2018, 51, 338–347. [Google Scholar] [CrossRef]
- Méndez, A.; Reyes, Y.; Trejo, G.; Stepień, K.; Ţălu, Ş. Micromorphological characterization of zinc/silver particle composite coatings. Microsc. Res. Technol. 2015, 78, 1082–1089. [Google Scholar] [CrossRef] [PubMed]
- Bruzzone, A.A.G.; Montanaro, J.S.; Ferrando, A.; Lonardo, P.M. Wavelet analysis for surface characterisation: An experimental assessment. CIRP Ann. Manuf. Technol. 2004, 53, 479–482. [Google Scholar] [CrossRef]
- Gogolewski, D.; Makieła, W.; Nowakowski, Ł. An assessment of applicability of the two-dimensional wavelet transform to assess the minimum chip thickness determination accuracy. Metrol. Meas. Syst. 2020, 27, 659–672. [Google Scholar]
- Pagac, M.; Hajnys, J.; Ma, Q.P.; Jancar, L.; Jansa, J.; Stefek, P.; Mesicek, J. A review of vat photopolymerization technology: Materials, applications, challenges, and future trends of 3d printing. Polymers 2021, 13, 598. [Google Scholar] [CrossRef] [PubMed]
- Budzik, G.; Przeszlowski, L.; Wieczorowski, M.; Rzucidlo, A.; Gapinski, B.; Krolczyk, G. Analysis of 3D printing parameters of gears for hybrid manufacturing. AIP Conf. Proc. 2018, 1960, 140005. [Google Scholar]
- Gogolewski, D.; Kozior, T.; Zmarzły, P.; Mathia, T.G. Morphology of Models Manufactured by SLM Technology and the Ti6Al4V Titanium Alloy Designed for Medical Applications. Materials 2021, 14, 6249. [Google Scholar] [CrossRef] [PubMed]
- Junk, S.; Rothe, N. Lightweight design of automotive components using generative design with fiber-reinforced additive manufacturing. Procedia CIRP 2022, 109, 119–124. [Google Scholar] [CrossRef]
- Sargini, M.I.M.; Masood, S.H.; Palanisamy, S.; Jayamani, E.; Kapoor, A. Additive manufacturing of an automotive brake pedal by metal fused deposition modelling. Mater. Today Proc. 2021, 45, 4601–4605. [Google Scholar] [CrossRef]
- Muvunzi, R.; Mpofu, K.; Daniyan, I.; Fameso, F. Analysis of potential materials for local production of a rail car component using additive manufacturing. Heliyon 2022, 8, e09405. [Google Scholar] [CrossRef]
- Gadwala, W.K.; Babu, R. Modeling and analysis of car wheel rim for weight optimization to use additive manufacturing process. Mater. Today Proc. 2022, 62, 336–345. [Google Scholar] [CrossRef]
- Edelmann, A.; Dubis, M.; Hellmann, R. Selective laser melting of patient individualized osteosynthesis plates—Digital to physical process chain. Materials 2020, 13, 5786. [Google Scholar] [CrossRef] [PubMed]
- Bedo, T.; Munteanu, S.I.; Popescu, I.; Chiriac, A.; Pop, M.A.; Milosan, I.; Munteanu, D. Method for translating 3D bone defects into personalized implants made by additive manufacturing. Mater. Today Proc. 2019, 19, 1032–1040. [Google Scholar] [CrossRef]
- Upadhyay, M.; Sivarupan, T.; El Mansori, M. 3D printing for rapid sand casting—A review. J. Manuf. Process. 2017, 29, 211–220. [Google Scholar] [CrossRef]
- Chun, S.; Kim, S.; Kim, W.; Lee, G.; Lee, M.; Ye, B.; Kim, H.; Hun, J.; Kim, T. Powder-bed-based 3D printing with cement for sustainable casting. J. Mater. Res. Technol. 2022, 22, 3192–3206. [Google Scholar] [CrossRef]
- Blasiak, S.; Laski, P.A.; Takosoglu, J.E. Rapid prototyping of pneumatic directional control valves. Polymers 2021, 13, 1458. [Google Scholar] [CrossRef]
- Saharudin, M.S.; Hajnys, J.; Kozior, T.; Gogolewski, D.; Zmarzły, P. Quality of Surface Texture and Mechanical Properties of PLA and PA-Based Material Reinforced with Carbon Fibers Manufactured by FDM and CFF 3D Printing Technologies. Polymers 2021, 13, 1671. [Google Scholar] [CrossRef]
- Kozior, T.; Mamun, A.; Trabelsi, M.; Sabantina, L.; Ehrmann, A. Quality of the Surface Texture and Mechanical Properties of FDM Printed Samples after Thermal and Chemical Treatment. Strojniški Vestn. J. Mech. Eng. 2020, 66, 105–113. [Google Scholar]
- Zárybnická, L.; Petrů, J.; Krpec, P.; Pagáč, M. Effect of Additives and Print Orientation on the Properties of Laser Sintering-Printed Polyamide 12 Components. Polymers 2022, 14, 1172. [Google Scholar] [CrossRef]
- Diaz, A. Surface texture characterization and optimization of metal additive manufacturing-produced components for aerospace applications. In Additive Manufacturing for the Aerospace Industry; Elsevier: Amsterdam, The Netherlands, 2019; pp. 341–374. [Google Scholar]
- Kozior, T.; Mamun, A.; Trabelsi, M.; Sabantina, L. Comparative Analysis of Polymer Composites Produced by FFF and PJM 3D Printing and Electrospinning Technologies for Possible Filter Applications. Coatings 2022, 12, 48. [Google Scholar] [CrossRef]
- Leach, R.; Thompson, A.; Senin, N.; Maskery, I. A metrology horror story: The additive surface. In Proceedings of the ASPEN/ASPE Spring Topical Meeting on Manufacture and Metrology of Structured and Freeform Surfaces for Functional Applications 2017, Hong Kong, China, 14–17 March 2017. [Google Scholar]
- Todhunter, L.D.; Leach, R.K.; Lawes, S.D.A.; Blateyron, F. Industrial survey of ISO surface texture parameters. CIRP J. Manuf. Sci. Technol. 2017, 19, 84–92. [Google Scholar] [CrossRef]
- Newton, L.; Senin, N.; Smith, B.; Leach, R. Feature-based characterisation of evolving surface topographies in finishing operations for additive manufacturing. In Proceedings of the European Society for Precision Engineering and Nanotechnology, Conference Proceedings—18th International Conference and Exhibition, EUSPEN 2018, Venice, Italy, 4–8 June 2018. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gogolewski, D. Multiscale Data Treatment in Additive Manufacturing. Materials 2023, 16, 3168. https://doi.org/10.3390/ma16083168
Gogolewski D. Multiscale Data Treatment in Additive Manufacturing. Materials. 2023; 16(8):3168. https://doi.org/10.3390/ma16083168
Chicago/Turabian StyleGogolewski, Damian. 2023. "Multiscale Data Treatment in Additive Manufacturing" Materials 16, no. 8: 3168. https://doi.org/10.3390/ma16083168
APA StyleGogolewski, D. (2023). Multiscale Data Treatment in Additive Manufacturing. Materials, 16(8), 3168. https://doi.org/10.3390/ma16083168






