Impact Responses and Wave Dissipation Investigation of a Composite Sandwich Shell Reinforced by Multilayer Negative Poisson’s Ratio Viscoelastic Polymer Material Honeycomb
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Equivalent Mechanical Parameters
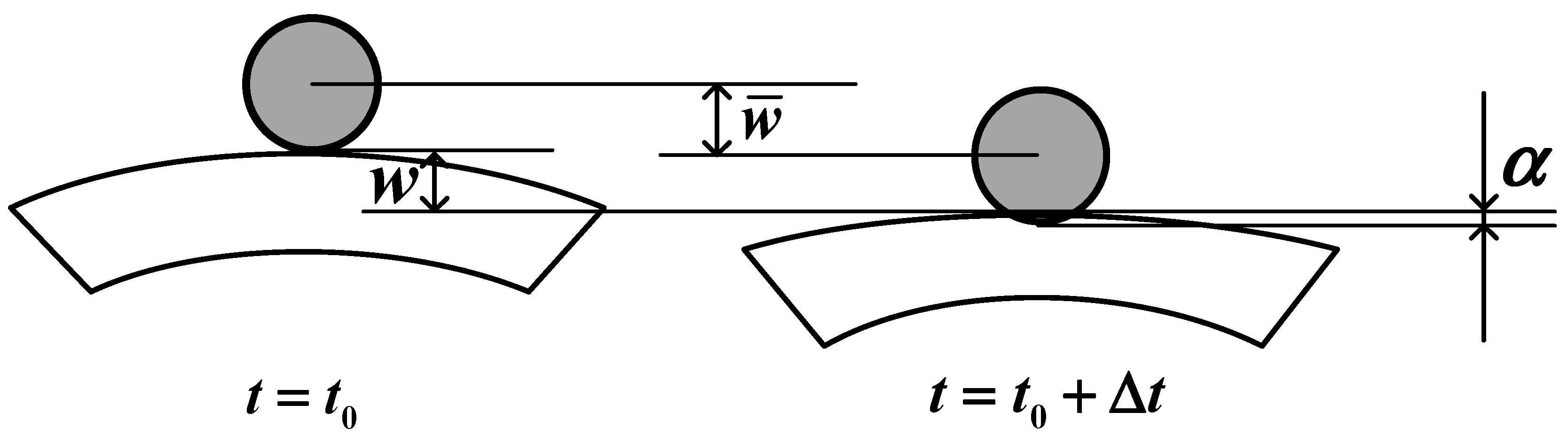
2.2. Impact Forces Determination
2.3. Constitutive Equations and In-Plane Variables Determination
2.4. Dynamic Equilibrium Equations
3. Solution Process
- where αD and βD are Rayleigh’s damping parameters, and those two parameters can be determined according to the viscoelastic material’s damping ratio ξ and the two fundamental frequencies ωi and ωj of the composite laminated shell, as shown in the following equation as:
- where the damping coefficients αD and βD are associated with the Rayleigh’s proportional damping model and can be determined based on the damping ratio ξ and the two natural frequencies of the structure ωi and ωj. The relationship between these parameters can be expressed as:
4. Results and Discussion
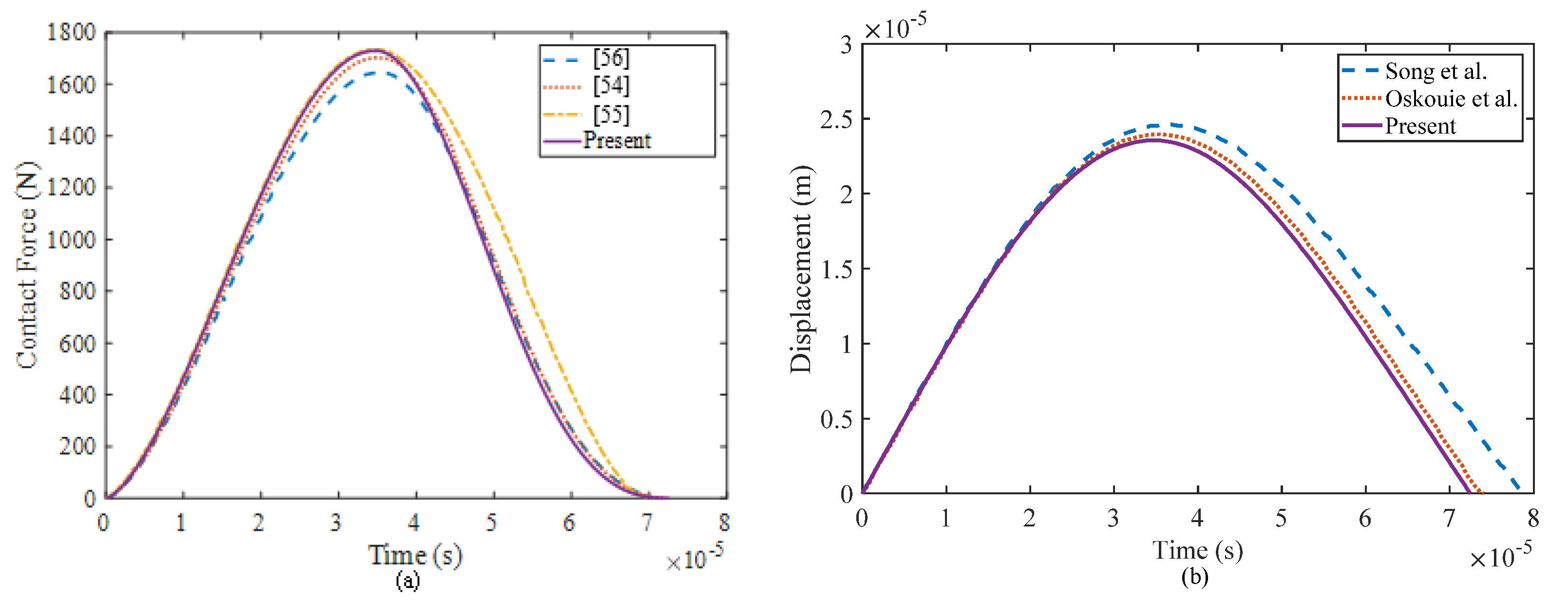
4.1. Validation
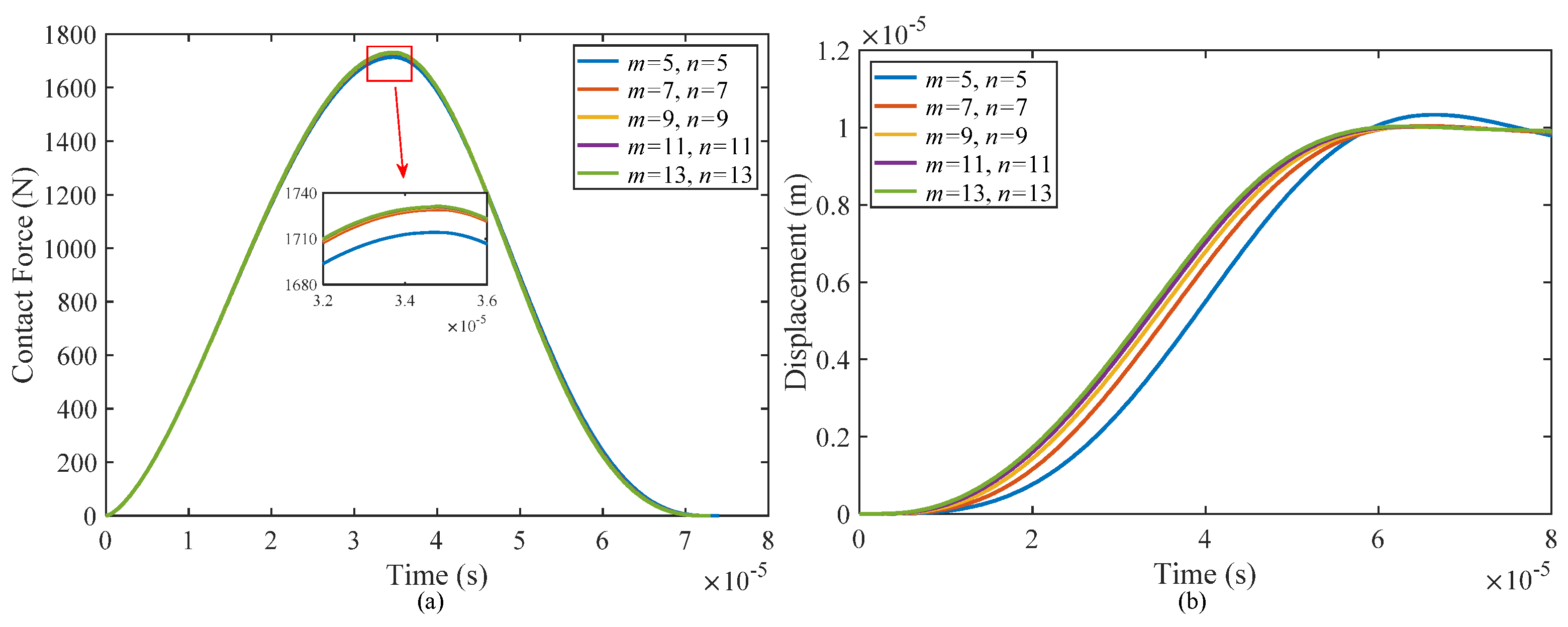
4.2. Parametric Analysis
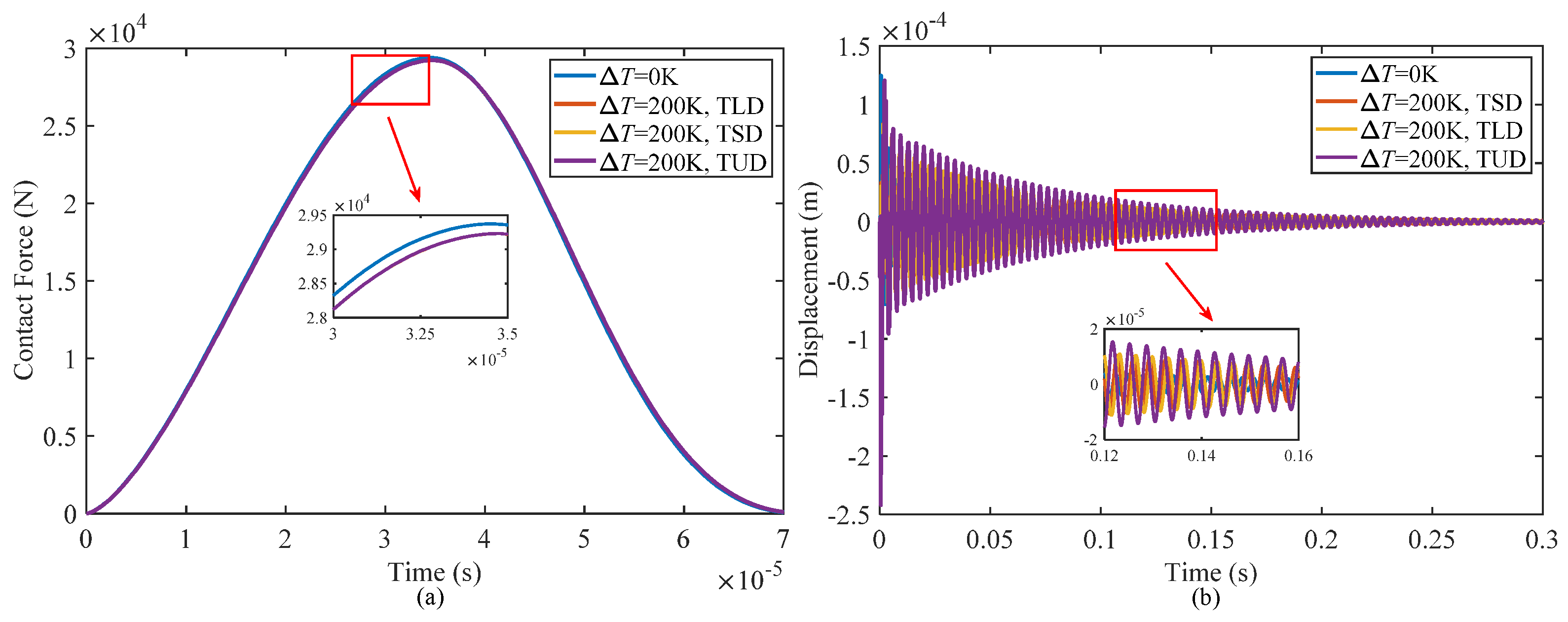
4.2.1. Effect of Temperature
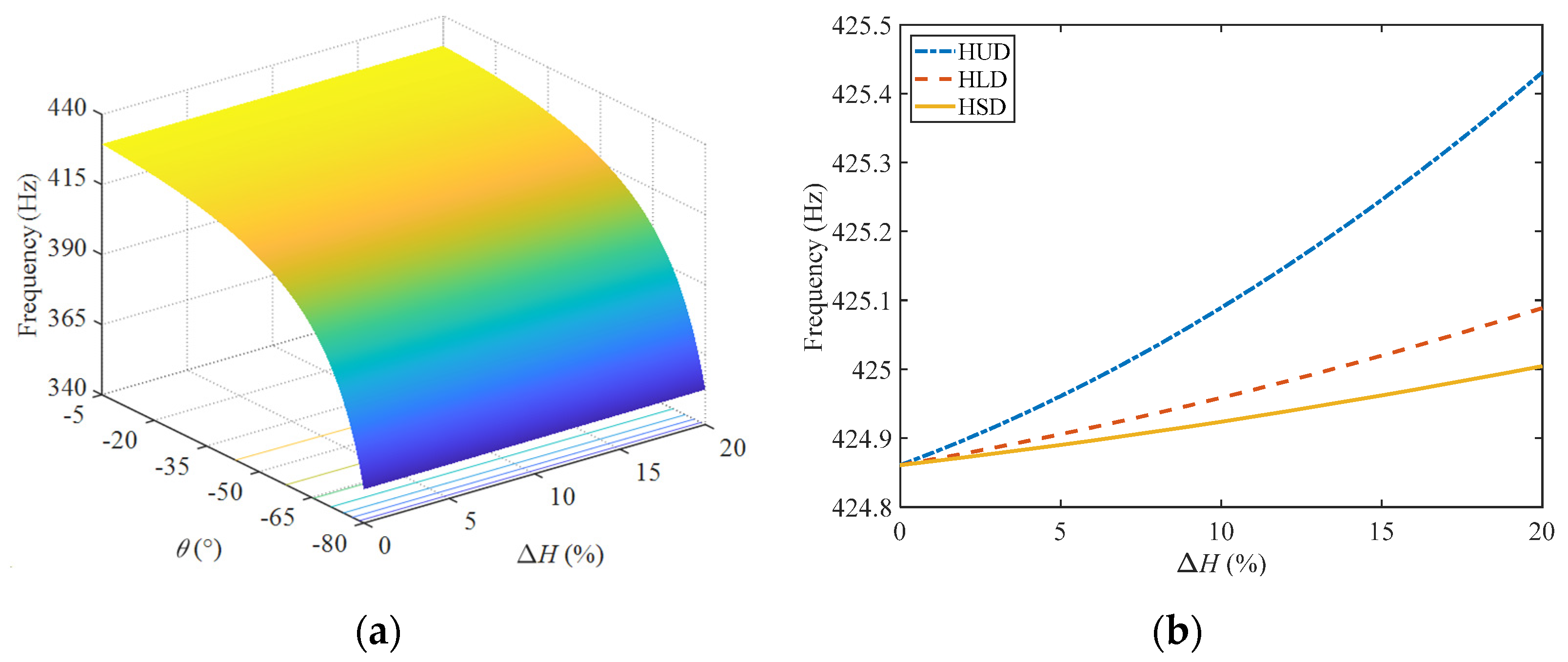
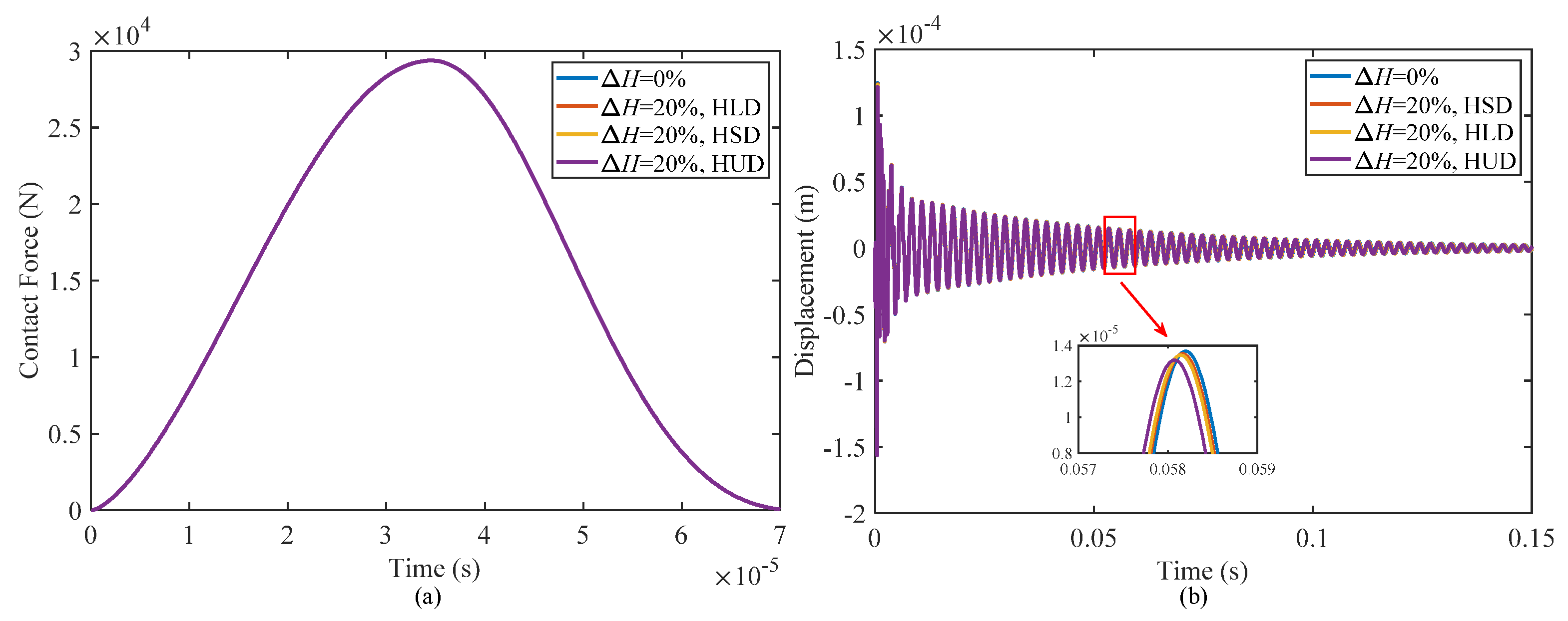
4.2.2. Effect of Moisture
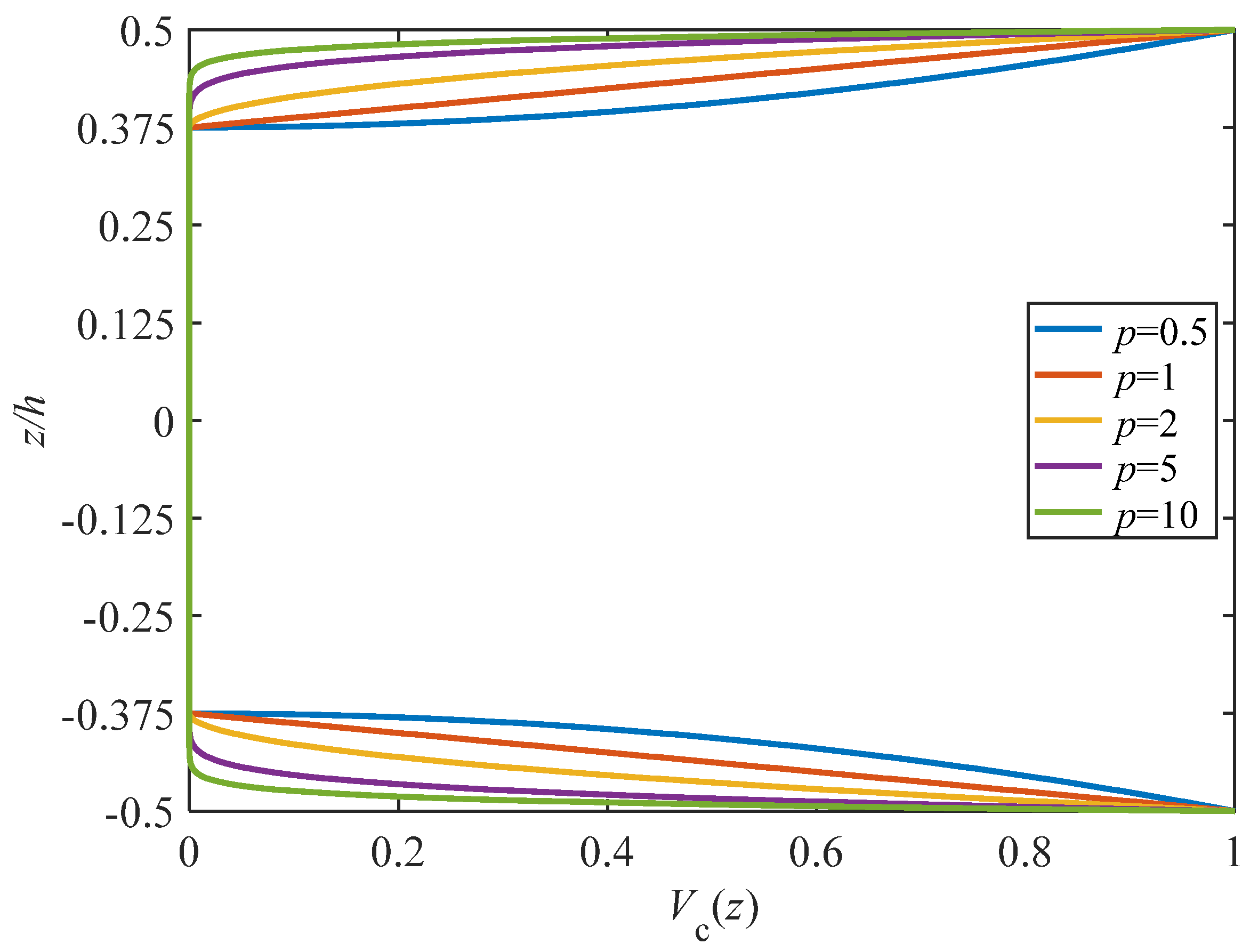
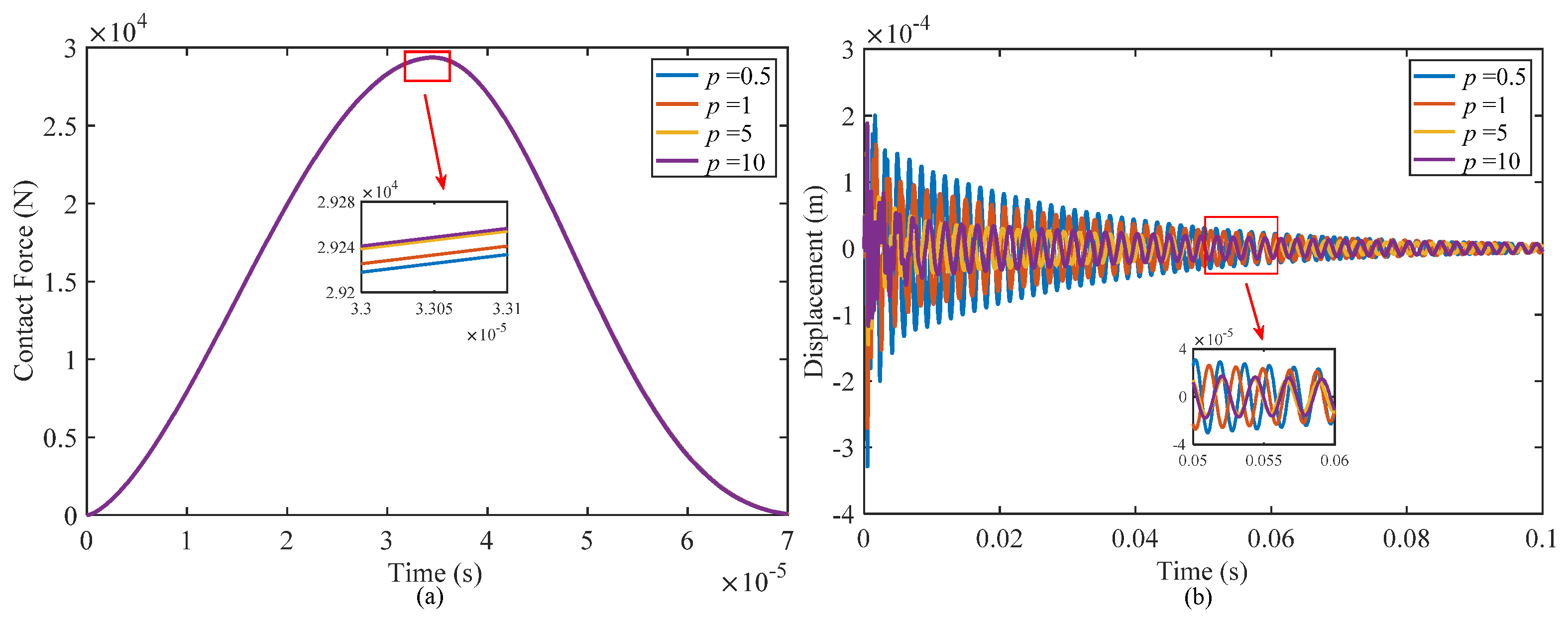
4.2.3. Effect of Power Law Index
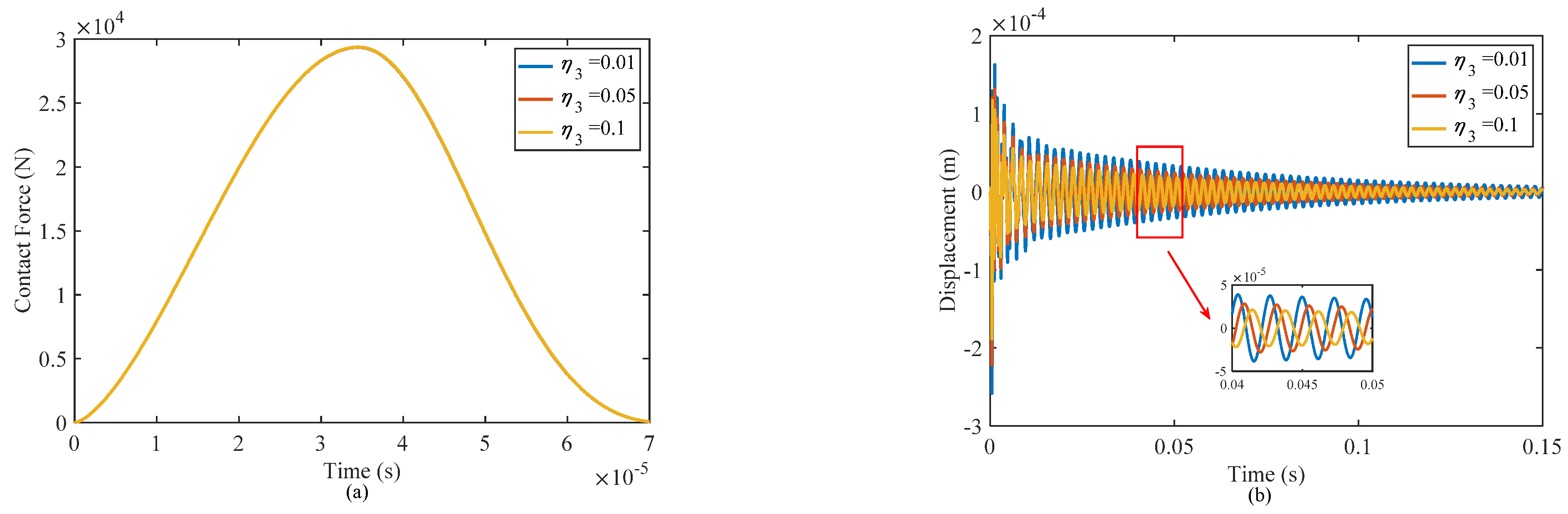
4.2.4. Effect of the Thickness of Honeycomb Wall
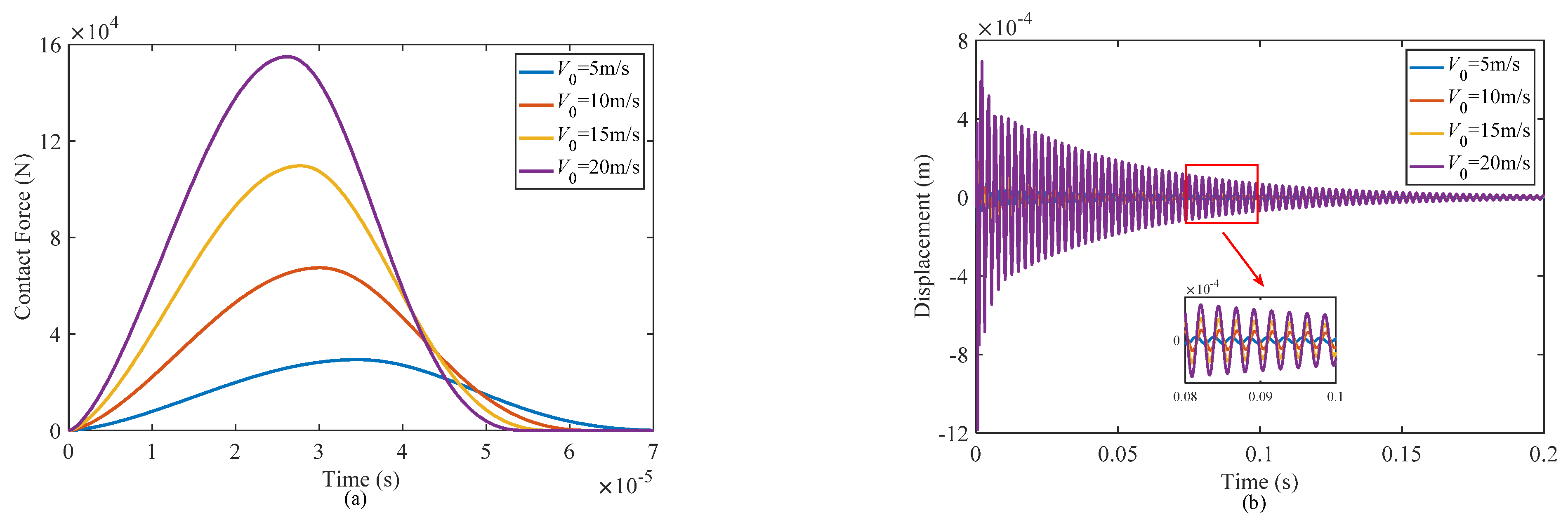
4.2.5. Effect of Initial Velocity of the Impactor
5. Conclusions
- (1)
- Increasing temperature will reduce the contact force during the impact process, and then the damping performance of the structure will deteriorate, resulting in an increase of displacement at the impact point and prolongation of the vibration decay time. There was no significant difference between the contact force under three different temperature distribution patterns, but the damping performance of the structure decreased most seriously when the temperature was uniformly distributed throughout the thickness.
- (2)
- Increasing moisture has almost no influence on the contact force during the impact process, but it will slightly reduce the displacement of the structure at the impact point and increase the vibration attenuation time. The structural stiffness is slightly improved due to the negative Poisson’s ratio effect, but the damping performance is significantly decreased.
- (3)
- The power law index has a direct effect on the mass and stiffness of the face-sheets of the structure. As the power law index increases, the contact force during the impact process increases slightly and the deformation resistance of the structure is enhanced, leading to a reduction of displacement at the impact point; however, the damping performance of the structure also decreases, and then the vibration dissipation time becomes longer.
- (4)
- Increasing the thickness of the honeycomb wall will increase the impact contact force, improving the overall stiffness and energy dissipation characteristics of the structure. Therefore, increasing the thickness of the honeycomb wall is an effective approach to improve both the stiffness and damping performance of the structure.
- (5)
- The contact force and central deflection of the structure experience a significant increase when the initial velocity of the impactor is raised. This amplification is attributed to the higher impact energy associated with the increased velocity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Galos, J. Thin-ply composite laminates: A review. Compos. Struct. 2020, 236, 111920. [Google Scholar] [CrossRef]
- Garg, A.; Chalak, H.D. A review on analysis of laminated composite and sandwich structures under hygrothermal conditions. Thin-Walled Struct. 2019, 142, 205–226. [Google Scholar] [CrossRef]
- Lopresto, V.; Langella, A.; Pagliarulo, V.; Papa, I. On low-velocity impact behaviour of composite laminates: Damage investigation and influence of matrix and temperature. Prog. Aerosp. Sci. 2022, 129, 100786. [Google Scholar] [CrossRef]
- Acanfora, V.; Zarrelli, M.; Riccio, A. Experimental and numerical assessment of the impact behaviour of a composite sandwich panel with a polymeric honeycomb core. Int. J. Impact Eng. 2023, 171, 104392. [Google Scholar] [CrossRef]
- Várdai, R.; Ferdinánd, M.; Lummerstorfer, T.; Pretschuh, C.; Jerabek, M.; Gahleitner, M.; Faludi, G.; Móczó, J.; Pukánszky, B. Impact modification of hybrid polypropylene composites with poly(vinyl alcohol) fibers. J. Reinf. Plast. Compos. 2022, 41, 399–410. [Google Scholar] [CrossRef]
- Fung, Y.C. Foundations of Solid Mechanics; Prentice Hall: Upper Saddle River, NJ, USA, 1965. [Google Scholar]
- Jastrzebski, Z.D. Nature and Properties of Engineering Materials; U.S. Department of Energy, Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1976. [Google Scholar]
- Wang, Y.-C.; Shen, M.-W.; Liao, S.-M. Microstructural Effects on the Poisson’s Ratio of Star-Shaped Two-Dimensional Systems. Physica Status Solidi 2017, 254, 1700024. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Lakes, R.S. Design Considerations for Materials with Negative Poisson’s Ratios. J. Mech. Des. 1993, 115, 696–700. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafström, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Lee, W.Y.; Stinton, D.P.; Berndt, C.C.; Erdogan, F.; Lee, Y.-D.; Mutasim, Z. Concept of Functionally Graded Materials for Advanced Thermal Barrier Coating Applications. J. Am. Ceram. Soc. 1996, 79, 3003–3012. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Wang, L. Low-velocity impact response of viscoelastic material filled FG honeycomb reinforced laminate plate in hygrothermal environments. Compos. Part B Eng. 2019, 165, 255–271. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional gradients and heterogeneities in biological materials: Design principles, functions, and bioinspired applications. Prog. Mater. Sci. 2017, 88, 467–498. [Google Scholar] [CrossRef]
- Vinh, P.V.; Son, L.T. A new first-order mixed beam element for static bending analysis of functionally graded graphene oxide powder-reinforced composite beams. Structures 2022, 36, 463–472. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Free vibrations of tapered and stepped, axially functionally graded beams with any number of attached masses. Eng. Struct. 2022, 267, 114696. [Google Scholar] [CrossRef]
- Zhou, X.; You, Q.; Gao, Y.; Hua, F.; Fu, W.; Huang, Q.; Wang, Y. Buckling Analysis on Resin Base Laminated Plate Reinforced with Uniform and Functional Gradient Distribution of Carbon Fiber in Thermal Environment. Polymers 2023, 15, 2086. [Google Scholar] [CrossRef]
- Aris, H.; Ahmadi, H. Using the higher-order shear deformation theory to analyze the free vibration of stiffened rotating FGM conical shells in a thermal environment. Thin-Walled Struct. 2023, 183, 110366. [Google Scholar] [CrossRef]
- Hua, F.; Fu, W.; You, Q.; Huang, Q.; Abad, F.; Zhou, X. A refined spectral element model for wave propagation in multiscale hybrid epoxy/carbon fiber/graphene platelet composite shells. Aerosp. Sci. Technol. 2023, 138, 108321. [Google Scholar] [CrossRef]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Szafran, M.; Konopka, K.; Bobryk, E.; Kurzydłowski, K.J. Ceramic matrix composites with gradient concentration of metal particles. J. Eur. Ceram. Soc. 2007, 27, 651–654. [Google Scholar] [CrossRef]
- Nieto, A.; Bisht, A.; Lahiri, D.; Zhang, C.; Agarwal, A. Graphene reinforced metal and ceramic matrix composites: A review. Int. Mater. Rev. 2017, 62, 241–302. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Review of research on the vibration and buckling of the FGM conical shells. Compos. Struct. 2019, 211, 301–317. [Google Scholar] [CrossRef]
- Bagheri, H.; Kiani, Y.; Eslami, M.R. Application of GDQ method to large amplitude response of FGM joined spherical-conical shells under rapid surface heating. Mech. Based Des. Struct. Mach. 2023, 1–33. [Google Scholar] [CrossRef]
- Bagheri, H.; Eslami, M.R.; Kiani, Y. Geometrically nonlinear response of FGM joined conical–conical shells subjected to thermal shock. Thin-Walled Struct. 2023, 182, 110171. [Google Scholar] [CrossRef]
- Fu, T.; Chen, Z.; Yu, H.; Wang, Z.; Liu, X. An analytical study of sound transmission through corrugated core FGM sandwich plates filled with porous material. Compos. Part B Eng. 2018, 151, 161–172. [Google Scholar] [CrossRef]
- Van Dung, D.; Chan, D.Q. Analytical investigation on mechanical buckling of FGM truncated conical shells reinforced by orthogonal stiffeners based on FSDT. Compos. Struct. 2017, 159, 827–841. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, D.; Barrera, O. Chapter Three—Mechanics constitutive models for viscoelastic solid materials: Development and a critical review. In Advances in Applied Mechanics; Bordas, S.P.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 189–321. [Google Scholar]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.Y.; Zhang, S.Q.; Wang, S. Research and applications of viscoelastic vibration damping materials: A review. Compos. Struct. 2016, 136, 460–480. [Google Scholar] [CrossRef]
- Qu, C.; Li, X.; Yang, Z.; Zhang, X.; Wang, T.; Wang, Q.; Chen, S. Damping, thermal, and mechanical performances of a novel semi-interpenetrating polymer networks based on polyimide/epoxy. J. Appl. Polym. Sci. 2019, 136, 48032. [Google Scholar] [CrossRef]
- Yuan, X.W.; Li, W.G.; Xiao, Z.M.; Zhang, Y.M. Prediction of temperature-dependent transverse strength of carbon fiber reinforced polymer composites by a modified cohesive zone model. Compos. Struct. 2023, 304, 116310. [Google Scholar] [CrossRef]
- Guzman, V.A.; Brøndsted, P. Effects of moisture on glass fiber-reinforced polymer composites. J. Compos. Mater. 2015, 49, 911–920. [Google Scholar] [CrossRef]
- Ye, J.-Y.; Zhang, L.-W. Damage evolution of polymer-matrix multiphase composites under coupled moisture effects. Comput. Methods Appl. Mech. Eng. 2022, 388, 114213. [Google Scholar] [CrossRef]
- Barba, D.; Arias, A.; Garcia-Gonzalez, D. Temperature and strain rate dependences on hardening and softening behaviours in semi-crystalline polymers: Application to PEEK. Int. J. Solids Struct. 2020, 182–183, 205–217. [Google Scholar] [CrossRef]
- Starkweather, H.W. Frequency-temperature relationships for relaxations in polymers. Thermochim. Acta 1993, 226, 1–5. [Google Scholar] [CrossRef]
- Mastroddi, F.; Martarelli, F.; Eugeni, M.; Riso, C. Time- and frequency-domain linear viscoelastic modeling of highly damped aerospace structures. Mech. Syst. Signal Process. 2019, 122, 42–55. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Krusser, A.I. Models of Viscoelastic Materials: A Review on Historical Development and Formulation; Springer International Publishing: Cham, Switzerland, 2022; pp. 285–326. [Google Scholar]
- Dammaß, F.; Ambati, M.; Kästner, M. A unified phase-field model of fracture in viscoelastic materials. Contin. Mech. Thermodyn. 2021, 33, 1907–1929. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R.; Haghi, P. Thermal effects on wave propagation characteristics of rotating strain gradient temperature-dependent functionally graded nanoscale beams. J. Therm. Stress. 2017, 40, 535–547. [Google Scholar] [CrossRef]
- Fu, W.; Hua, F.; You, Q.; Zhou, X. Impact response analysis on orthogrid stiffened composite sandwich plates embedded with viscoelastic material considering temperature and moisture effects. Int. J. Appl. Mech. 2023, 15, 2350072. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Gupta, A.; Pradyumna, S. Nonlinear dynamic analysis of sandwich shell panels with auxetic honeycomb core and curvilinear fibre reinforced facesheets. Eur. J. Mech.—A Solids 2022, 95, 104640. [Google Scholar] [CrossRef]
- Sun, C.T.; Chen, J.K. On the Impact of Initially Stressed Composite Laminates. J. Compos. Mater. 1985, 19, 490–504. [Google Scholar] [CrossRef]
- Abrate, S. Impact on Composite Structures; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sayyad, A.S.; Ghugal, Y.M. Static and free vibration analysis of laminated composite and sandwich spherical shells using a generalized higher-order shell theory. Compos. Struct. 2019, 219, 129–146. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Hygrothermal forced vibration of a viscoelastic laminated plate with magnetostrictive actuators resting on viscoelastic foundations. Int. J. Mech. Mater. Des. 2021, 17, 301–320. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z.X.; Habibi, M.; Ghabussi, A.; Alyousef, R. Low-velocity impact, resonance, and frequency responses of FG-GPLRC viscoelastic doubly curved panel. Compos. Struct. 2021, 269, 114000. [Google Scholar] [CrossRef]
- Sobhy, M. Buckling and free vibration of exponentially graded sandwich plates resting on elastic foundations under various boundary conditions. Compos. Struct. 2013, 99, 76–87. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Chaikittiratana, A. An analytical investigation on free vibration of FGM doubly curved shallow shells with stiffeners under thermal environment. Aerosp. Sci. Technol. 2015, 40, 181–190. [Google Scholar] [CrossRef]
- Pham, H.A.; Tran, H.Q.; Tran, M.T.; Nguyen, V.L.; Huong, Q.T. Free vibration analysis and optimization of doubly-curved stiffened sandwich shells with functionally graded skins and auxetic honeycomb core layer. Thin-Walled Struct. 2022, 179, 109571. [Google Scholar] [CrossRef]
- Wang, Z.X.; Xu, J.F.; Qiao, P.Z. Nonlinear low-velocity impact analysis of temperature-dependent nanotube-reinforced composite plates. Compos. Struct. 2014, 108, 423–434. [Google Scholar] [CrossRef]
- Oskouie, M.F.; Hassanzadeh-Aghdam, M.K.; Ansari, R. A new numerical approach for low velocity impact response of multiscale-reinforced nanocomposite plates. Eng. Comput. 2021, 37, 713–730. [Google Scholar] [CrossRef]
- Liu, Y.F.; Hu, W.Y.; Zhu, R.Z.; Safaei, B.; Qin, Z.Y.; Chu, F.L. Dynamic responses of corrugated cylindrical shells subjected to nonlinear low-velocity impact. Aerosp. Sci. Technol. 2022, 121, 107321. [Google Scholar] [CrossRef]
- Song, M.T.; Li, X.Q.; Kitipornchai, S.; Bi, Q.S.; Yang, J. Low-velocity impact response of geometrically nonlinear functionally graded graphene platelet-reinforced nanocomposite plates. Nonlinear Dyn. 2019, 95, 2333–2352. [Google Scholar] [CrossRef]
- Hua, F.F.; Fu, W.B.; Zhou, X.Q. Wave propagation analysis of sandwich plates with graphite particles filled viscoelastic material core in hygrothermal environments. Compos. Struct. 2022, 288, 115380. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Habibi, S. Nonlinear eccentric low-velocity impact response of a polymer-carbon nanotube-fiber multiscale nanocomposite plate resting on elastic foundations in hygrothermal environments. Mech. Adv. Mater. Struct. 2018, 25, 425–438. [Google Scholar] [CrossRef]
- Bisheh, H.; Wu, N. Wave propagation in smart laminated composite cylindrical shells reinforced with carbon nanotubes in hygrothermal environments. Compos. Part B Eng. 2019, 162, 219–241. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E.; Brincker, R. Damping estimation using free decays and ambient vibration tests. Mech. Syst. Signal Process. 2010, 24, 1274–1290. [Google Scholar] [CrossRef]
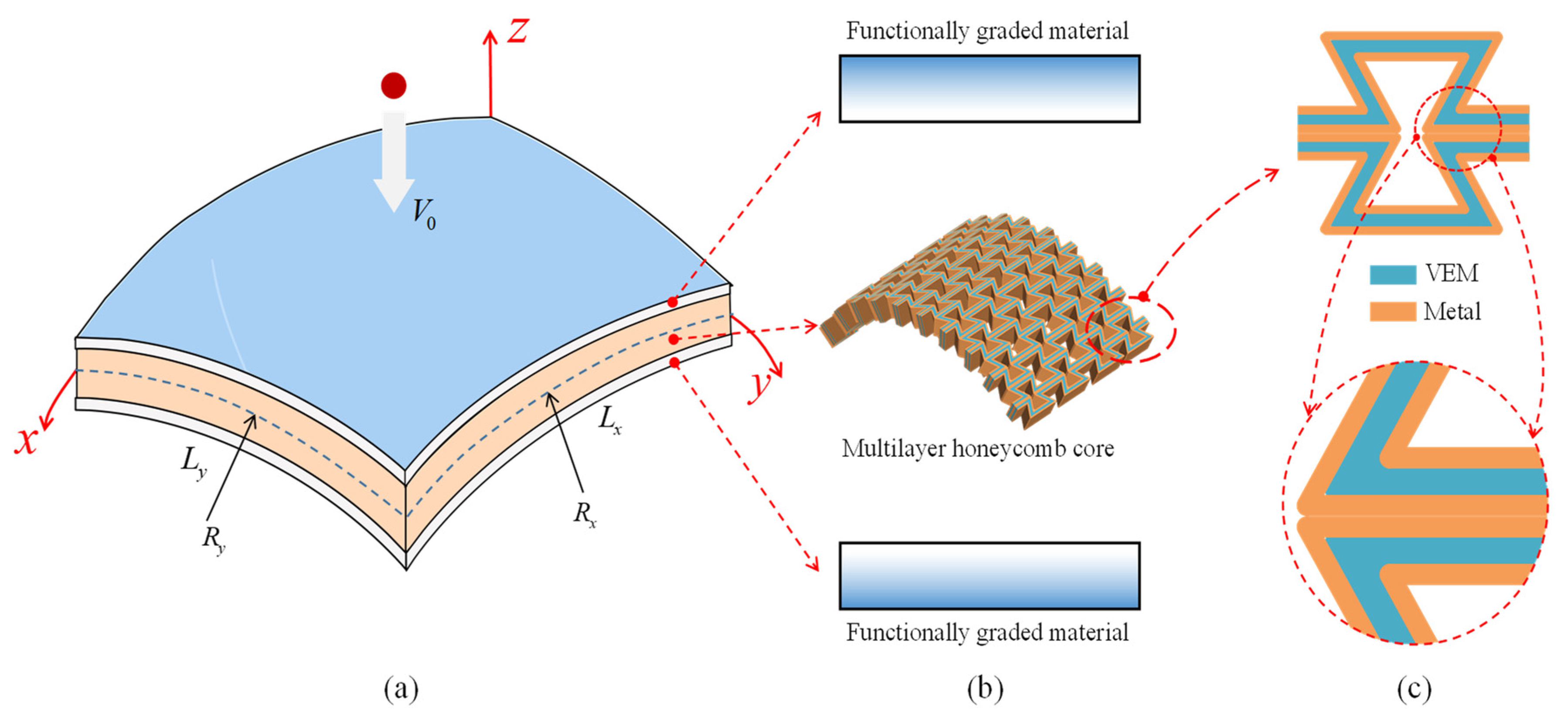
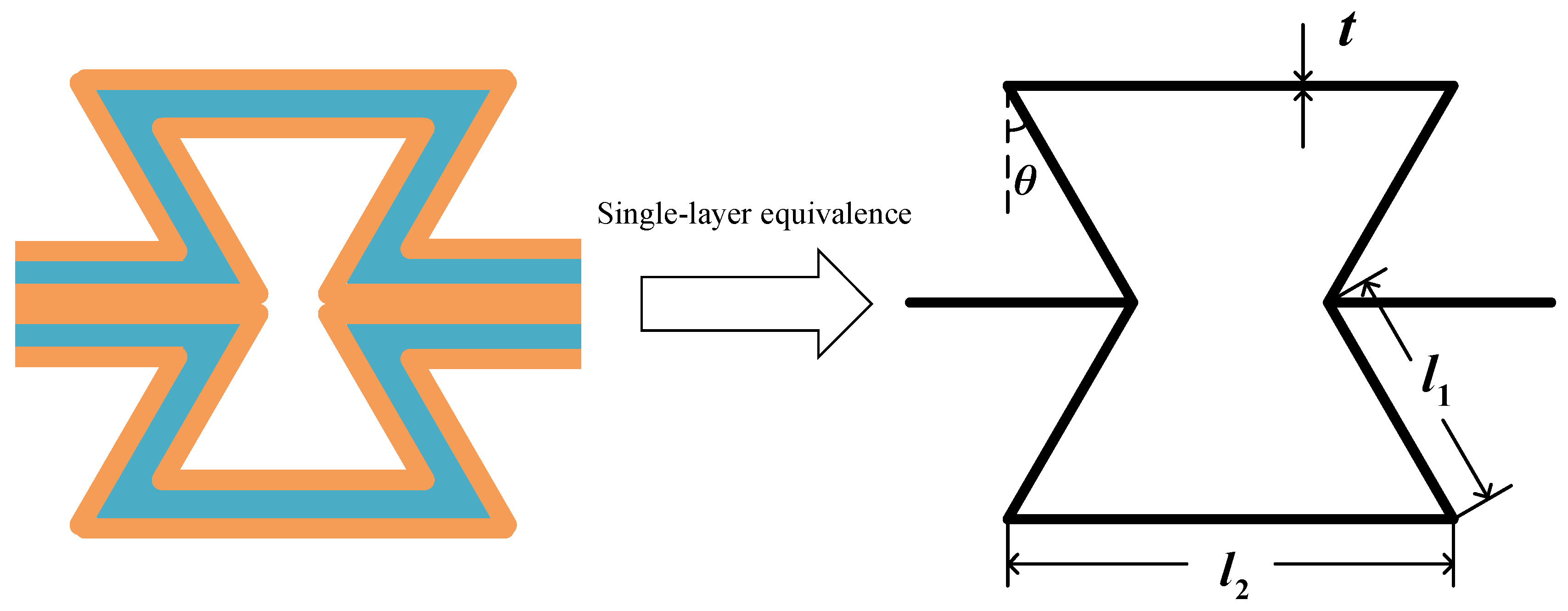

| Material | Property | P0 | P1 | P2 | P3 |
|---|---|---|---|---|---|
| Ceramic (Si3N4) | E (Pa) | 3.4843 × 1011 | −3.0700 × 10−4 | 2.1600 × 10−7 | −8.9460 × 10−11 |
| ρ (kg/m3) | 2370 | 0 | 0 | 0 | |
| ν | 0.24 | 0 | 0 | 0 | |
| α (K−1) | 5.8723 × 10−6 | 9.0950× 10−4 | 0 | 0 | |
| Metal (SUS304) | E (Pa) | 2.0104 × 1011 | 3.0790 × 10−4 | −6.5340 × 10−7 | 0 |
| ρ (kg/m3) | 8166 | 0 | 0 | 0 | |
| ν | 0.3262 | −2.0020 × 10−4 | 3.7970 × 10−7 | 0 | |
| α (K−1) | 1.2330 × 10−5 | 8.0860 × 10−4 | 0 | 0 |
| Functions | Boundary Conditions | ||
|---|---|---|---|
| SSSS | CSSS | CSCS | |
| Xm(x) | sin(λx) | sin(λx)(cos(λx)-1) | sin(λx)(cos(λx)-1) |
| Yn(y) | sin(μy) | sin(μy) | sin(μy)(cos(μy)-1) |
| Material | E (GPa) | ρ (kg/m3) | ν |
|---|---|---|---|
| Al | 69 | 2707 | 0.3 |
| Al2O3 | 380 | 3800 | 0.3 |
| Structure | Method | p = 0 | p = 0.5 | p = 1.0 | p = 4.0 | p = 10.0 |
|---|---|---|---|---|---|---|
| Plate (Lx/Rx = Ly/Ry = 0) | Ref. [51] | 0.0577 | 0.0490 | 0.0442 | 0.0382 | 0.0366 |
| Present | 0.0577 | 0.0490 | 0.0442 | 0.0381 | 0.0364 | |
| Cylindrical shell (Lx/Rx = 0.5, Ly/Ry = 0) | Ref. [51] | 0.0617 | 0.0527 | 0.0477 | 0.0407 | 0.0385 |
| Present | 0.0617 | 0.0527 | 0.0477 | 0.0405 | 0.0383 | |
| Spherical shell (Lx/Rx = Ly/Ry = 0.5) | Ref. [51] | 0.0746 | 0.0646 | 0.0588 | 0.0491 | 0.0455 |
| Present | 0.0746 | 0.0646 | 0.0588 | 0.0490 | 0.0453 |
| Structure | Method | p = 0.5 | p = 1.0 | p = 5.0 | p = 10.0 |
|---|---|---|---|---|---|
| Plate (Lx/Rx = Ly/Ry = 0) | Ref. [52] | 0.0181 | 0.0172 | 0.0137 | 0.0123 |
| Present | 0.0177 | 0.0167 | 0.0133 | 0.0119 | |
| Cylindrical shell (Lx/Rx = 0.5, Ly/Ry = 0) | Ref. [52] | 0.0186 | 0.0176 | 0.0140 | 0.0125 |
| Present | 0.0182 | 0.0171 | 0.0136 | 0.0123 | |
| Spherical shell (Lx/Rx = Ly/Ry = 0.5) | Ref. [52] | 0.0201 | 0.0189 | 0.0150 | 0.0135 |
| Present | 0.0197 | 0.0185 | 0.0146 | 0.0132 |
| Distribution Pattern | A (m) | B | t1 (s) |
|---|---|---|---|
| ΔT = 0 K | 4.874 × 10−5 | 21.77 | 0.0306 |
| ΔT = 200 K, TSD | 6.594 × 10−5 | 15.08 | 0.0566 |
| ΔT = 200 K, TLD | 6.844 × 10−5 | 14.93 | 0.0580 |
| ΔT = 200 K, TUD | 8.407 × 10−5 | 14.01 | 0.0695 |
| Distribution Pattern | A (m) | B | t1 (s) |
|---|---|---|---|
| ΔH = 0% | 4.874 × 10−5 | 21.77 | 0.0306 |
| ΔH = 20%, HSD | 4.708 × 10−5 | 20.52 | 0.0310 |
| ΔH = 20%, HLD | 4.707 × 10−5 | 20.62 | 0.0309 |
| ΔH = 20%, HUD | 4.424 × 10−5 | 20.49 | 0.0415 |
| p | A (m) | B | t1 (s) |
|---|---|---|---|
| 0.5 | 1.631 × 10−4 | 32.91 | 0.0273 |
| 1 | 1.154 × 10−4 | 28.65 | 0.0292 |
| 5 | 4.874 × 10−5 | 21.85 | 0.0298 |
| 10 | 5.393 × 10−5 | 20.59 | 0.0305 |
| η3 | A (m) | B | t1 (s) |
|---|---|---|---|
| 0.01 | 8.053 × 10−5 | 16.42 | 0.0377 |
| 0.5 | 6.480 × 10−5 | 18.84 | 0.0323 |
| 0.1 | 5.393 × 10−5 | 20.59 | 0.0305 |
| V0 (m/s) | A (m) | B | t1 (s) |
|---|---|---|---|
| 5 | 5.393 × 10−5 | 20.59 | 0.0305 |
| 10 | 1.610 × 10−4 | 20.25 | 0.0319 |
| 15 | 3.393 × 10−4 | 20.09 | 0.0339 |
| 20 | 5.405 × 10−4 | 20.03 | 0.0351 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Fu, W.; Wang, Y.; Yan, H.; Huang, Y. Impact Responses and Wave Dissipation Investigation of a Composite Sandwich Shell Reinforced by Multilayer Negative Poisson’s Ratio Viscoelastic Polymer Material Honeycomb. Materials 2024, 17, 233. https://doi.org/10.3390/ma17010233
Zhou X, Fu W, Wang Y, Yan H, Huang Y. Impact Responses and Wave Dissipation Investigation of a Composite Sandwich Shell Reinforced by Multilayer Negative Poisson’s Ratio Viscoelastic Polymer Material Honeycomb. Materials. 2024; 17(1):233. https://doi.org/10.3390/ma17010233
Chicago/Turabian StyleZhou, Xiaoqiang, Wanbiao Fu, Yun Wang, Hai Yan, and Yicang Huang. 2024. "Impact Responses and Wave Dissipation Investigation of a Composite Sandwich Shell Reinforced by Multilayer Negative Poisson’s Ratio Viscoelastic Polymer Material Honeycomb" Materials 17, no. 1: 233. https://doi.org/10.3390/ma17010233
APA StyleZhou, X., Fu, W., Wang, Y., Yan, H., & Huang, Y. (2024). Impact Responses and Wave Dissipation Investigation of a Composite Sandwich Shell Reinforced by Multilayer Negative Poisson’s Ratio Viscoelastic Polymer Material Honeycomb. Materials, 17(1), 233. https://doi.org/10.3390/ma17010233







