Interpretation of Frequency Effect for High-Strength Steels with Three Different Strength Levels via Crystal Plasticity Finite Element Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Specimens
2.2. Experimental Methods
2.3. Crystal Plasticity Theory
3. Crystal Plasticity Finite Element Simulation
3.1. Finite Element Modeling
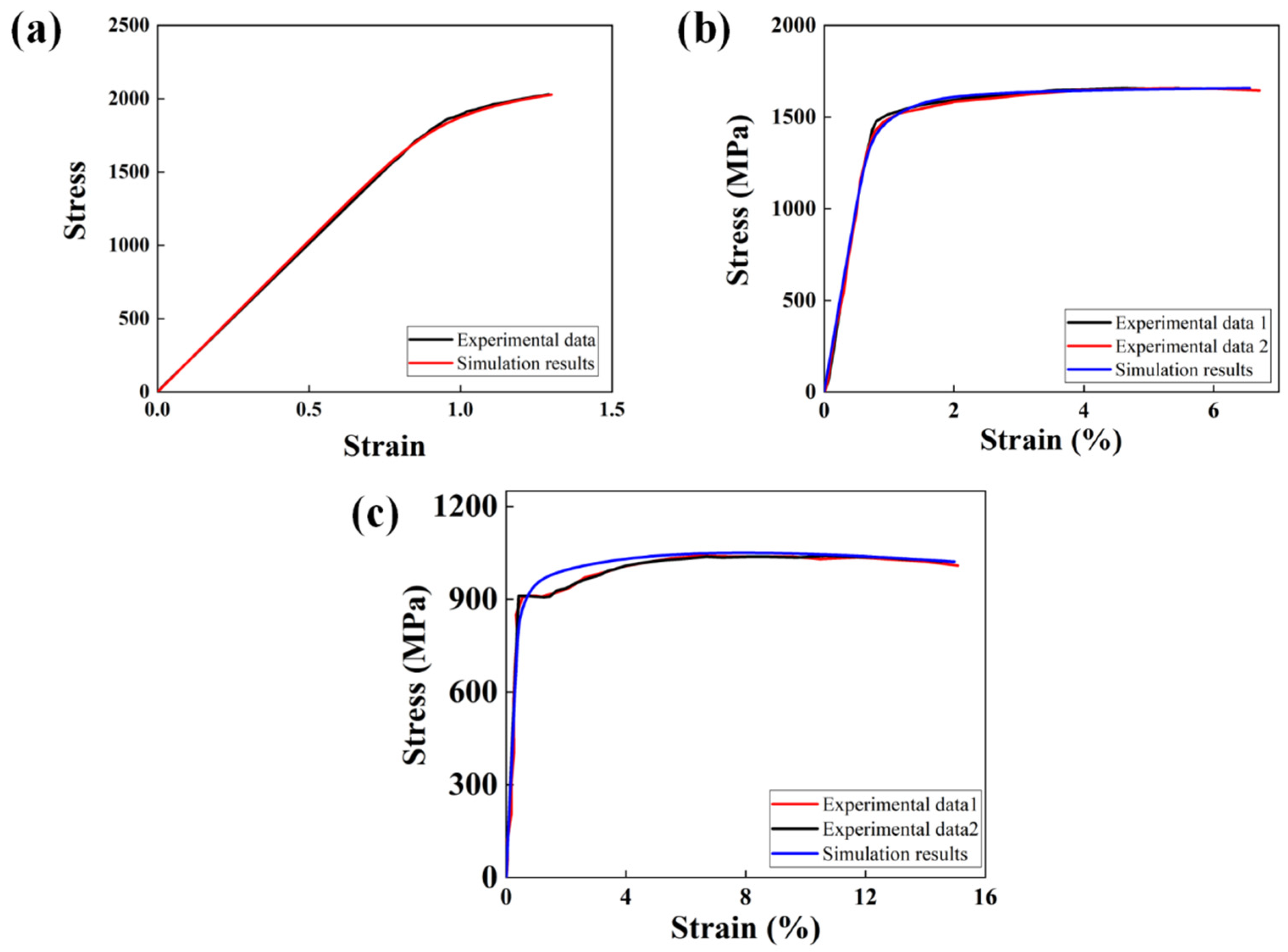
3.2. Model Parameter Calibration
4. Results and Discussion
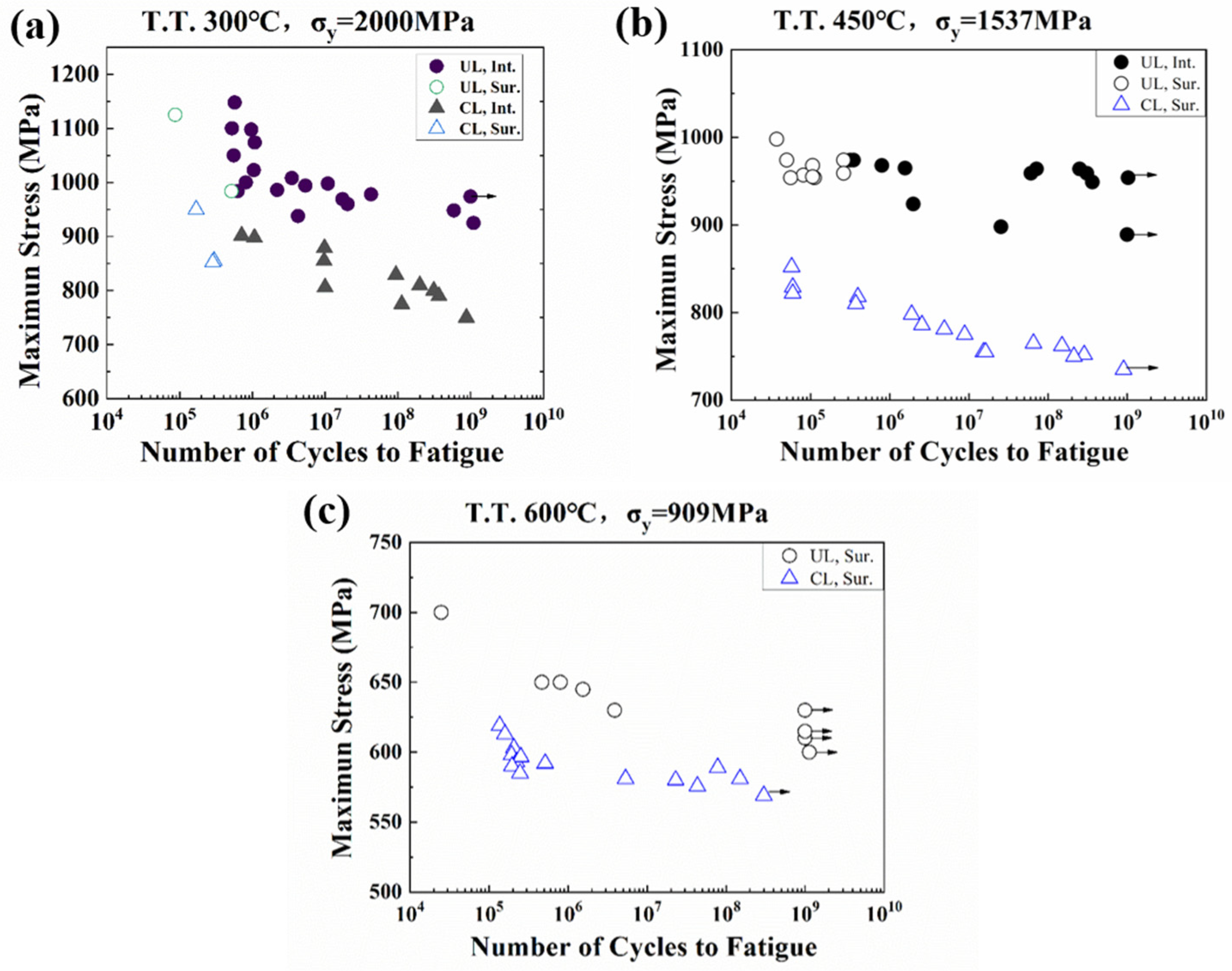
4.1. Fatigue Experimental Results
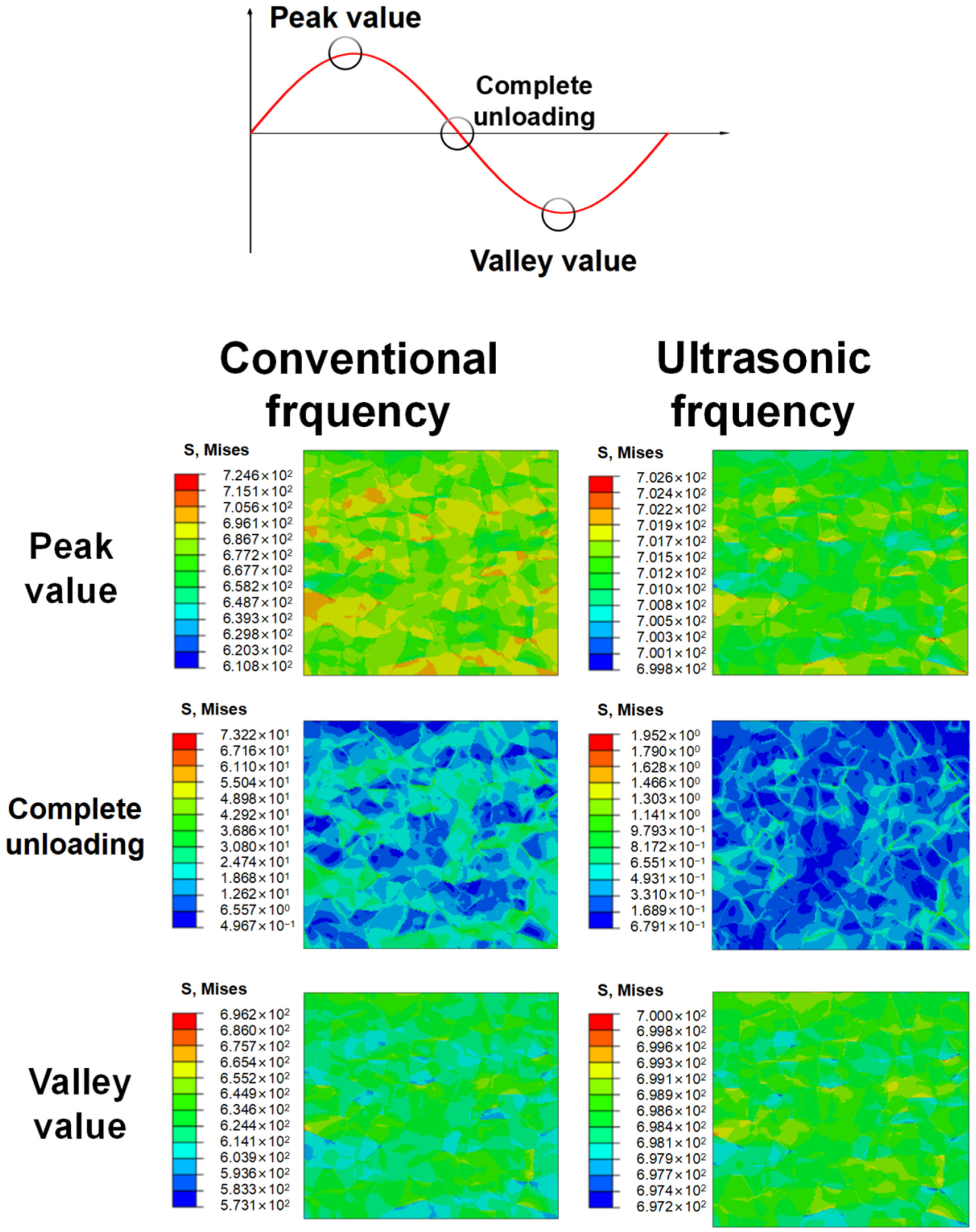
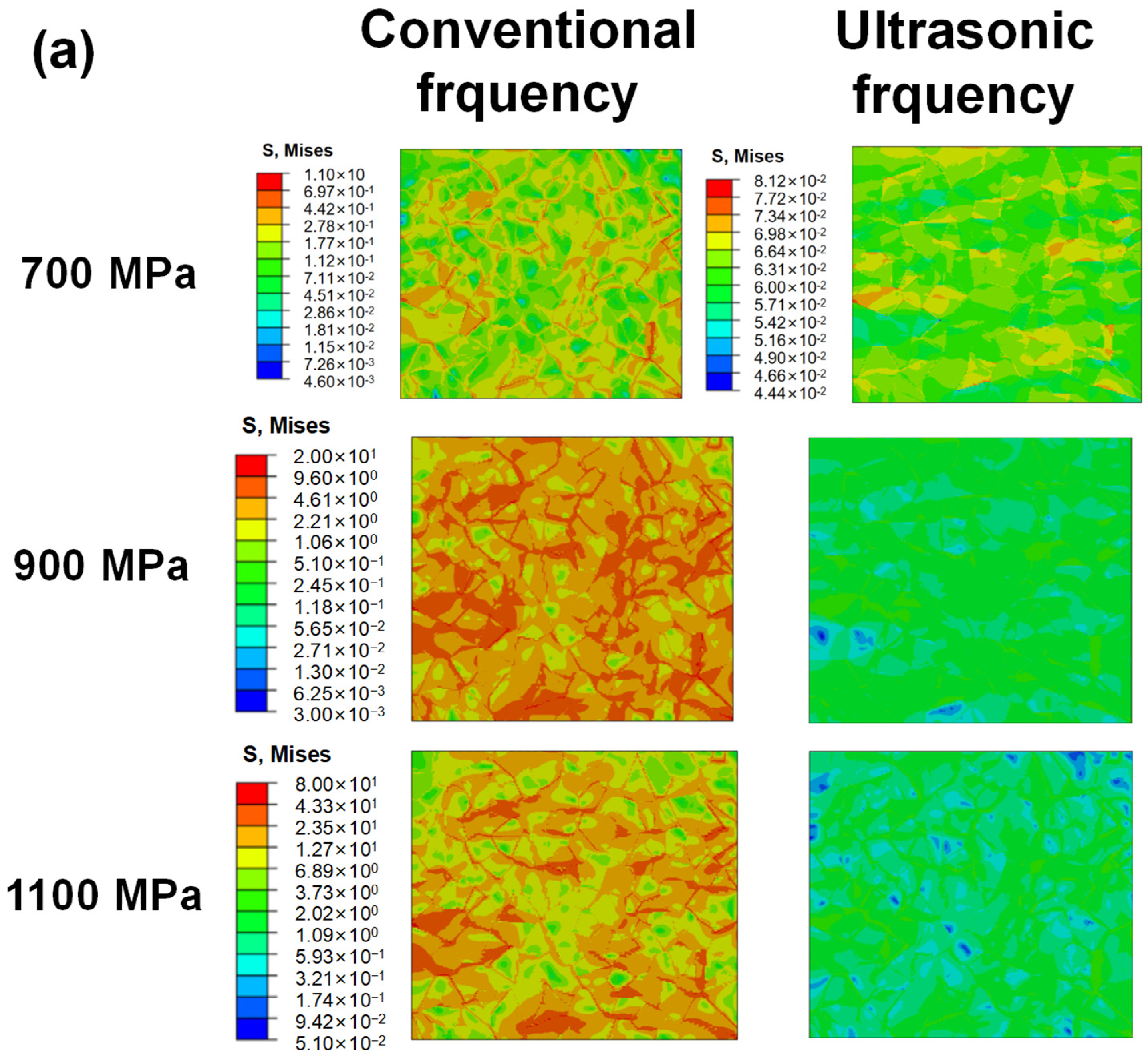
4.2. Local Residual Stress Distribution Calculated by CPFEM
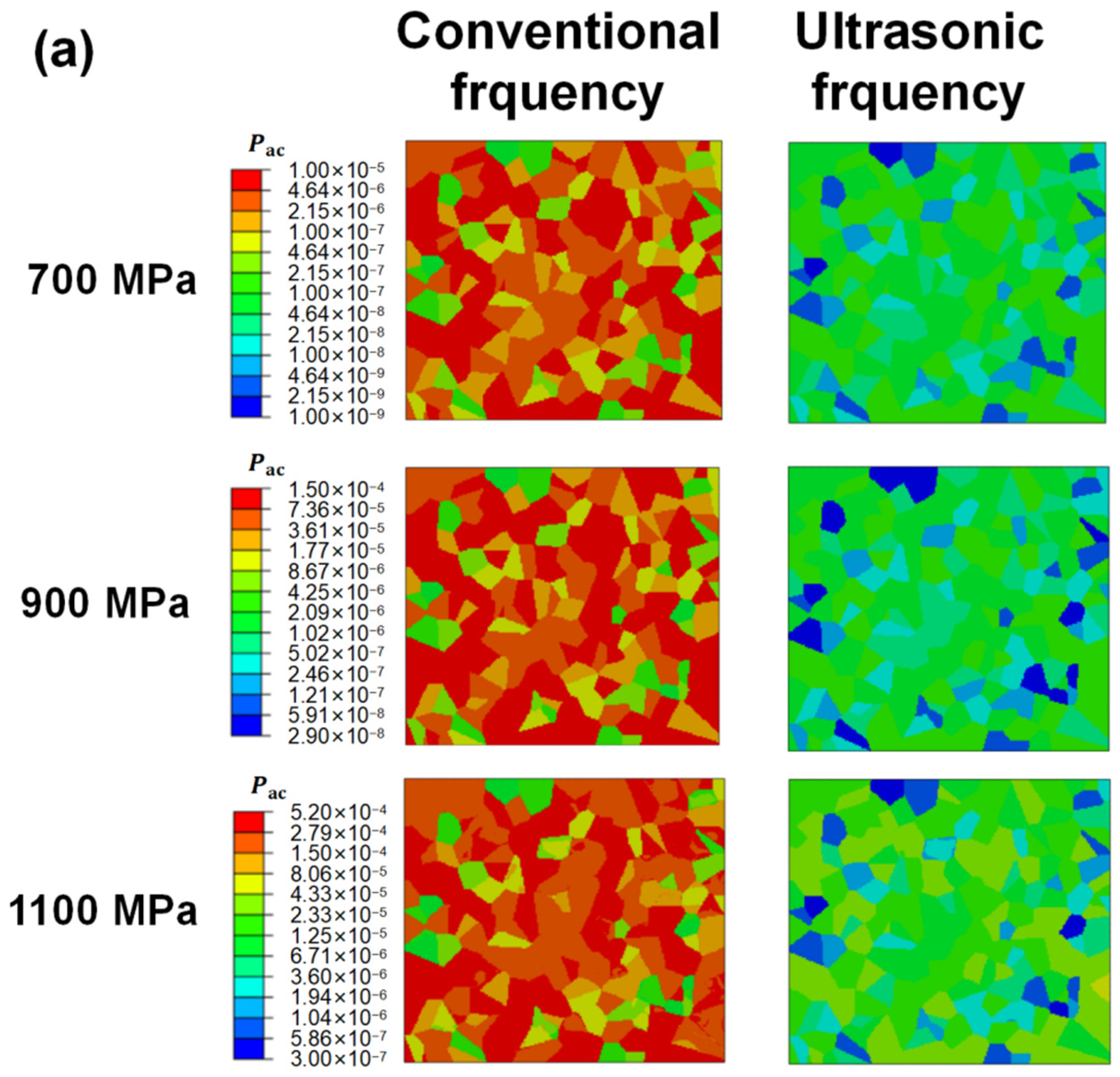
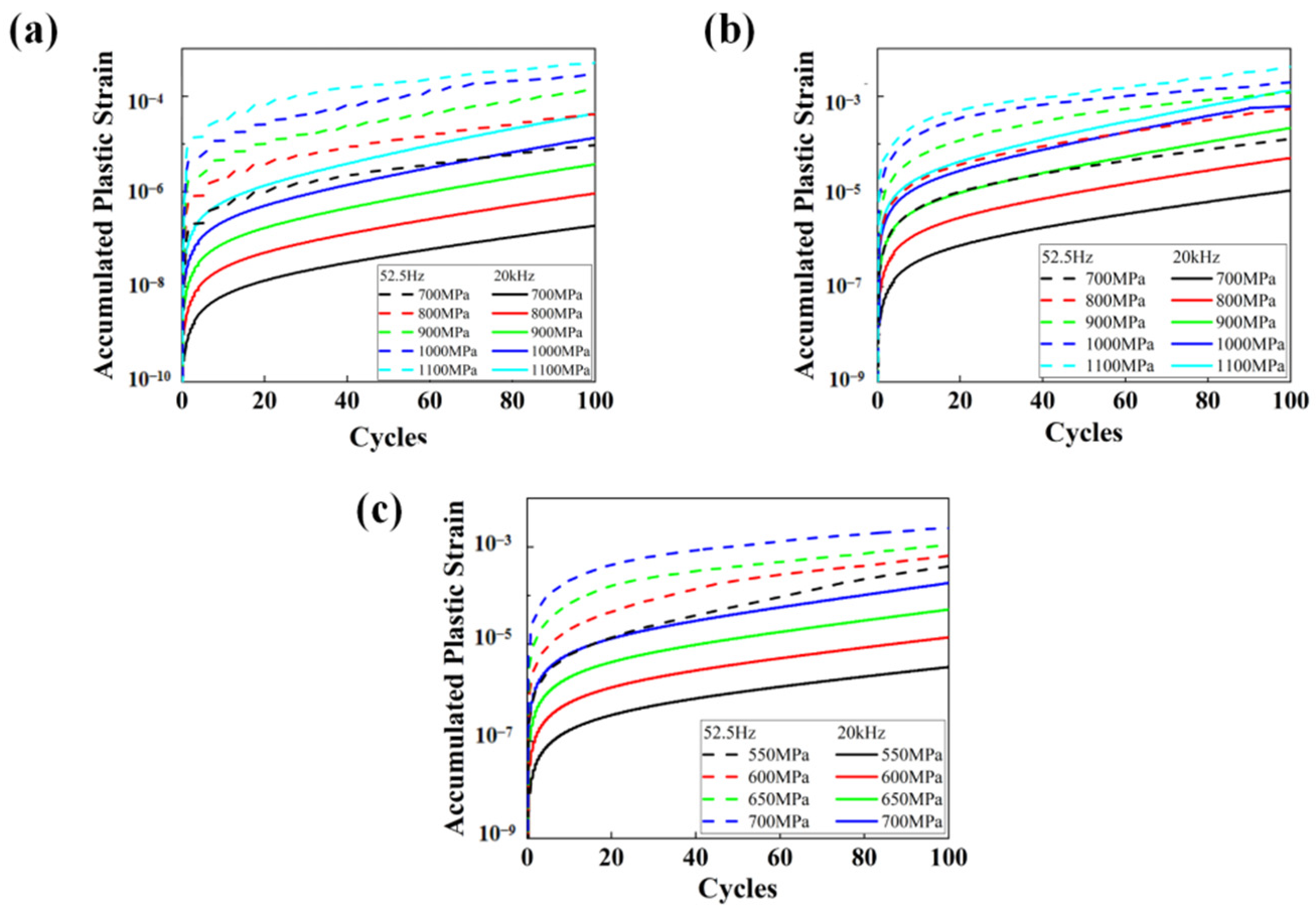
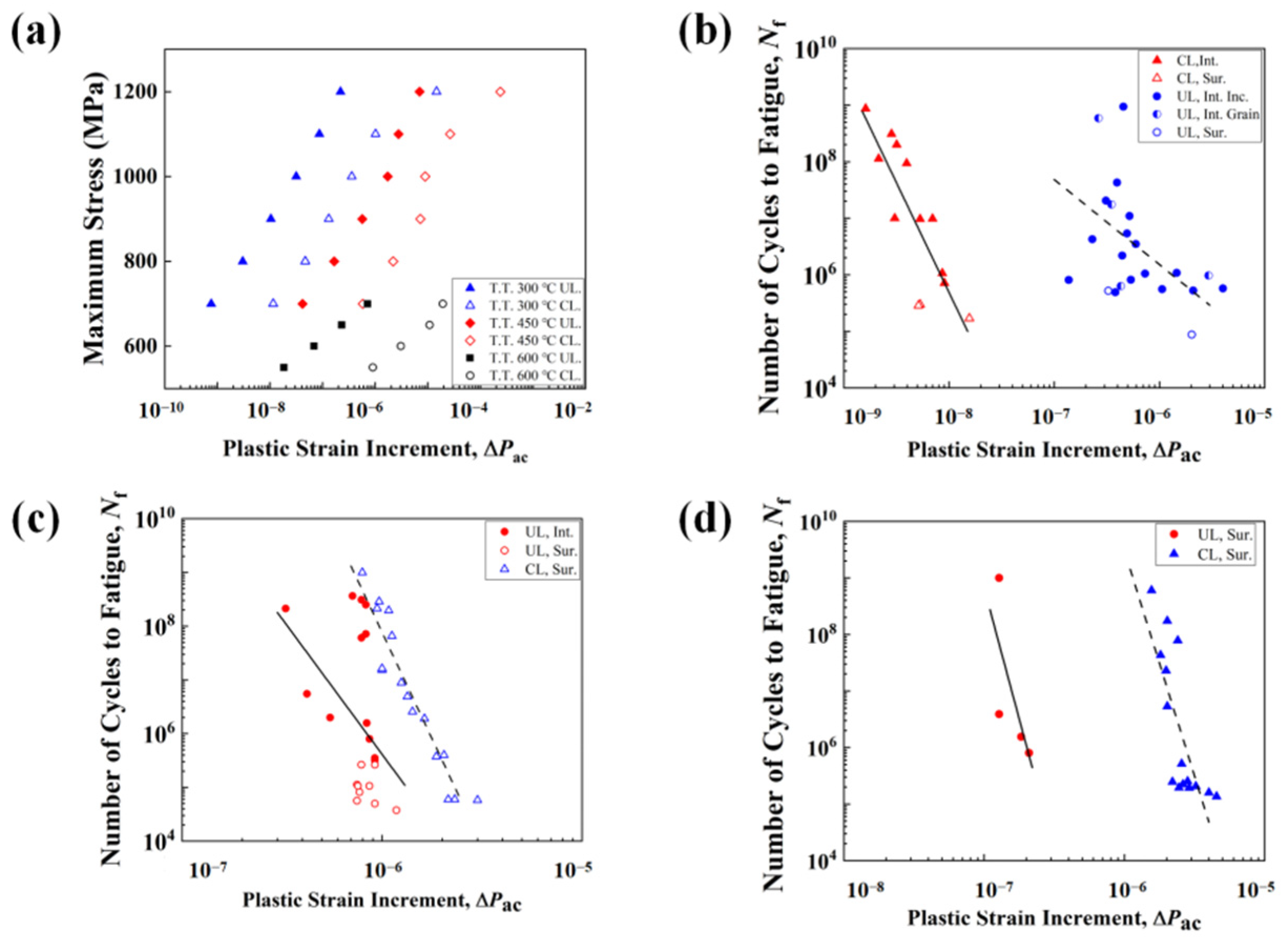
4.3. The Accumulated Plastic Strain
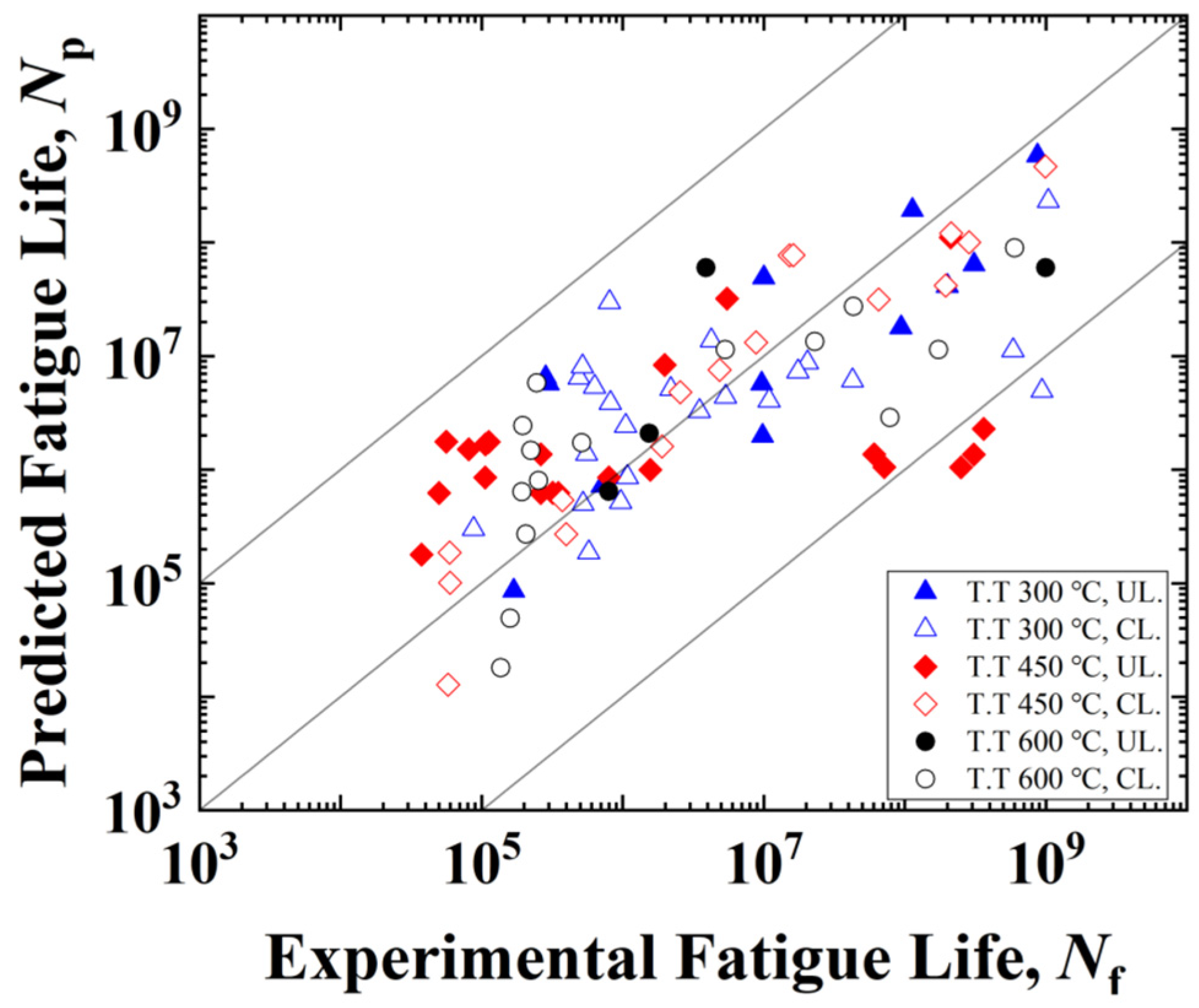
4.4. Fatigue Life Prediction Model
5. Conclusions
- (1)
- The yield strength of the high-carbon chromium-bearing steel lifts from 909 to 2000 MPa as the tempering temperature reduces from 600 °C to 300 °C. The S-N curves shift upward under ultrasonic frequency loading, suggesting that the fatigue lives were much larger at higher frequency loading under the same load stress amplitude. This frequency effect is obvious for all three groups of specimens.
- (2)
- The local residual stress distribution obtained under the same applied load but at different loading frequencies indicates that the maximum local stress is much lower at ultrasonic frequency loading. The maximum local stress increases with the applied loads under both loading frequencies.
- (3)
- Accumulated plastic strain can be taken as the fatigue indicator parameter to explain the frequency effect. For all three groups of specimens, the accumulated plastic strain obtained under ultrasonic loading frequency is several orders smaller than that obtained under conventional loading frequency, as the applied load is fixed. This is the reason for much higher fatigue lives under ultrasonic loading.
- (4)
- The increment of accumulated plastic strain and the load stress amplitude exhibited a linear relationship in the double logarithmic coordinate system. Based on that, an improved fatigue life prediction model was established. The predicted results and the experimental fatigue life are in good agreement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, X.; Du, L.; Qian, G.; Hong, Y. Microstructure features induced by fatigue crack initiation up to very-high-cycle regime for an additively manufactured aluminium alloy. J. Mater. Sci. Technol. 2023, 173, 247–260. [Google Scholar] [CrossRef]
- Yu, C.; Huang, Z.; Zhang, Z.; Wang, J.; Shen, J.; Xu, Z.J. Investigation of High-Cycle Fatigue Properties of Wire Arc Additive Manufacturing 13Cr4Ni Martensitic Stainless Steel. Mater. Res. Technol. 2022, 18, 29–43. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, P.; Wang, B.; Zhu, Y.; Xu, Z.; Zhang, Z. Fatigue cracking criterion of high-strength steels induced by inclusions under high-cycle fatigue. J. Mater. Sci. Technol. 2023, 154, 114–128. [Google Scholar] [CrossRef]
- Cheng, G.; Li, H.; Dai, H.; Gao, H.; Pang, J. Investigation of High-Cycle Fatigue Properties of Wire Arc Additive Manufacturing 13Cr4Ni Martensitic Stainless Steel. Metals 2023, 13, 1210. [Google Scholar] [CrossRef]
- Zou, C.; Pang, J.; Qiu, Y.; Liu, R.; Li, S.; Jing, G.; Xu, C.; Zhang, Z. The high-cycle fatigue fracture mechanism and fatigue strength prediction of compacted graphite iron. Int. J. Fatigue 2022, 161, 106881. [Google Scholar] [CrossRef]
- Wells, J.M.; Buck, O.; Roth, L.D.; Tien, J.K. Ultrasonic Fatique: Proceedings of the First International Conference on Fatigue and Corrosion Fatigue Up to Ultrasonic Frequencies; The Metallurgical Society of AIME: New York, NY, USA, 1982. [Google Scholar]
- Mayer, H. Fatigue crack growth and threshold measurements at very high frequencies. Int. Met. Rev. 1999, 44, 1–34. [Google Scholar] [CrossRef]
- Fitzka, M.; Schönbauer, B.M.; Rhein, R.K.; Sanaei, N.; Zekriardehani, S.; Tekalur, S.A.; Carroll, J.W.; Mayer, H. Usability of ultrasonic frequency testing for rapid generation of high and very high cycle fatigue data. Materials 2021, 14, 2245. [Google Scholar] [CrossRef] [PubMed]
- Furuya, Y.; Shimamura, Y.; Takanashi, M.; Ogawa, T. Standardization of an ultrasonic fatigue testing method in Japan. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2415–2420. [Google Scholar] [CrossRef]
- Mayer, H. Recent developments in ultrasonic fatigue. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 3–29. [Google Scholar] [CrossRef]
- Jeddi, D.; Palin-Luc, T. A review about the effects of structural and operational factors on the gigacycle fatigue of steels. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 969–990. [Google Scholar] [CrossRef]
- Hong, Y.; Hu, Y.; Zhao, A. Effects of loading frequency on fatigue behavior of metallic materials—A literature review. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 3077–3098. [Google Scholar] [CrossRef]
- Zhao, A.; Xie, J.; Sun, C.; Lei, Z.; Hong, Y. Effects of strength level and loading frequency on very-high-cycle fatigue behavior for a bearing steel. Int. J. Fatigue 2012, 38, 46–56. [Google Scholar] [CrossRef]
- Guennec, B.; Ueno, A.; Sakai, T.; Takanashi, M.; Itabashi, Y. Effect of the loading frequency on fatigue properties of JIS S15C low carbon steel and some discussions based on micro-plasticity behavior. Int. J. Fatigue 2014, 66, 29–38. [Google Scholar] [CrossRef]
- Guennec, B.; Ueno, A.; Sakai, T.; Takanashi, M.; Itabashi, Y.; Ota, M. Dislocation-based interpretation on the effect of the loading frequency on the fatigue properties of JIS S15C low carbon steel. Int. J. Fatigue 2015, 70, 328–341. [Google Scholar] [CrossRef]
- Schneider, N.; Bödecker, J.; Berger, C.; Oechsner, M. Frequency effect and influence of testing technique on the fatigue behaviour of quenched and tempered steel and aluminium alloy. Int. J. Fatigue 2016, 93, 224–231. [Google Scholar] [CrossRef]
- Torabian, N.; Favier, V.; Dirrenberger, J.; Adamski, F.; Ziaei-Rad, S.; Ranc, N. Correlation of the high and very high cycle fatigue response of ferrite based steels with strain rate-temperature conditions. Acta Mater. 2017, 134, 40–52. [Google Scholar] [CrossRef]
- Fintová, S.; Pokorný, P.; Fajkoš, R.; Hutař, P. EA4T railway axle steel fatigue behavior under very high-frequency fatigue loading. Eng. Fail. Anal. 2020, 115, 104668. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, C.; Xie, J.; Hong, Y. Effects of loading frequency and loading type on high-cycle and very-high-cycle fatigue of a high-strength steel. Materials 2018, 11, 1456. [Google Scholar] [CrossRef]
- Fu, Z.; Wu, P.; Zhang, Y.; Gan, K.; Yan, D.; Li, Z. Effects of hydrogen and load frequency on the fatigue crack propagation behavior of selective laser melted Inconel 718 alloy. Int. J. Fatigue 2022, 160, 106848. [Google Scholar] [CrossRef]
- Fitzka, M.; Mayer, H. Constant and variable amplitude fatigue testing of aluminum alloy 2024-T351 with ultrasonic and servo-hydraulic equipment. Int. J. Fatigue 2016, 91, 363–372. [Google Scholar] [CrossRef]
- Pessoa, D.F.; Kirchhoff, G.; Zimmermann, M. Influence of loading frequency and role of surface micro-defects on fatigue behavior of metastable austenitic stainless steel AISI 304. Int. J. Fatigue 2017, 103, 48–59. [Google Scholar] [CrossRef]
- Li, Y.; Song, Q.; Feng, S.; Sun, C. Effects of Loading Frequency and Specimen Geometry on High Cycle and Very High Cycle Fatigue Life of a High Strength Titanium Alloy. Materials 2018, 11, 1628. [Google Scholar] [CrossRef]
- Schmiedt, A.; Lücker, L.; Manka, M.; Tillmann, W.; Walther, F. Frequency-dependent fatigue and corrosion fatigue assessment of brazed AISI 304L/BNi-2 joints in air and synthetic exhaust gas condensate. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2338–2349. [Google Scholar] [CrossRef]
- Baya, R.; Schrock, D.; Akman, A.; Bland, L.; Thodla, R.; Locke, J. The effect of sensitization and fatigue loading frequency on corrosion fatigue of AA5083-H131. Int. J. Fatigue 2019, 124, 1–9. [Google Scholar] [CrossRef]
- Ren, W.; Liu, D.; Liu, Q.; Xin, R. Influence of texture distribution in magnesium welds on their non-uniform mechanical behavior: A CPFEM study. J. Mater. Sci. Technol. 2020, 46, 168–176. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Xu, D.; Teng, C.; Wang, H.; Yang, L.; Ju, H.; Xu, H.; Meng, Z.; Ma, Y.; et al. Phase field simulation of the stress-induced α microstructure in Ti–6Al–4 V alloy and its CPFEM properties evaluation. J. Mater. Sci. Technol. 2021, 90, 168–182. [Google Scholar] [CrossRef]
- Li, B.; Chen, C.; Qin, Z.; Xue, H. An energy-CP-combined model for predicting the fatigue life of polycrystalline materials under high cycle and very high cycle fatigue. Eng. Fract. Mech. 2023, 291, 109564. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, X.; Yang, X.; Zhang, T.; Jiang, Y.; Zhang, X.; Gong, J.; Tu, S. A generalized physical-based failure indicator parameter used in crystal plasticity model to predict fatigue life under low cycle fatigue and creep-fatigue loadings. Int. J. Fatigue 2023, 166, 107290. [Google Scholar] [CrossRef]
- Li, K.; Wang, R.; Zhang, X.; Tu, S. Creep-fatigue damage mechanisms and life prediction based on crystal plasticity combined with grain boundary cavity model in a nickel-based superalloy at 650 °C. Int. J. Plast. 2023, 165, 103601. [Google Scholar] [CrossRef]
- Li, K.; Wang, R.; Yuan, G.; Zhu, S.; Zhang, X.; Tu, S.; Miura, H. A crystal plasticity-based approach for creep-fatigue life prediction and damage evaluation in a nickel-based superalloy. Int. J. Fatigue 2021, 143, 106031. [Google Scholar] [CrossRef]
- Li, K.; Wang, R.; Cheng, L.; Lu, T.; Zhang, X.; Tu, S.; Zhang, G.; Fan, Z. Dislocation-based crystal plasticity modelling of a nickel-based superalloy under dwell-fatigue: From life prediction to residual life assessment. Int. J. Fatigue 2022, 159, 106569. [Google Scholar] [CrossRef]
- Lu, P.; Jin, X.; Li, P.; Sun, Y.; Fan, X. Crystal plasticity constitutive model and thermodynamics informed creep-fatigue life prediction model for Ni-based single crystal superalloy. Int. J. Fatigue 2023, 176, 107829. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, M.; Zhang, C.; He, P.; Dai, Y. Experimental investigation and crystal plasticity modeling of combined high and low cycle loading on AISI 4140 steel. Int. J. Fatigue 2023, 168, 107465. [Google Scholar] [CrossRef]
- Jiang, W.; Yao, W.; Li, P.; Luo, P. A fatigue life prediction method distinguishing fracture modes for Ni-based single crystal superalloys considering porosity defect. Theor. Appl. Fract. Mech. 2021, 112, 102883. [Google Scholar] [CrossRef]
- Li, L.; Wang, R.; Xu, L.; Zhang, C.; Xia, X.; Tang, M.; Zhang, M.; Zhang, X.; Tu, S. Life prediction and damage analysis of creep-fatigue combined with high-low cycle loading by using a crystal plasticity-based approach. Int. J. Fatigue 2022, 164, 107154. [Google Scholar] [CrossRef]
- Cong, T.; Li, R.; Zheng, Z.; Ma, X.; Wu, S.; Zhang, R.; Berto, F.; Sun, J.; Qian, G. Experimental and computational investigation of weathering steel Q450NQR1 under high cycle fatigue loading via crystal plasticity finite element method. Int. J. Fatigue 2022, 159, 106772. [Google Scholar] [CrossRef]
- Li, L.; Shen, L.; Proust, G. Fatigue crack initiation life prediction for aluminum alloy 7075 using crystal plasticity finite element simulations. Mech. Mater. 2015, 81, 84–93. [Google Scholar] [CrossRef]
- Shen, J.; Fan, H.; Wang, J.; Zhang, G.; Pan, R.; Huang, Z. Stored energy density research on the fatigue crack initiation at twin boundary and life prediction of Inconel718 superalloy. Int. J. Fatigue 2023, 171, 107590. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, Y.; Ma, X.; Qian, G.; Zhang, J.; Yang, Z.; Berto, F. Very-high-cycle fatigue behavior of AlSi10Mg manufactured by selected laser melting: Crystal plasticity modeling. Int. J. Fatigue 2021, 145, 106109. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Wu, S.; Zhang, W.; Sun, J.; Qian, G. High-cycle and very-high-cycle fatigue lifetime prediction of additively manufactured AlSi10Mg via crystal plasticity finite element method. Int. J. Fatigue 2022, 155, 106577. [Google Scholar] [CrossRef]
- Prithivirajan, V.; Sangid, M. Examining metrics for fatigue life predictions of additively manufactured IN718 via crystal plasticity modeling including the role of simulation volume and microstructural constraints. Mater. Sci. Eng. A 2020, 783, 139312. [Google Scholar] [CrossRef]
- Priddy, M.; Paulson, N.; Kalidindi, S.; McDowell, D. Strategies for rapid parametric assessment of microstructure-sensitive fatigue for HCP polycrystals. Int. J. Fatigue 2017, 104, 231–242. [Google Scholar] [CrossRef]
- Paulson, N.; Priddy, M.; McDowell, D.; Kalidindi, S. Reduced-order microstructure-sensitive protocols to rank-order the transition fatigue resistance of polycrystalline microstructures. Int. J. Fatigue 2019, 119, 1–10. [Google Scholar] [CrossRef]
- Sun, J.; Qian, G.; Li, J.; Li, R.; Jian, X.; Hong, Y.; Berto, F. A framework to simulate the crack initiation and propagation in very-high-cycle fatigue of an additively manufactured AlSi10Mg alloy. J. Mech. Phys. Solids 2023, 175, 105293. [Google Scholar] [CrossRef]
- Cheng, J.; Hu, X.; Kirka, M. A cycle-jump acceleration method for the crystal plasticity simulation of high cycle fatigue of the metallic microstructure. Int. J. Fatigue 2022, 165, 107185. [Google Scholar] [CrossRef]
- Ghosh, S.; Chakraborty, P. Microstructure and load sensitive fatigue crack nucleation in Ti-6242 using accelerated crystal plasticity FEM simulations. Int. J. Fatigue 2013, 48, 231–246. [Google Scholar] [CrossRef]
- Rice, J. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. A 1976, 348, 101–127. [Google Scholar]
- Peirce, D.; Asaro, R.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Opinsky, A.; Smoluchowski, R. The Crystallographic Aspect of Slip in Body-Centered Cubic Single Crystals. II. Interpretation of Experiments. J. Appl. Phys. 1951, 22, 1488–1492. [Google Scholar] [CrossRef]
- Tian, C.; Dehm, G.; Kirchlechner, C. Influence of strain rate on the activation of {110}, {112}, {123} slip in ferrite of DP800. Materialia 2021, 15, 100983. [Google Scholar] [CrossRef]

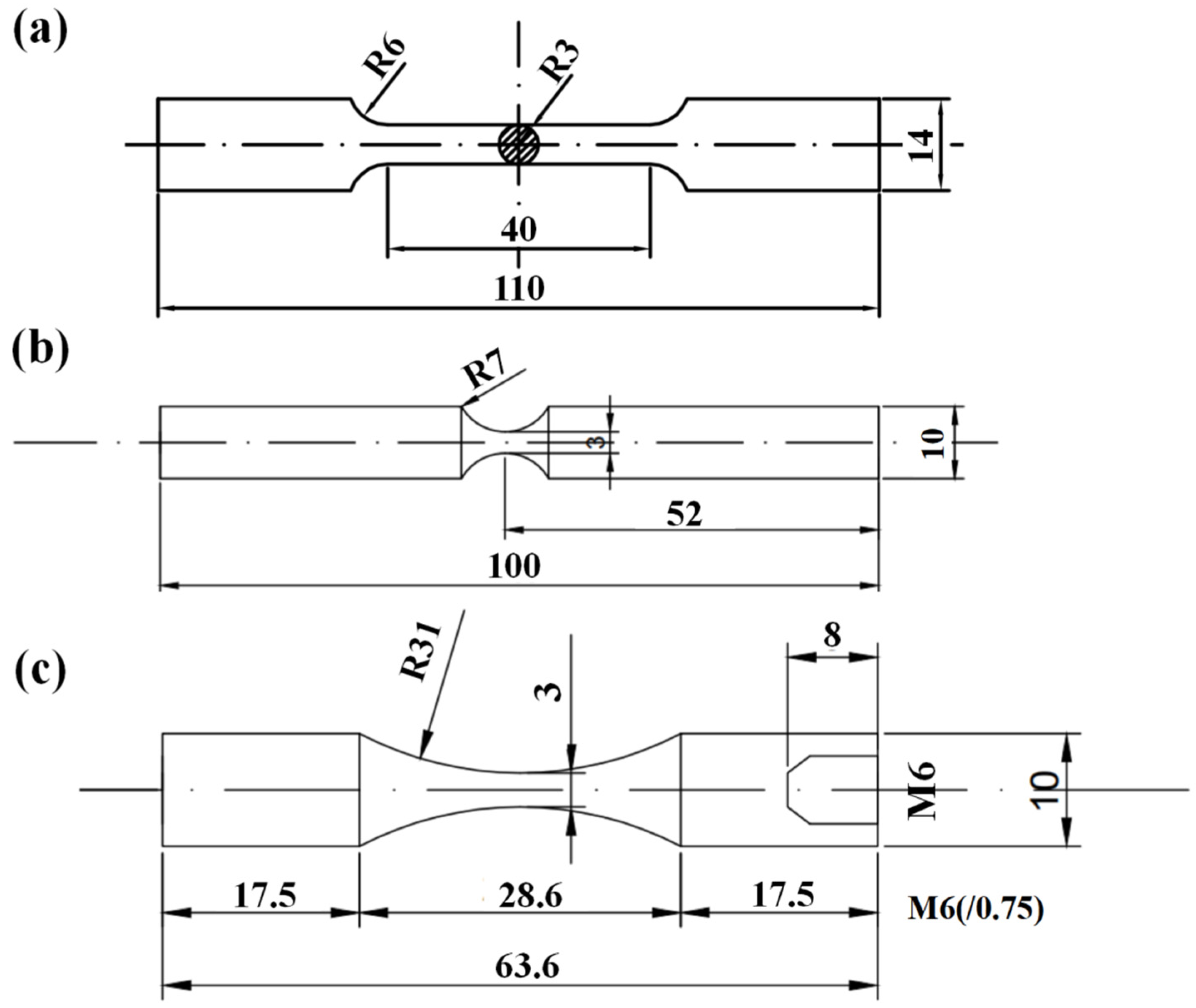
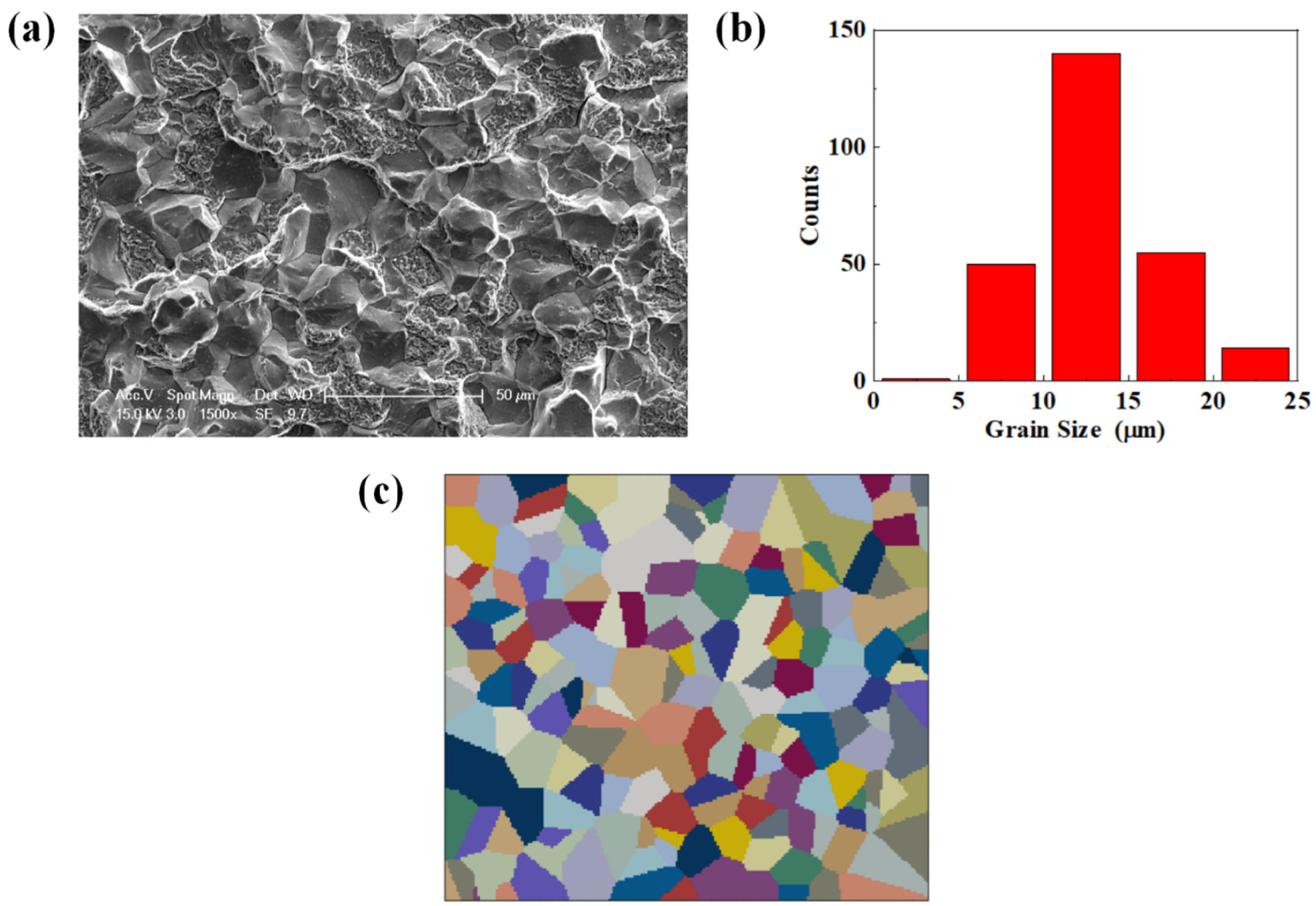




| C | Cr | Mn | Si | P | S | Fe |
|---|---|---|---|---|---|---|
| 1.01 | 1.45 | 0.35 | 0.28 | 0.015 | 0.01 | Balance |
| Tempering Temperature | Slip System | n | h0 (MPa) | τs (MPa) | τ0 (MPa) |
|---|---|---|---|---|---|
| 300 °C | {110}<111> | 10 | 390 | 1000 | 570 |
| {112}<111> | 10 | 290 | 1000 | 640 | |
| 450 °C | {110}<111> | 10 | 200 | 900 | 400 |
| {112}<111> | 10 | 150 | 910 | 400 | |
| 600 °C | {110}<111> | 10 | 300 | 330 | 270 |
| {112}<111> | 10 | 250 | 340 | 280 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wang, X.; Pan, L.; Wang, J.; Chen, L.; Xing, T.; Zhu, J.; Zhao, A. Interpretation of Frequency Effect for High-Strength Steels with Three Different Strength Levels via Crystal Plasticity Finite Element Method. Materials 2024, 17, 2350. https://doi.org/10.3390/ma17102350
Zhao Y, Wang X, Pan L, Wang J, Chen L, Xing T, Zhu J, Zhao A. Interpretation of Frequency Effect for High-Strength Steels with Three Different Strength Levels via Crystal Plasticity Finite Element Method. Materials. 2024; 17(10):2350. https://doi.org/10.3390/ma17102350
Chicago/Turabian StyleZhao, Yingxin, Xiaoya Wang, Like Pan, Jun Wang, Liming Chen, Tong Xing, Junchen Zhu, and Aiguo Zhao. 2024. "Interpretation of Frequency Effect for High-Strength Steels with Three Different Strength Levels via Crystal Plasticity Finite Element Method" Materials 17, no. 10: 2350. https://doi.org/10.3390/ma17102350
APA StyleZhao, Y., Wang, X., Pan, L., Wang, J., Chen, L., Xing, T., Zhu, J., & Zhao, A. (2024). Interpretation of Frequency Effect for High-Strength Steels with Three Different Strength Levels via Crystal Plasticity Finite Element Method. Materials, 17(10), 2350. https://doi.org/10.3390/ma17102350







