Comparative Study of the Optical and Dielectric Anisotropy of a Difluoroterphenyl Dimer and Trimer Forming Two Nematic Phases
Abstract
1. Introduction
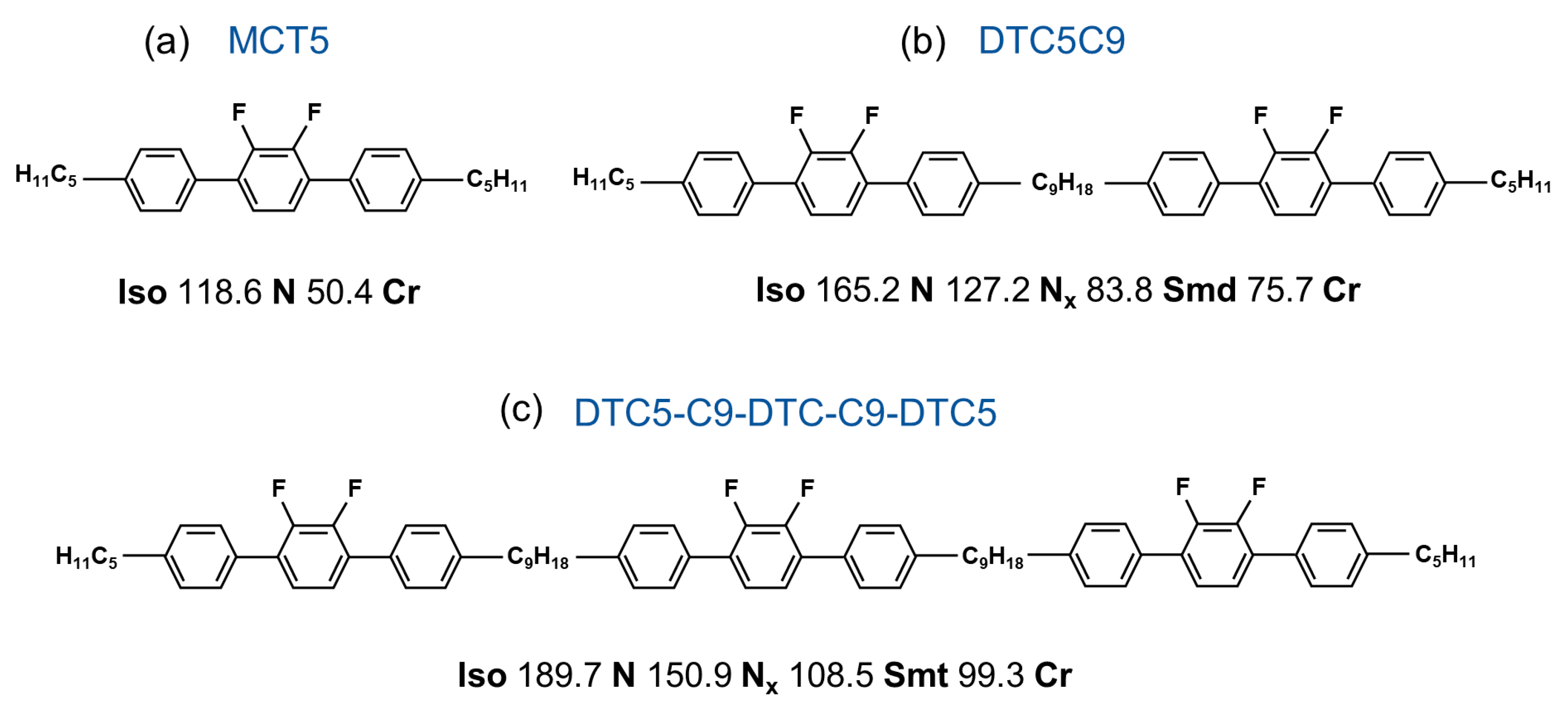
2. Materials and Methods
3. Results
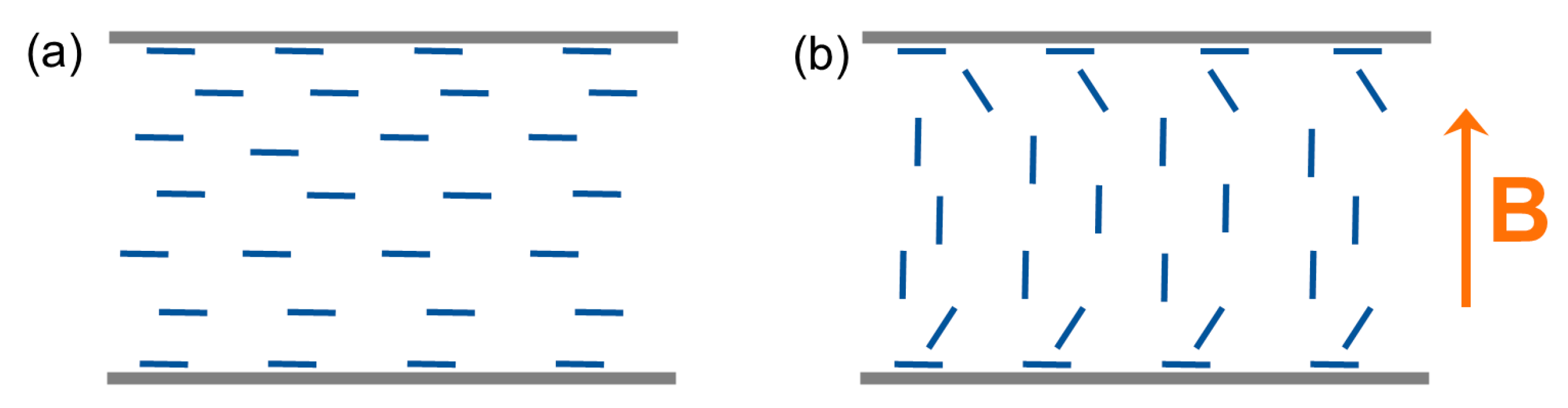
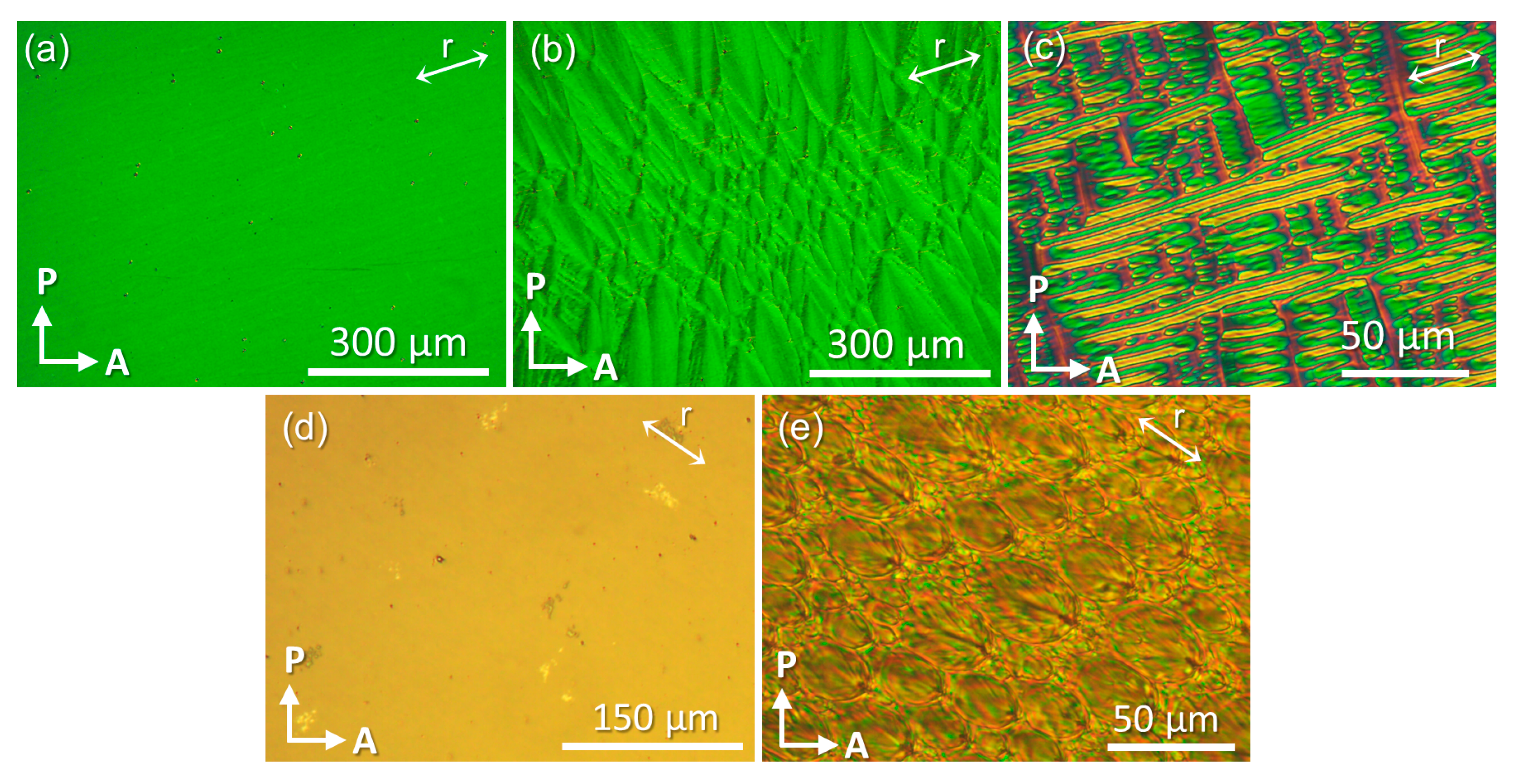
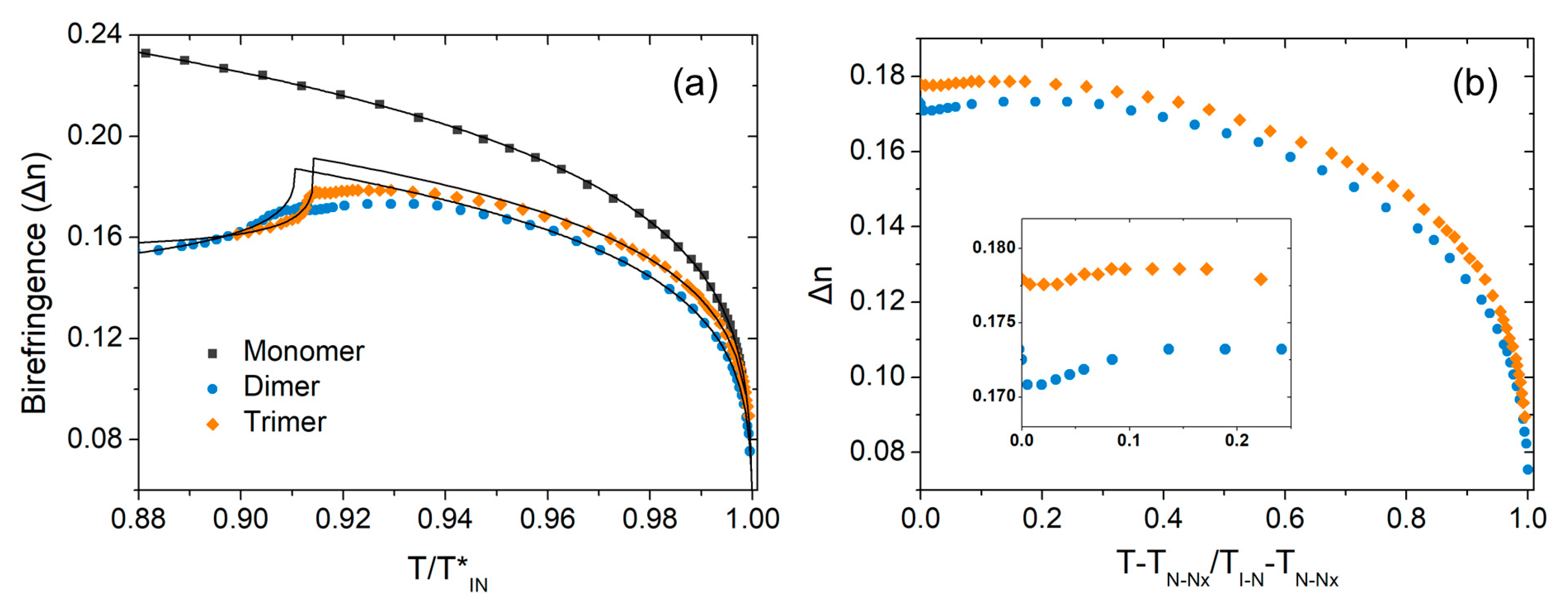
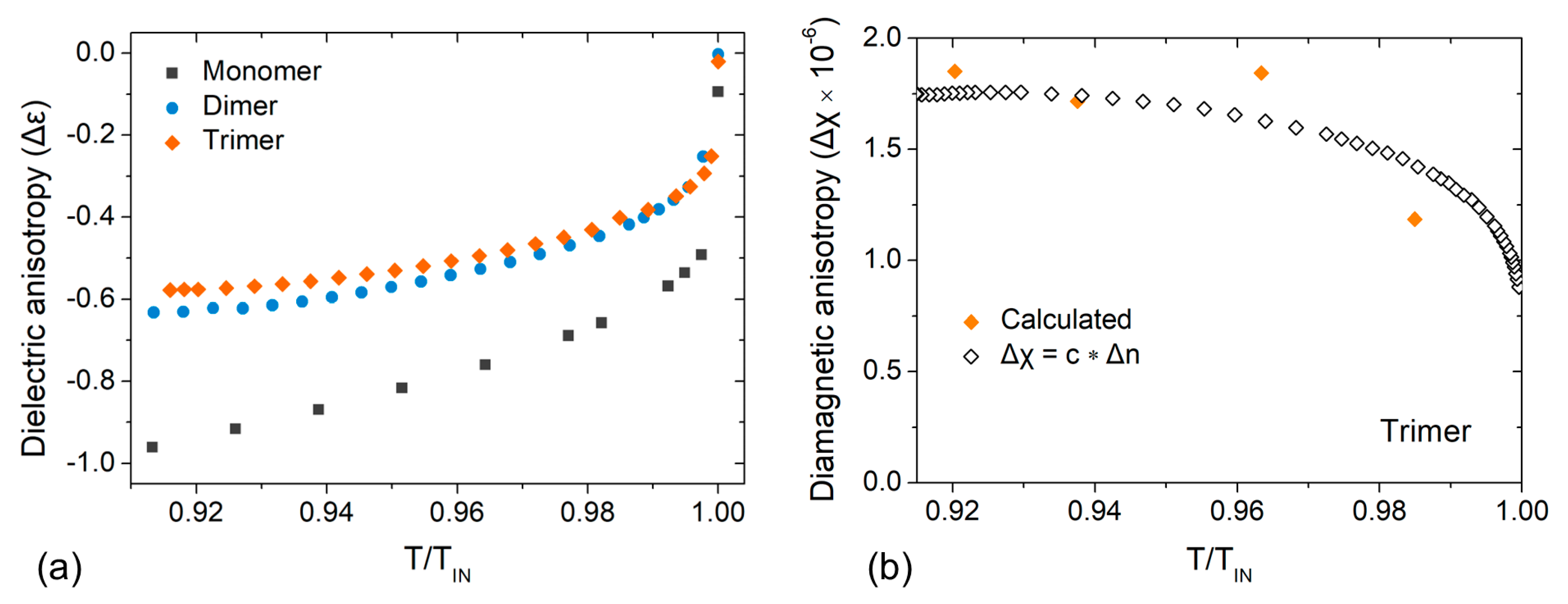
3.1. Optical Anisotropy Studies
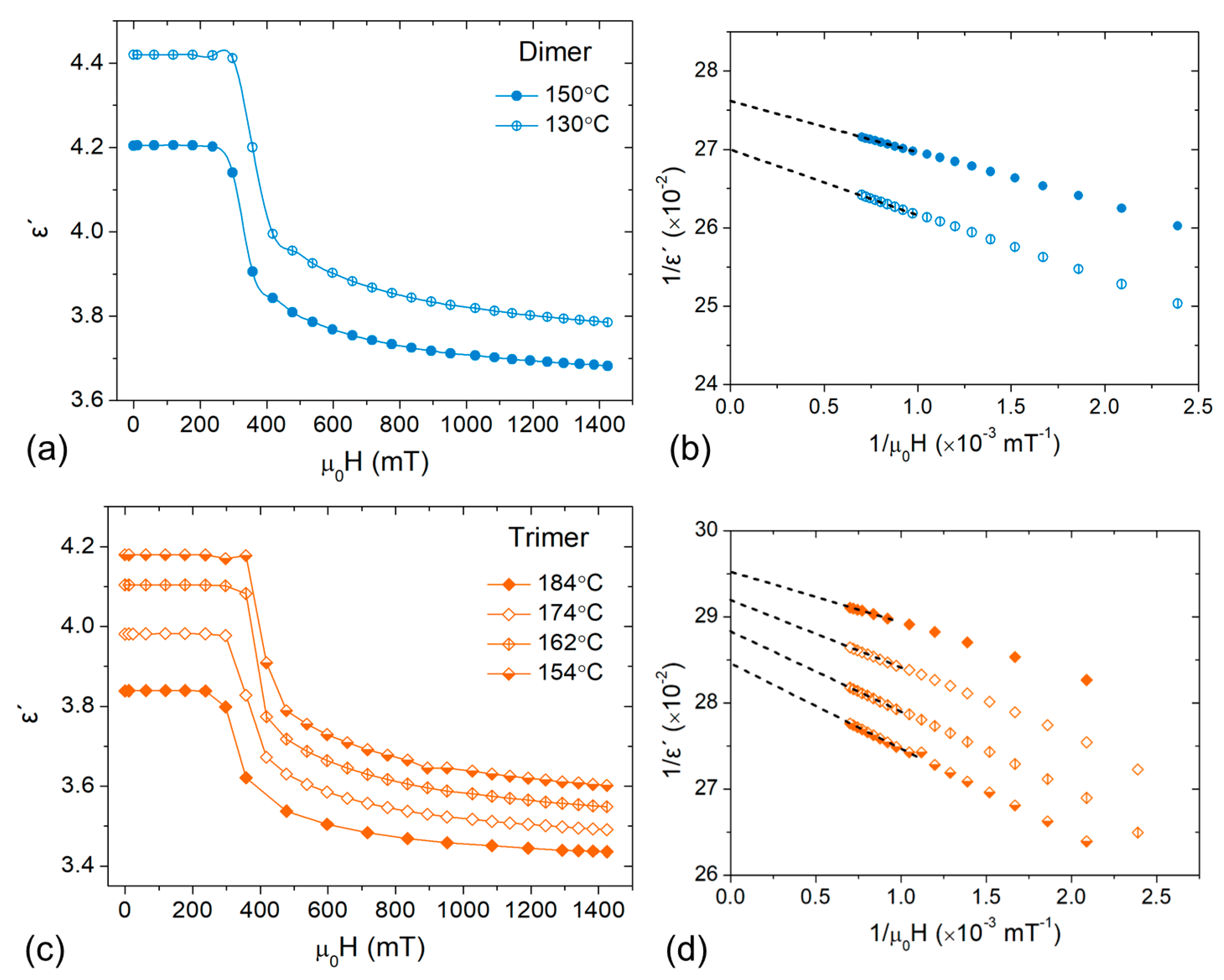
3.2. Dielectric Anisotropy Studies
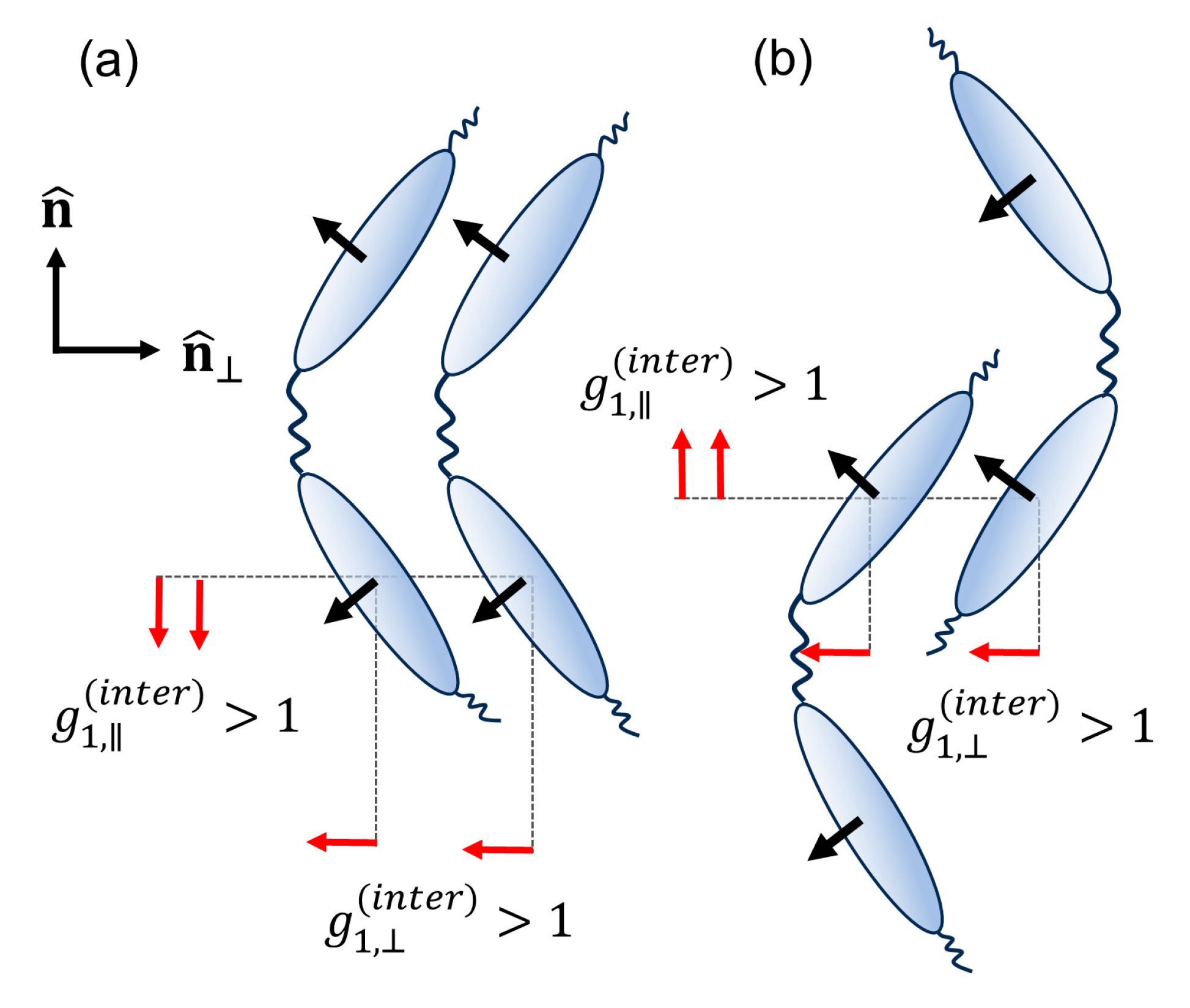
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vorländer, D. Über Die Natur Der Kohlenstoffketten in Kristallin-Flüssigen Substanzen. Z. Phys. Chem. 1927, 126U, 449–472. [Google Scholar] [CrossRef]
- Griffin, A.C.; Britt, T.R. Effect of Molecular Structure on Mesomorphism. Flexible-Center Siamese-Twin Liquid Crystalline Diesters-A “Prepolymer” Model. J. Am. Chem. Soc. 1981, 103, 4957–4959. [Google Scholar] [CrossRef]
- Emsley, J.W.; Luckhurst, G.R.; Shilstone, G.N.; Sage, I. The Preparation and Properties of the α,ω-Bis(4,4′-Cyanobiphenyloxy)Alkanes: Nematogenic Molecules with a Flexible Core. Mol. Cryst. Liq. Cryst. 1984, 102, 223–233. [Google Scholar] [CrossRef]
- Photinos, D.J.; Samulski, E.T.; Toriumi, H. Molecular Flexibility in Nematics: From Alkanes to Dimer Mesogens. J. Chem. Soc. Faraday Trans. 1992, 88, 1875–1883. [Google Scholar] [CrossRef]
- Imrie, C.T.; Henderson, P.A. Liquid Crystal Dimers and Higher Oligomers: Between Monomers and Polymers. Chem. Soc. Rev. 2007, 36, 2096–2124. [Google Scholar] [CrossRef]
- Panov, V.P.; Nagaraj, M.; Vij, J.K.; Panarin, Y.P.; Kohlmeier, A.; Tamba, M.G.; Lewis, R.A.; Mehl, G.H. Spontaneous Periodic Deformations in Nonchiral Planar-Aligned Bimesogens with a Nematic-Nematic Transition and a Negative Elastic Constant. Phys. Rev. Lett. 2010, 105, 167801. [Google Scholar]
- Borshch, V.; Kim, Y.K.; Xiang, J.; Gao, M.; Jákli, A.; Panov, V.P.; Vij, J.K.; Imrie, C.T.; Tamba, M.G.; Mehl, G.H.; et al. Nematic Twist-Bend Phase with Nanoscale Modulation of Molecular Orientation. Nat. Commun. 2013, 4, 2635. [Google Scholar] [CrossRef]
- Chen, D.; Porada, J.H.; Hooper, J.B.; Klittnick, A.; Shen, Y.; Tuchband, M.R.; Korblova, E.; Bedrov, D.; Walba, D.M.; Glaser, M.A.; et al. Chiral Heliconical Ground State of Nanoscale Pitch in a Nematic Liquid Crystal of Achiral Molecular Dimers. Proc. Natl. Acad. Sci. USA 2013, 110, 15931–15936. [Google Scholar] [CrossRef]
- Zhu, C.; Tuchband, M.R.; Young, A.; Shuai, M.; Scarbrough, A.; Walba, D.M.; Maclennan, J.E.; Wang, C.; Hexemer, A.; Clark, N.A. Resonant Carbon K-Edge Soft X-Ray Scattering from Lattice-Free Heliconical Molecular Ordering: Soft Dilative Elasticity of the Twist-Bend Liquid Crystal Phase. Phys. Rev. Lett. 2016, 116, 147803. [Google Scholar] [CrossRef]
- Stevenson, W.D.; Ahmed, Z.; Zeng, X.B.; Welch, C.; Ungar, G.; Mehl, G.H. Molecular Organization in the Twist–Bend Nematic Phase by Resonant X-Ray Scattering at the Se K-Edge and by SAXS, WAXS and GIXRD. Phys. Chem. Chem. Phys. 2017, 19, 13449–13454. [Google Scholar] [CrossRef]
- Cestari, M.; Diez-Berart, S.; Dunmur, D.A.; Ferrarini, A.; de la Fuente, M.R.; Jackson, D.J.B.; Lopez, D.O.; Luckhurst, G.R.; Perez-Jubindo, M.A.; Richardson, R.M.; et al. Phase Behavior and Properties of the Liquid-Crystal Dimer 1′′,7′′-Bis(4-Cyanobiphenyl-4′-Yl) Heptane: A Twist-Bend Nematic Liquid Crystal. Phys. Rev. E 2011, 84, 031704. [Google Scholar] [CrossRef]
- Longa, L.; Tomczyk, W. Twist–Bend Nematic Phase from the Landau–de Gennes Perspective. J. Phys. Chem. C 2020, 124, 22761–22775. [Google Scholar] [CrossRef]
- Meyer, R.B. Structural problems in liquid crystal physics. In Molecular Fluids, Les Houches Summer School in Theoretical Physics; Balian, R., Weill, G., Eds.; Gordon and Breach: New York, NY, USA, 1976. [Google Scholar]
- Dozov, I. On the Spontaneous Symmetry Breaking in the Mesophases of Achiral Banana-Shaped Molecules. Europhys. Lett. 2001, 56, 247. [Google Scholar] [CrossRef]
- Vanakaras, A.G.; Photinos, D.J. A Molecular Theory of Nematic-Nematic Phase Transitions in Mesogenic Dimers. Soft Matter 2016, 12, 2208–2220. [Google Scholar] [CrossRef]
- Vanakaras, A.G.; Photinos, D.J. Molecular Dynamics Simulations of Nematic Phases Formed by Cyano-Biphenyl Dimers. Liq. Cryst. 2018, 45, 2184–2196. [Google Scholar] [CrossRef]
- Samulski, E.T.; Reyes-Arango, D.; Vanakaras, A.G.; Photinos, D.J. All Structures Great and Small: Nanoscale Modulations in Nematic Liquid Crystals. Nanomaterials 2022, 12, 93. [Google Scholar] [CrossRef]
- Samulski, E.T. The Ever Elusive, Yet-to-Be-Discovered Twist-Bend Nematic Phase. Crystals 2023, 13, 1648. [Google Scholar] [CrossRef]
- Robles-Hernández, B.; Sebastián, N.; De La Fuente, M.R.; López, D.O.; Diez-Berart, S.; Salud, J.; Ros, M.B.; Dunmur, D.A.; Luckhurst, G.R.; Timimi, B.A. Twist, Tilt, and Orientational Order at the Nematic to Twist-Bend Nematic Phase Transition of 1″,9″-Bis(4-Cyanobiphenyl-4′-Yl) Nonane: A Dielectric, (2)H NMR, and Calorimetric Study. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2015, 92, 062505. [Google Scholar] [CrossRef]
- Paterson, D.A.; Abberley, J.P.; Harrison, W.T.A.; Storey, J.; Imrie, C.T. Cyanobiphenyl-Based Liquid Crystal Dimers and the Twist-Bend Nematic Phase. Liq. Cryst. 2017, 44, 127–146. [Google Scholar] [CrossRef]
- Mandle, R.J. The Dependency of Twist-Bend Nematic Liquid Crystals on Molecular Structure: A Progression from Dimers to Trimers, Oligomers and Polymers. Soft Matter 2016, 12, 7883–7901. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A. Dependency of the Twist-Bend Nematic Phase Formation on the Molecular Shape of Liquid Crystal Dimers: A View through the Lens of DFT. J. Mol. Liq. 2022, 354, 118858. [Google Scholar] [CrossRef]
- Panov, V.P.; Vij, J.K.; Mehl, G.H. Twist-Bend Nematic Phase in Cyanobiphenyls and Difluoroterphenyls Bimosogens. Liq. Cryst. 2017, 44, 147–159. [Google Scholar]
- Gray, G.W.; Hird, M.; Lacey, D.; Toyne, K.J. The Synthesis and Transition Temperatures of Some 4,4″-Dialkyl- and 4,4″-Alkoxyalkyl-1,1′:4′,1″-Terphenyls with 2,3- or 2′,3′-Difluoro Substituents and of Their Biphenyl Analogues. J. Chem. Soc. Perkin Trans. 1989, 2, 2041–2053. [Google Scholar] [CrossRef]
- Tamba, M.G.; Salili, S.M.; Zhang, C.; Jákli, A.; Mehl, G.H.; Stannarius, R.; Eremin, A. A Fibre Forming Smectic Twist–Bent Liquid Crystalline Phase. RSC Adv. 2015, 5, 11207–11211. [Google Scholar] [CrossRef]
- Sebastián, N.; Tamba, M.G.; Stannarius, R.; De La Fuente, M.R.; Salamonczyk, M.; Cukrov, G.; Gleeson, J.; Sprunt, S.; Jákli, A.; Welch, C.; et al. Mesophase Structure and Behaviour in Bulk and Restricted Geometry of a Dimeric Compound Exhibiting a Nematic–Nematic Transition. Phys. Chem. Chem. Phys. 2016, 18, 19299–19308. [Google Scholar] [CrossRef]
- Stevenson, W.D.; Zou, H.X.; Zeng, X.B.; Welch, C.; Ungar, G.; Mehl, G.H. Dynamic Calorimetry and XRD Studies of the Nematic and Twist-Bend Nematic Phase Transitions in a Series of Dimers with Increasing Spacer Length. Phys. Chem. Chem. Phys. 2018, 20, 25268–25274. [Google Scholar] [CrossRef]
- Panov, V.P.; Balachandran, R.; Vij, J.K.; Tamba, M.G.; Kohlmeier, A.; Mehl, G.H. Field-Induced Periodic Chiral Pattern in the Nx Phase of Achiral Bimesogens. Appl. Phys. Lett. 2012, 101, 234106. [Google Scholar] [CrossRef]
- Saha, R.; Feng, C.; Welch, C.; Mehl, G.H.; Feng, J.; Zhu, C.; Gleeson, J.; Sprunt, S.; Jákli, A. The Interplay between Spatial and Heliconical Orientational Order in Twist-Bend Nematic Materials. Phys. Chem. Chem. Phys. 2021, 23, 4055–4063. [Google Scholar] [CrossRef]
- Cukrov, G.; Mosaddeghian Golestani, Y.; Xiang, J.; Nastishin, Y.A.; Ahmed, Z.; Welch, C.; Mehl, G.H.; Lavrentovich, O.D. Comparative Analysis of Anisotropic Material Properties of Uniaxial Nematics Formed by Flexible Dimers and Rod-like Monomers. Liq. Cryst. 2016, 44, 219–231. [Google Scholar] [CrossRef]
- Parsouzi, Z.; Babakhanova, G.; Rajabi, M.; Saha, R.; Gyawali, P.; Turiv, T.; Wang, H.; Baldwin, A.R.; Welch, C.; Mehl, G.H.; et al. Pretransitional Behavior of Viscoelastic Parameters at the Nematic to Twist-Bend Nematic Phase Transition in Flexible n-Mers. Phys. Chem. Chem. Phys. 2019, 21, 13078–13089. [Google Scholar] [CrossRef] [PubMed]
- Babakhanova, G.; Wang, H.; Rajabi, M.; Li, D.; Li, Q.; Lavrentovich, O.D. Elastic and Electro-Optical Properties of Flexible Fluorinated Dimers with Negative Dielectric Anisotropy. Liq. Cryst. 2022, 49, 982–994. [Google Scholar] [CrossRef]
- Emsley, J.W.; Lelli, M.; Joy, H.; Tamba, M.G.; Mehl, G.H. Similarities and Differences between Molecular Order in the Nematic and Twist-Bend Nematic Phases of a Symmetric Liquid Crystal Dimer. Phys. Chem. Chem. Phys. 2016, 18, 9419–9430. [Google Scholar] [CrossRef]
- Merkel, K.; Loska, B.; Welch, C.; Mehl, G.H.; Kocot, A. The Role of Intermolecular Interactions in Stabilizing the Structure of the Nematic Twist-Bend Phase. RSC Adv. 2021, 11, 2917–2925. [Google Scholar] [CrossRef]
- Merkel, K.; Loska, B.; Welch, C.; Mehl, G.H.; Kocot, A. Molecular Biaxiality Determines the Helical Structure—Infrared Measurements of the Molecular Order in the Nematic Twist-Bend Phase of Difluoro Terphenyl Dimer. Phys. Chem. Chem. Phys. 2021, 23, 4151–4160. [Google Scholar] [CrossRef]
- Stevenson, W.D.; Zeng, X.; Welch, C.; Thakur, A.K.; Ungar, G.; Mehl, G.H. Macroscopic Chirality of Twist-Bend Nematic Phase in Bent Dimers Confirmed by Circular Dichroism. J. Mater. Chem. C 2020, 8, 1041–1047. [Google Scholar] [CrossRef]
- Saha, R.; Babakhanova, G.; Parsouzi, Z.; Rajabi, M.; Gyawali, P.; Welch, C.; Mehl, G.H.; Gleeson, J.; Lavrentovich, O.D.; Sprunt, S.; et al. Oligomeric Odd–Even Effect in Liquid Crystals. Mater. Horiz. 2019, 6, 1905–1912. [Google Scholar] [CrossRef]
- Ahmed, Z.; Welch, C.; Mehl, G.H. The Design and Investigation of the Self-Assembly of Dimers with Two Nematic Phases. RSC Adv. 2015, 5, 93513–93521. [Google Scholar] [CrossRef]
- Ramou, E. Investigation of the Mesomorphic Behaviour of Liquid Crystalline Oligomers and Binary Systems that Exhibit Two Nematic Phases. Ph.D. Thesis, University of Patras, Patras, Greece, 2018. [Google Scholar]
- Mandle, R.J. A Ten-Year Perspective on Twist-Bend Nematic Materials. Molecules 2022, 27, 2689. [Google Scholar] [CrossRef]
- Tuchband, M.R.; Paterson, D.A.; Salamończyk, M.; Norman, V.A.; Scarbrough, A.N.; Forsyth, E.; Garcia, E.; Wang, C.; Storey, J.M.D.; Walba, D.M.; et al. Distinct Differences in the Nanoscale Behaviors of the Twist–Bend Liquid Crystal Phase of a Flexible Linear Trimer and Homologous Dimer. Proc. Natl. Acad. Sci. USA 2019, 166, 10698–10704. [Google Scholar] [CrossRef]
- Zavvou, E.E.; Ramou, E.; Ahmed, Z.; Welch, C.; Mehl, G.H.; Vanakaras, A.G.; Karahaliou, P.K. Dipole–Dipole Correlations in the Nematic Phases of Symmetric Cyanobiphenyl Dimers and Their Binary Mixtures with 5CB. Soft Matter 2023, 19, 9224–9238. [Google Scholar] [CrossRef]
- Urban, S.; Kula, P.; Spadło, A.; Geppi, M.; Marini, A. Dielectric Properties of Selected Laterally Fluoro-Substituted 4,4′′-Dialkyl, Dialkoxy and Alkyl-Alkoxy [1:1′;4′:1′′]Terphenyls. Liq. Cryst. 2010, 37, 1321–1330. [Google Scholar] [CrossRef]
- Clark, M.G.; Raynes, E.P.; Smith, R.A.; Tough, R.J.A. Measurement of the Permittivity of Nematic Liquid Crystals in Magnetic and Electric Fields Using Extrapolation Procedures. J. Phys. Appl. Phys. 1980, 13, 2151. [Google Scholar] [CrossRef]
- Haller, I. Thermodynamic and Static Properties of Liquid Crystals. Prog. Solid State Chem. 1975, 10, 103–118. [Google Scholar] [CrossRef]
- Pociecha, D.; Crawford, C.A.; Paterson, D.A.; Storey, J.M.D.; Imrie, C.T.; Vaupotič, N.; Gorecka, E. Critical Behavior of the Optical Birefringence at the Nematic to Twist-Bend Nematic Phase Transition. Phys. Rev. E 2018, 98, 052706. [Google Scholar] [CrossRef]
- Majewska, M.M.; Forsyth, E.; Pociecha, D.; Wang, C.; Storey, J.M.D.; Imrie, C.T.; Gorecka, E. Controlling Spontaneous Chirality in Achiral Materials: Liquid Crystal Oligomers and the Heliconical Twist-Bend Nematic Phase. Chem. Commun. 2022, 58, 5285–5288. [Google Scholar] [CrossRef]
- Meyer, C.; Luckhurst, G.R.; Dozov, I. The Temperature Dependence of the Heliconical Tilt Angle in the Twist-Bend Nematic Phase of the Odd Dimer CB7CB. J. Mater. Chem. C 2014, 3, 318–328. [Google Scholar] [CrossRef]
- Gil-Villegas, A.; McGrother, S.C.; Jackson, G. Chain and Ring Structures in Smectic Phases of Molecules with Transverse Dipoles. Chem. Phys. Lett. 1997, 269, 441–447. [Google Scholar] [CrossRef]
- Berardi, R.; Orlandi, S.; Zannoni, C. Monte Carlo Simulations of Rod-like Gay–Berne Mesogens with Transverse Dipoles. Int. J. Mod. Phys. C 1999, 10, 477–484. [Google Scholar] [CrossRef]
- Mcdonnell, D.G.; Raynes, E.P.; Smith, R.A. The Physical Properties of Fluorine Derivatives of 4-Cyanobiphenyls. Mol. Cryst. Liq. Cryst. 1985, 123, 169–177. [Google Scholar] [CrossRef]
- McDonnell, D.G.; Raynes, E.P.; Smith, R.A. Dipole Moments and Dielectric Properties of Fluorine Substituted Nematic Liquid Crystals. Liq. Cryst. 1989, 6, 515–523. [Google Scholar] [CrossRef]
- Toriyama, K.; Dunmur, D.A.; Hunt, S.E. Transverse Dipole Association and Negative Dielectric Anisotropy of Nematic Liquid Crystals. Liq. Cryst. 1989, 5, 1001–1009. [Google Scholar] [CrossRef]
- Sebastián, N.; Robles-Hernández, B.; Diez-Berart, S.; Salud, J.; Luckhurst, G.R.; Dunmur, D.A.; López, D.O.; de la Fuente, M.R. Distinctive Dielectric Properties of Nematic Liquid Crystal Dimers. Liq. Cryst. 2016, 44, 177–190. [Google Scholar] [CrossRef]
- Heist, L.M.; Samulski, E.T.; Welch, C.; Ahmed, Z.; Mehl, G.H.; Vanakaras, A.G.; Photinos, D.J. Probing Molecular Ordering in the Nematic Phases of Para-Linked Bimesogen Dimers through NMR Studies of Flexible Prochiral Solutes. Liq. Cryst. 2020, 47, 2058–2073. [Google Scholar] [CrossRef]

| Compound | ||||||
|---|---|---|---|---|---|---|
| Monomer | 0.3480 | 0.189 | -- | -- | 393.84 | -- |
| Dimer | 0.2843 | 0.173 | 0.748 | 0.1905 | 440.27 | 400.91 |
| Trimer | 0.2841 | 0.161 | 0.590 | 0.1252 | 466.10 | 426.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavvou, E.E.; Welch, C.; Mehl, G.H.; Vanakaras, A.G.; Karahaliou, P.K. Comparative Study of the Optical and Dielectric Anisotropy of a Difluoroterphenyl Dimer and Trimer Forming Two Nematic Phases. Materials 2024, 17, 2555. https://doi.org/10.3390/ma17112555
Zavvou EE, Welch C, Mehl GH, Vanakaras AG, Karahaliou PK. Comparative Study of the Optical and Dielectric Anisotropy of a Difluoroterphenyl Dimer and Trimer Forming Two Nematic Phases. Materials. 2024; 17(11):2555. https://doi.org/10.3390/ma17112555
Chicago/Turabian StyleZavvou, Evangelia E., Chris Welch, Georg H. Mehl, Alexandros G. Vanakaras, and Panagiota K. Karahaliou. 2024. "Comparative Study of the Optical and Dielectric Anisotropy of a Difluoroterphenyl Dimer and Trimer Forming Two Nematic Phases" Materials 17, no. 11: 2555. https://doi.org/10.3390/ma17112555
APA StyleZavvou, E. E., Welch, C., Mehl, G. H., Vanakaras, A. G., & Karahaliou, P. K. (2024). Comparative Study of the Optical and Dielectric Anisotropy of a Difluoroterphenyl Dimer and Trimer Forming Two Nematic Phases. Materials, 17(11), 2555. https://doi.org/10.3390/ma17112555








