Failure Analysis for Overall Overturning of Concrete Single-Column Pier Bridges Induced by Temperature and Overloaded Vehicles
Abstract
1. Introduction
2. Numerical Analysis of the Overturning Process
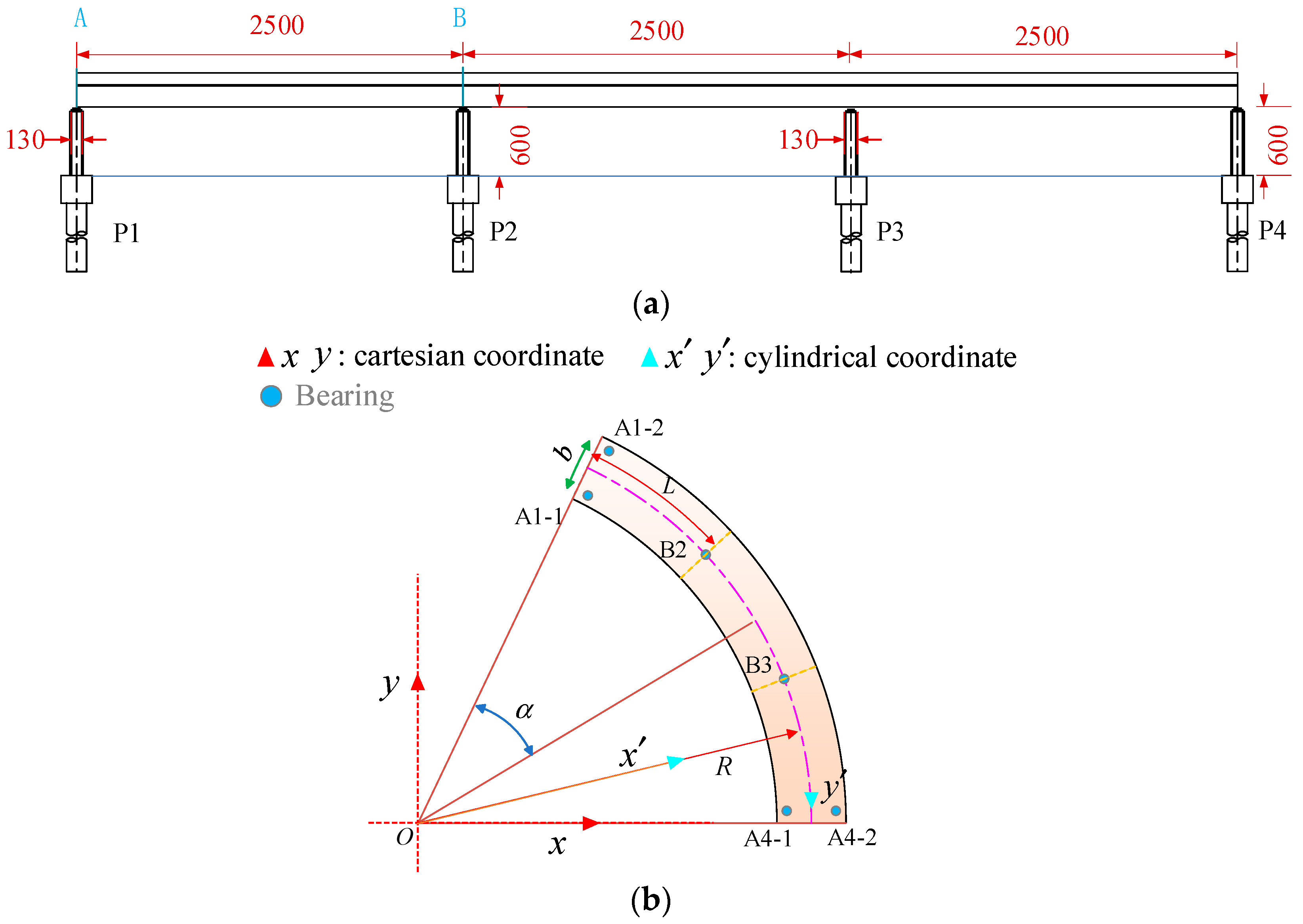
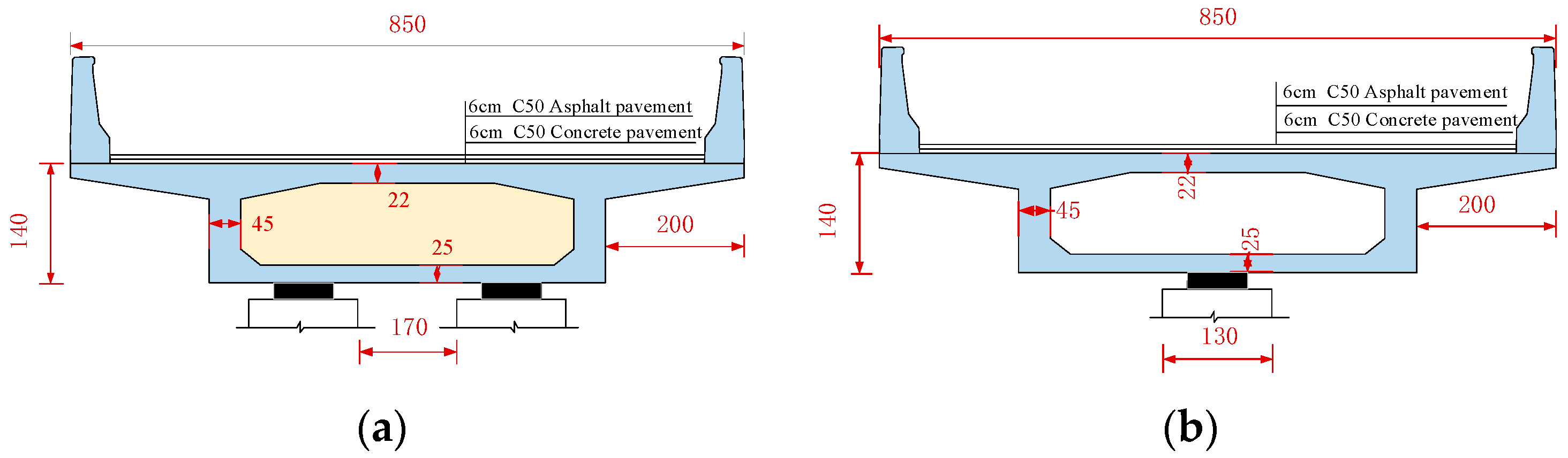
2.1. Prototype Bridge
2.2. Material Parameters
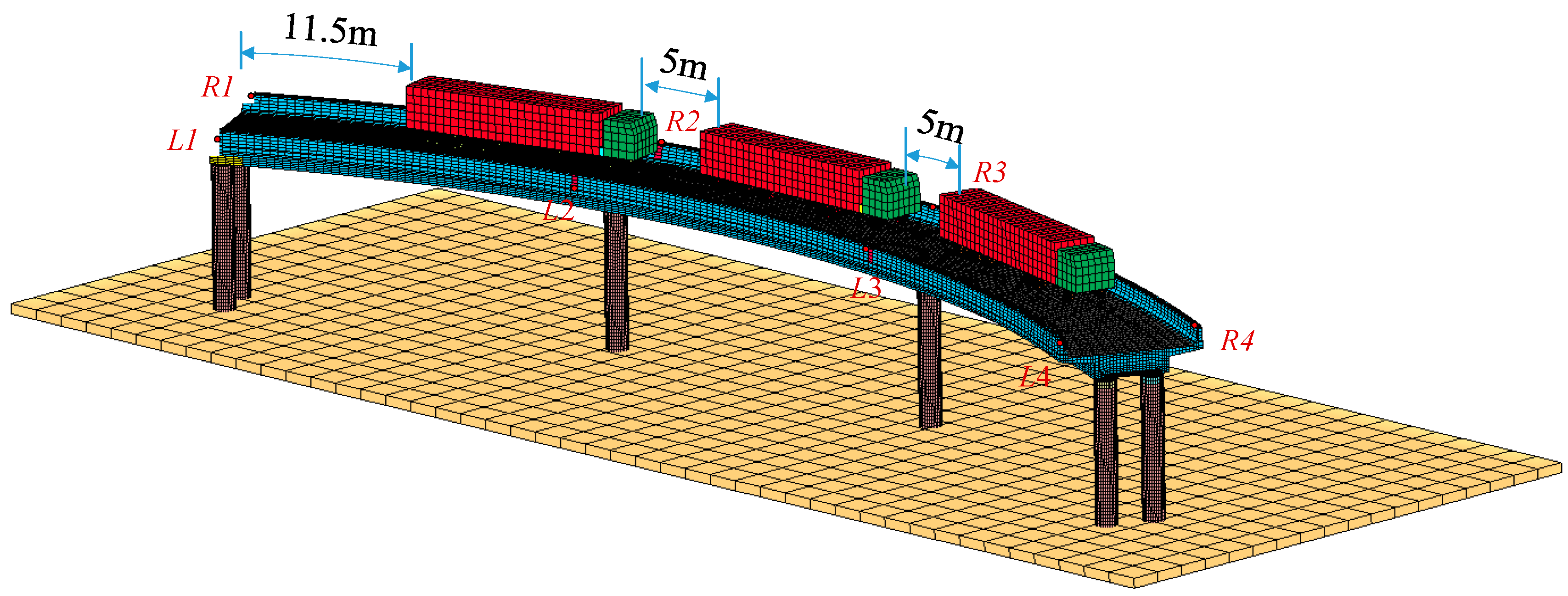
2.3. Load Setting
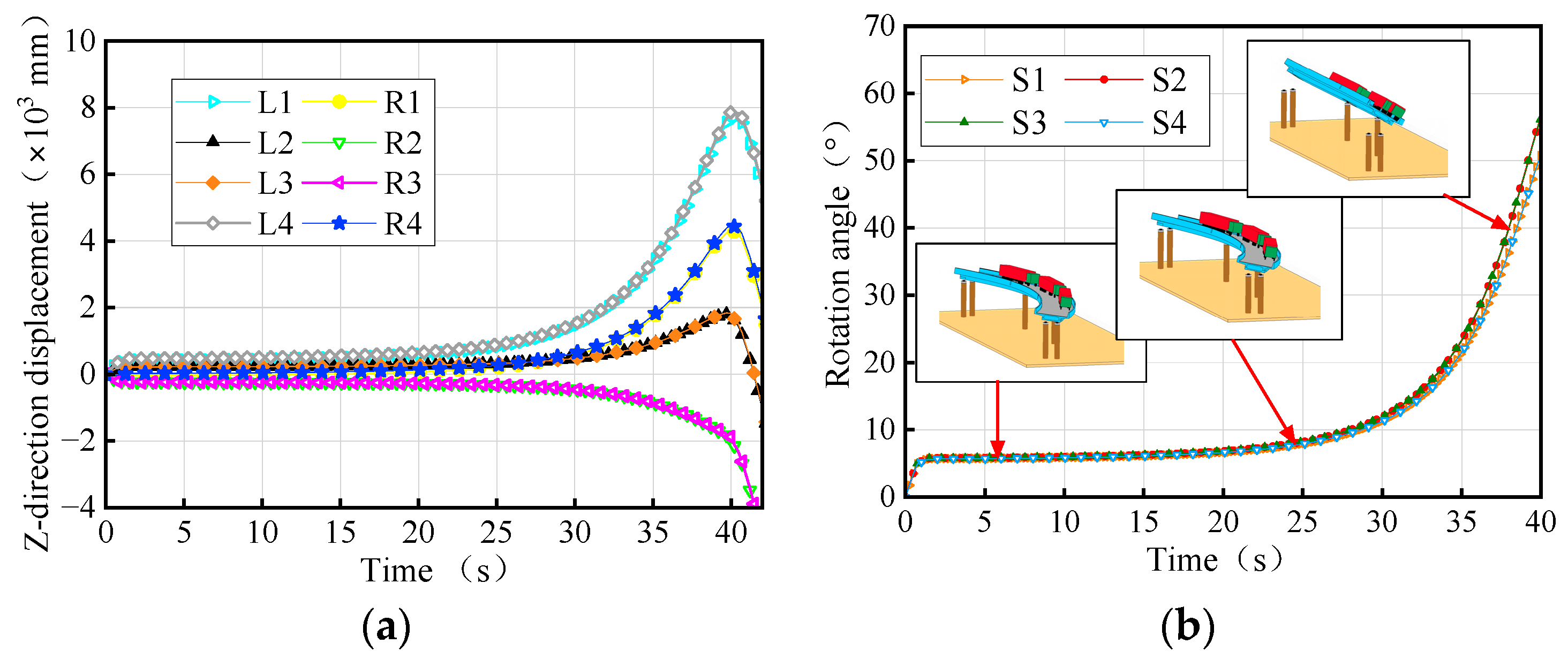
2.4. Overturning Process and Failure Characteristics
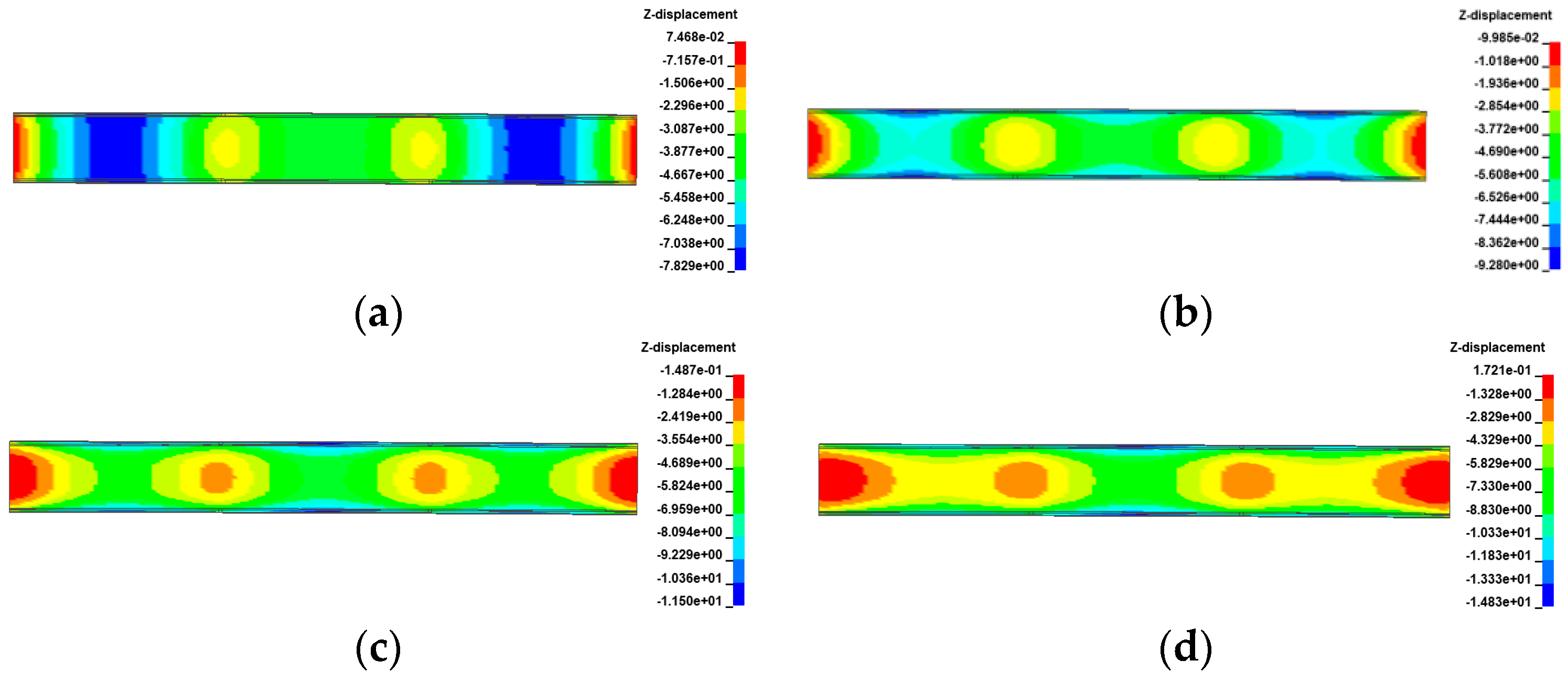
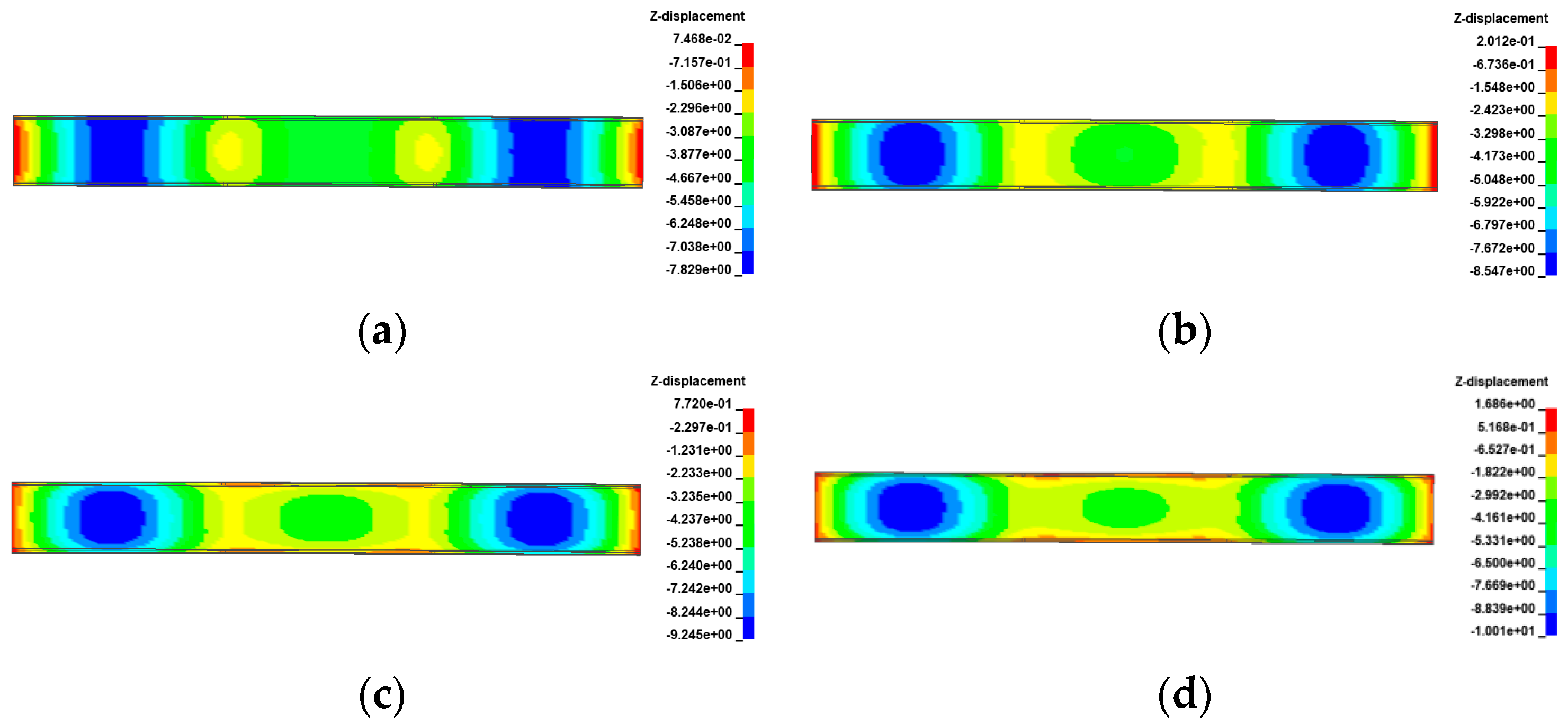
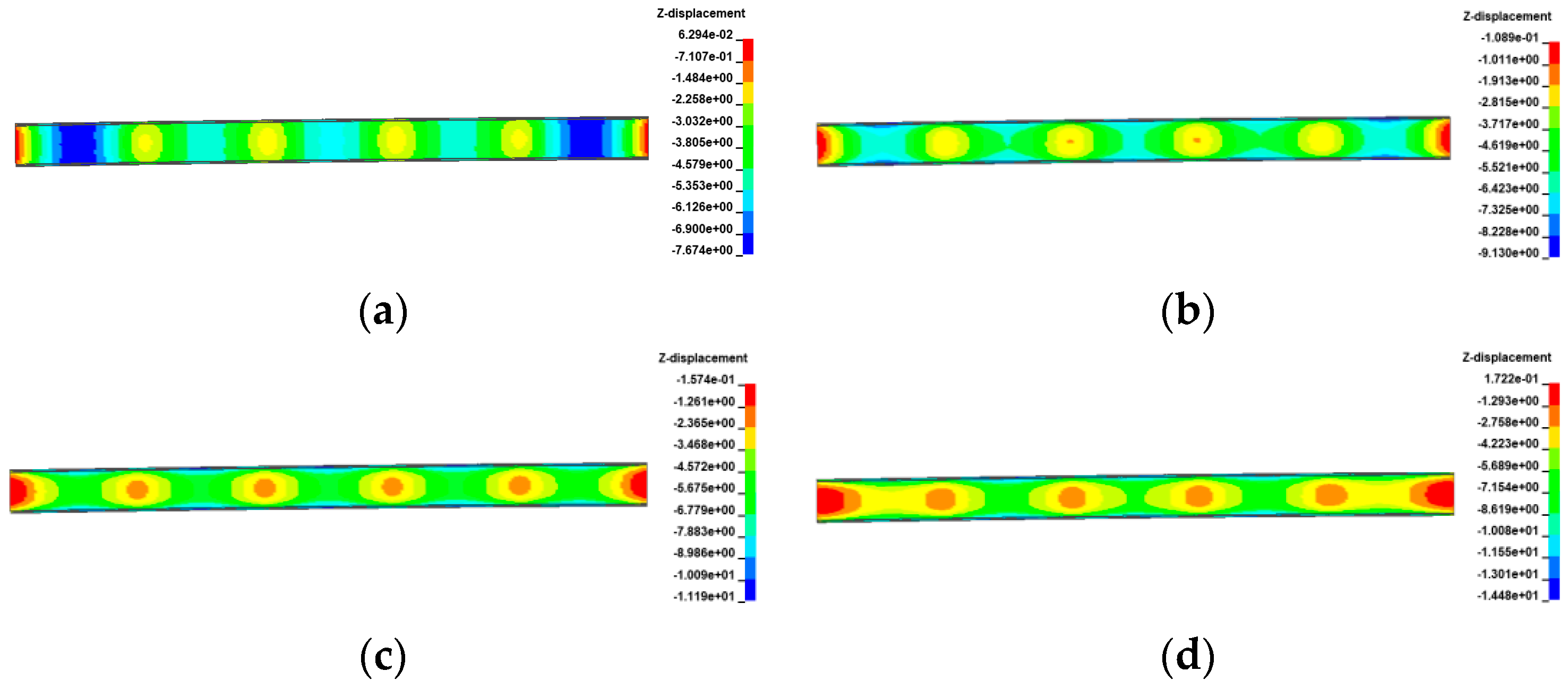
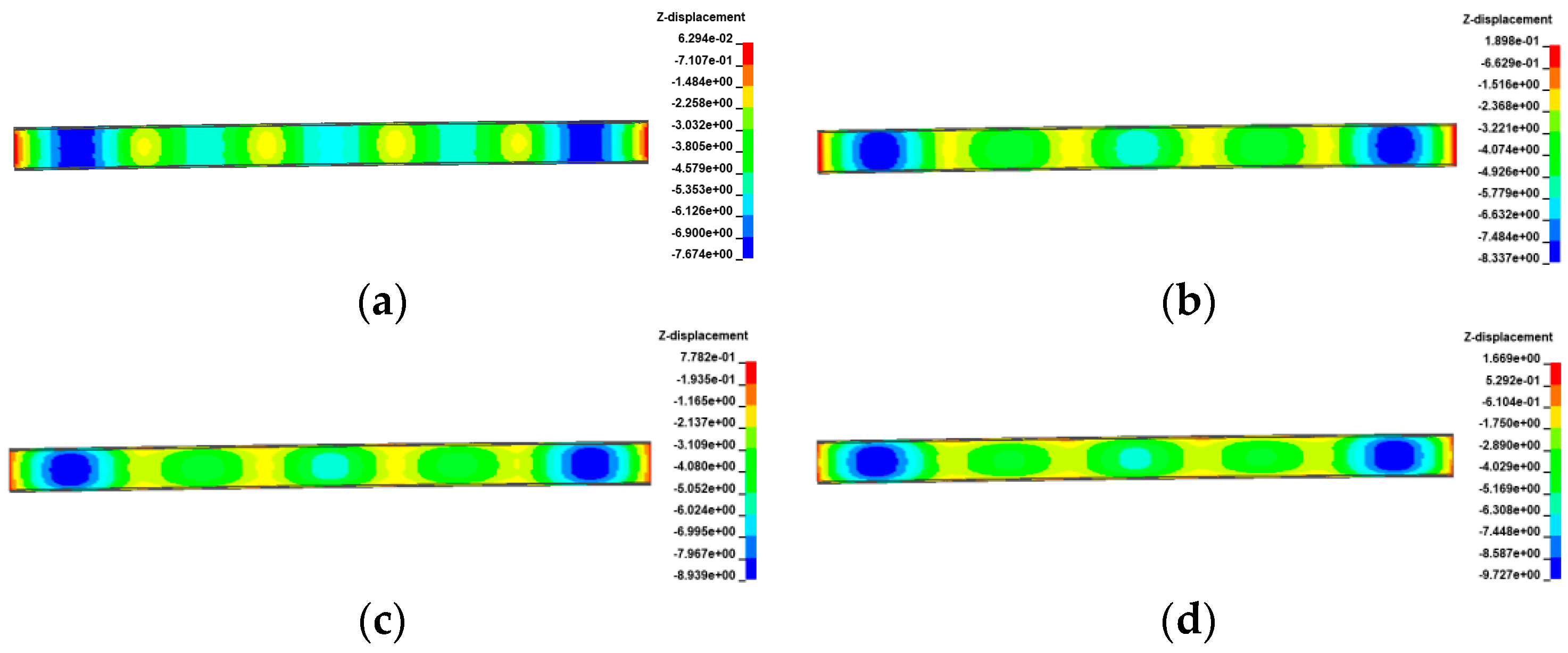
3. Overturning Effects of Bridge in Temperature Field
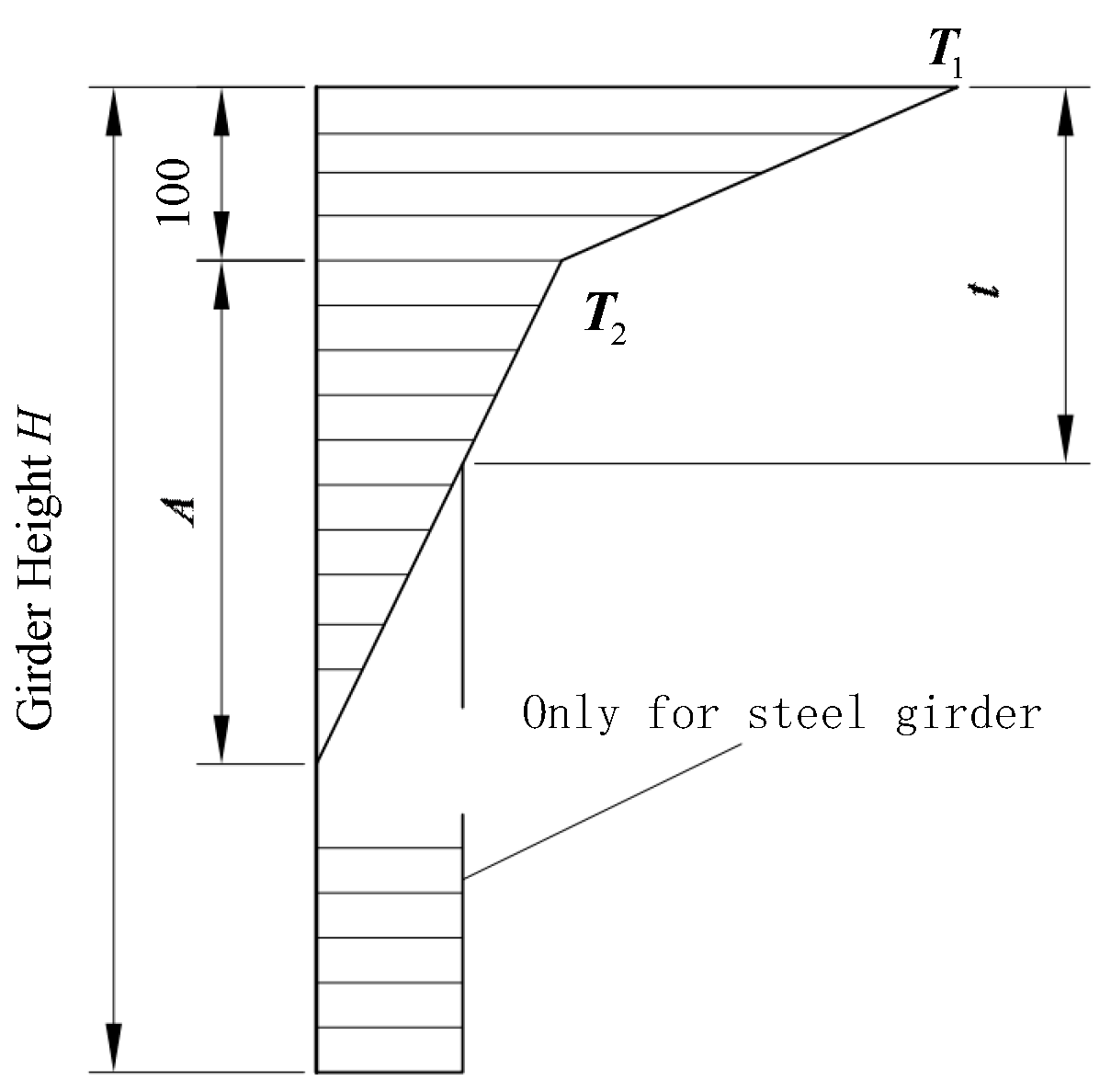
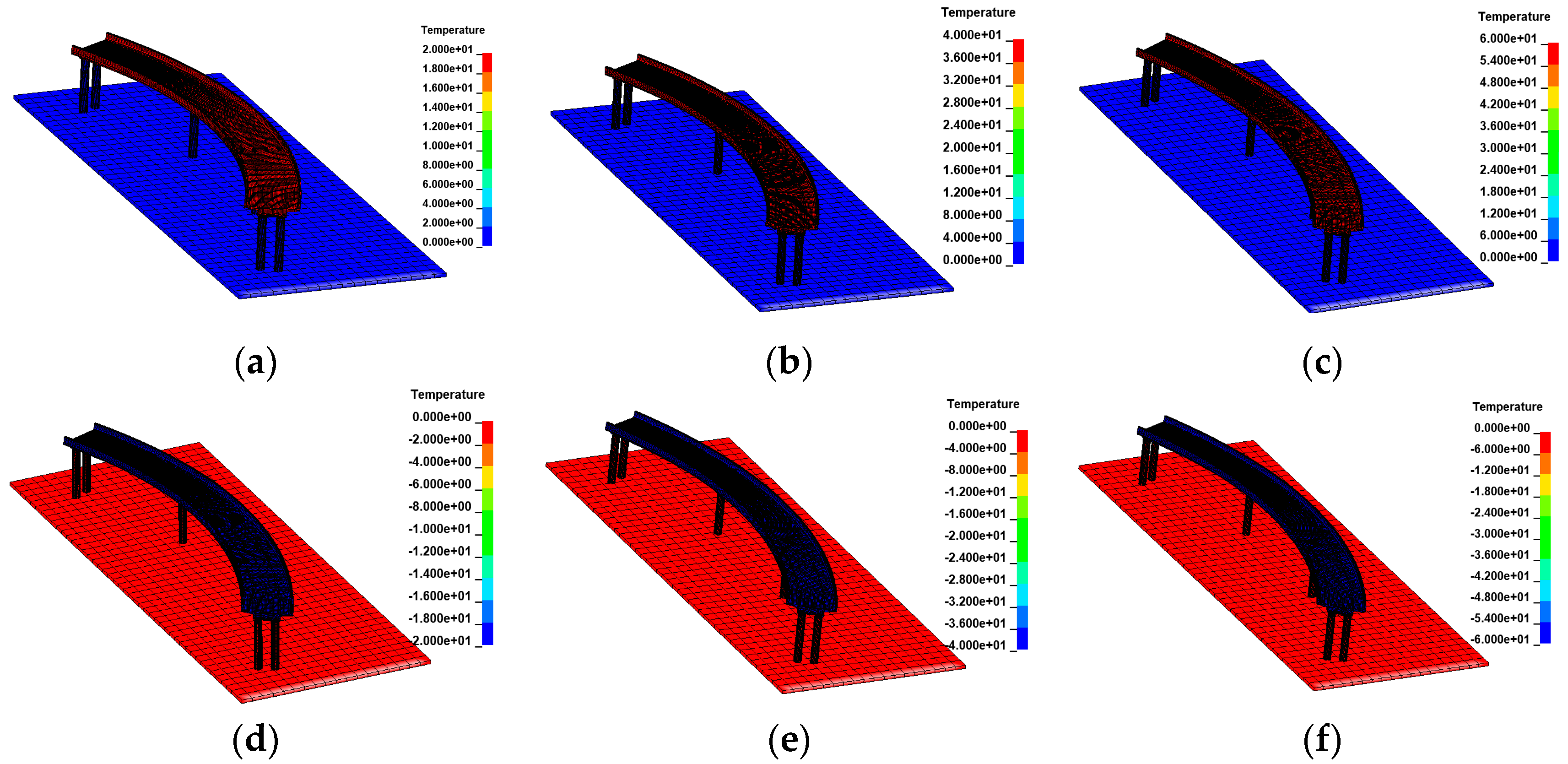
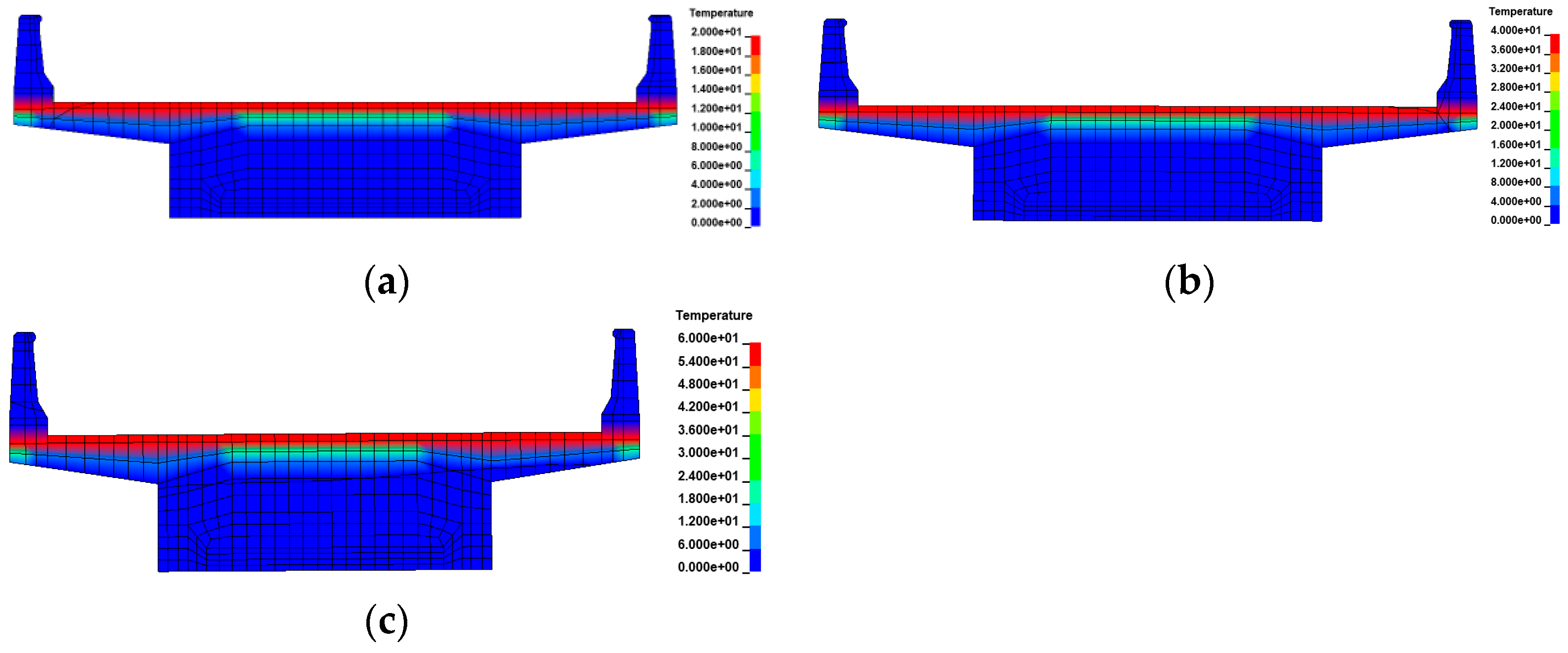
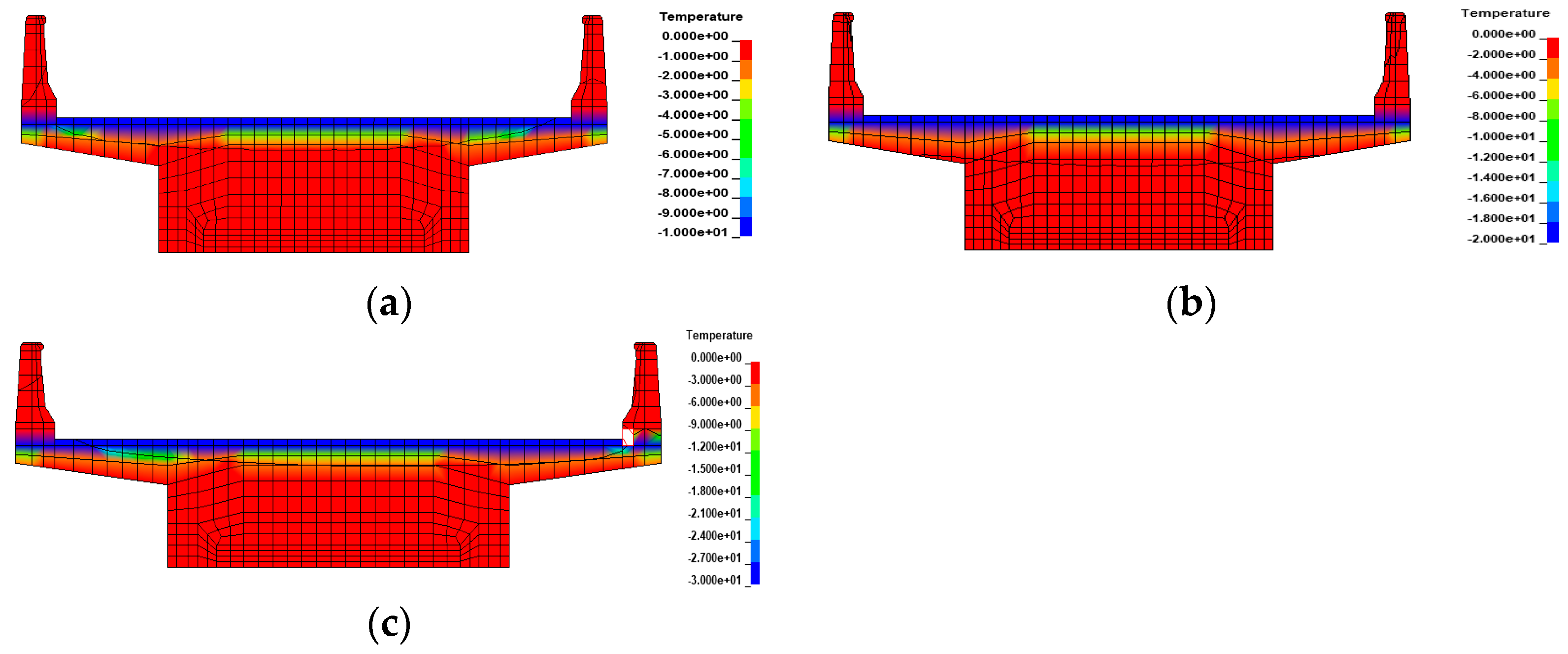
3.1. Temperature Model
3.2. Uniform Temperature Effects
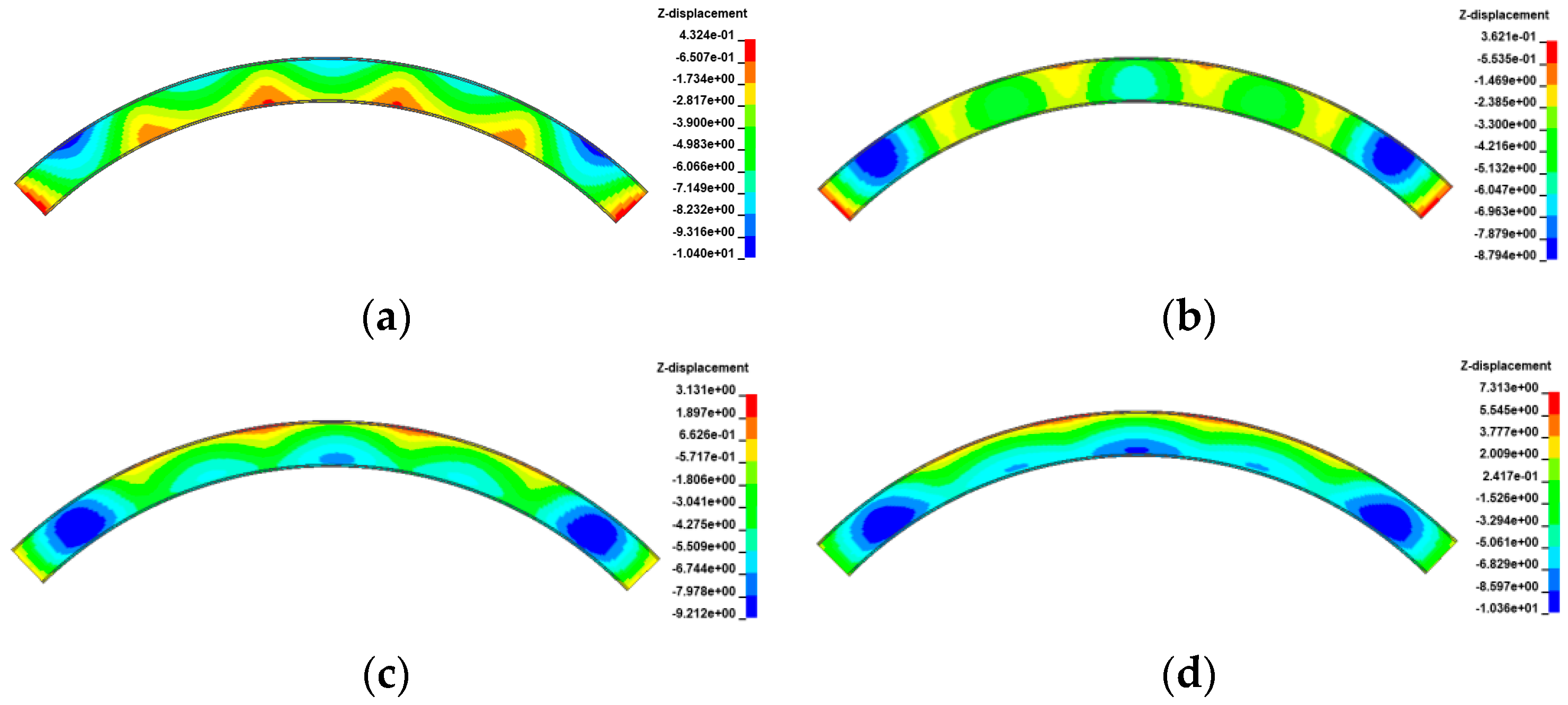
3.3. Gradient Temperature Effects
4. Overturning Mechanism of Bridges Induced by Gradient Temperatures
4.1. Overturning Mechanism for Curved Bridges
4.2. Overturning Mechanism for Straight Bridges
5. Conclusions
- (1)
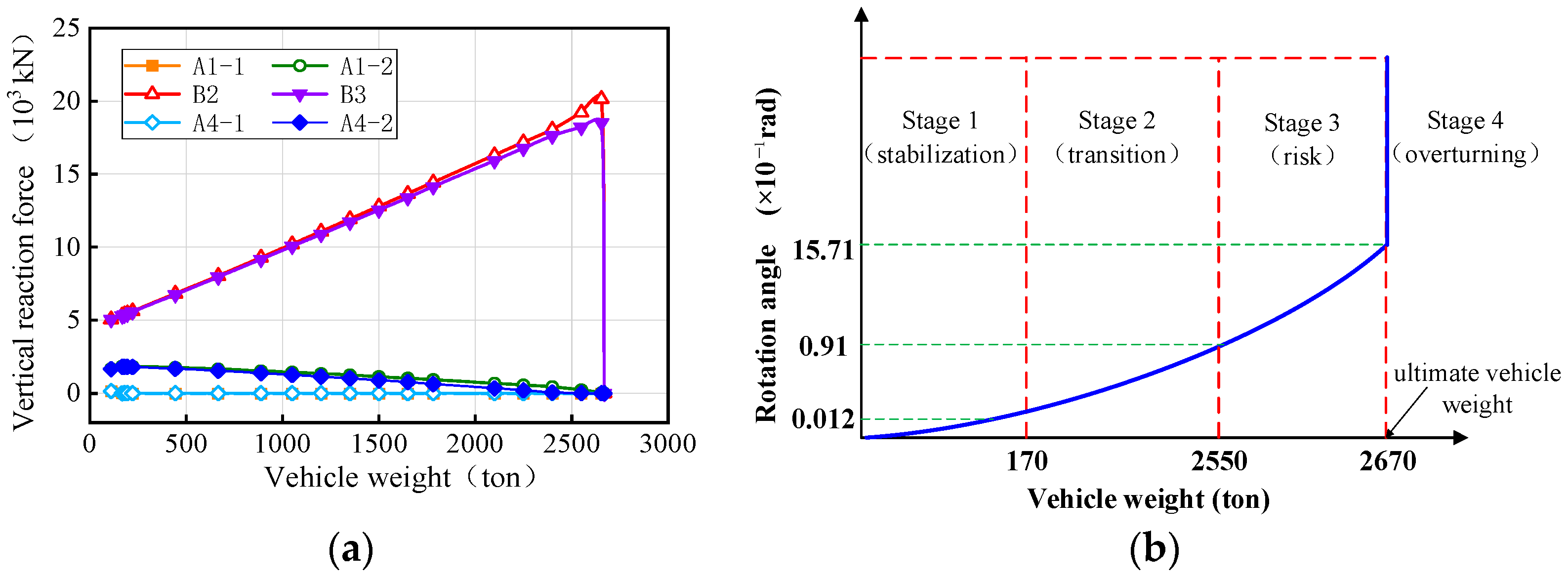
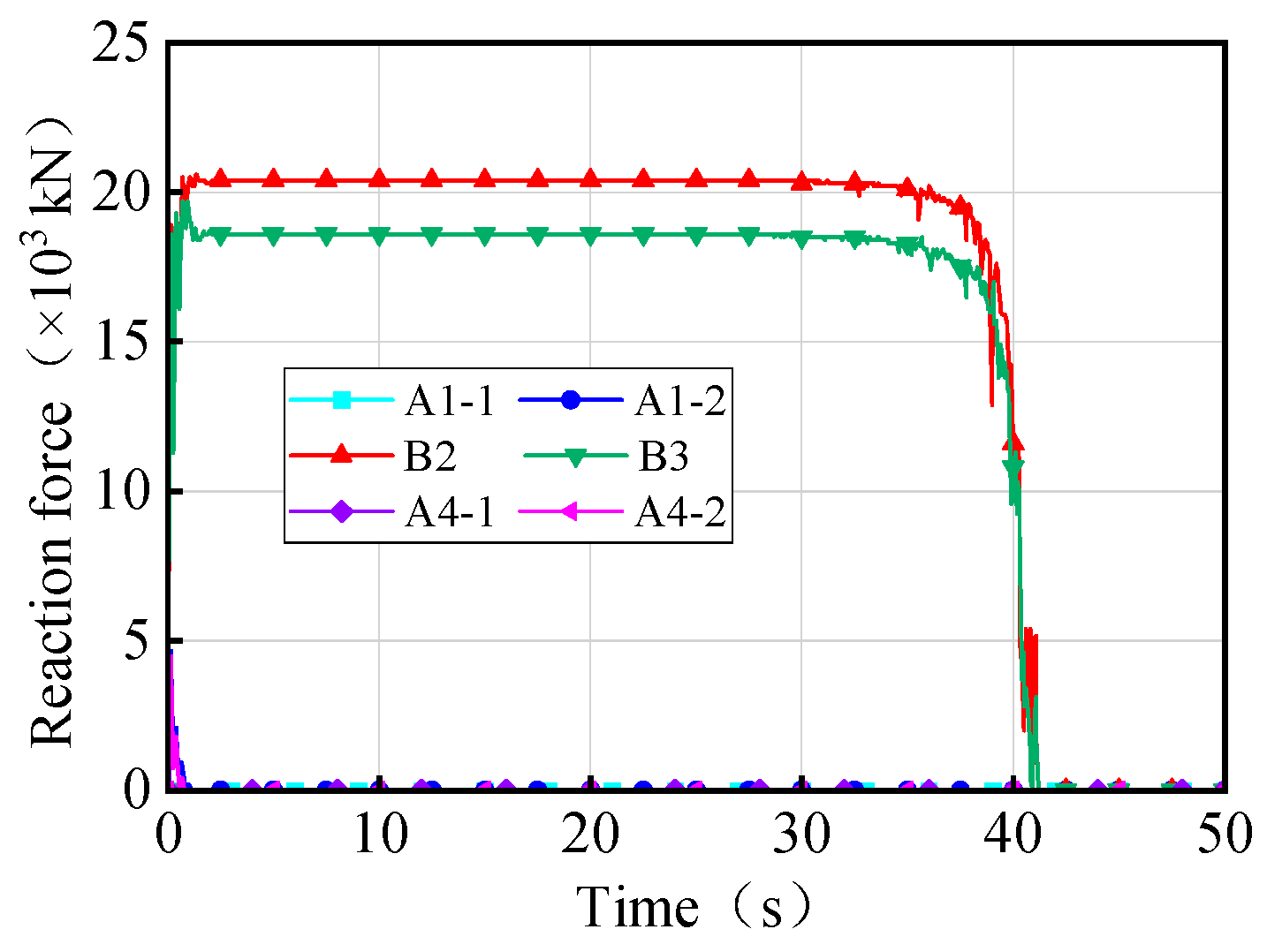
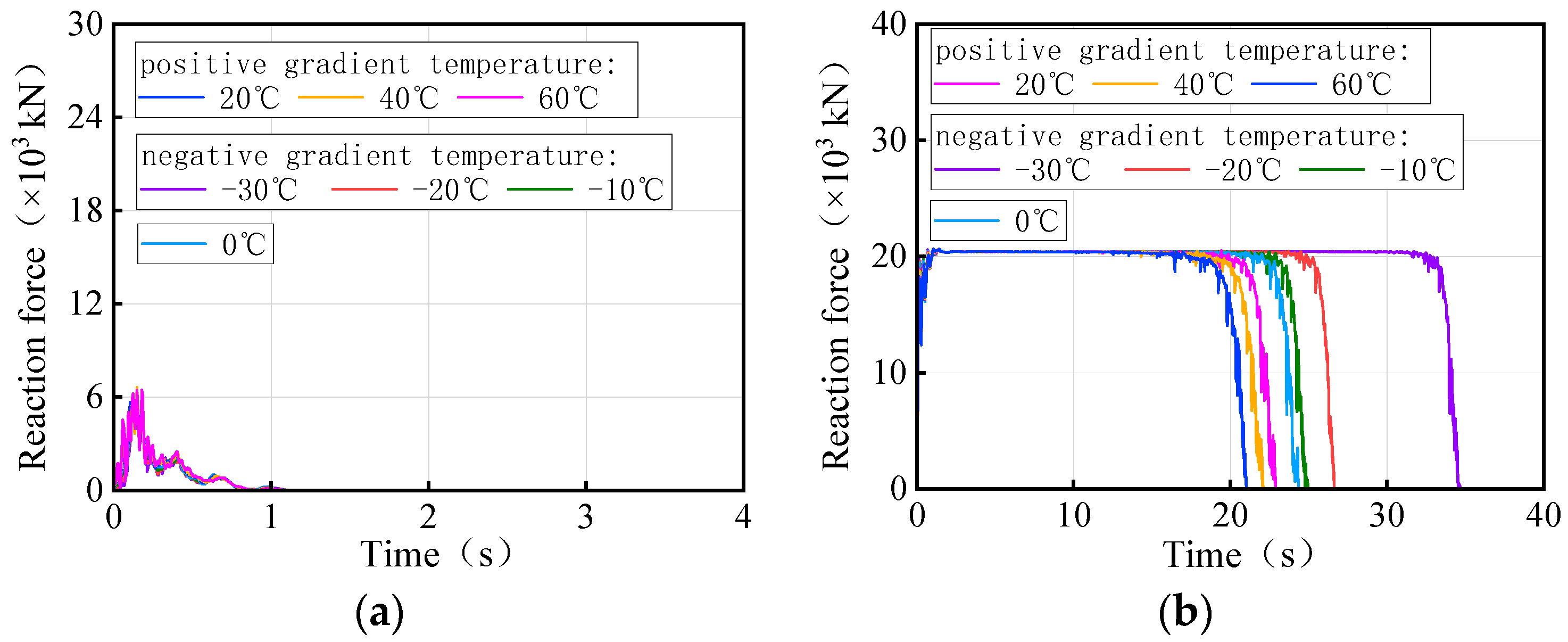
- For the 3 × 25 m curved single-column pier bridge, the rotation angles of all girder sections are similar, with a maximum difference of 6°. During girder overturning, failed bearings initiate from the inner curvature or non-overturning side and progress towards the overturning side, leading to evolving support conditions for the bridge. The overall overturning collapse process of bridges can be divided into four stages: stabilization stage, transition stage, risk stage, and overturning stage. The state corresponding to the two-bearing support of the bridge can be used as a failure criterion to assess the limit state of the bridge’s overall overturning.
- (2)
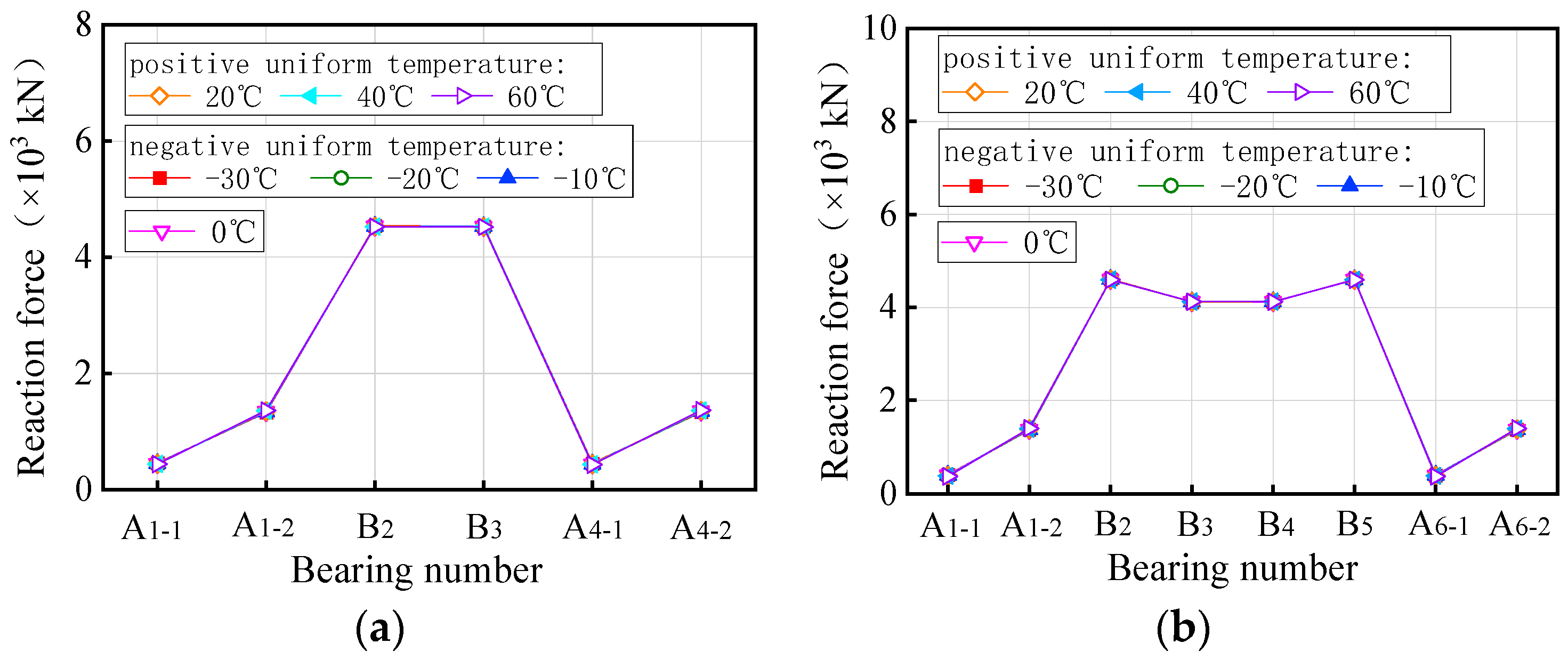
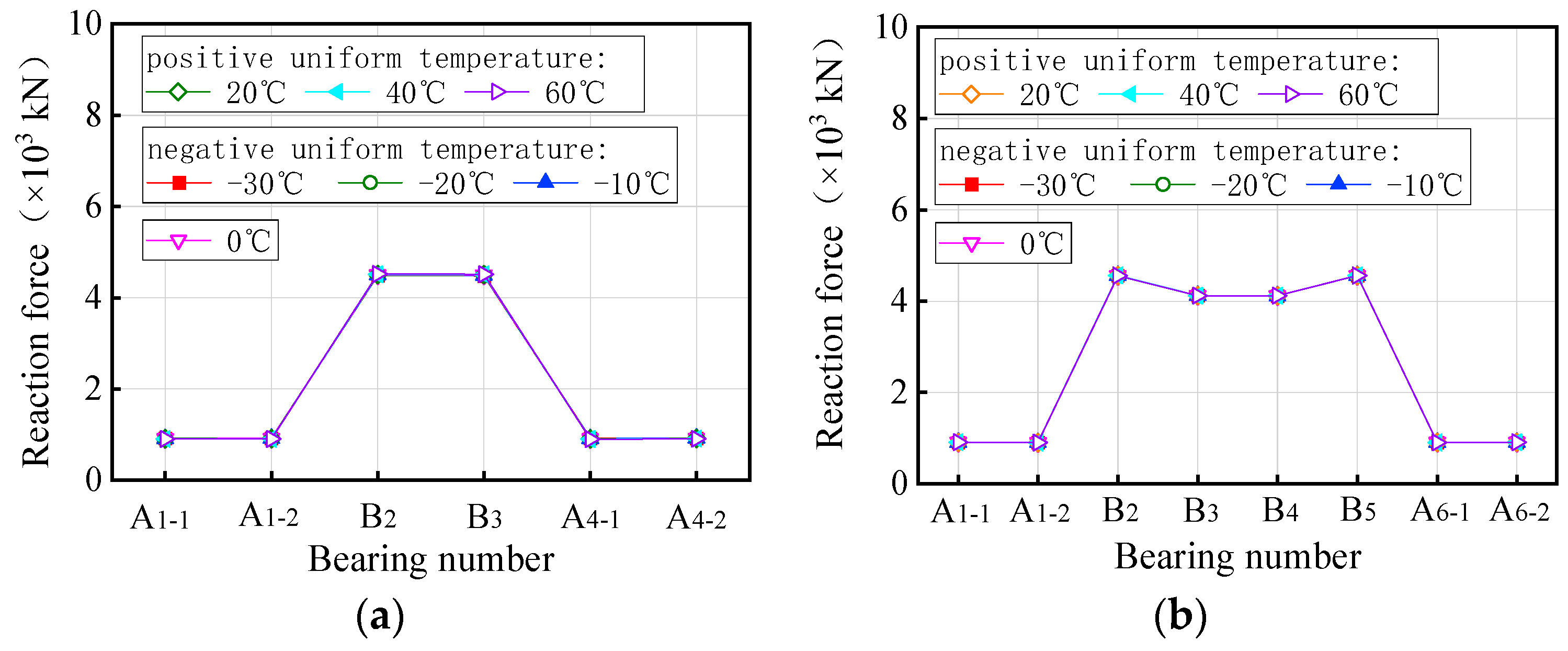
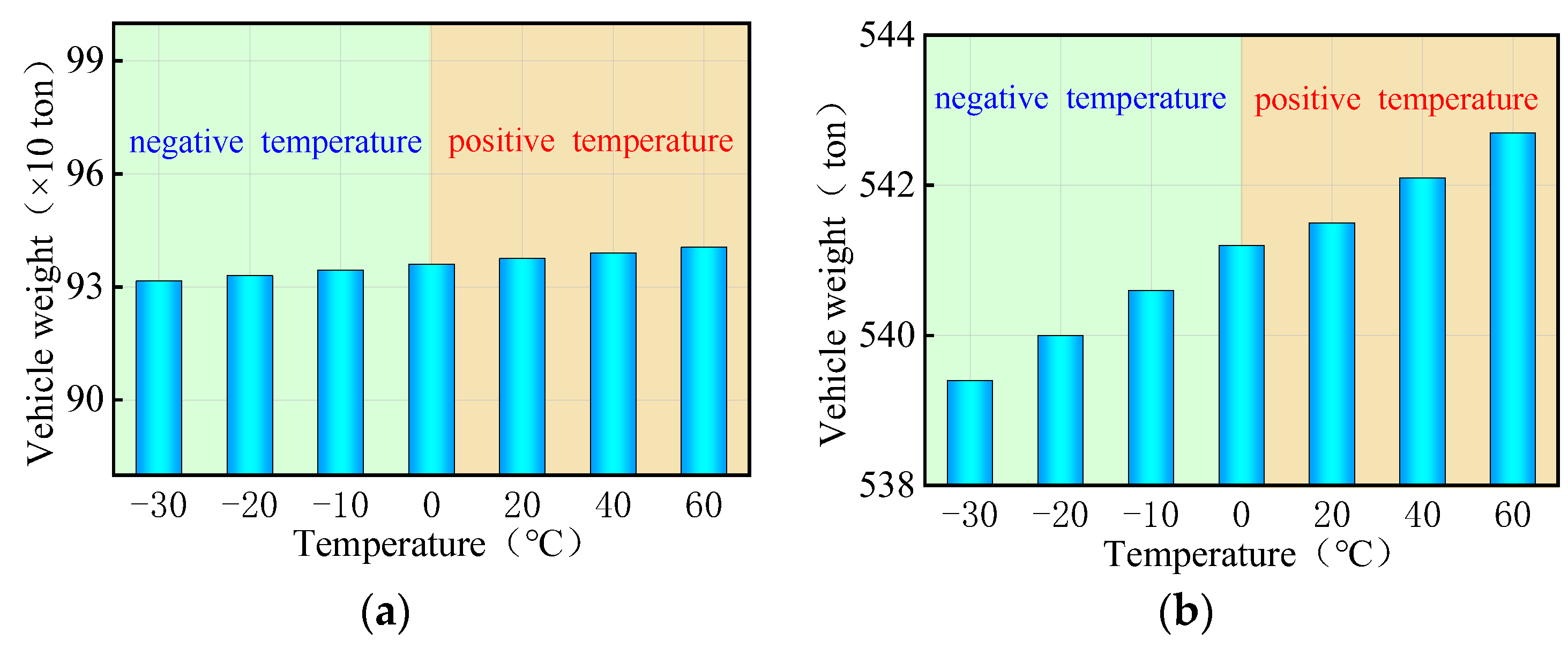
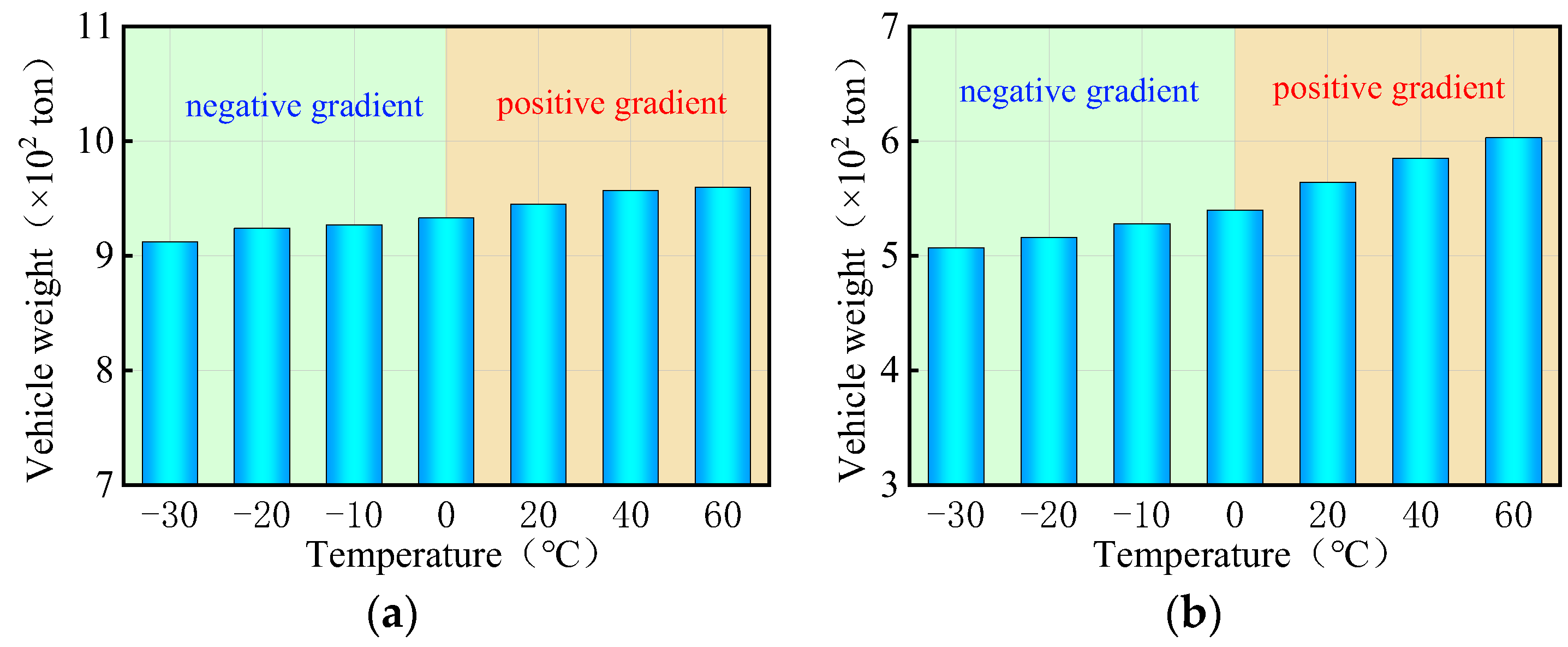
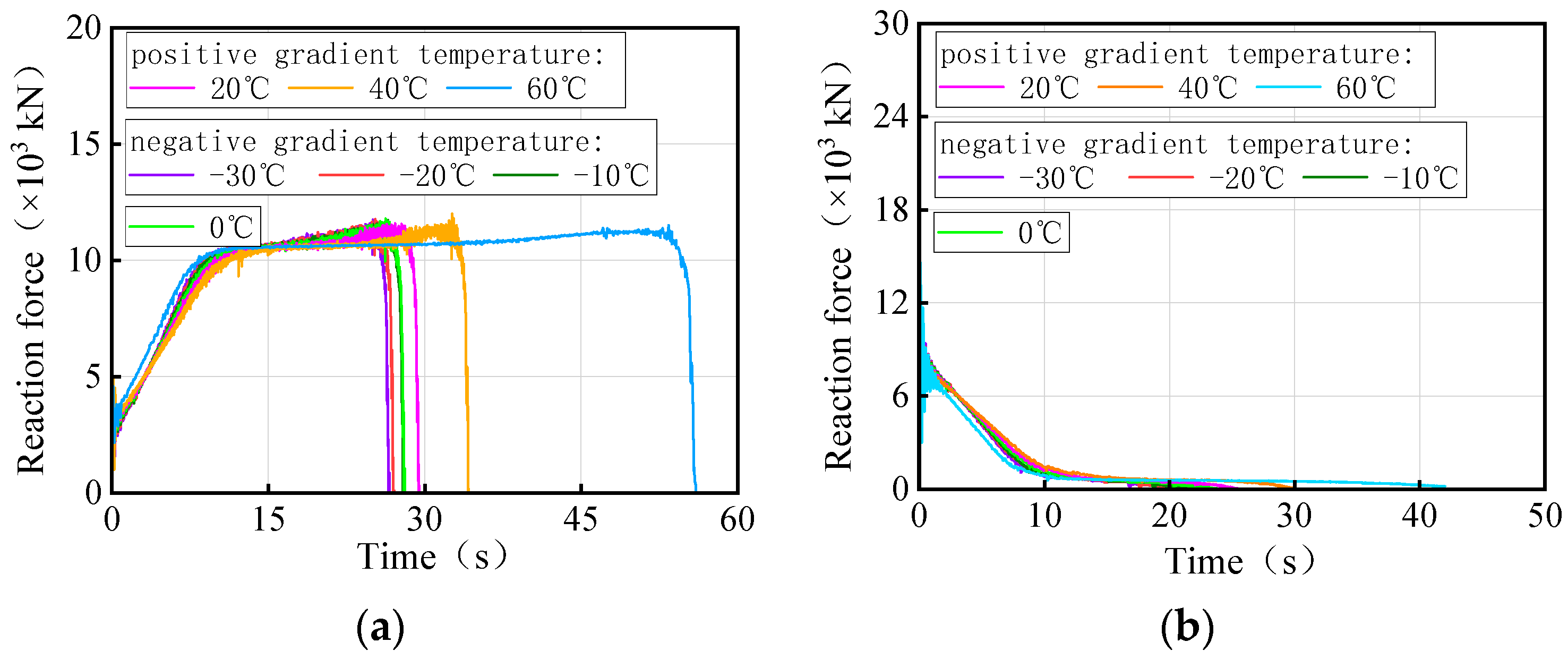
- As the uniform temperature fluctuates from −30 °C to 60 °C, the ultimate vehicle weights for the overall overturning of the 3 × 25 m and 5 × 25 m curved bridges gradually decrease by 0.1% to 0.7%. Conversely, the results for the straight bridges of the same dimensions showed an opposite trend, with an increase of 0.1% to 0.7% in ultimate vehicle weights. The effect of uniform temperatures on the ultimate vehicle weights of the bridges was found to be minimal, with changes of less than 1%, and can be considered negligible.
- (3)
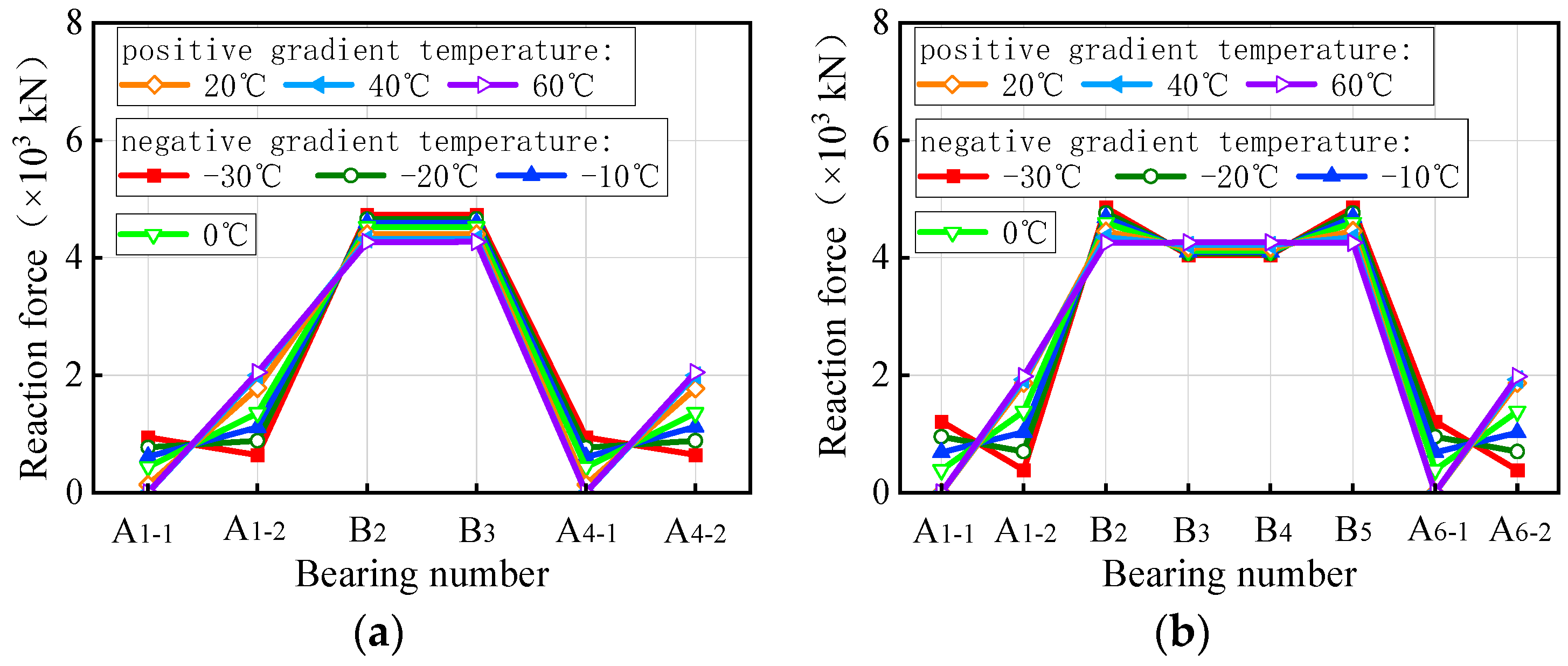
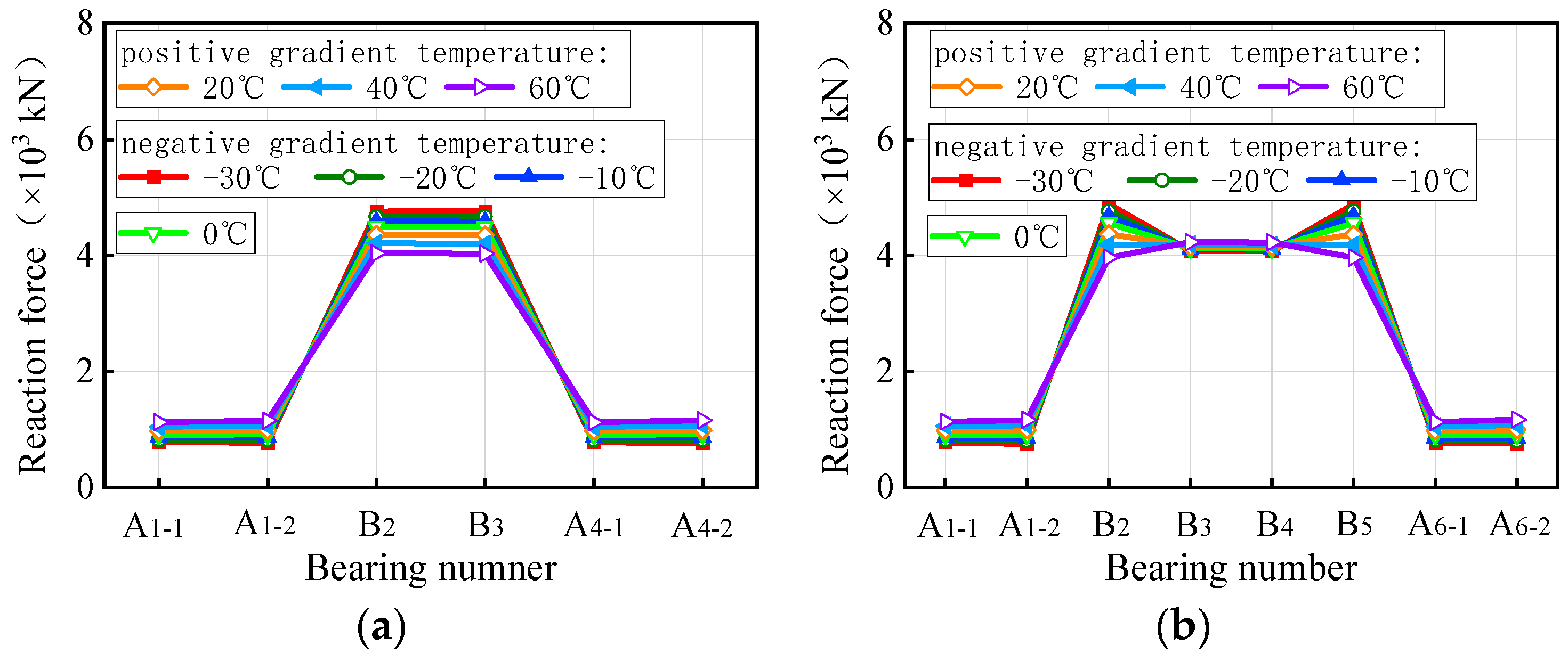
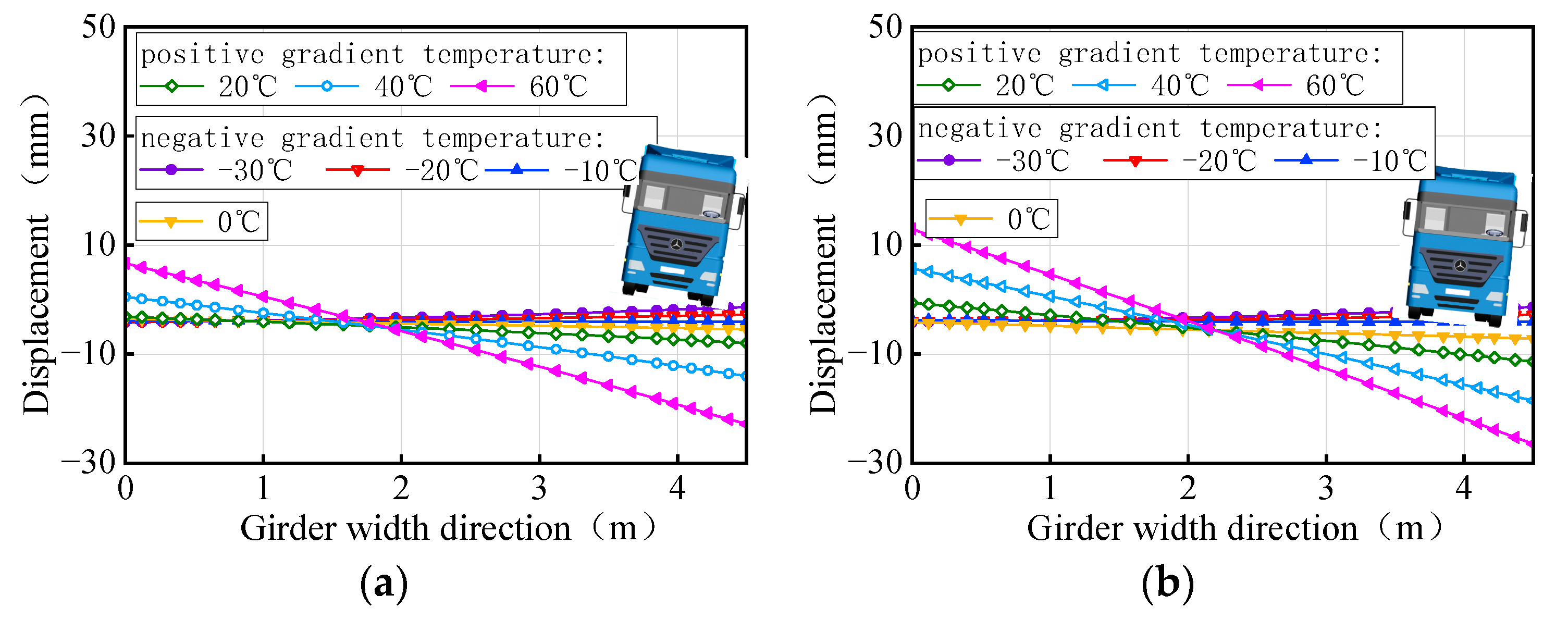
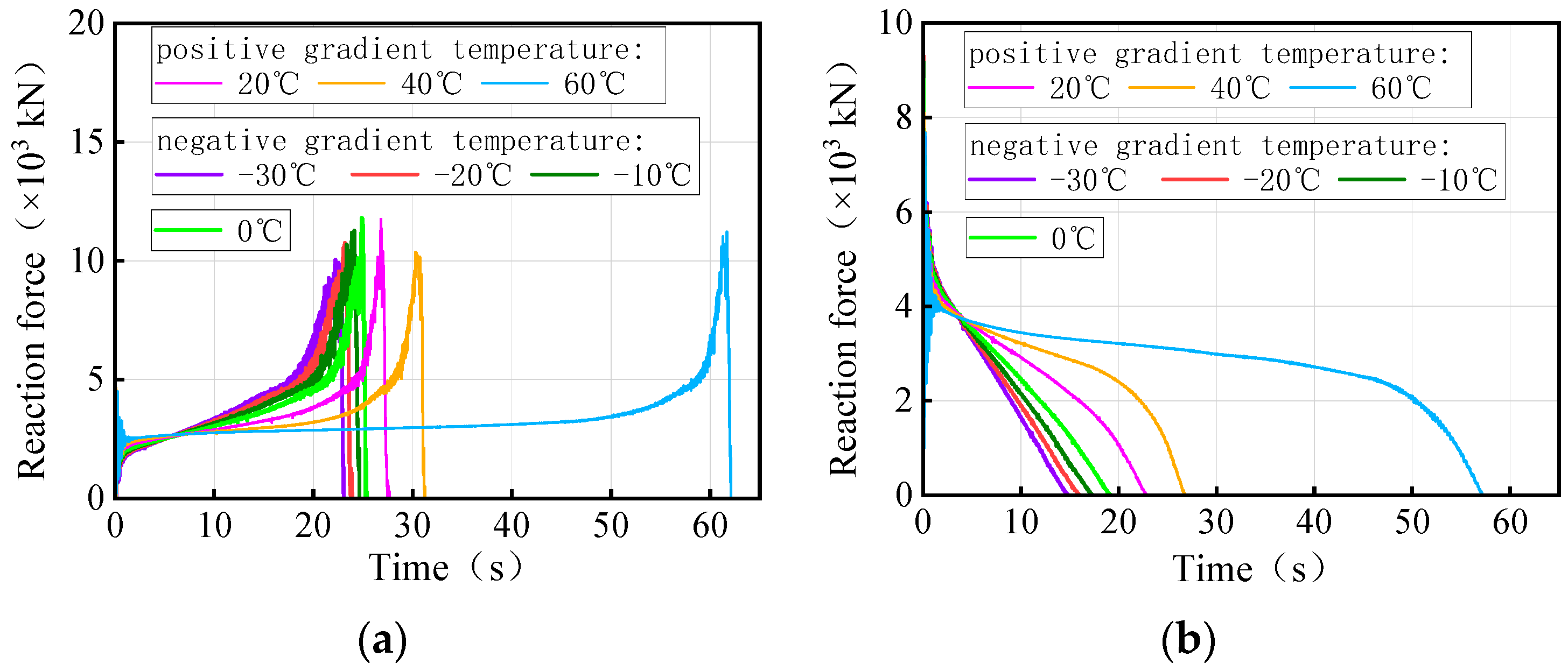
- The ultimate vehicle weights for the overall overturning of the 3 × 25 m and 5 × 25 m curved bridges decrease by 0.1% to 1.4% with a positive gradient temperature range of 0 °C to 60 °C. Conversely, under a negative gradient temperature range of 0 °C to −30 °C, the ultimate vehicle weights for the overall overturning of curved bridges increase by 0.1% to 0.8%. In contrast, the results for the 3 × 25 m and 5 × 25 m straight bridges show the opposite trend to the curved bridges. There is an increase in ultimate vehicle weights of 1.3% to 11.7% under positive temperature conditions and a decrease of 0.6% to 6.1% under negative gradient temperature conditions.
- (4)
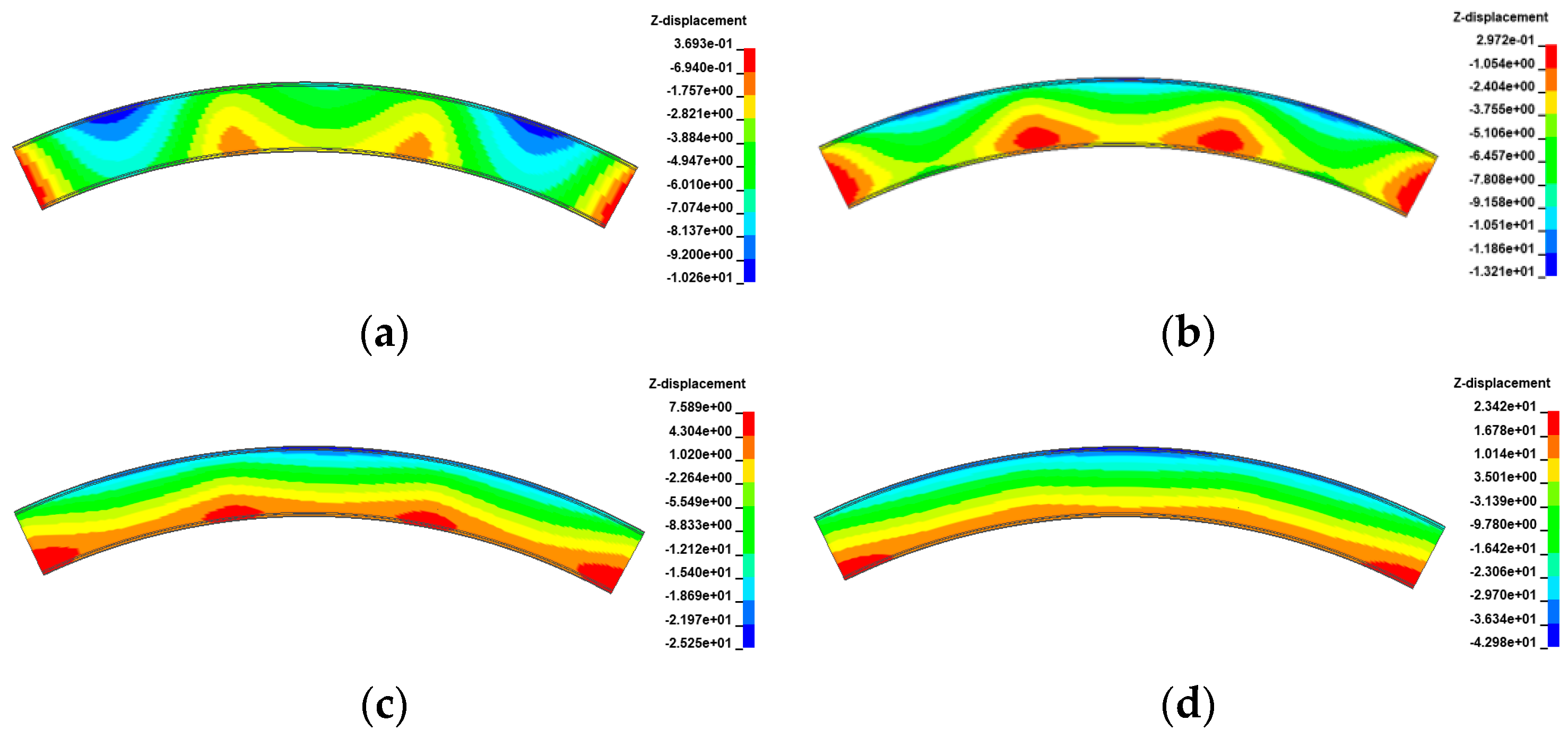
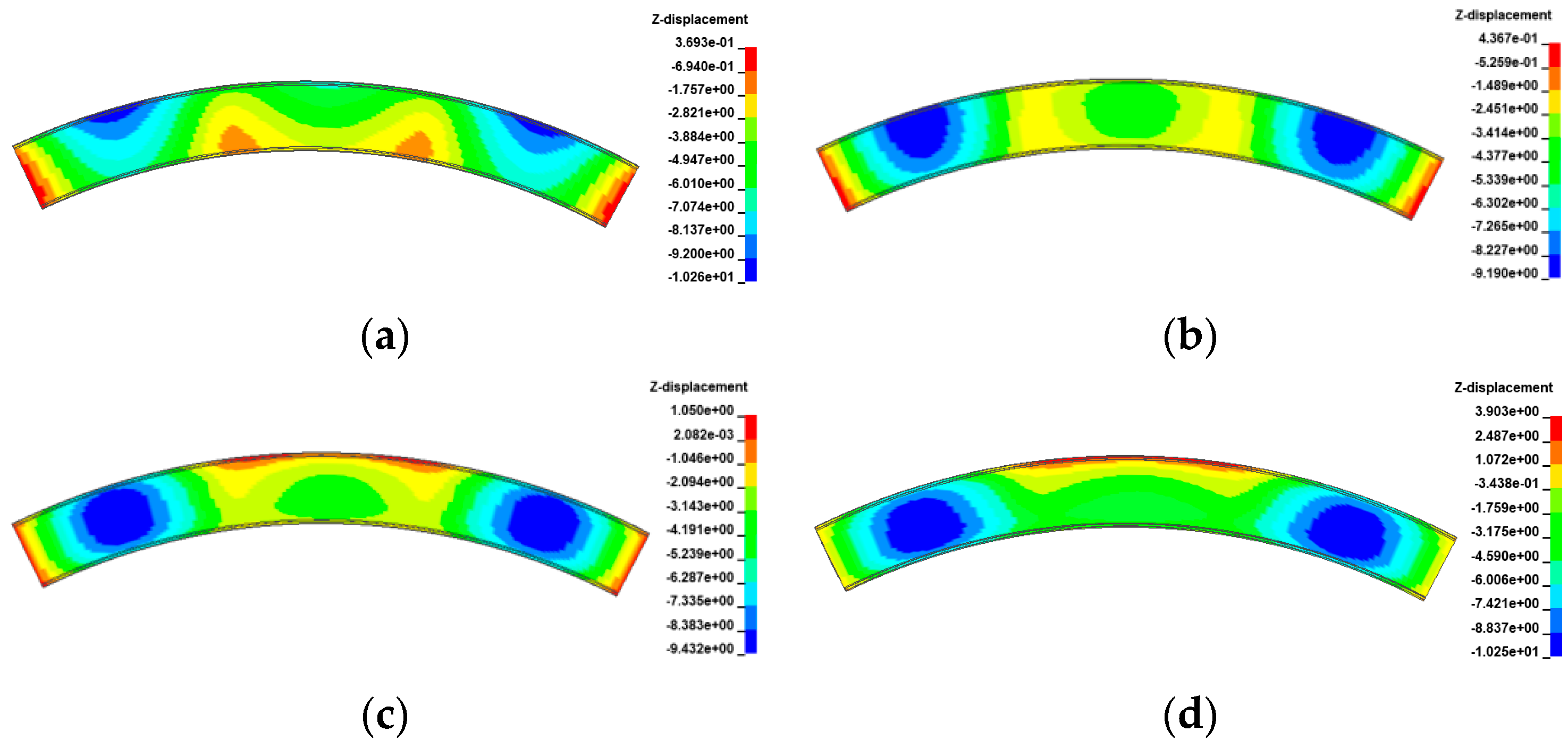
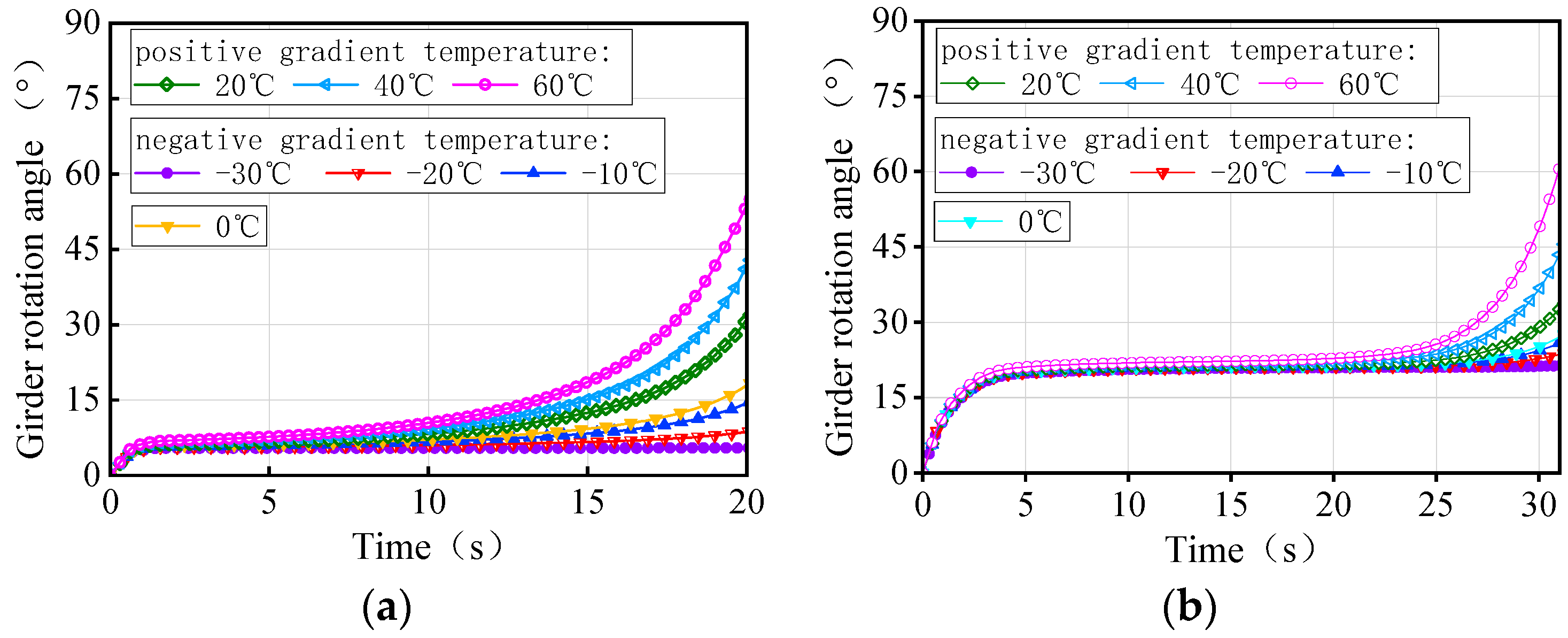
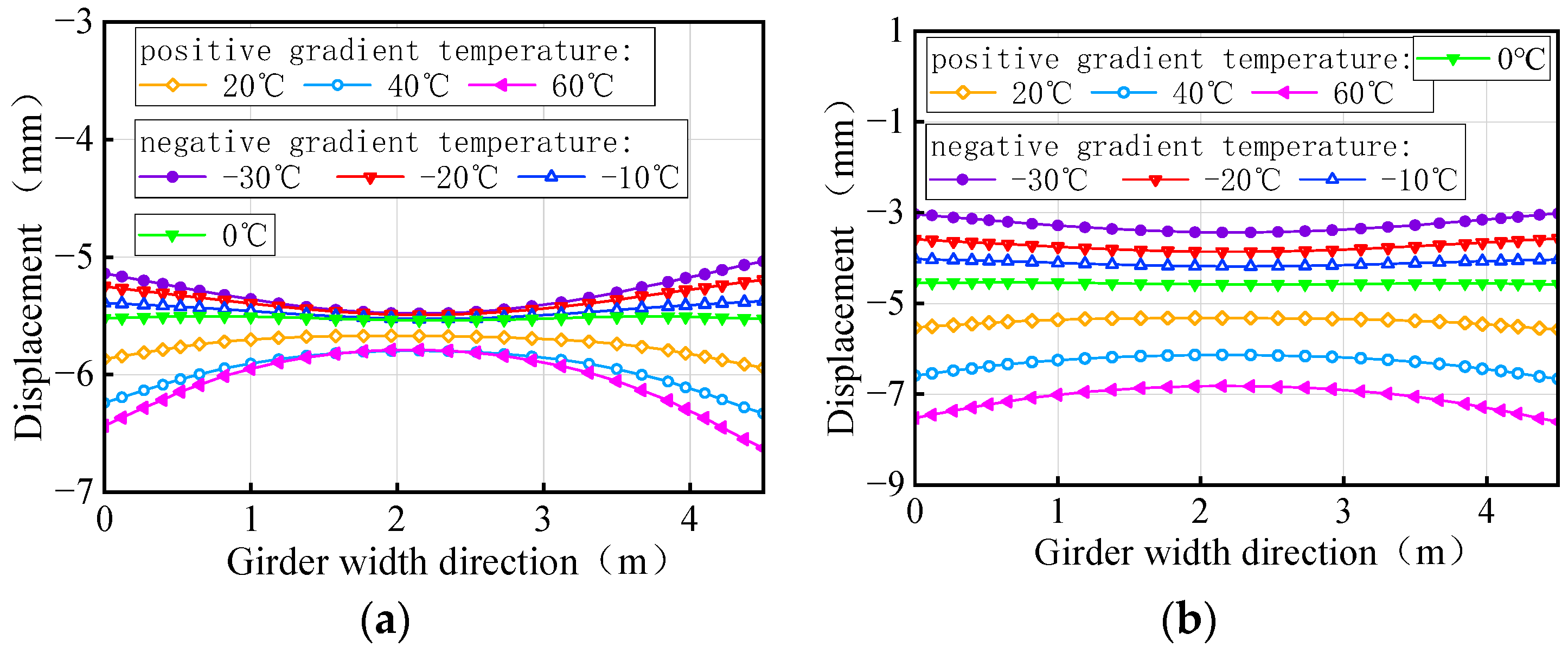
- The deformation of the girder of the curved bridges shifts from ‘down warp’ to ‘torsion’ as the gradient temperature changes. Positive gradient temperature leads to girder flips outward towards horizontal curvature, deteriorating the lateral stability of bridges, while inward flips improve stability. For the 3 × 25 m and 5 × 25 m curved bridges, bearing disengagement follows a specific temperature sequence. Delayed failures of mid-pier bearings at low temperatures are linked to higher overturning capacity, underscoring their significance in evaluating bridge stability.
- (5)
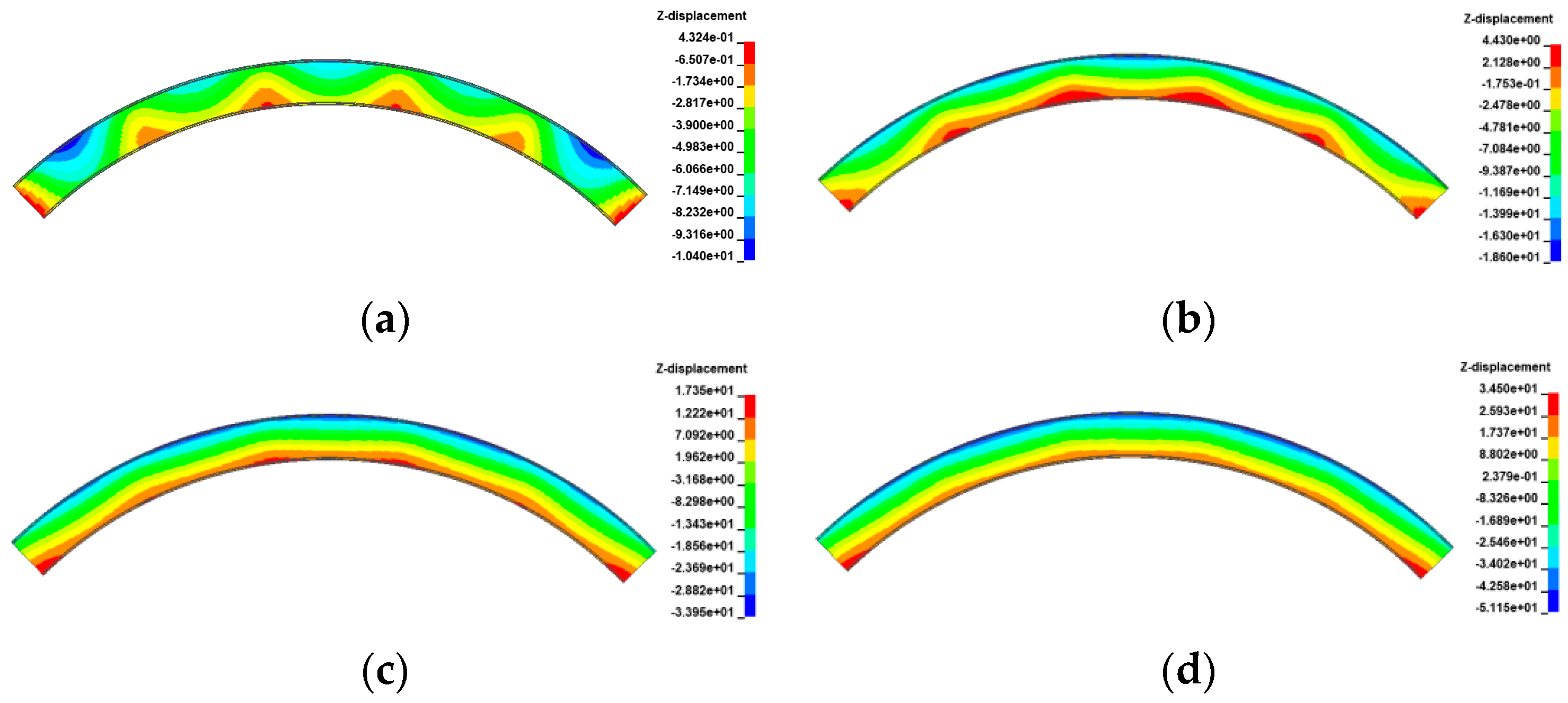
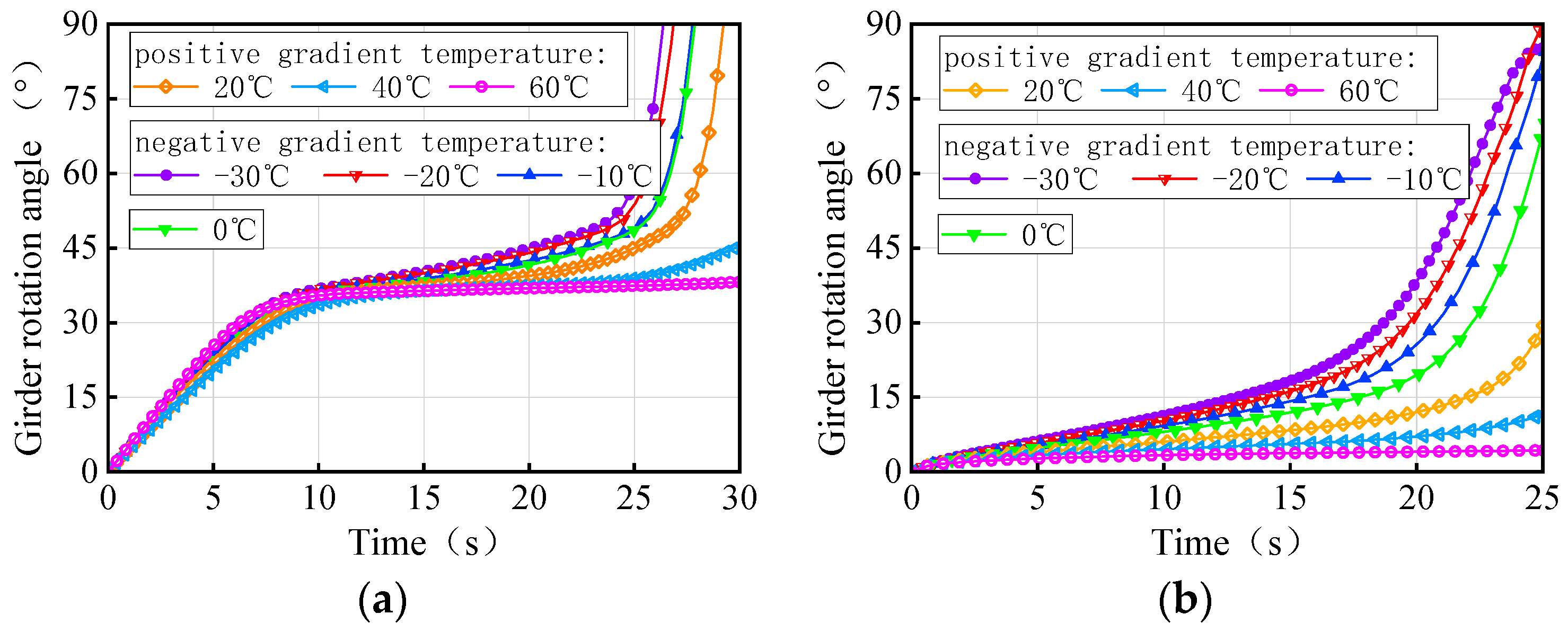
- Gradient temperature variations can cause ‘down warp’ or ‘upward warping’ as a whole in straight girders, influencing their separation from mid-pier bearings. Within the range of −30 °C to 60 °C, the higher the temperature, the lower the girder rotation angle and the higher the anti-overturning stability. There is an obvious time sequence for bearing failure caused by temperature gradient: for the same bearing, the lower the temperature, the earlier the bearing will disengage. Both the girder rotation angle and reaction force of the bearing can serve as a comparative indicator of stability for straight bridges.
- (6)
- This study focuses solely on the effect of temperature on the overall overturning mode of bridges. However, it is important to note that bridge failure modes also encompass girder slip failure, bearing extrusion failure, and pier failure. Investigating the influence and mechanisms of temperature on these specific damage modes may provide a more comprehensive understanding of bridge behavior. In addition, other factors affecting the stability of bridges are worth exploring, such as prestressing, foundation settlement, and some structural factors, and verifying by experimental trials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, T.; Zhang, J.; Li, S.; Wang, Y. Anti-overturning stability coefficient of curved girder bridges considering seismic action. J. Vibroeng. 2019, 21, 710–725. [Google Scholar] [CrossRef]
- Cao, L.; Zhou, H.; Peng, W.; Liu, J.; Chen, Y.F. Analytical analysis on the static support reactions of single-column pier bridges using the grey wolf optimizer. Structures 2023, 55, 2003–2012. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Wang, Y.L.; Zhao, Y.; Xue, Y.X.; Han, Z.Q. Review on research of anti-overturning of highway bridgers with single-column piers. J. Traffic Transp. Eng. 2022, 22, 46–66. [Google Scholar]
- Michaltsos, G.T.; Raftoyiannis, I.G. A mathematical model for the rocking, overturning and shifting problems in bridges. Eng. Struct. 2008, 30, 3587–3594. [Google Scholar] [CrossRef]
- Ge, L.; Dan, D.; Yan, X.; Zhang, K. Real time monitoring and evaluation of overturning risk of single-column-pier box-girder bridges based on identification of spatial distribution of moving loads. Eng. Struct. 2020, 210, 110383. [Google Scholar] [CrossRef]
- Xu, F.Y.; Zhang, M.J.; Wang, L.; Zhang, J.R. Recent highway bridge collapses in China: Review and discussion. J. Perform. Constr. Facil. 2016, 30, 04016030. [Google Scholar] [CrossRef]
- Lee, K.; Andrawes, B.; Lim, J.; Kim, H.; Kang, Y. A study on overturning failure of horizontally curved single steel box girders. Eng. Fail. Anal. 2019, 97, 20–31. [Google Scholar] [CrossRef]
- Xu, H.; Li, Q.; Li, D.; Jiang, H.; Wang, T.; Gao, Q. Experimental and numerical investigation of the anti-overturning theory of single-column pier bridges. Sustainability 2023, 15, 1545. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, Z.; Ma, H.; Emadi, S.; Cao, Z. Failure mechanism and design method for box girder bridge with interior hinged supports under eccentrically vertical loads. Structures 2023, 48, 438–449. [Google Scholar] [CrossRef]
- Peng, W.; Zhao, H.; Dai, F.; Taciroglu, E. Analytical method for overturning limit analysis of single-column pier bridges. J. Perform. Constr. Facil. 2017, 31, 04017007. [Google Scholar] [CrossRef]
- Fan, Y.; Zhu, J.; Pei, J.; Li, Z.; Wu, Y. Analysis for Yangmingtan bridge collapse. Eng. Fail. Anal. 2015, 56, 20–27. [Google Scholar] [CrossRef]
- Ji, X.L.; Zhu, L.; Su, R.K.L.; Wang, G.M. Lateral overturning process and failure mechanism of curved steel-concrete composite box-girder bridges under specific overloading vehicles. Structures 2022, 35, 638–649. [Google Scholar] [CrossRef]
- Deng, L.; Wang, W.; Yu, Y. State-of-the-art review on the causes and mechanisms of bridge collapse. J. Perform. Constr. Facil. 2016, 30, 04015005. [Google Scholar] [CrossRef]
- Jain, R.; Singh, A. Parametric study of horizontally curved box girders for torsional behavior and stability. Int. Res. J. Eng. Technol. 2016, 3, 1431–1436. [Google Scholar]
- Keke, P. Research on comprehensive evaluation method for antioverturning safety of bridges with bent-straight beam. IOP Conf. Ser. Mater. Sci. Eng. 2018, 423, 012012. [Google Scholar] [CrossRef]
- Dan, D.; Yu, X.; Yan, X.; Zhang, K. Monitoring and evaluation of overturning resistance of box girder bridges based on time-varying reliability analysis. J. Perform. Constr. Facil. 2020, 34, 04019101. [Google Scholar] [CrossRef]
- Song, T.; Deng, Q.; Li, G. Collapse mechanism and full-range analysis of overturning failure of continuous girder bridges. Adv. Mater. Sci. Eng. 2021, 2021, 5547300. [Google Scholar] [CrossRef]
- Zhuang, D.; Xiao, R.; Jia, L.; Sun, B. Failure analysis for overall stability against sliding and overturning of a girder bridge. Eng. Fail. Anal. 2020, 109, 104271. [Google Scholar] [CrossRef]
- Peng, W.B.; Zhu, Z.X.; Chen, G.J.; Zhu, H.H. Research on overturning failure mode of beam bridges and applicability of calculation method. China Civ. Eng. J. 2019, 52, 104–113. [Google Scholar]
- Liu, B.; Han, W.; Wang, T.; Feng, Y.; Wang, J.; Xu, K. Analytical method for overturning risk assessment of curved girder bridges with single-column piers under heavy-duty vehicles. Structures 2023, 57, 105084. [Google Scholar] [CrossRef]
- Xiong, W.; Cai, C.S.; Kong, B.; Ye, J. Overturning-collapse modeling and safety assessment for bridges supported by single-column piers. J. Bridge Eng. 2017, 22, 04017084. [Google Scholar] [CrossRef]
- Shi, X.; Cao, Z.; Ma, H.; Ruan, X. Failure analysis on a curved girder bridge collapse under eccentric heavy vehicles using explicit finite element method: Case study. J. Bridge Eng. 2018, 23, 05018001. [Google Scholar] [CrossRef]
- Streit, W.; Mang, R. Uberschlägiger Kippsicherheitsnachweis für Stahlbeton-und Spannbetonbinder. Bauingenieur 1984, 59, 433–439. [Google Scholar]
- Song, G.; Che, D.; Li, M. Overturning axis selection in curved box-girder bridges with single-column piers. Math. Probl. Eng. 2018, 2018, 9206138. [Google Scholar] [CrossRef]
- Li, H.C.; Liu, X.D.; Feng, M. Overturning risk management of box-girder ramp bridge in operation period. Highway 2016, 61, 88–93. [Google Scholar]
- JTG/T 3362-2018 (MTPRC 2018); Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. Standards Press: Beijing, China, 2018.
- Wang, J.F.; Xu, Z.Y.; Fan, X.L.; Lin, J.P. Thermal effects on curved steel box girder bridges and their countermeasures. J. Perform. Constr. Facil. 2017, 31, 04016091. [Google Scholar] [CrossRef]
- Wang, J.; Fang, Z. Temperature variation of concrete box girder bridge. Front. Archit. Civ. Eng. China 2009, 3, 407–413. [Google Scholar] [CrossRef]
- Song, G.; Che, D.; Li, M. Stability against overturning of curved continuous box-girder bridges with single column piers. IOP Conf. Ser. Mater. Sci. Eng. 2018, 452, 022105. [Google Scholar] [CrossRef]
- Tayşi, N.; Abid, S. Temperature distributions and variations in concrete box-girder bridges: Experimental and finite element parametric studies. Adv. Struct. Eng. 2015, 18, 469–486. [Google Scholar] [CrossRef]
- He, B.L. The sun runs away the bridge?—An analysis of an incident on a ramp bridge at an interchange in Shenzhen. Urban Roads Bridges Flood Control 2002, 2, 39–43. [Google Scholar]
- Qi, Z.; Huang, F.; Su, X.; Wang, S. Study on calculation method of anti overturning of continuous steel box girder. J. Phys. Conf. Ser. 2021, 2012, 012042. [Google Scholar] [CrossRef]
- Li, J.; Li, G.P. Analysis of the causes of lateral tilting and bearing dehiscence in curved continuous box girder bridge. In Proceedings of the National Key Technology of Cable-Stayed Bridge; China Highway and Transportation Society. China Communications Press: Xiamen, China, 2012; pp. 286–291. [Google Scholar]
- Zhao, C.G.; Wang, X.D.; Yang, D.H. Research on existing medium and small span curve bridges about the mechanisms of beam body radial moving. J. China Foreign Highw. 2018, 38, 162–167. [Google Scholar]
- Lei, N. Research and Application of Anti-Overturning and Structural-Reinforcement Technology of Single-Column Bearing Bridge. Master’s Thesis, Tsinghua University, Beijing, China, 2017. [Google Scholar]
- Xu, Z.; Lu, X.; Guan, H.; Lu, X.; Ren, A. Progressive-collapse simulation and critical region identification of a stone arch bridge. J. Perform. Constr. Facil. 2013, 27, 43–52. [Google Scholar] [CrossRef]
- JT/T 391-2009; Pot Bearings for Highway Bridges. China Communications Press: Beijing, China, 2009.
- Hossain, T.; Segura, S.; Okeil, A.M. Structural effects of temperature gradient on a continuous prestressed concrete girder bridge: Analysis and field measurements. Struct. Infrastruct. Eng. 2020, 16, 1539–1550. [Google Scholar] [CrossRef]
- Abid, S.R.; Xue, J.; Liu, J.; Tayşi, N.; Liu, Y.; Özakça, M.; Briseghella, B. Temperatures and gradients in concrete Bridges: Experimental, finite element analysis and design. Structures 2022, 37, 960–976. [Google Scholar] [CrossRef]
- Abid, S.R.; Tayşi, N.; Özakça, M. Experimental analysis of temperature gradients in concrete box-girders. Constr. Build. Mater. 2016, 106, 523–532. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Liu, J.; Xin, G.; Long, G.; Zhang, T. Experimental study and analysis for the long-term behavior of the steel-concrete composite girder bridge. Structures 2023, 51, 1305–1327. [Google Scholar] [CrossRef]
- Liu, X. Temperature Induced Stress Analysis for Concrete Structures; China Communications Press: Beijing, China, 1991; pp. 373–401. [Google Scholar]
- JTG D60-2015 (MTPRC 2015); General Specifications for Design of Highway Bridges and Culverts. Standards Press: Beijing, China, 2015.
- Peng, W.B.; Dai, F.; Taciroglu, E. Research on mechanism of overturning failure for single-column pier bridge. Comput. Civil Build. Eng. 2014, 1747–1754. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, Z.; Ruan, X. Failure analysis of a girder bridge collapse under eccentric heavy vehicles. J. Bridge Eng. 2016, 21, 05016009. [Google Scholar] [CrossRef]

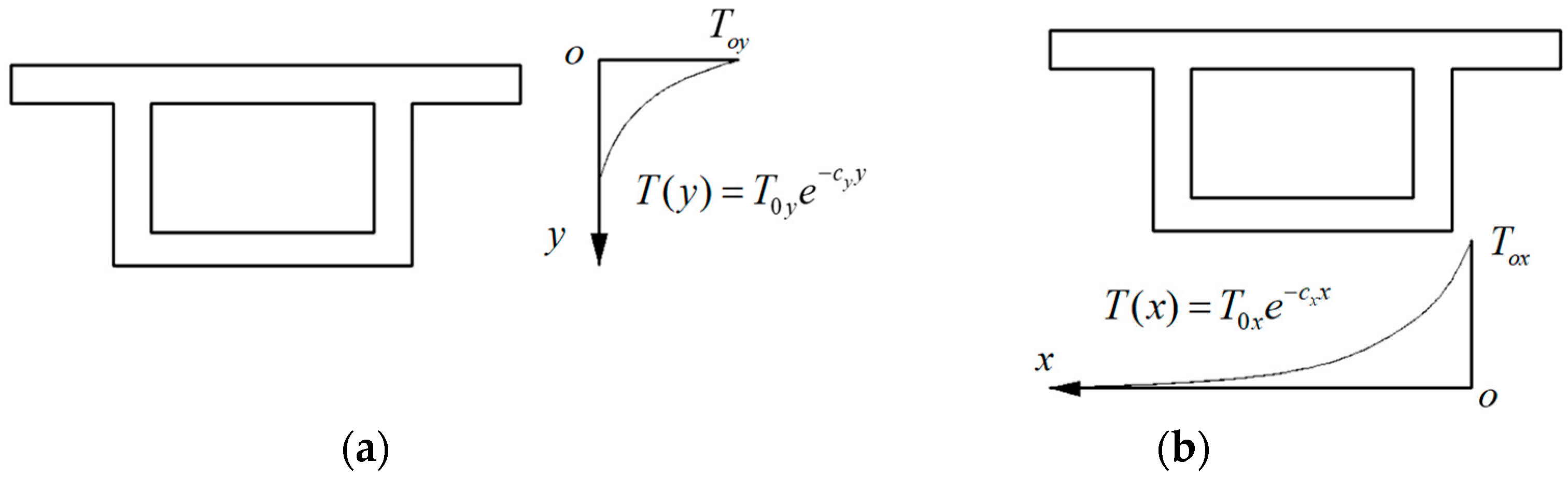



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, Y.; Xue, Y.; Yao, C.; Wang, K.; Luo, X. Failure Analysis for Overall Overturning of Concrete Single-Column Pier Bridges Induced by Temperature and Overloaded Vehicles. Materials 2024, 17, 2650. https://doi.org/10.3390/ma17112650
Wang Y, Zhou Y, Xue Y, Yao C, Wang K, Luo X. Failure Analysis for Overall Overturning of Concrete Single-Column Pier Bridges Induced by Temperature and Overloaded Vehicles. Materials. 2024; 17(11):2650. https://doi.org/10.3390/ma17112650
Chicago/Turabian StyleWang, Yelu, Yongjun Zhou, Yuxin Xue, Changwei Yao, Kailong Wang, and Xuchang Luo. 2024. "Failure Analysis for Overall Overturning of Concrete Single-Column Pier Bridges Induced by Temperature and Overloaded Vehicles" Materials 17, no. 11: 2650. https://doi.org/10.3390/ma17112650
APA StyleWang, Y., Zhou, Y., Xue, Y., Yao, C., Wang, K., & Luo, X. (2024). Failure Analysis for Overall Overturning of Concrete Single-Column Pier Bridges Induced by Temperature and Overloaded Vehicles. Materials, 17(11), 2650. https://doi.org/10.3390/ma17112650










