Assessment of the Influence of Fabric Structure on Their Electro-Conductive Properties
Abstract
:1. Introduction
2. Materials
3. Methods
4. Results and Discussion
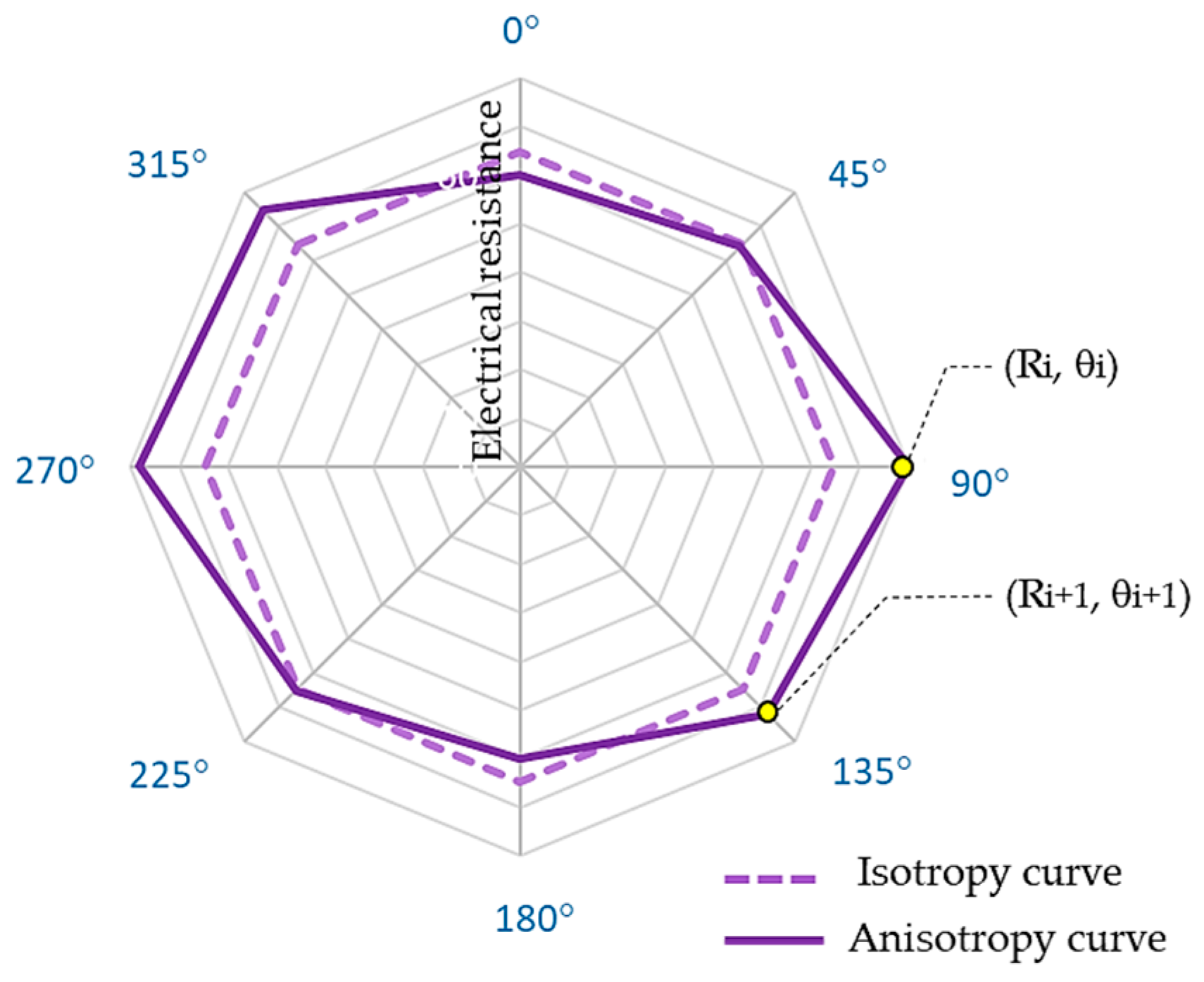
4.1. Electrical Anisotropy of Fabrics
4.2. Factors Affecting the Electrical Conductivity of Fabrics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- An, B.W.; Shin, J.H.; Kim, S.-Y.; Kim, J.; Ji, S.; Park, J.; Lee, Y.; Jang, J.; Park, Y.-G.; Cho, E.; et al. Smart sensor systems for wearable electronic devices. Polymers 2017, 9, 303. [Google Scholar] [CrossRef] [PubMed]
- Acar, G.; Ozturk, O.; Golparvar, A.J.; Elboshra, T.A.; Böhringer, K.; Yapici, M.K. Wearable and flexible textile electrodes for biopotential signal monitoring: A review. Electronics 2019, 8, 479. [Google Scholar] [CrossRef]
- Cherenack, K.; Van Pieterson, L. Smart textiles: Challenges and opportunities. J. Appl. Phys. 2012, 112, 091301. [Google Scholar] [CrossRef]
- Dhawan, A.; Seyam, A.M.; Ghosh, T.K.; Muth, J.F. Woven fabric-based electrical circuits: Part I: Evaluating interconnect methods. Text. Res. J. 2004, 74, 913–919. [Google Scholar] [CrossRef]
- Wu, X.; Yu, P.; Sun, X.; Wang, X.; Li, W. Modeling the thermal performance of anisotropic heat conduction fabric with different structural parameters. J. Nat. Fibers 2023, 20, 2181263. [Google Scholar] [CrossRef]
- Zuo, X.; Zhang, X.; Qu, L.; Miao, J. Smart fibers and textiles for personal thermal management in emerging wearable applications. Adv. Mater. Technol. 2023, 8, 2201137. [Google Scholar] [CrossRef]
- Leśnikowski, J. Effect of cyclical bending and rubbing on the characteristic impedance of textile signal lines. Materials 2021, 14, 6013. [Google Scholar] [CrossRef]
- Jeong, Y.R.; Lee, G.; Park, H.; Ha, J.S. Stretchable, skin-attachable electronics with integrated energy storage devices for biosignal monitoring. Acc. Chem. Res. 2019, 52, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Shak Sadi, M.; Kumpikaite, E. Advances in the robustness of wearable electronic textiles: Strategies, stability, washability and perspective. Nanomaterials 2022, 12, 2039. [Google Scholar] [CrossRef]
- Euler, L.; Guo, L.; Persson, N.-K. A review of textile-based electrodes developed for electrostimulation. Text. Res. J. 2022, 92, 1300–1320. [Google Scholar] [CrossRef]
- Stoppa, M.; Chiolerio, A. Wearable electronics and smart textiles: A critical review. Sensors 2014, 14, 11957–11992. [Google Scholar] [CrossRef] [PubMed]
- Palanisamy, S.; Tunakova, V.; Militky, J. Fiber-based structures for electromagnetic shielding–comparison of different materials and textile structures. Text. Res. J. 2018, 88, 1992–2012. [Google Scholar] [CrossRef]
- Sindhu, G.; Poornima, A. A brief synopsis on conductive textiles. Int. J. Adv. Biochem. Res. 2024, 8, 440–444. [Google Scholar] [CrossRef]
- Ojstršek, A.; Plohl, O.; Gorgieva, S.; Kurečič, M.; Jančič, U.; Hribernik, S.; Fakin, D. Metallisation of textiles and protection of conductive layers: An overview of application techniques. Sensors 2021, 21, 3508. [Google Scholar] [CrossRef] [PubMed]
- Pawlak, R.; Korzeniewska, E.; Koneczny, C.; Hałgas, B. Properties of thin metal layers deposited on textile composites by using the PVD method for textronic applications. Autex Res. J. 2017, 17, 229–237. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, X.; Qiu, B.; Yang, Z.; Cai, D.; He, P.; Jia, D.; Zhou, Y. Preparation and anisotropic properties of textured structural ceramics: A review. J. Adv. Ceram. 2019, 8, 289–332. [Google Scholar] [CrossRef]
- Pham, T.-T.-H.; Lo, Y.L. Extraction of effective parameters of anisotropic optical materials using a decoupled analytical method. J. Biomed. Opt. 2012, 17, 025006. [Google Scholar] [CrossRef] [PubMed]
- Qing, A.; Xu, X.; Gan, Y. Anisotropy of composite materials with inclusion. IEEE Trans. Antennas Propag. 2005, 53, 737–744. [Google Scholar] [CrossRef]
- Hrouda, F. Magnetic anisotropy of rocks and its application in geology and geophysics. Surv. Geophys. 1982, 5, 37–82. [Google Scholar] [CrossRef]
- Tokarska, M.; Miśkiewicz, P.; Pawlak, W. Research on the planar electrical anisotropy of conductive woven fabrics. Adv. Eng. Mater. 2023, 25, 2300019. [Google Scholar] [CrossRef]
- Gong, J.; Liu, Z.; Yu, J.; Dai, D.; Dai, W.; Du, S.; Li, C.; Jiang, N.; Zhan, Z.; Lin, C.-T. Graphene woven fabric-reinforced polyimide films with enhanced and anisotropic thermal conductivity. Compos. Part A Appl. Sci. Manuf. 2016, 87, 290–296. [Google Scholar] [CrossRef]
- Paul, O.; Plattner, L.; Baltes, H. A thermal van der Pauw test structure. In Proceedings of the ICMTS 1999—Proceedings of International Conference on Microelectronic Test Structures, Gothenburg, Sweden, 15–18 March 1999; pp. 56–61. [Google Scholar]
- Tokarska, M. Characterization of electro-conductive textile materials by its biaxial anisotropy coefficient and resistivity. J. Mater. Sci. Mater. Electron. 2019, 30, 4093–4103. [Google Scholar] [CrossRef]
- Van der Pauw, L.J. A method of measuring specific resistivity and Hall effect of discs of arbitrary shape. Philips Res. Rep. 1958, 13, 174–182. [Google Scholar]
- Majid, A.J. An innovative method of measuring semiconductors resistivity using Van der Pauw technique. Int. J. Sci. Eng. Res. 2011, 2, 1–6. [Google Scholar]
- Majid, A.J. Resistivity measurements of conductors and semiconductors of different geometrical shapes using Van der Pauw technique. Int. J. Sci. Eng. Res. 2011, 2, 1–5. [Google Scholar]
- Oliveira, F.S.; Cipriano, R.B.; da Silva, F.T.; Romão, E.C.; dos Santos, C.A.M. Simple analytical method for determining electrical resistivity and sheet resistance using the van der Pauw procedure. Sci. Rep. 2020, 10, 16379. [Google Scholar] [CrossRef] [PubMed]
- Zikulnig, J.; Roshanghias, A.; Rauter, L.; Hirschl, C. Evaluation of the sheet resistance of inkjet-printed Ag-layers on flexible, uncoated paper substrates using Van-der-Pauw’s method. Sensors 2020, 20, 2398. [Google Scholar] [CrossRef] [PubMed]
- Náhlík, J.; Kašpárková, I.; Fitl, P. Influence of non-ideal circumferential contacts on errors in the measurements of the resistivity of layers using the van der Pauw method. Measurement 2013, 46, 887–892. [Google Scholar] [CrossRef]
- Kazani, I.; De Mey, G.; Hertleer, C.; Banaszczyk, J.; Schwarz, A.; Guxho, G.; Van Langenhove, L. Van der Pauw method for measuring resistivities of anisotropic layers printed on textile substrates. Text. Res. J. 2011, 81, 2117–2124. [Google Scholar] [CrossRef]
- Tyurin, I.N.; Getmantseva, V.V.; Andreeva, E.G. Van der Pauw method for measuring the electrical conductivity of smart textiles. Fibre Chem. 2019, 51, 139–146. [Google Scholar] [CrossRef]
- Jiyong, H.; Xiaofeng, Z.; Guohao, L.; Xudong, Y.; Xin, D. Electrical properties of PPy-coated conductive fabrics for human joint motion monitoring. AUTEX Res. J. 2016, 16, 7–12. [Google Scholar] [CrossRef]
- Kazani, I.; De Mey, G.; Hertleer, C.; Banaszczyk, J.; Schwarz, A.; Guxho, G.; Van Langenhove, L. About the collinear four-probe techniques inability to measure the resistivity of anisotropic electroconductive fabrics. Text. Res. J. 2013, 83, 1587–1593. [Google Scholar] [CrossRef]
- Smits, F.M. Measurement of sheet resistivity with the four-point probe. Bell Syst. Tech. J. 1958, 37, 711–718. [Google Scholar] [CrossRef]
- Martin, N.; Sauget, J.; Nyberg, T. Anisotropic electrical resistivity during annealing of oriented columnar titanium films. Mater. Lett. 2013, 105, 20–23. [Google Scholar] [CrossRef]
- Yeboah-Forson, A.; Whitman, D. Electrical resistivity characterization of anisotropy in the biscayne aquifer. Groundwater 2014, 52, 728–736. [Google Scholar] [CrossRef] [PubMed]
- Semeraro, F.; Ferguson, J.C.; Acin, M.; Panerai, F.; Mansour, N.N. Anisotropic analysis of fibrous and woven materials part 2: Computation of effective conductivity. Comput. Mater. Sci. 2021, 186, 109956. [Google Scholar] [CrossRef]
- Shabani, A.; Hylli, M.; Kazani, I. Investigating properties of electrically conductive textiles: A review. Tekstilec 2022, 65, 194–217. [Google Scholar] [CrossRef]
- Zeng, W.; Shu, L.; Li, Q.; Chen, S.; Wang, F.; Tao, X.-M. Fiber-based wearable electronics: A review of materials, fabrication, devices, and applications. Adv. Mater. 2014, 26, 5310–5336. [Google Scholar] [CrossRef]
- Wisung, G. Method Evaluation. Electrical Surface Resistance Measurements on Coated Conductive Textiles. Master’s Thesis, The Swedish School of Textiles, University of Boras, Borås, Sweden, 2018. [Google Scholar]
- Tokarska, M.; Gniotek, K. Anisotropy of the electrical properties of flat textiles. J. Text. I. 2015, 106, 9–18. [Google Scholar] [CrossRef]
- Cho, G.; Jeong, K.; Paik, M.J.; Kwun, Y.; Sung, M. Performance evaluation of textile-based electrodes and motion sensors for smart clothing. IEEE Sens. J. 2011, 11, 3183–3193. [Google Scholar] [CrossRef]
- Bosowski, P.; Hoerr, M.; Mecnika, V.; Gries, T.; Jockenhövel, S. Design and manufacture of textile-based sensors. In Electronic Textiles. Smart Fabrics and Wearable Technology; Dias, T., Ed.; Woodhead Publishing: Sawston, UK, 2015; pp. 75–107. [Google Scholar]
- Hou, L.; Hayes, S.A. A resistance-based damage location sensor for carbon-fibre composites. Smart Mater. Struct. 2002, 11, 966–969. [Google Scholar] [CrossRef]
- Tokarska, M.; Czyżnik, N. Evaluation of electrically conducting fabrics for use as layers protecting against mechanical damages. Technol. Jakość Wyr. 2023, 68, 93–110. [Google Scholar]
- Kleiza, J.; Sapagovas, M.; Kleiza, V. The extension of the Van der Pauw method to anisotropic media. Informatica 2007, 18, 253–266. [Google Scholar] [CrossRef]
- Wąs-Gubała, J.; Skóra, K.; Brożek-Mucha, Z. Characterisation and discrimination of so-called metallised fibres found in clothing and decorative materials originating from the consumer market. Sci. Justice 2021, 61, 535–541. [Google Scholar] [CrossRef]
- Bera, T.K.; Mohamadou, Y.; Lee, K.; Wi, H.; Oh, T.I.; Woo, E.J.; Soleimani, M.; Seo, J.K. Electrical impedance spectroscopy for electro-mechanical characterization of conductive fabrics. Sensors 2014, 14, 9738–9754. [Google Scholar] [CrossRef]
- Khan, S.B.; Hou, M.; Shuang, S.; Zhang, Z. Morphological influence of TiO2 nanostructures (nanozigzag, nanohelics and nanorod) on photocatalytic degradation of organic dyes. Appl. Surf. Sci. 2017, 400, 184–193. [Google Scholar] [CrossRef]
- Renard, M.; Puszkarz, A.K. Modeling of heat transfer through firefighters multilayer protective clothing using the computational fluid dynamics assisted by X-ray microtomography and thermography. Materials 2022, 15, 5417. [Google Scholar] [CrossRef] [PubMed]
- Haupt, F.; Pult, J.R.W.; Hülsmann, M. Micro–computed tomographic evaluation of the shaping ability of 3 reciprocating single-file nickel-titanium systems on single-and double-curved root canals. J. Endod. 2020, 46, 1130–1135. [Google Scholar] [CrossRef] [PubMed]
- Erkkilä, A.-L.; Leppänen, T.; Puurtinen, A.; Ora, M.; Tuovinen, T. Hygroexpansivity of anisotropic sheets. Nord. Pulp Paper Res. J. 2015, 30, 326–335. [Google Scholar] [CrossRef]
- Miccoli, I.; Edler, F.; Pfnür, H.; Tegenkamp, C. The 100th anniversary of the four-point probe technique: The role of probe geometries in isotropic and anisotropic systems. J. Phys. Condens. Matter 2015, 27, 223201. [Google Scholar] [CrossRef]
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics for Non-Statisticians: A Step-by-Step Approach; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]

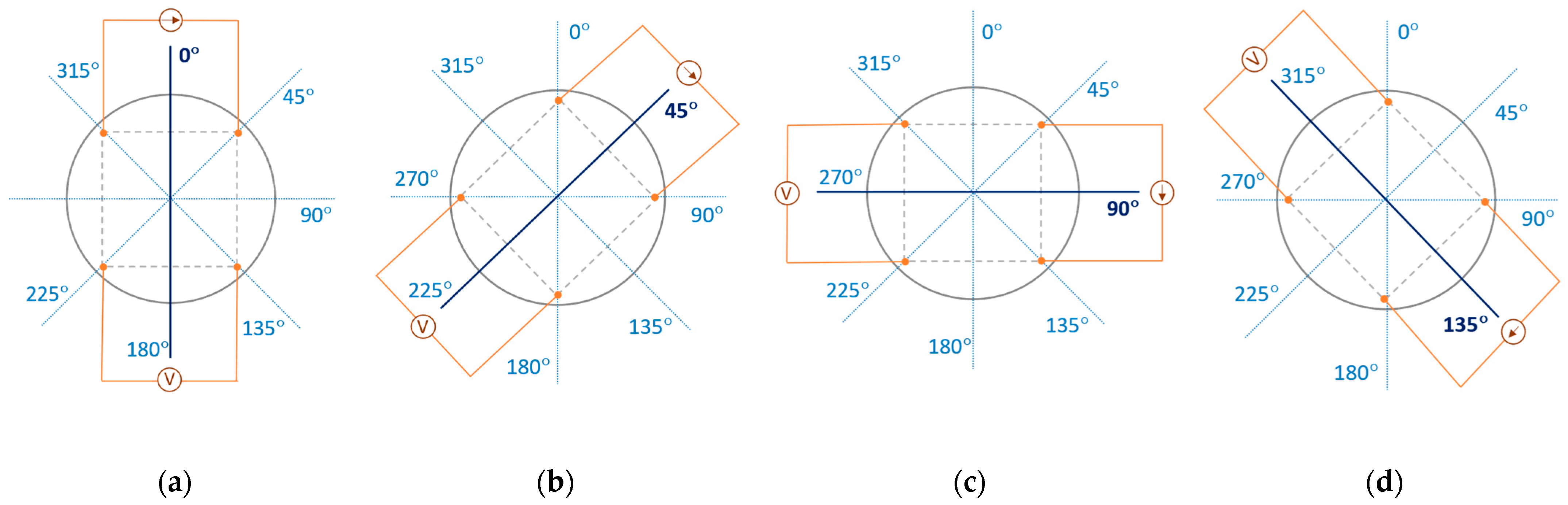
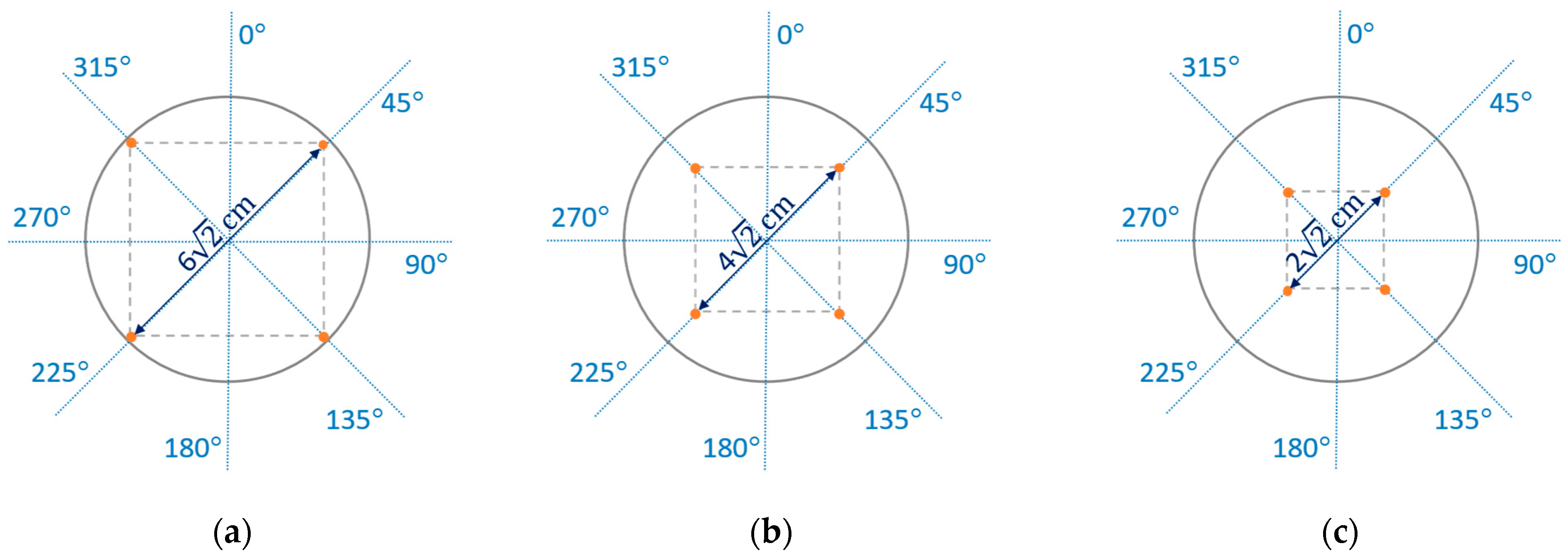
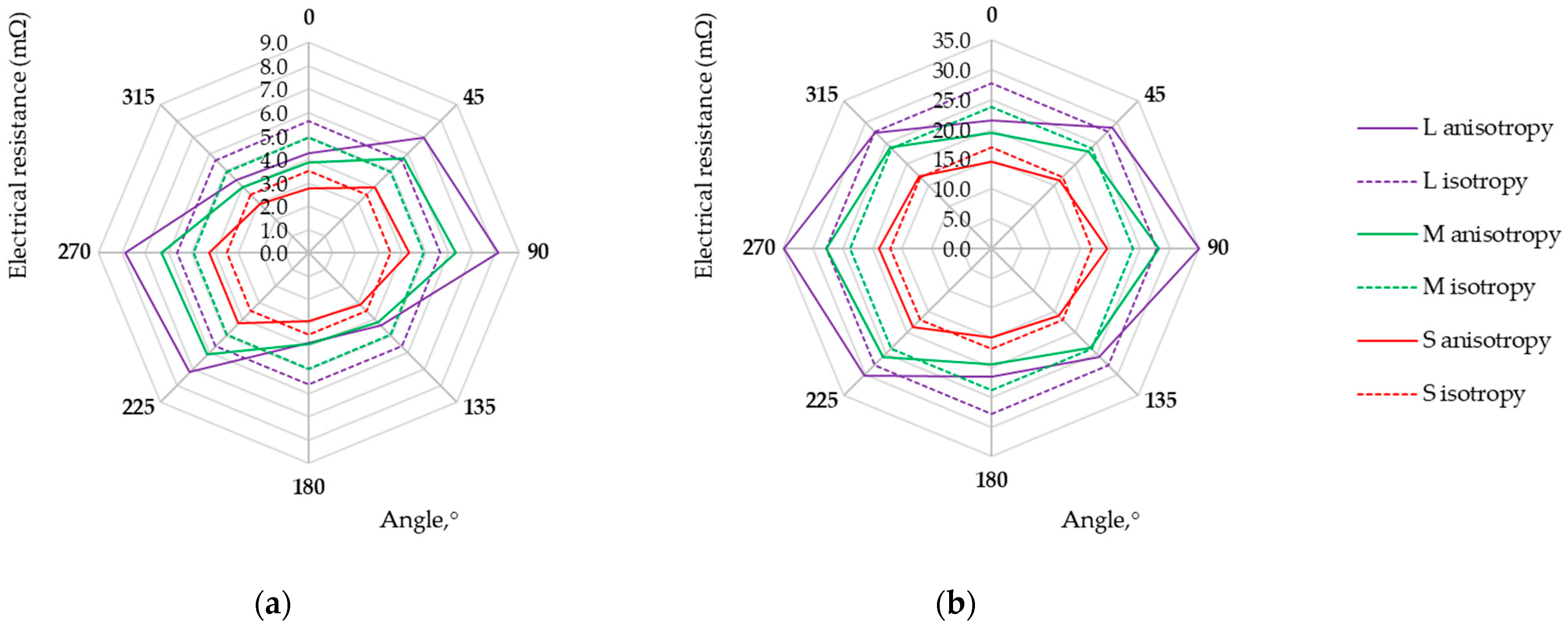
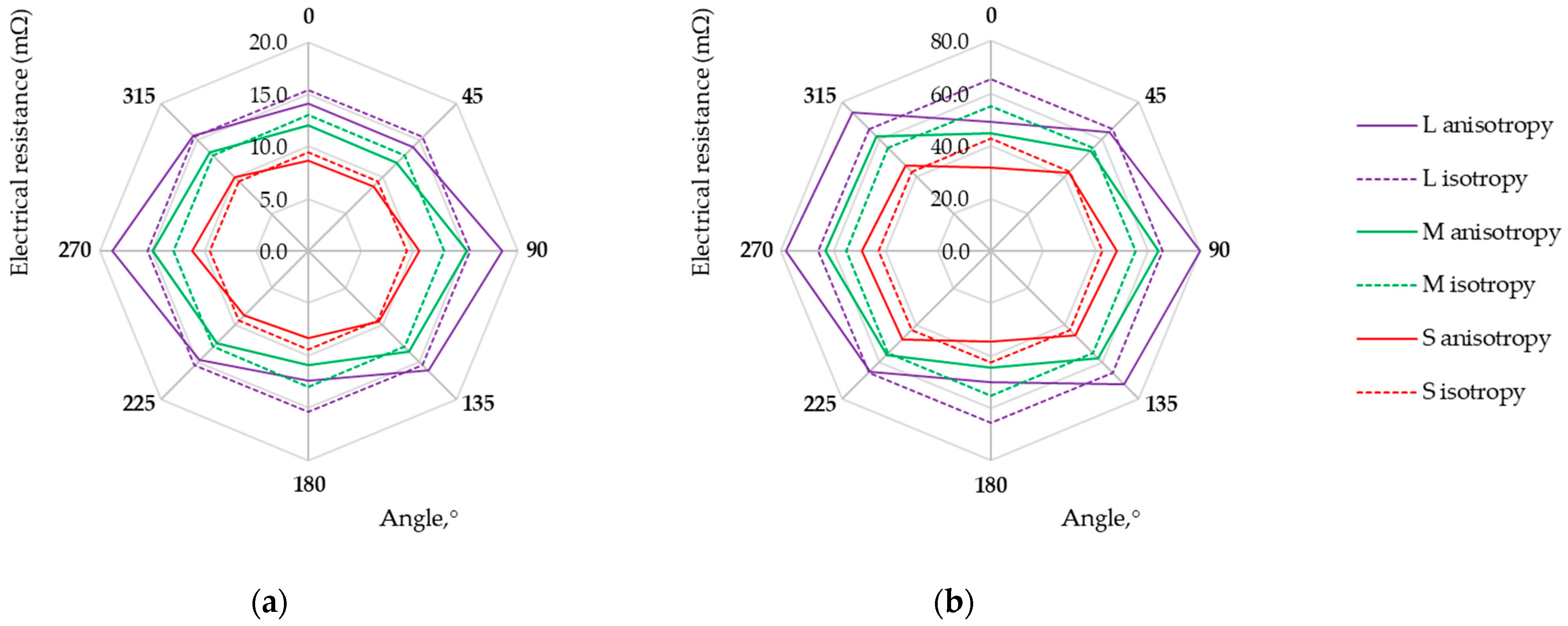
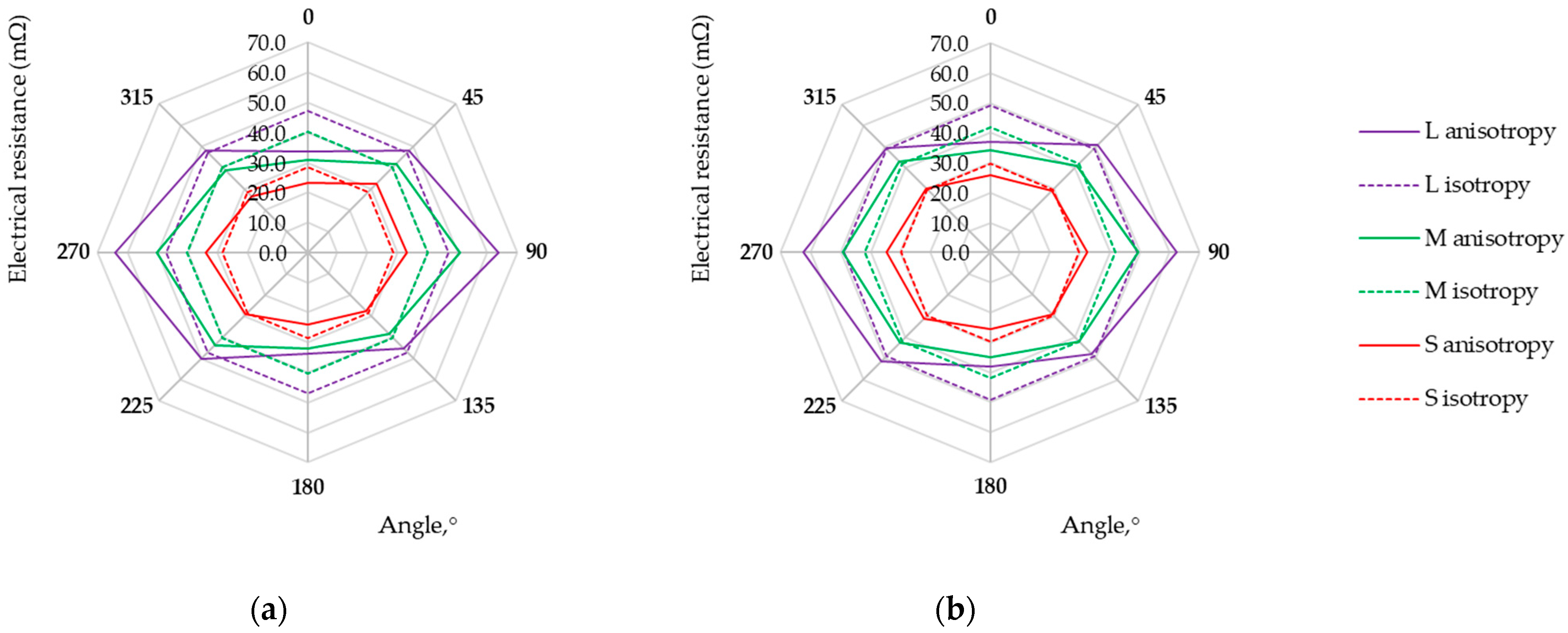
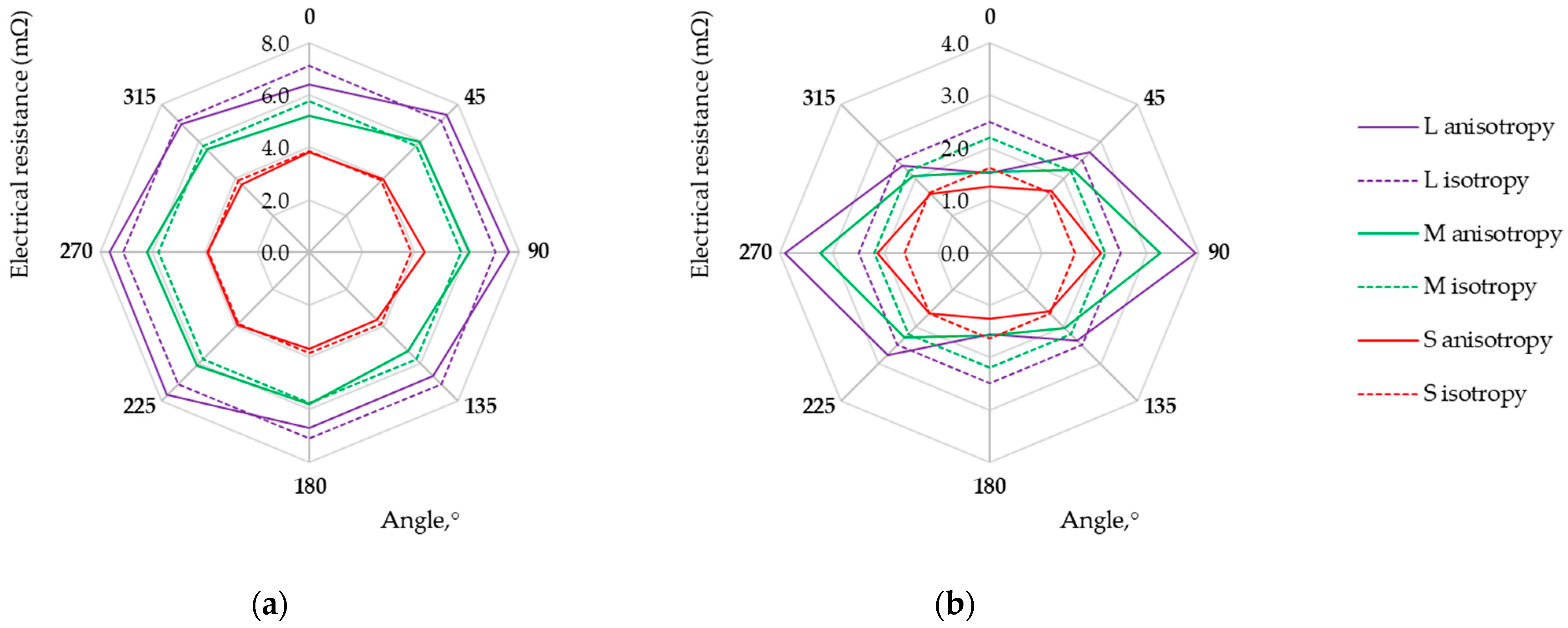
| Sample | Raw Material Composition (Supplier) | Electrical Resistance | Thickness ± SD 1 (mm) | Surface Mass (g m−2) |
|---|---|---|---|---|
| L525 | Copper and nickel metalized polyamide fabric (Laird) | <0.07 Ω | 0.12 ± 0.01 | 86 |
| M1 | Silver-coated polyamide yarns (Qingdao Hengtong X-Silver) | Conductive | 0.15 ± 0.01 | 84 |
| M6 | Silver-coated polyamide yarns (Qingdao Hengtong X-Silver) | Conductive | 0.35 ± 0.01 | 164 |
| M9 | Nickel metalized polyester fabric (Soliani EMC) | <0.40 Ω | 0.19 ± 0.01 | 65 |
| M10 | Nickel metalized polyester fabric (Soliani EMC) | <0.40 Ω | 0.08 ± 0.01 | 75 |
| M11 | Nickel metalized polyester fabric (Soliani EMC) | <0.40 Ω | 0.27 ± 0.01 | 152 |
| M12 | Nickel metalized polyester fabric (Soliani EMC) | <0.40 Ω | 0.15 ± 0.02 | 113 |
| U1 | Copper and tin metalized polyamide fabric (Shieldex) | <0.02 Ω | 0.12 ± 0.01 | 77 |
| Chemical Element→ Sample ↓ | Cu | Ni | Ag | Sn | P | Ti | Others |
|---|---|---|---|---|---|---|---|
| L525 | 12.1 ± 0.1 | 13.4 ± 0.1 | - | - | - | - | 74.6 |
| M1 | - | 53.0 ± 0.1 | - | - | - | 47.0 | |
| M6 | - | - | 62.9 ± 0.1 | - | - | - | 37.1 |
| M9 | - | 49.1 ± 0.1 | - | - | 0.6 ± 0.1 | 0.1 ± 0.1 | 50.2 |
| M10 | 82.7 ± 0.1 | 1.7 ± 0.1 | 15.6 | ||||
| M11 | 87.4 ± 0.1 | 0.6 ± 0.1 | 12.0 | ||||
| M12 | - | 60.6 ± 0.1 | - | - | 0.1 ± 0.1 | - | 39.3 |
| U1 | 76.7 ± 0.1 | - | 0.3 ± 0.1 | 12.5 ± 0.1 | - | - | 10.5 |
| Sample Parameter | L525 | M1 | M6 | M9 | M10 | M11 | M12 | U1 |
|---|---|---|---|---|---|---|---|---|
| Weave | Twill | Dobby | Twill | Plain | Plain | Twill | Plain | Ripstop |
| Weft density (mm−1) | 4.2 ± 0.11 | 3.1 ± 0.15 | 3.5 ± 0.094 | 1.9 ± 0.13 | 3.2 ± 0.099 | 3.6 ± 0.11 | 2.4 ± 0.079 | 4.6 ± 0.14 |
| Warp density (mm−1) | 6.3 ± 0.088 | 4.6 ± 0.18 | 7.3 ± 0.13 | 3.2 ± 0.20 | 4.2 ± 0.084 | 6.3 ± 0.15 | 3.2 ± 0.087 | 5.2 ± 0.18 |
| Major axis of elliptical weft cross-section (mm) | 0.24 ± 0.030 | 0.29 ± 0.051 | 0.25 ± 0.041 | 0.26 ± 0.035 | 0.29 ± 0.047 | 0.25 ± 0.065 | 0.31 ± 0.048 | 0.22 ± 0.052 |
| Minor axis of elliptical weft cross-section (mm) | 0.09 ± 0.004 | 0.08 ± 0.005 | 0.1 ± 0.009 | 0.08 ± 0.008 | 0.08 ± 0.007 | 0.1 ± 0.005 | 0.07 ± 0.007 | 0.05 ± 0.004 |
| Major axis of elliptical warp cross-section (mm) | 0.13 ± 0.023 | 0.19 ± 0.043 | 0.11 ± 0.021 | 0.35 ± 0.056 | 0.22 ± 0.045 | 0.14 ± 0.025 | 0.24 ± 0.059 | 0.16 ± 0.051 |
| Minor axis of elliptical warp cross-section (mm) | 0.04 ± 0.003 | 0.08 ± 0.004 | 0.09 ± 0.004 | 0.05 ± 0.003 | 0.05 ± 0.003 | 0.07 ± 0.004 | 0.08 ± 0.005 | 0.05 ± 0.003 |
| Sample | Electrode Arrangement | Rm (mΩ) (GSD) 4 | Diso (mΩ) | Daniso (mΩ) | D% |
|---|---|---|---|---|---|
| L525 | L | 5.63 (1.4) | 34.47 | 39.91 | 15.8% |
| M | 4.94 (1.3) | 30.24 | 32.91 | 8.8% | |
| S | 3.51 (1.2) | 21.49 | 22.84 | 6.3% | |
| M1 | L | 27.73 (1.2) | 169.81 | 179.84 | 5.9% |
| M | 23.75 (1.2) | 145.45 | 150.26 | 3.3% | |
| S | 16.91 (1.1) | 103.56 | 105.81 | 2.2% | |
| M6 | L | 15.43 (1.2) | 94.45 | 97.82 | 3.6% |
| M | 12.97 (1.1) | 79.40 | 81.27 | 2.4% | |
| S | 9.42 (1.1) | 57.68 | 58.84 | 2.0% | |
| M9 | L | 65.63 (1.2) | 401.87 | 425.69 | 5.9% |
| M | 55.24 (1.2) | 338.25 | 350.07 | 3.5% | |
| S | 42.68 (1.2) | 261.35 | 273.03 | 4.5% | |
| M10 | L | 47.05 (1.3) | 288.11 | 316.06 | 9.7% |
| M | 40.17 (1.2) | 245.97 | 260.07 | 5.7% | |
| S | 28.49 (1.2) | 174.42 | 180.72 | 3.6% | |
| M11 | L | 49.04 (1.2) | 300.26 | 318.68 | 6.1% |
| M | 41.81 (1.1) | 255.98 | 263.82 | 3.1% | |
| S | 29.64 (1.1) | 181.46 | 184.81 | 1.8% | |
| M12 | L | 7.11 (1.1) | 43.52 | 43.92 | 0.9% |
| M | 5.76 (1.1) | 35.29 | 35.57 | 0.8% | |
| S | 3.86 (1.1) | 23.65 | 23.81 | 0.7% | |
| U1 | L | 2.49 (1.4) | 15.28 | 18.42 | 20.5% |
| M | 2.20 (1.3) | 13.47 | 15.29 | 13.5% | |
| S | 1.63 (1.2) | 9.96 | 10.65 | 9.9% |
| Sample | K-W Test | Post Hoc Test | ||
|---|---|---|---|---|
| L-M | M-S | L-S | ||
| L525 | 0.0141 | 0.7088 | 0.2592 | 0.0112 |
| M1 | 0.0003 | 0.7962 | 0.0148 | 0.0003 |
| M6 | 0.0002 | 0.3853 | 0.0296 | 0.0001 |
| M9 | 0.0012 | 0.2496 | 0.1555 | 0.0007 |
| M10 | 0.0017 | 0.9666 | 0.0400 | 0.0016 |
| M11 | 0.0003 | 0.7300 | 0.0175 | 0.0003 |
| M12 | 0.0000 | 0.0709 | 0.0709 | 0.0000 |
| U1 | 0.0650 | 1.0000 | 0.3853 | 0.0647 |
| DEwe | DEwa | MAwe | MAwa | eChE | Rm L | Rm M | Rm S | D% L | D% M | D% S | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DEwe | 1.0000 | 0.7280 | −0.6897 | −0.8513 | 0.2004 | −0.5942 | −0.5868 | −0.6050 | 0.7589 | 0.7471 | 0.5335 |
| DEwa | 0.7280 | 1.0000 | −0.6084 | −0.8995 | 0.0158 | −0.3252 | −0.3201 | −0.3378 | 0.2399 | 0.2028 | 0.1158 |
| MAwe | −0.6897 | −0.6084 | 1.0000 | 0.4379 | −0.0605 | 0.1961 | 0.1949 | 0.1748 | −0.7120 | −0.7076 | −0.7269 |
| MAwa | −0.8513 | −0.8995 | 0.4379 | 1.0000 | −0.1346 | 0.5837 | 0.5766 | 0.6078 | −0.3130 | −0.2921 | −0.0618 |
| eChE | 0.2004 | 0.0158 | −0.0605 | −0.1346 | 1.0000 | 0.1777 | 0.1814 | 0.1504 | 0.0878 | 0.1457 | −0.1304 |
| Rm L | −0.5942 | −0.3252 | 0.1961 | 0.5837 | 0.1777 | 1.0000 | 0.9999 | 0.9985 | −0.3414 | −0.3811 | −0.1816 |
| Rm M | −0.5868 | −0.3201 | 0.1949 | 0.5766 | 0.1814 | 0.9999 | 1.0000 | 0.9980 | −0.3364 | −0.3770 | −0.1799 |
| Rm S | −0.6050 | −0.3378 | 0.1748 | 0.6078 | 0.1504 | 0.9985 | 0.9980 | 1.0000 | −0.3296 | −0.3677 | −0.1538 |
| D% L | 0.7589 | 0.2399 | −0.7120 | −0.3130 | 0.0878 | −0.3414 | −0.3364 | −0.3296 | 1.0000 | 0.9913 | 0.9278 |
| D% M | 0.7471 | 0.2028 | −0.7076 | −0.2921 | 0.1457 | −0.3811 | −0.3770 | −0.3677 | 0.9913 | 1.0000 | 0.9157 |
| D% S | 0.5335 | 0.1158 | −0.7269 | −0.0618 | −0.1304 | −0.1816 | −0.1799 | −0.1538 | 0.9278 | 0.9157 | 1.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokarska, M.; Gebremariam, A.; Puszkarz, A.K. Assessment of the Influence of Fabric Structure on Their Electro-Conductive Properties. Materials 2024, 17, 2692. https://doi.org/10.3390/ma17112692
Tokarska M, Gebremariam A, Puszkarz AK. Assessment of the Influence of Fabric Structure on Their Electro-Conductive Properties. Materials. 2024; 17(11):2692. https://doi.org/10.3390/ma17112692
Chicago/Turabian StyleTokarska, Magdalena, Ayalew Gebremariam, and Adam K. Puszkarz. 2024. "Assessment of the Influence of Fabric Structure on Their Electro-Conductive Properties" Materials 17, no. 11: 2692. https://doi.org/10.3390/ma17112692
APA StyleTokarska, M., Gebremariam, A., & Puszkarz, A. K. (2024). Assessment of the Influence of Fabric Structure on Their Electro-Conductive Properties. Materials, 17(11), 2692. https://doi.org/10.3390/ma17112692






