Strength of Composite Pressure Insulators for High Voltage Circuit Breakers: An Experimental and Numerical Investigation
Abstract
:1. Introduction
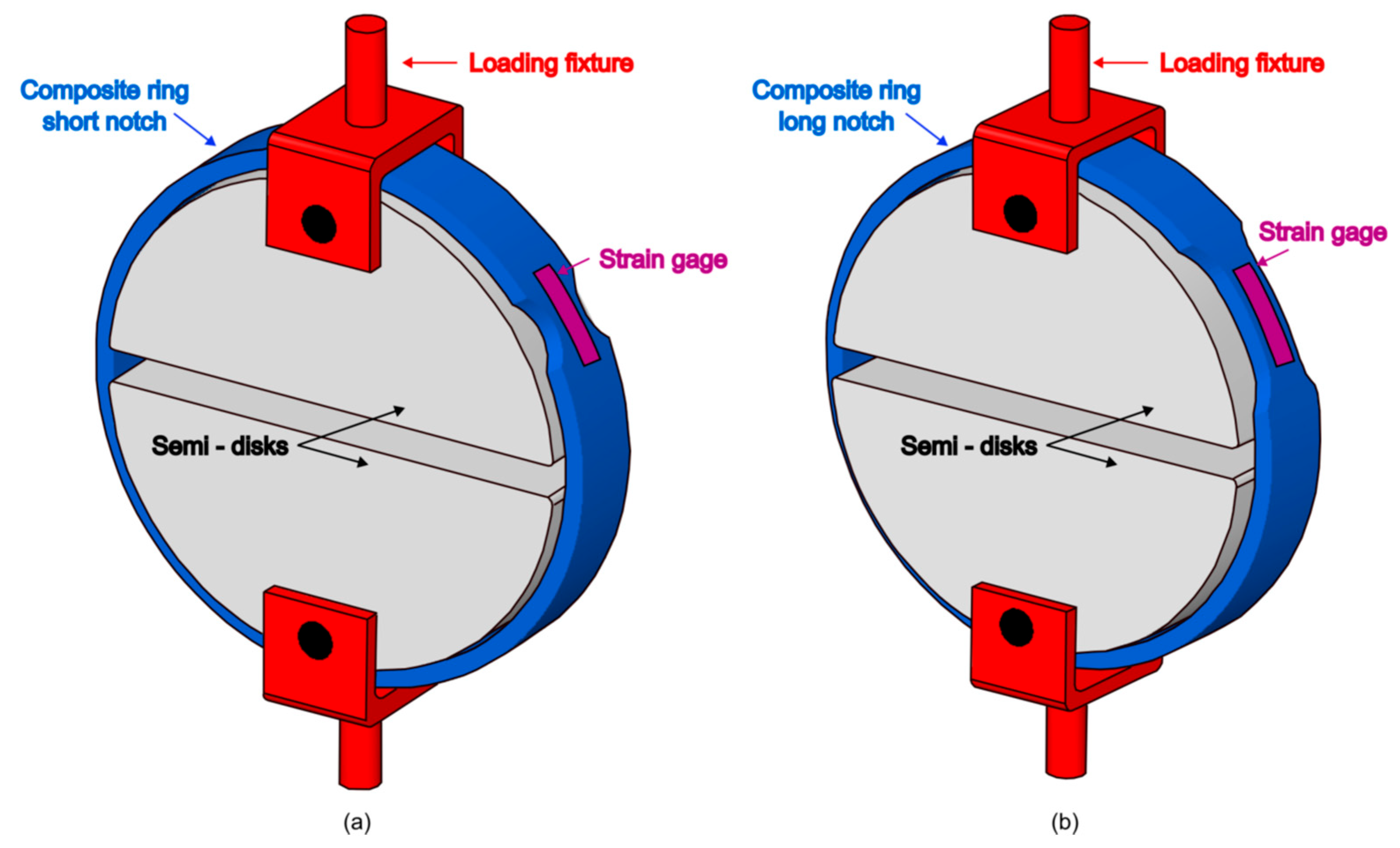
2. Materials and Experimental Methods
3. Experimental Results
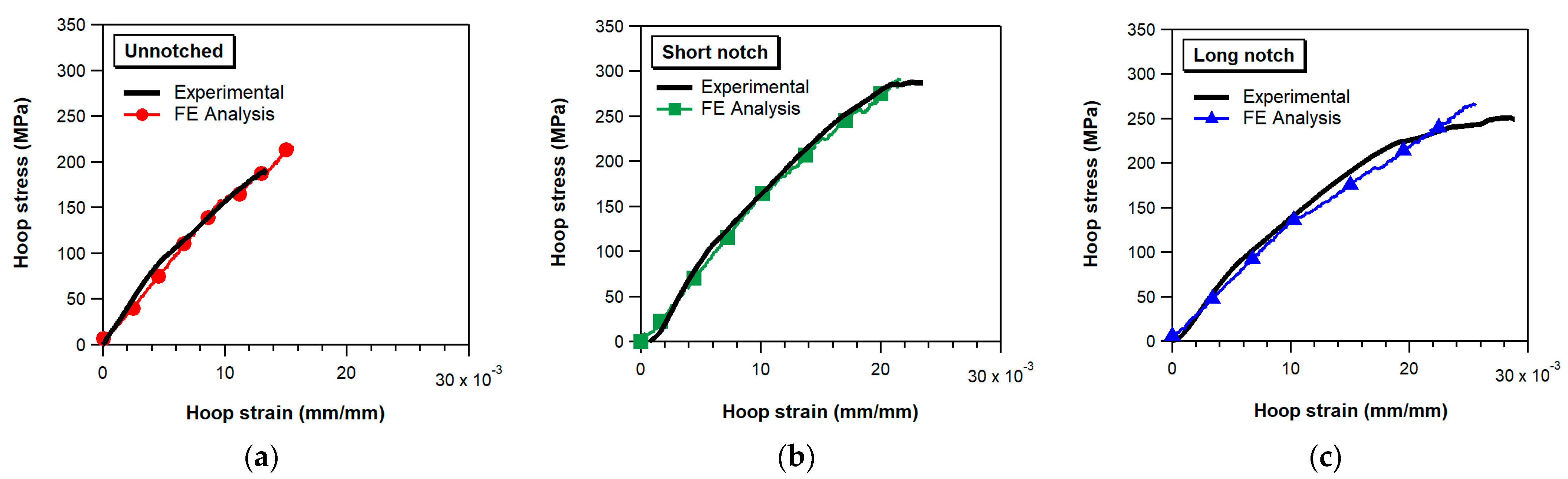
4. FE Model
5. Results and Discussion
6. Conclusions
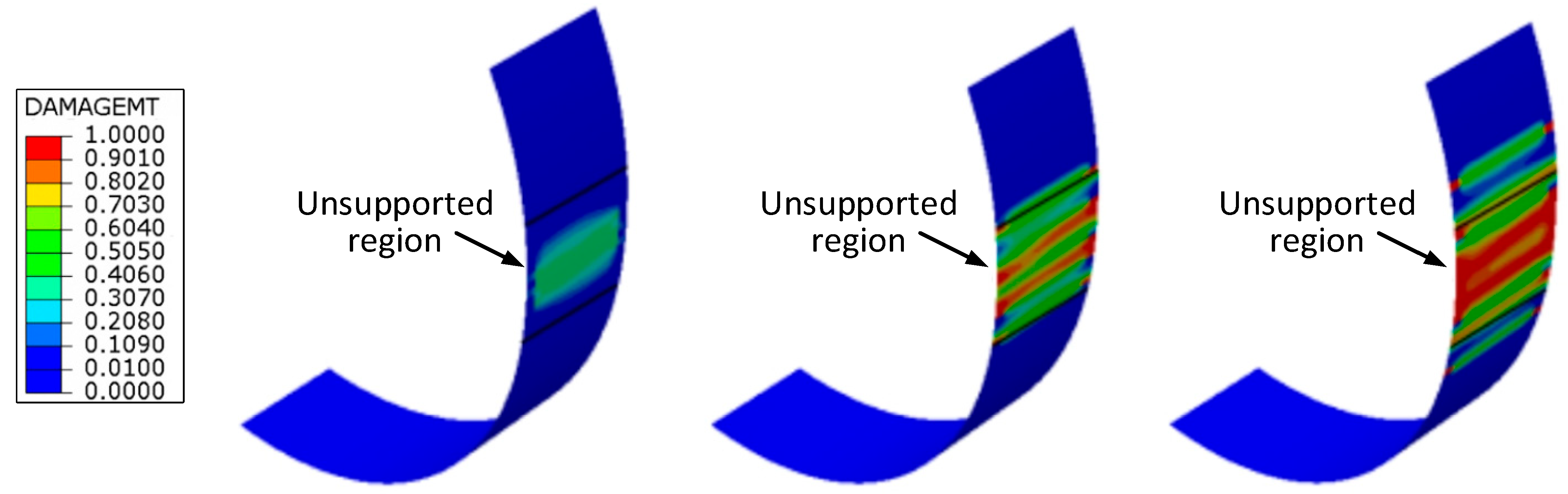
- Significant bending and stress concentration effects occur in the unsupported portion of the specimen at the gap between the semi-disks. The introduction of an area reduction via a notch is necessary to enforce failure in a region of the specimen not affected by these stress disturbances.
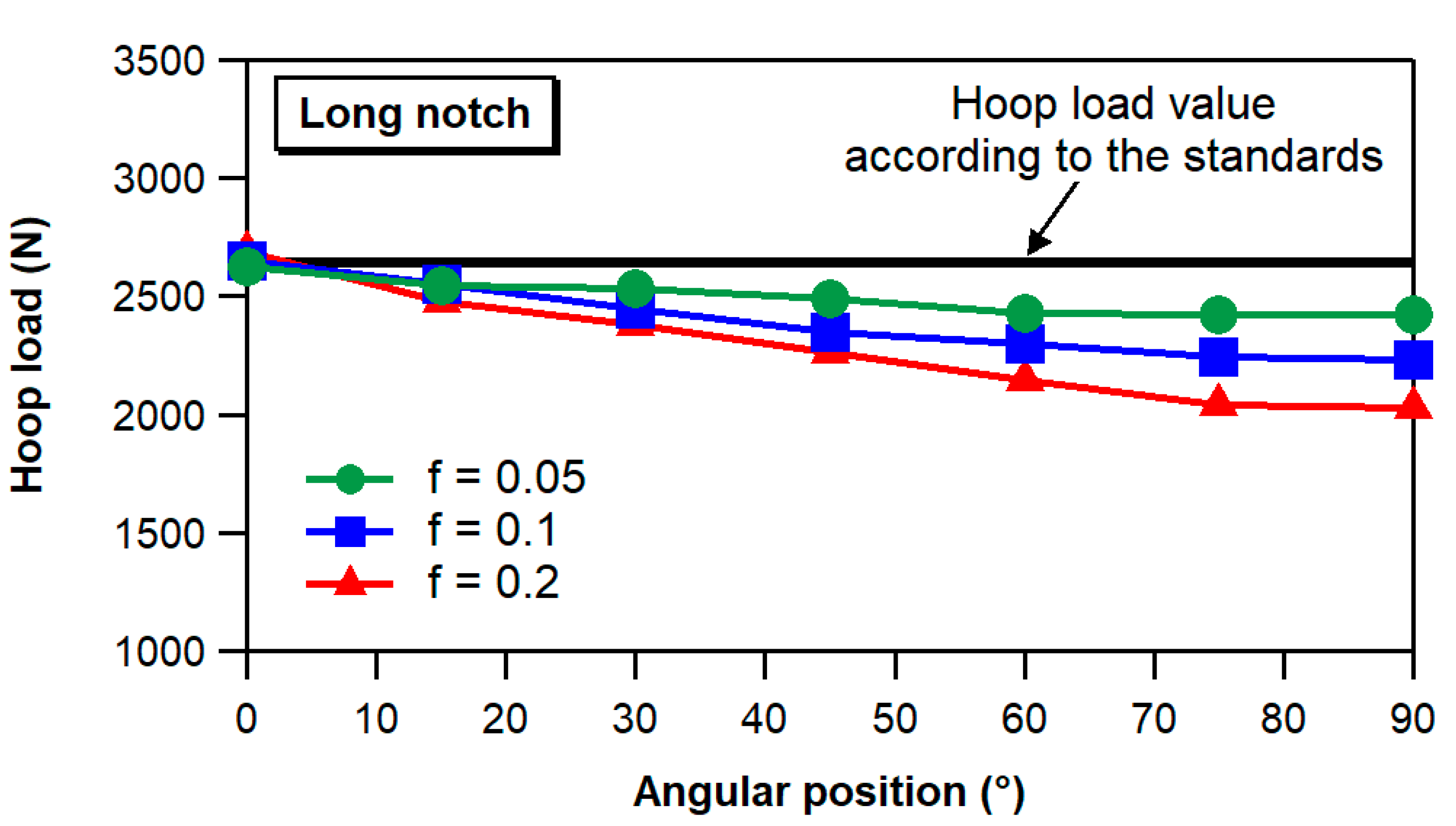
- The friction between the specimen and the semi-disks has a noteworthy effect on the hoop load applied to the specimen wall by the split-disk fixture. Large friction forces between the semi-disks and the specimen result in hoop load values greatly dependent on the angular position and significantly lower than those estimated in accordance with the ASTM and EN standards. In contrast, an almost constant distribution of the hoop load, which is thus representative of the real operating conditions of the pressurized insulator, can be achieved by careful lubrication of the disk/specimen contact surface.
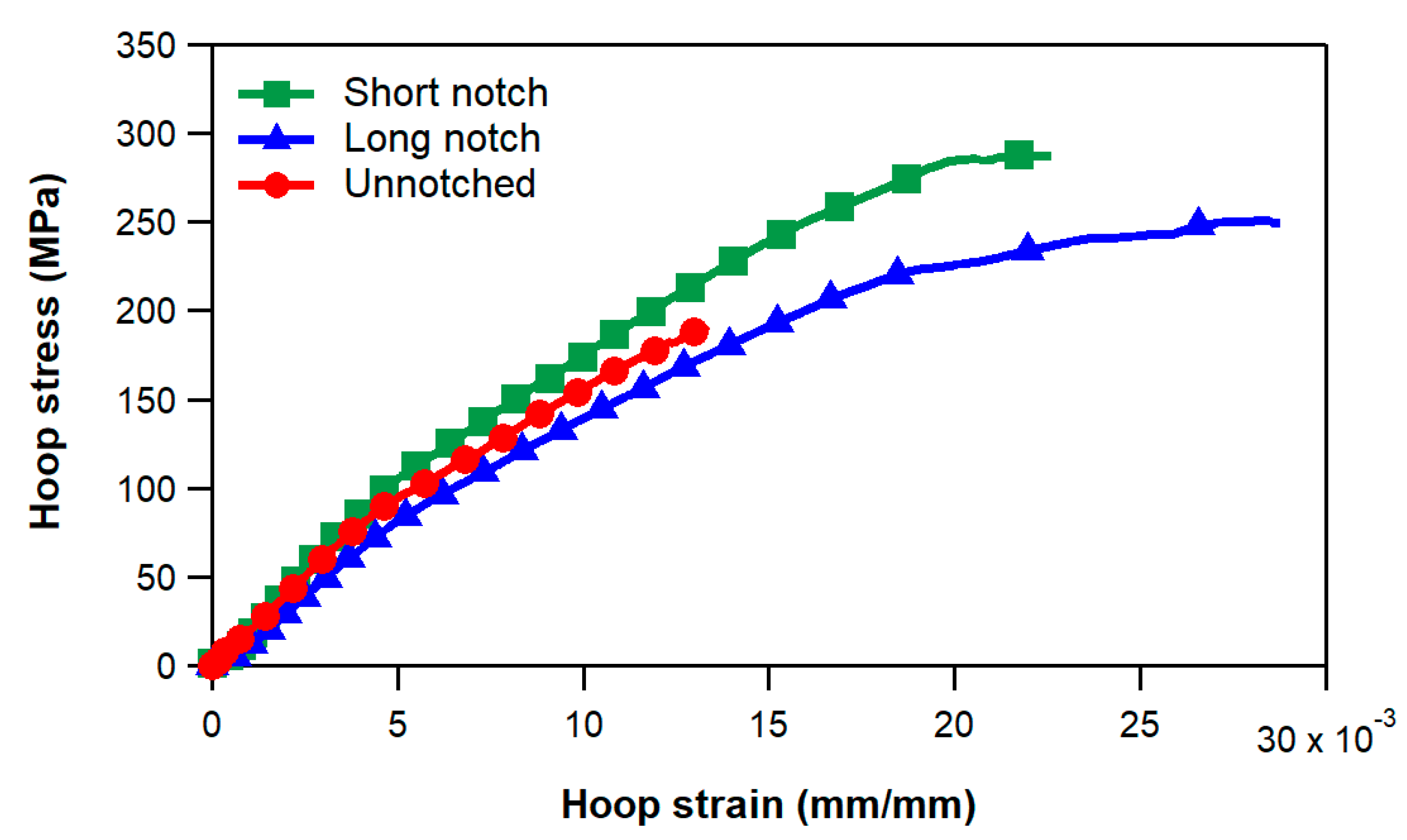
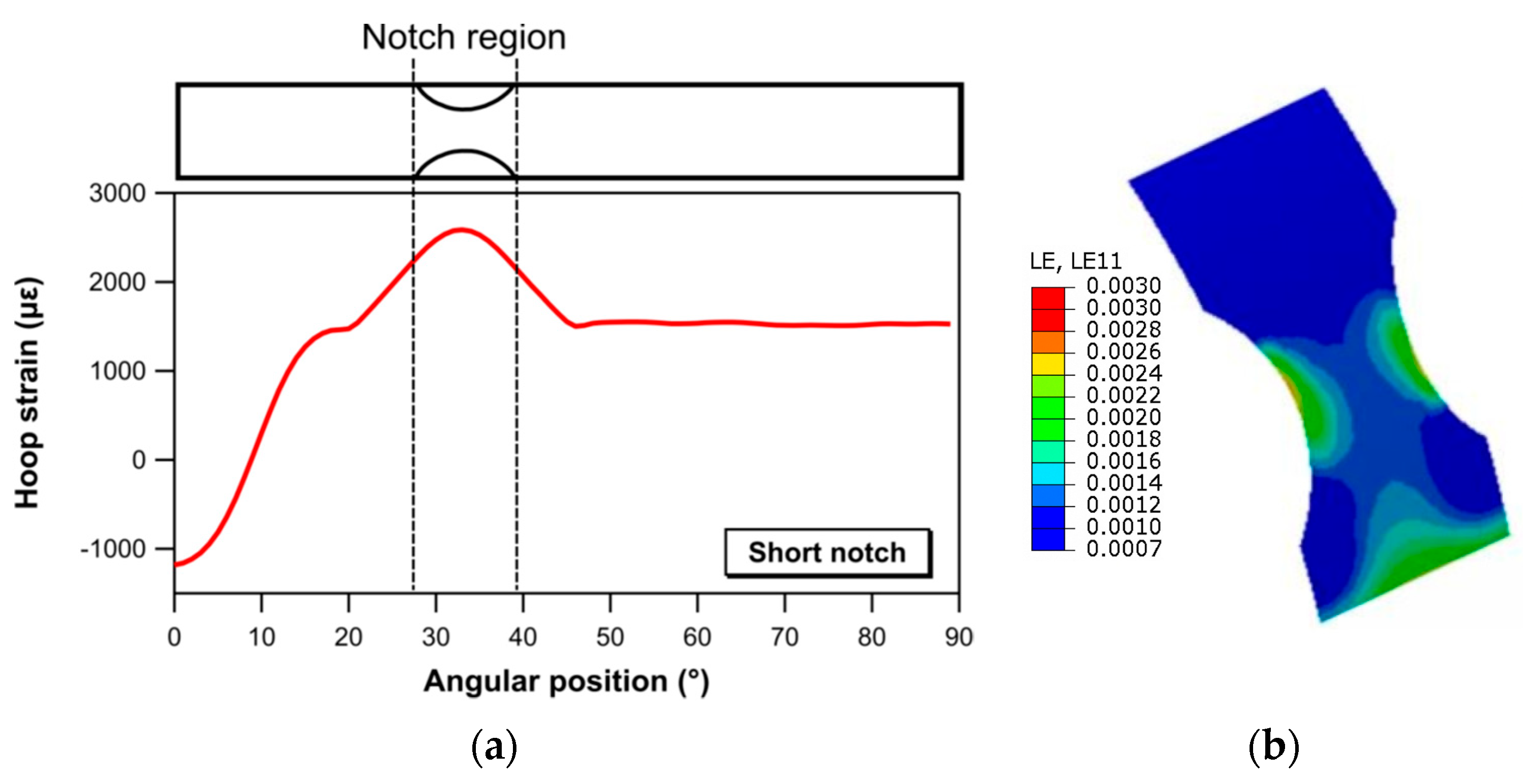
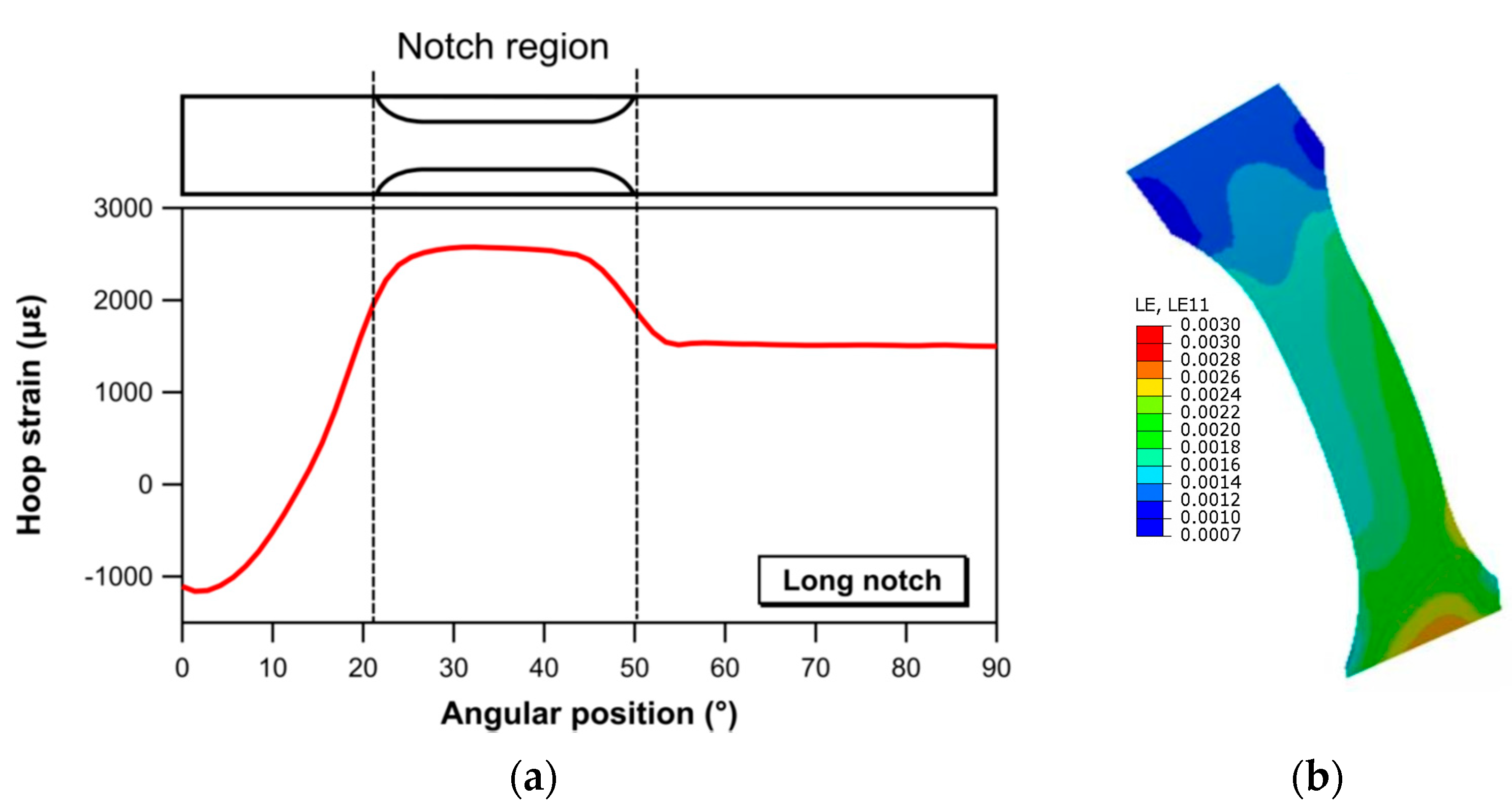
- The FE analyses show that the notch geometry specified by the ASTM and EN standards (short notch) for introducing an area reduction is not capable of generating a strain field with a uniform distribution. Conversely, a rather homogeneous strain distribution is achieved on the specimen with the notch geometry proposed in this study (long notch), which is characterized by a 20 mm long gauge length.
- The results of the experimental tests and of the FE analyses show that the hoop strength evaluated on the short notch specimens is higher than that determined on the long notch specimens. These results suggest that special caution must be taken when evaluating the hoop strength of the composite vessel using specimens with notch geometries that induce markedly non-uniform strain distributions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Imai, T. Polymer Composites for Switchgears. In Polymer Composites for Electrical Engineering; Huang, X., Tanaka, T., Eds.; Wiley: Hoboken, NJ, USA, 2021; pp. 339–375. ISBN 978-1-119-71960-1. [Google Scholar]
- Bosma, A.; Hammarsten, A.; Thomas, R. High-Voltage Live Tank Circuit-Breakers with Composite Insulators. In Proceedings of the PowerCon 2000, 2000 International Conference on Power System Technology, Proceedings (Cat. No.00EX409), Perth, WA, Australia, 4–7 December 2000; Volume 3, pp. 1217–1222. [Google Scholar]
- Peters, S.T. (Ed.) Composite Filament Winding; ASM International: Novelty, OH, USA, 2011; ISBN 978-1-61503-722-3. [Google Scholar]
- IEC Standard 61462; Composite Hollow Insulators-Pressurized and Unpressurized Insulators for Use in Electrical Equipment with Rated Voltage Greater than 1000 V—Definitions Test Methods Acceptance Criteria and Design Recommendations. IEC: Geneva, Switzerland, 2007.
- VSR.8.B.1—DM 1.12.1980; Regulation of Gas Pressure Containers with Mixed Membranes of Insulating and Metallic Material, Containing Active Parts of Equipment. Ministero delle Imprese e del Made in Italy: Roma, Italy, 1980. (In Italian)
- Perillo, G.; Vacher, R.; Grytten, F.; Sørbø, S.; Delhaye, V. Material Characterisation and Failure Envelope Evaluation of Filament Wound GFRP and CFRP Composite Tubes. Polym. Test. 2014, 40, 54–62. [Google Scholar] [CrossRef]
- Choi, S.; Pyo, S.; Suh, Y.S.; Seo, Y. Development of Notched Ring Test for Measuring Slow Cracking Resistance in Plastics Pipes and Fittings. Plast. Rubber Compos. 2007, 36, 219–225. [Google Scholar] [CrossRef]
- Cain, J.; Case, S.; Lesko, J. Testing of Hygrothermally Aged E-Glass/Epoxy Cylindrical Laminates Using a Novel Fixture for Simulating Internal Pressure. J. Compos. Constr. 2009, 13, 325–331. [Google Scholar] [CrossRef]
- Hwang, T.-K.; Park, J.-B.; Kim, H.-G. Evaluation of Fiber Material Properties in Filament-Wound Composite Pressure Vessels. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1467–1475. [Google Scholar] [CrossRef]
- Bois, C.; Pilato, A.; Wahl, J.-C.; Perry, N. Proposal for a Smart Pressurised Ring Test to Study Thick Composite Produced by Filament Winding. Compos. Part B Eng. 2013, 53, 382–390. [Google Scholar] [CrossRef]
- Horide, A.; Wakayama, S.; Kawahara, M. Characterization of Fracture Process during Ring Burst Test of FW-FRP Composites with Damage. Adv. Compos. Mater. 1999, 8, 139–151. [Google Scholar] [CrossRef]
- Kim, W.T.; Kim, S.S. Design of a Segment-Type Ring Burst Test Device to Evaluate the Pressure Resistance Performance of Composite Pressure Vessels. Compos. Struct. 2020, 242, 112199. [Google Scholar] [CrossRef]
- ASTM D2290-19a; Standard Test Method for Apparent Hoop Tensile Strength of Plastic or Reinforced Plastic Pipe. ASTM: West Conshohocken, PA, USA, 2019.
- EN 1394:1997; Plastics Piping Systems. Glass-Reinforced Thermosetting Plastics (GRP) Pipes. Determination of the Apparent Initial Circumferential Tensile Strength. American National Standards Institute: Washington, DC, USA, 2008.
- ISO 8521:2020; Glass-Reinforced Thermosetting Plastic (GRP) Pipes—Test Methods for the Determination of the Initial Circumferential Tensile Wall Strength. ISO: Geneva, Switzerland, 2020.
- Arsene, S.; Bai, J. A New Approach to Measuring Transverse Properties of Structural Tubing by a Ring Test. J. Test. Eval. 1996, 24, 386–391. [Google Scholar] [CrossRef]
- Walsh, E.J.; Adams, D.O. Development and Evaluation of the Quadrant Ring Test Method. Exp Mech. 2008, 48, 319–326. [Google Scholar] [CrossRef]
- Bilalis, E.P.; Tsouvalis, N.G. Finite Element Analysis of Filament Wound Composite Materials Split Disk Tests. In Advances in the Analysis and Design of Marine Structures, Proceedings of the 9th International Conference on Marine Structures (MARSTRUCT 2023), Gothenburg, Sweden, 3–5 April 2023; CRC Press: London, UK, 2023; pp. 691–698. ISBN 978-1-00-339975-9. [Google Scholar]
- Chatzinas, P.S.; Bilalis, E.P.; Papadakis, A.Z.; Tsouvalis, N.G. Effect of Manufacturing Parameters on the Mechanical Properties of Filament Wound Composite Materials. In Developments in the Analysis and Design of Marine Structures, Proceedings of the 8th International Conference on Marine Structures (MARSTRUCT 2021), Trondheim, Norway, 7–9 June 2021; CRC Press: London, UK, 2021; pp. 377–385. ISBN 978-1-00-323037-3. [Google Scholar]
- Jones, I.A.; Middleton, V.; Owen, M.J. Roller-Assisted Variant of the Split Disc Test for Filament-Wound Composites. Compos. Part A Appl. Sci. Manuf. 1996, 27, 287–294. [Google Scholar] [CrossRef]
- Kaynak, C.; Salim Erdiller, E.; Parnas, L.; Senel, F. Use of Split-Disk Tests for the Process Parameters of Filament Wound Epoxy Composite Tubes. Polym. Test. 2005, 24, 648–655. [Google Scholar] [CrossRef]
- Yoon, S.-H.; Kim, C.-G.; Cho, W.-M. Measurement of Tensile Properties Using Filament Wound Ring Specimens. J. Reinf. Plast. Compos. 1997, 16, 810–824. [Google Scholar] [CrossRef]
- Zhao, Y.; Druzhinin, P.; Ivens, J.; Vandepitte, D.; Lomov, S.V. Split-Disk Test with 3D Digital Image Correlation Strain Measurement for Filament Wound Composites. Compos. Struct. 2021, 263, 113686. [Google Scholar] [CrossRef]
- Demirci, M.T.; Tarakçıoğlu, N.; Avcı, A.; Akdemir, A.; Demirci, İ. Fracture Toughness (Mode I) Characterization of SiO2 Nanoparticle Filled Basalt/Epoxy Filament Wound Composite Ring with Split-Disk Test Method. Compos. Part B Eng. 2017, 119, 114–124. [Google Scholar] [CrossRef]
- Eggers, F.; Almeida, J.H.S.; Azevedo, C.B.; Amico, S.C. Mechanical Response of Filament Wound Composite Rings under Tension and Compression. Polym. Test. 2019, 78, 105951. [Google Scholar] [CrossRef]
- Kara, M.; Kirici, M.; Cagan, S.C. Effects of the Number of Fatigue Cycles on the Hoop Tensile Strength of Glass Fiber/Epoxy Composite Pipes. J. Fail. Anal. Prev. 2019, 19, 1181–1186. [Google Scholar] [CrossRef]
- Paessler, M.; Miaris, A.; Schledjewski, R.; Mitschang, P. Ring Winding Technology: Increased Process Efficiency and Effects on the Mechanical Properties of Ring Specimens. In Proceedings of the ASME 2011 Pressure Vessels and Piping Conference. Volume 6: Materials and Fabrication, Parts A and B, Baltimore, Maryland, USA, 17–21 July 2011; ASME: Baltimore, MD, USA, 2011; pp. 69–77. [Google Scholar]
- Shabani, P.; Taheri-Behrooz, F.; Maleki, S.; Hasheminasab, M. Life Prediction of a Notched Composite Ring Using Progressive Fatigue Damage Models. Compos. Part B Eng. 2019, 165, 754–763. [Google Scholar] [CrossRef]
- Srebrenkoska, S.; Kochoski, F.; Srebrenkoska, V.; Risteska, S.; Kotynia, R. Effect of Process Parameters on Thermal and Mechanical Properties of Filament Wound Polymer-Based Composite Pipes. Polymers 2023, 15, 2829. [Google Scholar] [CrossRef]
- Toh, W.; Tan, L.B.; Tse, K.M.; Giam, A.; Raju, K.; Lee, H.P.; Tan, V.B.C. Material Characterization of Filament-Wound Composite Pipes. Compos. Struct. 2018, 206, 474–483. [Google Scholar] [CrossRef]
- Simulia. ABAQUS Simulia, ABAQUS, User’s Manual; Version 6.22; Simulia: Providence, RI, USA, 2022. [Google Scholar]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A Fatigue Failure Criterion for Fiber Reinforced Materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Matzenmiller, A.; Lubliner, J.; Taylor, R.L. A Constitutive Model for Anisotropic Damage in Fiber-Composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Lapczyk, I.; Hurtado, J.A. Progressive Damage Modeling in Fiber-Reinforced Materials. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2333–2341. [Google Scholar] [CrossRef]
- Barbero, E.J.; Cosso, F.A.; Roman, R.; Weadon, T.L. Determination of Material Parameters for Abaqus Progressive Damage Analysis of E-Glass Epoxy Laminates. Compos. Part B Eng. 2013, 46, 211–220. [Google Scholar] [CrossRef]
- Soden, P.D.; Hinton, M.J.; Kaddour, A.S. Lamina Properties, Lay-up Configurations and Loading Conditions for a Range of Fibre-Reinforced Composite Laminates. Compos. Sci. Technol. 1998, 58, 1011–1022. [Google Scholar] [CrossRef]
- Tarfaoui, M.; Gning, P.B.; Hamitouche, L. Dynamic Response and Damage Modeling of Glass/Epoxy Tubular Structures: Numerical Investigation. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1–12. [Google Scholar] [CrossRef]
- Perillo, G.; Vedivik, N.; Echtermeyer, A. Numerical and Experimental Investigation of Impact on Filament Wound Glass Reinforced Epoxy Pipe. J. Compos. Mater. 2015, 49, 723–738. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Khosravani, M.R.; Hamzah, R.I.R.; Tamin, M.N. FE Model-Based Construction and Progressive Damage Processes of FRP Composite Laminates with Different Manufacturing Processes. Int. J. Mech. Sci. 2018, 141, 223–235. [Google Scholar] [CrossRef]
- Mahdavi, H.; Rahimi, G.H.; Farrokhabadi, A. Failure Analysis of (±55°)9 Filament-Wound GRE Pipes Using Explicit Finite Element Method: A Comparison with the Experimental Method. J. Fail. Anal. Prev. 2018, 18, 1526–1533. [Google Scholar] [CrossRef]
- Yao, L.; Wang, S.; Meng, X.; Zhang, C. Numerical and Experimental Investigation of the Burst Resistance of Glass-Fiber Thermoplastic Composite Pipes under Internal Pressure. Mech. Compos. Mater. 2021, 57, 211–224. [Google Scholar] [CrossRef]
- Ruggiero, A.; Merola, M.; Carlone, P.; Archodoulaki, V.-M. Tribo-Mechanical Characterization of Reinforced Epoxy Resin under Dry and Lubricated Contact Conditions. Compos. Part B Eng. 2015, 79, 595–603. [Google Scholar] [CrossRef]





| Unnotched | Short Notch | Long Notch | |
|---|---|---|---|
| Hoop strength (MPa) | 190 | 290 | 238 |
| Standard deviation (MPa) | 8.6 | 4.5 | 13.6 |
| Number of tested samples | 6 | 10 | 24 |
| Elastic Properties | Hashin Damage Model Parameters | ||
|---|---|---|---|
| ) | 38.6 GPa | ) | 950 MPa |
| ) | 6.0 GPa | ) | 500 MPa |
| ) | 6.0 GPa | ) | 50 MPa |
| ) | 2.0 GPa | ) | 320 MPa |
| Poisson’s coefficient | 0.27 | ) | 100 MPa |
| ) | 100 MPa | ||
| ) | 20 N/mm | ||
| ) | 20 N/mm | ||
| ) | 1.2 N/mm | ||
| ) | 1.2 N/mm | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferino, J.; Loi, G.; Meleddu, A.; Aymerich, F.; Mazzarelli, I.; Pichini, E. Strength of Composite Pressure Insulators for High Voltage Circuit Breakers: An Experimental and Numerical Investigation. Materials 2024, 17, 2741. https://doi.org/10.3390/ma17112741
Ferino J, Loi G, Meleddu A, Aymerich F, Mazzarelli I, Pichini E. Strength of Composite Pressure Insulators for High Voltage Circuit Breakers: An Experimental and Numerical Investigation. Materials. 2024; 17(11):2741. https://doi.org/10.3390/ma17112741
Chicago/Turabian StyleFerino, Jan, Gabriela Loi, Andrea Meleddu, Francesco Aymerich, Iuri Mazzarelli, and Elisa Pichini. 2024. "Strength of Composite Pressure Insulators for High Voltage Circuit Breakers: An Experimental and Numerical Investigation" Materials 17, no. 11: 2741. https://doi.org/10.3390/ma17112741
APA StyleFerino, J., Loi, G., Meleddu, A., Aymerich, F., Mazzarelli, I., & Pichini, E. (2024). Strength of Composite Pressure Insulators for High Voltage Circuit Breakers: An Experimental and Numerical Investigation. Materials, 17(11), 2741. https://doi.org/10.3390/ma17112741








