Analytical Modeling of Riveting Squeezing Force Considering Non-Uniform Deformation of Rivets in Aeronautical Structures
Abstract
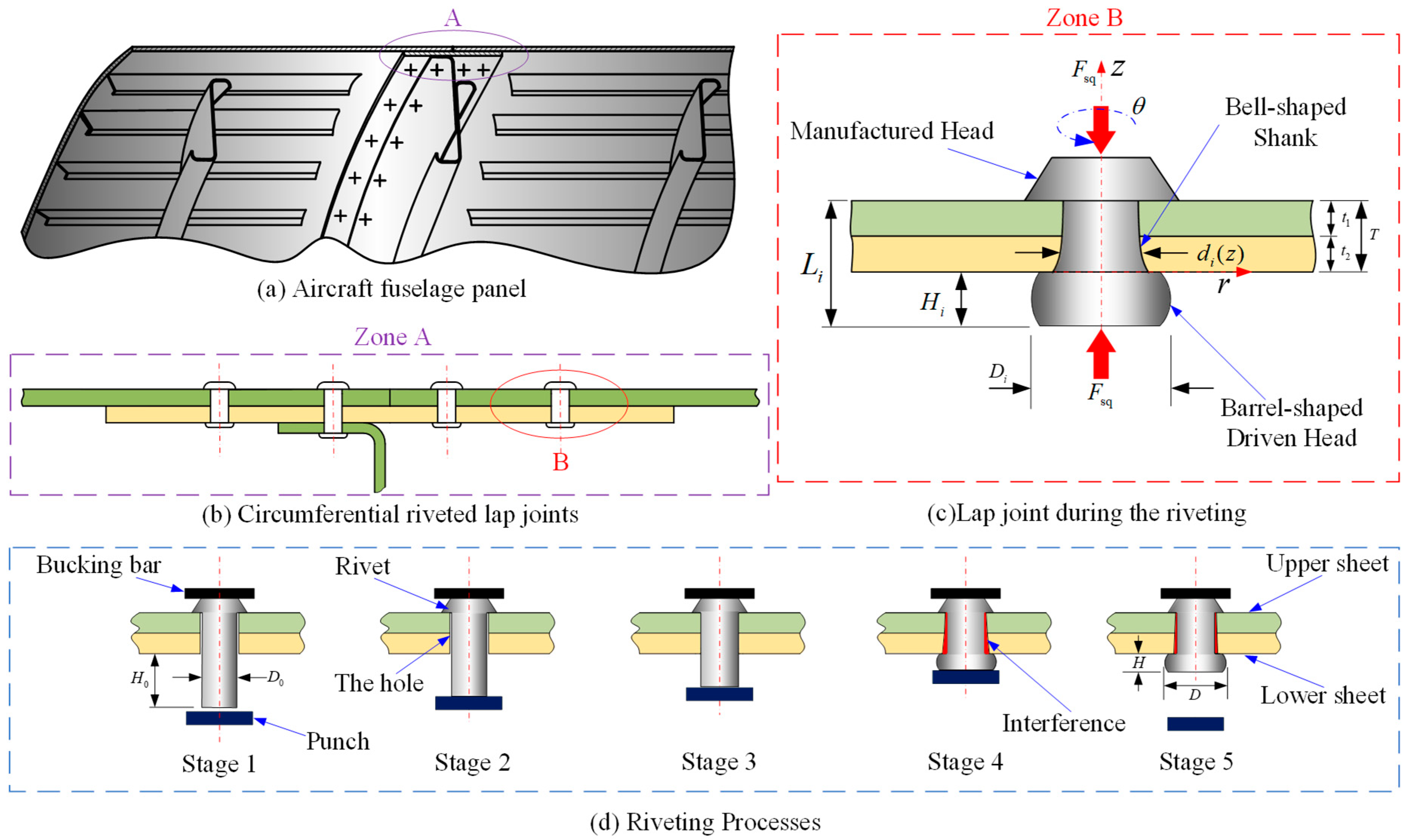
:1. Introduction
2. Squeeze Force Modeling Considering the Non-Uniform Deformation of the Rivet
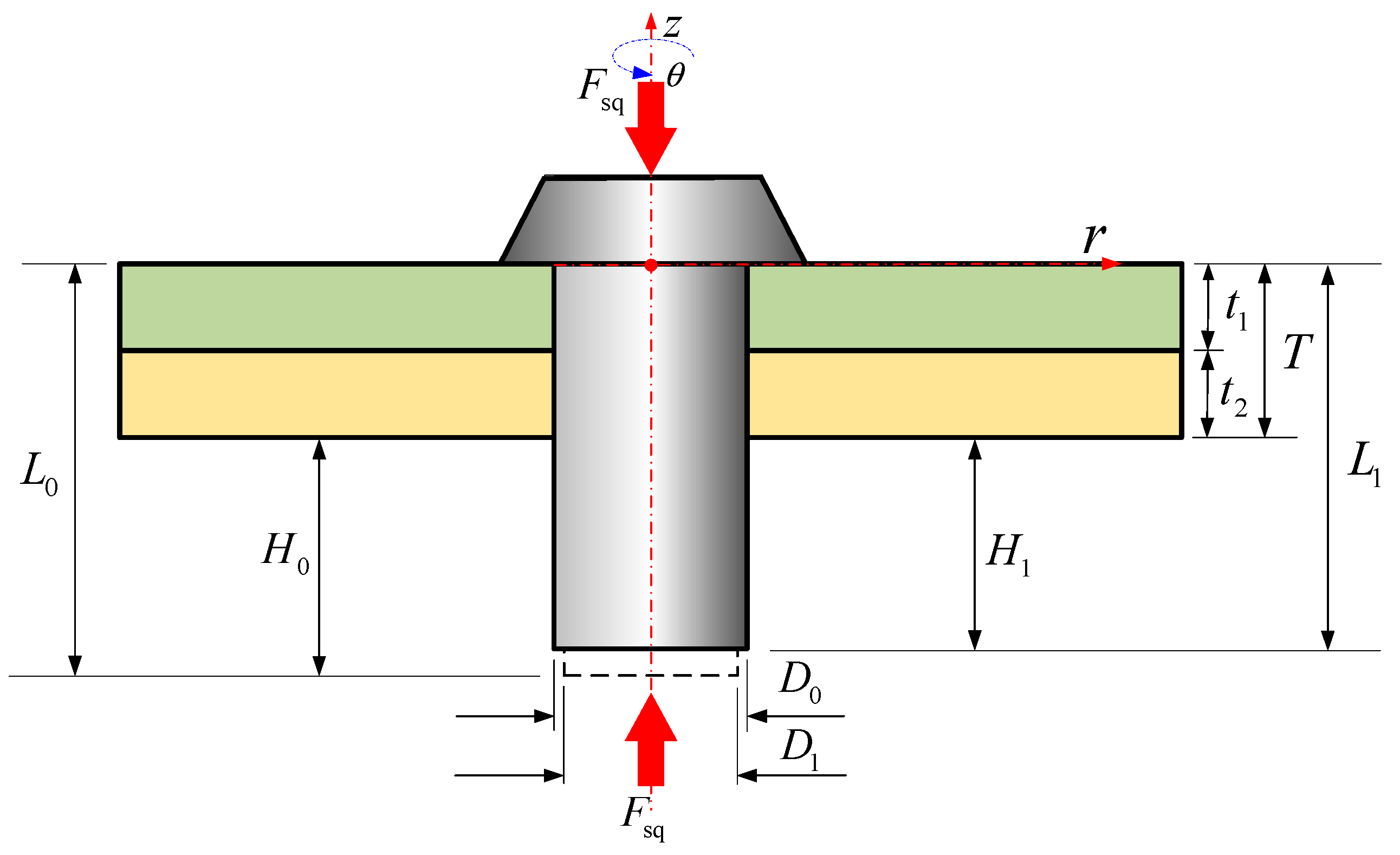
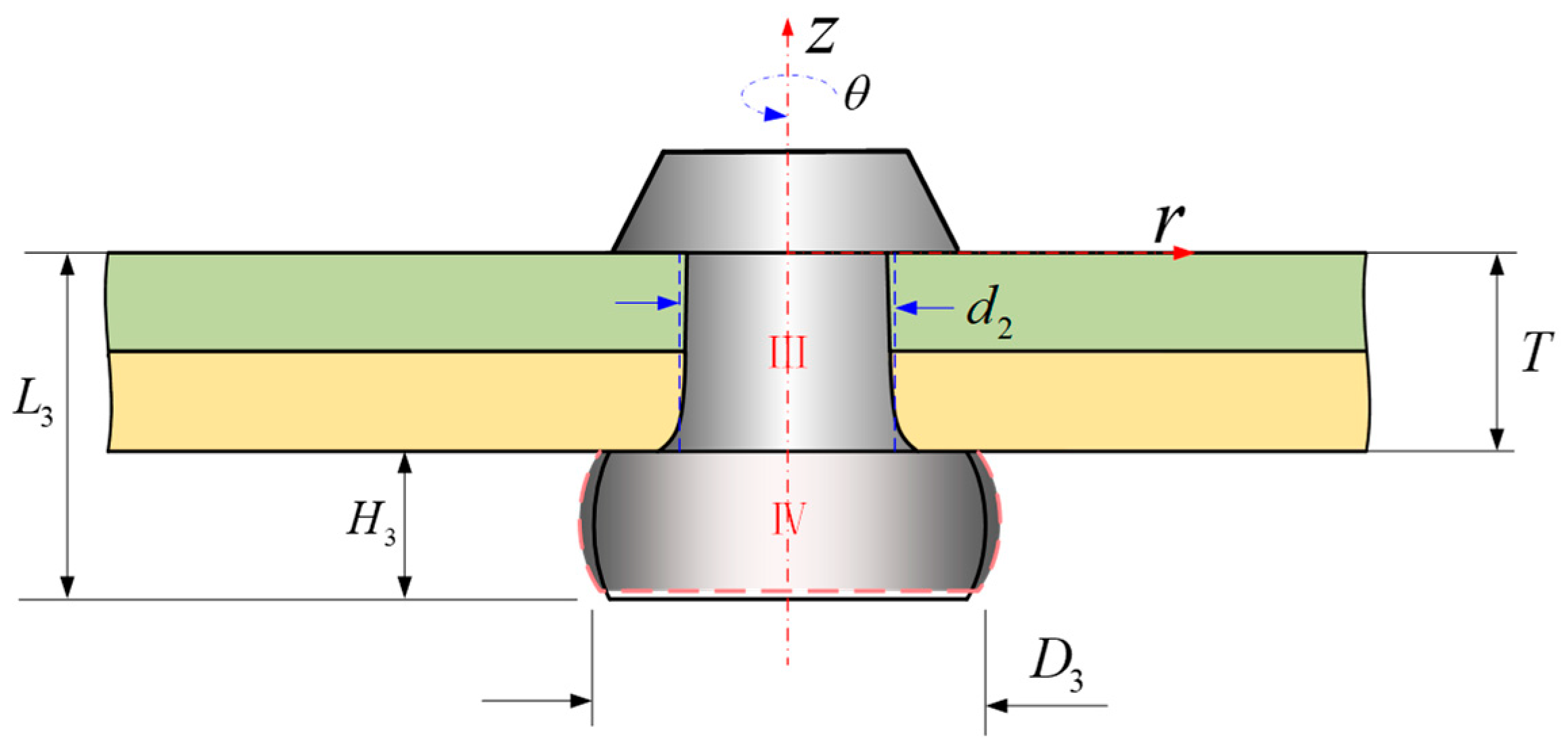
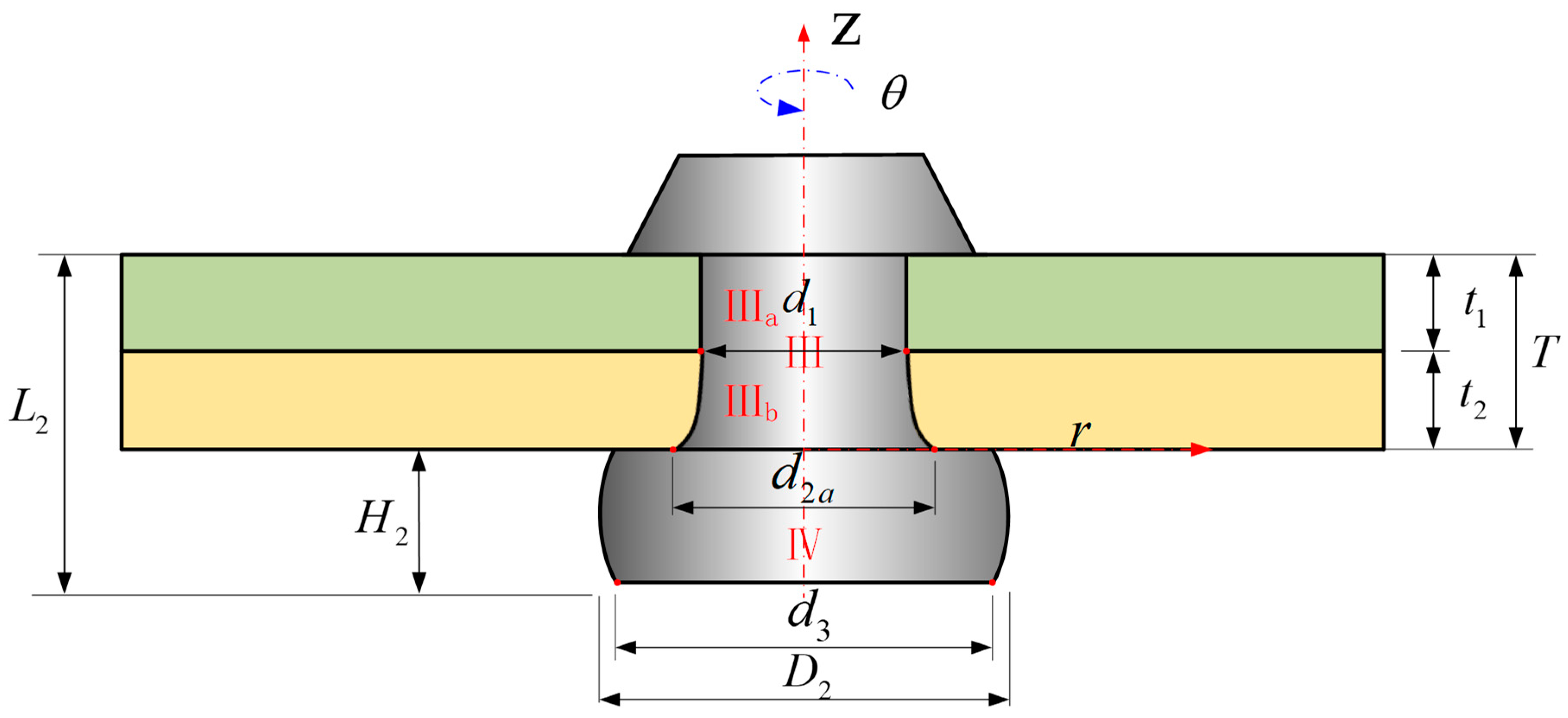
2.1. Determination of Rivet Volume at Various Stages
2.2. Riveting Squeezing Force Modeling
2.3. The Determination of the Unknown Parameters
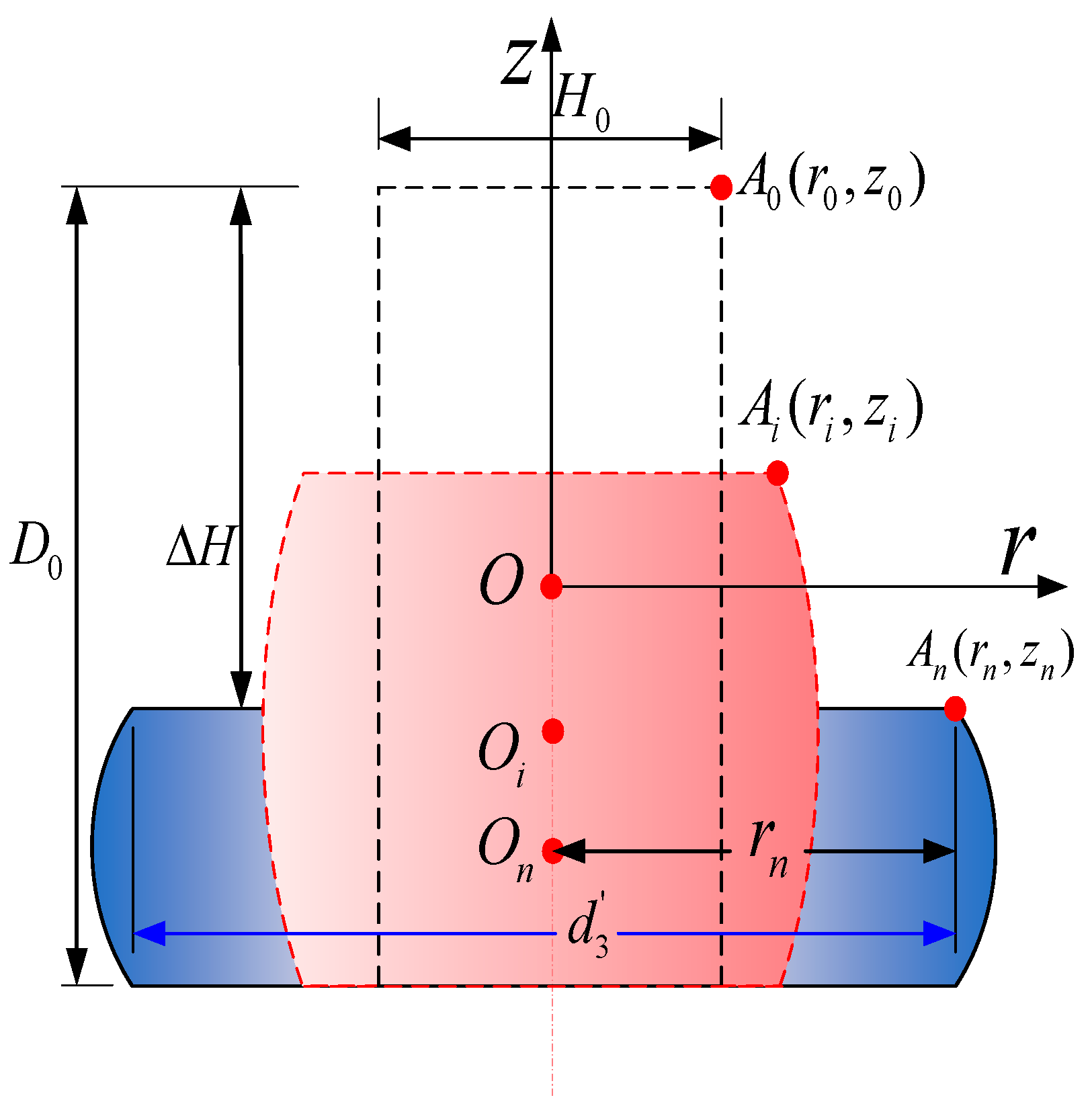
2.3.1. Estimation of Considering the Barrel-Shaped Effect
2.3.2. The Expanded Hole Diameter d2a Considering the Non-Uniform Interference Fit
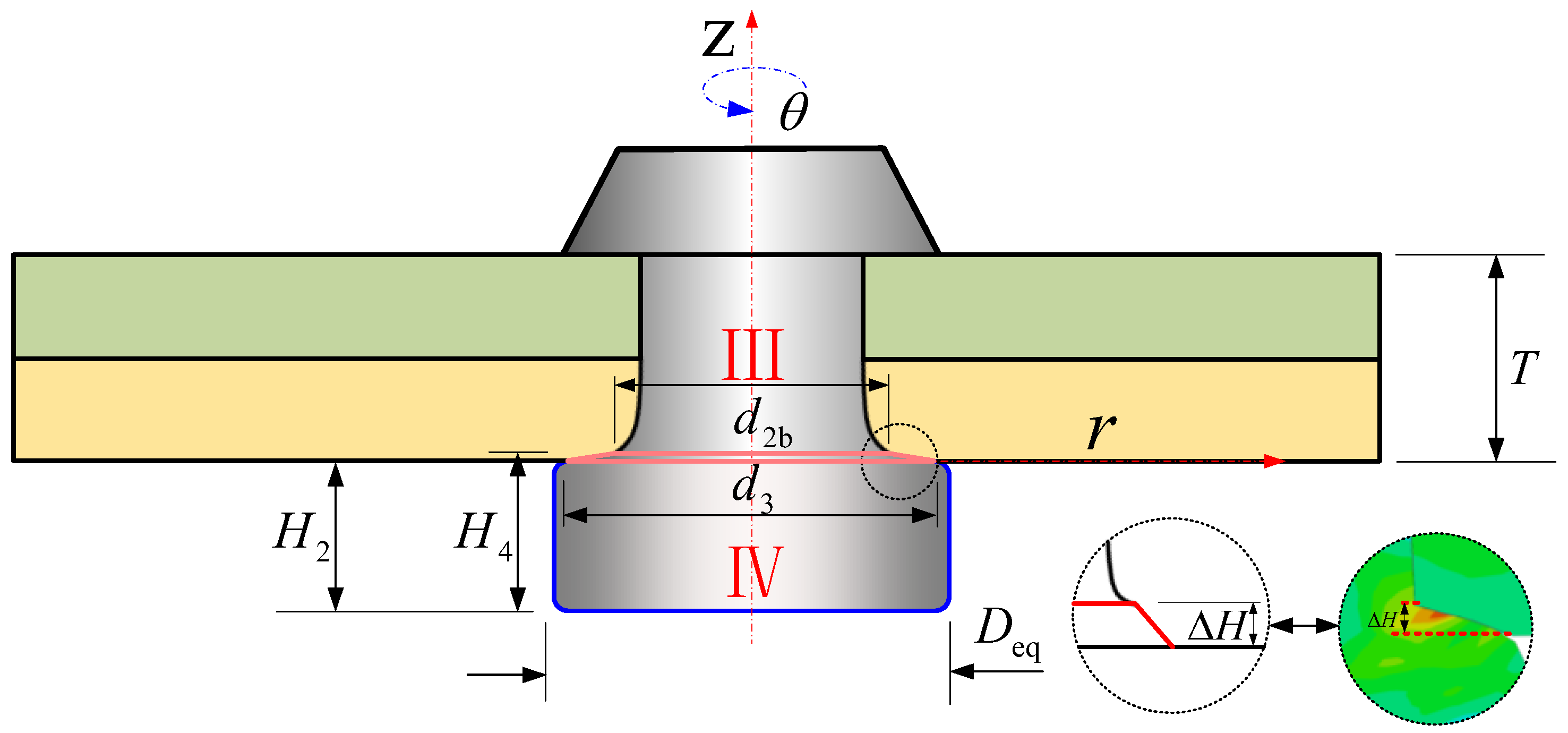
2.3.3. The Influence of the Material Inserted into the Hole on the Dimensions of the Driven Head
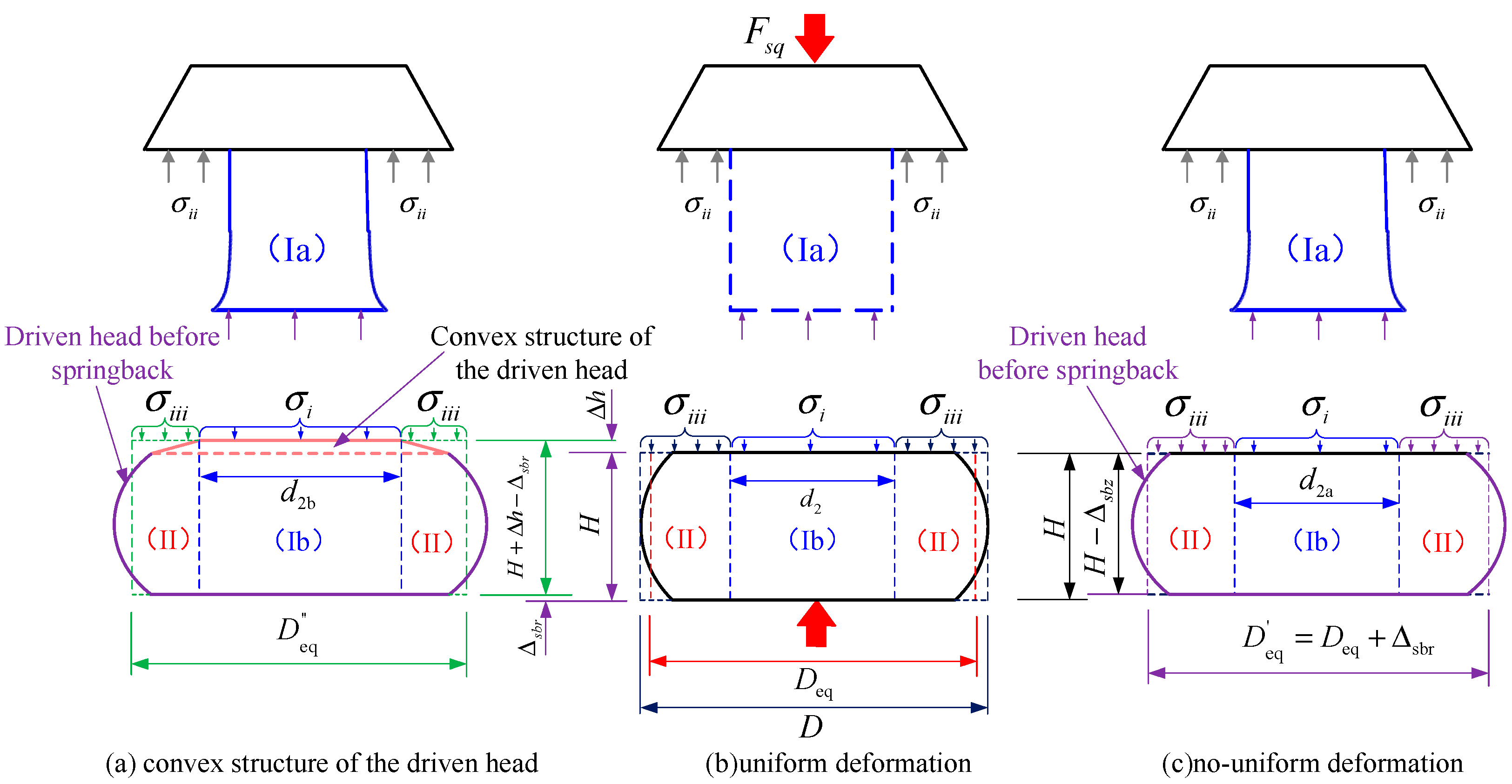
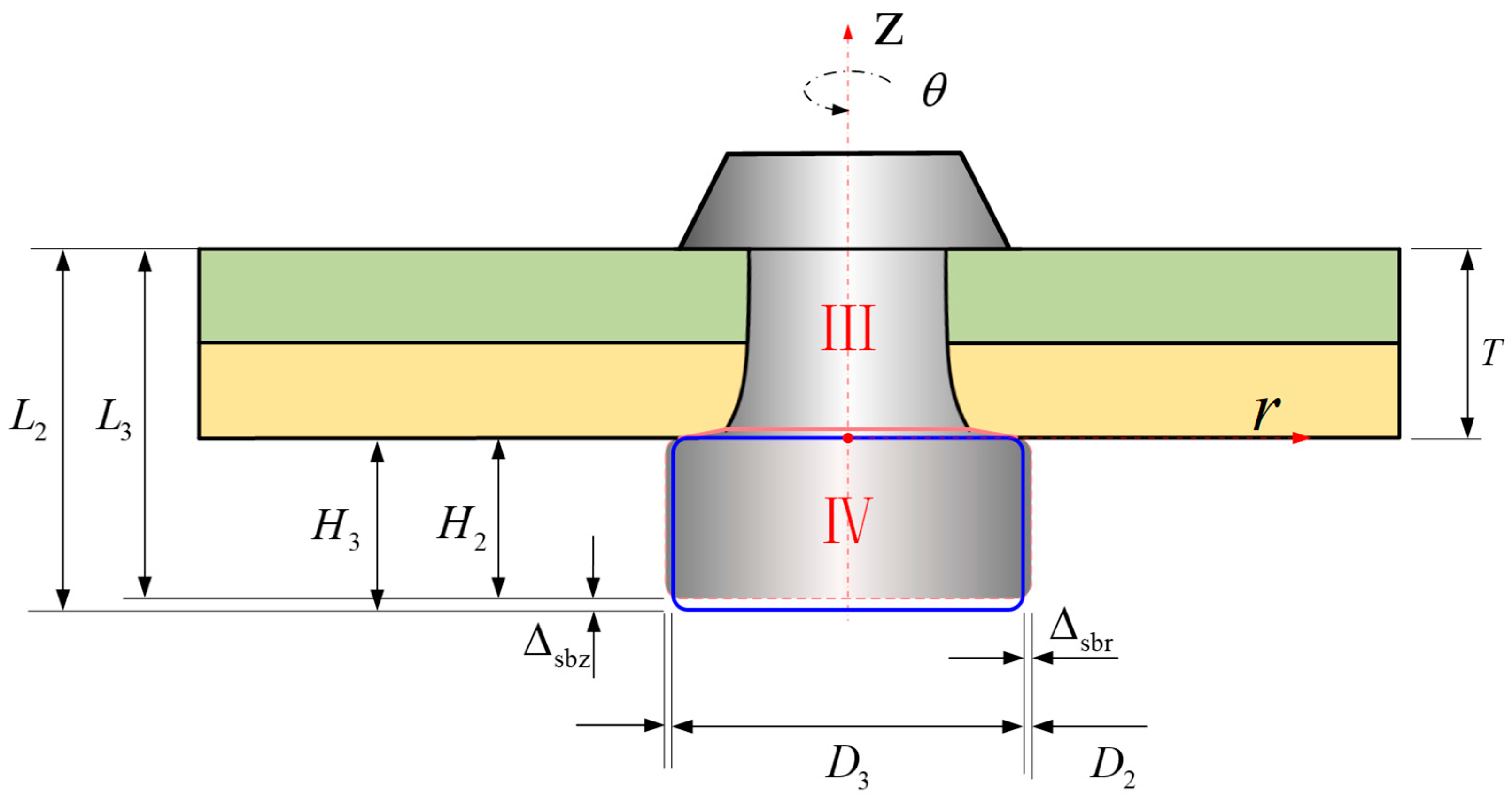
2.3.4. The Spring-Back and Influence of Rivet after the Pressure Has Been Removed
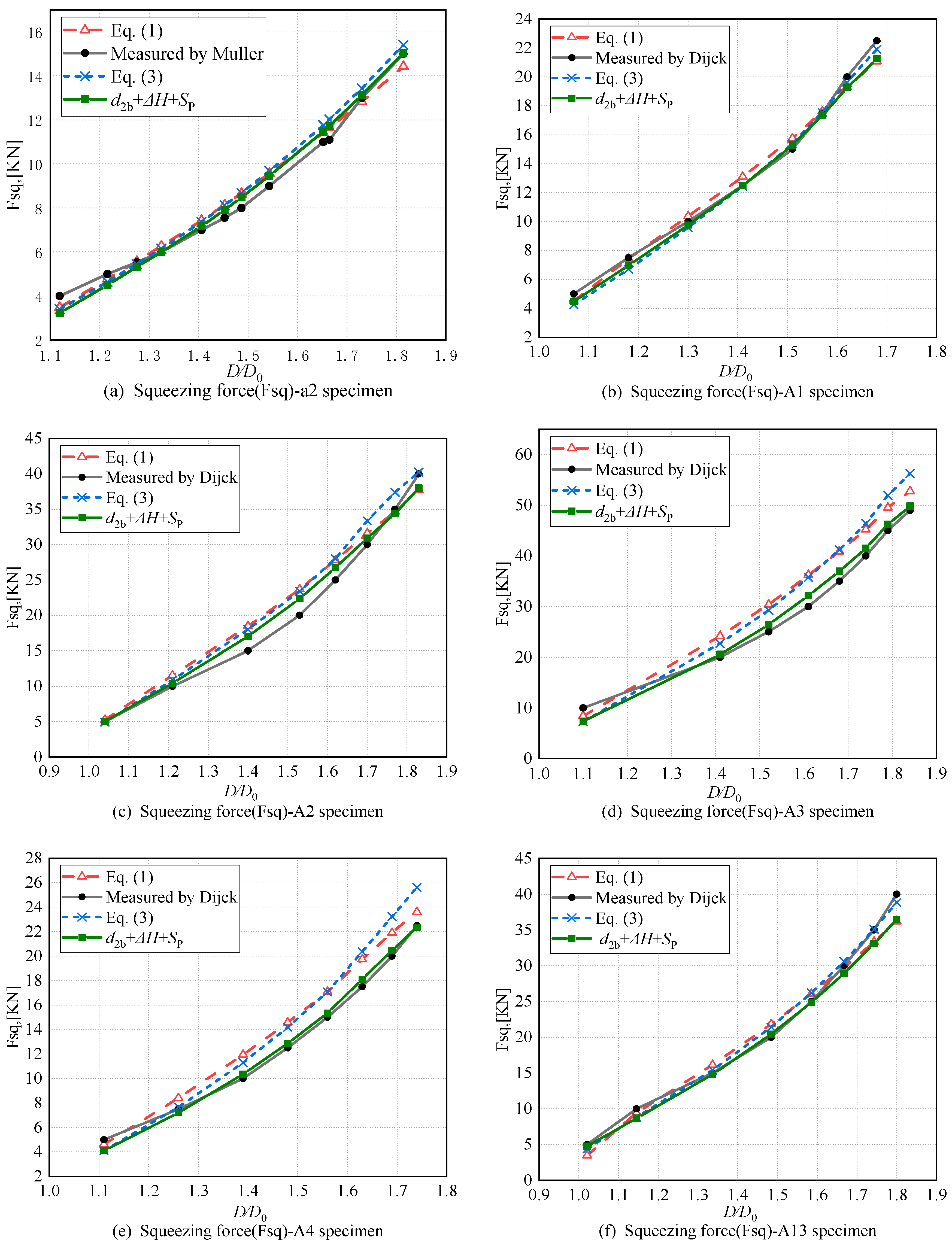
3. Calculation Results and Discussion
- (1)
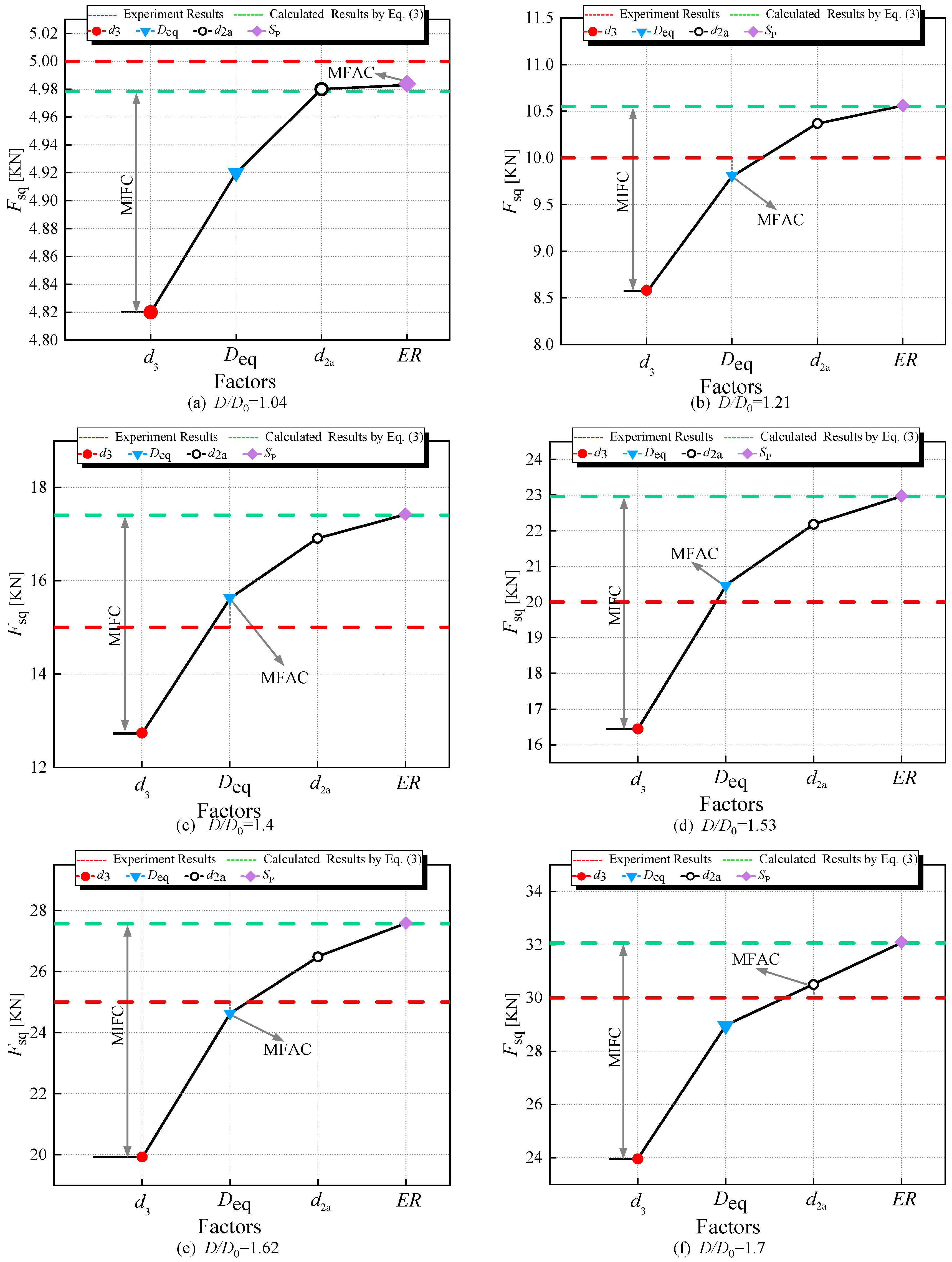
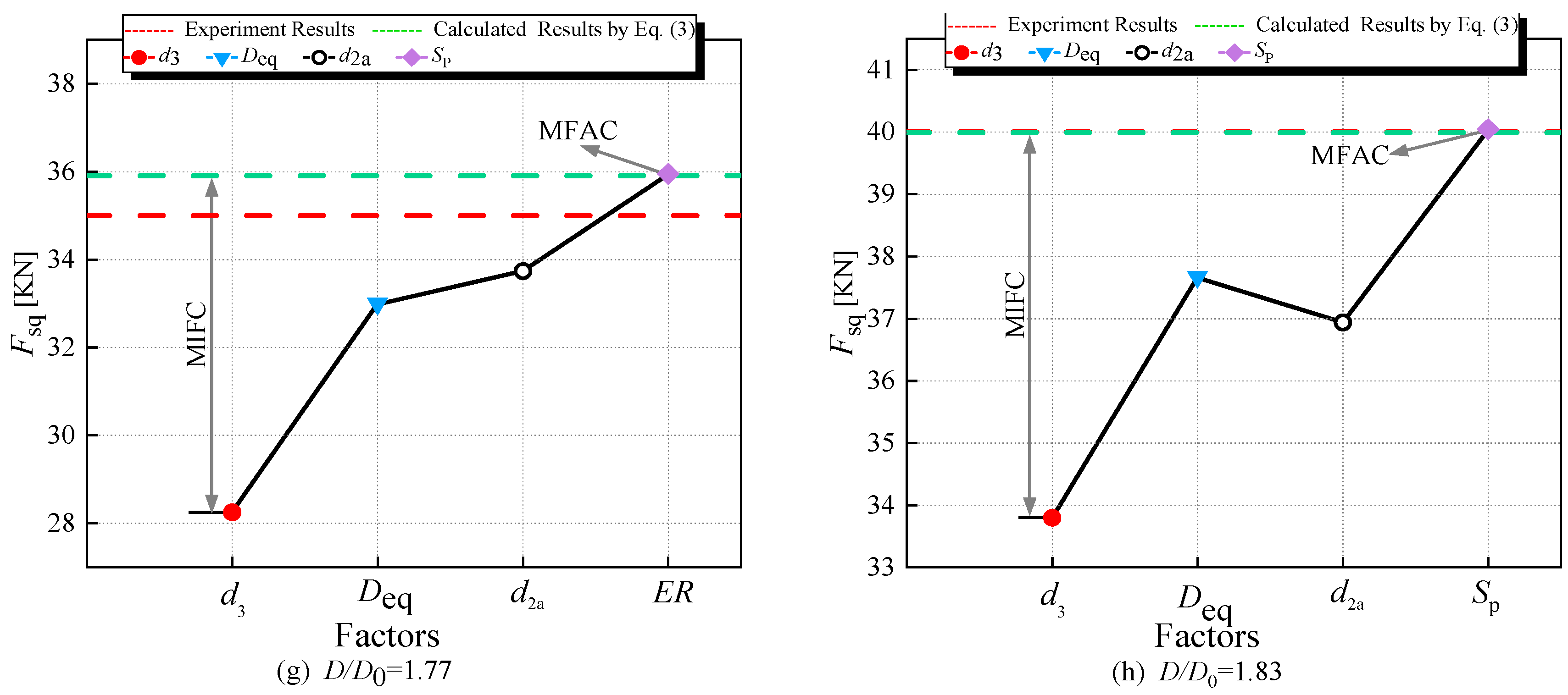
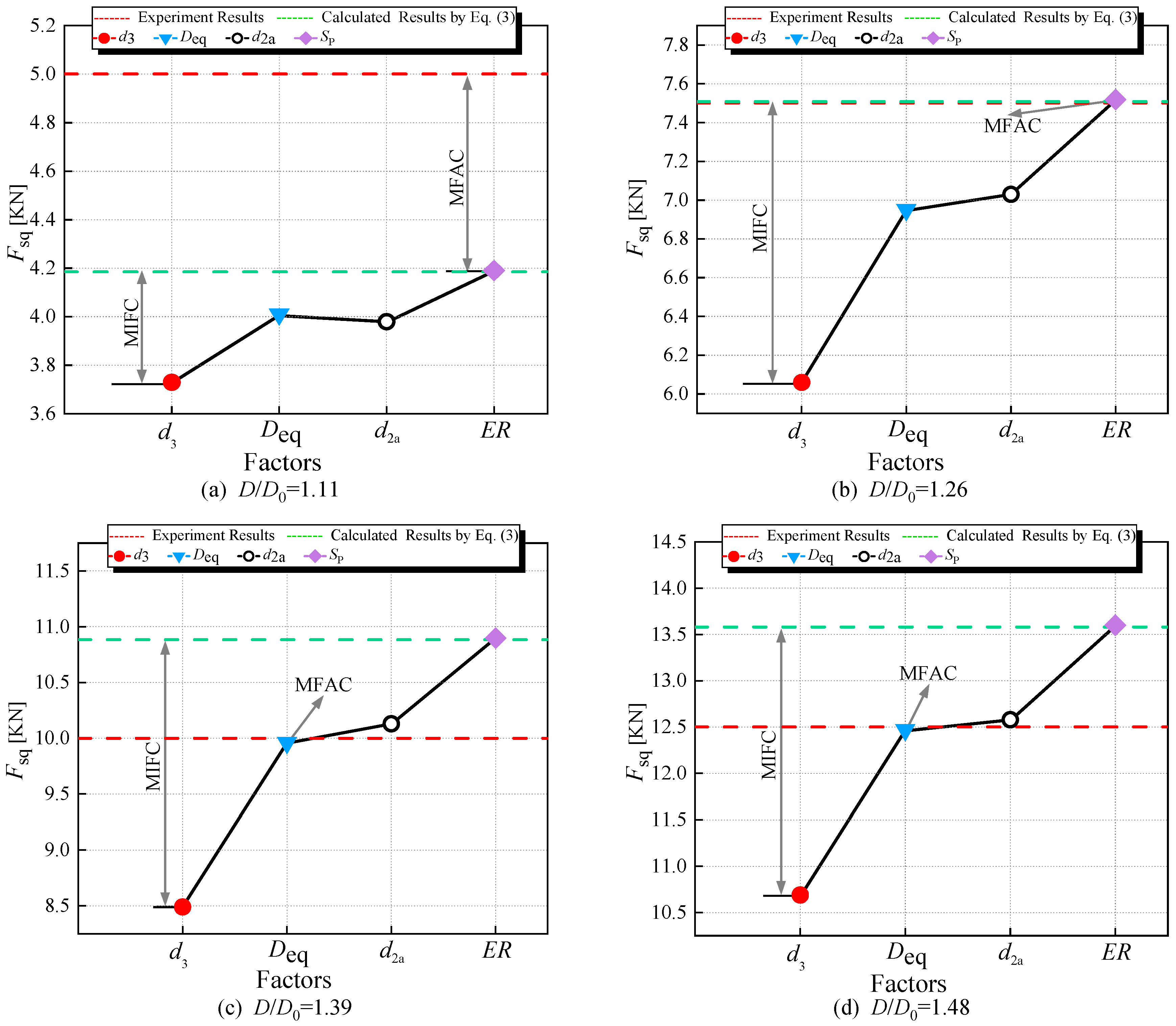
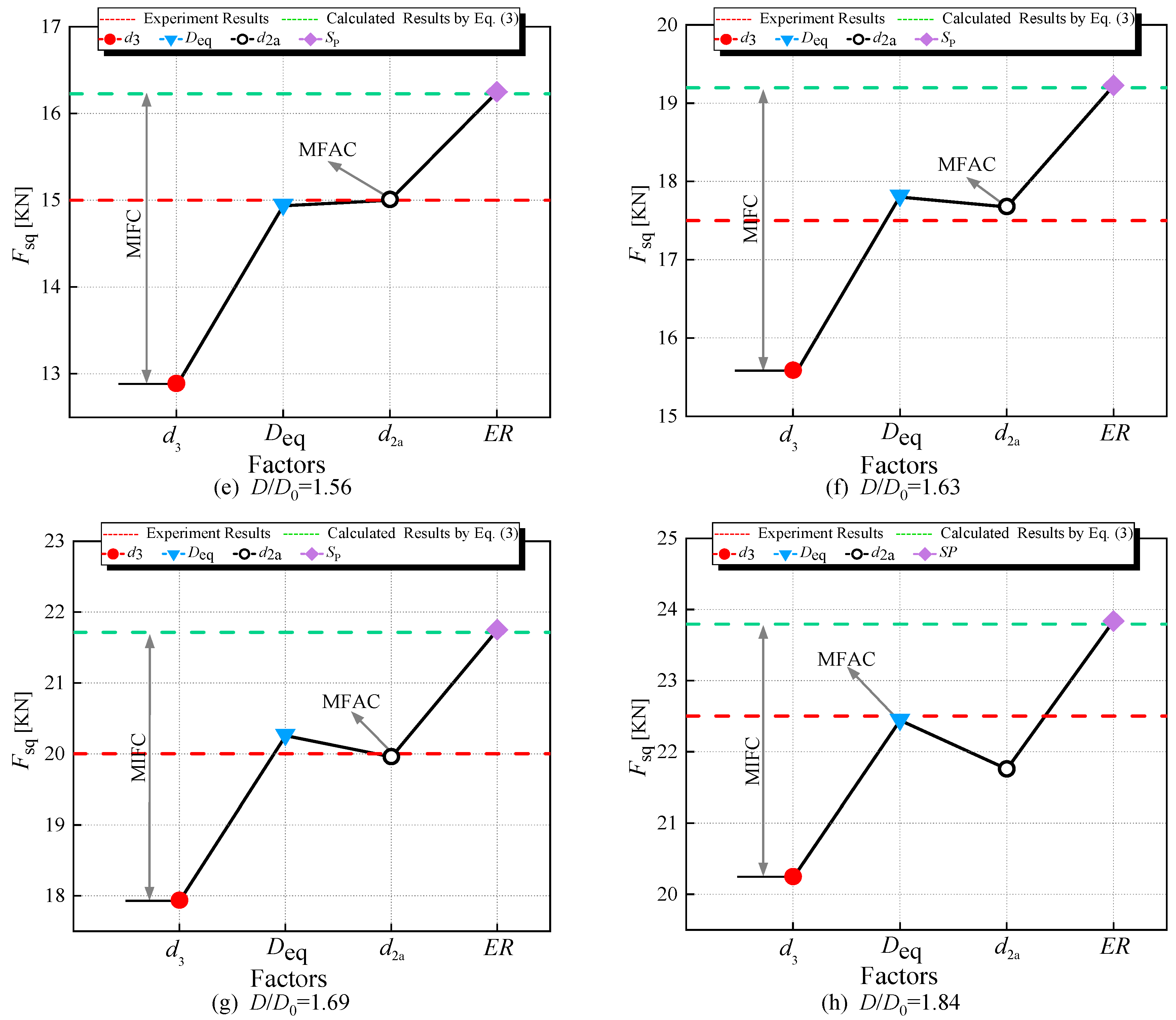
- Importance analysis of the proposed parameters including d3, Deq, d2a, and SP in squeezing force calculation, aiming to identify the factor exerting the most significant influence on squeezing force calculation.
- (2)
- (3)
| Specimens | Measured Values by Müller/De Rijck | Calculated Values | ||||
|---|---|---|---|---|---|---|
| Equation (1) | Equation (3) | |||||
| D/D0 | Fsq, kN | Fsq, kN | Deviation, % | Fsq, kN | Deviation, % | |
| a2 (D0 = 3.208 mm; t1 = t2 = 0.83 mm; NAS1097AD4) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.12 | 4.00 | 3.48 | −13.1 | 3.39 | −15.3 | |
| 1.22 | 5.00 | 4.77 | −4.5 | 4.65 | −7.1 | |
| 1.27 | 5.53 | 5.57 | 0.8 | 5.45 | −1.5 | |
| 1.32 | 6.00 | 6.27 | 4.4 | 6.15 | 2.5 | |
| 1.41 | 7.00 | 7.43 | 6.2 | 7.37 | 5.3 | |
| 1.45 | 7.55 | 8.14 | 7.8 | 8.12 | 7.5 | |
| 1.49 | 8.00 | 8.67 | 8.4 | 8.69 | 8.6 | |
| 1.54 | 9.00 | 9.57 | 6.3 | 9.67 | 7.4 | |
| 1.65 | 11.00 | 11.42 | 3.8 | 11.76 | 6.9 | |
| 1.66 | 11.10 | 11.64 | 4.9 | 12.02 | 8.3 | |
| 1.73 | 13.00 | 12.83 | −1.3 | 13.43 | 3.3 | |
| 1.81 | 15.00 | 14.43 | −3.8 | 15.41 | 2.8 | |
| A1 (D0 = 3.96 mm; H0 = 5.45 mm; t1 = t2 = 2.03 mm; NAS1097AD5-6) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.07 | 5.00 | 4.52 | −9.60 | 4.25 | −15.0 | |
| 1.18 | 7.50 | 7.43 | −1.00 | 6.70 | −10.7 | |
| 1.30 | 10.00 | 10.37 | 3.70 | 9.58 | −4.2 | |
| 1.41 | 12.50 | 13.10 | 4.80 | 12.45 | −0.4 | |
| 1.51 | 15.00 | 15.76 | 5.10 | 15.39 | 2.6 | |
| 1.57 | 17.50 | 17.61 | 0.60 | 17.56 | 0.3 | |
| 1.62 | 20.00 | 19.30 | −3.50 | 19.64 | −1.8 | |
| 1.68 | 22.50 | 21.07 | −6.40 | 21.92 | −2.6 | |
| A2 (D0 = 4.76 mm; H0 = 7.02 mm; t1 = t2 = 2.03 mm; NAS1097AD5-6) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.04 | 5.00 | 5.27 | 5.4 | 4.93 | −1.40 | |
| 1.21 | 10.00 | 11.56 | 15.6 | 10.89 | 8.90 | |
| 1.40 | 15.00 | 18.47 | 23.1 | 18.01 | 20.10 | |
| 1.53 | 20.00 | 23.70 | 18.5 | 23.40 | 17.0 | |
| 1.62 | 25.00 | 27.80 | 11.2 | 28.03 | 12.1 | |
| 1.70 | 30.00 | 31.59 | 5.3 | 33.36 | 11.2 | |
| 1.77 | 35.00 | 34.65 | −1.0 | 37.42 | 6.90 | |
| 1.83 | 40.00 | 37.73 | −5.7 | 40.25 | 0.60 | |
| A3 (D0 = 5.52 mm; H0 = 9.86 mm; t1 = t2 = 3.19 mm; EN6101D7-10) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.10 | 10.00 | 8.40 | −16.0 | 7.34 | −26.6 | |
| 1.41 | 20.00 | 24.18 | 20.9 | 22.69 | 13.4 | |
| 1.52 | 25.00 | 30.40 | 21.6 | 29.28 | 17.1 | |
| 1.61 | 30.00 | 36.21 | 20.7 | 35.74 | 19.1 | |
| 1.68 | 35.00 | 40.90 | 16.9 | 41.20 | 17.7 | |
| 1.74 | 40.00 | 45.19 | 13.0 | 46.40 | 16.0 | |
| 1.79 | 45.00 | 49.54 | 10.1 | 51.93 | 15.4 | |
| 1.84 | 49.00 | 52.77 | 7.7 | 56.23 | 14.8 | |
| A4 (D0 = 3.98 mm; H0 = 5.68 mm; t1 = t2 = 2.005 mm; NAS1097D5-6) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.11 | 5.00 | 4.62 | −7.5 | 4.10 | −18.0 | |
| 1.26 | 7.50 | 8.41 | 12.1 | 7.66 | 2.1 | |
| 1.39 | 10.00 | 11.94 | 19.4 | 11.29 | 12.9 | |
| 1.48 | 12.50 | 14.57 | 16.6 | 14.18 | 13.5 | |
| 1.56 | 15.00 | 17.08 | 13.8 | 17.08 | 13.9 | |
| 1.63 | 17.50 | 19.74 | 12.8 | 20.36 | 16.4 | |
| 1.69 | 20.00 | 21.92 | 9.6 | 23.24 | 16.2 | |
| 1.74 | 22.50 | 23.62 | 5.0 | 25.62 | 13.9 | |
| A13 (D0 = 4.75 mm; H0 = 6.08 mm; t1 = t2 = 2.00 mm; MS20470AD6-6-5) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.02 | 5.00 | 3.47 | −30.6 | 4.38 | −12.4 | |
| 1.15 | 10.00 | 9.43 | −5.7 | 8.81 | −11.9 | |
| 1.34 | 15.00 | 16.14 | 7.6 | 15.39 | 2.6 | |
| 1.48 | 20.00 | 21.82 | 9.1 | 21.41 | 7.1 | |
| 1.59 | 25.00 | 26.07 | 4.3 | 26.20 | 4.8 | |
| 1.67 | 30.00 | 29.76 | −0.8 | 30.59 | 2.0 | |
| 1.74 | 35.00 | 33.35 | −4.7 | 35.11 | 0.3 | |
| 1.80 | 40.00 | 36.16 | −9.6 | 38.85 | −2.9 | |
3.1. Analysis of Parameters’ Importance
- (1)
- For A2 and A4, in the majority of cases, substituting d3 or Deq with D, or d2a with d2, or applying SP to adjust the dimensions D and H of the driven head, resulting in a squeezing force calculation that is smaller than the computed value.
- (2)
- In Figure 16, d3 emerges as the major influencing factor for the calculation results (MIFC), while Deq is the major factor influencing the accuracy of the calculation (MFAC).
- (3)
- (4)
3.2. Considering Non-Uniform Deformation of the Rivet
3.3. Considering the Effect of the Material Inserted into the Hole on the Height of the Driven Head
| Specimens | Calculated Values | |||||||
|---|---|---|---|---|---|---|---|---|
| Values Measured by Müller/De Rijck | Equation (1) | d2 + Deq + ER (Equation (21)) | ΔH + d2b + ER (Equation (22)) | |||||
| D∕D0 | Fsq, kN | Fsq | Deviation, % | Fsq | Deviation, % | Fsq | Deviation, % | |
| a2 (D0 = 3.208 mm; t1 = t2 = 0.83 mm; NAS1097AD4) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.12 | 4.00 | 3.48 | −13.1 | 3.10 | −22.44 | 3.22 | −19.41 | |
| 1.22 | 5.00 | 4.77 | −4.5 | 4.25 | −15.04 | 4.50 | −9.99 | |
| 1.27 | 5.53 | 5.57 | 0.8 | 5.02 | −9.27 | 5.32 | −3.72 | |
| 1.32 | 6.00 | 6.27 | 4.4 | 5.63 | −6.22 | 6.00 | 0.03 | |
| 1.41 | 7.00 | 7.43 | 6.2 | 6.63 | −5.28 | 7.17 | 2.49 | |
| 1.45 | 7.55 | 8.14 | 7.8 | 7.33 | −2.98 | 7.91 | 4.82 | |
| 1.49 | 8.00 | 8.67 | 8.4 | 7.88 | −1.51 | 8.48 | 5.98 | |
| 1.54 | 9.00 | 9.57 | 6.3 | 8.75 | −2.83 | 9.46 | 5.06 | |
| 1.65 | 11.00 | 11.42 | 3.8 | 10.63 | −3.33 | 11.47 | 4.28 | |
| 1.66 | 11.10 | 11.64 | 4.9 | 10.86 | −2.12 | 11.73 | 5.65 | |
| 1.73 | 13.00 | 12.83 | −1.3 | 12.15 | −6.57 | 13.12 | 0.96 | |
| 1.81 | 15.00 | 14.43 | −3.8 | 13.96 | −6.95 | 15.03 | 0.22 | |
| A1 (D0 = 3.96 mm; H0 = 5.45 mm; t1 = t2 = 2.03 mm; NAS1097AD5-6) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.07 | 5.00 | 4.52 | −9.60 | 4.36 | −12.78 | 4.47 | −10.57 | |
| 1.18 | 7.50 | 7.43 | −1.00 | 6.57 | −12.38 | 6.97 | −7.10 | |
| 1.30 | 10.00 | 10.37 | 3.70 | 9.02 | −9.85 | 9.76 | −2.42 | |
| 1.41 | 12.50 | 13.10 | 4.80 | 11.41 | −8.73 | 12.48 | −0.15 | |
| 1.51 | 15.00 | 15.76 | 5.10 | 13.86 | −7.59 | 15.29 | 1.93 | |
| 1.57 | 17.50 | 17.61 | 0.60 | 15.80 | −9.69 | 17.33 | −0.97 | |
| 1.62 | 20.00 | 19.30 | −3.50 | 17.63 | −11.86 | 19.25 | −3.77 | |
| 1.68 | 22.50 | 21.07 | −6.40 | 19.57 | −13.02 | 21.25 | −5.55 | |
| A2 (D0 = 4.76 mm; H0 = 7.02 mm; t1 = t2 = 2.03 mm; NAS1097AD5-6) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.04 | 5.00 | 5.27 | 5.4 | 5.06 | 1.16 | 5.00 | 0.08 | |
| 1.21 | 10.00 | 11.56 | 15.6 | 9.85 | −1.53 | 10.44 | 4.36 | |
| 1.40 | 15.00 | 18.47 | 23.1 | 15.54 | 3.59 | 17.02 | 13.49 | |
| 1.53 | 20.00 | 23.70 | 18.5 | 20.25 | 1.25 | 22.35 | 11.74 | |
| 1.62 | 25.00 | 27.80 | 11.2 | 24.24 | −3.04 | 26.74 | 6.96 | |
| 1.70 | 30.00 | 31.59 | 5.3 | 28.18 | −6.08 | 30.91 | 3.05 | |
| 1.77 | 35.00 | 34.65 | −1.0 | 31.62 | −9.66 | 34.38 | −1.76 | |
| 1.83 | 40.00 | 37.73 | −5.7 | 35.35 | −11.61 | 37.99 | −5.04 | |
| A3 (D0 = 5.52 mm; H0 = 9.86 mm; t1 = t2 = 3.19 mm; EN6101D7-10) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.10 | 10.00 | 8.40 | −16.0 | 7.31 | −26.88 | 7.38 | −26.24 | |
| 1.41 | 20.00 | 24.18 | 20.9 | 20.07 | 0.37 | 20.53 | 2.67 | |
| 1.52 | 25.00 | 30.40 | 21.6 | 25.74 | 2.97 | 26.41 | 5.62 | |
| 1.61 | 30.00 | 36.21 | 20.7 | 30.06 | 0.19 | 32.14 | 7.12 | |
| 1.68 | 35.00 | 40.90 | 16.9 | 34.90 | −0.28 | 36.97 | 5.64 | |
| 1.74 | 40.00 | 45.19 | 13.0 | 39.38 | −1.56 | 41.50 | 3.75 | |
| 1.79 | 45.00 | 49.54 | 10.1 | 44.01 | −2.19 | 46.21 | 2.68 | |
| 1.84 | 49.00 | 52.77 | 7.7 | 47.61 | −2.84 | 49.83 | 1.70 | |
| A4 (D0 = 3.98 mm; H0 = 5.68mm; t1 = t2 = 2.005 mm; NAS1097D5-6) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.11 | 5.00 | 4.62 | −7.5 | 3.91 | −21.72 | 4.10 | −17.94 | |
| 1.26 | 7.50 | 8.41 | 12.1 | 6.66 | −11.16 | 7.21 | −3.93 | |
| 1.39 | 10.00 | 11.94 | 19.4 | 9.49 | −5.06 | 10.36 | 3.56 | |
| 1.48 | 12.50 | 14.57 | 16.6 | 11.81 | −5.50 | 12.87 | 2.96 | |
| 1.56 | 15.00 | 17.08 | 13.8 | 14.13 | −5.80 | 15.35 | 2.34 | |
| 1.63 | 17.50 | 19.74 | 12.8 | 16.75 | −4.28 | 18.11 | 3.48 | |
| 1.69 | 20.00 | 21.92 | 9.6 | 19.02 | −4.92 | 20.46 | 2.29 | |
| 1.74 | 22.50 | 23.62 | 5.0 | 20.92 | −7.03 | 22.36 | −0.63 | |
| A13 (D0 = 4.75 mm; H0 = 6.08 mm; t1 = t2 = 2.00 mm; MS20470AD6-6-5) | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1.02 | 5.00 | 3.47 | −30.6 | 4.82 | −3.58 | 4.77 | −4.60 | |
| 1.15 | 10.00 | 9.43 | −5.7 | 8.52 | −14.77 | 8.67 | −13.33 | |
| 1.34 | 15.00 | 16.14 | 7.6 | 14.29 | −4.74 | 14.78 | −1.43 | |
| 1.48 | 20.00 | 21.82 | 9.1 | 19.16 | −4.19 | 20.44 | 2.19 | |
| 1.59 | 25.00 | 26.07 | 4.3 | 23.45 | −6.21 | 24.85 | −0.61 | |
| 1.67 | 30.00 | 29.76 | −0.8 | 27.43 | −8.57 | 28.92 | −3.60 | |
| 1.74 | 35.00 | 33.35 | −4.7 | 31.52 | −9.95 | 33.09 | −5.45 | |
| 1.80 | 40.00 | 36.16 | −9.6 | 34.75 | −13.12 | 36.46 | −8.85 | |
4. Conclusions
- (1)
- The introduction of both d2a and Deq can reduce the calculated values of the riveting force, while the introduction of spring-back can slightly increase the calculated values of the riveting force compared to the previous model, as shown in Equation (3).
- (2)
- The new analytical models for calculating riveting squeezing force, represented by Equations (21) and (22), which take into account the non-uniform deformation of the rivet, significantly reduced the deviation between the calculated squeezing force and experimental data, especially in the medium squeeze ratio range (1.3 ≤ D/D0 ≤ 1.6). The previous formulation (Equations (1) and (3)) generally overestimates the required squeezing force due to an overestimation of the true strain of the rivet material within the hole vicinity. Equations (21) and (22) significantly improved the prediction accuracy, and the deviation from the experimental values is reduced to within 10% for some specimens (while the deviation for Equations (1) and (3) sometimes exceed 20%), this is because the non-uniform deformation of the rivet is considered fully.
- (3)
- After considering the convex structure of the driven head, the calculation accuracy is significantly improved, and most importantly, the consistency of the predicted squeezing force is improved, with a standard deviation of 8.46%. However, Equation (22) had a standard deviation of 17.66%.
- (4)
- For other types of sheet materials, such as CFRP, and different fasteners like headless rivets, the proposed model requires modifications to maintain accuracy. And, the current study did not account for the friction between the rivet shank and the hole. To further the research in this area, the proposed model must take into account the friction that occurs between the rivet shank and the holes. This improvement would help reduce the tendency to underestimate the riveting forces in the low squeeze ratio range.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the diameter of installed driven rivet head (or tail head diameter) | |
| the diameter of uninstalled or original rivet shank | |
| the diameter of rivet shank when shank touching sheet-hole wall (equal to d1) | |
| the maximum diameter of the formed driven head | |
| the final maximum diameter of the driven head after elastic recovery | |
| the height of installed driven rivet head (or tail head height) | |
| the height of driven head convex structure inserted into the hole | |
| the height of uninstalled rivet tail out of the sheet-hole | |
| the height of rivet tail when the shank touching sheet-hole wall | |
| the formed height of the driven head (equal to H) | |
| the final height of the driven head after spring-back | |
| the length of installed rivet shank | |
| the length of original rivet shank | |
| the length of rivet shank when the shank touching sheet-hole wall | |
| the formed length of rivet shank | |
| the formed length of rivet shank after elastic recovery | |
| the diameter of original sheet-hole (before rivet shank expansion) | |
| the diameter of expanded sheet-hole considering the uniform deformation | |
| the diameter of the bottom of expanded sheet-hole considering the non-uniform deformation | |
| the diameter of the bottom of expanded sheet-hole considering convex structure of the driven head | |
| the minimum diameter of the driven head | |
| the bottom diameter of the driven head | |
| material’s Young’s modulus | |
| Euler’s constant (natural number) | |
| riveting squeezing force | |
| sheet material strength coefficient | |
| rivet material strength coefficient | |
| sheet material strain hardening coefficient as per Hollomon, in which σ is equal to K(ε)n | |
| rivet material strain hardening coefficient | |
| the thickness of whole sheet | |
| the thickness of upper sheet | |
| the thickness of lower sheet | |
| squeeze true strain at rivet tail head | |
| friction coefficient (Coulomb friction) | |
| rivet squeeze stress in driven head | |
| sheet or material yield stress | |
| rivet material yield stress |
References
- Zhao, H.; Xi, J.; Zheng, K.; Shi, Z.; Lin, J.; Nikbin, K.; Duan, S.; Wang, B. A review on solid riveting techniques in aircraft assembling. Manuf. Rev. 2020, 7, 40. [Google Scholar] [CrossRef]
- Chowdhury, N.; Chiu, W.K.; Wang, J.; Chang, P. Static and fatigue testing thin riveted, bonded and hybrid carbon fiber double lap joints used in aircraft structures. Compos. Struct. 2015, 121, 315–323. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Z.; Zhu, R.; Chen, Z.; Ye, Q.; Duan, Y.; Jia, Y.; Zhang, Q. Experimental study on Q355 steel T-stubs connected through high-strength ring groove rivets. Thin Walled Struct. 2024, 195, 111399. [Google Scholar] [CrossRef]
- Wang, S.; Fan, J.; Li, H.; Wang, H.; Lan, Z.; Liu, J.; Peng, J.; Zhu, M. Fatigue failure analysis of CFRP single-lap adhesive-riveted hybrid joints. Tribol. Int. 2023, 188, 108854. [Google Scholar] [CrossRef]
- Liang, Q.; Zhang, T.; Zhu, C.; Bi, Y. Effect of riveting angle and direction on fatigue performance of riveted lap joints. Coatings 2021, 11, 236. [Google Scholar] [CrossRef]
- Zeng, C.; Xue, J.T.; Liu, X.Y.; Tian, W. Design variables influencing the fatigue of Al 2024-T3 in riveted aircraft lap joints: Squeeze force and initial fit tolerance. Int. J. Fatigue 2020, 140, 105751. [Google Scholar] [CrossRef]
- Zeng, C.; Liao, W.H.; Tian, W. Influence of initial fit tolerance and squeeze force on the residual stress in a riveted lap joint. Int. J. Adv. Manuf. Technol. 2015, 81, 1643–1656. [Google Scholar] [CrossRef]
- Jiang, K.; Liu, Z.; Yang, C.; Zhang, C.; Tian, Y.; Zhang, T. Effects of the joint surface considering asperity interaction on the bolted joint performance in the bolt tightening process. Tribol. Int. 2022, 167, 107408. [Google Scholar] [CrossRef]
- Mori, K.I.; Bay, N.; Fratini, L.; Micari, F.; Tekkaya, A.E. Joining by plastic deformation. CIRP Ann. 2013, 62, 673–694. [Google Scholar] [CrossRef]
- Müller, R.P.G. An Experimental and Analytical Investigation on the Fatigue Behavior of Fuselage Riveted Lap Joints. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1995. [Google Scholar]
- Schijve, J. Some Considerations on the Correlation between the Rivet Squeezing Force and the Dimensions of the Driven Rivet Head; Memorandum m-847; Delft University of Technology, Faculty of Aerospace Engineering: Delft, The Netherlands, 1998. [Google Scholar]
- De Rijck, J.J.M. Stress Analysis of Fatigue Cracks in Mechanically Fastened Joints: An Analytical and Experimental Investigation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2005. [Google Scholar]
- De Rijck, J.J.M.; Homan, J.J.; Schijve, J.; Benedictus, R. The driven rivet head dimensions as an indication of the fatigue performance of aircraft lap joints. Int. J. Fatigue 2007, 29, 2208–2218. [Google Scholar] [CrossRef]
- Figueira, J.A.N.; Trabasso, L.G. Riveting-Induced Deformations on Aircraft Structures. J. Aircr. 2015, 52, 2032–2050. [Google Scholar] [CrossRef]
- Figueira, J.A.N.; Trabasso, L.G. Riveting Squeezing Force Estimation: A Revised Algebraic Model. J. Aircr. 2022, 59, 1005–1019. [Google Scholar] [CrossRef]
- Cheraghi, S.H. Effect of variations in the riveting process on the quality of riveted joints. Int. J. Adv. Manuf. Technol. 2008, 39, 1144–1155. [Google Scholar] [CrossRef]
- Chang, Z.; Wang, Z.; Jiang, B.; Zhang, J.; Guo, F.; Kang, Y. Modeling and predicting of aeronautical thin-walled sheet metal parts riveting deformation. Assem. Autom. 2016, 36, 295–307. [Google Scholar] [CrossRef]
- Chang, Z.; Wang, Z.; Xie, L.; Kang, Y.; Xu, M.; Wang, Z. Prediction of riveting deformation for thin-walled structures using local-global finite element approach. Int. J. Adv. Manuf. Technol. 2018, 97, 2529–2544. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, H.; Yuan, L. Riveting process modeling and simulating for deformation analysis of aircraft’s thin-walled sheet-metal parts. Chin. J. Aeronaut. 2011, 24, 369–377. [Google Scholar] [CrossRef]
- Zeng, C.; Tian, W.; Liao, W.H. Improved model concerning driven rivet head dimensions based on material flow characteristics. J. Aircr. 2016, 53, 1180–1185. [Google Scholar] [CrossRef]
- Behrens, B.A.; Bouguecha, A.; Hadifi, T.; Mielke, J. Advanced friction modeling for bulk metal forming processes. Prod. Eng. 2011, 5, 621–627. [Google Scholar] [CrossRef]
- Tan, X. Comparisons of friction models in bulk metal forming. Tribol. Int. 2002, 35, 385–393. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, Y.C.; Kim, K.W. The effect of Coulomb friction on the static performance of foil journal bearings. Tribol. Int. 2010, 43, 1065–1072. [Google Scholar] [CrossRef]
- Dieter, G.E. Mechanical Metallurgy; McGraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Cho, S.W.; Choi, S.M.; Bae, C.S. Frictional modes of barrel shaped piston rings under flooded lubrication. Tribol. Int. 2000, 33, 545–551. [Google Scholar] [CrossRef]
- Narayanasamy, R.; Pandey, K.S. Phenomenon of barrelling in aluminium solid cylinders during cold upset-forming. J. Mater. Process. Technol. 1997, 70, 17–21. [Google Scholar] [CrossRef]
- Serebriakov, I.; Puchi-Cabrera, E.S.; Dubar, L.; Moreau, P.; Meresse, D.; La Barbera-Sosa, J.G. Friction analysis during deformation of steels under hot-working conditions. Tribol. Int. 2021, 158, 106928. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Zu, T.; Lu, Z. Elastic–plastic cylindrical rolling contact fatigue mechanism evolution and life prediction considering random surface topography. Tribol. Int. 2023, 188, 108809. [Google Scholar] [CrossRef]
- Sun, H. Analytical Calculation of Deformation of Deformation and Stress Field in Upsetting of Large Steel. Master’s Thesis, Yanshan Universit, Qinhuangdao, China, 2020. [Google Scholar]
- Zaharia, L.; Comaneci, R.; Chelariu, R.; Luca, D. A new severe plastic deformation method by repetitive extrusion and upsetting. Mater. Sci. Eng. A 2014, 595, 135–142. [Google Scholar] [CrossRef]
- Çetinarslan, C.S. Effect of aspect ratio on barreling contour and variation of total surface area during upsetting of cylindrical specimen. Mater. Des. 2007, 28, 1907–1913. [Google Scholar] [CrossRef]
- Liang, K.; Jiang, L.P.; Wei, H.Y.; Chen, W.L.; Jiang, H.Y.; Xu, R.W.; Wang, Y.B.; Yu, L. Interference Uniformity Analysis Based on the Clearance between the Hole and Rivet. Appl. Mech. Mater. 2013, 246, 28–32. [Google Scholar] [CrossRef]
- Rans, C.; Straznicky, P.V.; Alderliesten, R. Riveting process induced residual stresses around solid rivets in mechanical joints. J. Aircr. 2007, 44, 323–329. [Google Scholar] [CrossRef]
- Li, G.; Shi, G. Effect of the riveting process on the residual stress in fuselage lap joints. Can. Aeronaut. Space J. 2004, 50, 91–105. [Google Scholar] [CrossRef]
- Federal Aviation Administration. MMPDS-07. Aluminum Alloys, Chapter 3; Federal Aviation Administration: Washington, DC, USA, 2012. [Google Scholar]








| Data | Value |
|---|---|
| Coulomb’s friction coefficient μ (assumed value by default) | 0.15 |
| Strength coefficient K for sheet material Al 2024-T3 | 462 Mpa |
| Strain hardening coefficient n for sheet material Al 2024-T3 | 0.0769 |
| AL 2024-T3 Young’s modulus E | 73,773.9 MPa |
| AL 2024-T3 compression yield stress | 255.1 MPa |
| AL 2024-T3 Poisson’s ratio | 0.33 |
| Specimen a2: 2024-T3 bare; t1 = t2 = 0.83 mm; D0 = 3.208 mm; H0 = 4.8 mm; d1 = 3.296 mm; rivet type: NAS1097AD4 | |
| Data | Value |
|---|---|
| Coulomb’s friction coefficient μ (assumed value by default) | 0.15 |
| Strength coefficient Kr for rivet material AI 2117-T4 (AD) | 600 MPa |
| Strength coefficient Kr for rivet material Al 2017-T4 (D) | 600 MPa |
| Strain hardening coefficient nr for rivet material Al 2117-T4 (AD) | 0.30 |
| Strain hardening coefficient nr for rivet material Al 2017-T4 (D) | 0.45 |
| Specimen A1: 2024-T3 clad; t1 = t2 = 2.04 mm; D0 = 3.96 mm; H0 = 5.45 mm; d1 = 4.10 mm; rivet type: NAS1097AD5-6 | |
| Specimen A2: 2024-T3 clad; t1 = t2 = 2.03 mm; D0 = 4.76 mm; H0 = 7.02 mm; d1 = 4.90 mm; rivet type: NAS1097AD6-7 | |
| Specimen A3: 2024-T3 clad; t1 = t2 = 3.18 mm; D0 = 5.52 mm; H0 = 9.86 mm; d1 = 5.60 mm; rivet type: EN6101D7-10 | |
| Specimen A4: 2024-T3 clad; t1 = t2 = 2.01 mm; D0 = 3.98 mm; H0 = 5.68 mm; d1 = 4.10 mm; rivet type: NAS1097D5-6 | |
| Specimen A13: 2024-T3 clad; t1 = t2 = 2.00 mm; D0 = 4.75 mm; H0 = 6.08 mm; d1 = 4.90 mm; rivet type: MS20470AD6-6-5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Song, S.; Wang, T.; Kou, S.; Li, G.; Chen, Y. Analytical Modeling of Riveting Squeezing Force Considering Non-Uniform Deformation of Rivets in Aeronautical Structures. Materials 2024, 17, 2756. https://doi.org/10.3390/ma17112756
Kang Y, Song S, Wang T, Kou S, Li G, Chen Y. Analytical Modeling of Riveting Squeezing Force Considering Non-Uniform Deformation of Rivets in Aeronautical Structures. Materials. 2024; 17(11):2756. https://doi.org/10.3390/ma17112756
Chicago/Turabian StyleKang, Yonggang, Siren Song, Tianyu Wang, Shuaijia Kou, Guomao Li, and Yonggang Chen. 2024. "Analytical Modeling of Riveting Squeezing Force Considering Non-Uniform Deformation of Rivets in Aeronautical Structures" Materials 17, no. 11: 2756. https://doi.org/10.3390/ma17112756





