The Behavior of Long Thin Rectangular Plates under Normal Pressure—A Thorough Investigation
Abstract
1. Introduction
2. Materials, Methods, and Results
3. Discussion
4. Conclusions
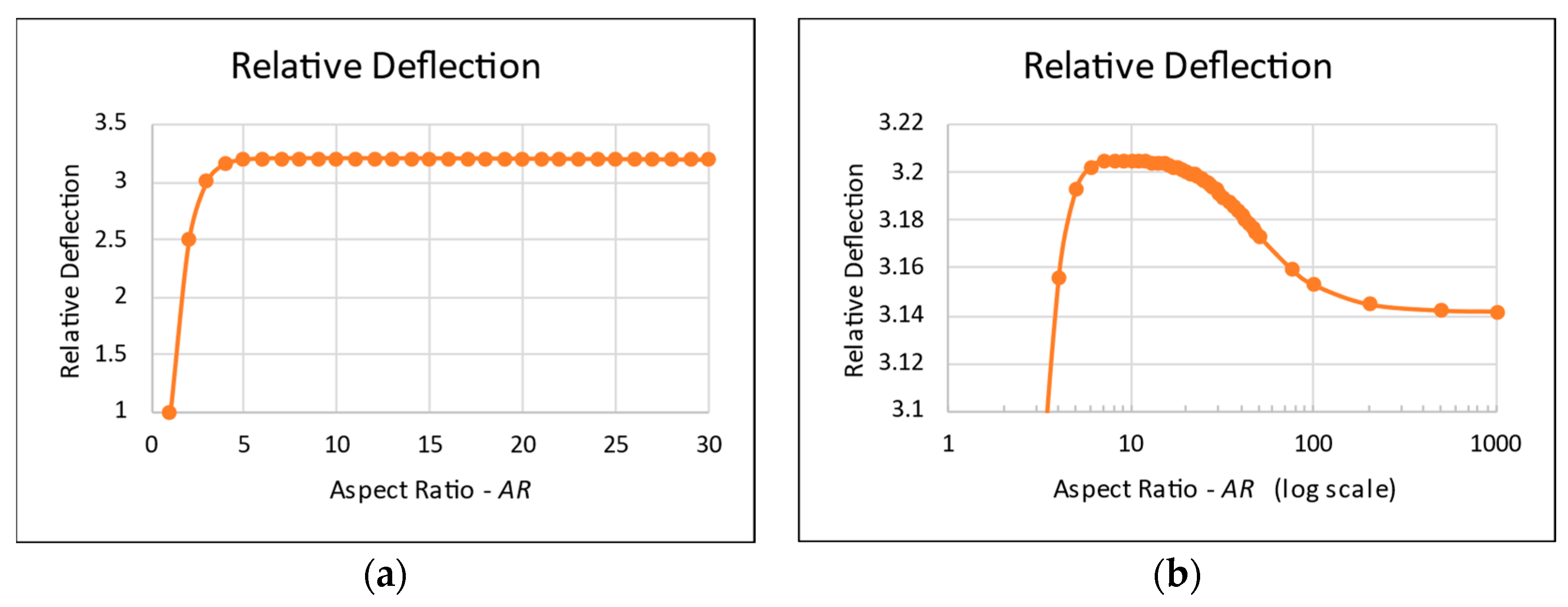
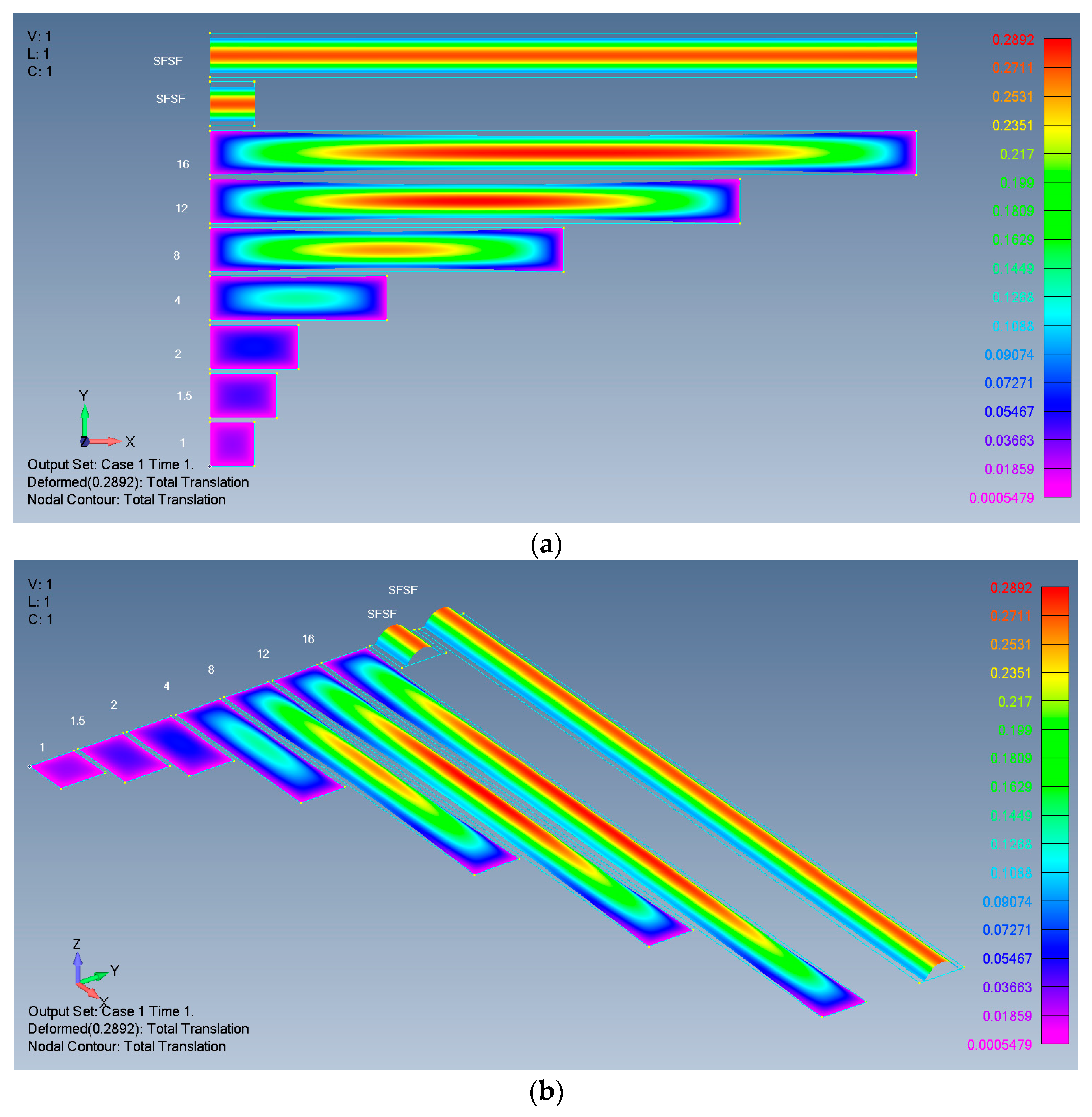
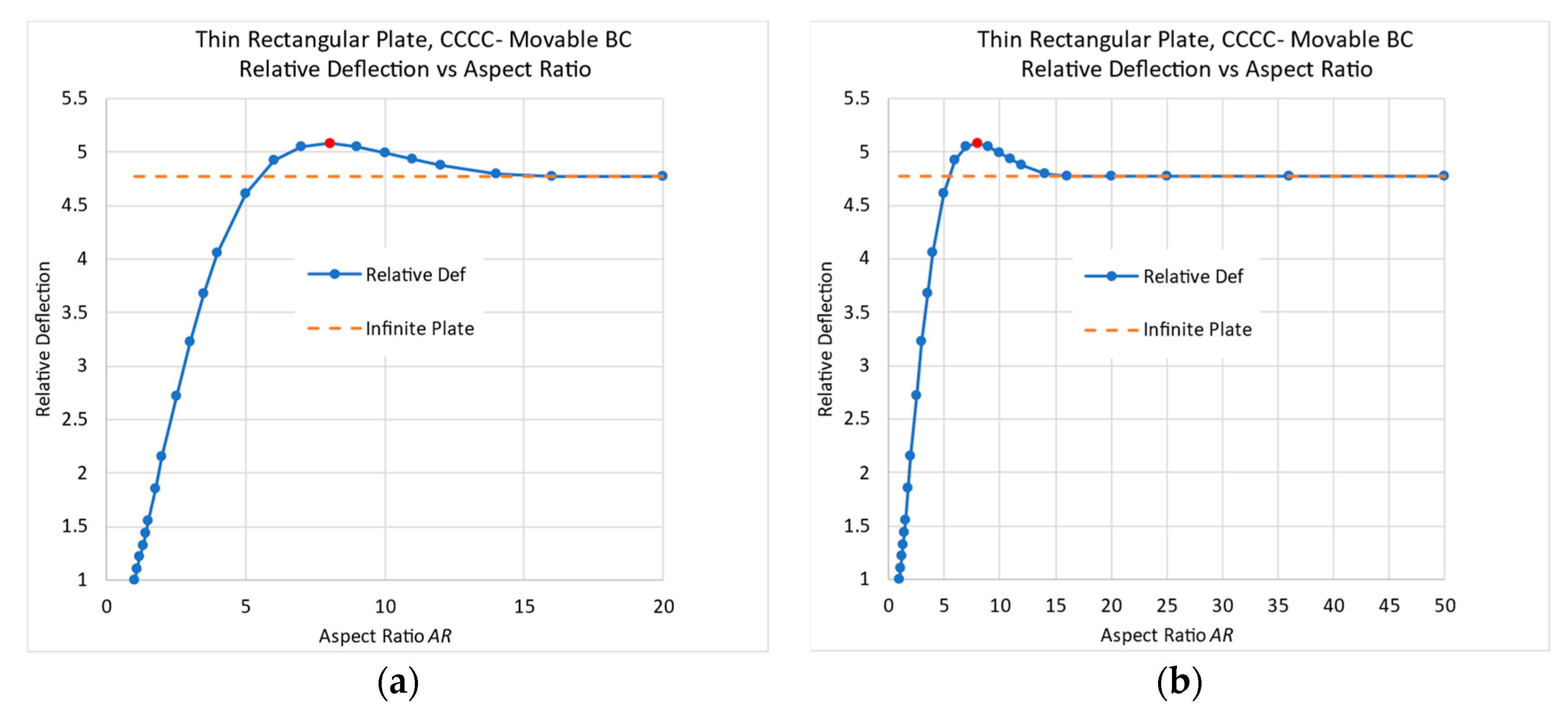
- High-AR rectangular plates (above a certain value) with movable edges cannot be considered infinitely long plates, but rather, the end influences are preserved near the ends.
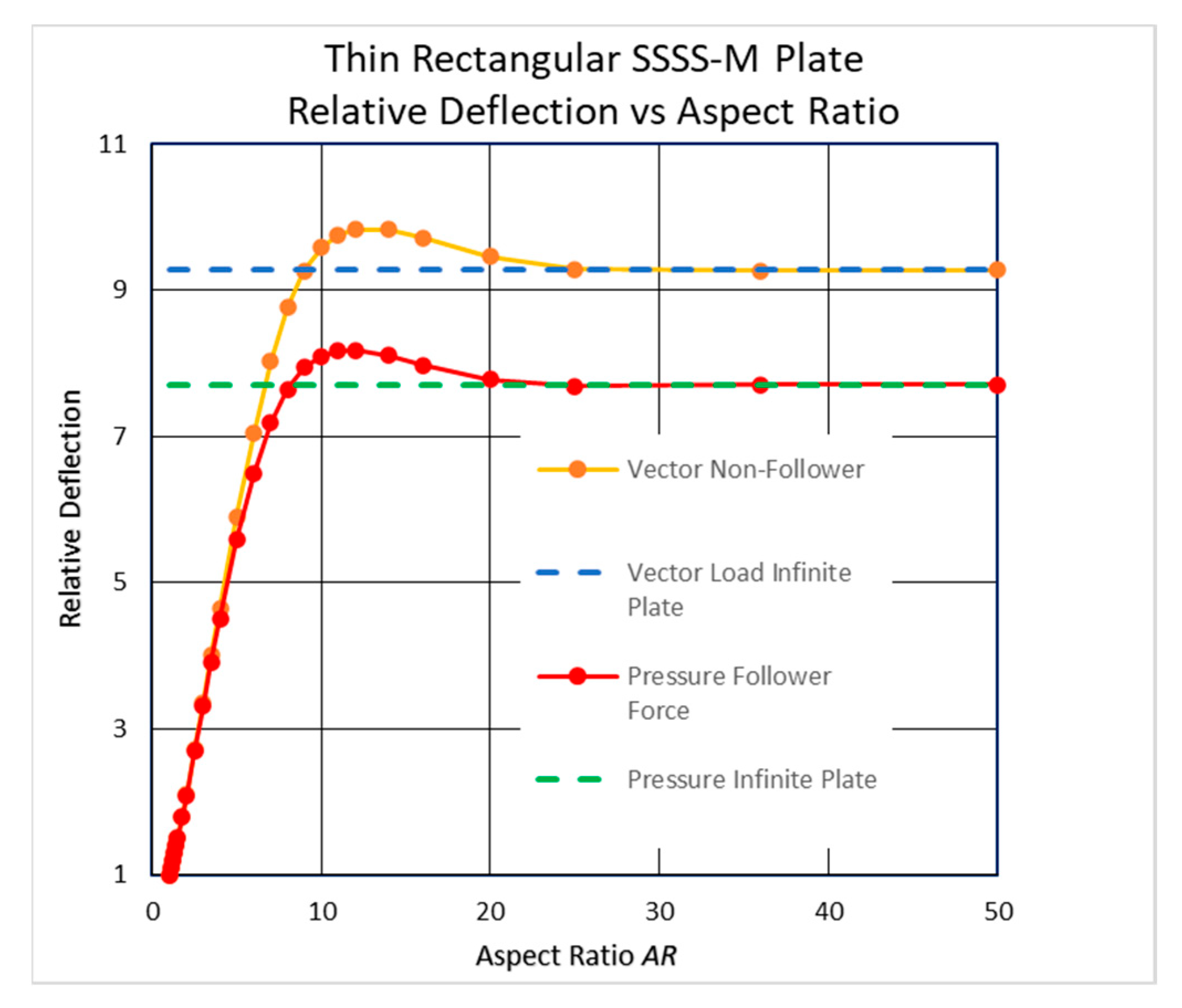
- The midpoint deflections of the SSSS-M case with 10 < AR < 20 and of the CCCC-M case with 6 < AR < 15 are higher than that of an infinitely long plate. A plausible explanation for this phenomenon might be the unusual shape of the deflections for these unique boundary conditions.
- This behavior has also been detected for small-deflection theory based on the classical Navier solution and all-around clamped plates in the small-deflection regime.
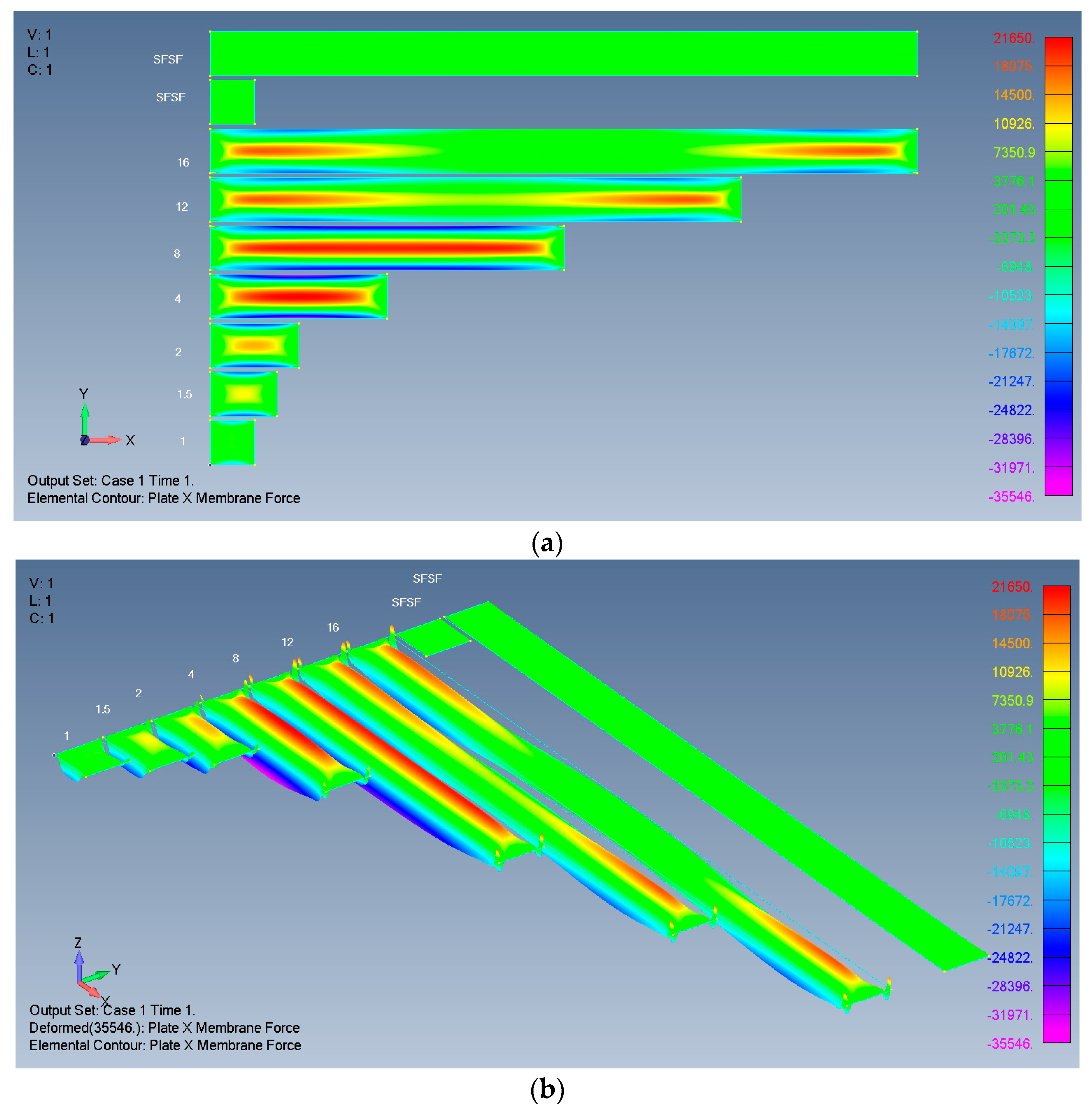
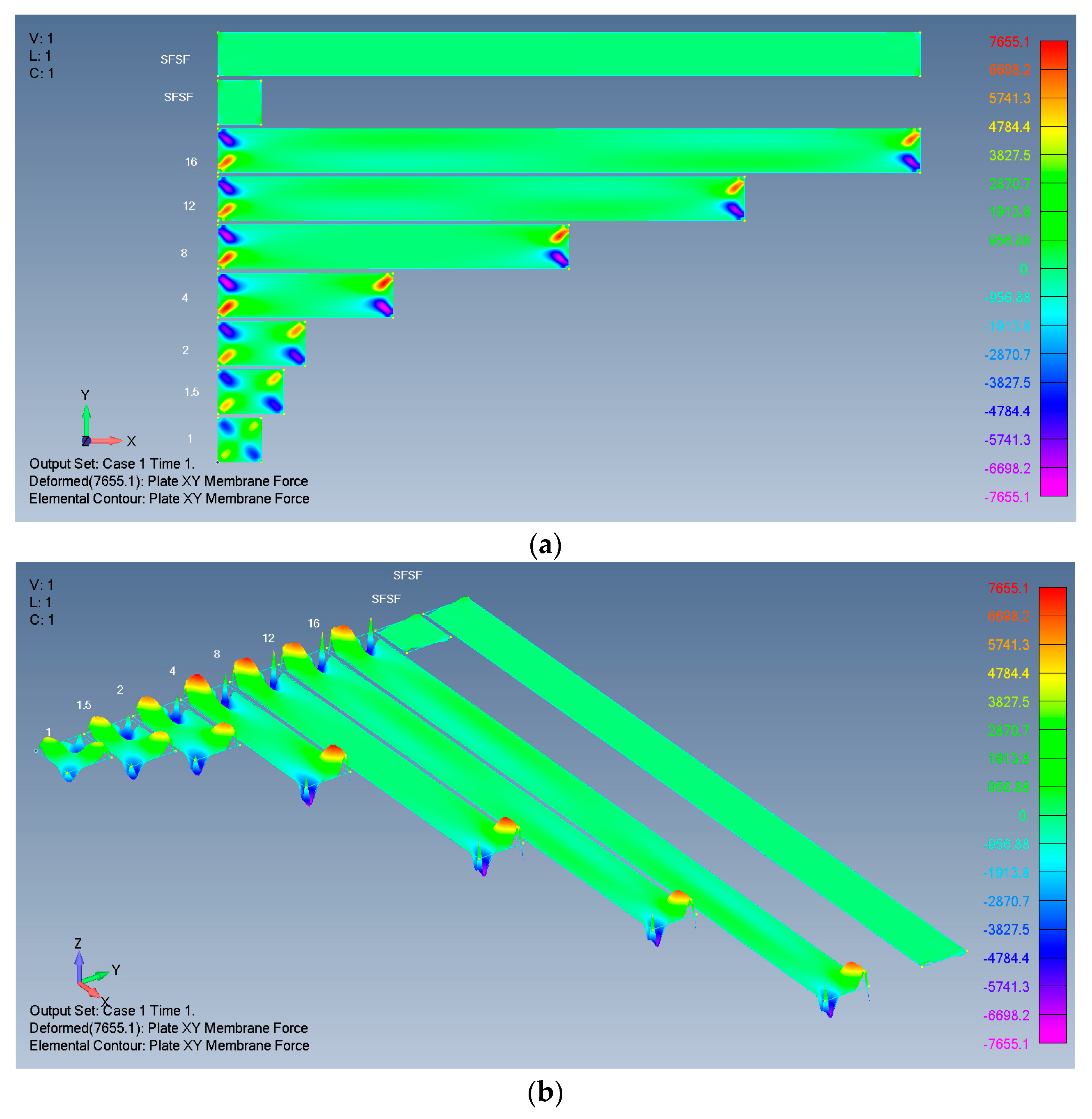
- The influence of the plate’s ends on the deflection and on the in-plane stresses penetrates from the far ends into the plate’s midpoint in different ways.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. (Based on [21])
- Finite element analysis (FEA) process description
- Model preparation:
- Geometry: create surfaces with the shape and dimensions of the requested plates—squares and rectangles.
- Define the material for the plate: isotropic polycarbonate with an E modulus of 2.4 GPa and Poisson’s ratio of 0.38. These two constants are enough here.
- Define the property for the plate element using the material from step 2 with a thickness of 0.005 m (5 mm); give all other inputs the default values.
- Mesh the surface with 50 × 50 mm quad plate elements using the property from step 3.
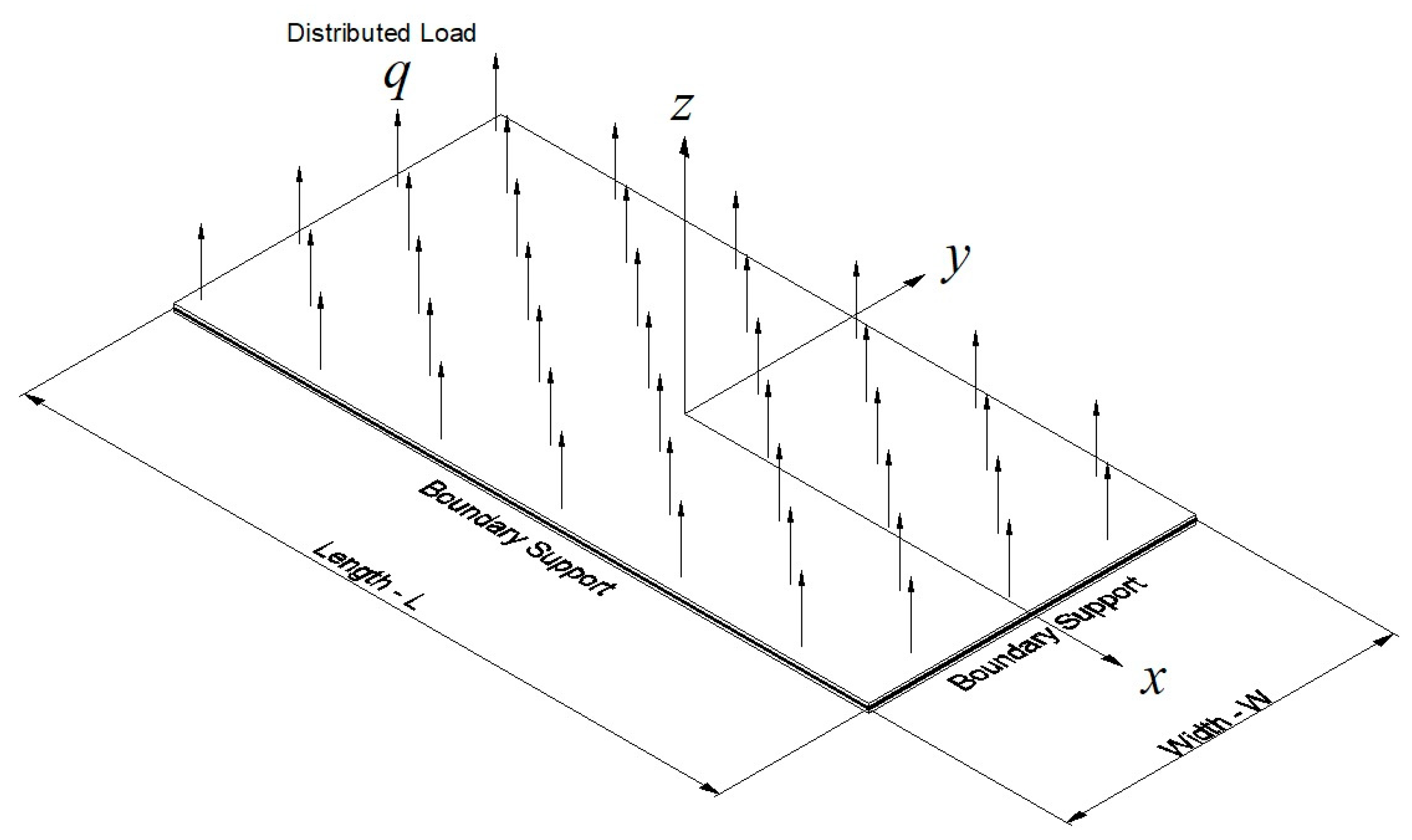
- Set the distributed load on the surface; use force per area on surface for a directional vector load and pressure on surface for a follower load. Set the load value to 1000 Pa in the Z direction.
- Define the boundary conditions, which are called constraints in the software. TX-1, TY-2, and TZ-3 relate to translation in the x,y,z directions. RX-4, RY-5, and RZ-6 relate to rotations around the x,y,z axes. The four types of BCs (simply supported, clamped, movable, immovable) are alternatively set on the surface perimeter:
- SSSS-M: TZ, designated 3 (in-plane movable BC);
- CCCC-M: TZ, RX, RY, designated 345 (in-plane movable BC);
- SSSS-I: TX, TY, TZ, designated T (in-plane immovable BC);
- CCCC-I: TX, TY, TZ, RX, RY, RZ, designated F (in-plane immovable BC).
Additionally, the FEA process requires that all free-body degrees of freedom (DOF) will be eliminated. For that, virtual (not participating) BCs are added where necessary: the plate midpoint may have a TX and TY designated 12, and one edge may have an additional TX or TY. - The last step is to define the type of analysis to run. Since large deflections with nonlinear effects are expected, we chose the analysis type “10..Nonlinear Static”. This analysis type has many input parameters that control its operation. From these, we set “Increments or Time Steps” to 20, and in “Output Control”, we collected “All” intermediate results. These settings enabled us to later see how various plate features developed as the load increased.
- Analyzing the model:
- Post-processing:
- Total translation (deflection);
- Plate X membrane force;
- Plate Y membrane force;
- Plate XY membrane force.
References
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells, 2nd ed.; 1959 Reissued 1987; McGraw-Hill Book Company: New York, NY, USA, 1987; ISBN 0-07-064779-8. [Google Scholar]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells, 2nd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2007. [Google Scholar] [CrossRef]
- Bakker, M.C.M.; Rosmanit, M.; Hofmeyer, H. Approximate large-deflection analysis of simply supported rectangular plates under transverse loading using plate post-buckling solutions. Thin-Walled Struct. 2008, 46, 1224–1235. [Google Scholar] [CrossRef]
- Bhaskar, K.; Varadan, T.K. Plates—Theories and Applications; Springer: Berlin/Heidelberg, Germany; ANE Books Pvt, Ltd.: New Delhi, India, 2021; ISBN 978-3-030-69423-4/978-3-030-69424-1. [Google Scholar] [CrossRef]
- McFarland, D.E.; Smith, B.I.; Bernhart, W.D. Analysis of Plates, 1st ed.; Spartan Books: New York, NY, USA, 1972; ISBN-10: 0876715609; ISBN-13: 978-0876715604. [Google Scholar]
- Onyeka, F.C.; Okeke, E.T.; Nwa-David, C.D.; Mama, B.O. Exact analytical solution for static bending of 3-D plate under transverse loading. J. Comput. Appl. Mech. 2022, 53, 309–331. [Google Scholar] [CrossRef]
- Paik, J.K. Ultimate Limit State Analysis and Design of Plated Structures, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018; Chapter 4; pp. 179–270. ISBN 978-1-119-36775-8. [Google Scholar]
- Bauer, F.; Bauer, L.; Becker, W.; Reiss, E.L. Bending of rectangular plates of finite deflections. J. Appl. Mech. 1965, 821–825. [Google Scholar] [CrossRef]
- Brown, C.J.; Goodey, R.J.; Rotter, J.M. Bending of rectangular plates subject to non-uniform pressure distributions relevant to containment structures. In Proceedings of the Eurosteel 2017, Copenhagen, Denmark, 13–15 September 2017. [Google Scholar] [CrossRef]
- Wang, D.; El-Sheikh, A.I. Large-Deflection Mathematical Analysis of Rectangular Plates. J. Eng. Mech. 2005, 131, 809–821. [Google Scholar] [CrossRef]
- Shao, C.J. Large Deflection of Rectangular Plate with High Aspect Ratio. Master’s Thesis, University of California, Berkeley, CA, USA, 1964. Available online: https://calhoun.nps.edu/handle/10945/12540 (accessed on 6 June 2024).
- Razdolsky, A.G. Large Deflections of Elastic Rectangular Plates. Int. J. Comput. Methods Eng. Sci. Mech. 2015, 16, 354–361. [Google Scholar] [CrossRef]
- Ostiguy, G.L.; Evan-lwanowski, R.M. Influence of the Aspect Ratio on the Dynamic Stability and Nonlinear Response of Rectangular Plates. J. Mech. Des. 1982, 104, 417–425. [Google Scholar] [CrossRef]
- Covestro AG. Leverkusen, Makrolon 2407 Datasheet. Available online: https://solutions.covestro.com/-/media/covestro/solution-center/products/datasheets/imported/makrolon/makrolon-2407_en_56977361-00009645-19213223.pdf (accessed on 6 June 2024).
- Sabic Lexan 940A Datasheet. Available online: https://www.matweb.com/search/datasheet.aspx?matguid=cda0ab793fed4ed6a7e5df4902937a4b&ckck=1 (accessed on 6 June 2024).
- Siemens. Simcenter Nastran Basic Nonlinear Analysis User’s Guide; Siemens Industry Software: Plano, TX, USA, 2020; Available online: https://docs.plm.automation.siemens.com/data_services/resources/scnastran/2020_1/help/tdoc/en_US/pdf/basic_nonlinear.pdf (accessed on 6 June 2024).
- Hakim, G.; Abramovich, H. Multiwall rectangular plates under transverse pressure—A non-linear experimental and numerical study. Materials 2023, 16, 2041. [Google Scholar] [CrossRef]
- Lee, H.-H. Finite Element Simulations with ANSYS Workbench 2023: Theory, Applications, Case Studies; SDC Publications: Mission, KS, USA, 2023; ISBN 1630576158/9781630576158. Available online: https://www.amazon.com/Finite-Element-Simulations-ANSYS-Workbench/dp/1630576158 (accessed on 6 June 2024).
- Ansys Internet Site. Available online: https://www.ansys.com/products/ansys-workbench (accessed on 6 June 2024).
- Hakim, G.; Abramovich, H. Homogenization of multiwall plates—An analytical, numerical and experimental study. Thin-Walled Struct. 2022, 185, 110583. [Google Scholar] [CrossRef]
- Hakim, G.; Abramovich, H. Large Deflections of Thin-Walled Plates under Transverse Loading—Investigation of the Generated In-Plane Stresses. Materials 2022, 15, 1577. [Google Scholar] [CrossRef]








| Young’s modulus E | 2.4 GPa |
| Poisson’s ratio ν | 0.38 |
| Thickness h | 0.005 m |
| Length a | varies |
| Width b | 1 m |
| Distributed load q | 100 Pa |
| The calculated bending rigidity D D = Eh3/12(1 − ν2) | 29.219 Nm |
| Summation indexes m and n | 1, 3, 5, …, 31 |
| Equivalent Eyt modulus | 228.56 | MPa |
| Equivalent Ext modulus | 318.77 | MPa |
| Equivalent Gxyt modulus | 83.417 | MPa |
| Poisson’s ratio νxyt | 0.37 | |
| Equivalent Exb modulus | 647.69 | MPa |
| Equivalent Eyb modulus | 370.51 | MPa |
| Equivalent Gxyb modulus | 13.55 | MPa |
| Poisson’s ratio νxyb | 0.37 | |
| Shear rigidity Sx | 136.27 | N/mm |
| Shear rigidity Sy | 3.8697 | N/mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hakim, G.; Abramovich, H. The Behavior of Long Thin Rectangular Plates under Normal Pressure—A Thorough Investigation. Materials 2024, 17, 2902. https://doi.org/10.3390/ma17122902
Hakim G, Abramovich H. The Behavior of Long Thin Rectangular Plates under Normal Pressure—A Thorough Investigation. Materials. 2024; 17(12):2902. https://doi.org/10.3390/ma17122902
Chicago/Turabian StyleHakim, Gilad, and Haim Abramovich. 2024. "The Behavior of Long Thin Rectangular Plates under Normal Pressure—A Thorough Investigation" Materials 17, no. 12: 2902. https://doi.org/10.3390/ma17122902
APA StyleHakim, G., & Abramovich, H. (2024). The Behavior of Long Thin Rectangular Plates under Normal Pressure—A Thorough Investigation. Materials, 17(12), 2902. https://doi.org/10.3390/ma17122902







