Bond Strength Assessment of Normal Strength Concrete–Ultra-High-Performance Fiber Reinforced Concrete Using Repeated Drop-Weight Impact Test: Experimental and Machine Learning Technique
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. NSC and UHPFRC
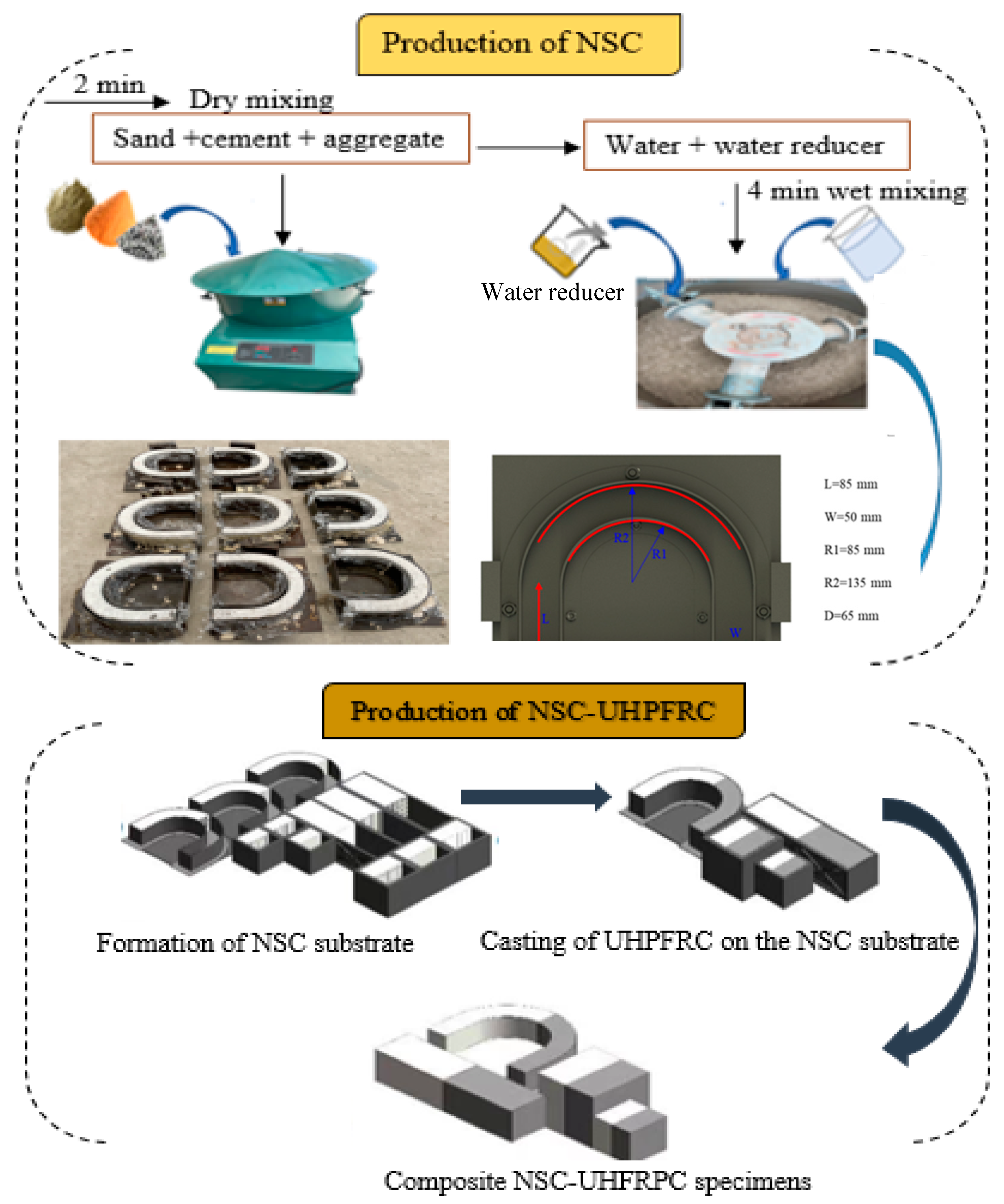
2.1.2. Sample Fabrications
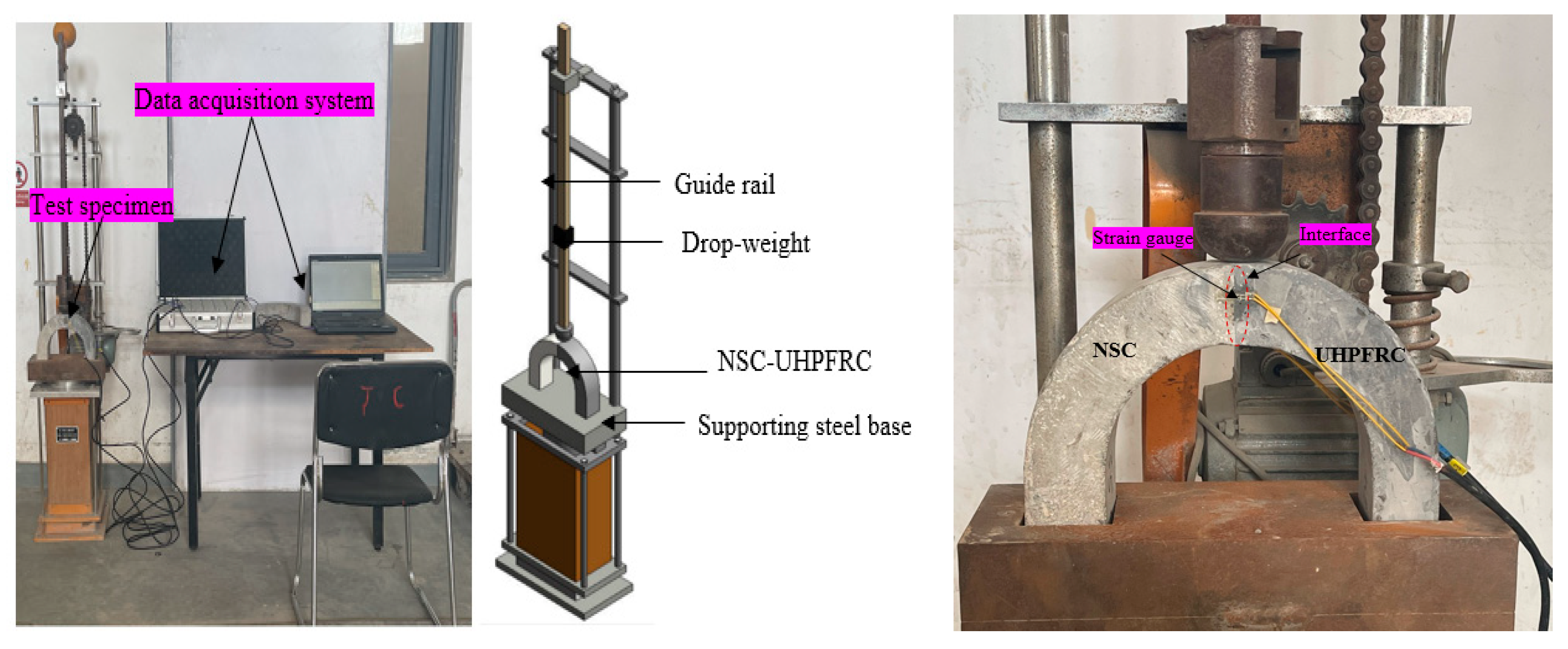
2.2. Testing Methods
Multiple Drop-Weight Impact Tests
2.3. Machine Learning Algorithms
2.3.1. CatBoost
2.3.2. XGBoost
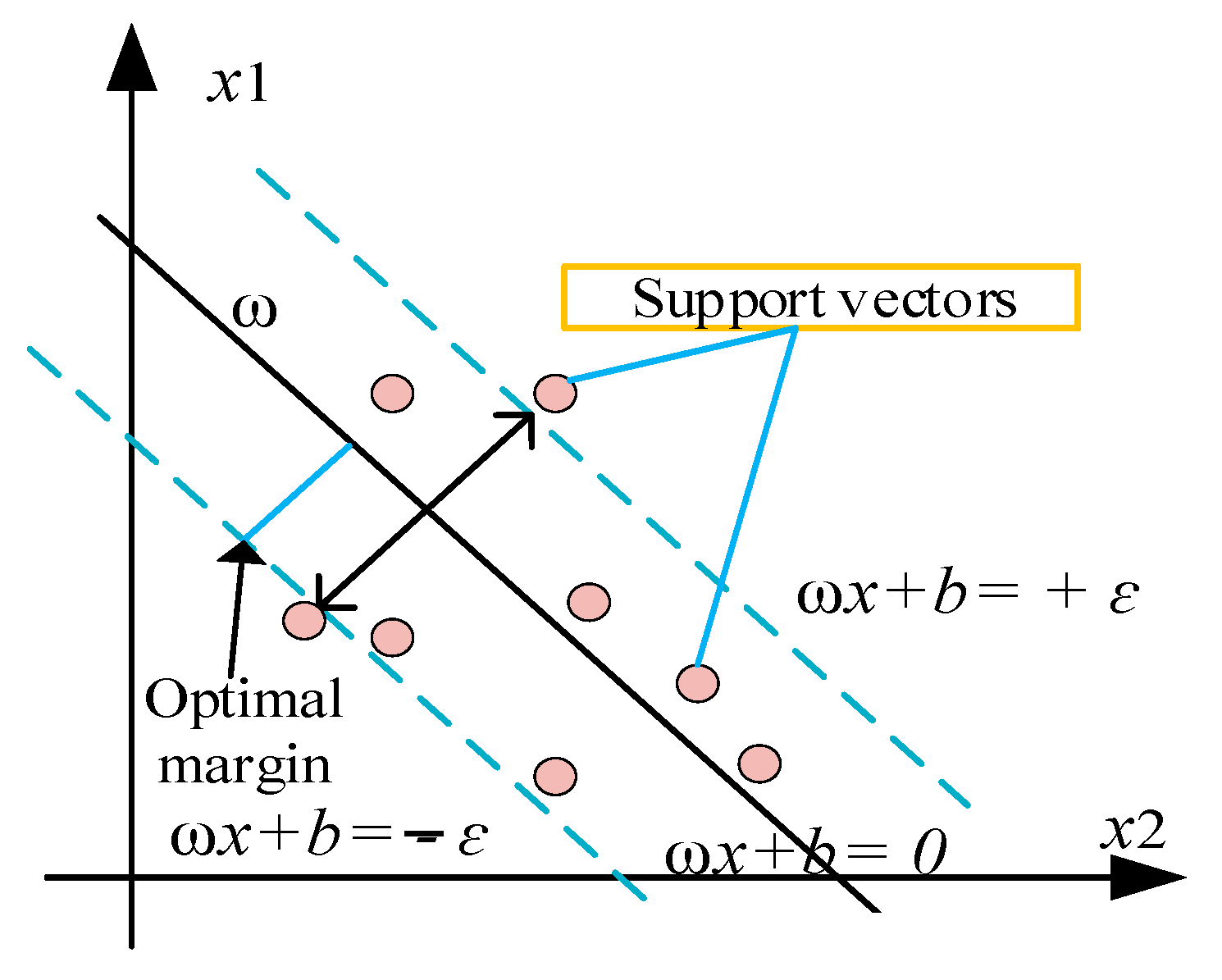
2.3.3. Support Vector Regression (SVR)
2.3.4. Generalized Linear Model (GLM)
2.3.5. Performance Evaluation Measures
3. Results and Discussions
3.1. Impact Resistance of NSC-UHPFRC
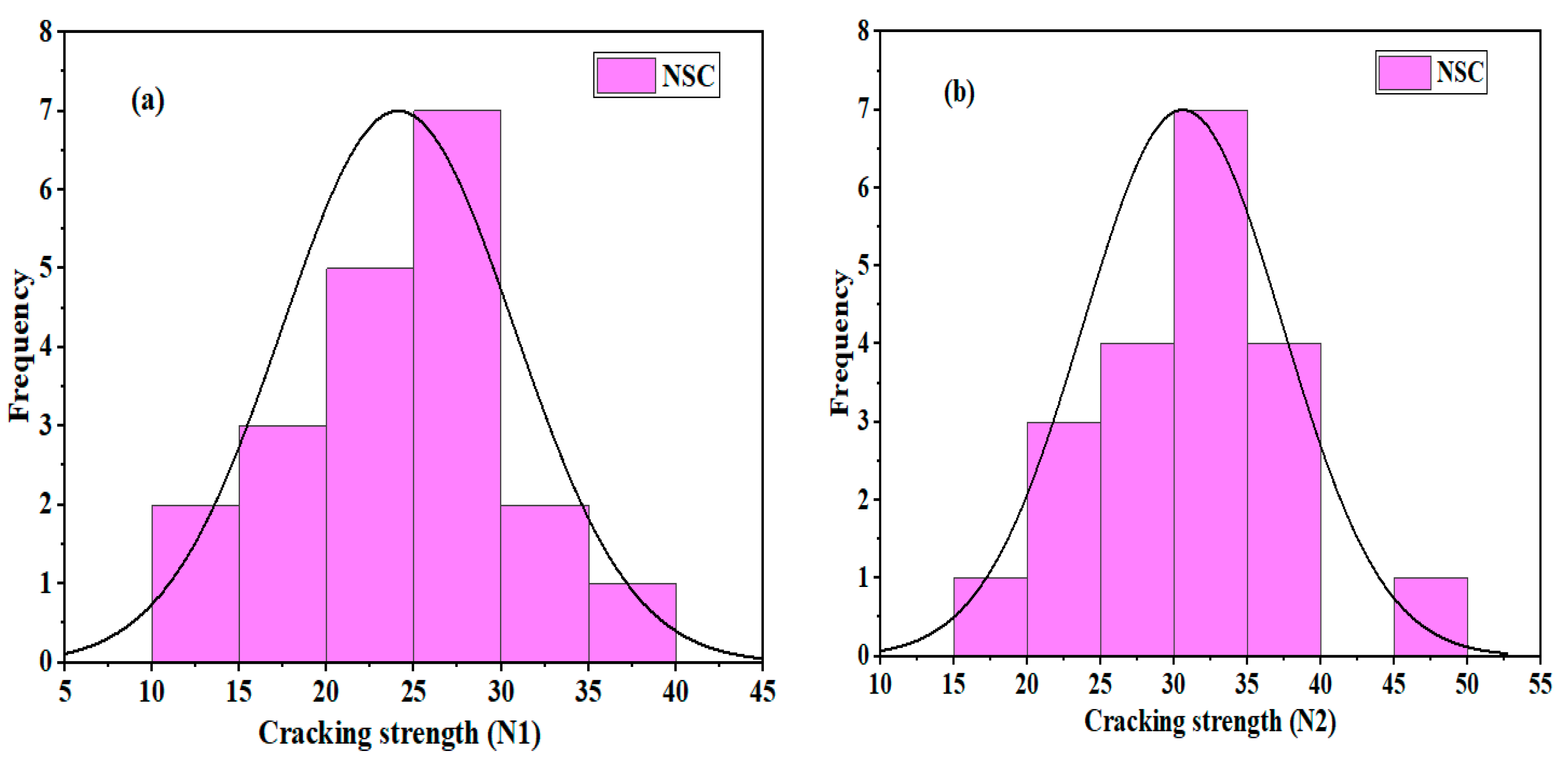
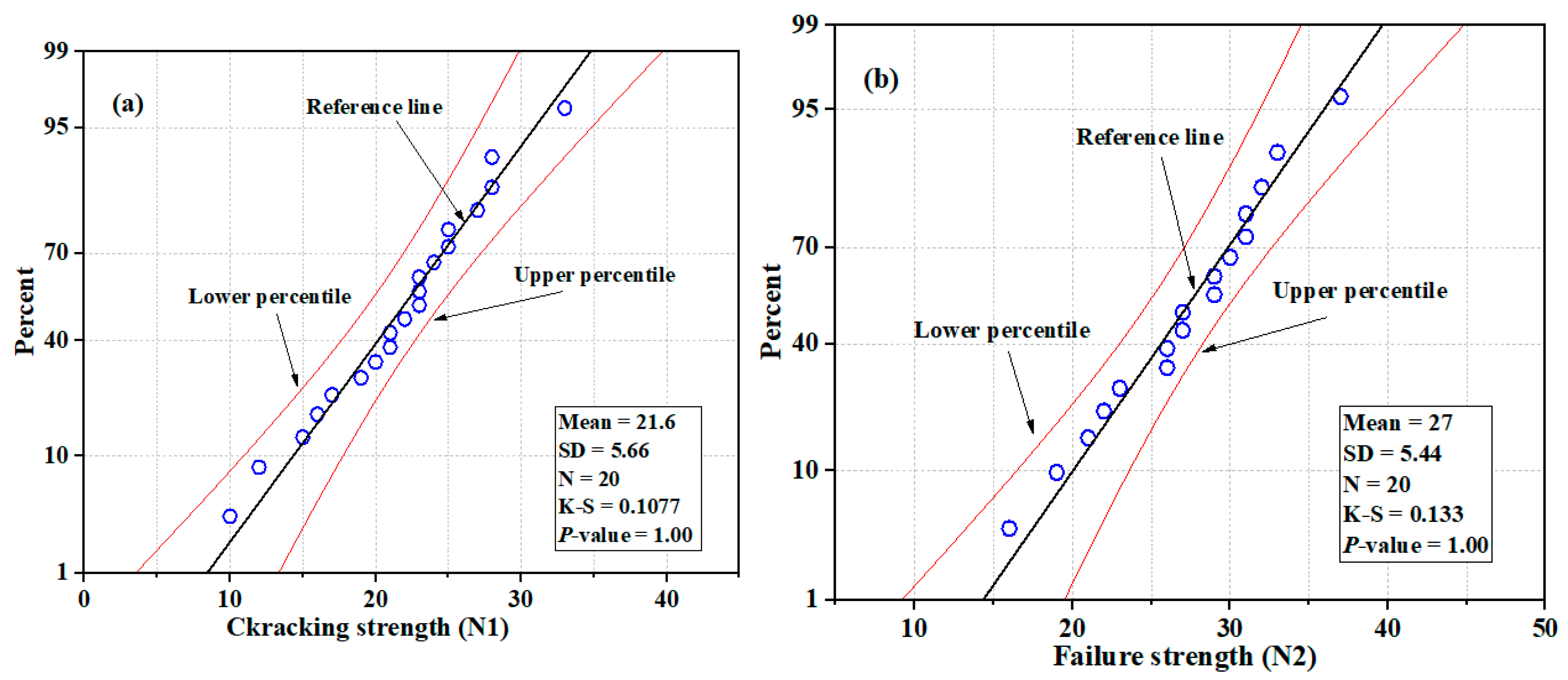
3.2. NSC
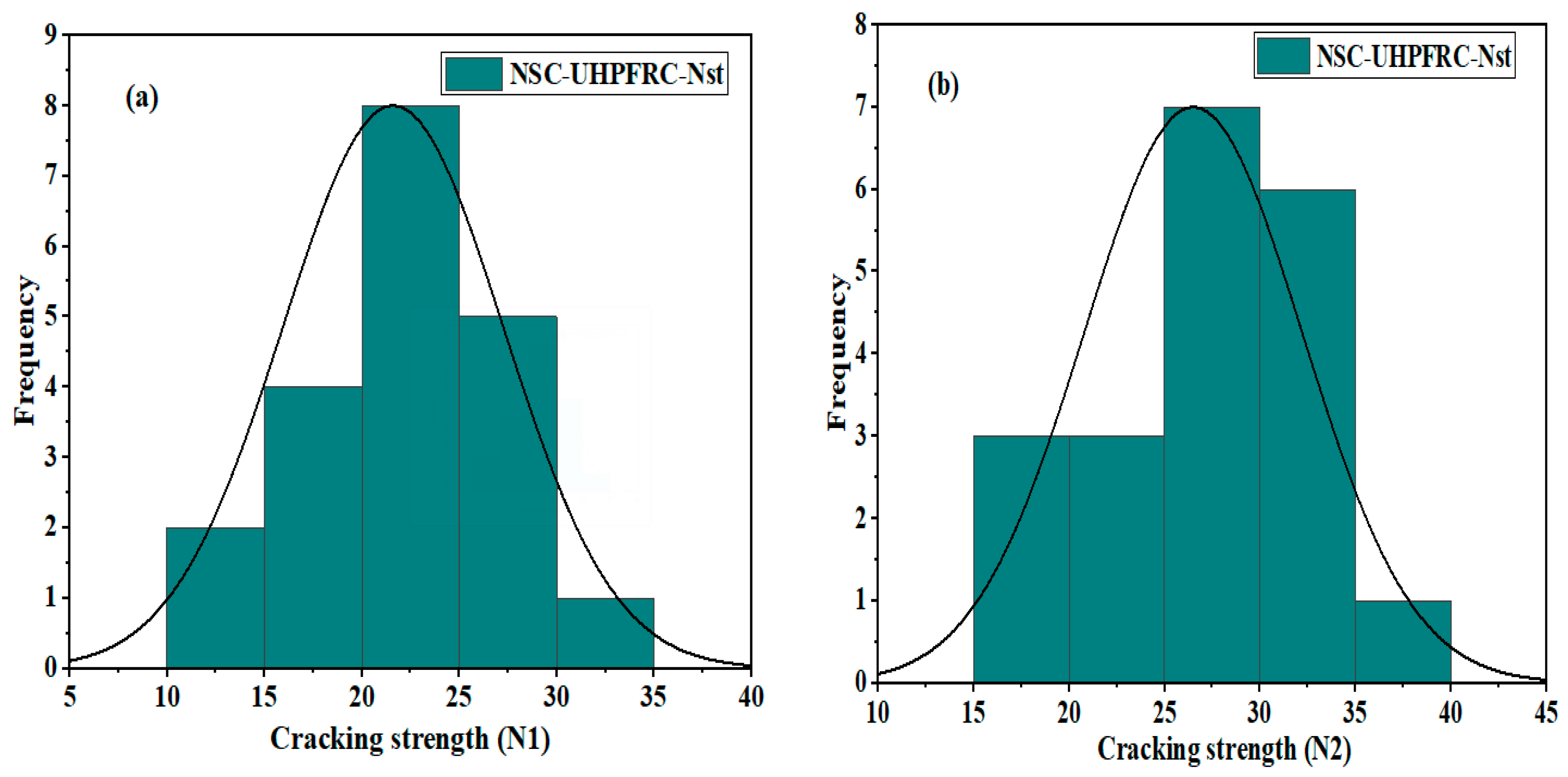
3.3. NSC-UHPFRC-Nst
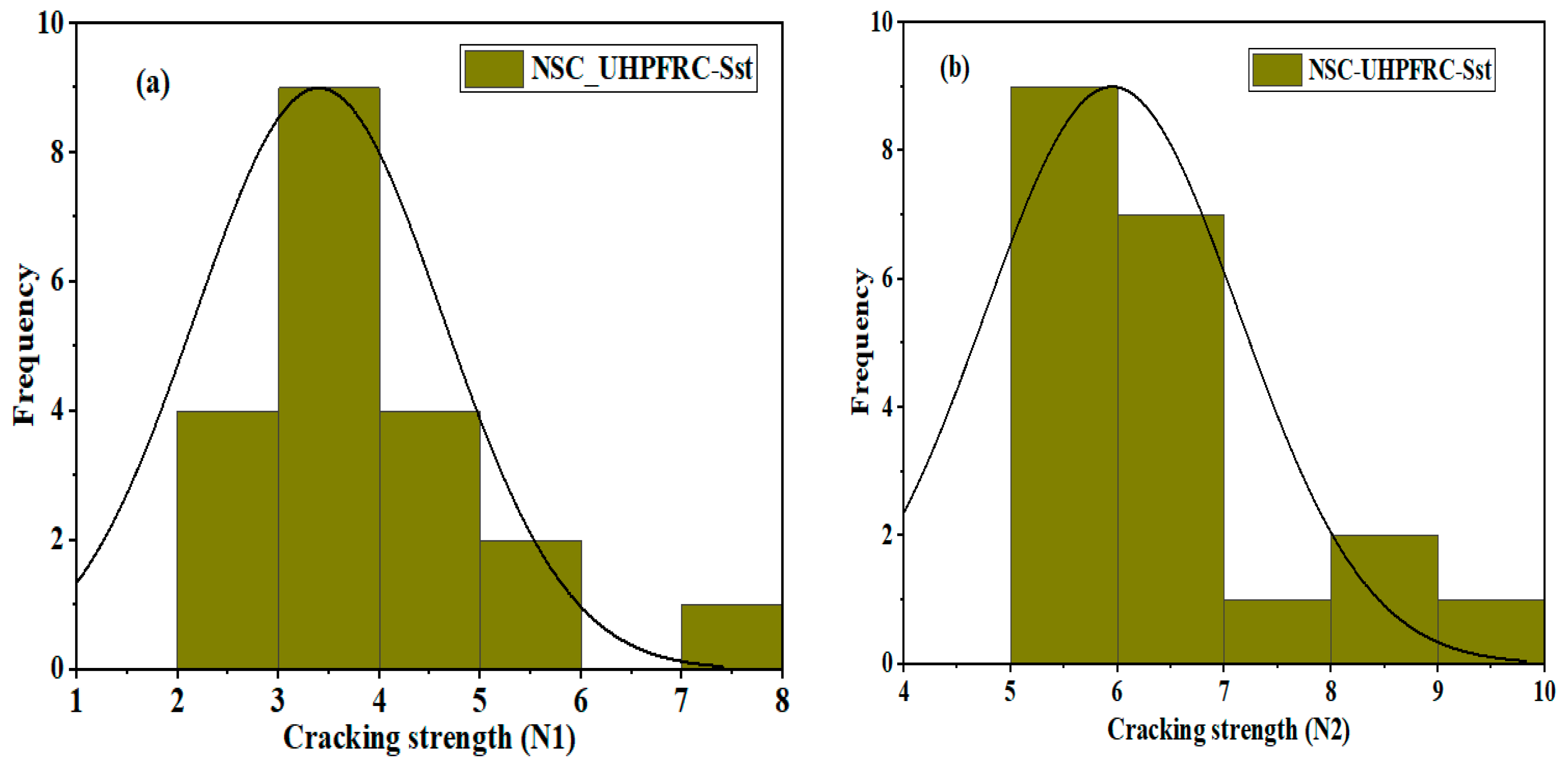
3.4. NSC-UHPFRC-Sst
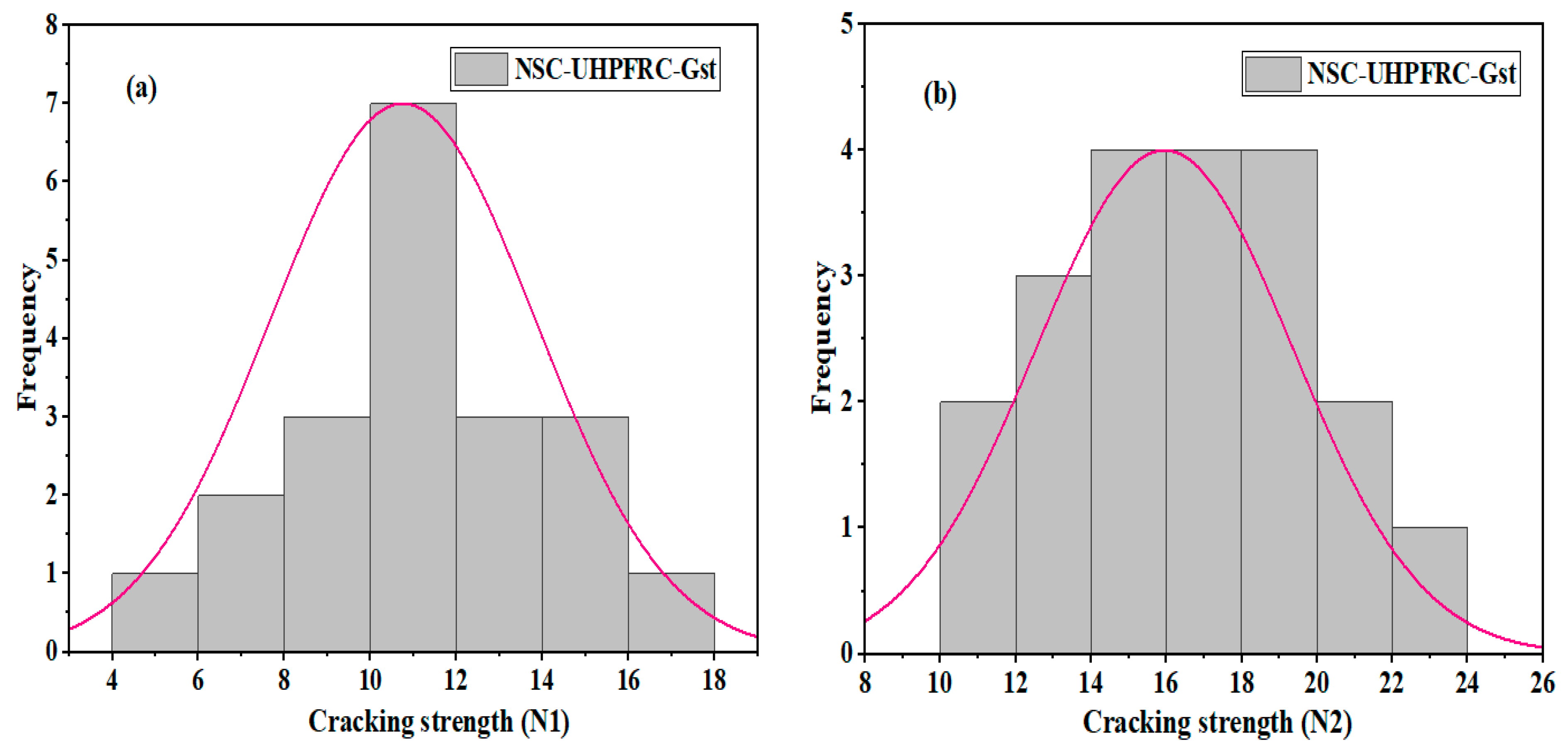
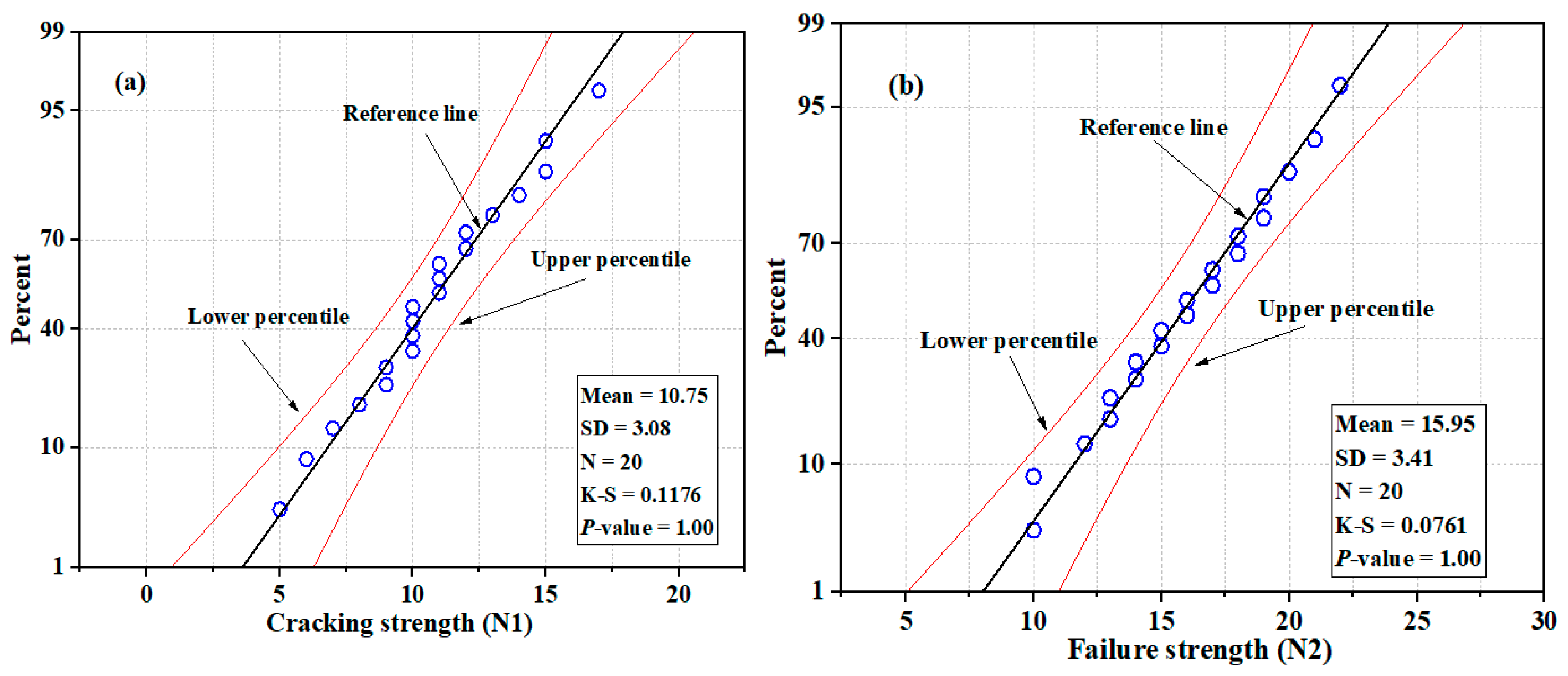
3.5. NSC-UHPFC-Gst
3.6. Results of the Ensemble Machine Learning Models
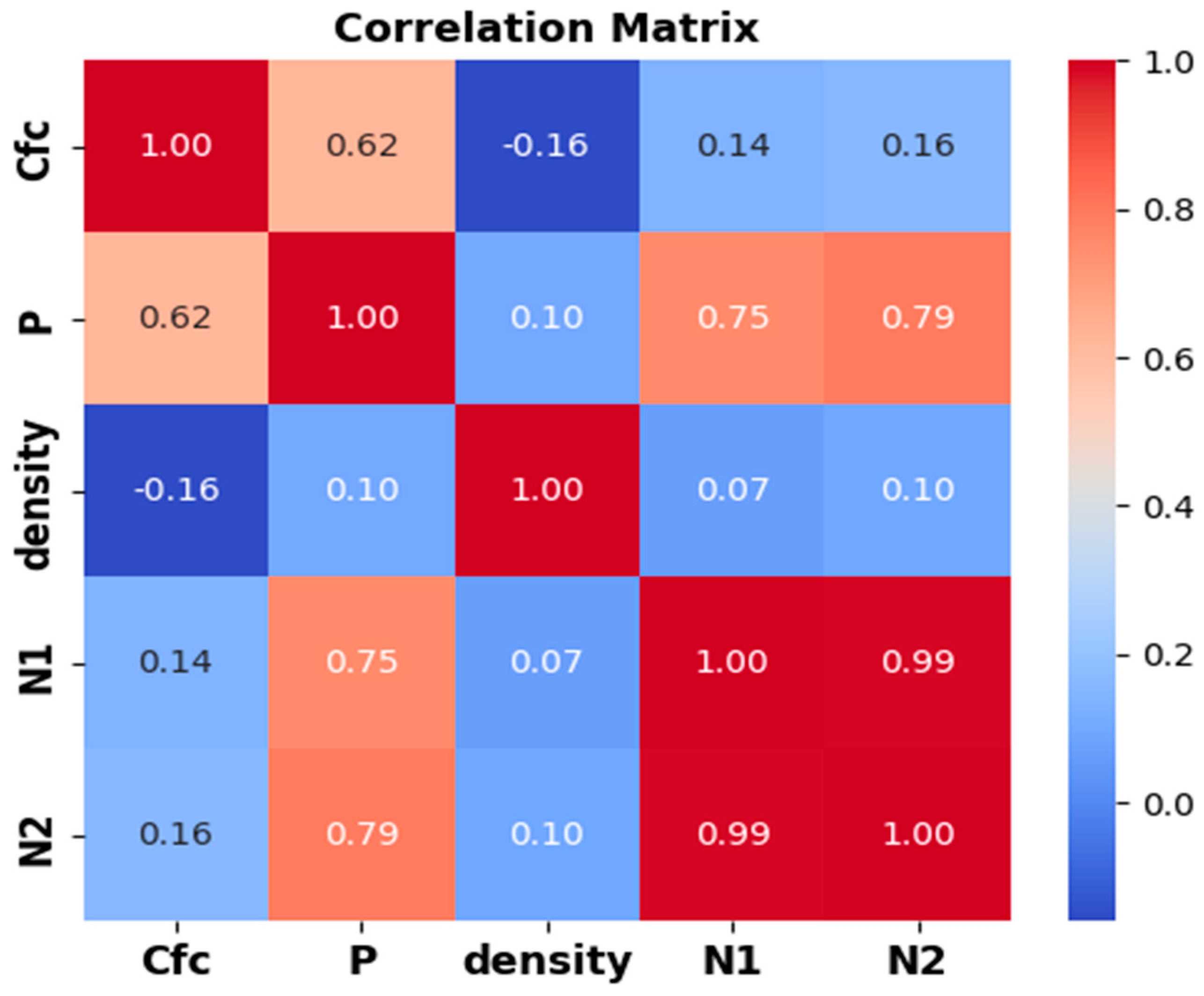
3.6.1. Sensitivity Analysis
3.6.2. XGBoost Model Results
3.6.3. CatBoost Model Results
3.6.4. SVR and GLM
4. Conclusions
- (1)
- The impact test result indicated that surface treatment plays a significant role in ensuring sufficient bond strength at the interface of NSC-UHPFRC composites, and the bond behavior between the NSC substrate under natural fracture and the UHPFRC layer can provide sufficient bond strength at the interface, resulting in a monolithic structure that can withstand dynamic loads under repeated drop-weight impact stress.
- (2)
- The reference NSC specimen requires a high number of drops to resist impact loads before initial crack (N1) occurrence, with the average number of drops equal to 24 blows compared to the NSC-UHPFRC composite samples. Remarkable reductions in impact strength properties were observed in all the composite U-shaped NSC-UHPFRC samples.
- (3)
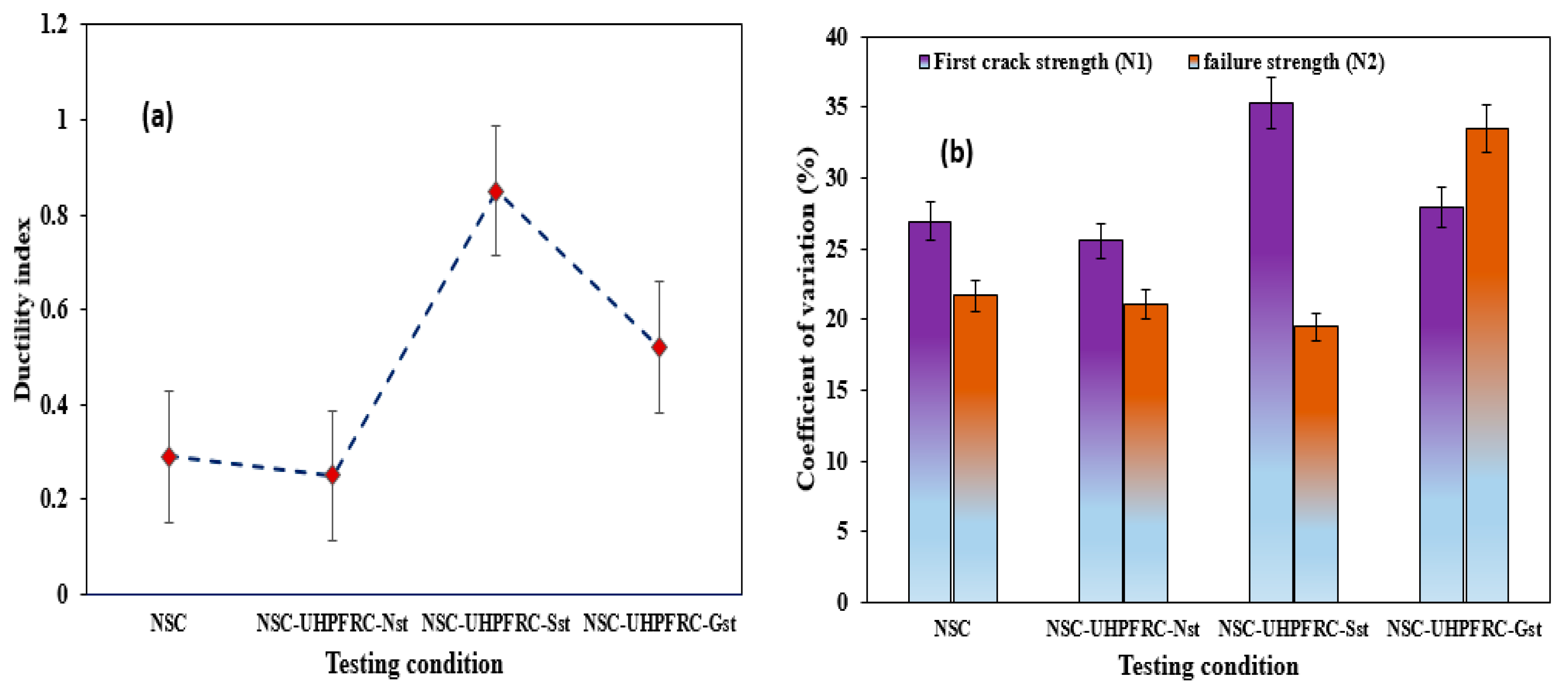
- The inclusion of steel fibers in the UHPFRC layer improved the composite U-shaped ductility, which transformed the composite specimens to a more ductile state and enhanced the impact strength of the NSC-UHPFRC sample. The DI values of the NSC-UHPFRC for each testing condition are less than unity. The COV of the impact data obtained in this work is lower than that found in several past studies that used the drop-weight impact testing approach ACI 544-2R.
- (4)
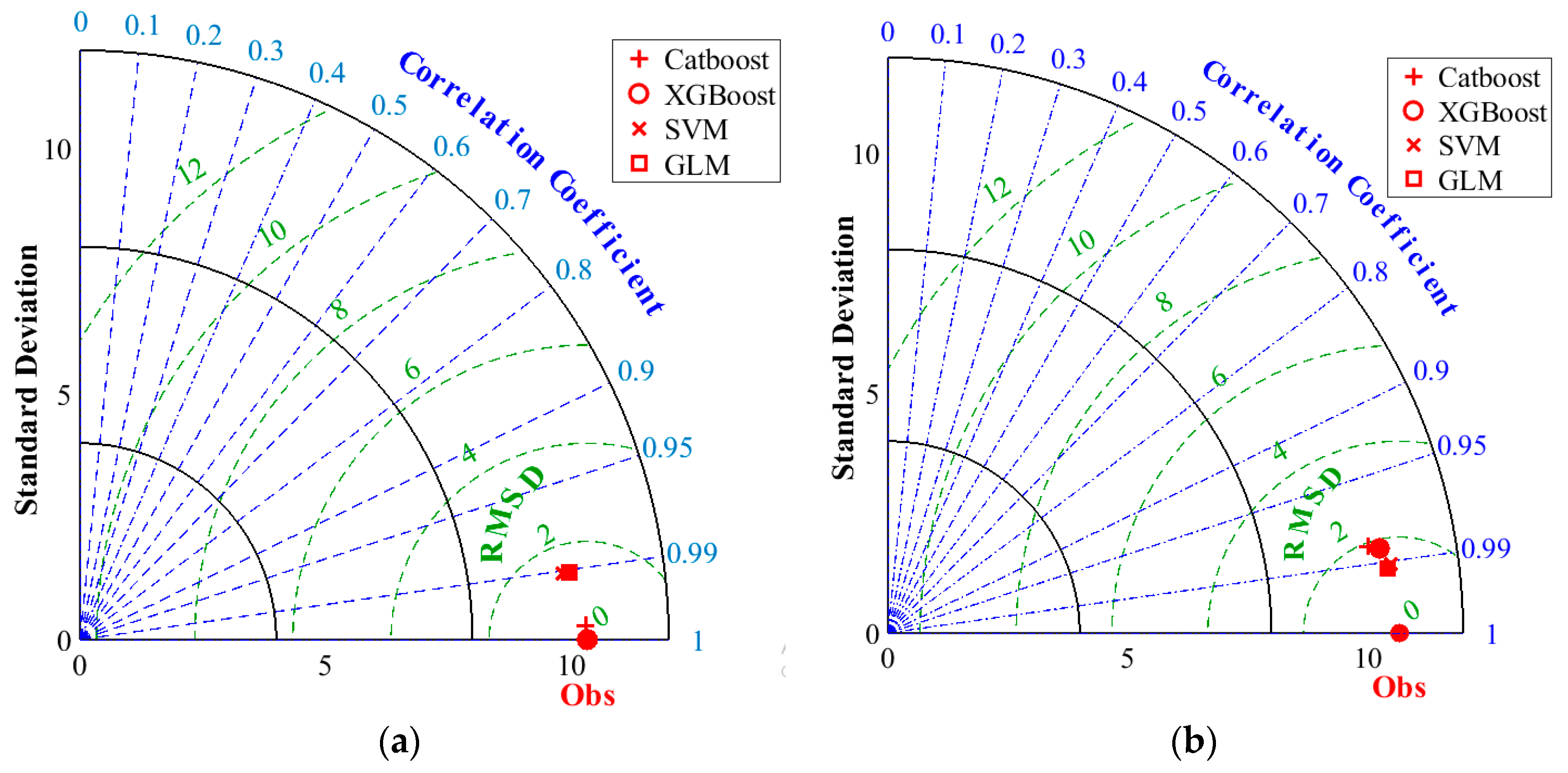
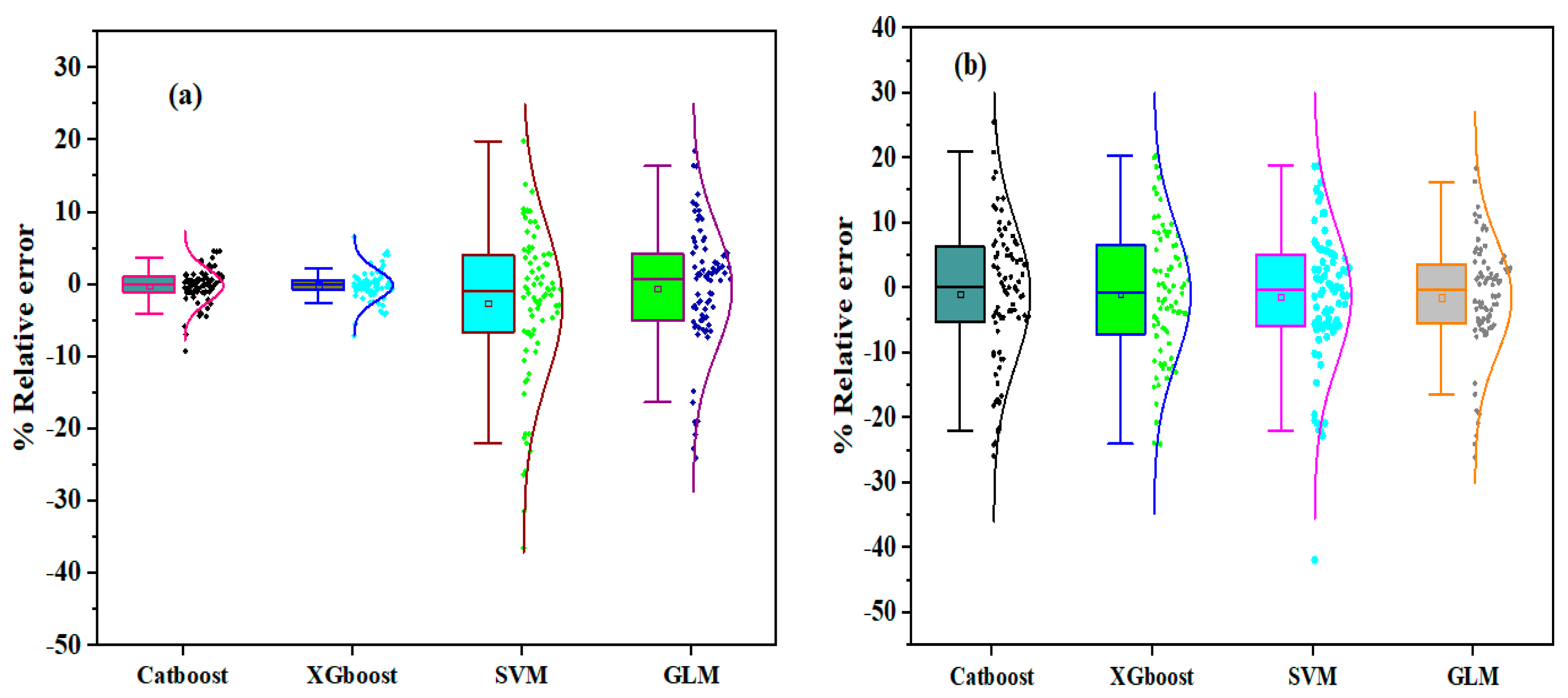
- The two ensemble ML approaches correctly estimated the impact strength of the NSC-UHPFRC composite. The XGBoost ensemble model gave coefficient of determination (R2) values of approximately 0.999 and 0.964 at the training and testing stages. Similarly, GLM outperformed other models in the testing phase, with an R2 value of 0.9805. The performance matrices were proven using the Taylor diagram and Boxplots.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Semendary, A.A.; Svecova, D. Factors affecting bond between precast concrete and cast in place ultra high performance concrete (UHPC). Eng. Struct. 2020, 216, 110746. [Google Scholar] [CrossRef]
- Beushausen, H.; Höhlig, B.; Talotti, M. The influence of substrate moisture preparation on bond strength of concrete overlays and the microstructure of the OTZ. Cem. Concr. Res. 2017, 92, 84–91. [Google Scholar] [CrossRef]
- Feng, S.; Xiao, H.; Geng, J. Bond strength between concrete substrate and repair mortar: Effect of fibre stiffness and substrate surface roughness. Cem. Concr. Compos. 2020, 114, 103746. [Google Scholar] [CrossRef]
- Mansour, W.; Sakr, M.A.; Seleemah, A.A.; Tayeh, B.A.; Khalifa, T.M. Bond behavior between concrete and prefabricated ultra high-performance fiber-reinforced concrete (UHPFRC) plates. Struct. Eng. Mech. 2022, 81, 305. [Google Scholar]
- Yu, J.; Zhang, B.; Chen, W.; Liu, H.; Li, H. Multi-scale study on interfacial bond failure between normal concrete (NC) and ultra-high performance concrete (UHPC). J. Build. Eng. 2022, 57, 104808. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, C.; Yang, J.; Wang, K. Experimental study on flexural behavior of precast hybrid UHPC-NSC beams. J. Build. Eng. 2023, 70, 106354. [Google Scholar] [CrossRef]
- Jongvivatsakul, P.; Thongchom, C.; Mathuros, A.; Prasertsri, T.; Adamu, M.; Orasutthikul, S.; Lenwari, A.; Charainpanitkul, T. Enhancing bonding behavior between carbon fiber-reinforced polymer plates and concrete using carbon nanotube reinforced epoxy composites. Case Stud. Constr. Mater. 2022, 17, e01407. [Google Scholar] [CrossRef]
- Haruna, S.I.; Zhu, H.; Jiang, W.; Shao, J. Evaluation of impact resistance properties of polyurethane-based polymer concrete for the repair of runway subjected to repeated drop-weight impact test. Constr. Build. Mater. 2021, 309, 125152. [Google Scholar] [CrossRef]
- Haruna, S.I.; Zhu, H.; Ibrahim, Y.E.; Shao, J.; Adamu, M.; Farouk, A.I.B. Experimental and Statistical Analysis of U-Shaped Polyurethane-Based Polymer Concrete under Static and Impact Loads as a Repair Material. Buildings 2022, 12, 1986. [Google Scholar] [CrossRef]
- Haruna, S.I.; Zhu, H.; Ibrahim, Y.E.; Shao, J.; Adamu, M.; Ahmed, O.S. Impact resistance and flexural behavior of U-shaped concrete specimen retrofitted with polyurethane grout. Case Stud. Constr. Mater. 2023, 19, e02547. [Google Scholar]
- Jia, P.C.; Wu, H.; Wang, R.; Fang, Q. Dynamic responses of reinforced ultra-high performance concrete members under low-velocity lateral impact. Int. J. Impact Eng. 2021, 150, 103818. [Google Scholar] [CrossRef]
- Zhai, Y.X.; Wu, H.; Fang, Q. Impact resistance of armor steel/ceramic/UHPC layered composite targets against 30CrMnSiNi2A steel projectiles. Int. J. Impact Eng. 2021, 154, 103888. [Google Scholar] [CrossRef]
- Zhang, F.; Shedbale, A.S.; Zhong, R.; Poh, L.H.; Zhang, M.-H. Ultra-high performance concrete subjected to high-velocity projectile impact: Implementation of K&C model with consideration of failure surfaces and dynamic increase factors. Int. J. Impact Eng. 2021, 155, 103907. [Google Scholar]
- Huang, L.; Su, L.; Xie, J.; Lu, Z.; Li, P.; Hu, R.; Yang, S. Dynamic splitting behaviour of ultra-high-performance concrete confined with carbon-fibre-reinforced polymer. Compos. Struct. 2022, 284, 115155. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; Khayat, K.H.; Xie, L. Effect of SCM and nano-particles on static and dynamic mechanical properties of UHPC. Constr. Build. Mater. 2018, 182, 118–125. [Google Scholar] [CrossRef]
- Yalin, L.; Ya, W. Drop-Weight Impact Resistance of Ultrahigh-Performance Concrete and the Corresponding Statistical Analysis. J. Mater. Civ. Eng. 2022, 34, 4021409. [Google Scholar]
- Yu, R.; Van Beers, L.; Spiesz, P.; Brouwers, H.J.H. Impact resistance of a sustainable Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) under pendulum impact loadings. Constr. Build. Mater. 2016, 107, 203–215. [Google Scholar] [CrossRef]
- Almustafa, M.K.; Nehdi, M.L. Machine learning model for predicting structural response of RC columns subjected to blast loading. Int. J. Impact Eng. 2022, 162, 104145. [Google Scholar] [CrossRef]
- Cao, Y.; Zandi, Y.; Rahimi, A.; Petković, D.; Denić, N.; Stojanović, J.; Spasić, B.; Vujović, V.; Khadimallah, M.A.; Assilzadeh, H. Evaluation and monitoring of impact resistance of fiber reinforced concrete by adaptive neuro fuzzy algorithm. Structures. 2021, 34, 3750–3756. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Nasiri, S.; Anders, D.; Weinberg, K. Prediction of dynamic properties of ultra-high performance concrete by an artificial intelligence approach. Adv. Eng. Softw. 2019, 127, 51–58. [Google Scholar] [CrossRef]
- Shao, R.; Wu, C.; Su, Y.; Liu, Z.; Liu, J.; Chen, G.; Xu, S. Experimental and numerical investigations of penetration resistance of ultra-high strength concrete protected with ceramic balls subjected to projectile impact. Ceram. Int. 2019, 45, 7961–7975. [Google Scholar] [CrossRef]
- GB175-2007; Common Portland Cement. Chinese National Standard: Beijing, China, 2007.
- JTG55-2011; Specification for Mix Proportion Design of Ordinary Concrete. Chinese National Standard: Beijing, China, 2011.
- Farouk, A.I.B.; Harunaa, S.I. Evaluation of Bond Strength between Ultra-High-Performance Concrete and Normal Strength Concrete: An Overview. J. Kejuruter. 2020, 32, 41–51. [Google Scholar] [CrossRef] [PubMed]
- ACI 544.2R-89; Measurement of Properties of Fiber Reinforced Concrete. American Concrete Institute: Farmington Hills, MI, USA, 1989; pp. 433–439.
- Al-shawafi, A.; Zhu, H.; Bo, Z.; Haruna, S.I.; Ibrahim, Y.E.; Farouk, A.I.B.; Laqsum, S.A.; Shao, J. Bond behavior between normal concrete and UHPC and PUC layers subjected to different loading conditions coupled with fracture analysis technique. J. Build. Eng. 2024, 86, 108880. [Google Scholar] [CrossRef]
- Malami, S.I.; Musa, A.A.; Haruna, S.I.; Aliyu, U.U.; Usman, A.G.; Abdurrahman, M.I.; Bashir, A.; Abba, S.I. Implementation of soft-computing models for prediction of flexural strength of pervious concrete hybridized with rice husk ash and calcium carbide waste. Model. Earth Syst. Environ. 2022, 8, 1933–1947. [Google Scholar] [CrossRef]
- Qian, L.; Chen, Z.; Huang, Y.; Stanford, R.J. Employing categorical boosting (CatBoost) and meta-heuristic algorithms for predicting the urban gas consumption. Urban Clim. 2023, 51, 101647. [Google Scholar] [CrossRef]
- Younsi, S.; Dabiri, H.; Marini, R.; Mazzanti, P.; Mugnozza, G.S.; Bozzano, F. Reconstructing missing InSAR data by the application of machine leaning-based prediction models: A case study of Rieti. J. Civ. Struct. Health Monit. 2024, 14, 143–161. [Google Scholar] [CrossRef]
- Dabiri, H.; Clementi, J.; Marini, R.; Mugnozza, G.S.; Bozzano, F.; Mazzanti, P. Machine learning-based analysis of historical towers. Eng. Struct. 2024, 304, 117621. [Google Scholar] [CrossRef]
- Lyu, F.; Fan, X.; Ding, F.; Chen, Z. Prediction of the axial compressive strength of circular concrete-filled steel tube columns using sine cosine algorithm-support vector regression. Compos. Struct. 2021, 273, 114282. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Support vector machines for classification and regression. Analyst 2010, 135, 230–267. [Google Scholar] [CrossRef]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized linear models. J. R. Stat. Soc. Ser. A Stat. Soc. 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Cao, H. Experimental investigation on the static and impact behaviors of basalt fiber-reinforced concrete. Open Civ. Eng. J. 2017, 11, 14–21. [Google Scholar] [CrossRef]
- Rai, B.; Singh, N.K. Statistical and experimental study to evaluate the variability and reliability of impact strength of steel-polypropylene hybrid fiber reinforced concrete. J. Build. Eng. 2021, 44, 102937. [Google Scholar] [CrossRef]
- Prasad, N.; Murali, G. Exploring the impact performance of functionally-graded preplaced aggregate concrete incorporating steel and polypropylene fibres. J. Build. Eng. 2021, 35, 102077. [Google Scholar] [CrossRef]
- Badr, A.; Ashour, A.F.; Platten, A.K. Statistical variations in impact resistance of polypropylene fibre-reinforced concrete. Int. J. Impact Eng. 2006, 32, 1907–1920. [Google Scholar] [CrossRef]
- Song, P.S.; Wu, J.C.; Hwang, S.; Sheu, B.C. Statistical analysis of impact strength and strength reliability of steel–polypropylene hybrid fiber-reinforced concrete. Constr. Build. Mater. 2005, 19, 1–9. [Google Scholar] [CrossRef]
- Haruna, S.I.; Zhu, H.; Shao, J. Experimental study, modeling, and reliability analysis of impact resistance of micro steel fiber-reinforced concrete modified with nano silica. Struct. Concr. 2022, 23, 1659–1674. [Google Scholar] [CrossRef]
- Farouk, A.I.B.; Jinsong, Z. Prediction of Interface Bond Strength between Ultra-High-Performance Concrete (UHPC) and Normal Strength Concrete (NSC) Using a Machine Learning Approach. Arab. J. Sci. Eng. 2022, 47, 5337–5363. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Pradhan, B. Vehicular traffic noise prediction and propagation modelling using neural networks and geospatial information system. Environ. Monit. Assess. 2019, 191, 190. [Google Scholar] [CrossRef] [PubMed]
- Yaseen, Z.M.; Ebtehaj, I.; Kim, S.; Sanikhani, H.; Asadi, H.; Ghareb, M.I.; Bonakdari, H.; Mohtar, W.H.W.; Al-Ansari, N.; Shahid, S. Novel Hybrid Data-Intelligence Model for Forecasting Monthly Rainfall with Uncertainty Analysis. Water 2019, 11, 502. [Google Scholar] [CrossRef]
- Zhu, S.; Heddam, S.; Wu, S.; Dai, J.; Jia, B. Extreme learning machine-based prediction of daily water temperature for rivers. Environ. Earth Sci. 2019, 78, 202. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 107, 7183–7192. [Google Scholar] [CrossRef]







| Materials | NSC | UHPFRC |
|---|---|---|
| OPC | 420 | 1000 |
| Fine aggregate | 573 | 1200 |
| Medium aggregate | 1273 | 0.00 |
| Water | 185 | 232 |
| Quartz powder | 0.00 | 50.0 |
| Water-reducing agent | 0.63 | 200 |
| Slag | 0.00 | 200 |
| Silica fumes | 0.00 | 250 |
| Steel Fiber (Vf%) | 0.00 | 1.0 |
| Properties | Length/mm | Diameter/mm | Aspect Ratio | Density/kg/m3 | Tensile Strength/MPa |
|---|---|---|---|---|---|
| 13.0 | 0.2 | 65.0 | 7800 | 2850 |
| S/N | NSC | NSC-UHPFRC-Nst | NSC-UHPFRC-Sst | NSC-UHPFRC-Gst | ||||
|---|---|---|---|---|---|---|---|---|
| N1 | N2 | N1 | N2 | N1 | N2 | N1 | N2 | |
| 1 | 24 | 28 | 22 | 26 | 3 | 5 | 10 | 14 |
| 2 | 27 | 34 | 23 | 30 | 7 | 9 | 12 | 19 |
| 3 | 12 | 17 | 10 | 15 | 4 | 6 | 5 | 10 |
| 4 | 25 | 33 | 28 | 32 | 3 | 5 | 11 | 19 |
| 5 | 23 | 32 | 20 | 26 | 5 | 8 | 10 | 16 |
| 6 | 28 | 34 | 25 | 30 | 2 | 5 | 12 | 17 |
| 7 | 26 | 35 | 23 | 27 | 3 | 6 | 11 | 15 |
| 8 | 20 | 25 | 17 | 22 | 2 | 5 | 8 | 13 |
| 9 | 15 | 24 | 12 | 16 | 3 | 6 | 6 | 10 |
| 10 | 23 | 29 | 21 | 26 | 3 | 5 | 10 | 15 |
| 11 | 37 | 46 | 33 | 37 | 4 | 6 | 17 | 21 |
| 12 | 17 | 25 | 15 | 19 | 3 | 5 | 9 | 13 |
| 13 | 18 | 23 | 16 | 21 | 3 | 5 | 7 | 12 |
| 14 | 24 | 30 | 21 | 27 | 2 | 5 | 10 | 16 |
| 15 | 29 | 36 | 24 | 29 | 3 | 6 | 13 | 18 |
| 16 | 25 | 31 | 23 | 29 | 4 | 6 | 11 | 17 |
| 17 | 34 | 39 | 28 | 33 | 3 | 6 | 15 | 20 |
| 18 | 32 | 36 | 27 | 31 | 2 | 5 | 14 | 18 |
| 19 | 29 | 34 | 25 | 31 | 4 | 7 | 15 | 22 |
| 20 | 14 | 21 | 19 | 23 | 5 | 8 | 9 | 14 |
| Mean | 24.10 | 30.60 | 21.60 | 26.50 | 3.40 | 5.95 | 10.75 | 15.95 |
| SD | 6.49 | 6.63 | 5.52 | 5.58 | 1.20 | 1.16 | 3.00 | 3.32 |
| COV. | 26.92 | 21.66 | 25.54 | 21.06 | 35.29 | 19.51 | 27.89 | 20.84 |
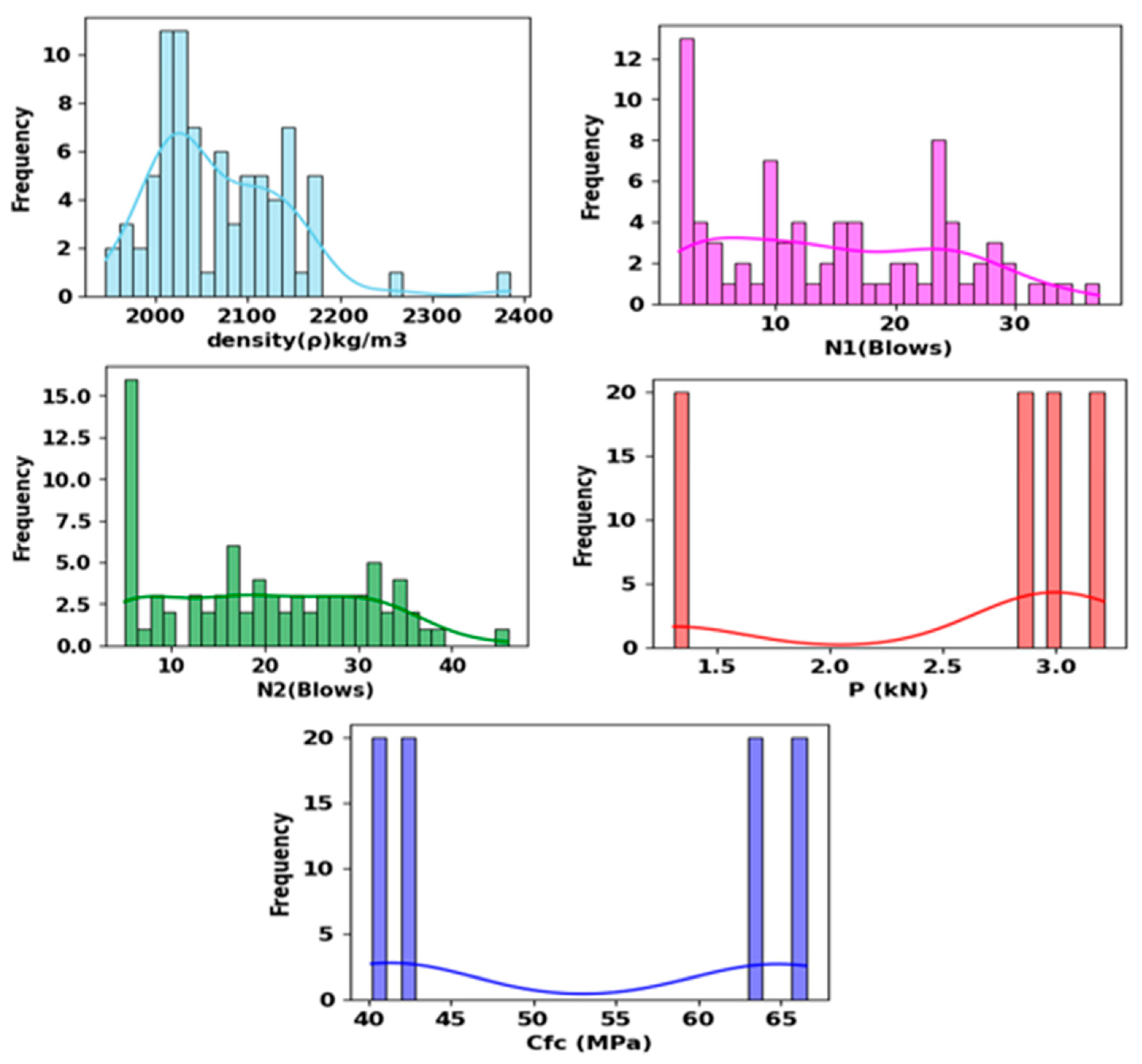
| Parameters | Symbol | Units | Min | Max | Mean | STD | Kurtosis | Skewness | |
|---|---|---|---|---|---|---|---|---|---|
| Input | Compressive strength of composite | Cfc | MPa | 40.20 | 66.50 | 53.08 | 11.89 | −1.99 | 0.017 |
| Flexural load | P | kN | 1.31 | 3.21 | 2.58 | 0.75 | −0.72 | −1.06 | |
| Density | ρ | kg/m | 1946.1 | 2385.03 | 2068.62 | 73.24 | 3.21 | 1.24 | |
| First crack strength | N1 | blows | 2 | 37 | 14.96 | 9.57 | −1.04 | 0.29 | |
| Output | Failure strength | N2 | blows | 5 | 46 | 19.75 | 10.74 | −1.03 | 0.15 |
| Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| MSE | RMSE | MAE | R2 | MSE | RMSE | MAE | R2 | |
| XGBoost | 0000035 | 0.0019 | 0.0014 | 1.0000 | 0.0000 | 0.0019 | 0.0014 | 0.9644 |
| CatBoost | 0.0638 | 0.2512 | 0.1950 | 0.9994 | 3.6676 | 1.6841 | 1.4128 | 0.9676 |
| SVM | 1.8663 | 1.3640 | 1.0410 | 0.9836 | 2.1014 | 1.4104 | 1.13836 | 0.9772 |
| GLM | 1.8784 | 1.3696 | 1.0395 | 0.9835 | 1.8784 | 1.3000 | 1.0395 | 0.9805 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haruna, S.I.; Ibrahim, Y.E.; Hassan, I.H.; Al-shawafi, A.; Zhu, H. Bond Strength Assessment of Normal Strength Concrete–Ultra-High-Performance Fiber Reinforced Concrete Using Repeated Drop-Weight Impact Test: Experimental and Machine Learning Technique. Materials 2024, 17, 3032. https://doi.org/10.3390/ma17123032
Haruna SI, Ibrahim YE, Hassan IH, Al-shawafi A, Zhu H. Bond Strength Assessment of Normal Strength Concrete–Ultra-High-Performance Fiber Reinforced Concrete Using Repeated Drop-Weight Impact Test: Experimental and Machine Learning Technique. Materials. 2024; 17(12):3032. https://doi.org/10.3390/ma17123032
Chicago/Turabian StyleHaruna, Sadi I., Yasser E. Ibrahim, Ibrahim Hayatu Hassan, Ali Al-shawafi, and Han Zhu. 2024. "Bond Strength Assessment of Normal Strength Concrete–Ultra-High-Performance Fiber Reinforced Concrete Using Repeated Drop-Weight Impact Test: Experimental and Machine Learning Technique" Materials 17, no. 12: 3032. https://doi.org/10.3390/ma17123032
APA StyleHaruna, S. I., Ibrahim, Y. E., Hassan, I. H., Al-shawafi, A., & Zhu, H. (2024). Bond Strength Assessment of Normal Strength Concrete–Ultra-High-Performance Fiber Reinforced Concrete Using Repeated Drop-Weight Impact Test: Experimental and Machine Learning Technique. Materials, 17(12), 3032. https://doi.org/10.3390/ma17123032








