Thermo-Chemo-Mechanical Modeling of Residual Stress in Unidirectional Carbon Fiber-Reinforced Polymers during Manufacture
Abstract
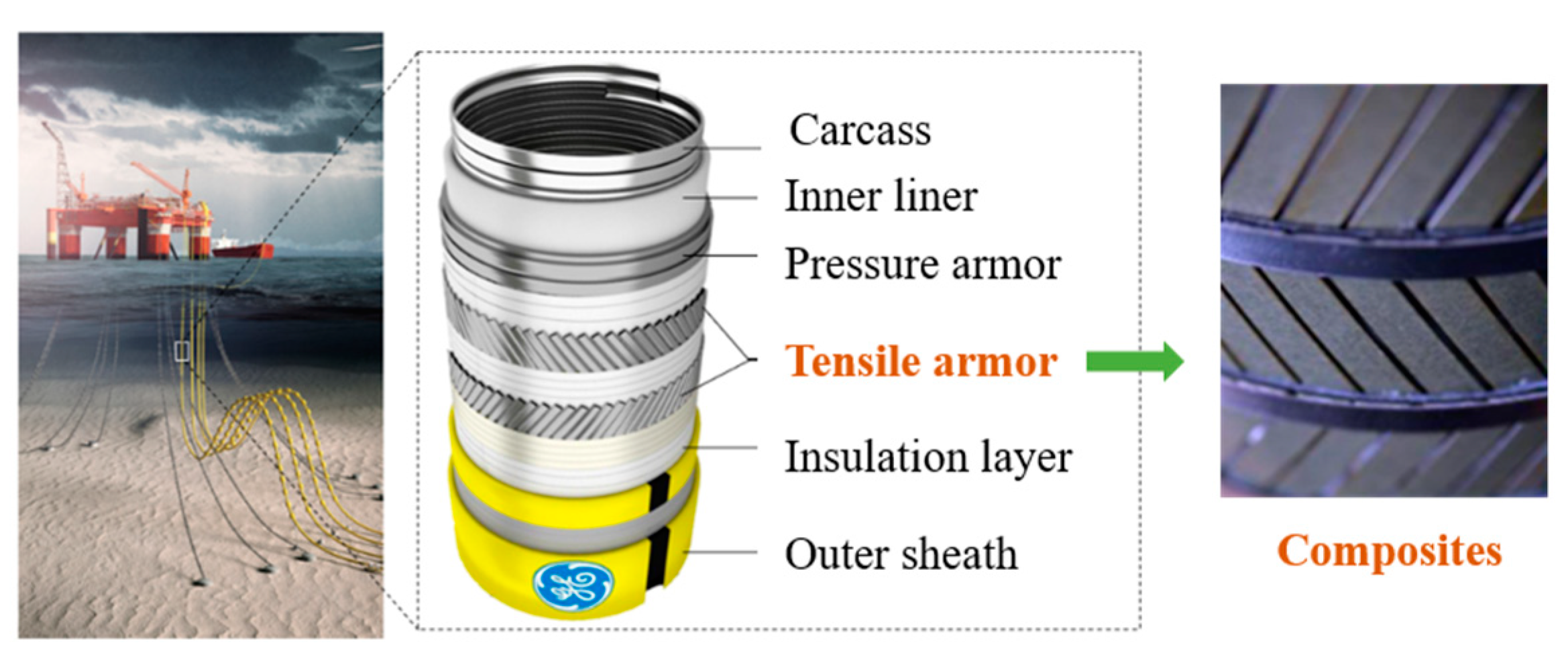
:1. Introduction
2. Multiscale Modeling Process
2.1. Resin Cure Kinetics
2.2. Cure-Dependent Modulus
2.3. Viscoelastic Constitutive Model
3. Model Verification and Numerical Implementation
3.1. Experimental Section
3.2. Numerical Model
4. Results and Discussion
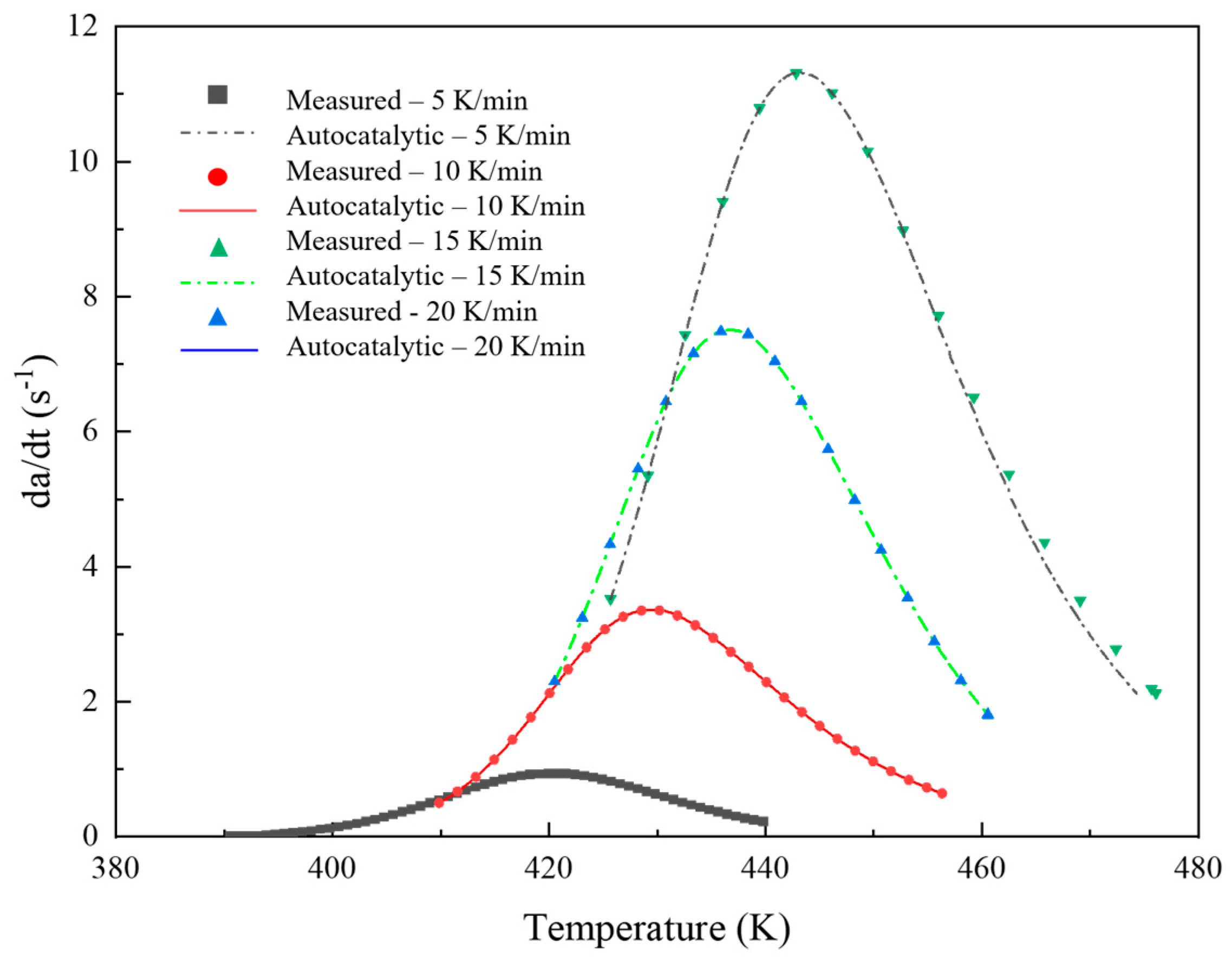
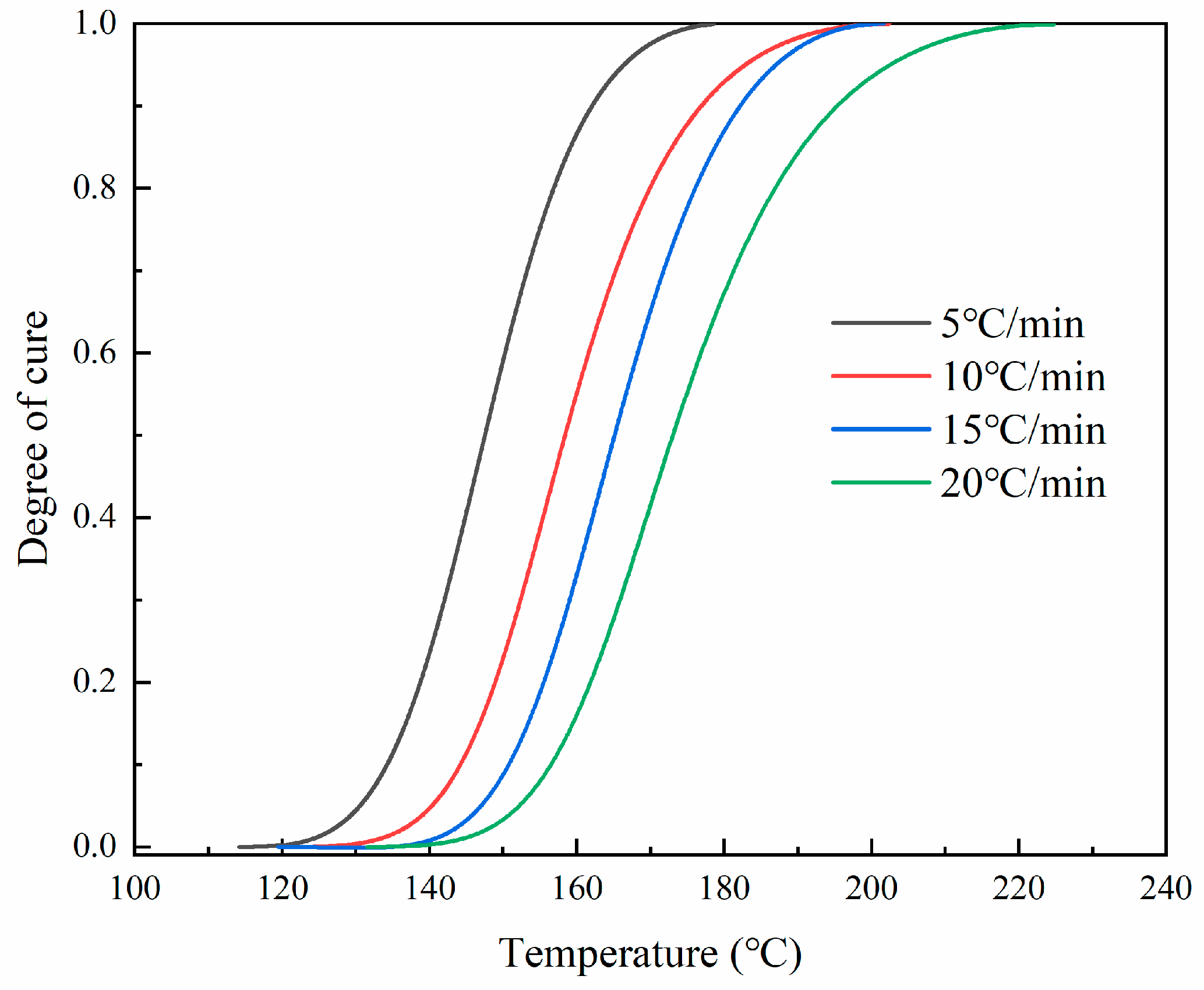
4.1. Cure Kinetics
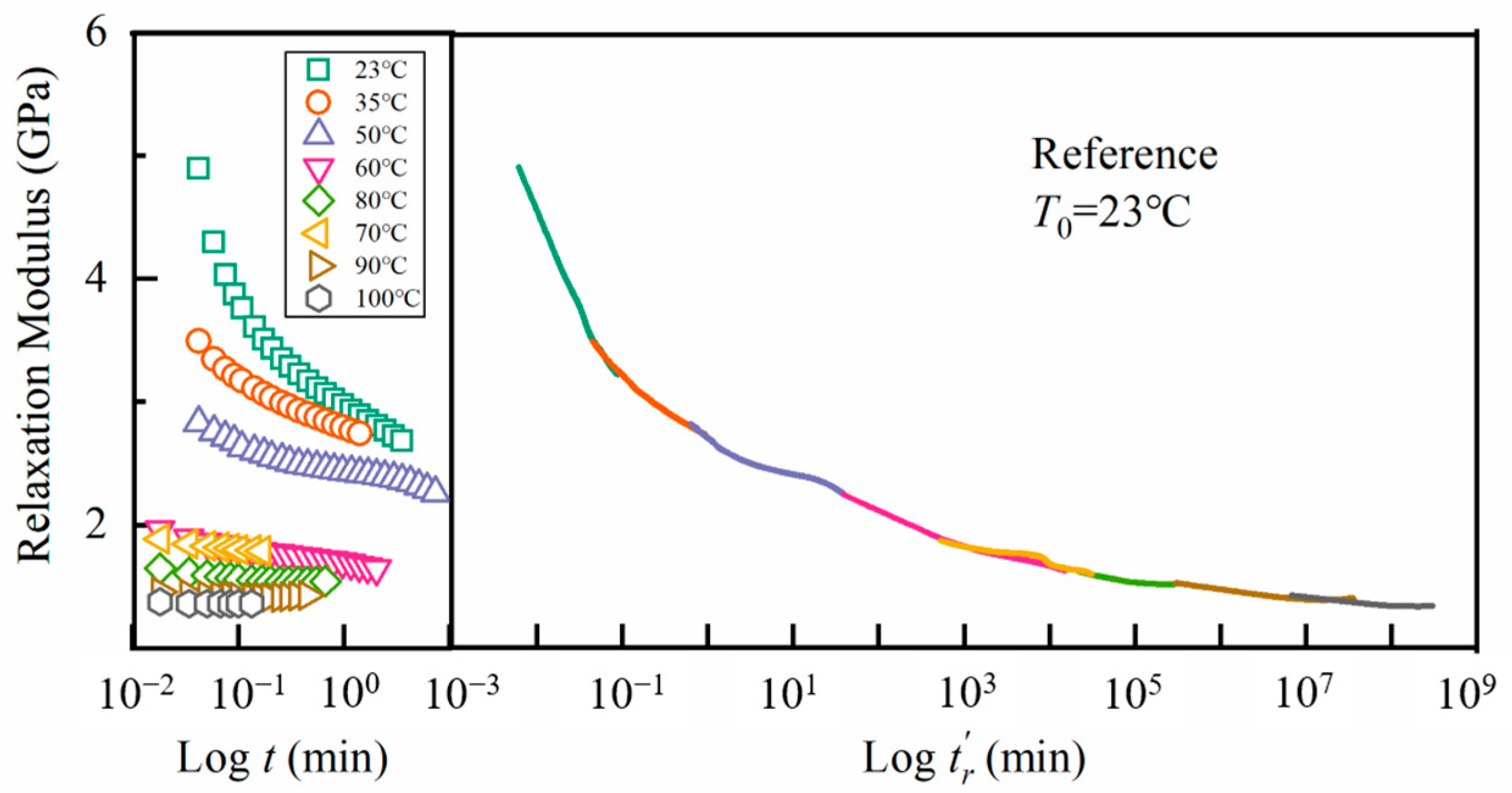
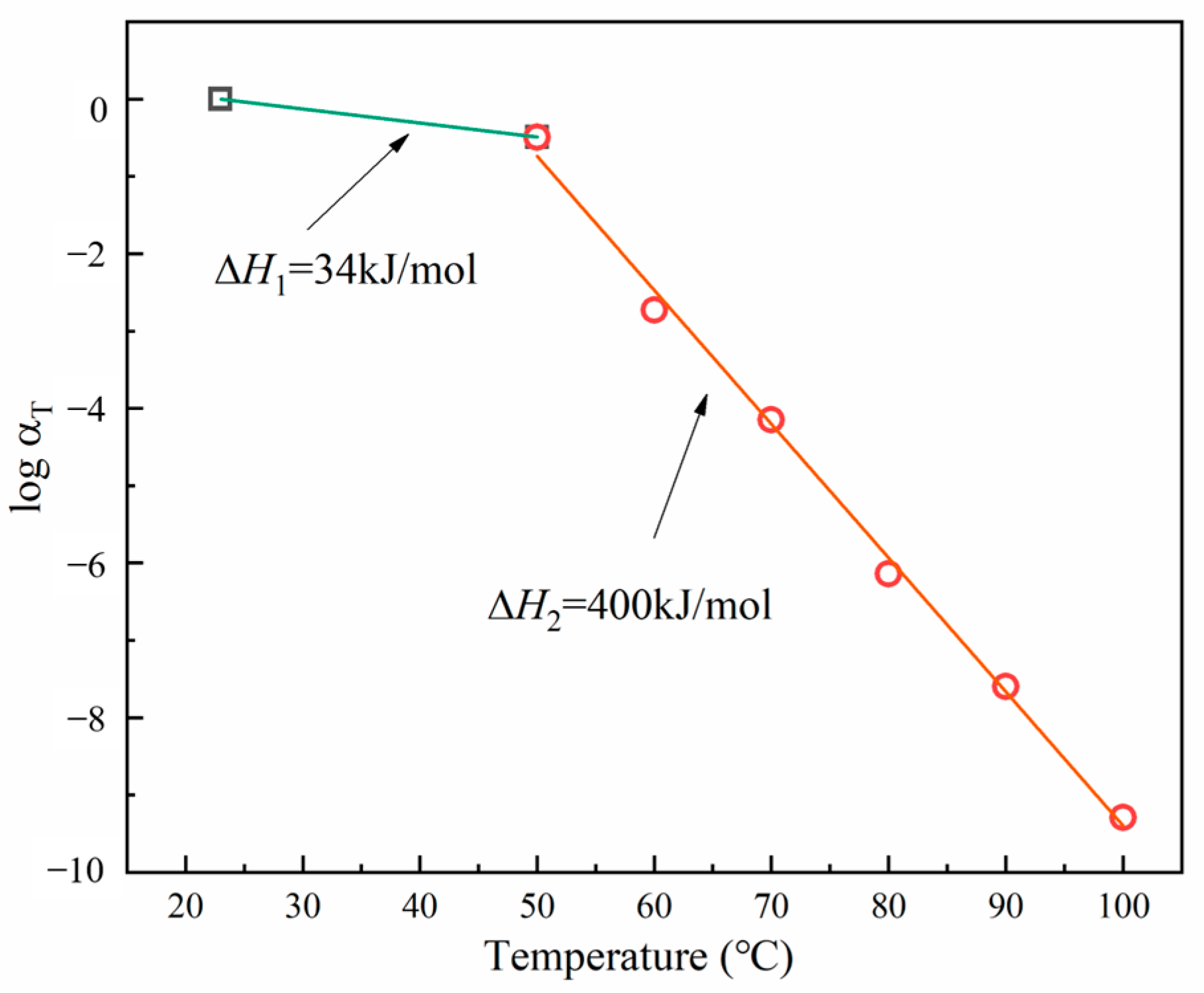
4.2. Material Modulus Characteristics
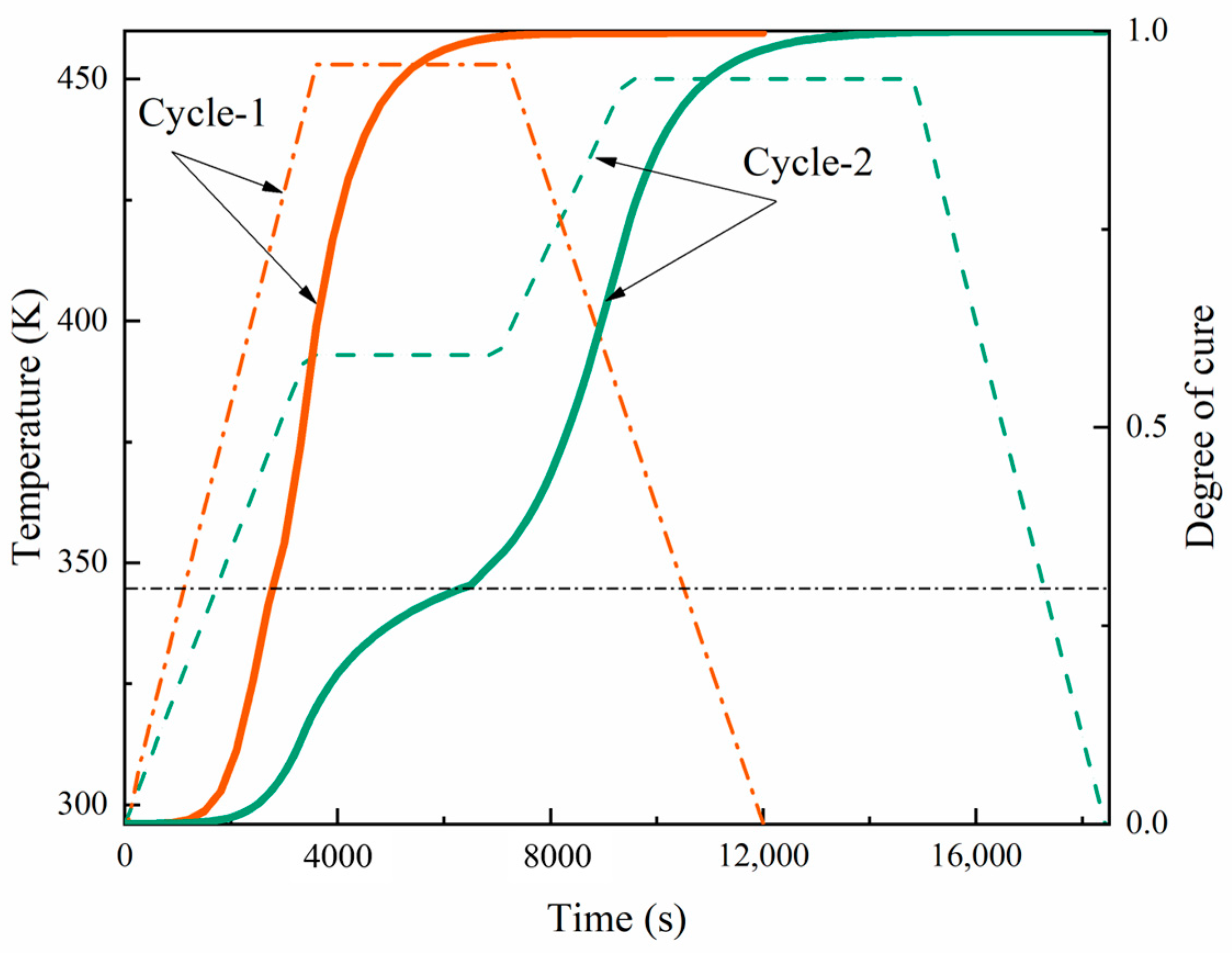
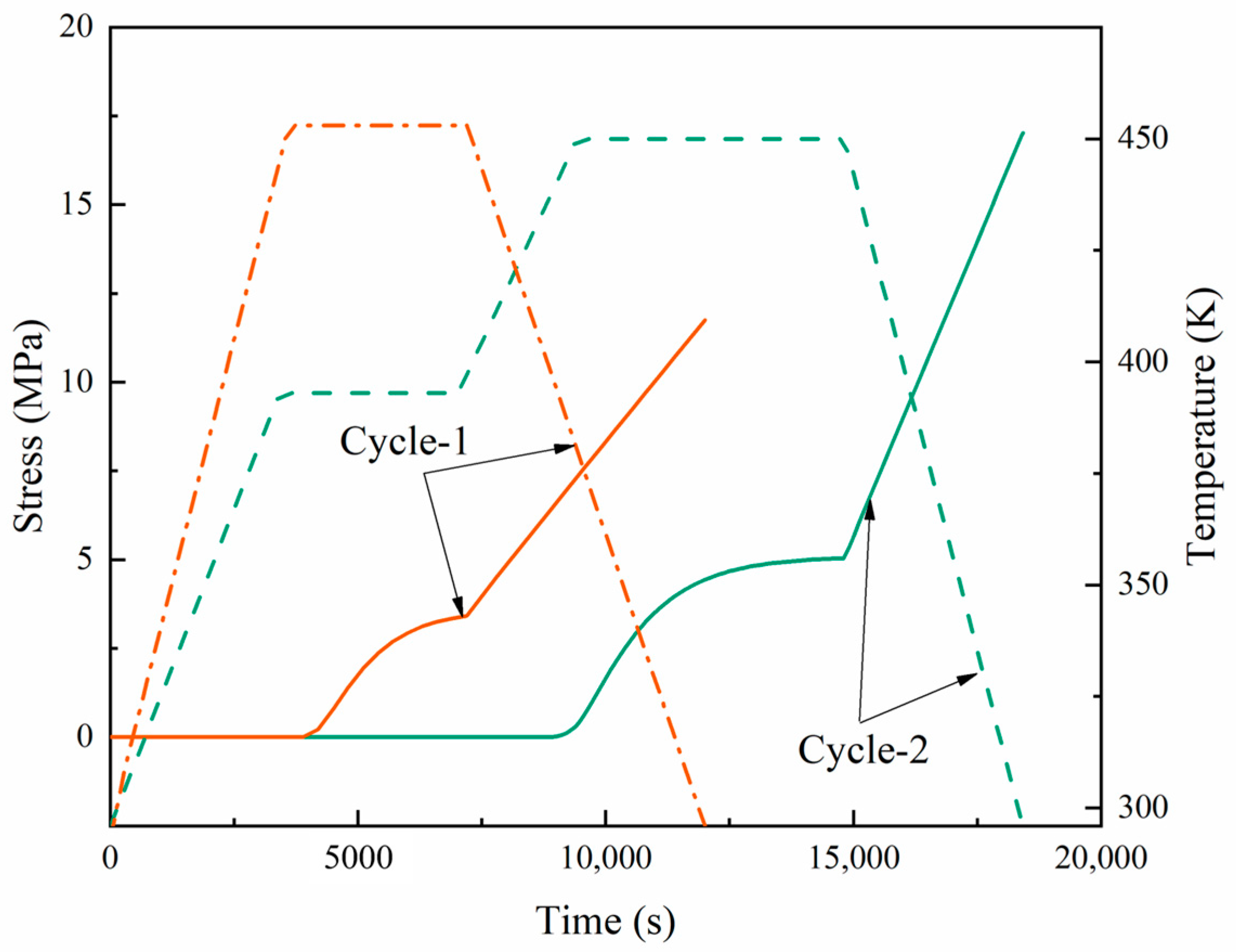
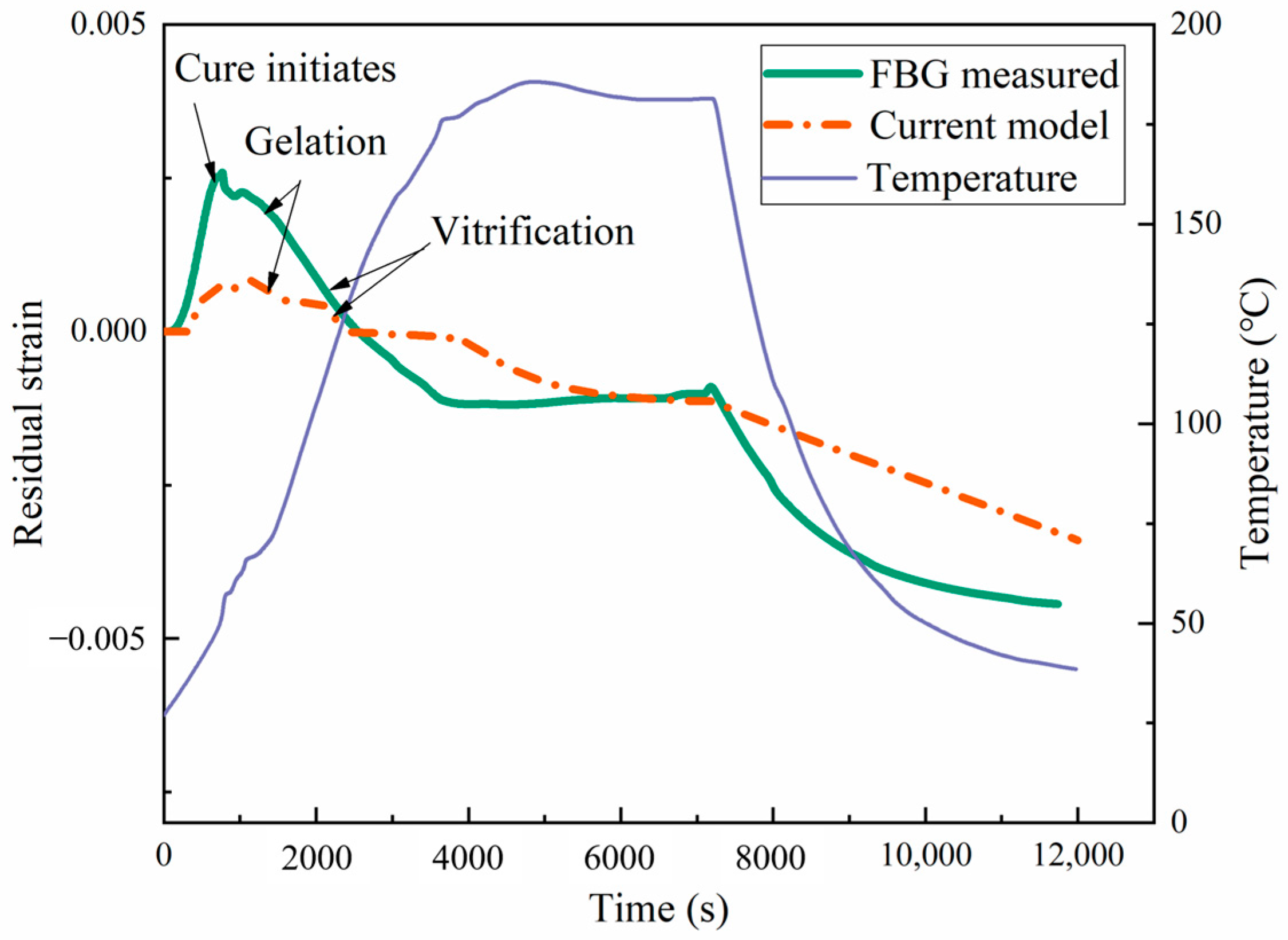
4.3. Residual Stress and Strain Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Ma, J.; Vaz, M.A.; Duan, M. Axisymmetric Structural Behaviours of Composite Tensile Armoured Flexible Pipes. Mar. Struct. 2020, 74, 102829. [Google Scholar] [CrossRef]
- Li, D.; Jiang, W.; Xing, Q.; Liu, Q. Axial Tensile Ultimate Strength of an Unbonded Flexible Riser Based on a Numerical Method. Materials 2024, 17, 2286. [Google Scholar] [CrossRef] [PubMed]
- Vedernikov, A.; Tucci, F.; Safonov, A.; Carlone, P.; Gusev, S.; Akhatov, I. Investigation on the Shape Distortions of Pultruded Profiles at Different Pulling Speed. Procedia Manuf. 2020, 47, 1–5. [Google Scholar] [CrossRef]
- Lee, W.I.; Loos, A.C.; Springer, G.S. Heat of Reaction, Degree of Cure, and Viscosity of Hercules 3501-6 Resin. J. Compos. Mater. 1982, 16, 510–520. [Google Scholar] [CrossRef]
- Dusi, M.R.; Lee, W.I.; Ciriscioli, P.R.; Springer, G.S. Cure Kinetics and Viscosity of Fiberite 976 Resin. J. Compos. Mater. 1987, 21, 243–261. [Google Scholar] [CrossRef]
- Mijović, J.; Kim, J.; Slaby, J. Cure Kinetics of Epoxy Formulations of the Type Used in Advanced Composites. J. Appl. Polym. Sci. 1984, 29, 1449–1462. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, X.; Yao, X. Mesoscopic Simulation on Curing Deformation and Residual Stresses of 3D Braided Composites. Compos. Struct. 2020, 246, 112387. [Google Scholar] [CrossRef]
- Che, L.; Fang, G.; Wu, Z.; Ma, Y.; Zhang, J.; Zhou, Z. Investigation of Curing Deformation Behavior of Curved Fiber Metal Laminates. Compos. Struct. 2020, 232, 111570. [Google Scholar] [CrossRef]
- Singleton, T.; Saeed, A.; Strawbridge, L.; Khan, Z.A. Finite Element Analysis of Manufacturing Deformation in Polymer Matrix Composites. Materials 2024, 17, 2228. [Google Scholar] [CrossRef]
- Stango, R.J.; Wang, S.S. Process-Induced Residual Thermal Stresses in Advanced Fiber-Reinforced Composite Laminates. J. Eng. Ind. 1984, 106, 48–54. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Kamali, S.M. Theoretical and Experimental Studies on Residual Stresses in Laminated Polymer Composites. J. Compos. Mater. 2005, 39, 2213–2225. [Google Scholar] [CrossRef]
- Schulz, W.A.; Myers, D.G.; Singer, T.N.; Ifju, P.G.; Haftka, R.T. Determination of Residual Stress and Thermal History for IM7/977-2 Composite Laminates. Compos. Sci. Technol. 2005, 65, 2014–2024. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Akbari, S.; Daneshvar, A. A Comparison between the Slitting Method and the Classical Lamination Theory in Determination of Macro-Residual Stresses in Laminated Composites. Compos. Struct. 2013, 96, 708–715. [Google Scholar] [CrossRef]
- Schapery, R.A. On the Characterization of Nonlinear Viscoelastic Materials. Polym. Eng. Sci. 1969, 9, 295–310. [Google Scholar] [CrossRef]
- Wang, T.-M.; Daniel, I.M.; Gotro, J.T. Thermoviscoelastic Analysis of Residual Stresses and Warpage in Composite Laminates. J. Compos. Mater. 1992, 26, 883–899. [Google Scholar] [CrossRef]
- White, S.R.; Hahn, H.T. Process Modeling of Composite Materials: Residual Stress Development during Cure. Part I. Model Formulation. J. Compos. Mater. 1992, 26, 2402–2422. [Google Scholar] [CrossRef]
- Adolf, D.; Martin, J.E. Calculation of Stresses in Crosslinking Polymers. J. Compos. Mater. 1996, 30, 13–34. [Google Scholar] [CrossRef]
- Kim, Y.K. Process-Induced Residual Stress Analysis by Resin Transfer Molding. J. Compos. Mater. 2004, 38, 959–972. [Google Scholar] [CrossRef]
- Merzlyakov, M.; McKenna, G.B.; Simon, S.L. Cure-Induced and Thermal Stresses in a Constrained Epoxy Resin. Compos. Part Appl. Sci. Manuf. 2006, 37, 585–591. [Google Scholar] [CrossRef]
- Kim, Y.K.; White, S.R. Stress Relaxation Behavior of 3501-6 Epoxy Resin during Cure. Polym. Eng. Sci. 1996, 36, 2852–2862. [Google Scholar] [CrossRef]
- Eom, Y.; Boogh, L.; Michaud, V.; Sunderland, P.; Månson, J. Time-cure-temperature Superposition for the Prediction of Instantaneous Viscoelastic Properties during Cure. Polym. Eng. Sci. 2000, 40, 1281–1292. [Google Scholar] [CrossRef]
- Prasatya, P.; McKenna, G.B.; Simon, S.L. A Viscoelastic Model for Predicting Isotropic Residual Stresses in Thermosetting Materials: Effects of Processing Parameters. J. Compos. Mater. 2001, 35, 826–848. [Google Scholar] [CrossRef]
- Bogetti, T.A.; Gillespie, J.W. Process-Induced Stress and Deformation in Thick-Section Thermoset Composite Laminates. J. Compos. Mater. 1992, 26, 626–660. [Google Scholar] [CrossRef]
- Shin, D.D.; Hahn, H.T. A Consistent Cure Kinetic Model for AS4/3502 Graphite/Epoxy. Compos. Part Appl. Sci. Manuf. 2000, 31, 991–999. [Google Scholar] [CrossRef]
- Kravchenko, O.G.; Kravchenko, S.G.; Pipes, R.B. Cure History Dependence of Residual Deformation in a Thermosetting Laminate. Compos. Part Appl. Sci. Manuf. 2017, 99, 186–197. [Google Scholar] [CrossRef]
- Kim, Y.K.; White, S.R. Process-Induced Stress Relaxation Analysis of AS4/3501-6 Laminate. J. Reinf. Plast. Compos. 1997, 16, 2–16. [Google Scholar] [CrossRef]
- Behseresht, S.; Park, Y.H. Additive Manufacturing of Composite Polymers: Thermomechanical FEA and Experimental Study. Materials 2024, 17, 1912. [Google Scholar] [CrossRef]
- Ganapathi, A.S.; Joshi, S.C.; Chen, Z. Influence of Cure Kinetic, Rheological and Thermo-Mechanical Behavior on Micro-Level Curing Strain of an Epoxy Prepreg. J. Therm. Anal. Calorim. 2016, 124, 305–316. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, X.; Gao, L.; Yan, L.; Song, G.; Zhang, S. Comparative Study on the Effect of Cure Parameters on Residual Deformation for Thermoset Composite Laminates. J. Compos. Mater. 2021, 55, 2591–2604. [Google Scholar] [CrossRef]
- Kim, S.S.; Murayama, H.; Kageyama, K.; Uzawa, K.; Kanai, M. Study on the Curing Process for Carbon/Epoxy Composites to Reduce Thermal Residual Stress. Compos. Part Appl. Sci. Manuf. 2012, 43, 1197–1202. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelasticity; Courier Corporation: New York, NY, USA, 2003. [Google Scholar]
- Stankiewicz, A. Sampling Points-Independent Identification of the Fractional Maxwell Model of Viscoelastic Materials Based on Stress Relaxation Experiment Data. Materials 2024, 17, 1527. [Google Scholar] [CrossRef] [PubMed]








| Laminate | Material Properties | |
|---|---|---|
| T700 | Elastic modulus | 115 GPa |
| −0.9 × 10−6/K | ||
| 7.2 × 10−6/K | ||
| Poisson’s ratio | 0.3 | |
| Epoxy | Thermal coefficient | 5.27 × 10−5/K |
| Volumetric shrinkage | 0.29 |
| Heating Rate/(K·min−1) | Autocatalytic Model | Nth-Order Model | |||||
|---|---|---|---|---|---|---|---|
| ln(A)/min−1 | m | n | R2 | ln(A)/min−1 | n | R2 | |
| 5 | 23.26 | 0.55 | 1.28 | 0.997 | 21.53 | 0.179 | 0.49 |
| 10 | 23.96 | 0.5 | 1.41 | 0.991 | |||
| 15 | 24.23 | 0.4 | 1.21 | 0.987 | |||
| 20 | 24.39 | 0.39 | 1.43 | 0.988 | |||
| Model | R2 | RMSE | AIC | BIC |
|---|---|---|---|---|
| Autocatalytic | 0.997 | 0.15 | 30.1 | 35.4 |
| Nth-order | 0.490 | 0.60 | 45.0 | 50.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, R.; Liu, J.; Xiao, Z.; Joshi, S.C. Thermo-Chemo-Mechanical Modeling of Residual Stress in Unidirectional Carbon Fiber-Reinforced Polymers during Manufacture. Materials 2024, 17, 3040. https://doi.org/10.3390/ma17123040
Bao R, Liu J, Xiao Z, Joshi SC. Thermo-Chemo-Mechanical Modeling of Residual Stress in Unidirectional Carbon Fiber-Reinforced Polymers during Manufacture. Materials. 2024; 17(12):3040. https://doi.org/10.3390/ma17123040
Chicago/Turabian StyleBao, Rui, Junpeng Liu, Zhongmin Xiao, and Sunil C. Joshi. 2024. "Thermo-Chemo-Mechanical Modeling of Residual Stress in Unidirectional Carbon Fiber-Reinforced Polymers during Manufacture" Materials 17, no. 12: 3040. https://doi.org/10.3390/ma17123040
APA StyleBao, R., Liu, J., Xiao, Z., & Joshi, S. C. (2024). Thermo-Chemo-Mechanical Modeling of Residual Stress in Unidirectional Carbon Fiber-Reinforced Polymers during Manufacture. Materials, 17(12), 3040. https://doi.org/10.3390/ma17123040








