Processing Optimization for Halbach Array Magnetic Field-Assisted Magnetic Abrasive Particles Polishing of Titanium Alloy
Abstract
:1. Introduction
2. Materials and Methods
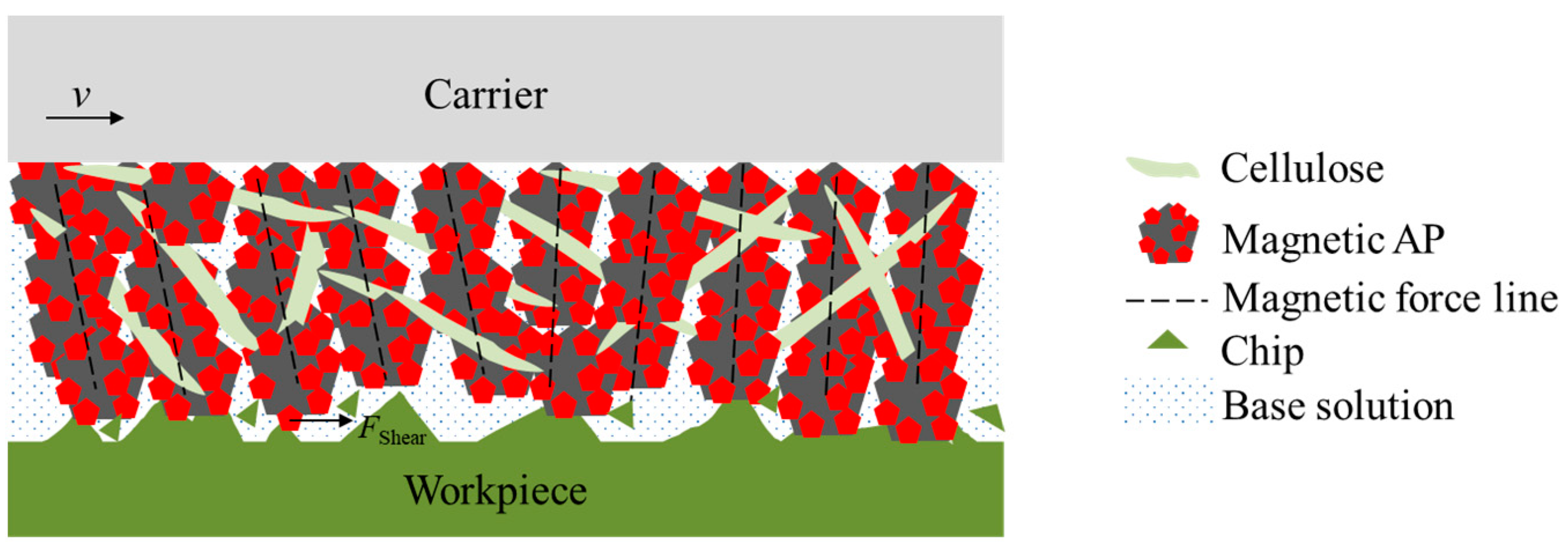
2.1. Principle and Device
2.2. Experimental
3. Results and Discussion
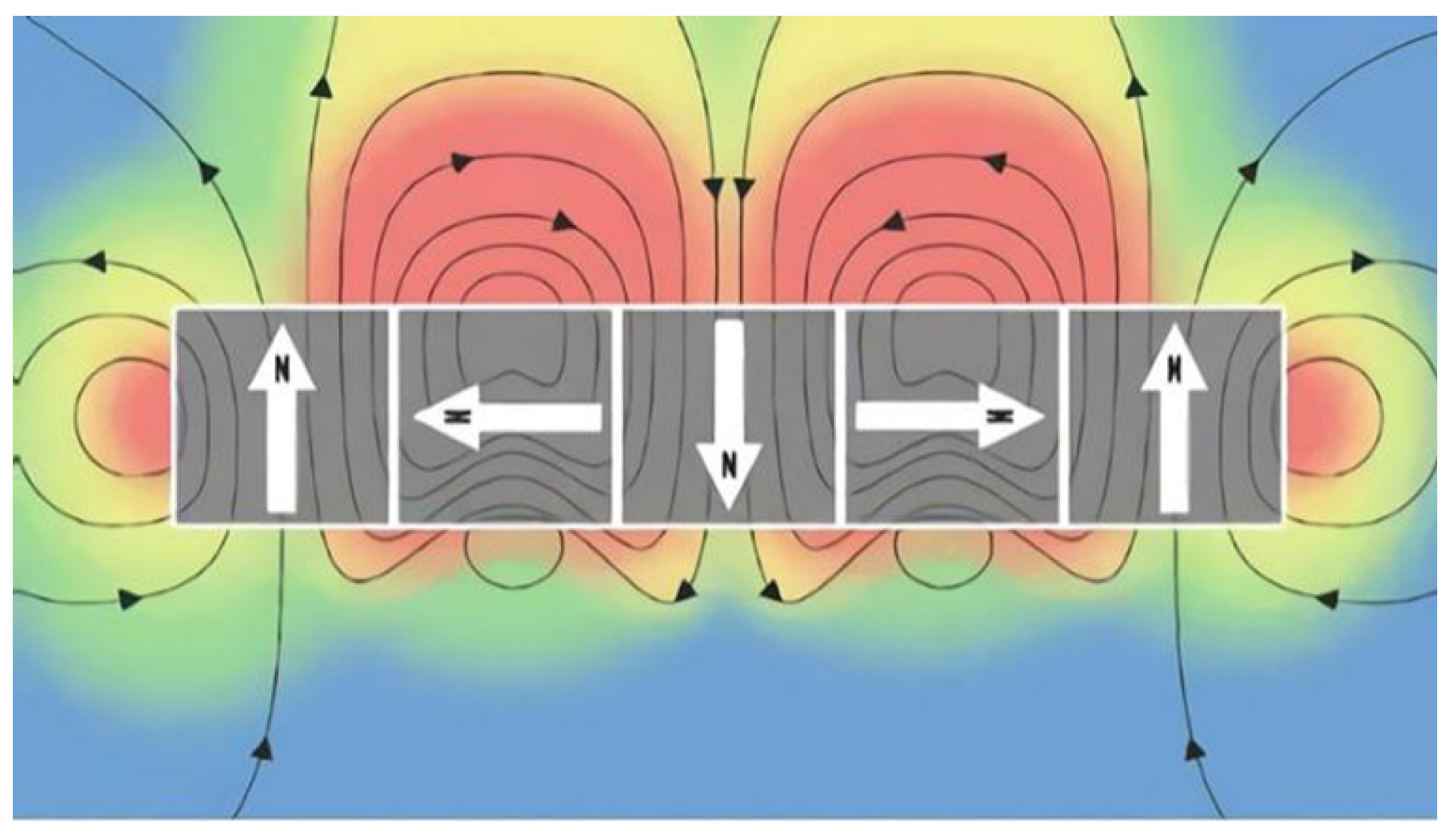
3.1. Magnetic Field Simulation
3.2. Polishing Performance
3.3. Response Surface Method Analysis
3.3.1. Variance Analysis of the Fitting Model for Shear Force
3.3.2. Variance Analysis of the Fitting Model for Surface Roughness
3.4. Interaction of Processing Parameters
3.4.1. Influence on Shear Force
3.4.2. Influence on Surface Roughness
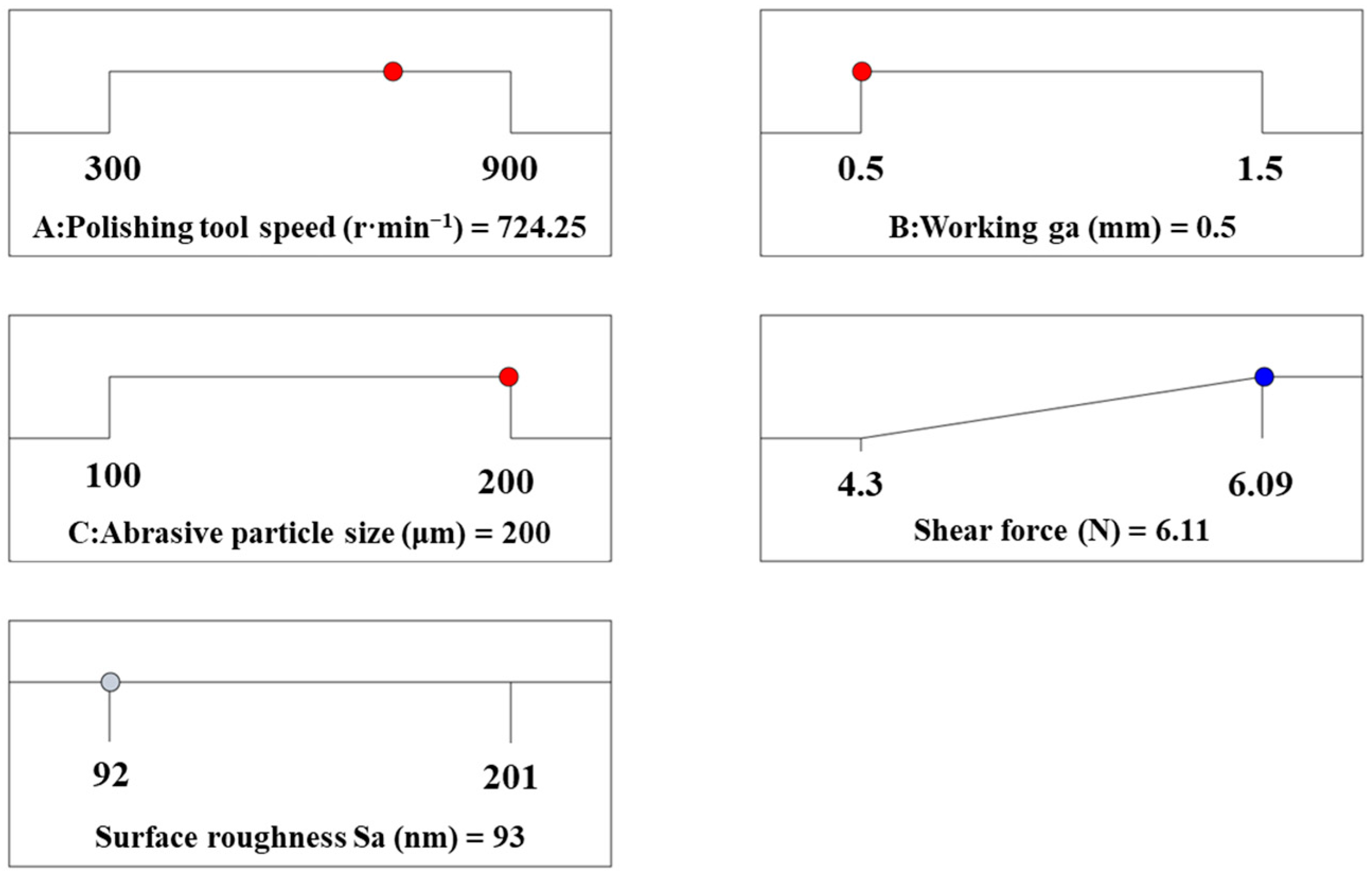
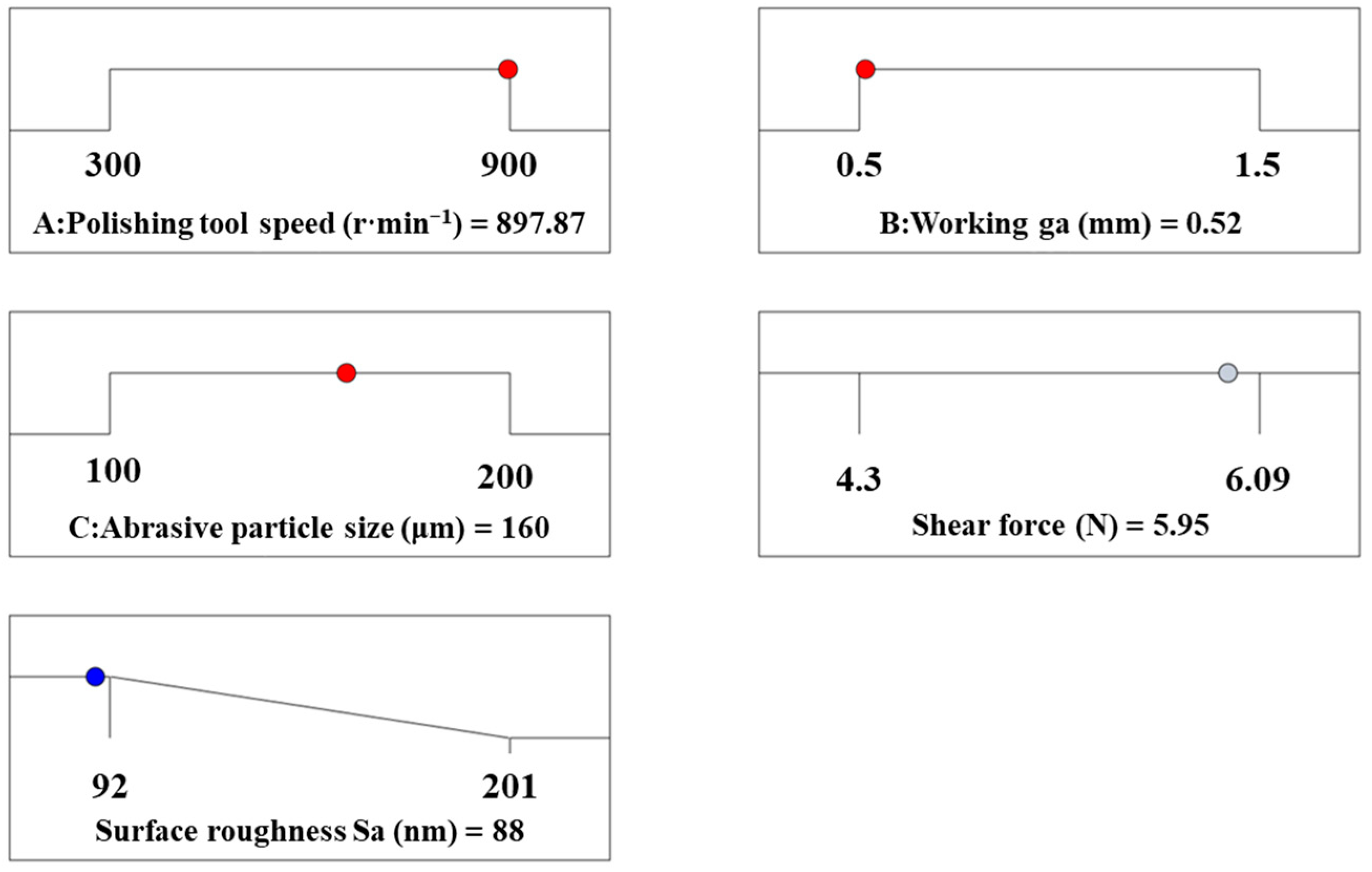
3.5. Verification
4. Conclusions
- (1)
- The magnetic field generated by the Halbach array exhibits periodic changes in magnetic field strength on the plane of the working gap. The distribution of the magnetic field strength was different as the radial diameter R increased.
- (2)
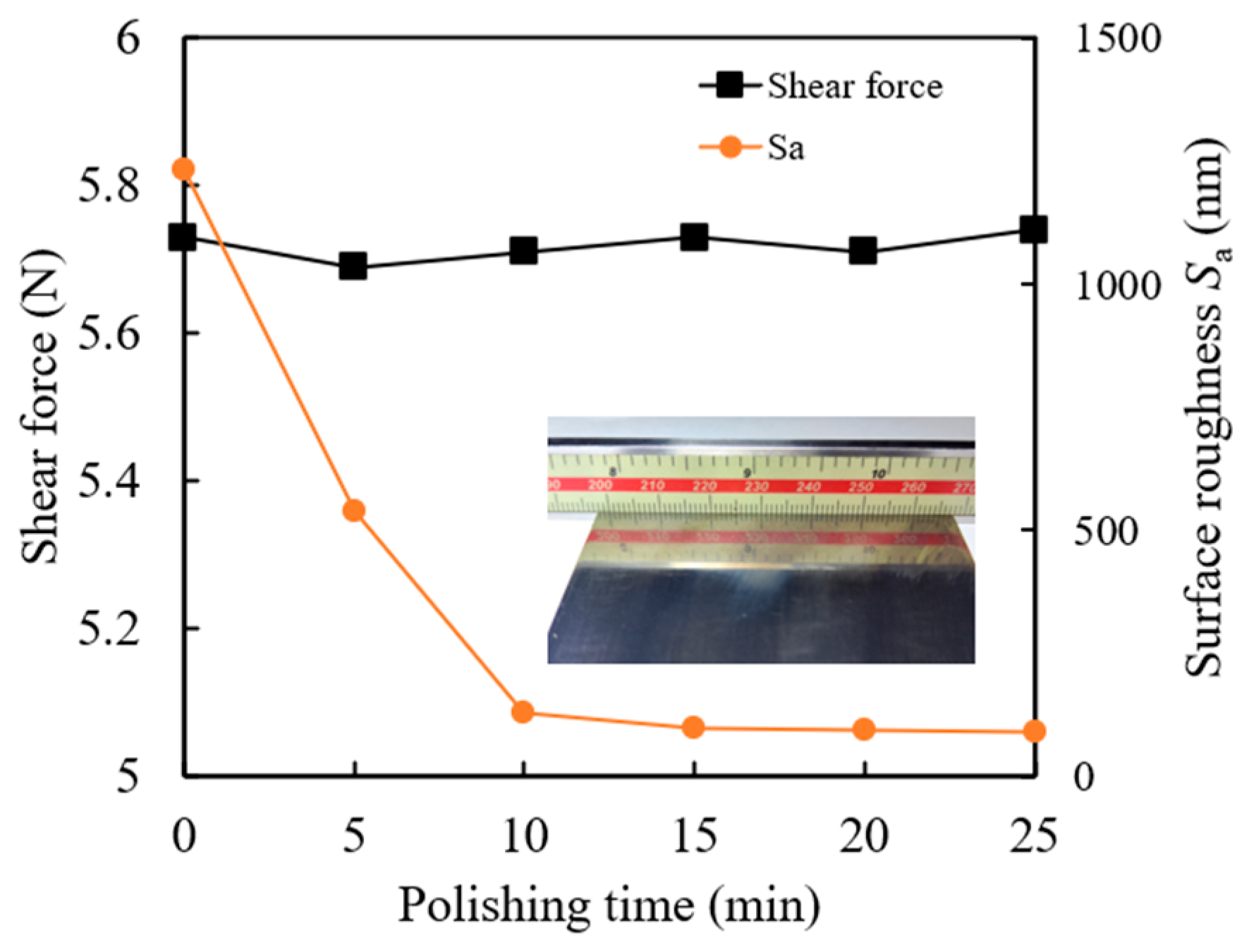
- The polishing time has a stable material removal capability for the magnetic polishing tool. Additionally, the surface roughness improved deeply as polishing time increased. However, this polishing method can induce comet-tail polishing marks on the workpiece surface, which is a common defect in magnetic slurry polishing.
- (3)
- The shear force and surface roughness can be affected to some extent by the combined action of the two process parameters. The correlation between the experimental results and predicted values indicates the reasonableness of the response surface prediction model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Dabrowski, R.; Solek, K. Formation of Microstructure and Mechanical Properties of Ti13Nb13Zr Medical Titanium Alloy. Eng. Sci. Technol.-Int. J.-Jestech 2023, 47, 101547. [Google Scholar] [CrossRef]
- Lei, L.; Zhao, Q.; Zhu, Q.; Yang, M.; Yang, W.; Zeng, W.; Zhao, Y. Twinning-induced High Impact Toughness of Titanium Alloy at Cryogenic Temperature. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2022, 860, 144258. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Li, X.W.; Fang, W.B. Microstructure and Mechanical Properties of TC4 Titanium Alloy at the Temperature of 77 K. Metals 2023, 13, 1086. [Google Scholar] [CrossRef]
- Li, L.; Pan, X.; Liu, B.; Liu, B.; Li, P.; Liu, Z. Strength and Toughness of Hot-Rolled TA15 Aviation Titanium Alloy after Heat Treatment. Aerospace 2023, 10, 436. [Google Scholar] [CrossRef]
- Li, Y.H.; Zuo, B.Q.; Cai, Y.S.; Lei, J. Effect of Low and High Double Heat Treatment on Fracture Toughness of TC4 Titanium Alloy Fabricated by Selective Laser Melting. Rare Met. Mater. Eng. 2022, 51, 1864–1872. [Google Scholar]
- Song, W.; Yang, Z.; Meng, D.; Wang, N.; Choi, S.B. Magnetorheological Polishing based on Honing Vertical Mechanism for Inner Surface of Titanium Alloy Pipes. Lubricants 2024, 12, 86. [Google Scholar] [CrossRef]
- Pasang, T.; Budiman, A.S.; Wang, J.C.; Jiang, C.P.; Boyer, R.; Williams, J.; Misiolek, W.Z. Additive manufacturing of Titanium Alloys-enabling re-Manufacturing of Aerospace and Biomedical Components. Microelectron. Eng. 2023, 270, 111935. [Google Scholar] [CrossRef]
- Satyanarayana, C.P.; Raju, L.S.; Dumpala, R.; Sunil, B.R. A Review on Strategies to enhance the Performance of the Titanium based Medical Implants. Mater. Today Commun. 2024, 38, 107985. [Google Scholar] [CrossRef]
- Loh, Y.M.; Gao, R.; Cheung, C.F.; Chen, Y.; Li, X.; Li, X.; Tsoi, J.K.H.; Wang, C. A Novel Magnetic Field assisted Automatic Batch Polishing Method for Dental Ceramic Crowns. Int. J. Adv. Manuf. Technol. 2023, 49, 26540–26547. [Google Scholar] [CrossRef]
- Wang, C.; Loh, Y.M.; Cheung, C.F.; Wang, S.; Chen, K.; Ho, L.T.; Cheng, E. Magnetic Field-assisted Batch Superfinishing on thin-walled Components. Int. J. Mech. Sci. 2022, 223, 107279. [Google Scholar] [CrossRef]
- Li, X.Y.; Huang, X.M.; Ming, Y.; Zhou, D.D.; Cai, Y.H. Carbide Twist Drill Surface Polishing and Cutting Edge Passivating based on Magnetic Field-assisted Shear Thickening. Int. J. Adv. Manuf. Technol. 2023, 126, 5649–5664. [Google Scholar] [CrossRef]
- Barman, A.; Das, M. Application of Magnetic Field assisted Finishing Process for Nanofinishing of Freeform Femoral Knee Joint and Performance Analysis of Finished Surface. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2024, 238, 3190–3203. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, X.; Chen, X.; Kaixiang, W.; Jinchao, R.; Rui, Y. Polishing Performance of Magnetic Composite Fluid based on Double Magnetic Field. Surf. Technol. 2022, 51, 360–372. [Google Scholar]
- Feng, M.; Wu, Y.; Wang, Y.; Zeng, J.; Bitoh, T.; Nomura, M.; Fujii, T. Effect of the Components of Magnetic Compound Fluid (MCF) Slurry on Polishing Characteristics in aspheric-surface Finishing with the doughnut-shaped MCF Tool. Precis. Eng. 2020, 65, 216–229. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, G.; Du, J.; Jiang, L.; Zhang, P.; Cui, Y. Removal Mechanism of Magnetic Abrasive Finishing on Aluminum and Magnesium Alloys. Int. J. Adv. Manuf. Technol. 2021, 114, 1717–1729. [Google Scholar] [CrossRef]
- Khalil, A.K.; Yip, W.S.; To, S. Theoretical and Experimental Investigations of Magnetic Field assisted Ultra-Precision Machining of Titanium Alloys. J. Mater. Process. Technol. 2022, 300, 117429. [Google Scholar] [CrossRef]
- Lou, Y.; Chen, L.; Wu, H.; To, S. Influence of Cutting Velocity on Surface Roughness during the Ultra-Precision Cutting of Titanium Alloys based on a Comparison between Simulation and Experiment. PLoS ONE 2023, 18, e0288502. [Google Scholar] [CrossRef]
- Yang, G.; Ming, P.; Niu, S.; Qin, G.; Liu, H.; Li, D.; Zhang, A. An Investigation of the Efficient-Precise Continuous Electrochemical Grinding Process of Ti-6Al-4V. Materials 2024, 17, 1729. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhao, Y.; Chen, S.; Li, L.; Han, B. Finishing Internal Surface of 6061 Aluminum Alloy Bend Pipe Based on Rotating Magnetic Field. China Surf. Eng. 2018, 31, 73–81. [Google Scholar]
- Zhou, Q.; Peng, K.; Chen, Y. Design and Experiment of Magnetic Field Generator Device in Magnetorheological Polishing Process. Surf. Technol. 2020, 49, 337–344. [Google Scholar]
- Gill, J.S.; Singh, L. Magnetic Abrasive Polishing of Stainless Steel SS304 with Diamond-Based Sintered Magnetic Abrasives. J. Adv. Manuf. Syst. 2022, 21, 797–811. [Google Scholar] [CrossRef]
- Verma, G.C.; Kala, P.; Pandey, P.M. Experimental Investigations into Internal Magnetic Abrasive Finishing of Pipes. Int. J. Adv. Manuf. Technol. 2017, 88, 1657–1668. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.; Li, W.; Ding, Y.; Bai, X.; Yan, T. Magnetic Field Design and Experimental Research based on Halbach Array in Magnetic Abrasives Finishing. Surf. Technol. 2020, 49, 47–54. [Google Scholar]
- Guo, Y.; Yin, S.; Huang, S. Study on Machining Characteristic and its Mechanism of Magnetorheological Polishing with Halbach Array and Other Excitation Modes. J. Mech. Eng. 2023, 59, 341–353. [Google Scholar]
- Winter, M.; Li, W.; Kara, S.; Herrmann, C. Determining optimal process parameters to increase the eco-efficiency of grinding processes. J. Clean. Prod. 2014, 66, 644–654. [Google Scholar] [CrossRef]
- Tran, H.C.; Lo, Y.L. Systematic approach for determining optimal processing parameters to produce parts with high density in selective laser melting process. Int. J. Adv. Manuf. Technol. 2019, 105, 4443–4460. [Google Scholar] [CrossRef]
- Mehat, N.M.; Kamaruddin, S. Optimization of mechanical properties of recycled plastic products via optimal processing parameters using the Taguchi method. J. Mater. Process. Technol. 2011, 211, 1989–1994. [Google Scholar] [CrossRef]
- Liberini, M.; Astarita, A.; Campatelli, G.; Scippa, A.; Montevecchi, F.; Venturini, G.; Durante, M.; Boccarusso, L.; Minutolo, F.M.C.; Squillace, A. Selection of optimal process parameters for wire arc additive manufacturing. Procedia Cirp 2017, 62, 470–474. [Google Scholar] [CrossRef]
- Rao, C.J.; Sreeamulu, D.; Mathew, A.T. Analysis of tool life during turning operation by determining optimal process parameters. Procedia Eng. 2014, 97, 241–250. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, J.; Wang, H.; Kumar, A.S.; Chaudhari, A. A novel magnetically driven polishing technique for internal surface finishing. Precis. Eng. 2018, 54, 222–232. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Mathematical modeling and FDM process parameters optimization using response surface methodology based on Q-optimal design. Appl. Math. Model. 2016, 40, 10052–10073. [Google Scholar] [CrossRef]






| Level | Factors | ||
|---|---|---|---|
| Revolution Speed of Carrier nc r·min−1 A | Working Gap h mm B | Abrasive Diameter μm C | |
| −1 | 300 | 0.5 | 100 |
| 0 | 600 | 1 | 150 |
| 1 | 900 | 1.5 | 200 |
| Carbonyl Iron Powder (wt.%) | Base Liquid (wt.%) | Cellulose (wt.%) |
|---|---|---|
| 85 | 10 | 5 |
| Number | Factors | Result | |||
|---|---|---|---|---|---|
| A r·min−1 | B mm | C mm | x N | y nm | |
| 1 | 300 | 0.5 | 150 | 5.31 | 112 |
| 2 | 900 | 0.5 | 150 | 5.72 | 92 |
| 3 | 300 | 1.5 | 150 | 4.70 | 164 |
| 4 | 900 | 1.5 | 150 | 5.13 | 142 |
| 5 | 300 | 1 | 100 | 4.30 | 183 |
| 6 | 900 | 1 | 100 | 4.83 | 168 |
| 7 | 300 | 1 | 200 | 4.92 | 161 |
| 8 | 900 | 1 | 200 | 5.43 | 132 |
| 9 | 600 | 0.5 | 100 | 5.12 | 139 |
| 10 | 600 | 1.5 | 100 | 4.57 | 173 |
| 11 | 600 | 0.5 | 200 | 6.09 | 104 |
| 12 | 600 | 1.5 | 200 | 4.47 | 201 |
| 13 | 600 | 1 | 150 | 4.53 | 192 |
| 14 | 600 | 1 | 150 | 4.54 | 187 |
| 15 | 600 | 1 | 150 | 4.47 | 183 |
| 16 | 600 | 1 | 150 | 4.67 | 178 |
| 17 | 600 | 1 | 150 | 4.83 | 173 |
| Source | Sum of Deviation Square | Freedom Degree | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 3.62 | 9 | 0.4022 | 12.75 | 0.0014 |
| A | 0.4418 | 1 | 0.4418 | 14.01 | 0.0072 |
| B | 1.42 | 1 | 1.42 | 45 | 0.0003 |
| C | 0.546 | 1 | 0.546 | 17.31 | 0.0042 |
| AB | 0.0001 | 1 | 0.0001 | 0.0032 | 0.9567 |
| AC | 0.0001 | 1 | 0.0001 | 0.0032 | 0.9567 |
| BC | 0.2862 | 1 | 0.2862 | 9.07 | 0.0196 |
| A2 | 0.1809 | 1 | 0.1809 | 5.73 | 0.0479 |
| B2 | 0.6728 | 1 | 0.6728 | 21.33 | 0.0024 |
| C2 | 0.0126 | 1 | 0.0126 | 0.4001 | 0.5471 |
| Residual | 0.2208 | 7 | 0.0315 | ||
| Lack of fit | 0.1379 | 3 | 0.046 | 2.22 | 0.2284 |
| Pure error | 0.0829 | 4 | 0.0207 | ||
| Total | 3.84 | 16 |
| Source | Sum of Deviation Square | Freedom Degree | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 3.61 | 6 | 0.6012 | 25.73 | <0.0001 |
| A | 0.4418 | 1 | 0.4418 | 18.91 | 0.0014 |
| B | 1.42 | 1 | 1.42 | 60.76 | <0.0001 |
| C | 0.546 | 1 | 0.546 | 23.37 | 0.0007 |
| BC | 0.2862 | 1 | 0.2862 | 12.25 | 0.0057 |
| A2 | 0.1864 | 1 | 0.1864 | 7.98 | 0.018 |
| B2 | 0.6845 | 1 | 0.6845 | 29.3 | 0.0003 |
| Residual error | 0.2336 | 10 | 0.0234 | ||
| Lack of fit | 0.1507 | 6 | 0.0251 | 1.21 | 0.4455 |
| Pure Error | 0.0829 | 4 | 0.0207 | ||
| Total | 3.84 | 16 |
| Model | Correlation Coefficient | Adjusted Correlation Coefficient | Predictive Correlation Coefficient | Variable Coefficient | Signal-to-Noise Ratio |
|---|---|---|---|---|---|
| R2 | R2Adj | R2Pre | C.V.% | SNR | |
| Initial | 0.9425 | 0.8686 | 0.3917 | 3.61 | 12.0672 |
| Post-optimization | 0.9392 | 0.9027 | 0.7227 | 3.11 | 16.7081 |
| Source | Sum of Deviation Square | Freedom Degree | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 16,119.81 | 9 | 1791.09 | 19.23 | 0.0004 |
| A | 924.5 | 1 | 924.5 | 9.93 | 0.0161 |
| B | 6786.12 | 1 | 6786.12 | 72.86 | <0.0001 |
| C | 528.13 | 1 | 528.13 | 5.67 | 0.0488 |
| AB | 1 | 1 | 1 | 0.0107 | 0.9204 |
| AC | 49 | 1 | 49 | 0.5261 | 0.4918 |
| BC | 992.25 | 1 | 992.25 | 10.65 | 0.0138 |
| A2 | 2460.76 | 1 | 2460.76 | 26.42 | 0.0013 |
| B2 | 4026.76 | 1 | 4026.76 | 43.24 | 0.0003 |
| C2 | 27.92 | 1 | 27.92 | 0.2998 | 0.601 |
| Residual | 651.95 | 7 | 93.14 | ||
| Lack of fit | 430.75 | 3 | 143.58 | 2.6 | 0.1896 |
| Pure error | 221.2 | 4 | 55.3 | ||
| Total | 16,771.76 | 16 |
| Source | Sum of Deviation Square | Freedom Degree | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 16,041.9 | 6 | 2673.65 | 36.63 | <0.0001 |
| A | 924.5 | 1 | 924.5 | 12.67 | 0.0052 |
| B | 6786.13 | 1 | 6786.13 | 92.98 | <0.0001 |
| C | 528.13 | 1 | 528.13 | 7.24 | 0.0227 |
| BC | 992.25 | 1 | 992.25 | 13.59 | 0.0042 |
| A2 | 2440.01 | 1 | 2440.01 | 33.43 | 0.0002 |
| B2 | 4002.63 | 1 | 4002.63 | 54.84 | <0.0001 |
| Residual | 729.87 | 10 | 72.99 | ||
| Lack of fit | 508.67 | 6 | 84.78 | 1.53 | 0.3537 |
| Pure error | 221.2 | 4 | 55.3 | ||
| Total | 16,771.76 | 16 |
| Model | Correlation Coefficient | Adjusted Correlation Coefficient | Predictive Correlation Coefficient | Variable Coefficient | Signal-to-Noise Ratio |
|---|---|---|---|---|---|
| R2 | R2Adj | R2Pre | C.V.% | SNR | |
| Initial | 0.9611 | 0.9111 | 0.5685 | 6.11 | 13.8988 |
| Post-optimization | 0.9565 | 0.9304 | 0.7957 | 5.41 | 18.3624 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Feng, M.; Cao, Q. Processing Optimization for Halbach Array Magnetic Field-Assisted Magnetic Abrasive Particles Polishing of Titanium Alloy. Materials 2024, 17, 3213. https://doi.org/10.3390/ma17133213
Qin J, Feng M, Cao Q. Processing Optimization for Halbach Array Magnetic Field-Assisted Magnetic Abrasive Particles Polishing of Titanium Alloy. Materials. 2024; 17(13):3213. https://doi.org/10.3390/ma17133213
Chicago/Turabian StyleQin, Jia, Ming Feng, and Qipeng Cao. 2024. "Processing Optimization for Halbach Array Magnetic Field-Assisted Magnetic Abrasive Particles Polishing of Titanium Alloy" Materials 17, no. 13: 3213. https://doi.org/10.3390/ma17133213
APA StyleQin, J., Feng, M., & Cao, Q. (2024). Processing Optimization for Halbach Array Magnetic Field-Assisted Magnetic Abrasive Particles Polishing of Titanium Alloy. Materials, 17(13), 3213. https://doi.org/10.3390/ma17133213





