Experimental Study of the Flexural Performance of GFRP-Reinforced Seawater Sea Sand Concrete Beams with Built-In GFRP Tubes
Abstract
1. Introduction
2. Experiment Design
2.1. Beam
2.2. Materials
2.2.1. Concrete
2.2.2. GFRP
2.3. Test Loading
3. Test Process
3.1. Destruction Process
3.2. Damage Patterns
4. Test Analysis
4.1. Effects of GFRP Tube
4.2. Effects of Reinforcement Ratio
4.3. Effects of the Strengths Grade of Concrete inside and outside Tube
4.4. Ductility Analysis
5. Ultimate Capacity
5.1. Strain
5.2. Interaction
5.2.1. Impact Factor of Tube Height ψG
5.2.2. Impact Factor of Reinforcement Ratio ψρ
5.2.3. Impact Factor of the Strength of Concrete outside Tube ψco
5.2.4. Impact Factor of the Strength of Concrete inside Tube ψci
5.2.5. Equation of the Interaction
5.3. Flexural Capacity
5.3.1. Assumption
5.3.2. Ultimate Capacity of Part I
5.3.3. Ultimate Capacity of Part II
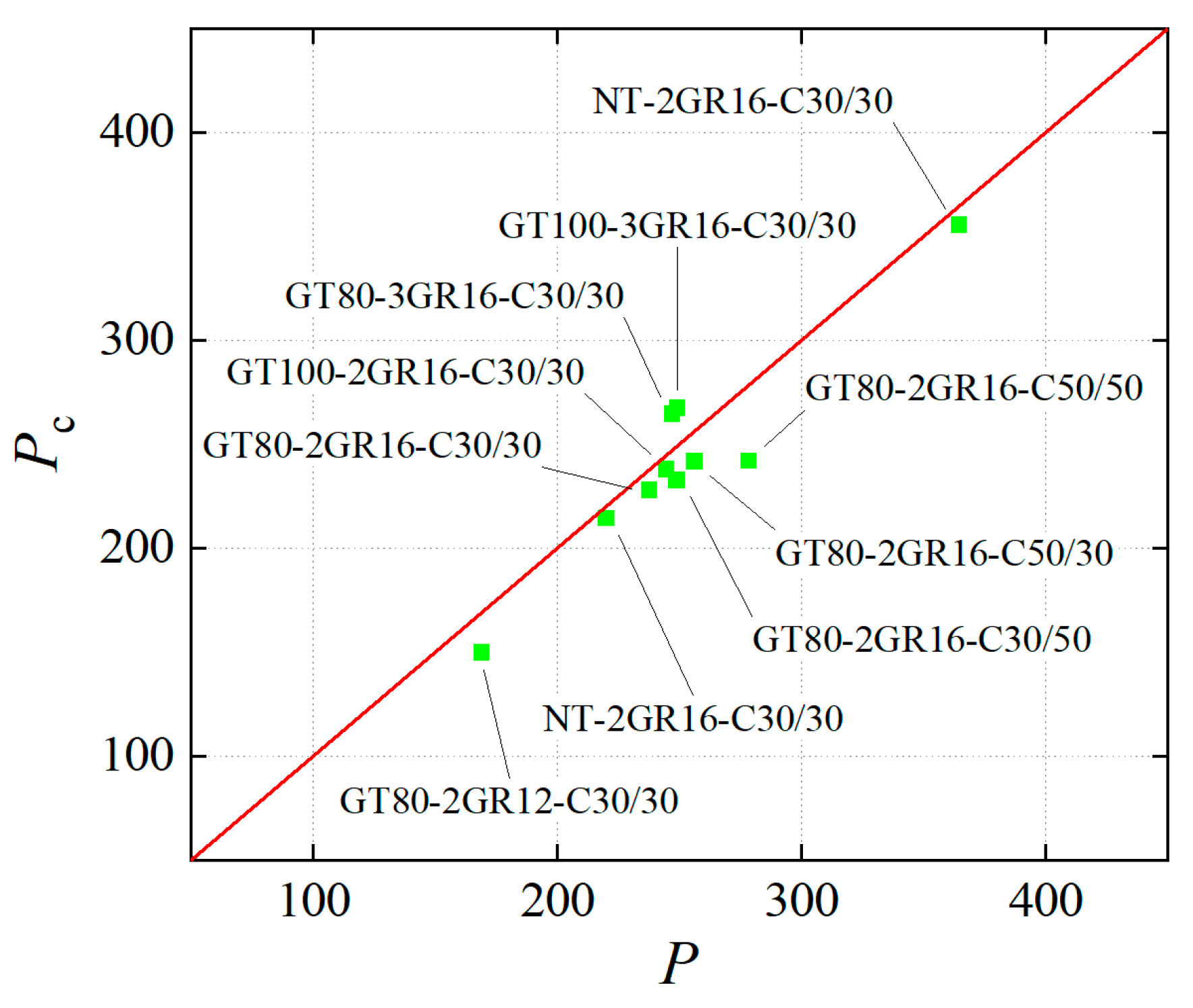
5.4. Verification
6. Conclusions
- (1)
- The beam crack distribution was significantly affected by the reinforcement ratio and concrete strength. The increase in reinforcement ratio and the strength of concrete inside the tube led to a denser crack distribution, while the increased strength of concrete outside the tube made the crack distribution sparser. The height of the built-in GFRP tube had a limited effect on the crack distribution.
- (2)
- The equipment of GFRP tubes could change rare-reinforced damage which should have occurred into over-reinforced damage. Under low-reinforcement-ratio conditions, the GFRP tube had little impact on the damage modes. In addition, the arrangement of GFRP tubes significantly increased the ultimate load and post-cracking stiffness of beams, and the improvement raised with the increasing reinforcement ratio and tube height.
- (3)
- The ductility of the SSSC beams with built-in GFRP tubes was reduced compared to that of the beam without tube. The ductility decreased with the increase of reinforcement ratio, and the favorable beam ductility realized when the strength of the concrete inside and outside the tube was similar and low.
- (4)
- The two parts, the concrete outside the tube, the tube and the concrete inside the tube, basically conformed to the flat cross-sectional assumption. Using the test results, the expression for the interaction between the GFRP tube and concrete was obtained by fitting, and the proposed formula was effective to predict the normal section flexural capacity of GFRP-reinforced SSSC beam with GFRP tubes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variable | Explanation |
| EGT | Axial elastic modulus |
| EGR | GFRP bar elastic modulus |
| Ec1 | Elastic modulus of concrete in the GFRP tube |
| Ec | Concrete elastic modulus |
| Average concrete elastic modulus | |
| fGR | GFRP bar tensile strength |
| fc1 | Concrete strength outside the GFRP tube |
| fc2 | Concrete strength in the GFRP tube |
| fc | Concrete compressive strength |
| Average concrete compressive strength | |
| t | Thickness of the GFRP tube |
| h | Height of beam |
| bG | Width of the GFRP tube |
| b | Beam width |
| h0 | Effective height of beam section |
| hG | Height of the GFRP tube |
| ρ | Reinforcement ratio |
| ρb | Boundary reinforcement ratio |
| P | Peak load |
| Pc | Calculated load capacity |
| l | Beam length |
| w | Mid-span deflections of beams |
| με | Microstrain |
| x | Height of the relative compression zone |
| xc | Height of the compression zone |
| xG | Distance from the neutral axis of the GFRP tube to the edge of the compression zone of the tube |
| β1 | Height conversion factor of equivalent rectangular stress |
| εc | Concrete strain |
| εcu | Ultimate compressive strain of concrete |
| εr | Basic strain reference |
| εG1 | Upper wall compressive strain |
| εG2 | Lower wall compressive strain |
| εr1 | Upper wall compressive strain of the GFRP tube in GT80-2GR16-C30/30 |
| εr2 | Upper wall compressive strain of the GFRP tube in GT100-2GR16-C30/30 |
| εr3 | Upper wall compressive strain of the GFRP tube in GT80-2GR16-C30/50 |
| εr4 | Upper wall compressive strain of the GFRP tube in GT80-2GR16-C50/30 |
| aGR | Distance from the action point of the combined forces of the tension bars to the tensile edge of the concrete |
| AGR | Area of the tension reinforcement |
| α1 | Strength conversion factor for the equivalent rectangular stress |
| aGT | Distance between the upper wall of the GFRP tube and the edge of the compressed concrete |
| ψG | Impact factor of the GFRP tube’s height |
| ψρ | Impact factor of reinforcement ratio |
| ψco | Impact factor of the strength of concrete outside tube |
| ψci | Impact factor of the strength of concrete inside tube |
| DR | Deformation capacity reserve factor |
| CR | Load capacity reserve factor |
| J | Overall performance factor |
| M1 | Bending capacity of Part I |
| M2 | Bending capacity of Part II |
| M | Total bending capacity |
| M0.001 | Bending moment when the compressive strain of the compressed concrete reaches 0.001 |
| Mu | Ultimate bending moment |
| Curvature when the compressive strain of the compressed concrete reaches 0.001 | |
| Ultimate curvature | |
| C1 | Upper wall force of the compression zone |
| C2 | Side wall force of the compression zone |
| C3 | Compressive force of the internal concrete of the compression zone |
| T1 | Lower wall forces of the tension zone |
| T2 | Side wall force of the tension zone |
References
- Sun, Z.; Li, X.; Liu, Q.; Tang, Q.; Lin, X.; Fan, X.; Huang, X.; Gan, M.; Chen, X.; Ji, Z. Recent advances in alkali-activated materials with seawater and sea sand. Materials 2023, 16, 3571. [Google Scholar] [CrossRef]
- Dhondy, T.; Remennikov, A.; Sheikh, M. Properties and application of sea sand in sea sand-seawater concrete. J. Mater. Civ. Eng. 2020, 32, 04020392. [Google Scholar] [CrossRef]
- Xiao, J.; Qiang, C.; Nanni, A.; Zhang, K. Use of sea-sand and seawater in concrete construction: Current status and future opportunities. Constr. Build. Mater. 2017, 155, 1101–1111. [Google Scholar] [CrossRef]
- Xiang, Y.; Al-Saadi, S.; Zhao, X.; Raman, R. Electrochemical investigations of steels in seawater sea sand concrete environments. Materials 2021, 14, 5713. [Google Scholar] [CrossRef]
- Sun, X.; Li, T.; Shi, F.; Liu, X.; Zong, Y.; Hou, B.; Tian, H. Sulphate corrosion mechanism of ultra-high-performance concrete (UHPC) prepared with seawater and sea sand. Polymers 2022, 14, 971. [Google Scholar] [CrossRef]
- Guo, F.; Al-Saadi, S.; Raman, R.; Zhao, X. Durability of fiber reinforced polymer (FRP) in simulated seawater sea sand concrete (SWSSC) environment. Corros. Sci. 2018, 141, 1–13. [Google Scholar] [CrossRef]
- Ahmed, A.; Guo, S.; Zhang, Z.; Shi, C.; Zhu, D. A review on durability of fiber reinforced polymer (FRP) bars reinforced seawater sea sand concrete. Constr. Build. Mater. 2020, 256, 119484. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Xian, G.; Wu, G.; Raman, R.; Al-Saadi, S. Effect of sustained load and seawater and sea sand concrete environment on durability of basalt- and glass-fibre reinforced polymer (B/GFRP) bars. Corros. Sci. 2018, 138, 200–218. [Google Scholar] [CrossRef]
- Dong, Z.; Wu, G.; Zhao, X.; Zhu, H.; Lian, J. The durability of seawater sea-sand concrete beams reinforced with metal bars or non-metal bars in the ocean environment. Adv. Struct. Eng. 2020, 23, 334–347. [Google Scholar] [CrossRef]
- Wei, B.; He, X.; Zhou, M.; Wang, H.; He, J. Experimental study on flexural behaviors of FRP and steel bars hybrid reinforced concrete beams. Case Stud. Constr. Mater. 2024, 20, e02759. [Google Scholar] [CrossRef]
- Ortiz, J.; Dolati, S.; Malla, P.; Nanni, A.; Mehrabi, A. FRP-reinforced/strengthened concrete: State-of-the-art review on durability and mechanical effects. Materials 2023, 16, 1990. [Google Scholar] [CrossRef]
- GB50608-2020; Technical Standard for Fiber Reinforced Polymer in Construction. Ministry of Housing and Urban-Rural Development of the People’s Republic of China and State Administration for Market Regulation: Beijing, China, 2020. (In Chinese)
- Xie, Q.; Xiao, J.; Zhang, K.; Zong, Z. Compressive behavior and microstructure of concrete mixed with natural seawater and sea sand. Front. Struct. Civ. Eng. 2021, 15, 1347–1357. [Google Scholar] [CrossRef]
- Wang, X.; Dong, C.; Xu, S.; Song, Q.; Ren, J.; Zhu, J. Influence of seawater and sea sand on early-age performance and cracking sensitivity of concrete. J. Build. Eng. 2023, 79, 107811. [Google Scholar] [CrossRef]
- Chen, Z.; Mo, L.; Song, C.; Zhang, Y. Investigation on compression properties of seawater-sea sand concrete. Adv. Concr. Constr. 2021, 12, 93–103. [Google Scholar] [CrossRef]
- Pan, D.; Yaseen, S.; Chen, K.; Niu, D.; Leung, C.; Li, Z. Study of the influence of seawater and sea sand on the mechanical and microstructural properties of concrete. J. Build. Eng. 2021, 42, 103006. [Google Scholar] [CrossRef]
- Younis, A.; Ebead, U.; Suraneni, P.; Nanni, A. Fresh and hardened properties of seawater-mixed concrete. Constr. Build. Mater. 2018, 190, 276–286. [Google Scholar] [CrossRef]
- Li, L.; Zeng, L.; Xu, S.; Guo, Y. Experimental study on axial compressive behavior of hybrid FRP confined concrete columns. Comput. Concr. 2017, 19, 395–404. [Google Scholar] [CrossRef]
- Won, J.; Park, C. Effect of environmental exposure on the mechanical and bonding properties of hybrid FRP reinforcing bars for concrete structures. J. Compos. Mater. 2006, 40, 1063–1076. [Google Scholar] [CrossRef]
- You, Y.; Park, Y.; Kim, H.; Park, J. Hybrid effect on tensile properties of FRP rods with various material compositions. Compos. Struct. 2007, 80, 117–122. [Google Scholar] [CrossRef]
- Ge, W.; Wang, Y.; Ashour, A.; Lu, W.; Cao, D. Flexural performance of concrete beams reinforced with steel-FRP composite bars. Arch. Civ. Mech. Eng. 2020, 20, 56. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Huang, C.; Fu, F. Comparative study of steel-FRP, FRP and steel-reinforced coral concrete beams in their flexural performance. Materials 2020, 13, 2097. [Google Scholar] [CrossRef]
- Yun, H.; Lim, S.; Choi, W. Effects of reinforcing fiber strength on mechanical properties of high-strength concrete. Fibers 2019, 7, 93. [Google Scholar] [CrossRef]
- Haktanir, T.; Ari, K.; Altun, F.; Karahan, O. A comparative experimental investigation of concrete, reinforced-concrete and steel-fibre concrete pipes under three-edge-bearing test. Constr. Build. Mater. 2007, 21, 1702–1708. [Google Scholar] [CrossRef]
- Bencardino, F.; Rizzuti, L.; Spadea, G.; Swamy, R. Fatigue experimental evaluation of fiber reinforced concrete fracture properties. Compos. Part B—Eng. 2010, 41, 17–24. [Google Scholar] [CrossRef]
- Iqbal, S.; Ali, I.; Room, S.; Khann, S.; Ali, A. Enhanced mechanical properties of fiber reinforced concrete using closed steel fibers. Mater. Struct. 2019, 52, 56. [Google Scholar] [CrossRef]
- Qeshta, I.; Shafigh, P.; Jumaat, M.; Abdulla, A.; Ibrahim, Z.; Alengaram, U. The use of wire mesh–epoxy composite for enhancing the flexural performance of concrete beams. Mater. Des. 2014, 60, 250–259. [Google Scholar] [CrossRef]
- Chen, C.; Li, X.; Li, C.; Zhou, Y.; Sui, L. Optimized flax FRP stirrup in reinforced concrete beam: Material property and shear performance. Compos. Struct. 2022, 302, 116219. [Google Scholar] [CrossRef]
- Fahmy, M.; Abd-ElShafy, Z.; Wu, Z. Experimental and numerical evaluation of the shear behavior of reinforced concrete t-beams with hybrid steel-FRP stirrups. J. Compos. Constr. 2017, 21, 04017007. [Google Scholar] [CrossRef]
- Zhao, J.; Bao, X.; Yang, S.; Wang, Z.; He, H.; Xu, X. Experimental and theoretical studies on the shear performance of concrete beams reinforced with fiber-reinforced polymer stirrups. Materials 2024, 17, 593. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Y.; Wang, G.; Cheng, X.; Li, G. Influence of the cross-sectional shape and corner radius on the compressive behaviour of concrete columns confined by FRP and stirrups. Polymers 2022, 14, 341. [Google Scholar] [CrossRef]
- Dong, H.; Wang, D.; Wang, Z.; Sun, Y. Axial compressive behavior of square concrete columns reinforced with innovative closed-type winding GFRP stirrups. Compos. Struct. 2018, 192, 115–125. [Google Scholar] [CrossRef]
- Fakharifar, M.; Dalvand, A.; Sharbatdar, M.; Chen, G.; Sneed, L. Innovative hybrid reinforcement constituting conventional longitudinal steel and FRP stirrups for improved seismic strength and ductility of RC structures. Front. Struct. Civ. Eng. 2016, 10, 44–62. [Google Scholar] [CrossRef]
- Chen, C.; Li, C.; Zhou, Y.; Sui, L.; Li, X. Applying flax FRP in an innovative closed-shape stirrup for concrete beams. Materials 2022, 15, 2927. [Google Scholar] [CrossRef]
- Li, W.; Huang, W.; Fang, Y.; Zhang, K.; Liu, Z.; Kong, Z. Experimental and theoretical analysis on shear behavior of RC beams reinforced with GFRP stirrups. Structures 2022, 46, 1753–1763. [Google Scholar] [CrossRef]
- Hadi, M.; Elbasha, N. Effects of tensile reinforcement ratio and compressive strength on the behaviour of over-reinforced helically confined HSC beams. Constr. Build. Mater. 2007, 21, 269–276. [Google Scholar] [CrossRef]
- Priastiwi, Y.A.; Imran, I. The effect of different shapes of confinement in compression zone on beam’s ductility subjected to monotonic loading. Procedia Eng. 2015, 125, 918–924. [Google Scholar] [CrossRef][Green Version]
- Renic, T.; Kisicek, T. Ductility of concrete beams reinforced with FRP rebars. Buildings 2021, 11, 424. [Google Scholar] [CrossRef]
- Renic, T.; Kisicek, T.; Koscak, J. Experimental testing of FRP reinforced concrete beams with steel compression reinforcement and a compression area confined with steel stirrups. Mater. Struct. 2023, 56, 10. [Google Scholar] [CrossRef]
- Michael, A.; Hamilton, H. Experimental ductility of compression-controlled flexural members using CFRP grid to confine concrete. Materials 2021, 14, 5163. [Google Scholar] [CrossRef]
- Mohamed, H.; Masmoudi, R. Flexural strength and behavior of steel and FRP-reinforced concrete-filled FRP tube beams. Eng. Struct. 2010, 32, 3789–3800. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, C.; Yan, L.; Kasal, B. Flexural behavior of u-shape FRP profile-RC composite beams with inner GFRP tube confinement at concrete compression zone. Compos. Struct. 2018, 184, 674–687. [Google Scholar] [CrossRef]
- Dong, Z.; Wu, G.; Zhu, H.; Zhao, X.; Wei, Y.; Qian, H. Flexural behavior of seawater sea-sand coral concrete–UHPC composite beams reinforced with BFRP bars. Constr. Build. Mater. 2020, 265, 120279. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, J.; Mai, Z.; Liu, P.; Lu, Z.; Li, L. Durability of GFRP bar-reinforced seawater–sea sand concrete beams: Coupled effects of sustained loading and exposure to a chloride environment. Eng. Struct. 2023, 283, 115814. [Google Scholar] [CrossRef]
- Hua, Y.; Yin, S.; Peng, Z. Crack development and calculation method for the flexural cracks in BFRP reinforced seawater sea-sand concrete (SWSSC) beams. Constr. Build. Mater. 2020, 255, 119328. [Google Scholar] [CrossRef]
- Su, C.; Wang, X.; Ding, L.; Chen, Z.; Liu, S.; Wu, Z. Experimental study on the seismic behavior of seawater sea sand concrete beams reinforced with steel-FRP composite bars. Eng. Struct. 2021, 248, 113269. [Google Scholar] [CrossRef]
- Hu, X.; Xiao, J.; Zhang, K.; Zhang, Q. Evaluation of cracking and deflection of GFRP bar reinforced recycled concrete beams with seawater and sea sand. J. Build. Eng. 2023, 80, 108092. [Google Scholar] [CrossRef]
- Li, Z.; Dong, F.; Qian, H.; Qiu, P.; Shi, Y. Shear performance of seawater sea-sand concrete beams reinforced with shape memory alloy longitudinal and stirrup bars. Constr. Build. Mater. 2024, 421, 135685. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, Y.; Zhou, J.; Dai, S. Parametric study, finite element analysis, and load capacity calculation for flexural behaviour of seawater and sea sand concrete beams reinforced with GFRP bars. Structures 2024, 63, 106424. [Google Scholar] [CrossRef]
- ASTM D1141–98; Standard Practice for the Preparation of Substitute Ocean Water. ASTM International: West Conshohocken, PA, USA, 2013.
- GB/T 30022-2013; Test method for Basic Mechanical Properties of Fiber Reinforced Polymer Bar. Standardization Administration of the People’s Republic of China: Beijing, China, 2013. (In Chinese)
- GB/T 3354-2014; Test Method for Tensile Properties of Orientation Fiber Reinforced Polymer Matrix Composite Materials. Standardization Administration of the People’s Republic of China: Beijing, China, 2020. (In Chinese)
- Jaeger, L.; Mufti, A.; Tadros, G. Balanced Section Ductility and Deformability in Concrete with FRP Reinforcement; West Virginia University: Morgantown, VA, USA, 1995. [Google Scholar]
- Spadea, G.; Bencardino, F.; Swamy, R. Optimizing the performance characteristics of beams strengthened with bonded CFRP laminates. Mater. Struct. 2020, 33, 119–126. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015. (In Chinese)
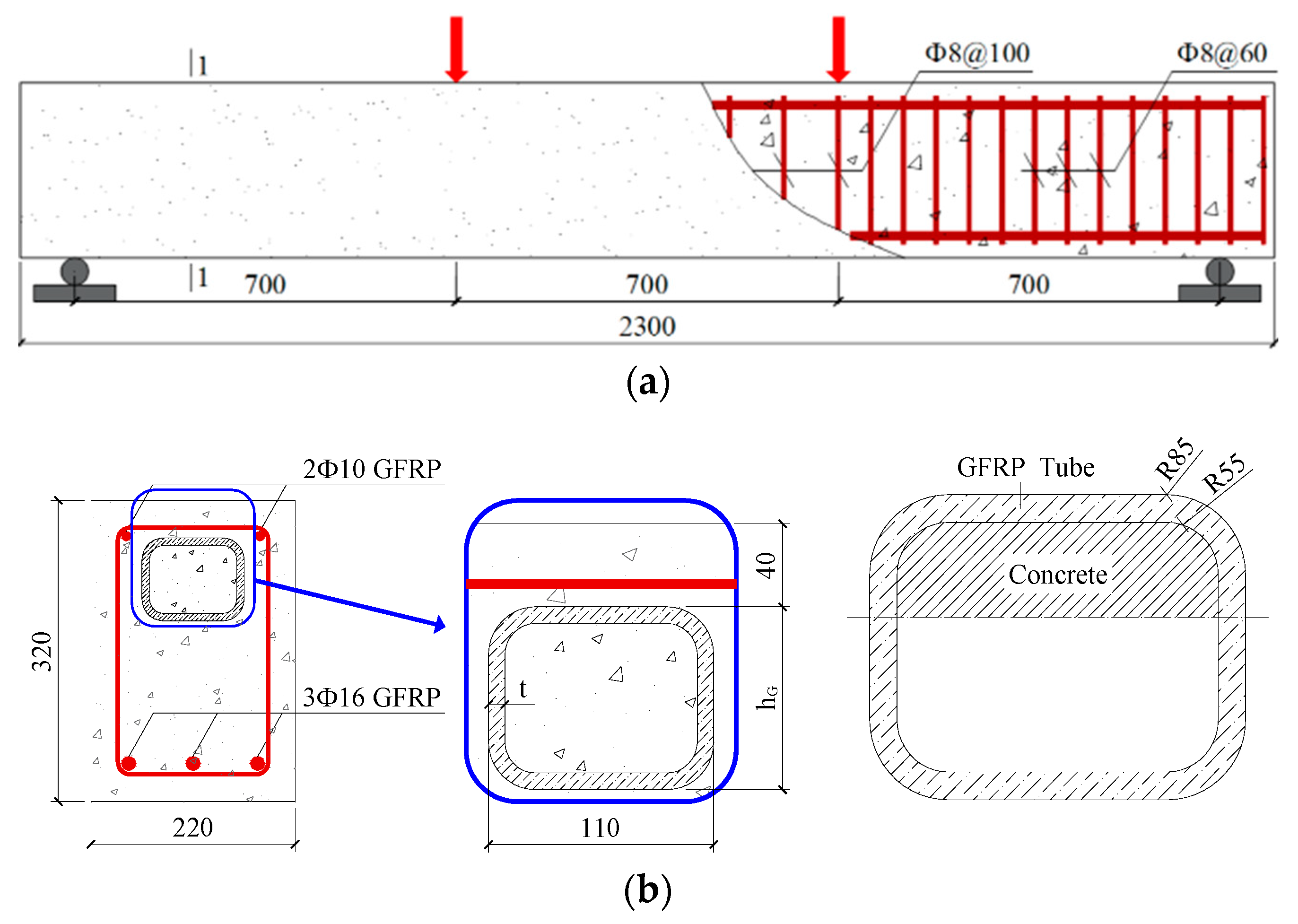





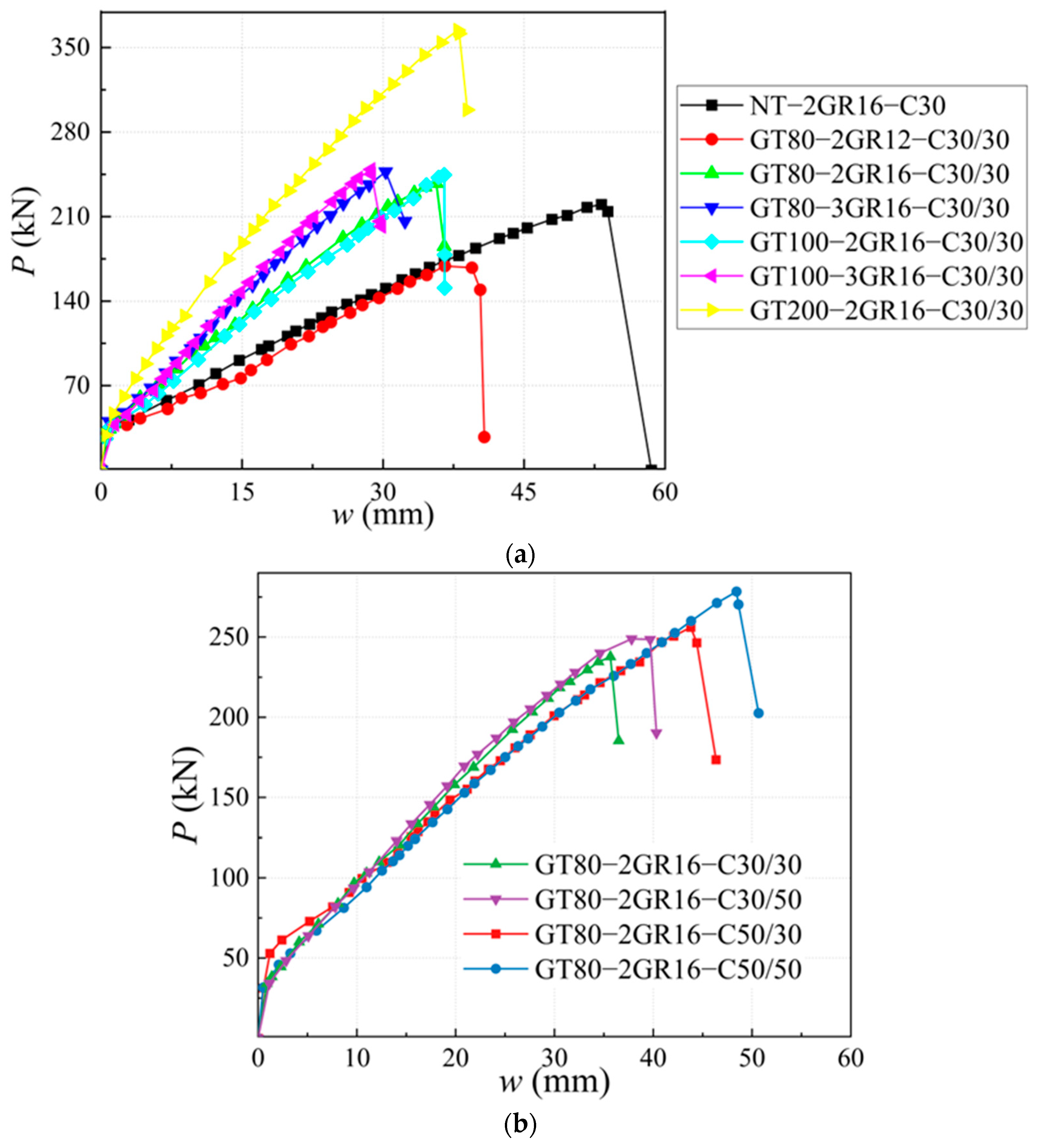
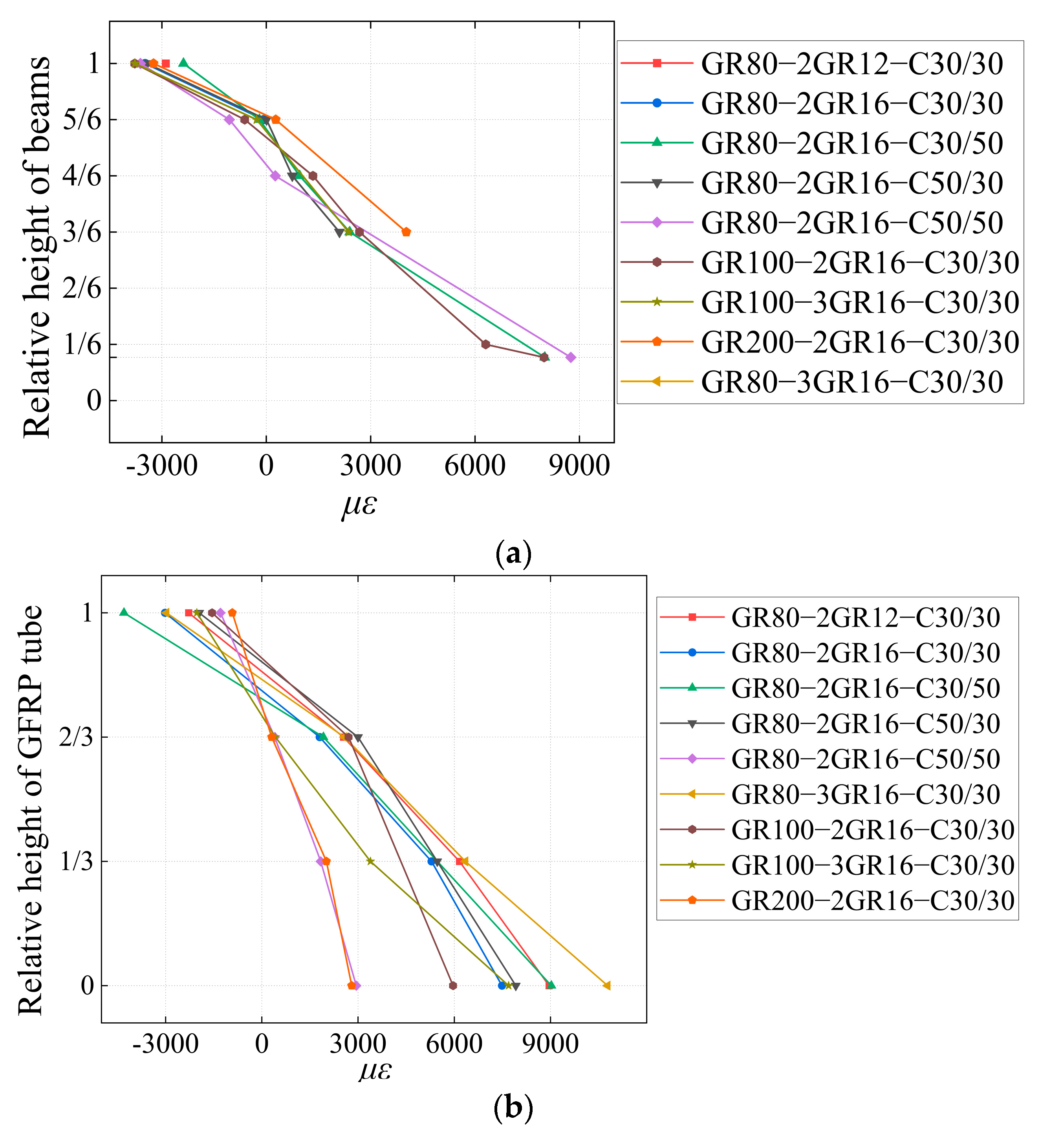
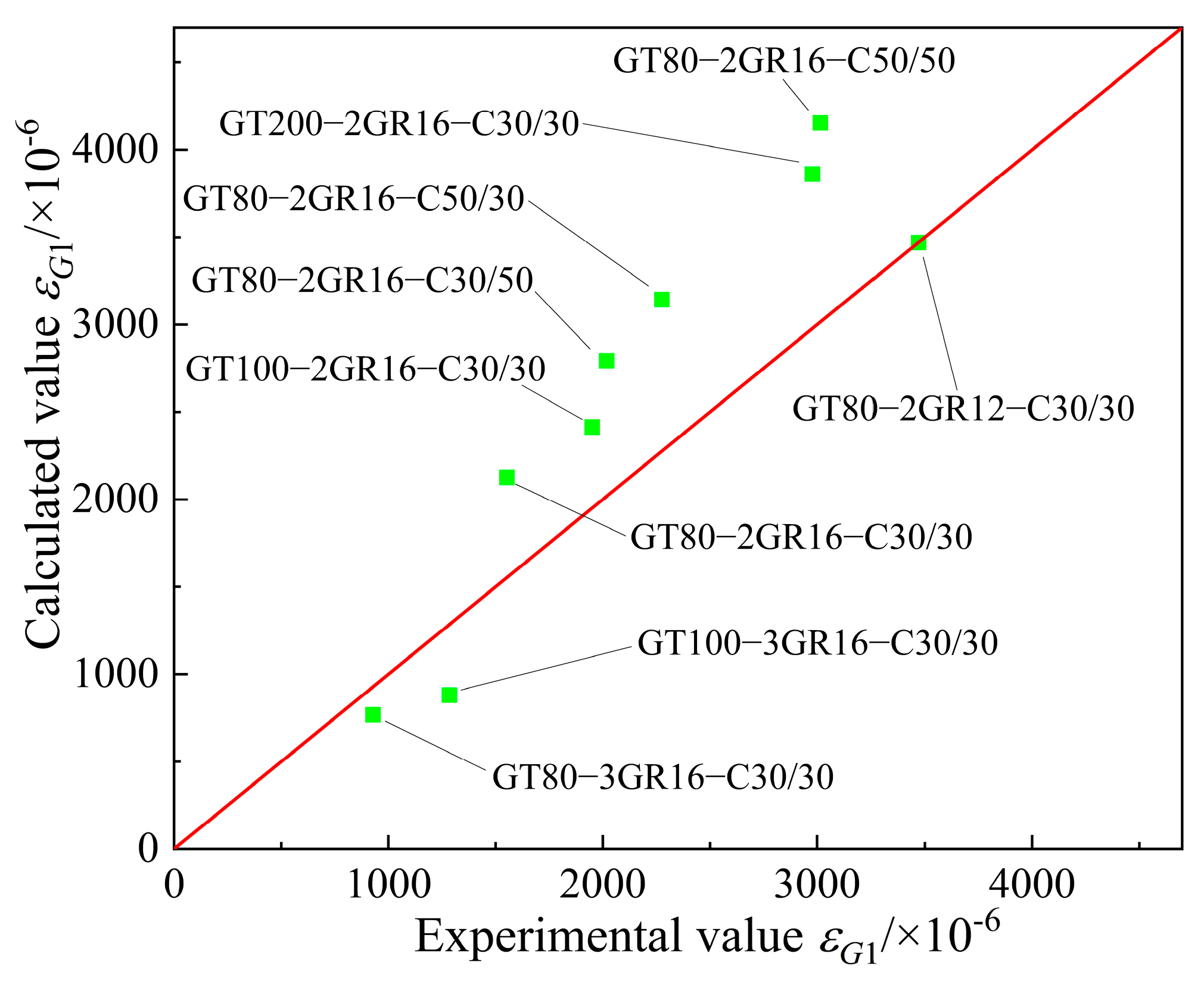

| No. | Beam | Tube Height hG/mm | Reinforcement | Concrete outside the Tube | Concrete inside the Tube |
|---|---|---|---|---|---|
| 1 | NT-2GR16-C30 | — | 2Ф16 | C30 | — |
| 2 | GT80-2GR12-C30/30 | 80 | 2Ф12 | C30 | C30 |
| 3 | GT80-2GR16-C30/30 | 80 | 2Ф16 | C30 | C30 |
| 4 | GT80-2GR16-C30/50 | 80 | 2Ф16 | C30 | C50 |
| 5 | GT80-2GR16-C50/30 | 80 | 2Ф16 | C50 | C30 |
| 6 | GT80-2GR16-C50/50 | 80 | 2Ф16 | C50 | C50 |
| 7 | GT80-3GR16-C30/30 | 80 | 3Ф16 | C30 | C30 |
| 8 | GT100-2GR16-C30/30 | 100 | 2Ф16 | C30 | C30 |
| 9 | GT100-3GR16-C30/30 | 100 | 3Ф16 | C30 | C30 |
| 10 | GT200-2GR16-C30/30 | 200 | 2Ф16 | C30 | C30 |
| Ingredient | NaCl | MgCl2 | Na2SO4 | CaCl2 |
|---|---|---|---|---|
| Content | 24.53 | 5.20 | 4.09 | 1.16 |
| Concrete Grade | Seawater | Cement | Sand | Crushed Stone | Water Reducer |
|---|---|---|---|---|---|
| C30 | 215 | 447 | 611 | 1242 | 0.537 |
| C50 | 229 | 653 | 595 | 1202 | 1.045 |
| Concrete Grade | Batch | Size/mm | Ec/ GPa | /GPa | σ(Ec) /GPa | Strength Conversion Factor | fc /MPa | /MPa | σ(fc) /MPa |
|---|---|---|---|---|---|---|---|---|---|
| C30 | 1 | 150 × 150 × 300 | 30.95 | 28.72 | 1.98 | — | — | — | — |
| 27.17 | — | — | — | ||||||
| 28.04 | — | — | — | ||||||
| 1 | 100 × 100 × 100 | — | — | — | 0.95 | 31.06 | 29.43 | 1.48 | |
| — | — | — | 28.18 | ||||||
| — | — | — | 29.06 | ||||||
| 2 | 150 × 150 × 150 | — | — | — | 1 | 31.34 | 32.43 | 1.59 | |
| — | — | — | 34.25 | ||||||
| — | — | — | 31.70 | ||||||
| 3 | 150 × 150 × 150 | — | — | — | 1 | 29.61 | 30.08 | 1.00 | |
| — | — | — | 29.4 | ||||||
| — | — | — | 31.22 | ||||||
| C50 | 1 | 150 × 150 × 300 | 30.27 | 32.31 | 1.84 | — | — | — | — |
| 32.81 | — | — | — | ||||||
| 33.85 | — | — | — | ||||||
| 1 | 100 × 100 × 100 | — | — | — | 0.95 | 50.81 | 51.60 | 0.85 | |
| — | — | — | 51.48 | ||||||
| — | — | — | 52.5 | ||||||
| 2 | 150 × 150 × 150 | — | — | — | 1 | 51.44 | 52.52 | 1.19 | |
| — | — | — | 53.82 | ||||||
| — | — | — | 52.52 |
| Type | Diameter | No | Peak Load/ kN | Destruction Mode | Strength/ MPa | Average Strength/ MPa | Standard Error of Mean | Elastic Modulus/ GPa | Average Elastic Modulus/ GPa | Standard Error of Mean |
|---|---|---|---|---|---|---|---|---|---|---|
| GFRP bar | 16 mm | GR16-1 | 138.4 | Pull apart | 688.35 | 725.65 | 46.59 | 45.39 | 43.72 | 3.38 |
| GR16-2 | 156.4 | Explosive pull | 777.87 | 39.83 | ||||||
| GR16-3 | 142.9 | Pull apart | 710.73 | 45.93 | ||||||
| 12 mm | GR12-1 | 71.7 | Pull away | — | 733.88 | 45.01 | — | 47.10 | 0.71 | |
| GR12-2 | 86.6 | Pull away | 765.71 | 47.60 | ||||||
| GR12-3 | 79.4 | Explosive pull | 702.05 | 46.60 | ||||||
| GFRP tube | Axial tensile | GTA-1 | 49.15 | - | 245.8 | 231.7 | 14.68 | 13.55 | 13.96 | 1.28 |
| GTA-2 | 50.85 | 254.3 | 15.39 | |||||||
| GTA-3 | 38.90 | 194.5 | 12.93 | |||||||
| GTA-4 | 43.30 | 216.5 | 11.70 | |||||||
| GTA-5 | 46.55 | 232.8 | 15.63 | |||||||
| Circumferential tensile | GTC-1 | 22.30 | - | 557.5 | 543.4 | 9.36 | 54.38 | 52.32 | 2.57 | |
| GTC-2 | 21.35 | 533.8 | 53.13 | |||||||
| GTC-3 | 21.05 | 526.3 | 49.44 | |||||||
| GTC-4 | 22.10 | 552.5 | 55.57 | |||||||
| GTC-5 | 21.75 | 543.8 | 47.22 |
| No | Beam | Crack Distribution and Destruction Features | Crack Development and Load Order → Load (kN) |
|---|---|---|---|
| 1 | NT-2GR16-C30 |  | ① → 38.71② →40.65 ③ → 45.61④ → 45.48⑤ → 45.48⑥ → 57.74⑦ → 62.26⑧ → 90.97⑨ → 102.90 |
| 2 | GT80-2GR12-C30 |  | ① → 35.16② → 36.13③ → 42.90④ → 59.68⑤ → 68.39⑥ → 71.29 |
| 3 | GT80-2GR16-C30/30 |  | ① → 28.39② → 37.10③ → 39.68④ → 50.00⑤ → 49.03⑥ → 59.35⑦ → 806.65⑧ → 86.45⑨ → 92.90 |
| 4 | GT80-2GR16-C30/50 |  | ① → 34.19② → 34.19③ → 40.32④ → 42.26⑤ → 53.23⑥ → 67.74⑦ → 68.39⑧ → 78.06 |
| 5 | GT80-2GR16-C50/30 |  | ① → 35.48② → 52.90③ → 58.39④ → 66.45⑤ → 72.90⑥ → 70.97⑦ → 70.97⑧ → 84.84⑨ → 99.68⑩ → 104.84⑪ → 148.39⑫ → 234.19 |
| 6 | GT80-2GR16-C50/50 |  | ① → 31.61② → 32.90③ → 45.81④ → 53.23⑤ → 50.65⑥ → 67.10⑦ → 65.48⑧ → 81.29⑨ → 104.52 |
| 7 | GT80-3GR16-C30/30 |  | ① → 40.32② → 42.58③ → 41.94④ → 47.74⑤ → 50.32⑥ → 59.35⑦ → 62.58⑧ → 68.06⑨ → 72.58⑩ → 93.87⑪ → 176.13 |
| 8 | GT100-2GR16-C30/30 |  | ① → 33.55② → 37.74③ → 41.61④ → 45.16⑤ → 43.55⑥ → 54.19⑦ → 69.35⑧ → 73.87⑨ → 130.97 |
| 9 | GT100-3GR16-C30/30 |  | ① → 37.74② → 40.32③ → 42.90④ → 46.77⑤ → 54.19⑥ → 57.42⑦ → 61.29⑧ → 63.87⑨ → 63.87⑩ → 65.81⑪ → 83.55⑫ → 83.55⑬ → 167.10 |
| 10 | GT200-2GR16-C30/30 |  | ① → 26.45② → 30.65③ → 42.58④ → 61.61⑤ → 69.03⑥ → 80.00⑦ → 107.13⑧ → 107.13⑨ → 106.13⑩ → 144.19⑪ → 171.29⑫ → 187.74⑬ → 218.06⑭ → 230.65⑮ → 283.87 |
| Beam | /m−1 | M0.001/kN·m | /m−1 | Mu/kN·m | DR | CR | J |
|---|---|---|---|---|---|---|---|
| NT-2GR16C-30 | 0.0144 | 20.44 | 0.0833 | 84.33 | 82.7% | 73.5% | 21.732 |
| GT80-2GR12-C30/30 | 0.0140 | 17.05 | 0.0575 | 64.79 | 75.7% | 71.2% | 14.290 |
| GT80-2GR16-C30/30 | 0.0128 | 27.23 | 0.0571 | 91.11 | 77.5% | 67.3% | 13.574 |
| GT80-2GR16-C30/50 | 0.0145 | 29.81 | 0.0597 | 95.41 | 75.7% | 65.8% | 12.021 |
| GT80-2GR16-C50/30 | 0.0207 | 38.05 | 0.0677 | 98.18 | 69.5% | 57.6% | 7.719 |
| GT80-2GR16-C50/50 | 0.0206 | 36.24 | 0.0748 | 106.72 | 72.4% | 62.8% | 9.748 |
| GT80-3GR16-C30/30 | 0.0156 | 35.90 | 0.0473 | 94.72 | 67.0% | 58.5% | 7.295 |
| GT100-2GR16-C30/30 | 0.0145 | 33.99 | 0.0573 | 93.73 | 74.7% | 60.3% | 9.970 |
| GT100-3GR16-C30/30 | 0.0156 | 32.85 | 0.0464 | 95.46 | 66.4% | 62.3% | 7.907 |
| GT200-2GR16-C30/30 | 0.0137 | 41.60 | 0.0596 | 139.69 | 77.1% | 67.4% | 13.390 |
| Beam | hG/mm | εG1/×10−6 | εG1/εr |
|---|---|---|---|
| GT80-2GR16-C30/30 | 80 | −1551 | 1.703 |
| GT100-2GR16-C30/30 | 100 | −1953 | 2.144 |
| GT200-2GR16-C30/30 | 200 | −2974 | 3.265 |
| Beam | Reinforcement Ratio ρ | εG1/×10−6 | εG1/εr1 | εG1/εr2 |
|---|---|---|---|---|
| GT80-2GR12-C30/30 | 0.366% | −3479 | 2.243 | — |
| GT80-2GR16-C30/30 | 0.655% | −1551 | 1 | — |
| GT80-3GR16-C30/30 | 0.983% | −923 | 0.595 | — |
| GT100-2GR16-C30/30 | 0.655% | −1953 | — | 1 |
| GT100-3GR16-C30/30 | 0.983% | −1290 | — | 0.661 |
| Beam | fc1/MPa | εG1/×10−6 | εG1/εr1 | εG1/εr3 |
|---|---|---|---|---|
| GT80-2GR16-C30/30 | 30 | −1551 | 1 | — |
| GT80-2GR16-C50/30 | 50 | −2281 | 1.471 | — |
| GT80-2GR16-C30/50 | 30 | −2028 | — | 1 |
| GT80-2GR16-C50/50 | 50 | −3019 | — | 1.489 |
| Beam | fc2/MPa | εG1/×10−6 | εG1/εr1 | εG1/εr4 |
|---|---|---|---|---|
| GT80-2GR16-C30/30 | 30 | −1551 | 1 | — |
| GT80-2GR16-C30/50 | 50 | −2028 | 1.308 | — |
| GT80-2GR16-C50/30 | 30 | −2281 | — | 1 |
| GT80-2GR16-C50/50 | 50 | −3019 | — | 1.324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; Tang, S.; Tang, J.; Liu, S.; Yang, S. Experimental Study of the Flexural Performance of GFRP-Reinforced Seawater Sea Sand Concrete Beams with Built-In GFRP Tubes. Materials 2024, 17, 3221. https://doi.org/10.3390/ma17133221
Deng X, Tang S, Tang J, Liu S, Yang S. Experimental Study of the Flexural Performance of GFRP-Reinforced Seawater Sea Sand Concrete Beams with Built-In GFRP Tubes. Materials. 2024; 17(13):3221. https://doi.org/10.3390/ma17133221
Chicago/Turabian StyleDeng, Xiaoqi, Song Tang, Jinyu Tang, Shutong Liu, and Shutong Yang. 2024. "Experimental Study of the Flexural Performance of GFRP-Reinforced Seawater Sea Sand Concrete Beams with Built-In GFRP Tubes" Materials 17, no. 13: 3221. https://doi.org/10.3390/ma17133221
APA StyleDeng, X., Tang, S., Tang, J., Liu, S., & Yang, S. (2024). Experimental Study of the Flexural Performance of GFRP-Reinforced Seawater Sea Sand Concrete Beams with Built-In GFRP Tubes. Materials, 17(13), 3221. https://doi.org/10.3390/ma17133221






